浙教版八下数学期中期末复习——4-5单元基础卷(含答案)
文档属性
| 名称 | 浙教版八下数学期中期末复习——4-5单元基础卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 520.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 09:57:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平
浙教版八下数学期中期末复习——4-5单元基础卷(含解析)
一、单选题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.B.C. D.
2.下列不能判断一个四边形是平行四边形的条件是( )
A.一组对边相等,另一组对边平行 B.一组对边平行且相等
C.一组对边平行且一组对角相等 D.任何一个内角都与相邻内角互补
3.如图,在 ABCD中,AD>AB,用直尺和圆规在边AD上确定一点E,使AE=AB,则下列作法错误的是( )
A.B.C.D.
4.点位于平面直角坐标系第四象限,且到轴的距离是5,到轴的距离是2,则点关于原点对称的的坐标是( )
A. B. C. D.
5.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A.4 B.3 C.2 D.1
6.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是( )
A.60 B.30 C.20 D.16
7.下列说法正确的是( )
A.在两条边和一个角对应相等的两个三角形全等
B.六边形的内角和是
C.矩形对角线互相垂直平分
D.已知在中,D、E分别是的中点,,则的长度是.
8.如图所示,点E为内一点,连接,,,,,已知 的面积为2,的面积为10,则阴影部分的面积为( )
A. B. C. D.
9.如图,,其中,,,M为BC中点,EF过点M交AC、BD于点E、F,连接BE、CF,则下列结论错误的是( ).
A.四边形BECF为平行四边形
B.当时,四边形BECF为矩形
C.当时,四边形BECF为菱形
D.四边形BECF不可能为正方形
10.如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为,,有如下三个结论:
①正方形ABCD的面积等于的一半;②正方形EFGH的面积等于的一半;③.上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.③ D.①②③
二、填空题
11.一个多边形的内角和等于外角和的5倍,则这个多边形的边数为
12.如图,在菱形ABCD中,∠=∠EAF=,∠BAE=,则∠CEF= .
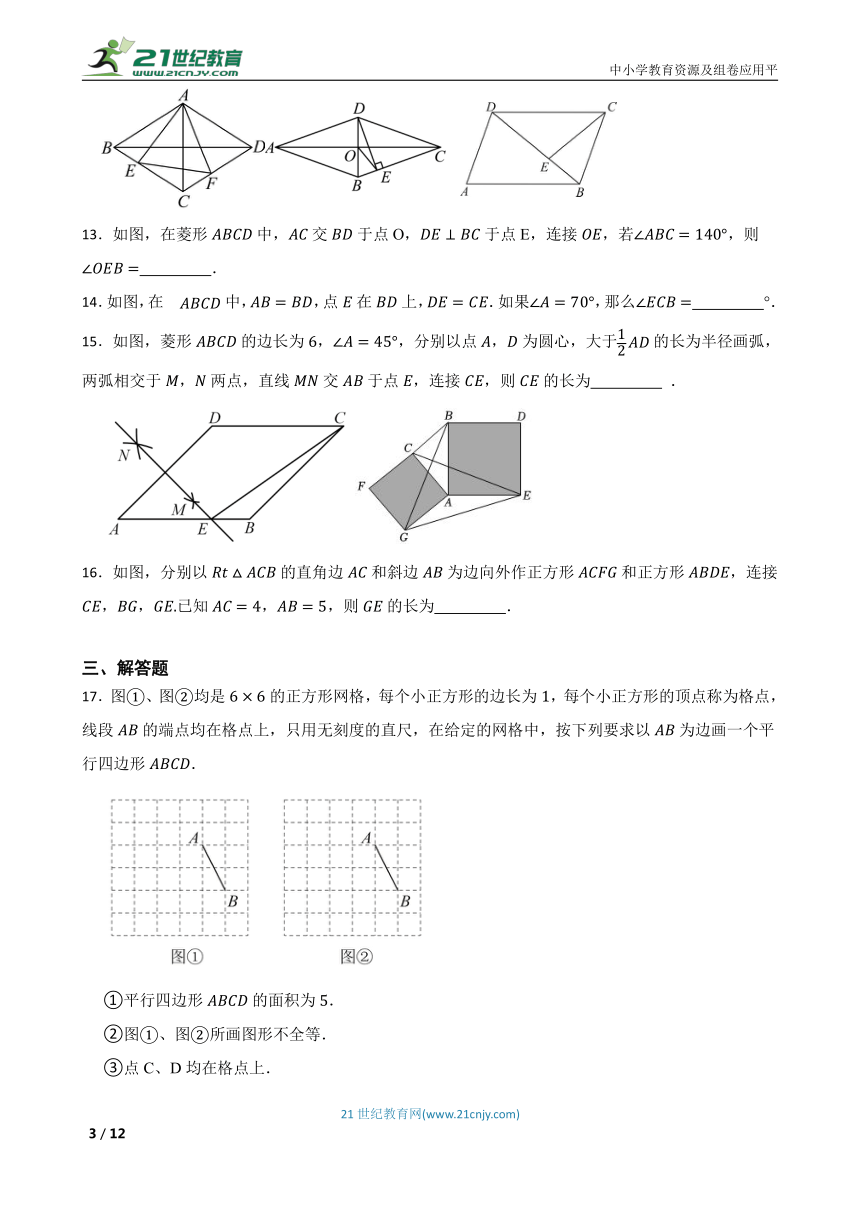
13.如图,在菱形中,交于点O,于点E,连接,若,则 .
14.如图,在中,,点在上,.如果,那么 °.
15.如图,菱形的边长为,,分别以点,为圆心,大于的长为半径画弧,两弧相交于,两点,直线交于点,连接,则的长为 .
16.如图,分别以的直角边和斜边为边向外作正方形和正方形,连接,,已知,,则的长为 .
三、解答题
17.图、图均是的正方形网格,每个小正方形的边长为,每个小正方形的顶点称为格点,线段的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以为边画一个平行四边形.
①平行四边形的面积为.
②图、图所画图形不全等.
③点C、D均在格点上.
18.(1)求满足条件的x的值;
(2)一个多边形的内角和比它的外角和的7倍还多,求这个多边形的边数 .
19.如图,平行四边形的对角线,相交于点O,且,,周长为.
(1)求的长.
(2)求的周长.
20.如图,四边形中,,点E,F在边上,平分,.
(1)求证:;
(2)若,,求证:.
21.如图,在 Rt△ABC 中,∠BAC=90°,以AB为一边作□ABDE,且AD∥BC,连结EC 交DA 的延长线于点F,延长EA 交 BC 于点G.
(1)求证:A 是EG 的中点.
(2)若DF⊥EC,DE=2BD=6,求BC 的长.
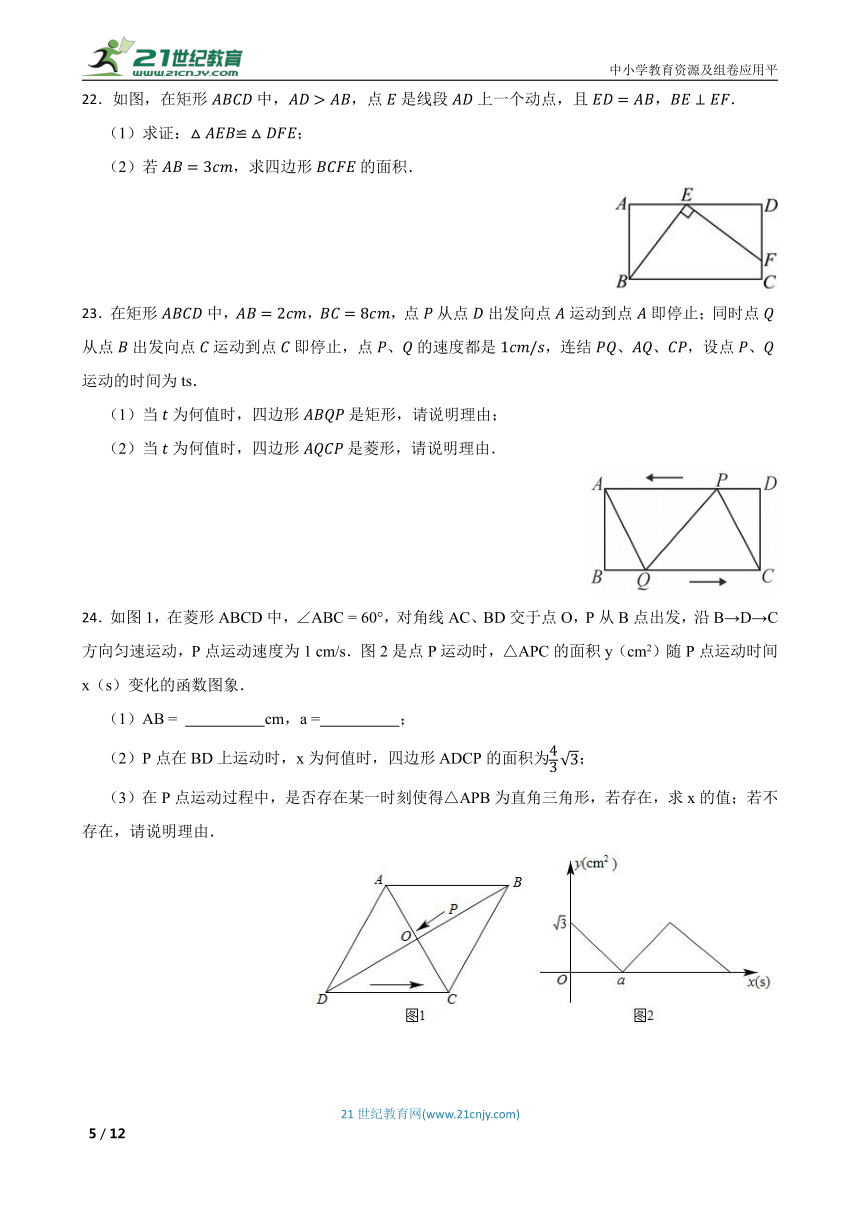
22.如图,在矩形中,,点是线段上一个动点,且,.
(1)求证:;
(2)若,求四边形的面积.
23.在矩形中,,,点从点出发向点运动到点即停止;同时点从点出发向点运动到点即停止,点、的速度都是,连结、、,设点、运动的时间为ts.
(1)当为何值时,四边形是矩形,请说明理由;
(2)当为何值时,四边形是菱形,请说明理由.
24.如图1,在菱形ABCD中,∠ABC = 60°,对角线AC、BD交于点O,P从B点出发,沿B→D→C方向匀速运动,P点运动速度为1 cm/s.图2是点P运动时,△APC的面积y(cm2)随P点运动时间x(s)变化的函数图象.
(1)AB = cm,a = ;
(2)P点在BD上运动时,x为何值时,四边形ADCP的面积为;
(3)在P点运动过程中,是否存在某一时刻使得△APB为直角三角形,若存在,求x的值;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】D
【解析】【解答】解:∵ 点M位于平面直角坐标系第四象限,
∴ 点M横坐标大于0,纵坐标小于0,
又∵ 到轴的距离是5,到轴的距离是2,
∴纵坐标为-5,横坐标为2,
∴点,
∵ 点与点关于原点对称,
∴
故答案为:D.
【分析】先根据点的坐标特征写出点M的坐标,再利用关于原点对称的性质写出的坐标即可.
5.【答案】D
【解析】【解答】解:由题意知是的中位线
∴
∵正方形ABCD的周长为8
∴
∴
故答案为:D.
【分析】由题意可得OH为△BCD的中位线,则OH=BC,根据正方形的性质结合周长为8可得BC=2,据此求解.
6.【答案】C
7.【答案】D
【解析】【解答】解:对于A、两边及其夹角分别对应相等的两个三角形全等;故A错误,不符合题意;
对于B、六边形的内角和是,故B错误,不符号题意;
对于C、矩形的对角线相等且互相平分,故C错误,不符合题意;
对于D、根据三角形中位线定理可得,故D正确.
故选:D.
【分析】直接利用全等三角形的判定、矩形的性质、多边形的内角和、三角形中位线逐项判断即可解答.
8.【答案】B
9.【答案】B
10.【答案】B
【解析】【解答】解:设甲正方形网格中每一小格长度为a,乙正方形网格中每一小格长度为b,
则,,,,
∴S正方形ABCD=,S正方形EFGH=,
∴正方形ABCD的面积大于的一半;正方形EFGH的面积等于的一半;
∵S正方形ABCD=S正方形EFGH,
∴,
∴,
∴,即,
∴符合题意结论的序号是②③,
故答案为:B.
【分析】先求出正方形ABCD的面积大于的一半;正方形EFGH的面积等于的一半,再结合S正方形ABCD=S正方形EFGH,可得,再求出,即可得到,即。
11.【答案】12
【解析】【解答】解:设这个多边形的边数为n,根据题意得
(n-2)×180°=5×360°,
解之:n=12.
故答案为:12
【分析】利用n边形的内角和为(n-2)×180°,外角和为360°,根据一个多边形的内角和等于外角和的5倍,可得到关于n的方程,解方程求出n的值.
12.【答案】20°
13.【答案】
14.【答案】30
【解析】【解答】解:∵四边形ABCD是平行四边形,且∠A=70°
∴∠DCB=∠A=70°
∠ADC=180°-∠A
=110°
∵AB=BD
∴∠ADB=∠A=70°
∴∠CDE=40°
∵DE=CE
∴∠DCE=∠CDE=40°
∴∠ECB=∠DCB-∠DCE
=30°
故答案为:30.
【分析】根据平行四边形的性质求出∠ADC、∠DCB的度数,再根据等边对等角即可求解。
15.【答案】
16.【答案】
17.【答案】解:按要求作图如下:
图①:,
以为边的正方形的面积为,
正方形即为所求;
图②:以为一边,以高作平行四边形,
四边形的面积为,
平行四边形即为所求.
【解析】【分析】画出一个边长为的正方形即可;画出一个底为,高为的平行四边形即可.
18.【答案】(1)或;(2)15
19.【答案】(1)
(2)
20.【答案】(1)证明:∵,
∴,
又∵平分,
∴,
∴,
∴,
又∵,
∴,
∴四边形是菱形,
∴;
(2)解:证明:∵四边形是菱形,
∴,
又∵,
∴,
∵,
∴四边形是平行四边形,
∴,
∴,
又∵,
∴,
由三角形内角和定理可得:,
∴.
【解析】【分析】(1)根据直线平行性质可得,根据角平分线性质得,继而得到,再利用菱形性质即可求出答案。
(2)根据菱形性质可判断四边形是平行四边形,根据平行四边形性质可得,利用三角形内角和定理即可求出答案。
21.【答案】(1)证明:∵四边形ABDE是平行四边形.
∴BD=AE,BD∥EG.
又∵AD∥BC.
∴四边形BGAD是平行四边形.
∴BD=AG.
∵BD=AE.
∴AG=AE.
∴A 是EG 的中点.
(2)解:∵四边形ADBG是平行四边形,DE=2BD=6.
∴BD=AG=DE=3.
∵AD∥BC,DF⊥EC.
∴BC⊥EC.
∴∠ECG=90°.
又∵A 是EG 的中点.
∴AC=EG,EG=2AG=2BD=6.
∴AC=3.
∵四边形ADBG是平行四边形.
∴DE=AB=6.
∴在Rt△ABC中,BC=
【解析】【分析】(1)先通过已知条件证明出四边形ADBG是平行四边形,进而得出BD=AG,由此即可得出A 是EG 的中点.
(2)首先根据平行四边形的性质和DE=2BD=6这一条件求出BD的长,然后根据直角三角形的性质求出AC的长,最后根据勾股定理求出BC的长即可.
22.【答案】(1)证明:四边形为矩形,
,
,
,
,
,
,
;
(2)解:,
,,
.
【解析】【分析】(1)由矩形的性质可得∠A=∠B=90°,由同角的余角相等得出∠DEF=∠ABE,再根据AAS证明;
(2)根据全等三角形的性质的对应边相等,结合,计算即可得出答案.
23.【答案】(1)解:当四边形是矩形时,,即:,
解得.
答:当时,四边形是矩形;
(2)解:设秒后,四边形是菱形
当,即时,四边形为菱形.
解得:.
答:当时,四边形是菱形.
【解析】【分析】(1)根据矩形的性质可得:,列出方程,解方程即可求出答案.
(2)根据菱形的性质可得:,,列出方程,解方程即可求出答案.
24.【答案】(1)2,
(2)
(3)存在,的值为或或.
21世纪教育网(www.21cnjy.com)
1 / 1
浙教版八下数学期中期末复习——4-5单元基础卷(含解析)
一、单选题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.B.C. D.
2.下列不能判断一个四边形是平行四边形的条件是( )
A.一组对边相等,另一组对边平行 B.一组对边平行且相等
C.一组对边平行且一组对角相等 D.任何一个内角都与相邻内角互补
3.如图,在 ABCD中,AD>AB,用直尺和圆规在边AD上确定一点E,使AE=AB,则下列作法错误的是( )
A.B.C.D.
4.点位于平面直角坐标系第四象限,且到轴的距离是5,到轴的距离是2,则点关于原点对称的的坐标是( )
A. B. C. D.
5.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A.4 B.3 C.2 D.1
6.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是( )
A.60 B.30 C.20 D.16
7.下列说法正确的是( )
A.在两条边和一个角对应相等的两个三角形全等
B.六边形的内角和是
C.矩形对角线互相垂直平分
D.已知在中,D、E分别是的中点,,则的长度是.
8.如图所示,点E为内一点,连接,,,,,已知 的面积为2,的面积为10,则阴影部分的面积为( )
A. B. C. D.
9.如图,,其中,,,M为BC中点,EF过点M交AC、BD于点E、F,连接BE、CF,则下列结论错误的是( ).
A.四边形BECF为平行四边形
B.当时,四边形BECF为矩形
C.当时,四边形BECF为菱形
D.四边形BECF不可能为正方形
10.如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为,,有如下三个结论:
①正方形ABCD的面积等于的一半;②正方形EFGH的面积等于的一半;③.上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.③ D.①②③
二、填空题
11.一个多边形的内角和等于外角和的5倍,则这个多边形的边数为
12.如图,在菱形ABCD中,∠=∠EAF=,∠BAE=,则∠CEF= .
13.如图,在菱形中,交于点O,于点E,连接,若,则 .
14.如图,在中,,点在上,.如果,那么 °.
15.如图,菱形的边长为,,分别以点,为圆心,大于的长为半径画弧,两弧相交于,两点,直线交于点,连接,则的长为 .
16.如图,分别以的直角边和斜边为边向外作正方形和正方形,连接,,已知,,则的长为 .
三、解答题
17.图、图均是的正方形网格,每个小正方形的边长为,每个小正方形的顶点称为格点,线段的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以为边画一个平行四边形.
①平行四边形的面积为.
②图、图所画图形不全等.
③点C、D均在格点上.
18.(1)求满足条件的x的值;
(2)一个多边形的内角和比它的外角和的7倍还多,求这个多边形的边数 .
19.如图,平行四边形的对角线,相交于点O,且,,周长为.
(1)求的长.
(2)求的周长.
20.如图,四边形中,,点E,F在边上,平分,.
(1)求证:;
(2)若,,求证:.
21.如图,在 Rt△ABC 中,∠BAC=90°,以AB为一边作□ABDE,且AD∥BC,连结EC 交DA 的延长线于点F,延长EA 交 BC 于点G.
(1)求证:A 是EG 的中点.
(2)若DF⊥EC,DE=2BD=6,求BC 的长.
22.如图,在矩形中,,点是线段上一个动点,且,.
(1)求证:;
(2)若,求四边形的面积.
23.在矩形中,,,点从点出发向点运动到点即停止;同时点从点出发向点运动到点即停止,点、的速度都是,连结、、,设点、运动的时间为ts.
(1)当为何值时,四边形是矩形,请说明理由;
(2)当为何值时,四边形是菱形,请说明理由.
24.如图1,在菱形ABCD中,∠ABC = 60°,对角线AC、BD交于点O,P从B点出发,沿B→D→C方向匀速运动,P点运动速度为1 cm/s.图2是点P运动时,△APC的面积y(cm2)随P点运动时间x(s)变化的函数图象.
(1)AB = cm,a = ;
(2)P点在BD上运动时,x为何值时,四边形ADCP的面积为;
(3)在P点运动过程中,是否存在某一时刻使得△APB为直角三角形,若存在,求x的值;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】D
【解析】【解答】解:∵ 点M位于平面直角坐标系第四象限,
∴ 点M横坐标大于0,纵坐标小于0,
又∵ 到轴的距离是5,到轴的距离是2,
∴纵坐标为-5,横坐标为2,
∴点,
∵ 点与点关于原点对称,
∴
故答案为:D.
【分析】先根据点的坐标特征写出点M的坐标,再利用关于原点对称的性质写出的坐标即可.
5.【答案】D
【解析】【解答】解:由题意知是的中位线
∴
∵正方形ABCD的周长为8
∴
∴
故答案为:D.
【分析】由题意可得OH为△BCD的中位线,则OH=BC,根据正方形的性质结合周长为8可得BC=2,据此求解.
6.【答案】C
7.【答案】D
【解析】【解答】解:对于A、两边及其夹角分别对应相等的两个三角形全等;故A错误,不符合题意;
对于B、六边形的内角和是,故B错误,不符号题意;
对于C、矩形的对角线相等且互相平分,故C错误,不符合题意;
对于D、根据三角形中位线定理可得,故D正确.
故选:D.
【分析】直接利用全等三角形的判定、矩形的性质、多边形的内角和、三角形中位线逐项判断即可解答.
8.【答案】B
9.【答案】B
10.【答案】B
【解析】【解答】解:设甲正方形网格中每一小格长度为a,乙正方形网格中每一小格长度为b,
则,,,,
∴S正方形ABCD=,S正方形EFGH=,
∴正方形ABCD的面积大于的一半;正方形EFGH的面积等于的一半;
∵S正方形ABCD=S正方形EFGH,
∴,
∴,
∴,即,
∴符合题意结论的序号是②③,
故答案为:B.
【分析】先求出正方形ABCD的面积大于的一半;正方形EFGH的面积等于的一半,再结合S正方形ABCD=S正方形EFGH,可得,再求出,即可得到,即。
11.【答案】12
【解析】【解答】解:设这个多边形的边数为n,根据题意得
(n-2)×180°=5×360°,
解之:n=12.
故答案为:12
【分析】利用n边形的内角和为(n-2)×180°,外角和为360°,根据一个多边形的内角和等于外角和的5倍,可得到关于n的方程,解方程求出n的值.
12.【答案】20°
13.【答案】
14.【答案】30
【解析】【解答】解:∵四边形ABCD是平行四边形,且∠A=70°
∴∠DCB=∠A=70°
∠ADC=180°-∠A
=110°
∵AB=BD
∴∠ADB=∠A=70°
∴∠CDE=40°
∵DE=CE
∴∠DCE=∠CDE=40°
∴∠ECB=∠DCB-∠DCE
=30°
故答案为:30.
【分析】根据平行四边形的性质求出∠ADC、∠DCB的度数,再根据等边对等角即可求解。
15.【答案】
16.【答案】
17.【答案】解:按要求作图如下:
图①:,
以为边的正方形的面积为,
正方形即为所求;
图②:以为一边,以高作平行四边形,
四边形的面积为,
平行四边形即为所求.
【解析】【分析】画出一个边长为的正方形即可;画出一个底为,高为的平行四边形即可.
18.【答案】(1)或;(2)15
19.【答案】(1)
(2)
20.【答案】(1)证明:∵,
∴,
又∵平分,
∴,
∴,
∴,
又∵,
∴,
∴四边形是菱形,
∴;
(2)解:证明:∵四边形是菱形,
∴,
又∵,
∴,
∵,
∴四边形是平行四边形,
∴,
∴,
又∵,
∴,
由三角形内角和定理可得:,
∴.
【解析】【分析】(1)根据直线平行性质可得,根据角平分线性质得,继而得到,再利用菱形性质即可求出答案。
(2)根据菱形性质可判断四边形是平行四边形,根据平行四边形性质可得,利用三角形内角和定理即可求出答案。
21.【答案】(1)证明:∵四边形ABDE是平行四边形.
∴BD=AE,BD∥EG.
又∵AD∥BC.
∴四边形BGAD是平行四边形.
∴BD=AG.
∵BD=AE.
∴AG=AE.
∴A 是EG 的中点.
(2)解:∵四边形ADBG是平行四边形,DE=2BD=6.
∴BD=AG=DE=3.
∵AD∥BC,DF⊥EC.
∴BC⊥EC.
∴∠ECG=90°.
又∵A 是EG 的中点.
∴AC=EG,EG=2AG=2BD=6.
∴AC=3.
∵四边形ADBG是平行四边形.
∴DE=AB=6.
∴在Rt△ABC中,BC=
【解析】【分析】(1)先通过已知条件证明出四边形ADBG是平行四边形,进而得出BD=AG,由此即可得出A 是EG 的中点.
(2)首先根据平行四边形的性质和DE=2BD=6这一条件求出BD的长,然后根据直角三角形的性质求出AC的长,最后根据勾股定理求出BC的长即可.
22.【答案】(1)证明:四边形为矩形,
,
,
,
,
,
,
;
(2)解:,
,,
.
【解析】【分析】(1)由矩形的性质可得∠A=∠B=90°,由同角的余角相等得出∠DEF=∠ABE,再根据AAS证明;
(2)根据全等三角形的性质的对应边相等,结合,计算即可得出答案.
23.【答案】(1)解:当四边形是矩形时,,即:,
解得.
答:当时,四边形是矩形;
(2)解:设秒后,四边形是菱形
当,即时,四边形为菱形.
解得:.
答:当时,四边形是菱形.
【解析】【分析】(1)根据矩形的性质可得:,列出方程,解方程即可求出答案.
(2)根据菱形的性质可得:,,列出方程,解方程即可求出答案.
24.【答案】(1)2,
(2)
(3)存在,的值为或或.
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
