浙江中考复习——集训精选题(四)(含解析)
文档属性
| 名称 | 浙江中考复习——集训精选题(四)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 09:58:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江中考复习——集训精选题(四)
一、选择题
1.(2025·金华模拟)如图是铺设在人行道上地板砖的一部分,它由正六边形和菱形无缝隙镶嵌而成.为各多边形顶点,已知正六边形的边长为,则四边形的面积为( )
A. B. C. D.
2.(2024九下·瓯海模拟)如图1是我国传统的计重工具—秤,当秤钩处挂上物品,移动秤砣使得秤杆处于水平位置时即可称出物品的重量,这用到了杠杆原理(如图2杠杆平衡时,动力动力臂阻力阻力臂).已知一杆秤的秤砣重,秤钮和秤钩的水平距离为,当秤杆处于水平位置时,已知秤砣到秤钮的水平距离为,秤钩所挂物品重为,则关于的函数关系图象是( )
A.B.C.D.
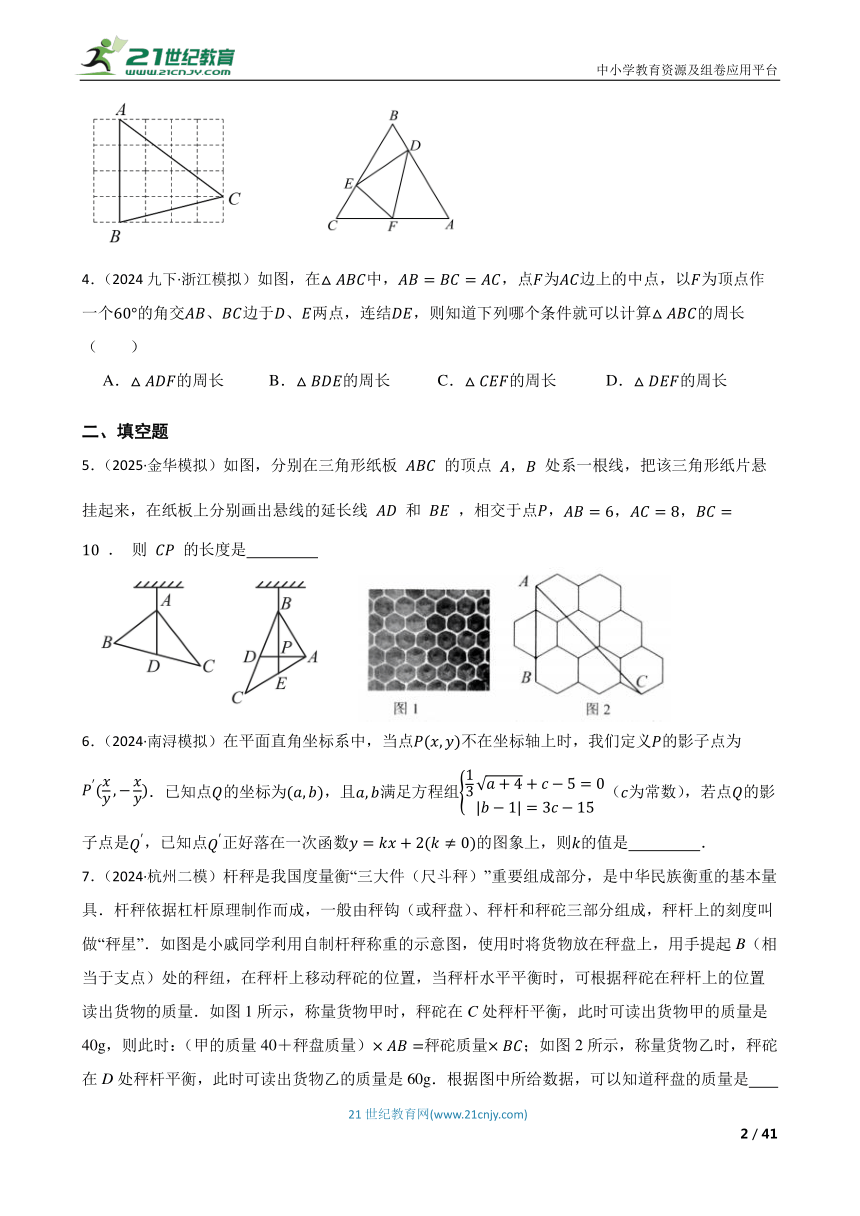
3.(2025九下·武义月考)如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
4.(2024九下·浙江模拟)如图,在中,,点为边上的中点,以为顶点作一个的角交、边于、两点,连结,则知道下列哪个条件就可以计算的周长( )
A.的周长 B.的周长 C.的周长 D.的周长
二、填空题
5.(2025·金华模拟)如图,分别在三角形纸板 的顶点 处系一根线,把该三角形纸片悬挂起来,在纸板上分别画出悬线的延长线 和 ,相交于点, . 则 的长度是
6.(2024·南浔模拟)在平面直角坐标系中,当点不在坐标轴上时,我们定义的影子点为.已知点的坐标为,且满足方程组(为常数),若点的影子点是,已知点正好落在一次函数的图象上,则的值是 .
7.(2024·杭州二模)杆秤是我国度量衡“三大件(尺斗秤)”重要组成部分,是中华民族衡重的基本量具.杆秤依据杠杆原理制作而成,一般由秤钩(或秤盘)、秤杆和秤砣三部分组成,秤杆上的刻度叫做“秤星”.如图是小戚同学利用自制杆秤称重的示意图,使用时将货物放在秤盘上,用手提起B(相当于支点)处的秤纽,在秤杆上移动秤砣的位置,当秤杆水平平衡时,可根据秤砣在秤杆上的位置读出货物的质量.如图1所示,称量货物甲时,秤砣在C处秤杆平衡,此时可读出货物甲的质量是40g,则此时:(甲的质量40+秤盘质量)秤砣质量;如图2所示,称量货物乙时,秤砣在D处秤杆平衡,此时可读出货物乙的质量是60g.根据图中所给数据,可以知道秤盘的质量是 克,这把杆秤的秤星E对应的刻度是 克.
图1 图2
8.(2025·临平模拟)图1为蜂巢的巢房,图2为其横截面示意图,由边长都相等的正六边形组成,A,B,C为顶点,则tan∠BAC的值为 .
三、尺规作图
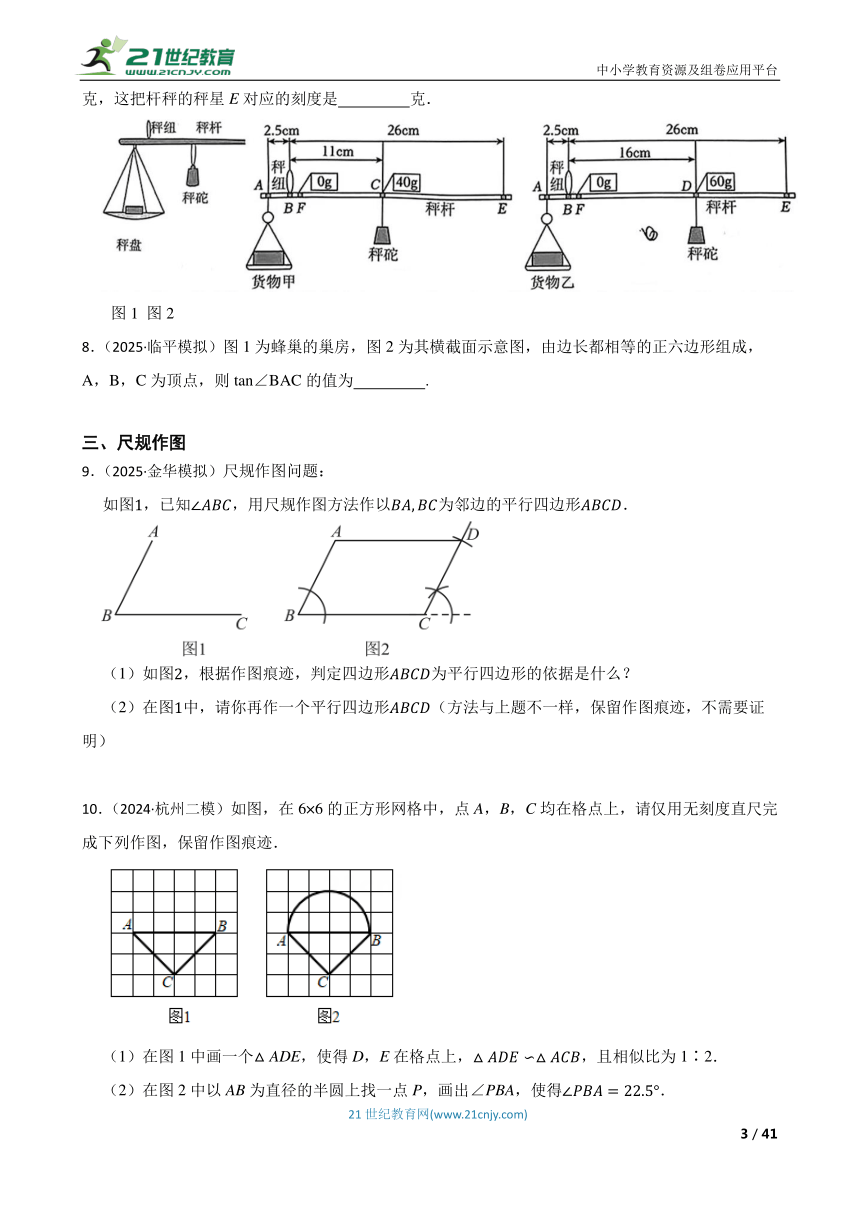
9.(2025·金华模拟)尺规作图问题:
如图,已知,用尺规作图方法作以为邻边的平行四边形.
(1)如图,根据作图痕迹,判定四边形为平行四边形的依据是什么?
(2)在图中,请你再作一个平行四边形(方法与上题不一样,保留作图痕迹,不需要证明)
10.(2024·杭州二模)如图,在6×6的正方形网格中,点A,B,C均在格点上,请仅用无刻度直尺完成下列作图,保留作图痕迹.
(1)在图1中画一个△ADE,使得D,E在格点上,,且相似比为1∶2.
(2)在图2中以AB为直径的半圆上找一点P,画出∠PBA,使得.
四、一次函数与反比例函数
11.(2024·杭州二模)如图,直线(k,b为常数)与双曲线(m为常数)相交于,两点.
(1)求双曲线和直线的表达式:
(2)在双曲线上任取两点和,若,试比较和的大小,并写出推理过程;
(3)请直接写出关于x的不等式的解集.
12.(2024九下·浙江模拟)如图,一次函数与反比例函数的图象相交于两点.
(1)求的值;
(2)直接写出不等式的解集;
(3)过两点分别作轴的平行线和垂线,四条直线的另两个交点为C、D,求证:直线经过原点.
13.(2025·嘉兴模拟)在一条高速公路上依次有A,B,C三地,甲车从A地出发匀速驶向C地,到达C地休息后调头(调头时间忽略不计)按原路原速驶向B地,甲车从A地出发后,乙车从C地出发匀速驶向A地,两车同时到达目的地.两车距A地路程与甲车行驶时间之间的函数关系如图所示.请结合图象信息,解答下列问题:
(1)甲车行驶的速度是_____,乙车行驶的速度是_____.
(2)求图中线段所表示的y与x之间的函数解析式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时,两车距各自出发地路程的差是?请直接写出答案.
五、概率与统计
14.(2025·杭州模拟)第二十二届中国绿色食品博览会上,我省采用多种形式,全方位展示“寒地黑土”“绿色有机”金字招牌,大力推介以下绿色优质农产品:A.“龙江奶”;B.“龙江肉”;C.“龙江米”;D.“龙江杂粮”;E.“龙江菜”;F.“龙江山珍”等,为了更好地了解某社区对以上六类绿色优质农产品的关注程度,某校学生对社区居民进行了抽样调查(每位居民只选最关注的一项),根据调查统计结果,绘制了如图所示的不完整统计图.请根据两幅统计图中的信息,解答下列问题:
(1)本次参与调查的居民有多少人?
(2)通过计算补全条形统计图,并求出在扇形统计图中C类的圆心角度数;
(3)如果该社区有4000人,估计关注“龙江杂粮”的居民有多少人?
15.(2025九上·苏州月考)5月12日是我国“防灾减灾日”.为增强学生防灾减灾意识,某区举行防灾减灾安全知识竞赛.竞赛结束后,发现所有参赛学生的成绩(满分100分)均不低于60分.小明将自己所在学校参加竞赛学生的成绩(用表示)分为四组:组组组,组,绘制了如下不完整的频数分布直方图和扇形统计图.
根据以上信息,解答下列问题:
(1)通过计算补全频数分布直方图;
(2)扇形统计图中组所对应的圆心角的度数为 ;
(3)根据小明学校成绩,估计全区参加竞赛的5000名学生中有多少人的成绩不低于80分?
六、解直角三角形
16.(2024九下·南浔模拟)如图1,某社区服务中心在墙外安装了遮阳棚,便于居民休憩.在如图2的侧面示意图中,遮阳棚长为5米,其与墙面的夹角,其靠墙端离地高米,是为了增加纳凉面积加装的一块前挡板(前挡板垂直于地面).
(1)求出遮阳棚前端到墙面的距离;
(2)已知本地夏日正午的太阳高度角(太阳光线与地面夹角)最小为,若此时房前恰好有米宽的阴影,则加装的前挡板的宽度的长是多少?
(结果精确到0.01,参考数据:,,,)
17.(2024·杭州模拟)如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,GP是杠杆,弹袋挂在点G,重锤挂在点P,点A为支点,点D是水平底板BC上的一点,米,米.
(1)投石车准备时,点G恰好与点B重合,此时AG和AC垂直,求AG
(2)投石车投石瞬间,AP的延长线交线段DC于点E,若DE:CE=5:1,则点G的上升高度为米.
18.(2024九下·浙江模拟)某临街商铺想做一款落地窗以展示商品,为防止商品久晒受损,需保证冬至日正午时分太阳光不能照进落地窗.如图,已有的遮阳棚,遮阳棚前段下摆的自然垂直长度,遮阳棚的固定高度,.
(1)如图1,求遮阳棚上的点到墙面的距离;
(2)如图2,冬至日正午时,该商铺所在地区的太阳的高度角约是(光线与地面的夹角),请通过计算判断该商铺的落地窗方案是否可行.(参考数据)
七、二次函数
19.(2024·南浔模拟)已知二次函数.
(1)若它的图象经过点和点.
①求该二次函数的表达式;
②当自变量的值满足时,求的取值范围.
(2)若它的图象经过点,且,求的取值范围.
20.(2025·龙湾模拟)已知二次函数的解析式为.
(1)若点在该二次函数的图象上,求的值;
(2)若该二次函数图象的顶点在轴上,求该二次函数的解析式;
(3)当时,函数有最大值和最小值,求证:.
21.(2025九上·仙居期末)二次函数的图象经过点,且对称轴为直线.
(1)求这个二次函数的解析式.
(2)图象上的点称为函数的不动点,求这个函数不动点的坐标.
(3)若是二次函数图象上不动点之间的点(包括端点),求的最大值与最小值的差.
八、圆的几何图形
22.(2025·龙湾模拟)如图,在四边形中,,的平分线交于,过三点的圆交于,且恰好是圆的切线,是上一点,连接.
(1)求的度数;
(2)当是圆的直径,
①求证:四边形是平行四边形;
②若是的中点,,求的长.
23.(2024九下·浙江模拟)如图,四边形是的内接四边形,.
(1) .
(2)如图,若半径.
①求证:;
②若,求的值;
③如图,过作于点,交于点的延长线恰好经过点,若,,求的长.
24.(2024·拱墅模拟)如图1,四边形内接于,为直径,上存在点E,满足,连接并延长交的延长线于点F,与交于点G.
(1)若,请用含的代数式表列.
(2)如图2,连接.求证;.
(3)如图3,在(2)的条件下,连接,.
①若,求的周长.
②求的最小值.
答案解析部分
1.【答案】B
【解析】【解答】解:如图,连接、,,,过作于点,
由正六边形的性质得,
∴,
∵四边形是菱形,
∴,,,,
∴,即点、、共线,
同理:点、、共线,
∴、、、共线,
∵,
∴,
∴是等边三角形,
∴,,
同理:,
∴,,
∴,
同理可得,
∴四边形是菱形,是等边三角形,
∵,
∴,,
∴四边形的面积为.
故答案为∶.
【分析】连接、,,,过作于点,得到、、、共线,根据勾股定理求出,即可得到四边形是菱形,是等边三角形,然后根据勾股定理求出AJ长解题即可.
2.【答案】C
【解析】【解答】解:∵一杆秤的秤砣重,秤钮和秤钩的水平距离为,当秤杆处于水平位置时,秤砣到秤钮的水平距离为,秤钩所挂物品重为,
∴根据平衡条件可得:,
整理得:,
∴y是的正比例函数,
把代入得:,
∴图象经过点,
∴C选项的函数图象符合题意,
故答案为:C.
【分析】根据平衡条件可得y与x之间的函数解析式,再把x=5代入求得的函数关系式计算可得图象经过点(5,200),然后再结合各选项判断即可求解.
3.【答案】D
【解析】【解答】解:如图,过作于,则,
=5.
.
故答案为:D
【分析】过作于,根据勾股定理可得AC=5,再根据锐角三角函数的定义即可求出答案.
4.【答案】B
【解析】【解答】解:如图,取中点,连接,在上取一点,使,连接,
∵,
∴ 是等边三角形,
∴,
∵以为顶点作一个的角交、边于、两点,
∴,
,
,
,
,,
∵点为边上的中点,
∴,
,
∴,
,
,
∴,,
在和中,
,
∴,
∴,
又∵点是中点,点是中点,
∴,
∵,
∴,
∵,
∴是等边三角形,
,
,
∵,,
∴,
在和中,
,
,
,
,
即为周长的一半,
故答案为:B.
【分析】取中点,连接,在上取一点,使,连接,易证 是等边三角形,根据等边三角形的性质得,从而得,进而证明,得、,根据,得出,证得,得到,,然后可证,得出,接下来证出是等边三角形,得,于是得,可证明,得到,即可得出,据此即可求解.
5.【答案】
【解析】【解答】解:如图所示,连接并延长交于点,
∵
∴
∴是直角三角形,
依题意,为的重心
∴
在中,
∴
故答案为:.
【分析】先利用勾股定理的逆定理得到是直角三角形,即可得到为的重心,连接并延长交于点,根据勾股定理求得长,根据重心定理解题即可.
6.【答案】
【解析】【解答】解:∵满足方程组(为常数) ,
即,
∴,
∴a+4=0,b-1=0,
即a=-4,b=1,
∴点Q的坐标为(-4,1),
∵定义的影子点为,点的影子点是,点正好落在一次函数的图象上,
∴点的影子点的坐标为(-4,4),
代入,得-4k+2=4,
即.
故答案为:.
【分析】将方程组变形得到,即可得到,求出a、b的值,即可得到点Q的坐标与点的影子点的坐标,将点的坐标代入一次函数,即可得到答案.
7.【答案】4;100
【解析】【解答】解:设秤盘的质量为x克,秤砣的质量为y克,
∴
解得:
设这把秤杆的秤星E对应的刻度为m克,
∴
∴
故答案为:4,100.
【分析】设秤盘的质量为x克,秤砣的质量为y克,根据杠杆平衡原理以及题中的图片信息得到方程组,求出x和y的值,最后再根据"(甲的质量40+秤盘质量)秤砣质量",即可求出这把杆秤的秤星E对应的刻度.
8.【答案】
【解析】【解答】解:如图2,延长CE交AB的延长线于点D,
在 中, 作 于G点,
即
中,
故答案为:
【分析】根据题意,延长CE交AB的延长线于点D,得到 再分别求出CD,AD长,即可得到结果.
9.【答案】(1)解:由作图可知,,
四边形是平行四边形,
判定四边形为平行四边形的依据是:一组对边平行且相等的四边形是平行四边形;
(2)解:如图所示:
.
【解析】【分析】(1)根据作图,利用平行四边形的判定定理解答即可;
(2)根据两组对边分别相等的四边形是平行四边形作图即可.
(1)解:由作图可知,,
四边形是平行四边形,
判定四边形为平行四边形的依据是:一组对边平行且相等的四边形是平行四边形;
(2)解:如图所示:
.
10.【答案】(1)解:如图,即为所求,
.
(2)解:如图即为所求,
.
11.【答案】(1)解:∵在双曲线 上,
∴
∴
∴
∴
把代入直线,
∴
∴.
(2)解:由题意可知分两种情况讨论,
①当M、N在双曲线同一支上时,
∵双曲线k=-2<0,
∴在同一支上时函数值随x增大而增大,
∴当时,
②当M、N不在双曲线同一支上时,
∵,
∴
∴
此时,.
(3)不等式的解集为:,
【解析】【解答】解:(3)根据图象,即一次函数值大于反比例函数值
∵,
∴不等式的解集为:,
【分析】(1)先根据点B的坐标求出双曲线的解析式,进而求出点A的坐标,最后把代入直线,即可求出其解析式;
(2)由题意可知分两种情况讨论,①当M、N在双曲线同一支上时,②当M、N不在双曲线同一支上时,分别根据双曲线的增减性,分析即可求解;
(3)根据图象,即一次函数值大于反比例函数值,结合点A和点B的坐标即可求解.
12.【答案】(1)解:∵ 一次函数与反比例函数的图象相交于两点 ,
∴当时,,
,
,
,
,;
(2)解:由(1)可知一次函数与反比例函数的图象相交于,,
∴根据函数图象可知不等式的解集为:或;
(3)证明:由(1)可知,,,
根据题意可得,,
设直线解析式为,代入、坐标得:,
解得:,
直线解析式为,
当时,,
∴直线经过原点.
【解析】【分析】(1)将点坐标代入一次函数解析式可得的值,根据反比例函数图象上点的坐标特征、结合的值可求出的值;
(2)根据一次函数与反比例函数的交点问题,结合(1)中的坐标可直接写出不等式解集;
(3)根据的坐标,结合题意可得,,然后用待定系数法求出直线解析式,再令,则,即可得证结论.
13.【答案】(1),
(2)解:设线段所在直线的解析式为.
∵,在直线上,
∴.
解得:.
线段所在直线的解析式为.
(3)解:设乙车出发时,
∵在中,当时,,
∴,
∵乙车行驶速度为,甲车行驶速度为且两车同时到达目的地,
∴乙到达目的地时,甲距离A地的距离为,
∴,,
∴两车距各自出发地路程的差是,
当时,此时甲在到达C地前,
,
解得:,(不合题意,舍去);
当时,此时甲在C地休息,
,
解得:,(不合题意,舍去);
当时,此时甲在返回B地中,
解得:,(不合题意,舍去)
综上所述,乙车出发或,两车距各自出发地路程的差是.
【解析】【解答】解:(1)由图可得,即甲出发3时后与地相距,
∴甲车行驶速度为;
由题意可得,,即乙车出发行驶,
∴乙车行驶速度为,
故答案为:,;
【分析】(1)结合函数图象中点的坐标的实际意义求速度;
(2)利用待定系数法求函数解析式;
(3)先求得点E、F坐标,然后分情况列方程求解.
14.【答案】(1)解:∵关注E种类有34人,占17%,
∴(人),
答:本次参与调查的居民有200人;
(2)解:选择B.“龙江肉”的学生人数为:(人);
补全条形统计图如图所示:
在扇形统计图中C类的圆心角度数是.
(3)解:∵ 本次参与调查的关注“龙江杂粮”的有46人,
∴(人),
答:该社区有4000人,估计关注“龙江杂粮”的居民约为920人.
【解析】【分析】(1)根据关注E种类的人数与占的百分比,可求得本次参与调查的人数;
(2)先根据关注B的占的百分比,可求出样本中选择B.“龙江肉”的人数,再可补全条形统计图,根据C类的人数,可求出在扇形统计图中C类的圆心角度数;
(3)根据本次参与调查的关注D.“龙江杂粮”的学生所占的百分比,可估计总体中选择D.“龙江杂粮”所占的百分比,从而求出相应的人数.
15.【答案】(1)解:根据题意,得参加竞赛学生总人数为:(人),
∴B组的人数为:(人)
∴补全频数分布直方图如下图:
(2)解:根据题意,得A组所对应的圆心角的度数为:,
故答案为:36°;
(3)解:(人),
∴估计全区参加竞赛的5000名学生中有3500人的成绩不低于80分.
【解析】【分析】(1)用C组人数除以C组所占百分比得参加竞赛学生的总人数,然后用总人数乘B组所占百分比得B组人数,再补全频数分布直方图即可;
(2)用360°乘A组人数所占比即可求解;
(3)利用样本估计总体,将5000乘成绩不低于80分的人数所占比即可求解.
16.【答案】(1)解:如图,所示过点M作,垂足为N,
在,米,,
而,
∴米.
因此遮阳棚前端M到墙面的距离为米.
(2)解:如图所示,过点E作,垂足为H,
在,米,,
∴米,
∵米,
∴米,
由(1)可知米,
∵米,米,
米,
在中,米,
米.
因此加装的前挡板的宽度的长是米.
【解析】【分析】(1)在直角三角形AMN中,斜边AM已知,sin75°条件也给出,因此利用正弦值进行计算即可求出MN的长度;
(2)AB的长度已知,AN可以利用余弦值来求出,此时BN的长度即可计算得出;结合(1)的结论MN的长度已知,BC为阴影部分的长度也已知,即可计算出CH的长度。利用正切值计算出EH的长度,ME的长度即可计算得出。
17.【答案】(1)解:如图,连接AB,过A点作AF⊥BC于F,
∵AD=AC=3米,CD=3.6米,
CF=DF=1.8米,
∴,
∵
∴,
∵,
∴,
∴,
∴,
∴,
∴AG的长为4米,
(2)过点G作GF⊥DC于点F,过点A作AH⊥CD于点H,则∠AHE=∠GFE=90°,如图所示:
∵CD=3.6米,DE:CE=5:1,
∴CE=0.6米,
∴EH=1.8-0.6=1.2米,
∴AE=米,
∵∠AEH=∠GEF,
∴△EAH∽△EGF,
∴,
∴,
解得:GF=,
∴点G上升的高度为()米,
【解析】【分析】(1)连接AB,过点A作AF⊥CB于点F,用勾股定理求出AF的长,证△AFB∽△CFA,根据对应线段成比例求出BF的长,再用勾股定理求解即可;
(2)过点G作GF⊥DC于点F,过点A作AH⊥CD于点H,则∠AHE=∠GFE=90°,先证出△EAH∽△EGF,可得,再将数据代入求出GF的长即可.
18.【答案】(1)解:如图1,过点作于,
∴,
∵,
∴,
∴点到墙面的距离为;
(2)解:如图2,延长光线交于点,延长交于点,
根据题意,可得,,
∴,
∴四边形是矩形,
∴,,
,,
,
∵,
∴,
∵,
∴,
在中,,
,
∴,
,
∴,
∴光线刚好不能照射到商户内,方案可行.
【解析】【分析】(1)过点作于,在中,解直角三角形求出的值即可;
(2)延长光线交于点,延长交于点,易证四边形是矩形,得,,利用勾股定理求得,从而得,进而得,在中,再根据,求出的长与比较大小即可得出结论.
19.【答案】(1)解:①∵二次函数的图象经过点和点,
∴,
解得:,
∴二次函数的表达式为;
②,
当时,,
当时,,
当时,,
∴当时,y随x增大而增大,当时,y随x增大而减小,
∴当时,;
(2)解:根据题意可知,对称轴为,
当x=0时,y=2,
∴图像经过点(0,2),
∵抛物线开口向下,
∴在对称轴左侧y随x增大而增大,在对称轴右侧y随x增大而减小,
∴点(0,2),(6,n)在对称轴左侧或两侧,
当点(0,2),(6,n)在对称轴左侧时,
∵点(p-4,m)在对称轴左侧, 且 ,
∴p-4>6,
即p>10;
当点(0,2),(6,n)在对称轴两侧时,
∴(p,m),(6,n)在右侧,(0,2)在左侧,
∴,
即5综上所述,p>10或5【解析】【分析】(1)①根据待定系数法即可求出二次函数的表达式;
②将表达式化为,再根据增减性即可得到答案;
(2)根据题意得到对称轴为,即图像过点(0,2),根据图象经过点,且,得到点(0,2),(6,n)在对称轴左侧或两侧,分别求出点与对称轴的距离即可得到答案.
20.【答案】(1)解:∵点在该二次函数的图象上,
∴将代入,
得:,
解得:或;
(2)解:∵,
∴二次函数的顶点坐标为,
∵该二次函数图象的顶点在轴上,
∴,
解得:,
∴该二次函数的解析式为;
(3)解:∵,其中二次项系数,对称轴为直线,
∴抛物线开口向上,抛物线上的点离对称轴距离越远其函数值越大,
又∵|-1-1|>|2-1|,
∴ 当时
∴当时函数取得最小值;
当时函数取得最大值;
∴,
即.
【解析】【分析】(1)根据二次函数图象上点的坐标特点,将代入,求解一元二次方程即可;
(2)先利用配方法将解析式配成顶点式,求出顶点坐标,由该抛物线顶点在x轴上可得顶点的纵坐标为零,据此建立方程求出c的值,从而即可得到抛物线的解析式;
(3)由二次项系数大于零,得抛物线开口向上,抛物线上的点离对称轴距离越远其函数值越大,据此结合x的取值范围,求出二次函数的最大值和最小值,再利用配方法判定即可.
(1)解:∵点在该二次函数的图象上,
∴将代入,
得:,
解得:或;
(2)解:∵,
∴二次函数的顶点坐标为,
∵该二次函数图象的顶点在轴上,
∴,
解得:,
∴该二次函数的解析式为;
(3)解:∵,
其中,对称轴为直线,
∴在时,随的增大而减小;在时,随的增大而增大;
∴当时函数取得最小值;
当时函数取得最大值;
∴,
即.
21.【答案】(1)解:∵ 二次函数的图象经过点,且对称轴为直线,
∴,解得,
∴该二次函数的解析式为.
(2)解:∵ 图象上的点称为函数的不动点,
∴,
解得:,,
∴这个函数不动点的坐标为和.
(3)解:∵,该抛物线的开口向上,对称轴为直线,,
∴当时,y有最小值,
当时,y有最大值5,
∴的最大值与最小值的差为.
【解析】【分析】(1)先根据点(4,-1)及对称轴,得到关于b,c的方程组求解,再代回解析式,求得函数表达式;
(2)将点代入解析式中,得到关于x的方程求解,求出不动点的坐标;
(3)先将解析式化为顶点式,再根据二次函数的性质求出最大值和最小值,进而求解即可.
(1)解:由题意,,解得,
∴该二次函数的解析式为;
(2)解:将代入中,得,
即,
解得,,
∴这个函数不动点的坐标为和;
(3)解:由(2)知,,
∵,该抛物线的开口向上,对称轴为直线,
∴当时,y有最小值,
当时,y有最大值5,
∴的最大值与最小值的差为.
22.【答案】(1)解:连接,
∵,
∴是直径.
∵是圆的切线,
∴.
∵的平分线交于,
∴,
∴,
∵,
∴;
(2)①证明:连接,
∵,是圆的直径,
∴,
∴,
∴,
∵
∴,
∴,
∴四边形是平行四边形;
②解:延长相较于点H,
∵,
∴,
∵,
∴.
∵,
∴.
∵是的中点,
∴.
∵,
∴,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
【解析】【分析】(1)连接CE,根据圆心角、弧、弦的关系可证明CE是直径,根据圆的切线垂直经过切点的半径得,由角平分线定义及三角形内角和定理求出,然后根据等弧所对的圆周角相等即可求解;
(2)①连接EF,由直径所对的圆周角是直角得,由同旁内角互补,两直线平行,可证,由二直线平行,内错角相等及等量代换可得,从而由同位角相等,两直线平行,可得,从而根据两组对边分别平行的四边形是平行四边形,可证四边形是平行四边形;
②延长BC、AD相交于H,由等角对等边得BE=CE,由等腰直角三角形性质求出,,由等弧所对的圆周角相等及平行线的性质可推出,由等角对等边得出,由有两组角对应相等的两个三角形相似得,由相似三角形对应边成比例得,代入数据即可求解.
(1)解:连接,
∵,
∴是直径.
∵是圆的切线,
∴.
∵的平分线交于,
∴,
∴,
∵,
∴
(2)①证明:连接,
∵,是圆的直径,
∴,
∴,
∴,
∵
∴,
∴,
∴四边形是平行四边形;
②解:延长相较于点H,
∵,
∴,
∵,
∴.
∵,
∴.
∵是的中点,
∴.
∵,
∴,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
23.【答案】(1)解:如图,连接,
,
,
,
∵,
∴,
,
故答案为:90°;
(2)①证明:如图,连接,
,
,
,
,
,
,
,
,
,
,
,
∵,
∴,
,
,
;
②如图,连接,连接并延长交于点,
∵,
∴,
,
,
∴,
,
∴,
∵,
∴,
,
,
,
,
,
,
,
,
,
设,则,
在中,,
,
,
在中,,
;
③如图,过点作交于点,
,
,
,
,
∵,
∴,
,
∴,
,
,
,
∴,
在和中,
,
,
,
同②可得,,
∵,
∴,
在和中,
,
,
,
∴,
在和中,
,
∴,
∴,,
∴,
设,
∵,
∴,
∵,
在和中,,
解得:,
,
,
,
,
,
,
,
.
【解析】【分析】(1)连接,根据圆周角定理、等腰三角形”等边对等角“的性质得,,然后由三角形内角和定理得,可推导出;
(2)①连接,根据平行线的性质得,根据圆周角定理、等腰三角形”等边对等角“的性质得,,然后由三角形内角和定理得,可得,接下来证出,进行等量代换可推导出;
②连接,连接并延长交于点,根据垂径定理的推论得,结合圆周角定理得,从而得,根据等腰三角形”等边对等角“性质得,即可证明,可推导出,设,则,利用勾股定理、三角形面积公式求出,,,即可得;
③过点作交于点,先证明,可得,再证明,得,从而得,进而证明,得,,则,设,,在和中,利用勾股定理得方程组,解方程即可求出,再求,可得,根据,最后求得,即可求.
24.【答案】解:(1)∵为的直径,
∴,
∵,
∴,
∴.
(2)∵为的直径,
∴,
∴,
∴,
∵,
∴.
又∵,
在△CFE和△BDG中
∴,
∴.
(3)①如图,连接.
∵为的直径,
∴.
在中,,,
∴.
∵,
∴,
即,
∴.
∵,
∴.
∵在中,,
∴,
∴.
∵在中,,
∴.
在中,,
∴,
∴的周长为.
②如图,过点C作于H.
∵,
∴.
∵,
在△CFE和△BDG中
∴.
∴,
∵,
∴.
∵,
∴.
∵,
∴,
∵,
∴,
∴.
设,
∴,
∴.
在中, ,
∴,
当时,的最小值为3,
∴的最小值为.
【解析】【分析】(1)利用圆周角定理求得,再根据,求得,即可得到答案;
(2)由,得到,由同角的补角相等可得,结合已知用角边角可证,再根据全等三角形的对应边相等可求解;
(3)①连接.利用已知求出,证得,得到,在中,根据锐角三角函数sin∠AGB=求出∠AGB的度数,由30度角所对的直角边等于斜边的一半求出AG的长,由线段的和差EF=DG=AD-AG求出EF的长,在中,,由30度角所对的直角边等于斜边的一半求出EG及DE,在Rt△FED中,用勾股定理求出DF的长,然后三角形FGD的周长可求解;
②过点C作于H,由题意,用角角边可证,由全等三角形的对应边相等可得,再根据有两个角对应相等的两个三角形相似可得,于是可得比例式,设,整理得,用勾股定理得到 ,求得,然后根据函数的性质即可求解.
21世纪教育网(www.21cnjy.com)
浙江中考复习——集训精选题(四)
一、选择题
1.(2025·金华模拟)如图是铺设在人行道上地板砖的一部分,它由正六边形和菱形无缝隙镶嵌而成.为各多边形顶点,已知正六边形的边长为,则四边形的面积为( )
A. B. C. D.
2.(2024九下·瓯海模拟)如图1是我国传统的计重工具—秤,当秤钩处挂上物品,移动秤砣使得秤杆处于水平位置时即可称出物品的重量,这用到了杠杆原理(如图2杠杆平衡时,动力动力臂阻力阻力臂).已知一杆秤的秤砣重,秤钮和秤钩的水平距离为,当秤杆处于水平位置时,已知秤砣到秤钮的水平距离为,秤钩所挂物品重为,则关于的函数关系图象是( )
A.B.C.D.
3.(2025九下·武义月考)如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,则的值为( )
A. B. C. D.
4.(2024九下·浙江模拟)如图,在中,,点为边上的中点,以为顶点作一个的角交、边于、两点,连结,则知道下列哪个条件就可以计算的周长( )
A.的周长 B.的周长 C.的周长 D.的周长
二、填空题
5.(2025·金华模拟)如图,分别在三角形纸板 的顶点 处系一根线,把该三角形纸片悬挂起来,在纸板上分别画出悬线的延长线 和 ,相交于点, . 则 的长度是
6.(2024·南浔模拟)在平面直角坐标系中,当点不在坐标轴上时,我们定义的影子点为.已知点的坐标为,且满足方程组(为常数),若点的影子点是,已知点正好落在一次函数的图象上,则的值是 .
7.(2024·杭州二模)杆秤是我国度量衡“三大件(尺斗秤)”重要组成部分,是中华民族衡重的基本量具.杆秤依据杠杆原理制作而成,一般由秤钩(或秤盘)、秤杆和秤砣三部分组成,秤杆上的刻度叫做“秤星”.如图是小戚同学利用自制杆秤称重的示意图,使用时将货物放在秤盘上,用手提起B(相当于支点)处的秤纽,在秤杆上移动秤砣的位置,当秤杆水平平衡时,可根据秤砣在秤杆上的位置读出货物的质量.如图1所示,称量货物甲时,秤砣在C处秤杆平衡,此时可读出货物甲的质量是40g,则此时:(甲的质量40+秤盘质量)秤砣质量;如图2所示,称量货物乙时,秤砣在D处秤杆平衡,此时可读出货物乙的质量是60g.根据图中所给数据,可以知道秤盘的质量是 克,这把杆秤的秤星E对应的刻度是 克.
图1 图2
8.(2025·临平模拟)图1为蜂巢的巢房,图2为其横截面示意图,由边长都相等的正六边形组成,A,B,C为顶点,则tan∠BAC的值为 .
三、尺规作图
9.(2025·金华模拟)尺规作图问题:
如图,已知,用尺规作图方法作以为邻边的平行四边形.
(1)如图,根据作图痕迹,判定四边形为平行四边形的依据是什么?
(2)在图中,请你再作一个平行四边形(方法与上题不一样,保留作图痕迹,不需要证明)
10.(2024·杭州二模)如图,在6×6的正方形网格中,点A,B,C均在格点上,请仅用无刻度直尺完成下列作图,保留作图痕迹.
(1)在图1中画一个△ADE,使得D,E在格点上,,且相似比为1∶2.
(2)在图2中以AB为直径的半圆上找一点P,画出∠PBA,使得.
四、一次函数与反比例函数
11.(2024·杭州二模)如图,直线(k,b为常数)与双曲线(m为常数)相交于,两点.
(1)求双曲线和直线的表达式:
(2)在双曲线上任取两点和,若,试比较和的大小,并写出推理过程;
(3)请直接写出关于x的不等式的解集.
12.(2024九下·浙江模拟)如图,一次函数与反比例函数的图象相交于两点.
(1)求的值;
(2)直接写出不等式的解集;
(3)过两点分别作轴的平行线和垂线,四条直线的另两个交点为C、D,求证:直线经过原点.
13.(2025·嘉兴模拟)在一条高速公路上依次有A,B,C三地,甲车从A地出发匀速驶向C地,到达C地休息后调头(调头时间忽略不计)按原路原速驶向B地,甲车从A地出发后,乙车从C地出发匀速驶向A地,两车同时到达目的地.两车距A地路程与甲车行驶时间之间的函数关系如图所示.请结合图象信息,解答下列问题:
(1)甲车行驶的速度是_____,乙车行驶的速度是_____.
(2)求图中线段所表示的y与x之间的函数解析式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时,两车距各自出发地路程的差是?请直接写出答案.
五、概率与统计
14.(2025·杭州模拟)第二十二届中国绿色食品博览会上,我省采用多种形式,全方位展示“寒地黑土”“绿色有机”金字招牌,大力推介以下绿色优质农产品:A.“龙江奶”;B.“龙江肉”;C.“龙江米”;D.“龙江杂粮”;E.“龙江菜”;F.“龙江山珍”等,为了更好地了解某社区对以上六类绿色优质农产品的关注程度,某校学生对社区居民进行了抽样调查(每位居民只选最关注的一项),根据调查统计结果,绘制了如图所示的不完整统计图.请根据两幅统计图中的信息,解答下列问题:
(1)本次参与调查的居民有多少人?
(2)通过计算补全条形统计图,并求出在扇形统计图中C类的圆心角度数;
(3)如果该社区有4000人,估计关注“龙江杂粮”的居民有多少人?
15.(2025九上·苏州月考)5月12日是我国“防灾减灾日”.为增强学生防灾减灾意识,某区举行防灾减灾安全知识竞赛.竞赛结束后,发现所有参赛学生的成绩(满分100分)均不低于60分.小明将自己所在学校参加竞赛学生的成绩(用表示)分为四组:组组组,组,绘制了如下不完整的频数分布直方图和扇形统计图.
根据以上信息,解答下列问题:
(1)通过计算补全频数分布直方图;
(2)扇形统计图中组所对应的圆心角的度数为 ;
(3)根据小明学校成绩,估计全区参加竞赛的5000名学生中有多少人的成绩不低于80分?
六、解直角三角形
16.(2024九下·南浔模拟)如图1,某社区服务中心在墙外安装了遮阳棚,便于居民休憩.在如图2的侧面示意图中,遮阳棚长为5米,其与墙面的夹角,其靠墙端离地高米,是为了增加纳凉面积加装的一块前挡板(前挡板垂直于地面).
(1)求出遮阳棚前端到墙面的距离;
(2)已知本地夏日正午的太阳高度角(太阳光线与地面夹角)最小为,若此时房前恰好有米宽的阴影,则加装的前挡板的宽度的长是多少?
(结果精确到0.01,参考数据:,,,)
17.(2024·杭州模拟)如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,GP是杠杆,弹袋挂在点G,重锤挂在点P,点A为支点,点D是水平底板BC上的一点,米,米.
(1)投石车准备时,点G恰好与点B重合,此时AG和AC垂直,求AG
(2)投石车投石瞬间,AP的延长线交线段DC于点E,若DE:CE=5:1,则点G的上升高度为米.
18.(2024九下·浙江模拟)某临街商铺想做一款落地窗以展示商品,为防止商品久晒受损,需保证冬至日正午时分太阳光不能照进落地窗.如图,已有的遮阳棚,遮阳棚前段下摆的自然垂直长度,遮阳棚的固定高度,.
(1)如图1,求遮阳棚上的点到墙面的距离;
(2)如图2,冬至日正午时,该商铺所在地区的太阳的高度角约是(光线与地面的夹角),请通过计算判断该商铺的落地窗方案是否可行.(参考数据)
七、二次函数
19.(2024·南浔模拟)已知二次函数.
(1)若它的图象经过点和点.
①求该二次函数的表达式;
②当自变量的值满足时,求的取值范围.
(2)若它的图象经过点,且,求的取值范围.
20.(2025·龙湾模拟)已知二次函数的解析式为.
(1)若点在该二次函数的图象上,求的值;
(2)若该二次函数图象的顶点在轴上,求该二次函数的解析式;
(3)当时,函数有最大值和最小值,求证:.
21.(2025九上·仙居期末)二次函数的图象经过点,且对称轴为直线.
(1)求这个二次函数的解析式.
(2)图象上的点称为函数的不动点,求这个函数不动点的坐标.
(3)若是二次函数图象上不动点之间的点(包括端点),求的最大值与最小值的差.
八、圆的几何图形
22.(2025·龙湾模拟)如图,在四边形中,,的平分线交于,过三点的圆交于,且恰好是圆的切线,是上一点,连接.
(1)求的度数;
(2)当是圆的直径,
①求证:四边形是平行四边形;
②若是的中点,,求的长.
23.(2024九下·浙江模拟)如图,四边形是的内接四边形,.
(1) .
(2)如图,若半径.
①求证:;
②若,求的值;
③如图,过作于点,交于点的延长线恰好经过点,若,,求的长.
24.(2024·拱墅模拟)如图1,四边形内接于,为直径,上存在点E,满足,连接并延长交的延长线于点F,与交于点G.
(1)若,请用含的代数式表列.
(2)如图2,连接.求证;.
(3)如图3,在(2)的条件下,连接,.
①若,求的周长.
②求的最小值.
答案解析部分
1.【答案】B
【解析】【解答】解:如图,连接、,,,过作于点,
由正六边形的性质得,
∴,
∵四边形是菱形,
∴,,,,
∴,即点、、共线,
同理:点、、共线,
∴、、、共线,
∵,
∴,
∴是等边三角形,
∴,,
同理:,
∴,,
∴,
同理可得,
∴四边形是菱形,是等边三角形,
∵,
∴,,
∴四边形的面积为.
故答案为∶.
【分析】连接、,,,过作于点,得到、、、共线,根据勾股定理求出,即可得到四边形是菱形,是等边三角形,然后根据勾股定理求出AJ长解题即可.
2.【答案】C
【解析】【解答】解:∵一杆秤的秤砣重,秤钮和秤钩的水平距离为,当秤杆处于水平位置时,秤砣到秤钮的水平距离为,秤钩所挂物品重为,
∴根据平衡条件可得:,
整理得:,
∴y是的正比例函数,
把代入得:,
∴图象经过点,
∴C选项的函数图象符合题意,
故答案为:C.
【分析】根据平衡条件可得y与x之间的函数解析式,再把x=5代入求得的函数关系式计算可得图象经过点(5,200),然后再结合各选项判断即可求解.
3.【答案】D
【解析】【解答】解:如图,过作于,则,
=5.
.
故答案为:D
【分析】过作于,根据勾股定理可得AC=5,再根据锐角三角函数的定义即可求出答案.
4.【答案】B
【解析】【解答】解:如图,取中点,连接,在上取一点,使,连接,
∵,
∴ 是等边三角形,
∴,
∵以为顶点作一个的角交、边于、两点,
∴,
,
,
,
,,
∵点为边上的中点,
∴,
,
∴,
,
,
∴,,
在和中,
,
∴,
∴,
又∵点是中点,点是中点,
∴,
∵,
∴,
∵,
∴是等边三角形,
,
,
∵,,
∴,
在和中,
,
,
,
,
即为周长的一半,
故答案为:B.
【分析】取中点,连接,在上取一点,使,连接,易证 是等边三角形,根据等边三角形的性质得,从而得,进而证明,得、,根据,得出,证得,得到,,然后可证,得出,接下来证出是等边三角形,得,于是得,可证明,得到,即可得出,据此即可求解.
5.【答案】
【解析】【解答】解:如图所示,连接并延长交于点,
∵
∴
∴是直角三角形,
依题意,为的重心
∴
在中,
∴
故答案为:.
【分析】先利用勾股定理的逆定理得到是直角三角形,即可得到为的重心,连接并延长交于点,根据勾股定理求得长,根据重心定理解题即可.
6.【答案】
【解析】【解答】解:∵满足方程组(为常数) ,
即,
∴,
∴a+4=0,b-1=0,
即a=-4,b=1,
∴点Q的坐标为(-4,1),
∵定义的影子点为,点的影子点是,点正好落在一次函数的图象上,
∴点的影子点的坐标为(-4,4),
代入,得-4k+2=4,
即.
故答案为:.
【分析】将方程组变形得到,即可得到,求出a、b的值,即可得到点Q的坐标与点的影子点的坐标,将点的坐标代入一次函数,即可得到答案.
7.【答案】4;100
【解析】【解答】解:设秤盘的质量为x克,秤砣的质量为y克,
∴
解得:
设这把秤杆的秤星E对应的刻度为m克,
∴
∴
故答案为:4,100.
【分析】设秤盘的质量为x克,秤砣的质量为y克,根据杠杆平衡原理以及题中的图片信息得到方程组,求出x和y的值,最后再根据"(甲的质量40+秤盘质量)秤砣质量",即可求出这把杆秤的秤星E对应的刻度.
8.【答案】
【解析】【解答】解:如图2,延长CE交AB的延长线于点D,
在 中, 作 于G点,
即
中,
故答案为:
【分析】根据题意,延长CE交AB的延长线于点D,得到 再分别求出CD,AD长,即可得到结果.
9.【答案】(1)解:由作图可知,,
四边形是平行四边形,
判定四边形为平行四边形的依据是:一组对边平行且相等的四边形是平行四边形;
(2)解:如图所示:
.
【解析】【分析】(1)根据作图,利用平行四边形的判定定理解答即可;
(2)根据两组对边分别相等的四边形是平行四边形作图即可.
(1)解:由作图可知,,
四边形是平行四边形,
判定四边形为平行四边形的依据是:一组对边平行且相等的四边形是平行四边形;
(2)解:如图所示:
.
10.【答案】(1)解:如图,即为所求,
.
(2)解:如图即为所求,
.
11.【答案】(1)解:∵在双曲线 上,
∴
∴
∴
∴
把代入直线,
∴
∴.
(2)解:由题意可知分两种情况讨论,
①当M、N在双曲线同一支上时,
∵双曲线k=-2<0,
∴在同一支上时函数值随x增大而增大,
∴当时,
②当M、N不在双曲线同一支上时,
∵,
∴
∴
此时,.
(3)不等式的解集为:,
【解析】【解答】解:(3)根据图象,即一次函数值大于反比例函数值
∵,
∴不等式的解集为:,
【分析】(1)先根据点B的坐标求出双曲线的解析式,进而求出点A的坐标,最后把代入直线,即可求出其解析式;
(2)由题意可知分两种情况讨论,①当M、N在双曲线同一支上时,②当M、N不在双曲线同一支上时,分别根据双曲线的增减性,分析即可求解;
(3)根据图象,即一次函数值大于反比例函数值,结合点A和点B的坐标即可求解.
12.【答案】(1)解:∵ 一次函数与反比例函数的图象相交于两点 ,
∴当时,,
,
,
,
,;
(2)解:由(1)可知一次函数与反比例函数的图象相交于,,
∴根据函数图象可知不等式的解集为:或;
(3)证明:由(1)可知,,,
根据题意可得,,
设直线解析式为,代入、坐标得:,
解得:,
直线解析式为,
当时,,
∴直线经过原点.
【解析】【分析】(1)将点坐标代入一次函数解析式可得的值,根据反比例函数图象上点的坐标特征、结合的值可求出的值;
(2)根据一次函数与反比例函数的交点问题,结合(1)中的坐标可直接写出不等式解集;
(3)根据的坐标,结合题意可得,,然后用待定系数法求出直线解析式,再令,则,即可得证结论.
13.【答案】(1),
(2)解:设线段所在直线的解析式为.
∵,在直线上,
∴.
解得:.
线段所在直线的解析式为.
(3)解:设乙车出发时,
∵在中,当时,,
∴,
∵乙车行驶速度为,甲车行驶速度为且两车同时到达目的地,
∴乙到达目的地时,甲距离A地的距离为,
∴,,
∴两车距各自出发地路程的差是,
当时,此时甲在到达C地前,
,
解得:,(不合题意,舍去);
当时,此时甲在C地休息,
,
解得:,(不合题意,舍去);
当时,此时甲在返回B地中,
解得:,(不合题意,舍去)
综上所述,乙车出发或,两车距各自出发地路程的差是.
【解析】【解答】解:(1)由图可得,即甲出发3时后与地相距,
∴甲车行驶速度为;
由题意可得,,即乙车出发行驶,
∴乙车行驶速度为,
故答案为:,;
【分析】(1)结合函数图象中点的坐标的实际意义求速度;
(2)利用待定系数法求函数解析式;
(3)先求得点E、F坐标,然后分情况列方程求解.
14.【答案】(1)解:∵关注E种类有34人,占17%,
∴(人),
答:本次参与调查的居民有200人;
(2)解:选择B.“龙江肉”的学生人数为:(人);
补全条形统计图如图所示:
在扇形统计图中C类的圆心角度数是.
(3)解:∵ 本次参与调查的关注“龙江杂粮”的有46人,
∴(人),
答:该社区有4000人,估计关注“龙江杂粮”的居民约为920人.
【解析】【分析】(1)根据关注E种类的人数与占的百分比,可求得本次参与调查的人数;
(2)先根据关注B的占的百分比,可求出样本中选择B.“龙江肉”的人数,再可补全条形统计图,根据C类的人数,可求出在扇形统计图中C类的圆心角度数;
(3)根据本次参与调查的关注D.“龙江杂粮”的学生所占的百分比,可估计总体中选择D.“龙江杂粮”所占的百分比,从而求出相应的人数.
15.【答案】(1)解:根据题意,得参加竞赛学生总人数为:(人),
∴B组的人数为:(人)
∴补全频数分布直方图如下图:
(2)解:根据题意,得A组所对应的圆心角的度数为:,
故答案为:36°;
(3)解:(人),
∴估计全区参加竞赛的5000名学生中有3500人的成绩不低于80分.
【解析】【分析】(1)用C组人数除以C组所占百分比得参加竞赛学生的总人数,然后用总人数乘B组所占百分比得B组人数,再补全频数分布直方图即可;
(2)用360°乘A组人数所占比即可求解;
(3)利用样本估计总体,将5000乘成绩不低于80分的人数所占比即可求解.
16.【答案】(1)解:如图,所示过点M作,垂足为N,
在,米,,
而,
∴米.
因此遮阳棚前端M到墙面的距离为米.
(2)解:如图所示,过点E作,垂足为H,
在,米,,
∴米,
∵米,
∴米,
由(1)可知米,
∵米,米,
米,
在中,米,
米.
因此加装的前挡板的宽度的长是米.
【解析】【分析】(1)在直角三角形AMN中,斜边AM已知,sin75°条件也给出,因此利用正弦值进行计算即可求出MN的长度;
(2)AB的长度已知,AN可以利用余弦值来求出,此时BN的长度即可计算得出;结合(1)的结论MN的长度已知,BC为阴影部分的长度也已知,即可计算出CH的长度。利用正切值计算出EH的长度,ME的长度即可计算得出。
17.【答案】(1)解:如图,连接AB,过A点作AF⊥BC于F,
∵AD=AC=3米,CD=3.6米,
CF=DF=1.8米,
∴,
∵
∴,
∵,
∴,
∴,
∴,
∴,
∴AG的长为4米,
(2)过点G作GF⊥DC于点F,过点A作AH⊥CD于点H,则∠AHE=∠GFE=90°,如图所示:
∵CD=3.6米,DE:CE=5:1,
∴CE=0.6米,
∴EH=1.8-0.6=1.2米,
∴AE=米,
∵∠AEH=∠GEF,
∴△EAH∽△EGF,
∴,
∴,
解得:GF=,
∴点G上升的高度为()米,
【解析】【分析】(1)连接AB,过点A作AF⊥CB于点F,用勾股定理求出AF的长,证△AFB∽△CFA,根据对应线段成比例求出BF的长,再用勾股定理求解即可;
(2)过点G作GF⊥DC于点F,过点A作AH⊥CD于点H,则∠AHE=∠GFE=90°,先证出△EAH∽△EGF,可得,再将数据代入求出GF的长即可.
18.【答案】(1)解:如图1,过点作于,
∴,
∵,
∴,
∴点到墙面的距离为;
(2)解:如图2,延长光线交于点,延长交于点,
根据题意,可得,,
∴,
∴四边形是矩形,
∴,,
,,
,
∵,
∴,
∵,
∴,
在中,,
,
∴,
,
∴,
∴光线刚好不能照射到商户内,方案可行.
【解析】【分析】(1)过点作于,在中,解直角三角形求出的值即可;
(2)延长光线交于点,延长交于点,易证四边形是矩形,得,,利用勾股定理求得,从而得,进而得,在中,再根据,求出的长与比较大小即可得出结论.
19.【答案】(1)解:①∵二次函数的图象经过点和点,
∴,
解得:,
∴二次函数的表达式为;
②,
当时,,
当时,,
当时,,
∴当时,y随x增大而增大,当时,y随x增大而减小,
∴当时,;
(2)解:根据题意可知,对称轴为,
当x=0时,y=2,
∴图像经过点(0,2),
∵抛物线开口向下,
∴在对称轴左侧y随x增大而增大,在对称轴右侧y随x增大而减小,
∴点(0,2),(6,n)在对称轴左侧或两侧,
当点(0,2),(6,n)在对称轴左侧时,
∵点(p-4,m)在对称轴左侧, 且 ,
∴p-4>6,
即p>10;
当点(0,2),(6,n)在对称轴两侧时,
∴(p,m),(6,n)在右侧,(0,2)在左侧,
∴,
即5
②将表达式化为,再根据增减性即可得到答案;
(2)根据题意得到对称轴为,即图像过点(0,2),根据图象经过点,且,得到点(0,2),(6,n)在对称轴左侧或两侧,分别求出点与对称轴的距离即可得到答案.
20.【答案】(1)解:∵点在该二次函数的图象上,
∴将代入,
得:,
解得:或;
(2)解:∵,
∴二次函数的顶点坐标为,
∵该二次函数图象的顶点在轴上,
∴,
解得:,
∴该二次函数的解析式为;
(3)解:∵,其中二次项系数,对称轴为直线,
∴抛物线开口向上,抛物线上的点离对称轴距离越远其函数值越大,
又∵|-1-1|>|2-1|,
∴ 当时
∴当时函数取得最小值;
当时函数取得最大值;
∴,
即.
【解析】【分析】(1)根据二次函数图象上点的坐标特点,将代入,求解一元二次方程即可;
(2)先利用配方法将解析式配成顶点式,求出顶点坐标,由该抛物线顶点在x轴上可得顶点的纵坐标为零,据此建立方程求出c的值,从而即可得到抛物线的解析式;
(3)由二次项系数大于零,得抛物线开口向上,抛物线上的点离对称轴距离越远其函数值越大,据此结合x的取值范围,求出二次函数的最大值和最小值,再利用配方法判定即可.
(1)解:∵点在该二次函数的图象上,
∴将代入,
得:,
解得:或;
(2)解:∵,
∴二次函数的顶点坐标为,
∵该二次函数图象的顶点在轴上,
∴,
解得:,
∴该二次函数的解析式为;
(3)解:∵,
其中,对称轴为直线,
∴在时,随的增大而减小;在时,随的增大而增大;
∴当时函数取得最小值;
当时函数取得最大值;
∴,
即.
21.【答案】(1)解:∵ 二次函数的图象经过点,且对称轴为直线,
∴,解得,
∴该二次函数的解析式为.
(2)解:∵ 图象上的点称为函数的不动点,
∴,
解得:,,
∴这个函数不动点的坐标为和.
(3)解:∵,该抛物线的开口向上,对称轴为直线,,
∴当时,y有最小值,
当时,y有最大值5,
∴的最大值与最小值的差为.
【解析】【分析】(1)先根据点(4,-1)及对称轴,得到关于b,c的方程组求解,再代回解析式,求得函数表达式;
(2)将点代入解析式中,得到关于x的方程求解,求出不动点的坐标;
(3)先将解析式化为顶点式,再根据二次函数的性质求出最大值和最小值,进而求解即可.
(1)解:由题意,,解得,
∴该二次函数的解析式为;
(2)解:将代入中,得,
即,
解得,,
∴这个函数不动点的坐标为和;
(3)解:由(2)知,,
∵,该抛物线的开口向上,对称轴为直线,
∴当时,y有最小值,
当时,y有最大值5,
∴的最大值与最小值的差为.
22.【答案】(1)解:连接,
∵,
∴是直径.
∵是圆的切线,
∴.
∵的平分线交于,
∴,
∴,
∵,
∴;
(2)①证明:连接,
∵,是圆的直径,
∴,
∴,
∴,
∵
∴,
∴,
∴四边形是平行四边形;
②解:延长相较于点H,
∵,
∴,
∵,
∴.
∵,
∴.
∵是的中点,
∴.
∵,
∴,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
【解析】【分析】(1)连接CE,根据圆心角、弧、弦的关系可证明CE是直径,根据圆的切线垂直经过切点的半径得,由角平分线定义及三角形内角和定理求出,然后根据等弧所对的圆周角相等即可求解;
(2)①连接EF,由直径所对的圆周角是直角得,由同旁内角互补,两直线平行,可证,由二直线平行,内错角相等及等量代换可得,从而由同位角相等,两直线平行,可得,从而根据两组对边分别平行的四边形是平行四边形,可证四边形是平行四边形;
②延长BC、AD相交于H,由等角对等边得BE=CE,由等腰直角三角形性质求出,,由等弧所对的圆周角相等及平行线的性质可推出,由等角对等边得出,由有两组角对应相等的两个三角形相似得,由相似三角形对应边成比例得,代入数据即可求解.
(1)解:连接,
∵,
∴是直径.
∵是圆的切线,
∴.
∵的平分线交于,
∴,
∴,
∵,
∴
(2)①证明:连接,
∵,是圆的直径,
∴,
∴,
∴,
∵
∴,
∴,
∴四边形是平行四边形;
②解:延长相较于点H,
∵,
∴,
∵,
∴.
∵,
∴.
∵是的中点,
∴.
∵,
∴,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
23.【答案】(1)解:如图,连接,
,
,
,
∵,
∴,
,
故答案为:90°;
(2)①证明:如图,连接,
,
,
,
,
,
,
,
,
,
,
,
∵,
∴,
,
,
;
②如图,连接,连接并延长交于点,
∵,
∴,
,
,
∴,
,
∴,
∵,
∴,
,
,
,
,
,
,
,
,
,
设,则,
在中,,
,
,
在中,,
;
③如图,过点作交于点,
,
,
,
,
∵,
∴,
,
∴,
,
,
,
∴,
在和中,
,
,
,
同②可得,,
∵,
∴,
在和中,
,
,
,
∴,
在和中,
,
∴,
∴,,
∴,
设,
∵,
∴,
∵,
在和中,,
解得:,
,
,
,
,
,
,
,
.
【解析】【分析】(1)连接,根据圆周角定理、等腰三角形”等边对等角“的性质得,,然后由三角形内角和定理得,可推导出;
(2)①连接,根据平行线的性质得,根据圆周角定理、等腰三角形”等边对等角“的性质得,,然后由三角形内角和定理得,可得,接下来证出,进行等量代换可推导出;
②连接,连接并延长交于点,根据垂径定理的推论得,结合圆周角定理得,从而得,根据等腰三角形”等边对等角“性质得,即可证明,可推导出,设,则,利用勾股定理、三角形面积公式求出,,,即可得;
③过点作交于点,先证明,可得,再证明,得,从而得,进而证明,得,,则,设,,在和中,利用勾股定理得方程组,解方程即可求出,再求,可得,根据,最后求得,即可求.
24.【答案】解:(1)∵为的直径,
∴,
∵,
∴,
∴.
(2)∵为的直径,
∴,
∴,
∴,
∵,
∴.
又∵,
在△CFE和△BDG中
∴,
∴.
(3)①如图,连接.
∵为的直径,
∴.
在中,,,
∴.
∵,
∴,
即,
∴.
∵,
∴.
∵在中,,
∴,
∴.
∵在中,,
∴.
在中,,
∴,
∴的周长为.
②如图,过点C作于H.
∵,
∴.
∵,
在△CFE和△BDG中
∴.
∴,
∵,
∴.
∵,
∴.
∵,
∴,
∵,
∴,
∴.
设,
∴,
∴.
在中, ,
∴,
当时,的最小值为3,
∴的最小值为.
【解析】【分析】(1)利用圆周角定理求得,再根据,求得,即可得到答案;
(2)由,得到,由同角的补角相等可得,结合已知用角边角可证,再根据全等三角形的对应边相等可求解;
(3)①连接.利用已知求出,证得,得到,在中,根据锐角三角函数sin∠AGB=求出∠AGB的度数,由30度角所对的直角边等于斜边的一半求出AG的长,由线段的和差EF=DG=AD-AG求出EF的长,在中,,由30度角所对的直角边等于斜边的一半求出EG及DE,在Rt△FED中,用勾股定理求出DF的长,然后三角形FGD的周长可求解;
②过点C作于H,由题意,用角角边可证,由全等三角形的对应边相等可得,再根据有两个角对应相等的两个三角形相似可得,于是可得比例式,设,整理得,用勾股定理得到 ,求得,然后根据函数的性质即可求解.
21世纪教育网(www.21cnjy.com)
同课章节目录
