20.2数据的集中趋势同步练习(含解析)
文档属性
| 名称 | 20.2数据的集中趋势同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 556.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 10:01:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
20.2数据的集中趋势
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小红在“养成阅读习惯,快乐阅读,健康成长”读书大赛活动中,随机调查了本校初二年级20名同学,在近5个月内每人阅读课外书的数量,数据如下表所示:
人数 3 4 8 5
课外书数量(本) 12 13 15 18
则阅读课外书数量的中位数和众数分别是( )
A.13,15 B.14,15 C.13,18 D.15,15
2.某品牌专营店店主对上一周新进的某款衬衫销售情况统计如下:
尺码 39 40 41 42 43 44 45
平均每天销售数量/件 10 23 30 35 28 21 8
该店主决定本周进货时,增加一些42码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.中位数 C.众数 D.加权平均数
3.一组数据,,,,的平均数和众数分别是( )
A., B., C., D.,
4.数据 0,1,1,3,3,4 的中位数和平均数分别是( )
A.2和2.4 B.2和2 C.1和2 D.3和2
5.某校篮球队五名主力队员的身高分别是174,179,180,174,178(单位:cm),则这五名队员身高的中位数是( )
A.174cm B.177cm C.178cm D.180cm
6.在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,50,55,这组数据的众数和中位数分别是( ).
A.50元,30元 B.50元,40元
C.50元,50元 D.55元,50元
7.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,甲组12户家庭用水量统计表
用水量(吨) 4 5 6 9
户数 4 5 2 1
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A.甲组比乙组大 B.甲、乙两组相同
C.乙组比甲组大 D.无法判断
8.某校在“绿色是生命的源泉,绿色是生命的希望”的主题创建活动中,组织全校学生开展了植树造林活动,该校八年级7个班同学种植树苗棵数依次为:77,80,79,77,80,79,80.这组数据的中位数是( )
A.77 B.79 C.79.5 D.80
9.某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天用水量的中位数是( )
A.30吨 B.36吨 C.32吨 D.34吨
10.在某校“人工智能与人类未来”的演讲比赛中,前6名同学的成绩(分)依次为:98、96、96、96、95、93,这组数据的众数、中位数依次为( )
A.98、93 B.96、96 C.96、95 D.95,96
11.下表为某校八年级72位女生在规定时间内的立定投篮数统计,
投进的个数 5 6 7 8 9 10 11 12 13 14 15
人数 3 7 6 10 11 8 13 7 1 4 2
若投篮投进个数的中位数为,众数为,则的值为( )
A.20 B.21 C.22 D.23
12.某班在开展劳动教育课程调查中发现,第一小组6名同学每周做家务的天数依次为3,7,5,6,5,4(单位:天),则这组数据的众数和中位数分别为( )
A.5和5 B.5和4 C.5和6 D.6和5
二、填空题
13.给定一组数据,那么描述这组数据的中位数一定只有一个.( )
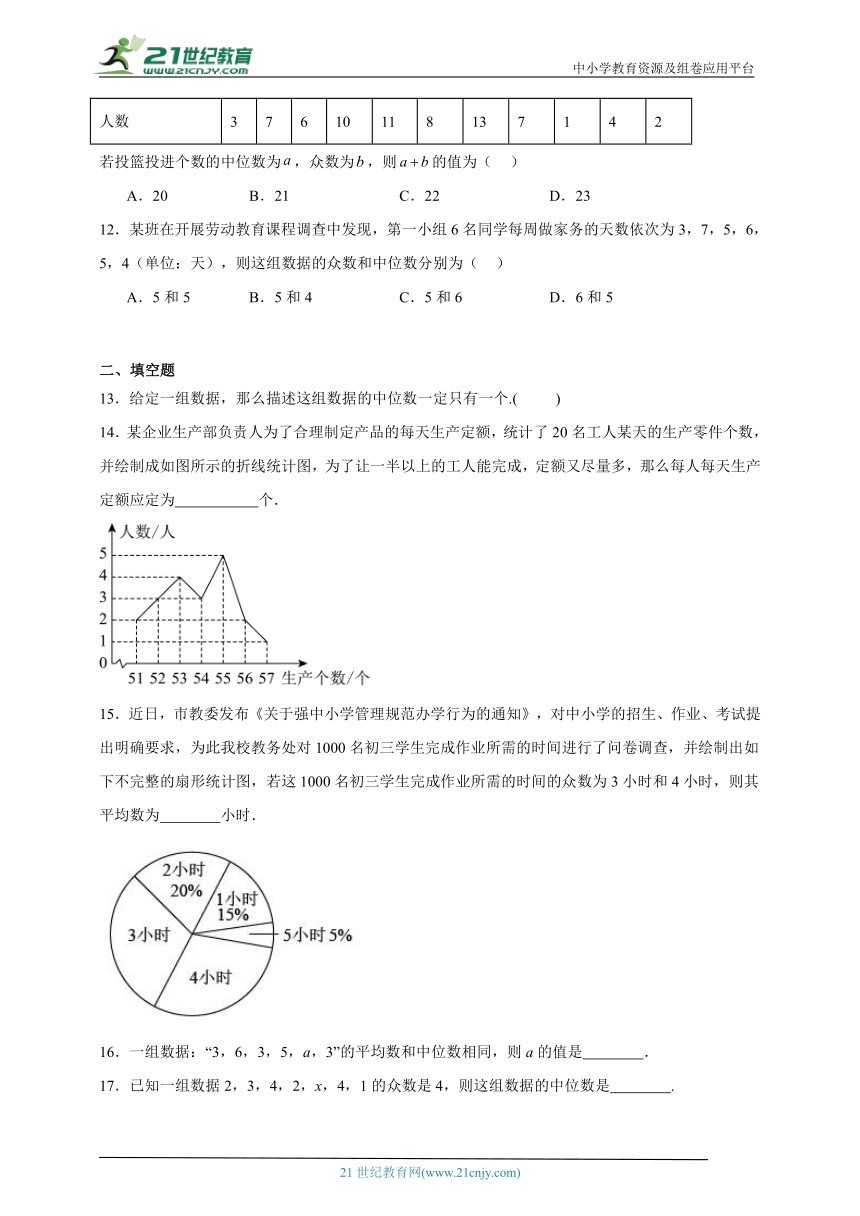
14.某企业生产部负责人为了合理制定产品的每天生产定额,统计了20名工人某天的生产零件个数,并绘制成如图所示的折线统计图,为了让一半以上的工人能完成,定额又尽量多,那么每人每天生产定额应定为 个.
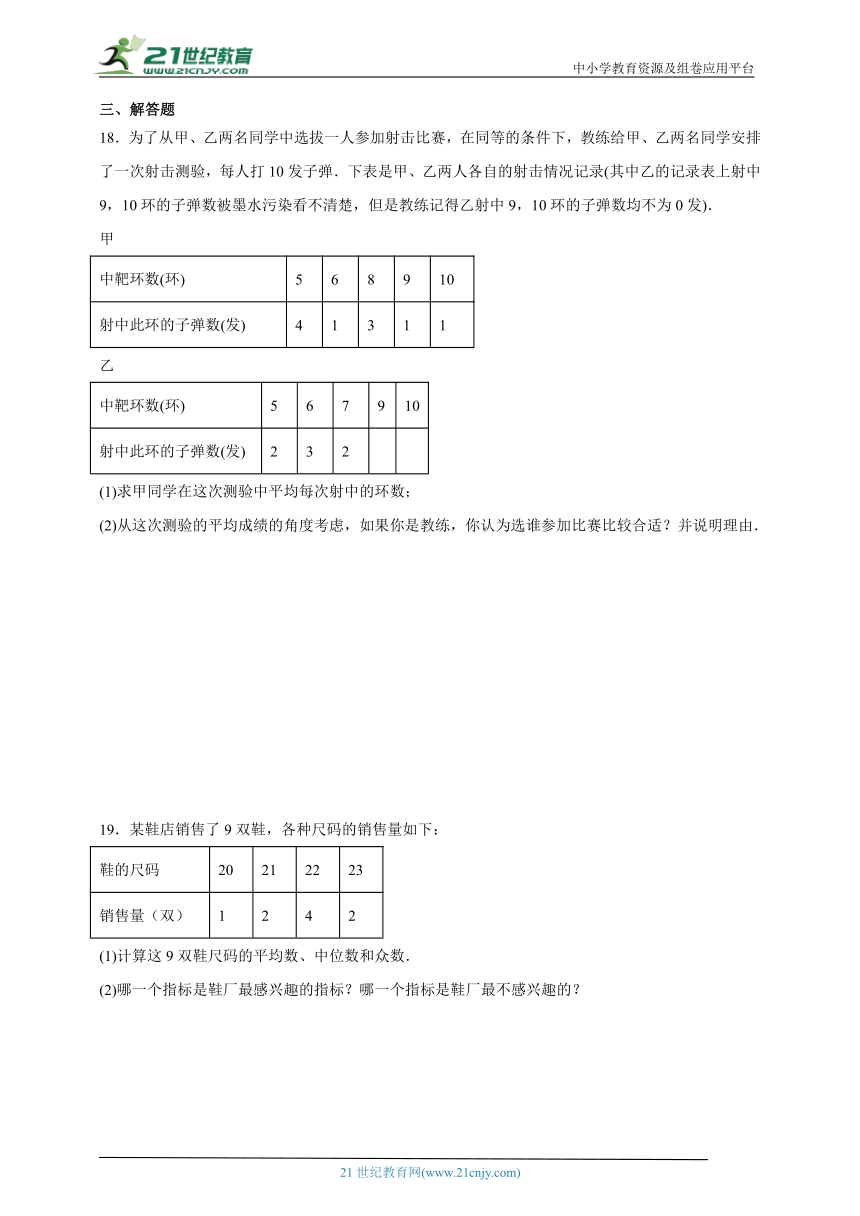
15.近日,市教委发布《关于强中小学管理规范办学行为的通知》,对中小学的招生、作业、考试提出明确要求,为此我校教务处对1000名初三学生完成作业所需的时间进行了问卷调查,并绘制出如下不完整的扇形统计图,若这1000名初三学生完成作业所需的时间的众数为3小时和4小时,则其平均数为 小时.
16.一组数据:“3,6,3,5,a,3”的平均数和中位数相同,则a的值是 .
17.已知一组数据2,3,4,2,x,4,1的众数是4,则这组数据的中位数是 .
三、解答题
18.为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹.下表是甲、乙两人各自的射击情况记录(其中乙的记录表上射中9,10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发).
甲
中靶环数(环) 5 6 8 9 10
射中此环的子弹数(发) 4 1 3 1 1
乙
中靶环数(环) 5 6 7 9 10
射中此环的子弹数(发) 2 3 2
(1)求甲同学在这次测验中平均每次射中的环数;
(2)从这次测验的平均成绩的角度考虑,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.
19.某鞋店销售了9双鞋,各种尺码的销售量如下:
鞋的尺码 20 21 22 23
销售量(双) 1 2 4 2
(1)计算这9双鞋尺码的平均数、中位数和众数.
(2)哪一个指标是鞋厂最感兴趣的指标?哪一个指标是鞋厂最不感兴趣的?
20.男子马拉松长跑比赛中,抽得12名选手所用的时间(单位:)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是,他的成绩如何?
21.某公司10名销售员,去年完成的销售额情况如下表:
销售额/万元 3 4 5 6 7 8 10
销售员人数/人 1 3 2 1 1 1 1
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元.
22.为了了解八年级学生的课外阅读情况,学校随机调查了该年级25名学生,得到他们上周双休日课外阅读时间(记为t,单位:时)的一组样本数据,其扇形统计图如图所示.
(1)阅读时间为4小时的占百分之几?
(2)试确定这个样本的中位数和众数,并求出平均数.
23.某鞋厂为了了解初中学生穿鞋的尺码情况,对某中学八年级(1)班的20名男生进行了调查,结果如图所示.
(1)写出这20个数据的平均数、中位数、众数;
(2)在平均数、中位数和众数中,鞋厂最感兴趣的是哪一个?
24.荆州古城是闻名遐迩的历史文化名城,下表是荆州古城某历史景点一周的抽样统计参观人数,如图是门票价格统计.
星期 一 二 三 四 五 六 日
人数
(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数,众数和平均数,分析表中数据还可得到一些信息,如双休日参观人数远远高于平时等,尝试再写出两条相关信息.
(2)若“五一”黄金周有甲、乙两旅行团到该景点参观,两团人数之和恰为上述样本数 据的中位数,乙团不超过人,设两团分别购票共付元,甲团人数人.
①求与的函数关系式;
②若甲团人数不超过人,说明两团合起来购票比分开购票最多可节约多少元?
《20.2数据的集中趋势》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B B C C B B C B
题号 11 12
答案 A A
1.D
【分析】利用中位数,众数的定义即可解决问题.
【详解】解:中位数为第10个和第11个的平均数,众数为15.
故选:D.
【点睛】本题考查了中位数和众数,解题的关键是掌握平均数、中位数和众数的概念.
2.C
【分析】销量大的尺码就是这组数据的众数.
【详解】解:由于众数是数据中出现次数最多的数,故影响该店主决策的统计量是众数.
故选:C.
【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
3.B
【分析】本题考查了众数和平均数的知识,一组数据中出现次数最多的数据叫做众数;平均数是指在一组数据中所有数据之和再除以数据的个数.根据众数和平均数的概念求解.
【详解】解:平均数为:,
∵1出现的次数最多,
∴众数为1.
故选:B.
4.B
【详解】试题分析:中位数是一组数据从小到大(或从大到小)排列后,最中间的那个数(最中间两个数的平均数).因此这组数据的中位数是第3,4个数的平均数:.
平均数是指在一组数据中所有数据之和再除以数据的个数.因此这组数据的平均数是:.
故选B.
5.C
【分析】中位数是指将一组数据按大小顺序排列后,处在最中间的一个数(或处在最中间的两个数的平均数).
【详解】数据从小到大的顺序排列为174,174,178,179,180,
∴这组数据的中位数是178.
故选:C.
6.C
【详解】50出现了3次,出现的次数最多,
则众数是50;
把这组数据从小到大排列为:20,25,30,50,50,50,55,
最中间的数是50,
则中位数是50.
故选C.
7.B
【详解】试题分析:将两组数据按从小到大的顺序排列为,甲:4,4,4,4,5,5,5,5,5,6,6,9;乙:4,4,4,5,5,5,5,6,6,6,2,2,所以甲组的中位数是(5+5)÷2=5,乙组的中位数是(5+5)÷2=5,甲乙两组的中位数相同,故答案选B.
考点:中位数,扇形统计图.
8.B
【分析】本题考查了中位数.根据按大小排列的数组中间的一个数据或中间两个数据的平均数是中位数计算即可.
【详解】解:将这组数据从小到大排列为:77,77,79,79,80,80,80,
中间数据是79,
故中位数是79.
故选:B.
9.C
【分析】将1日至5日每天用水量按照从小到大打的顺序排列一下,即可得出中位数.
【详解】由图可知:六月份1日至5日每天用水量为:30吨,32吨,36吨,28吨,34吨.
由小到大排列为:28吨,30吨,32吨,34吨,36吨.
这5天用水量的中位数是:32吨.
故答案为C.
【点睛】本题考查了中位数,熟练掌握中位数的概念是解题的关键.
10.B
【分析】本题考查中位数,众数的定义,掌握相关定义是解题的关键.根据众数,中位数的定义求解.
【详解】解:将各数从大到小排列后得:98、96、96、96、95、93,其中96出现次数最多,众数为96,处于中间的两个数为96、96,中位数为.
故选:B.
11.A
【分析】根据中位数与众数的求法,分别求出投中个数的中位数与众数再相加即可解答.
【详解】第36 与37人投中的个数均为9,故中位数a=9,
11出现了13次,次数最多,故众数b=11,
所以a+b=9+11=20.
故选A.
【点睛】本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
12.A
【解析】略
13.∨
【分析】根据中位数的定义进行判断即可解答.
【详解】给定一组数据,则这组数据的中位数一定只有一个,故正确.
故答案为√.
【点睛】本题属于基础题,考查了确定一组数据的中位数的能力.注意找中位数的时候一定要先排好顺序,然后再根据数据个数来确定中位数,如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两个数的平均数.
14.
【分析】本题考查的是从折线统计图中获取信息,理解折线图的含义是解本题的关键.
【详解】解:由折线图得,第10,11个数据个,个,
∴中位数为,
而完成个(含个)以上的人数有(个)
∴每人每天生产定额应定为54个.因为这个数值,一半以上的工人能完成.
故答案为:54.
15.2.9
【分析】结合题意,根据扇形统计图、众数的性质计算得学生完成作业所需的时间为3小时和4小时的百分比,再根据平均数的定义即可解决问题.
【详解】学生完成作业所需的时间的众数为3小时和4小时,
学生完成作业所需的时间为3小时和4小时的百分比,
名初三学生完成作业所需的时间的平均数(小时),
故答案为:2.9.
【点睛】本题考查了众数、平均数的知识;解题的关键是熟练掌握众数、平均数的性质,从而完成求解.
16.
【分析】根据一组数据“3,6,3,5,a,3”的平均数和中位数相同和分类讨论的方法,可以求得a的值.
【详解】解:∵一组数据:“3,6,3,5,a,3”的平均数和中位数相同,
∴当时,
,
解得;
当时,
,
解得(不合题意,舍去);
当时,
,
解得(不合题意,舍去);
故答案为:.
【点睛】本题考查中位数、算术平均数,解答本题的关键是明确题意,求出a的值.
17.3
【详解】试题解析:根据题意由有唯一的众数4,可知x=4,
将数据从小到大排列为:1,2,2,3,4,4,4,
则中位数为:3.
18.(1)6.9环;(2)选乙同学参加比赛比较合适.理由见解析.
【分析】第(1)问中直接根据平均数的求法,算出结果即
第(2)问中由于数字模糊,可分情况讨论乙的平均数,再与甲进行比较即可
【详解】(1)甲同学在这次测验中平均每次射中的环数是(环).
(2)选乙同学参加比赛比较合适.理由:①若乙同学射中9环的子弹数为1发,则射中10环的子弹数为2发.乙同学在这次测验中平均每次射中的环数是(环).
因为,故在这次测验中乙同学的成绩比甲同学的成绩好,这时应选择乙同学参加射击比赛;
②若乙同学射中9环的子弹数为2发,则射中10环的子弹数为1发.乙同学在这次测验中平均每次射中的环数是(环).
因为,故在这次测验中乙同学的成绩比甲同学的成绩好,这时应选择乙同学参加射击比赛.综上所述,选择乙同学参加射击比赛比较合适.
【点睛】本题主要考查平均数的计算,掌握平均数的计算方法是关键;
19.(1)平均数21.8,中位数22,众数22
(2)众数,平均数
【分析】本题主要考查众数,加权平均数及中位数,解题的关键是掌握众数、加权平均数及中位数的定义.
(1)分别根据加权平均数、中位数和众数的概念求解可得;
(2)众数是数量最大的,也是销量最多的,所以鞋厂对众数最感兴趣;平均数不是整数,不会生产这种鞋号的鞋子,所以鞋厂对平均数最不感兴趣.
【详解】(1)解:平均数为,
共9个数,第五个数是22,故中位数是22,
22出现了4次,出现的次数最多,故众数是22;
(2)鞋厂最感兴趣的指标是众数,因为它表明工厂应该生产最多这一鞋号的鞋;
鞋厂最不感兴趣的指标是平均数,因为平均数不是整数,不会生产这种鞋号的鞋子.
20.(1)样本数据的中位数是147;(2)推测他的成绩比一半以上选手的成绩好.
【分析】(1)根据中位数的定义直接求解即可;
(2)根据这名选手的成绩与中位数相比较即可判断.
【详解】(1)先将样本数据按照由小到大的顺序排列:
124 129 136 140 145 146
148 154 158 165 175 180
这组数据的中位数为处于中间的两个数146,148的平均数,即.
因此样本数据的中位数是147.
(2)根据(1)中得到的样本数据的中位数,可以估计,在这次马拉松比赛中,大约有一半选手的成绩快于,有一半选手的成绩慢于.这名选手的成绩是,快于中位数,可以推测他的成绩比一半以上选手的成绩好.
【点睛】本题考查了中位数的定义:把一组数据按从小到大(或从大到小)排列,最中间那个数(或最中间两个数的平均数)叫这组数据的中位数.
21.(1)平均数为5.6万元;众数是4万元;中位数是5万元;(2)把5万元定为标准比较合理,理由见解析
【分析】(1)根据平均数公式求得平均数,根据次数出现最多的数确定众数,按从小到大顺序排列好后求得中位数.
(2)根据平均数,中位数,众数的意义回答.
【详解】解:(1)平均数为:(万元);
出现次数最多的是4万元,所以众数是4万元;
将这10个数据按从小到大的顺序排列后,第5、6个数据都是5万元,所以中位数是5万元;
(2)若规定平均数5.6万元为标准,则多数人无法或不可能超额完成,会挫伤员工的积极性;若规定众数4万元为标准,则大多数人不必努力就可以超额完成,不利于提高年销售额;若规定中位数5万元为标准,则大多数人能完成或超额完成,少数人经过努力也能完成因此把5万元定为标准比较合理.
【点睛】本题为众数,中位数,平均数的意义.解题的关键是根据众数,中位数,平均数的意义求出答案.
22.(1)28%;(2)中位数是3小时,众数是4小时,平均数是3.36小时
【分析】(1)各个部分所占百分比的和为1,即可求出t=4小时所占的百分比;
(2)根据中位数、众数、平均数的计算方法分别进行计算即可.
【详解】解:(1)1-12%-16%-24%-12%-8%=28%,
答:阅读时间为4小时的占28%;
(2)阅读时间出现最多的是4小时,占28%,因此阅读时间的众数是4小时,
从小到大排列,所占百分比处在50%的阅读时间是3小时,因此阅读时间的中位数是3小时,
=(1×12%+2×16%+3×24%+4×28%+5×12%+6×8%)=3.36(时),
答:学生上周双休日课外阅读时间的众数是4小时,中位数是3小时,平均数是3.36小时.
【点睛】本题考查中位数、众数、平均数的意义和计算方法,掌握扇形统计图的各个部分所占百分比的和为1是前提,理解加权平均数的意义是正确计算的关键.
23.(1)平均数为39.1码,中位数为39码,众数为40码;(2)鞋厂最感兴趣的是众数
【分析】(1)根据平均数、众数与中位数的定义求解分析.40出现的次数最多为众数,第10、11个数的平均数为中位数.
(2)鞋厂最感兴趣的是使用的人数,即众数.
【详解】解:(1)平均数=(37×3+38×4+39×4+40×7+41×1+42×1)÷20=39.1.
观察图表可知:有7人的鞋号为40,人数最多,即众数是40;
中位数是第10、11人的平均数,(39+39)÷2=39,
故答案为:平均数为39.1码,中位数为39码,众数为40码;
(2)鞋厂最感兴趣的是使用的人数,即众数,
故答案为:鞋厂最感兴趣的是众数.
【点睛】本题考查平均数,众数与中位数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.众数是数据中出现最多的一个数.正确理解中位数、众数及平均数的概念,是解决本题的关键.
24.(1)这个样本的中位数是,众数是,平均数是.相关信息:①双休日参观人数为平时的倍左右.②参观人数自周五开始明显上升等均可
(2)①且为正整数;且为正整数;②元
【分析】本题主要考查了算术平均数,中位数,众数;一次函数的应用.
(1)利用众数就是出现次数最多的数,中位数就是大小处于中间位置的数,以及平均数的公式即可求出答案;
(2)根据(1)可知,两团人数之和是人,所有①与的函数关系式是,②求出团购需付的钱数,即可求出答案
【详解】(1)解:这个样本的中位数是,众数是,平均数是.
相关信息:①双休日参观人数为平时的倍左右.②参观人数自周五开始明显上升等均可.
(2)①当甲团人数为人时,乙团人数为人,且为正整数;
由题意:,得.
若,则两团购票的总费用;
若,则两团购票的总费用.
②两团合起购票的花费为元元.
由①知当时,设节省元,
两团合起购票比分开购票可节省,
当时,元.
当时,两团合起购票比分开购票可节省,
故当时,元.
综上所述,两团合起来购票比分开购票最多省元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
20.2数据的集中趋势
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小红在“养成阅读习惯,快乐阅读,健康成长”读书大赛活动中,随机调查了本校初二年级20名同学,在近5个月内每人阅读课外书的数量,数据如下表所示:
人数 3 4 8 5
课外书数量(本) 12 13 15 18
则阅读课外书数量的中位数和众数分别是( )
A.13,15 B.14,15 C.13,18 D.15,15
2.某品牌专营店店主对上一周新进的某款衬衫销售情况统计如下:
尺码 39 40 41 42 43 44 45
平均每天销售数量/件 10 23 30 35 28 21 8
该店主决定本周进货时,增加一些42码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.中位数 C.众数 D.加权平均数
3.一组数据,,,,的平均数和众数分别是( )
A., B., C., D.,
4.数据 0,1,1,3,3,4 的中位数和平均数分别是( )
A.2和2.4 B.2和2 C.1和2 D.3和2
5.某校篮球队五名主力队员的身高分别是174,179,180,174,178(单位:cm),则这五名队员身高的中位数是( )
A.174cm B.177cm C.178cm D.180cm
6.在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,50,55,这组数据的众数和中位数分别是( ).
A.50元,30元 B.50元,40元
C.50元,50元 D.55元,50元
7.甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,甲组12户家庭用水量统计表
用水量(吨) 4 5 6 9
户数 4 5 2 1
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A.甲组比乙组大 B.甲、乙两组相同
C.乙组比甲组大 D.无法判断
8.某校在“绿色是生命的源泉,绿色是生命的希望”的主题创建活动中,组织全校学生开展了植树造林活动,该校八年级7个班同学种植树苗棵数依次为:77,80,79,77,80,79,80.这组数据的中位数是( )
A.77 B.79 C.79.5 D.80
9.某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天用水量的中位数是( )
A.30吨 B.36吨 C.32吨 D.34吨
10.在某校“人工智能与人类未来”的演讲比赛中,前6名同学的成绩(分)依次为:98、96、96、96、95、93,这组数据的众数、中位数依次为( )
A.98、93 B.96、96 C.96、95 D.95,96
11.下表为某校八年级72位女生在规定时间内的立定投篮数统计,
投进的个数 5 6 7 8 9 10 11 12 13 14 15
人数 3 7 6 10 11 8 13 7 1 4 2
若投篮投进个数的中位数为,众数为,则的值为( )
A.20 B.21 C.22 D.23
12.某班在开展劳动教育课程调查中发现,第一小组6名同学每周做家务的天数依次为3,7,5,6,5,4(单位:天),则这组数据的众数和中位数分别为( )
A.5和5 B.5和4 C.5和6 D.6和5
二、填空题
13.给定一组数据,那么描述这组数据的中位数一定只有一个.( )
14.某企业生产部负责人为了合理制定产品的每天生产定额,统计了20名工人某天的生产零件个数,并绘制成如图所示的折线统计图,为了让一半以上的工人能完成,定额又尽量多,那么每人每天生产定额应定为 个.
15.近日,市教委发布《关于强中小学管理规范办学行为的通知》,对中小学的招生、作业、考试提出明确要求,为此我校教务处对1000名初三学生完成作业所需的时间进行了问卷调查,并绘制出如下不完整的扇形统计图,若这1000名初三学生完成作业所需的时间的众数为3小时和4小时,则其平均数为 小时.
16.一组数据:“3,6,3,5,a,3”的平均数和中位数相同,则a的值是 .
17.已知一组数据2,3,4,2,x,4,1的众数是4,则这组数据的中位数是 .
三、解答题
18.为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹.下表是甲、乙两人各自的射击情况记录(其中乙的记录表上射中9,10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发).
甲
中靶环数(环) 5 6 8 9 10
射中此环的子弹数(发) 4 1 3 1 1
乙
中靶环数(环) 5 6 7 9 10
射中此环的子弹数(发) 2 3 2
(1)求甲同学在这次测验中平均每次射中的环数;
(2)从这次测验的平均成绩的角度考虑,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.
19.某鞋店销售了9双鞋,各种尺码的销售量如下:
鞋的尺码 20 21 22 23
销售量(双) 1 2 4 2
(1)计算这9双鞋尺码的平均数、中位数和众数.
(2)哪一个指标是鞋厂最感兴趣的指标?哪一个指标是鞋厂最不感兴趣的?
20.男子马拉松长跑比赛中,抽得12名选手所用的时间(单位:)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是,他的成绩如何?
21.某公司10名销售员,去年完成的销售额情况如下表:
销售额/万元 3 4 5 6 7 8 10
销售员人数/人 1 3 2 1 1 1 1
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元.
22.为了了解八年级学生的课外阅读情况,学校随机调查了该年级25名学生,得到他们上周双休日课外阅读时间(记为t,单位:时)的一组样本数据,其扇形统计图如图所示.
(1)阅读时间为4小时的占百分之几?
(2)试确定这个样本的中位数和众数,并求出平均数.
23.某鞋厂为了了解初中学生穿鞋的尺码情况,对某中学八年级(1)班的20名男生进行了调查,结果如图所示.
(1)写出这20个数据的平均数、中位数、众数;
(2)在平均数、中位数和众数中,鞋厂最感兴趣的是哪一个?
24.荆州古城是闻名遐迩的历史文化名城,下表是荆州古城某历史景点一周的抽样统计参观人数,如图是门票价格统计.
星期 一 二 三 四 五 六 日
人数
(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数,众数和平均数,分析表中数据还可得到一些信息,如双休日参观人数远远高于平时等,尝试再写出两条相关信息.
(2)若“五一”黄金周有甲、乙两旅行团到该景点参观,两团人数之和恰为上述样本数 据的中位数,乙团不超过人,设两团分别购票共付元,甲团人数人.
①求与的函数关系式;
②若甲团人数不超过人,说明两团合起来购票比分开购票最多可节约多少元?
《20.2数据的集中趋势》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B B C C B B C B
题号 11 12
答案 A A
1.D
【分析】利用中位数,众数的定义即可解决问题.
【详解】解:中位数为第10个和第11个的平均数,众数为15.
故选:D.
【点睛】本题考查了中位数和众数,解题的关键是掌握平均数、中位数和众数的概念.
2.C
【分析】销量大的尺码就是这组数据的众数.
【详解】解:由于众数是数据中出现次数最多的数,故影响该店主决策的统计量是众数.
故选:C.
【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
3.B
【分析】本题考查了众数和平均数的知识,一组数据中出现次数最多的数据叫做众数;平均数是指在一组数据中所有数据之和再除以数据的个数.根据众数和平均数的概念求解.
【详解】解:平均数为:,
∵1出现的次数最多,
∴众数为1.
故选:B.
4.B
【详解】试题分析:中位数是一组数据从小到大(或从大到小)排列后,最中间的那个数(最中间两个数的平均数).因此这组数据的中位数是第3,4个数的平均数:.
平均数是指在一组数据中所有数据之和再除以数据的个数.因此这组数据的平均数是:.
故选B.
5.C
【分析】中位数是指将一组数据按大小顺序排列后,处在最中间的一个数(或处在最中间的两个数的平均数).
【详解】数据从小到大的顺序排列为174,174,178,179,180,
∴这组数据的中位数是178.
故选:C.
6.C
【详解】50出现了3次,出现的次数最多,
则众数是50;
把这组数据从小到大排列为:20,25,30,50,50,50,55,
最中间的数是50,
则中位数是50.
故选C.
7.B
【详解】试题分析:将两组数据按从小到大的顺序排列为,甲:4,4,4,4,5,5,5,5,5,6,6,9;乙:4,4,4,5,5,5,5,6,6,6,2,2,所以甲组的中位数是(5+5)÷2=5,乙组的中位数是(5+5)÷2=5,甲乙两组的中位数相同,故答案选B.
考点:中位数,扇形统计图.
8.B
【分析】本题考查了中位数.根据按大小排列的数组中间的一个数据或中间两个数据的平均数是中位数计算即可.
【详解】解:将这组数据从小到大排列为:77,77,79,79,80,80,80,
中间数据是79,
故中位数是79.
故选:B.
9.C
【分析】将1日至5日每天用水量按照从小到大打的顺序排列一下,即可得出中位数.
【详解】由图可知:六月份1日至5日每天用水量为:30吨,32吨,36吨,28吨,34吨.
由小到大排列为:28吨,30吨,32吨,34吨,36吨.
这5天用水量的中位数是:32吨.
故答案为C.
【点睛】本题考查了中位数,熟练掌握中位数的概念是解题的关键.
10.B
【分析】本题考查中位数,众数的定义,掌握相关定义是解题的关键.根据众数,中位数的定义求解.
【详解】解:将各数从大到小排列后得:98、96、96、96、95、93,其中96出现次数最多,众数为96,处于中间的两个数为96、96,中位数为.
故选:B.
11.A
【分析】根据中位数与众数的求法,分别求出投中个数的中位数与众数再相加即可解答.
【详解】第36 与37人投中的个数均为9,故中位数a=9,
11出现了13次,次数最多,故众数b=11,
所以a+b=9+11=20.
故选A.
【点睛】本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
12.A
【解析】略
13.∨
【分析】根据中位数的定义进行判断即可解答.
【详解】给定一组数据,则这组数据的中位数一定只有一个,故正确.
故答案为√.
【点睛】本题属于基础题,考查了确定一组数据的中位数的能力.注意找中位数的时候一定要先排好顺序,然后再根据数据个数来确定中位数,如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两个数的平均数.
14.
【分析】本题考查的是从折线统计图中获取信息,理解折线图的含义是解本题的关键.
【详解】解:由折线图得,第10,11个数据个,个,
∴中位数为,
而完成个(含个)以上的人数有(个)
∴每人每天生产定额应定为54个.因为这个数值,一半以上的工人能完成.
故答案为:54.
15.2.9
【分析】结合题意,根据扇形统计图、众数的性质计算得学生完成作业所需的时间为3小时和4小时的百分比,再根据平均数的定义即可解决问题.
【详解】学生完成作业所需的时间的众数为3小时和4小时,
学生完成作业所需的时间为3小时和4小时的百分比,
名初三学生完成作业所需的时间的平均数(小时),
故答案为:2.9.
【点睛】本题考查了众数、平均数的知识;解题的关键是熟练掌握众数、平均数的性质,从而完成求解.
16.
【分析】根据一组数据“3,6,3,5,a,3”的平均数和中位数相同和分类讨论的方法,可以求得a的值.
【详解】解:∵一组数据:“3,6,3,5,a,3”的平均数和中位数相同,
∴当时,
,
解得;
当时,
,
解得(不合题意,舍去);
当时,
,
解得(不合题意,舍去);
故答案为:.
【点睛】本题考查中位数、算术平均数,解答本题的关键是明确题意,求出a的值.
17.3
【详解】试题解析:根据题意由有唯一的众数4,可知x=4,
将数据从小到大排列为:1,2,2,3,4,4,4,
则中位数为:3.
18.(1)6.9环;(2)选乙同学参加比赛比较合适.理由见解析.
【分析】第(1)问中直接根据平均数的求法,算出结果即
第(2)问中由于数字模糊,可分情况讨论乙的平均数,再与甲进行比较即可
【详解】(1)甲同学在这次测验中平均每次射中的环数是(环).
(2)选乙同学参加比赛比较合适.理由:①若乙同学射中9环的子弹数为1发,则射中10环的子弹数为2发.乙同学在这次测验中平均每次射中的环数是(环).
因为,故在这次测验中乙同学的成绩比甲同学的成绩好,这时应选择乙同学参加射击比赛;
②若乙同学射中9环的子弹数为2发,则射中10环的子弹数为1发.乙同学在这次测验中平均每次射中的环数是(环).
因为,故在这次测验中乙同学的成绩比甲同学的成绩好,这时应选择乙同学参加射击比赛.综上所述,选择乙同学参加射击比赛比较合适.
【点睛】本题主要考查平均数的计算,掌握平均数的计算方法是关键;
19.(1)平均数21.8,中位数22,众数22
(2)众数,平均数
【分析】本题主要考查众数,加权平均数及中位数,解题的关键是掌握众数、加权平均数及中位数的定义.
(1)分别根据加权平均数、中位数和众数的概念求解可得;
(2)众数是数量最大的,也是销量最多的,所以鞋厂对众数最感兴趣;平均数不是整数,不会生产这种鞋号的鞋子,所以鞋厂对平均数最不感兴趣.
【详解】(1)解:平均数为,
共9个数,第五个数是22,故中位数是22,
22出现了4次,出现的次数最多,故众数是22;
(2)鞋厂最感兴趣的指标是众数,因为它表明工厂应该生产最多这一鞋号的鞋;
鞋厂最不感兴趣的指标是平均数,因为平均数不是整数,不会生产这种鞋号的鞋子.
20.(1)样本数据的中位数是147;(2)推测他的成绩比一半以上选手的成绩好.
【分析】(1)根据中位数的定义直接求解即可;
(2)根据这名选手的成绩与中位数相比较即可判断.
【详解】(1)先将样本数据按照由小到大的顺序排列:
124 129 136 140 145 146
148 154 158 165 175 180
这组数据的中位数为处于中间的两个数146,148的平均数,即.
因此样本数据的中位数是147.
(2)根据(1)中得到的样本数据的中位数,可以估计,在这次马拉松比赛中,大约有一半选手的成绩快于,有一半选手的成绩慢于.这名选手的成绩是,快于中位数,可以推测他的成绩比一半以上选手的成绩好.
【点睛】本题考查了中位数的定义:把一组数据按从小到大(或从大到小)排列,最中间那个数(或最中间两个数的平均数)叫这组数据的中位数.
21.(1)平均数为5.6万元;众数是4万元;中位数是5万元;(2)把5万元定为标准比较合理,理由见解析
【分析】(1)根据平均数公式求得平均数,根据次数出现最多的数确定众数,按从小到大顺序排列好后求得中位数.
(2)根据平均数,中位数,众数的意义回答.
【详解】解:(1)平均数为:(万元);
出现次数最多的是4万元,所以众数是4万元;
将这10个数据按从小到大的顺序排列后,第5、6个数据都是5万元,所以中位数是5万元;
(2)若规定平均数5.6万元为标准,则多数人无法或不可能超额完成,会挫伤员工的积极性;若规定众数4万元为标准,则大多数人不必努力就可以超额完成,不利于提高年销售额;若规定中位数5万元为标准,则大多数人能完成或超额完成,少数人经过努力也能完成因此把5万元定为标准比较合理.
【点睛】本题为众数,中位数,平均数的意义.解题的关键是根据众数,中位数,平均数的意义求出答案.
22.(1)28%;(2)中位数是3小时,众数是4小时,平均数是3.36小时
【分析】(1)各个部分所占百分比的和为1,即可求出t=4小时所占的百分比;
(2)根据中位数、众数、平均数的计算方法分别进行计算即可.
【详解】解:(1)1-12%-16%-24%-12%-8%=28%,
答:阅读时间为4小时的占28%;
(2)阅读时间出现最多的是4小时,占28%,因此阅读时间的众数是4小时,
从小到大排列,所占百分比处在50%的阅读时间是3小时,因此阅读时间的中位数是3小时,
=(1×12%+2×16%+3×24%+4×28%+5×12%+6×8%)=3.36(时),
答:学生上周双休日课外阅读时间的众数是4小时,中位数是3小时,平均数是3.36小时.
【点睛】本题考查中位数、众数、平均数的意义和计算方法,掌握扇形统计图的各个部分所占百分比的和为1是前提,理解加权平均数的意义是正确计算的关键.
23.(1)平均数为39.1码,中位数为39码,众数为40码;(2)鞋厂最感兴趣的是众数
【分析】(1)根据平均数、众数与中位数的定义求解分析.40出现的次数最多为众数,第10、11个数的平均数为中位数.
(2)鞋厂最感兴趣的是使用的人数,即众数.
【详解】解:(1)平均数=(37×3+38×4+39×4+40×7+41×1+42×1)÷20=39.1.
观察图表可知:有7人的鞋号为40,人数最多,即众数是40;
中位数是第10、11人的平均数,(39+39)÷2=39,
故答案为:平均数为39.1码,中位数为39码,众数为40码;
(2)鞋厂最感兴趣的是使用的人数,即众数,
故答案为:鞋厂最感兴趣的是众数.
【点睛】本题考查平均数,众数与中位数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.众数是数据中出现最多的一个数.正确理解中位数、众数及平均数的概念,是解决本题的关键.
24.(1)这个样本的中位数是,众数是,平均数是.相关信息:①双休日参观人数为平时的倍左右.②参观人数自周五开始明显上升等均可
(2)①且为正整数;且为正整数;②元
【分析】本题主要考查了算术平均数,中位数,众数;一次函数的应用.
(1)利用众数就是出现次数最多的数,中位数就是大小处于中间位置的数,以及平均数的公式即可求出答案;
(2)根据(1)可知,两团人数之和是人,所有①与的函数关系式是,②求出团购需付的钱数,即可求出答案
【详解】(1)解:这个样本的中位数是,众数是,平均数是.
相关信息:①双休日参观人数为平时的倍左右.②参观人数自周五开始明显上升等均可.
(2)①当甲团人数为人时,乙团人数为人,且为正整数;
由题意:,得.
若,则两团购票的总费用;
若,则两团购票的总费用.
②两团合起购票的花费为元元.
由①知当时,设节省元,
两团合起购票比分开购票可节省,
当时,元.
当时,两团合起购票比分开购票可节省,
故当时,元.
综上所述,两团合起来购票比分开购票最多省元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
