第二十章数据的整理与初步处理同步练习(含解析)
文档属性
| 名称 | 第二十章数据的整理与初步处理同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 528.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十章数据的整理与初步处理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某外卖员三月份的送餐统计数据如下表:
送餐距离(公里)
占比
送餐费 3元/单 5元/单
则该外卖员三月份平均每单的送餐费是( )
A.3.4元 B.3.8元 C.4元 D.4.2元
2.某校九年级(1)班全体学生2018年初中毕业体育考试的成绩统计如表:
成绩(分) 35 39 42 44 45 48 50
人数(人) 2 5 6 6 8 7 6
根据如表的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是44分
D.该班学生这次考试最高成绩是50分
3.若样本数据3,4,2,6,x的平均数为5,则这个样本的方差是( )
A.3 B.5 C.8 D.
4.一组数据3、4、4、5,若添加一个数4后得到一组新数据,则前后两组数据的统计量会发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
5.已知一组数据20、30、40、50、50、50、60、70、80,其中平均数、中位数、众数的大小关系是( )
A.平均数>中位数>众数 B.平均数<中位数<众数
C.中位数<众数<平均数 D.平均数=中位数=众数
6.已知一组数据2,a,4,5的众数为5,则这组数据的平均数为( )
A.3 B.4 C.5 D.6
7.5G是新一代信息技术的发展方向和数字经济的重要基础,预计我国5G商用将直接创造更多的就业岗位.小明准备到一家公司应聘普通员,他了解到该公司全体员工的月收入如下:
月收入/元 45000 19000 10000 5000 4500 3000 2000
人数 1 2 3 6 1 11 1
对这家公司全体员工的月收入,能为小明提供更为有用的信息的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
8.已知一组数据:,,,,.则这组数据的平均数是( )
A. B. C. D.
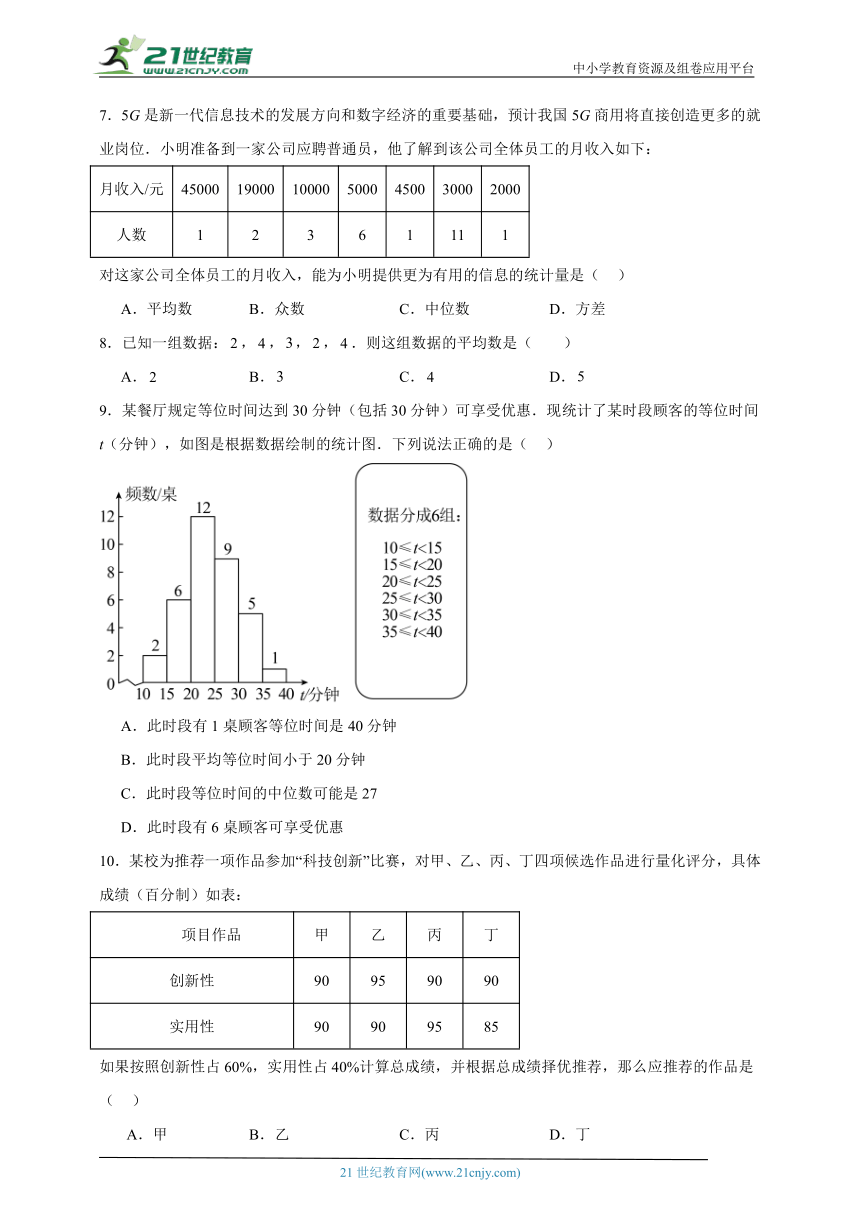
9.某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟),如图是根据数据绘制的统计图.下列说法正确的是( )
A.此时段有1桌顾客等位时间是40分钟
B.此时段平均等位时间小于20分钟
C.此时段等位时间的中位数可能是27
D.此时段有6桌顾客可享受优惠
10.某校为推荐一项作品参加“科技创新”比赛,对甲、乙、丙、丁四项候选作品进行量化评分,具体成绩(百分制)如表:
项目作品 甲 乙 丙 丁
创新性 90 95 90 90
实用性 90 90 95 85
如果按照创新性占60%,实用性占40%计算总成绩,并根据总成绩择优推荐,那么应推荐的作品是( )
A.甲 B.乙 C.丙 D.丁
11.2022年将在北京——张家口举办冬季奥运会,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 队员2 队员3 队员4 队员5 队员6
甲组 176 176 175 177 177 175
乙组 183 175 170 174 178 176
设两队队员身高的平均数依次为,,方差依次为,下列关系中正确的是( )
A. B.
C. D.
12.甲、乙、丙、丁四名射击运动员参加射击预选赛,每人射击20发子弹.他们射击成绩的平均数及标准差如表所示.
人员 成绩 甲 乙 丙 丁
平均数(环) 8.6 8.6 9.1 9.1
标准差S(环) 1.3 1.5 1.0 1.2
若要选一名成绩较好且又稳定的运动员参赛,则应选运动( )
A.甲 B.乙 C.丙 D.丁
二、填空题
13.若数据a,b,c的平均数是2,数据d,e的平均数是3,则a,b,c,4,d,e这组数据的平均数是 .
14.一组数据按从小到大的顺序排列为1,2,3,,4,5,若这组数据的中位数为3,则这组数据的方差是 .
15.如果一组数据的平均数是3,那么数据,,,,的平均数是 .
16.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2:
甲 乙 丙 丁
平均数(cm) 561 560 561 560
方差s2(cm2) 3.5 3.5 15.5 16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 .
17.数据4,0,2,1,-2的方差是 ,标准差是 .
三、解答题
18.某学校规定:学生的学期总评成绩由三部分组成:平时作业、期中测验、期末测验,并分别按50%、20%、30%的比例计入学期总评成绩.小明同学的平时作业、期中测验、期末测验的数学成绩依次是98分、80分、90分,这学期小明的数学总评成绩是多少?
19.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
分别计算这些运动员成绩的平均数、中位数、众数(结果保留小数点后两位).
20.某超市招聘收银员一名,对3名申请人进行了三项素质测试,下面是三名候选人的素质测试成绩:
素质测试 测试成绩
小赵 小钱 小孙
计算机 90 65 70
语言 75 55 50
商品知识 35 80 80
公司根据实际需要对计算机、语言、商品知识三项测试成绩分别赋予权4、3、3,这三人中谁将被录用.
21.体育课上,小明记录了本小组同学跳绳的成绩(单位:个)
.
请计算这个小组同学跳绳的平均成绩.
22.一组数1,2,3,的平均数是4.
(1)求三数的平均数;
(2)求,,的平均数.
23.甲、乙两台包装机同时包装的糖果,从中各抽出10袋,测得实际质量(g)
如下:
甲:501 505 508 508 494 508 506 508 507 499
乙:508 507 505 498 507 506 508 507 507 506
(1)分别计算两组数据的平均数(结果四舍五入保留整数)和方差;
(2)哪台包装机包装糖果的质量比较稳定?
24.甲乙两台机床同时生产一种零件,在10天中,两台机床每天出次品的数量如下表:
甲 0 1 0 2 2 0 3 1 2 4
乙 2 3 1 1 0 2 1 1 0 1
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果看,在10天中,那台机床出次品的平均数较小?那台机床出次品的波动性较小.
《第二十章数据的整理与初步处理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D D B B B D B
题号 11 12
答案 A C
1.B
【分析】本题主要考查了求加权平均数,熟练掌握加权平均数的公式是解题的关键.本题主要考查了求加权平均数,熟练掌握加权平均数的公式是解题的关键.
【详解】解:该外卖员三月份平均每单送餐费为(元),
故选:B.
2.C
【分析】根据总数,众数,中位数的定义即可一一判断;
【详解】该班一共有:2+5+6+6+8+7+6=40(人),众数是45分,最高成绩为50分,中位数为45分,
故A、B、D正确,C错误,
故选:C.
【点睛】此题考查总数,众数,中位数的定义,解题的关键是熟练掌握基本知识,属于中考基础题.
3.C
【分析】先由平均数是5计算出x的值,再计算方差.
【详解】解:∵数据3,4,2,6,x的平均数为5,
∴ ,
解得:x=10,
则方差为×[(3﹣5)2+(4﹣5)2+(2﹣5)2+(6﹣5)2+(10﹣5)2]=8,
故选C.
【点睛】本题考查的是平均数和方差的求法.计算方差的步骤是:①计算数据的平均数;②计算偏差,即每个数据与平均数的差;③计算偏差的平方和;④偏差的平方和除以数据个数.
4.D
【分析】计算出原数据与新数据的平均数、中位数、众数与方差,然后进行比较即可得出结果.
【详解】解:原数据3,4,4,5的平均数为,中位数为4,众数为4,方差为,
新数据3,4,4,4,5的平均数为,中位数为4,众数为4,方差为,
综合可得:平均数、中位数、众数均未发生变化,方差发生变化,
故选:D.
【点睛】题目主要考查求数据的平均数、中位数、众数与方差,熟练掌握各个统计量的求法是解题关键.
5.D
【详解】从小到大数据排列为20、30、40、50、50、50、60、70、80,
50出现了3次,为出现次数最多的数,故众数为50;共9个数据,第5个数为50,故中位数是50;平均数=(20+30+40+50+50+50+60+70+80)÷9=50.∴平均数=中位数=众数.故选D.
6.B
【分析】本题考查了平均数与众数的意义,要求平均数只要求出数据之和再除以总个数即可;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.依此先求出a,再求这组数据的平均数.
【详解】解:众数是5,已知的三个数都只出现了一次,
就可以知道,
所以平均数.
故选:B.
7.B
【分析】平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.既然小明想了解到该公司全体员工的月收入,那么应该是看多数员工的工资情况,故值得关注的是众数.
【详解】解:由于众数是数据中出现次数最多的数,故小明应最关心这组数据中的众数.
故选:B.
【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
8.B
【分析】此题主要考查了平均数,根据平均数的公式进行计算即可得出答案,熟练掌握平均数的计算公式是解题的关键.
【详解】解:,
故选:.
9.D
【分析】根据直方图,逐一进行判断即可.
【详解】解:A、由直方图可知:有1桌顾客等位时间在35至40分钟,不能说是40分钟,选项错误,不符合题意;
B、平均等位时间为:(分钟),大于20分钟,选项错误,不符合题意;
C、因为样本容量是35,中位数落在之间,选项错误,不符合题意;
D、30分钟以上的桌数为,选项正确,符合题意.
故选:D.
【点睛】本题考查频数分布直方图,求平均数,中位数.解题的关键是从统计图中有效的获取信息.
10.B
【分析】利用加权平均数计算总成绩,比较判断即可
【详解】根据题意,得:
甲:90×60%+90×40%=90;
乙:95×60%+90×40%=93;
丙:90×60%+95×40%=92;
丁:90×60%+85×40%=88;
故选B
【点睛】本题考查了加权平均数的计算,熟练掌握加权平均数的计算方法是解题的关键.
11.A
【分析】先根据平均数的定义分别计算出甲乙的平均数,然后根据方程公式计算出甲乙的方差即可对各选项进行判断.
【详解】解:,
,
,
∴.
故选:A
【点睛】本题考查了方差和平均数,熟练掌握一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差是解题的关键.
12.C
【分析】先比较平均数,再比较标准差,然后得出丙的方差小于丁的方差,从而得出答案.
【详解】解:由图可知,丙和丁的平均成绩好,
∵丙的标准差小于丁的标准差,
∴丙的方差小于丁的方差,
∴若要选一名成绩较好且发挥稳定的运动员参赛,则应选择丙,
故选:C.
【点睛】本题考查标准差、方差和算术平均数,掌握方差反映了一组数据的波动大小,方差越大,波动越大,方差越小,数据越稳定是解题的关键.
13.
【分析】本题主要考查了平均数.解决本题的关键是熟练掌握平均数的定义.
根据a,b,c的平均数是2,求出a,b,c的和,根据d,e的平均数是3,求出d,e的和,即可求a,b,c,4,d,e的平均数.
【详解】∵数据a,b,c的平均数是2,数据d,e的平均数是3,
∴,,
∴a,b,c,4,d,e的平均数是,
.
故答案为:.
14.
【详解】试题分析:根据中位数的求法可知=3,解得x=3,因此这组数的平均数为=,所以方差为s==.
考点:数据的分析
15.1
【分析】根据数据的平均数为3,可知,据此可得出的值.
【详解】
解:数据的平均数为3,
,
,
数据,,,,的平均数是1.
故答案为:1.
【点睛】本题考查了平均数:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
16.甲
【分析】首先比较平均数,平均数相同时选择方差较小的运动员参加.
【详解】∵ ,
∴从甲和丙中选择一人参加比赛,
∵ ,
∴选择甲参赛,
故答案为甲.
【点睛】此题考查了平均数和方差,关键是根据方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17. 4; 2.
【分析】先根据平均数的计算公式求出这组数据的平均数,再根据方差公式求出方差,从而得出标准差.
【详解】解:这组数据4、0、2、1、-2的平均数是:(4+0+2+1-2)=1;
方差S2=[(4-1)2+(0-1)2+(2-1)2+(1-1)2+(-2-1)2]=4,标准差S=2.
故答案为: (1). 4 (2). 2
【点睛】本题考查平均数,方差和标准差,用到的知识点是平均数、方差和标准差的计算公式,关键是根据题意和公式列出算式.
18.92分
【分析】根据加权平均数的计算公式列式进行计算即可求得.
【详解】由题意得:=92(分),
答:这学期小明的数学总评成绩是92分.
【点睛】本题考查了加权平均数的应用,正确理解题意,熟练应用加权平均数的公式是解题的关键.
19.这些运动员成绩的平均数、中位数、众数分别为1.67,1.70,1.75.
【分析】由平均数的计算公式即可算出平均数;把各运动员的成绩按从低到高排列,正中间的数是中位数;成绩人数最多的数便是众数
【详解】平均数为:
由成绩表知,正中间的数是1.70,故中位数为1.70
由于成绩为1.70米的学生人数最多,故众数这1.75
所以这些运动员成绩的平均数、中位数、众数分别为1.67,1.70,1.75.
【点睛】本题考查了求一组数据的平均数、中位数、众数,掌握它们的概念及计算方法是关键.
20.小赵被录用
【分析】本题考查加权平均数,根据表格中数据分别算出三人各自的加权平均数,并进行比较,即可解题.
【详解】解:根据题意可得:
小赵总成绩为:,
小钱总成绩为:,
小孙总成绩为:,
,
小赵被录用.
21.177个
【分析】设定180为标准,然后根据正与负相对进行解答即可.
【详解】解:把超过180个的个数用正数表示,不足180个的个数用负数表示,
本小组同学跳绳的成绩与180个的差值分别为: ;
∴;
因此,这个小组同学跳绳的平均成绩为:(个).
【点睛】本题主要考查的是正负数的应用,掌握正与负相对是解题的关键.
22.(1)6 ;(2)30.
【分析】(1)根据平均数的计算公式先求出的值,再除以3即可得出答案;
(2)根据(1)得出的的平均数,再根据平均数的变化规律即可得出答案.
【详解】解:(1)因为,
所以,
所以三数的平均数为;
(2)由(1)得,
所以
,
所以,,的平均数为.
【点睛】此题考查了平均数,掌握平均数的计算公式是本题的关键,注意平均数的变化规律.
23.(1),,,,(2)乙包装机包装糖果的质量比较稳定.
【分析】(1)根据平均数就是对每组数求和后除以数的个数;根据方差公式计算即可;
(2)方差大说明这组数据波动大,方差小则波动小,就比较稳定.依此判断即可.
【详解】(1),
,
.
,
(2),
乙包装机包装糖果的质量比较稳定.
【点睛】本题考查平均数、方差的计算以及它们的意义,掌握平均数、方差的计算是解题的关键.
24.(1) ,,见详解;(2)在10天中,乙台机床出次品的平均数较小,乙台机床出次品的波动较小,见详解.
【分析】(1)由表格及平均数、方差计算公式可直接求出答案;
(2)根据(1)可直接判断出
【详解】解:(1)由表格及题意可得:
,,
,
;
(2)由(1)可得:
,
在10天中,乙台机床出次品的平均数较小,乙台机床出次品的波动较小.
答:在10天中,乙台机床出次品的平均数较小,乙台机床出次品的波动较小.
【点睛】本题主要考查数据统计分析,熟练掌握平均数及方差的求法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十章数据的整理与初步处理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某外卖员三月份的送餐统计数据如下表:
送餐距离(公里)
占比
送餐费 3元/单 5元/单
则该外卖员三月份平均每单的送餐费是( )
A.3.4元 B.3.8元 C.4元 D.4.2元
2.某校九年级(1)班全体学生2018年初中毕业体育考试的成绩统计如表:
成绩(分) 35 39 42 44 45 48 50
人数(人) 2 5 6 6 8 7 6
根据如表的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是44分
D.该班学生这次考试最高成绩是50分
3.若样本数据3,4,2,6,x的平均数为5,则这个样本的方差是( )
A.3 B.5 C.8 D.
4.一组数据3、4、4、5,若添加一个数4后得到一组新数据,则前后两组数据的统计量会发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
5.已知一组数据20、30、40、50、50、50、60、70、80,其中平均数、中位数、众数的大小关系是( )
A.平均数>中位数>众数 B.平均数<中位数<众数
C.中位数<众数<平均数 D.平均数=中位数=众数
6.已知一组数据2,a,4,5的众数为5,则这组数据的平均数为( )
A.3 B.4 C.5 D.6
7.5G是新一代信息技术的发展方向和数字经济的重要基础,预计我国5G商用将直接创造更多的就业岗位.小明准备到一家公司应聘普通员,他了解到该公司全体员工的月收入如下:
月收入/元 45000 19000 10000 5000 4500 3000 2000
人数 1 2 3 6 1 11 1
对这家公司全体员工的月收入,能为小明提供更为有用的信息的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
8.已知一组数据:,,,,.则这组数据的平均数是( )
A. B. C. D.
9.某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟),如图是根据数据绘制的统计图.下列说法正确的是( )
A.此时段有1桌顾客等位时间是40分钟
B.此时段平均等位时间小于20分钟
C.此时段等位时间的中位数可能是27
D.此时段有6桌顾客可享受优惠
10.某校为推荐一项作品参加“科技创新”比赛,对甲、乙、丙、丁四项候选作品进行量化评分,具体成绩(百分制)如表:
项目作品 甲 乙 丙 丁
创新性 90 95 90 90
实用性 90 90 95 85
如果按照创新性占60%,实用性占40%计算总成绩,并根据总成绩择优推荐,那么应推荐的作品是( )
A.甲 B.乙 C.丙 D.丁
11.2022年将在北京——张家口举办冬季奥运会,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 队员2 队员3 队员4 队员5 队员6
甲组 176 176 175 177 177 175
乙组 183 175 170 174 178 176
设两队队员身高的平均数依次为,,方差依次为,下列关系中正确的是( )
A. B.
C. D.
12.甲、乙、丙、丁四名射击运动员参加射击预选赛,每人射击20发子弹.他们射击成绩的平均数及标准差如表所示.
人员 成绩 甲 乙 丙 丁
平均数(环) 8.6 8.6 9.1 9.1
标准差S(环) 1.3 1.5 1.0 1.2
若要选一名成绩较好且又稳定的运动员参赛,则应选运动( )
A.甲 B.乙 C.丙 D.丁
二、填空题
13.若数据a,b,c的平均数是2,数据d,e的平均数是3,则a,b,c,4,d,e这组数据的平均数是 .
14.一组数据按从小到大的顺序排列为1,2,3,,4,5,若这组数据的中位数为3,则这组数据的方差是 .
15.如果一组数据的平均数是3,那么数据,,,,的平均数是 .
16.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2:
甲 乙 丙 丁
平均数(cm) 561 560 561 560
方差s2(cm2) 3.5 3.5 15.5 16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 .
17.数据4,0,2,1,-2的方差是 ,标准差是 .
三、解答题
18.某学校规定:学生的学期总评成绩由三部分组成:平时作业、期中测验、期末测验,并分别按50%、20%、30%的比例计入学期总评成绩.小明同学的平时作业、期中测验、期末测验的数学成绩依次是98分、80分、90分,这学期小明的数学总评成绩是多少?
19.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
分别计算这些运动员成绩的平均数、中位数、众数(结果保留小数点后两位).
20.某超市招聘收银员一名,对3名申请人进行了三项素质测试,下面是三名候选人的素质测试成绩:
素质测试 测试成绩
小赵 小钱 小孙
计算机 90 65 70
语言 75 55 50
商品知识 35 80 80
公司根据实际需要对计算机、语言、商品知识三项测试成绩分别赋予权4、3、3,这三人中谁将被录用.
21.体育课上,小明记录了本小组同学跳绳的成绩(单位:个)
.
请计算这个小组同学跳绳的平均成绩.
22.一组数1,2,3,的平均数是4.
(1)求三数的平均数;
(2)求,,的平均数.
23.甲、乙两台包装机同时包装的糖果,从中各抽出10袋,测得实际质量(g)
如下:
甲:501 505 508 508 494 508 506 508 507 499
乙:508 507 505 498 507 506 508 507 507 506
(1)分别计算两组数据的平均数(结果四舍五入保留整数)和方差;
(2)哪台包装机包装糖果的质量比较稳定?
24.甲乙两台机床同时生产一种零件,在10天中,两台机床每天出次品的数量如下表:
甲 0 1 0 2 2 0 3 1 2 4
乙 2 3 1 1 0 2 1 1 0 1
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果看,在10天中,那台机床出次品的平均数较小?那台机床出次品的波动性较小.
《第二十章数据的整理与初步处理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D D B B B D B
题号 11 12
答案 A C
1.B
【分析】本题主要考查了求加权平均数,熟练掌握加权平均数的公式是解题的关键.本题主要考查了求加权平均数,熟练掌握加权平均数的公式是解题的关键.
【详解】解:该外卖员三月份平均每单送餐费为(元),
故选:B.
2.C
【分析】根据总数,众数,中位数的定义即可一一判断;
【详解】该班一共有:2+5+6+6+8+7+6=40(人),众数是45分,最高成绩为50分,中位数为45分,
故A、B、D正确,C错误,
故选:C.
【点睛】此题考查总数,众数,中位数的定义,解题的关键是熟练掌握基本知识,属于中考基础题.
3.C
【分析】先由平均数是5计算出x的值,再计算方差.
【详解】解:∵数据3,4,2,6,x的平均数为5,
∴ ,
解得:x=10,
则方差为×[(3﹣5)2+(4﹣5)2+(2﹣5)2+(6﹣5)2+(10﹣5)2]=8,
故选C.
【点睛】本题考查的是平均数和方差的求法.计算方差的步骤是:①计算数据的平均数;②计算偏差,即每个数据与平均数的差;③计算偏差的平方和;④偏差的平方和除以数据个数.
4.D
【分析】计算出原数据与新数据的平均数、中位数、众数与方差,然后进行比较即可得出结果.
【详解】解:原数据3,4,4,5的平均数为,中位数为4,众数为4,方差为,
新数据3,4,4,4,5的平均数为,中位数为4,众数为4,方差为,
综合可得:平均数、中位数、众数均未发生变化,方差发生变化,
故选:D.
【点睛】题目主要考查求数据的平均数、中位数、众数与方差,熟练掌握各个统计量的求法是解题关键.
5.D
【详解】从小到大数据排列为20、30、40、50、50、50、60、70、80,
50出现了3次,为出现次数最多的数,故众数为50;共9个数据,第5个数为50,故中位数是50;平均数=(20+30+40+50+50+50+60+70+80)÷9=50.∴平均数=中位数=众数.故选D.
6.B
【分析】本题考查了平均数与众数的意义,要求平均数只要求出数据之和再除以总个数即可;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.依此先求出a,再求这组数据的平均数.
【详解】解:众数是5,已知的三个数都只出现了一次,
就可以知道,
所以平均数.
故选:B.
7.B
【分析】平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.既然小明想了解到该公司全体员工的月收入,那么应该是看多数员工的工资情况,故值得关注的是众数.
【详解】解:由于众数是数据中出现次数最多的数,故小明应最关心这组数据中的众数.
故选:B.
【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
8.B
【分析】此题主要考查了平均数,根据平均数的公式进行计算即可得出答案,熟练掌握平均数的计算公式是解题的关键.
【详解】解:,
故选:.
9.D
【分析】根据直方图,逐一进行判断即可.
【详解】解:A、由直方图可知:有1桌顾客等位时间在35至40分钟,不能说是40分钟,选项错误,不符合题意;
B、平均等位时间为:(分钟),大于20分钟,选项错误,不符合题意;
C、因为样本容量是35,中位数落在之间,选项错误,不符合题意;
D、30分钟以上的桌数为,选项正确,符合题意.
故选:D.
【点睛】本题考查频数分布直方图,求平均数,中位数.解题的关键是从统计图中有效的获取信息.
10.B
【分析】利用加权平均数计算总成绩,比较判断即可
【详解】根据题意,得:
甲:90×60%+90×40%=90;
乙:95×60%+90×40%=93;
丙:90×60%+95×40%=92;
丁:90×60%+85×40%=88;
故选B
【点睛】本题考查了加权平均数的计算,熟练掌握加权平均数的计算方法是解题的关键.
11.A
【分析】先根据平均数的定义分别计算出甲乙的平均数,然后根据方程公式计算出甲乙的方差即可对各选项进行判断.
【详解】解:,
,
,
∴.
故选:A
【点睛】本题考查了方差和平均数,熟练掌握一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差是解题的关键.
12.C
【分析】先比较平均数,再比较标准差,然后得出丙的方差小于丁的方差,从而得出答案.
【详解】解:由图可知,丙和丁的平均成绩好,
∵丙的标准差小于丁的标准差,
∴丙的方差小于丁的方差,
∴若要选一名成绩较好且发挥稳定的运动员参赛,则应选择丙,
故选:C.
【点睛】本题考查标准差、方差和算术平均数,掌握方差反映了一组数据的波动大小,方差越大,波动越大,方差越小,数据越稳定是解题的关键.
13.
【分析】本题主要考查了平均数.解决本题的关键是熟练掌握平均数的定义.
根据a,b,c的平均数是2,求出a,b,c的和,根据d,e的平均数是3,求出d,e的和,即可求a,b,c,4,d,e的平均数.
【详解】∵数据a,b,c的平均数是2,数据d,e的平均数是3,
∴,,
∴a,b,c,4,d,e的平均数是,
.
故答案为:.
14.
【详解】试题分析:根据中位数的求法可知=3,解得x=3,因此这组数的平均数为=,所以方差为s==.
考点:数据的分析
15.1
【分析】根据数据的平均数为3,可知,据此可得出的值.
【详解】
解:数据的平均数为3,
,
,
数据,,,,的平均数是1.
故答案为:1.
【点睛】本题考查了平均数:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
16.甲
【分析】首先比较平均数,平均数相同时选择方差较小的运动员参加.
【详解】∵ ,
∴从甲和丙中选择一人参加比赛,
∵ ,
∴选择甲参赛,
故答案为甲.
【点睛】此题考查了平均数和方差,关键是根据方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17. 4; 2.
【分析】先根据平均数的计算公式求出这组数据的平均数,再根据方差公式求出方差,从而得出标准差.
【详解】解:这组数据4、0、2、1、-2的平均数是:(4+0+2+1-2)=1;
方差S2=[(4-1)2+(0-1)2+(2-1)2+(1-1)2+(-2-1)2]=4,标准差S=2.
故答案为: (1). 4 (2). 2
【点睛】本题考查平均数,方差和标准差,用到的知识点是平均数、方差和标准差的计算公式,关键是根据题意和公式列出算式.
18.92分
【分析】根据加权平均数的计算公式列式进行计算即可求得.
【详解】由题意得:=92(分),
答:这学期小明的数学总评成绩是92分.
【点睛】本题考查了加权平均数的应用,正确理解题意,熟练应用加权平均数的公式是解题的关键.
19.这些运动员成绩的平均数、中位数、众数分别为1.67,1.70,1.75.
【分析】由平均数的计算公式即可算出平均数;把各运动员的成绩按从低到高排列,正中间的数是中位数;成绩人数最多的数便是众数
【详解】平均数为:
由成绩表知,正中间的数是1.70,故中位数为1.70
由于成绩为1.70米的学生人数最多,故众数这1.75
所以这些运动员成绩的平均数、中位数、众数分别为1.67,1.70,1.75.
【点睛】本题考查了求一组数据的平均数、中位数、众数,掌握它们的概念及计算方法是关键.
20.小赵被录用
【分析】本题考查加权平均数,根据表格中数据分别算出三人各自的加权平均数,并进行比较,即可解题.
【详解】解:根据题意可得:
小赵总成绩为:,
小钱总成绩为:,
小孙总成绩为:,
,
小赵被录用.
21.177个
【分析】设定180为标准,然后根据正与负相对进行解答即可.
【详解】解:把超过180个的个数用正数表示,不足180个的个数用负数表示,
本小组同学跳绳的成绩与180个的差值分别为: ;
∴;
因此,这个小组同学跳绳的平均成绩为:(个).
【点睛】本题主要考查的是正负数的应用,掌握正与负相对是解题的关键.
22.(1)6 ;(2)30.
【分析】(1)根据平均数的计算公式先求出的值,再除以3即可得出答案;
(2)根据(1)得出的的平均数,再根据平均数的变化规律即可得出答案.
【详解】解:(1)因为,
所以,
所以三数的平均数为;
(2)由(1)得,
所以
,
所以,,的平均数为.
【点睛】此题考查了平均数,掌握平均数的计算公式是本题的关键,注意平均数的变化规律.
23.(1),,,,(2)乙包装机包装糖果的质量比较稳定.
【分析】(1)根据平均数就是对每组数求和后除以数的个数;根据方差公式计算即可;
(2)方差大说明这组数据波动大,方差小则波动小,就比较稳定.依此判断即可.
【详解】(1),
,
.
,
(2),
乙包装机包装糖果的质量比较稳定.
【点睛】本题考查平均数、方差的计算以及它们的意义,掌握平均数、方差的计算是解题的关键.
24.(1) ,,见详解;(2)在10天中,乙台机床出次品的平均数较小,乙台机床出次品的波动较小,见详解.
【分析】(1)由表格及平均数、方差计算公式可直接求出答案;
(2)根据(1)可直接判断出
【详解】解:(1)由表格及题意可得:
,,
,
;
(2)由(1)可得:
,
在10天中,乙台机床出次品的平均数较小,乙台机床出次品的波动较小.
答:在10天中,乙台机床出次品的平均数较小,乙台机床出次品的波动较小.
【点睛】本题主要考查数据统计分析,熟练掌握平均数及方差的求法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
