9.3.2 向量坐标表示与运算 2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 9.3.2 向量坐标表示与运算 2024-2025学年高一数学苏教版(2019)必修第二册 | 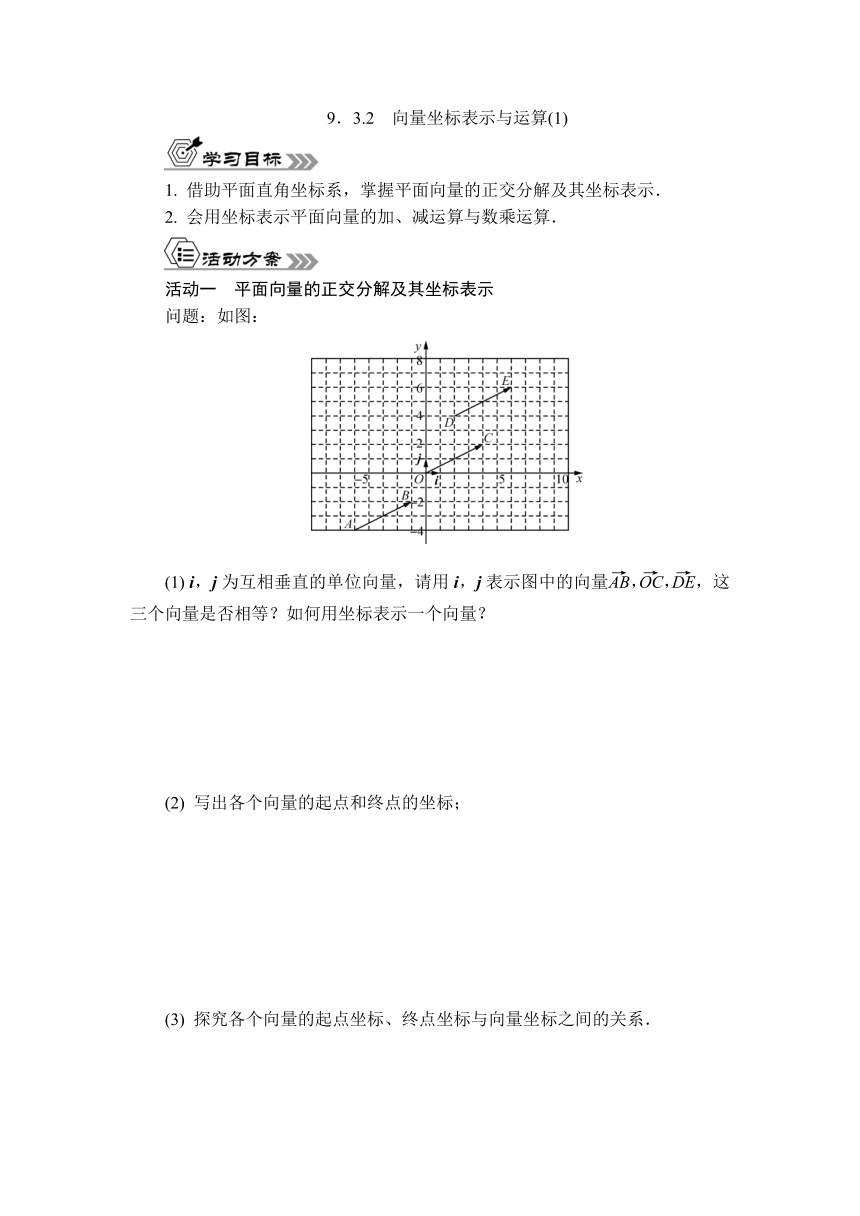 | |
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 17:48:17 | ||
图片预览





文档简介
9.3.2 向量坐标表示与运算(1)
1. 借助平面直角坐标系,掌握平面向量的正交分解及其坐标表示.
2. 会用坐标表示平面向量的加、减运算与数乘运算.
活动一 平面向量的正交分解及其坐标表示
问题:如图:
(1) i,j为互相垂直的单位向量,请用i,j表示图中的向量,,,这三个向量是否相等?如何用坐标表示一个向量?
(2) 写出各个向量的起点和终点的坐标;
(3) 探究各个向量的起点坐标、终点坐标与向量坐标之间的关系.
例1 如图,已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,求向量的坐标.
从原点引出的向量的坐标(x,y)就是点M的坐标.
如图,取与x轴,y轴相同方向的两个单位向量i,j作为基底,分别用i,j表示,,,并求出它们的坐标.
活动二 平面向量线性运算的坐标表示
1. 平面向量的坐标运算.
根据平面向量坐标表示的几何意义及向量的运算性质思考下列问题:
思考1
已知a=(x1,y1),b=(x2,y2),求a+b,a-b.
思考2
已知a=(x,y)和实数λ,求λa.
2. 平面向量坐标运算的应用.
例2 在平面直角坐标系中,O为坐标原点,已知点A(-1,3),B(1,-3),C(4,1),D(3,4),求向量,,,的坐标.
思考3
例2中的四边形OCDA是平行四边形吗?为什么?
一个向量的坐标等于该向量终点的坐标减去起点的坐标.
已知a=(3,4),b=(-1,4),求a+b,a-b,2a-3b的坐标.
已知a=(10,-4),b=(3,1),c=(-2,3),试用b,c表示a.
1. (教材改编)已知O为坐标原点,若向量=(3,2),=(-4,5),则点A的坐标为( )
A. (-1,7) B. (7,-3) C. (-1,-3) D. (7,7)
2. (2024成都期中)已知点O(0,0),向量=(2,3),=(6,-3),P是线段AB上靠近点A的三等分点,则点P的坐标为( )
A. B. C. D.
3. (多选)(2024张家口期中)已知平行四边形的三个顶点的坐标分别为(2,2),(-2,4),(0,0),则另一个顶点的坐标可以是( )
A. (0,-6) B. (0,6) C. (4,-2) D. (-4,2)
4. (2024北京期中)已知O为坐标原点,点A(3,-6),B(-5,2),=(+),则点C的坐标为________.
5. 已知a=(2,-4),b=(-1,3),c=(6,5),p=a+2b-c,试用a,b表示p.
9.3.2 向量坐标表示与运算(2)
1. 能用坐标表示平面向量的数量积及夹角.
2. 能用坐标表示平面向量垂直的条件.
活动一 掌握平面向量数量积的坐标表示
1. 两个非零平面向量垂直的等价条件:
2. 设i,j分别是与x轴,y轴正方向相同的两个单位向量,则i·i=________,j·j=________,i·j=j·i=________.
3. 探究:若两个向量a=(x1,y1),b=(x2,y2),i,j分别是与x轴,y轴正方向相同的单位向量.
(1) 将a,b用向量i和j表示;
(2) 根据向量数量积的定义及上面的结论计算a·b;
(3) 由(1)(2)得出用a,b的坐标来表示它们的数量积a·b.
4. 平面向量数量积的坐标表示.
(1) 平面向量数量积的坐标表示:
根据上述探究,如果两个向量a=(x1,y1),b=(x2,y2),那么平面两向量数量积的坐标表示为:
特别地,设a=(x,y),则a·a的几何意义是什么?你能得到什么结论?(|a|2=?即|a|=?)
(2) 平面内两点间的距离公式:
①已知两点A(x1,y1),B(x2,y2),求;
②能否用(1)的结论求||
③||的几何意义是什么?
根据①②③得出A(x1,y1),B(x2,y2)两点间的距离公式为:
(3) 两向量夹角的余弦(0≤θ≤π):
①设两个非零向量a=(x1,y1),b=(x2,y2),它们的夹角是θ,根据向量数量积的定义,如何用向量a和b的坐标来表示它们夹角的余弦?
②特别地,若a⊥b,则向量a和b的坐标满足什么条件?
③反之,向量a和b的坐标满足上述条件,则a⊥b成立吗?
由此得出:a⊥b a·b=0 _____________.
活动二 掌握平面向量数量积的坐标表示的应用
例1 已知△ABC的三个顶点坐标分别为A(1,2),B(2,3),C(-2,5),求证:△ABC是直角三角形.
因为两个平面向量垂直的充要条件是a·b=0,又两个向量的数量积的坐标运算为a·b=x1x2+y1y2,所以在平面直角坐标系中,要得到垂直关系,只要说明x1x2+y1y2=0,其中(x1,y1),(x2,y2)分别表示两个向量的坐标.
在△ABC中,=(2,3),=(1,k),且△ABC是直角三角形,求k的值.
例2 已知a=(3,-1),b=(1,2),求满足x·a=9与x·b=4的向量x.
已知a=(4,3),则与a垂直的单位向量的坐标是____________________.
例3 已知平面向量a=(-,),b=(-,-1).
(1) 求证:a⊥b;
(2) 若存在不同时为零的实数k,t,使得x=a+(t2-2)b,y=-ka+t2b,且x⊥y,试把k表示为t的函数.
利用两个平面向量垂直的充要条件x1x2+y1y2=0,列出相应的关系式,从而解决一些相关问题.
在平面直角坐标系xOy中,已知向量a=(,-1),b=(cos 60°,sin 60°).
(1) 求证:|a|=2|b|,且a⊥b;
(2) 设向量x=a+(t+4)b,y=a+tb,且x⊥y,求实数t的值.
1. (教材改编)已知向量a=(2,1),b=(-2,4),则|a-b|等于( )
A. 2 B. 3 C. 4 D. 5
2. (2024芜湖期中)已知向量a=(1,-2),b=(m,1),若a⊥b,则b与a+b夹角的余弦值为( )
A. B. C. D. -
3. (多选)(教材改编)已知向量a=(-1,3),b=(x,2),且(a-2b)⊥a,则下列结论中正确的是( )
A. b=(1,2)
B. |2a-b|=25
C. 向量a与向量b的夹角是45°
D. 向量a在向量b上投影向量的坐标是(1,2)
4. (2023潍坊四中月考)已知O为坐标原点,且=(1,2),=(-2,-1),若2=,则||=________.
5. (2024株洲月考)在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1).
(1) 求·;
(2) 若实数t满足(-t)·=0,求t的值.
9.3.2 向量坐标表示与运算(1)
【活动方案】
问题:(1) ===4i+2j.
存在有序实数对(x,y)使a=xi+yj,把有序数对(x,y)称为向量a的直角坐标.
(2) :A(-5,-4),B(-1,-2);
:O(0,0),C(4,2);
:D(2,4),E(6,6).
(3) 向量坐标=终点坐标-起点坐标.
例1 设点A的坐标为(x,y),
则x=OA·cos 60°=2,
y=OA·sin 60°=6,
即点A的坐标为(2,6),
所以=(2-0,6-0)=(2,6).
跟踪训练 =6i+2j,=2i+4j,=-=-4i+2j.
所以=(6,2),=(2,4),=(-4,2).
思考1:a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2).
思考2:λa=(λx,λy).
例2 =(-1,3),=(1,-3),=(1,-3),=(-1,3).
思考3:是,因为与为相等向量且不重合,所以OA∥CD,OA=CD,所以四边形OCDA是平行四边形.
跟踪训练1 a+b=(2,8),a-b=(4,0),2a-3b=(9,-4).
跟踪训练2 设a=mb+nc,则a=(3m-2n,m+3n),即解得所以a=2b-2c.
【检测反馈】
1. B 因为=(3,2),=(-4,5),所以=-=(3,2)-(-4,5)=(7,-3),所以点A的坐标为(7,-3).
2. B 因为=(2,3),=(6,-3),所以=-=(4,-6).因为P是线段AB上靠近点A的三等分点,所以==,则=+=,可得点P的坐标为.
3. BCD 记点(2,2),(-2,4),(0,0)分别为A,B,O,第4个顶点为C.当线段AB为平行四边形的对角线时,==(2,2),可得点C的坐标为(0,6),故B正确;当线段OB为平行四边形的对角线时,==(-4,2),可得点C 的坐标为(-4,2),故D正确;当线段OA为平行四边形的对角线时,==(4,-2),可得点C的坐标为(4,-2),故C正确.故选BCD.
4. (-1,-2) 由=(+),得C为线段AB的中点.又A(3,-6),B(-5,2),则C(-1,-2).
5. 由题意,得p=a+2b-c=(-6,-3).
设p=ma+nb,
则解得
所以p=-a-15b.
9.3.2 向量坐标表示与运算(2)
【活动方案】
1. a·b=0
2. 1 1 0
3. (1) a=x1i+y1j,b=x2i+y2j.
(2) a·b=(x1i+y1j)·(x2i+y2j)=x1x2+y1y2.
(3) a·b=x1x2+y1y2.
4. (1) a·b=x1x2+y1y2.
a·a的几何意义是向量a在向量a上的投影向量与向量a的数量积.
|a|2=x2+y2,即|a|=.
(2) ①=(x2-x1,y2-y1).
②||=.
③表示A,B两点间的距离.
AB=.
(3) ①cos θ=.
②x1x2+y1y2=0.
③成立.
x1x2+y1y2=0
例1 由题意,得=(1,1),=(-3,3),
所以·=0,即AB⊥AC,
所以△ABC是直角三角形.
跟踪训练 由题意,得=-=(-1,k-3).
①当A=90°,
即·=2+3k=0时,k=-;
②当B=90°,
即·=-2+3k-9=0时,k=;
③当C=90°,
即·=-1+k2-3k=0时,k=.
综上,k的值为-或或或.
例2 设x=(m,n),
则解得
所以x=.
跟踪训练 或 设单位向量为(x,y),则解得或所以所求的单位向量为或(-,).
例3 (1) 因为a·b=·(-,-1)=-=0,所以a⊥b.
(2) |a|2=+=1,|b|2=3+1=4,
x·y=[a+(t2-2)b]·(-ka+t2b)=0,
即-k+4t2(t2-2)+(t2-kt2+2k)a·b=0,
所以k=4t4-8t2.
跟踪训练 (1) 由题意,得b=,|a|=2,
则|b|=1,所以|a|=2|b|.
因为a·b=-=0,所以a⊥b.
(2) 因为x⊥y,所以x·y=0.
由(1)得x·y=[a+(t+4)b]·(a+tb)=a2+t(t+4)b2=t2+4t+4=(t+2)2=0,
解得t=-2.
【检测反馈】
1. D 因为a-b=(2,1)-(-2,4)=(4,-3),所以|a-b|==5.
2. A 设b与a+b的夹角是θ,因为a⊥b,所以a·b=m-2=0,即m=2,所以b=(2,1),可得a+b=(3,-1),所以cos θ====.
3. ACD 由a=(-1,3),b=(x,2),得a-2b=(-1-2x,-1).由(a-2b)⊥a,得2x+1-3=0,解得x=1.对于A,b=(1,2),故A正确;对于B,2a-b=(-3,4),则|2a-b|==5,故B错误;对于C,设向量a与向量b的夹角是θ,易得|a|=,|b|=,a·b=-1×1+3×2=5,则cos θ===.又0°≤θ≤180°,所以θ=45°,故C正确;对于D,向量a在向量b上的投影向量为b=b=(1,2),故D正确.故选ACD.
4. 因为O为坐标原点,=(1,2),=(-2,-1),且2=,所以P为线段AB的中点,则=(+)=,所以||==.
5. (1) 由题意,得=(2,3)-(-1,-2)=(3,5),=(-2,-1)-(-1,-2)=(-1,1),
所以·=3×(-1)+5×1=2.
(2) 由题意,得-t=(3,5)-t(-2,-1)=(3+2t,5+t),=(2,3).
因为(-t)·=0,
所以2(3+2t)+3(5+t)=0,
解得t=-3.
1. 借助平面直角坐标系,掌握平面向量的正交分解及其坐标表示.
2. 会用坐标表示平面向量的加、减运算与数乘运算.
活动一 平面向量的正交分解及其坐标表示
问题:如图:
(1) i,j为互相垂直的单位向量,请用i,j表示图中的向量,,,这三个向量是否相等?如何用坐标表示一个向量?
(2) 写出各个向量的起点和终点的坐标;
(3) 探究各个向量的起点坐标、终点坐标与向量坐标之间的关系.
例1 如图,已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,求向量的坐标.
从原点引出的向量的坐标(x,y)就是点M的坐标.
如图,取与x轴,y轴相同方向的两个单位向量i,j作为基底,分别用i,j表示,,,并求出它们的坐标.
活动二 平面向量线性运算的坐标表示
1. 平面向量的坐标运算.
根据平面向量坐标表示的几何意义及向量的运算性质思考下列问题:
思考1
已知a=(x1,y1),b=(x2,y2),求a+b,a-b.
思考2
已知a=(x,y)和实数λ,求λa.
2. 平面向量坐标运算的应用.
例2 在平面直角坐标系中,O为坐标原点,已知点A(-1,3),B(1,-3),C(4,1),D(3,4),求向量,,,的坐标.
思考3
例2中的四边形OCDA是平行四边形吗?为什么?
一个向量的坐标等于该向量终点的坐标减去起点的坐标.
已知a=(3,4),b=(-1,4),求a+b,a-b,2a-3b的坐标.
已知a=(10,-4),b=(3,1),c=(-2,3),试用b,c表示a.
1. (教材改编)已知O为坐标原点,若向量=(3,2),=(-4,5),则点A的坐标为( )
A. (-1,7) B. (7,-3) C. (-1,-3) D. (7,7)
2. (2024成都期中)已知点O(0,0),向量=(2,3),=(6,-3),P是线段AB上靠近点A的三等分点,则点P的坐标为( )
A. B. C. D.
3. (多选)(2024张家口期中)已知平行四边形的三个顶点的坐标分别为(2,2),(-2,4),(0,0),则另一个顶点的坐标可以是( )
A. (0,-6) B. (0,6) C. (4,-2) D. (-4,2)
4. (2024北京期中)已知O为坐标原点,点A(3,-6),B(-5,2),=(+),则点C的坐标为________.
5. 已知a=(2,-4),b=(-1,3),c=(6,5),p=a+2b-c,试用a,b表示p.
9.3.2 向量坐标表示与运算(2)
1. 能用坐标表示平面向量的数量积及夹角.
2. 能用坐标表示平面向量垂直的条件.
活动一 掌握平面向量数量积的坐标表示
1. 两个非零平面向量垂直的等价条件:
2. 设i,j分别是与x轴,y轴正方向相同的两个单位向量,则i·i=________,j·j=________,i·j=j·i=________.
3. 探究:若两个向量a=(x1,y1),b=(x2,y2),i,j分别是与x轴,y轴正方向相同的单位向量.
(1) 将a,b用向量i和j表示;
(2) 根据向量数量积的定义及上面的结论计算a·b;
(3) 由(1)(2)得出用a,b的坐标来表示它们的数量积a·b.
4. 平面向量数量积的坐标表示.
(1) 平面向量数量积的坐标表示:
根据上述探究,如果两个向量a=(x1,y1),b=(x2,y2),那么平面两向量数量积的坐标表示为:
特别地,设a=(x,y),则a·a的几何意义是什么?你能得到什么结论?(|a|2=?即|a|=?)
(2) 平面内两点间的距离公式:
①已知两点A(x1,y1),B(x2,y2),求;
②能否用(1)的结论求||
③||的几何意义是什么?
根据①②③得出A(x1,y1),B(x2,y2)两点间的距离公式为:
(3) 两向量夹角的余弦(0≤θ≤π):
①设两个非零向量a=(x1,y1),b=(x2,y2),它们的夹角是θ,根据向量数量积的定义,如何用向量a和b的坐标来表示它们夹角的余弦?
②特别地,若a⊥b,则向量a和b的坐标满足什么条件?
③反之,向量a和b的坐标满足上述条件,则a⊥b成立吗?
由此得出:a⊥b a·b=0 _____________.
活动二 掌握平面向量数量积的坐标表示的应用
例1 已知△ABC的三个顶点坐标分别为A(1,2),B(2,3),C(-2,5),求证:△ABC是直角三角形.
因为两个平面向量垂直的充要条件是a·b=0,又两个向量的数量积的坐标运算为a·b=x1x2+y1y2,所以在平面直角坐标系中,要得到垂直关系,只要说明x1x2+y1y2=0,其中(x1,y1),(x2,y2)分别表示两个向量的坐标.
在△ABC中,=(2,3),=(1,k),且△ABC是直角三角形,求k的值.
例2 已知a=(3,-1),b=(1,2),求满足x·a=9与x·b=4的向量x.
已知a=(4,3),则与a垂直的单位向量的坐标是____________________.
例3 已知平面向量a=(-,),b=(-,-1).
(1) 求证:a⊥b;
(2) 若存在不同时为零的实数k,t,使得x=a+(t2-2)b,y=-ka+t2b,且x⊥y,试把k表示为t的函数.
利用两个平面向量垂直的充要条件x1x2+y1y2=0,列出相应的关系式,从而解决一些相关问题.
在平面直角坐标系xOy中,已知向量a=(,-1),b=(cos 60°,sin 60°).
(1) 求证:|a|=2|b|,且a⊥b;
(2) 设向量x=a+(t+4)b,y=a+tb,且x⊥y,求实数t的值.
1. (教材改编)已知向量a=(2,1),b=(-2,4),则|a-b|等于( )
A. 2 B. 3 C. 4 D. 5
2. (2024芜湖期中)已知向量a=(1,-2),b=(m,1),若a⊥b,则b与a+b夹角的余弦值为( )
A. B. C. D. -
3. (多选)(教材改编)已知向量a=(-1,3),b=(x,2),且(a-2b)⊥a,则下列结论中正确的是( )
A. b=(1,2)
B. |2a-b|=25
C. 向量a与向量b的夹角是45°
D. 向量a在向量b上投影向量的坐标是(1,2)
4. (2023潍坊四中月考)已知O为坐标原点,且=(1,2),=(-2,-1),若2=,则||=________.
5. (2024株洲月考)在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1).
(1) 求·;
(2) 若实数t满足(-t)·=0,求t的值.
9.3.2 向量坐标表示与运算(1)
【活动方案】
问题:(1) ===4i+2j.
存在有序实数对(x,y)使a=xi+yj,把有序数对(x,y)称为向量a的直角坐标.
(2) :A(-5,-4),B(-1,-2);
:O(0,0),C(4,2);
:D(2,4),E(6,6).
(3) 向量坐标=终点坐标-起点坐标.
例1 设点A的坐标为(x,y),
则x=OA·cos 60°=2,
y=OA·sin 60°=6,
即点A的坐标为(2,6),
所以=(2-0,6-0)=(2,6).
跟踪训练 =6i+2j,=2i+4j,=-=-4i+2j.
所以=(6,2),=(2,4),=(-4,2).
思考1:a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2).
思考2:λa=(λx,λy).
例2 =(-1,3),=(1,-3),=(1,-3),=(-1,3).
思考3:是,因为与为相等向量且不重合,所以OA∥CD,OA=CD,所以四边形OCDA是平行四边形.
跟踪训练1 a+b=(2,8),a-b=(4,0),2a-3b=(9,-4).
跟踪训练2 设a=mb+nc,则a=(3m-2n,m+3n),即解得所以a=2b-2c.
【检测反馈】
1. B 因为=(3,2),=(-4,5),所以=-=(3,2)-(-4,5)=(7,-3),所以点A的坐标为(7,-3).
2. B 因为=(2,3),=(6,-3),所以=-=(4,-6).因为P是线段AB上靠近点A的三等分点,所以==,则=+=,可得点P的坐标为.
3. BCD 记点(2,2),(-2,4),(0,0)分别为A,B,O,第4个顶点为C.当线段AB为平行四边形的对角线时,==(2,2),可得点C的坐标为(0,6),故B正确;当线段OB为平行四边形的对角线时,==(-4,2),可得点C 的坐标为(-4,2),故D正确;当线段OA为平行四边形的对角线时,==(4,-2),可得点C的坐标为(4,-2),故C正确.故选BCD.
4. (-1,-2) 由=(+),得C为线段AB的中点.又A(3,-6),B(-5,2),则C(-1,-2).
5. 由题意,得p=a+2b-c=(-6,-3).
设p=ma+nb,
则解得
所以p=-a-15b.
9.3.2 向量坐标表示与运算(2)
【活动方案】
1. a·b=0
2. 1 1 0
3. (1) a=x1i+y1j,b=x2i+y2j.
(2) a·b=(x1i+y1j)·(x2i+y2j)=x1x2+y1y2.
(3) a·b=x1x2+y1y2.
4. (1) a·b=x1x2+y1y2.
a·a的几何意义是向量a在向量a上的投影向量与向量a的数量积.
|a|2=x2+y2,即|a|=.
(2) ①=(x2-x1,y2-y1).
②||=.
③表示A,B两点间的距离.
AB=.
(3) ①cos θ=.
②x1x2+y1y2=0.
③成立.
x1x2+y1y2=0
例1 由题意,得=(1,1),=(-3,3),
所以·=0,即AB⊥AC,
所以△ABC是直角三角形.
跟踪训练 由题意,得=-=(-1,k-3).
①当A=90°,
即·=2+3k=0时,k=-;
②当B=90°,
即·=-2+3k-9=0时,k=;
③当C=90°,
即·=-1+k2-3k=0时,k=.
综上,k的值为-或或或.
例2 设x=(m,n),
则解得
所以x=.
跟踪训练 或 设单位向量为(x,y),则解得或所以所求的单位向量为或(-,).
例3 (1) 因为a·b=·(-,-1)=-=0,所以a⊥b.
(2) |a|2=+=1,|b|2=3+1=4,
x·y=[a+(t2-2)b]·(-ka+t2b)=0,
即-k+4t2(t2-2)+(t2-kt2+2k)a·b=0,
所以k=4t4-8t2.
跟踪训练 (1) 由题意,得b=,|a|=2,
则|b|=1,所以|a|=2|b|.
因为a·b=-=0,所以a⊥b.
(2) 因为x⊥y,所以x·y=0.
由(1)得x·y=[a+(t+4)b]·(a+tb)=a2+t(t+4)b2=t2+4t+4=(t+2)2=0,
解得t=-2.
【检测反馈】
1. D 因为a-b=(2,1)-(-2,4)=(4,-3),所以|a-b|==5.
2. A 设b与a+b的夹角是θ,因为a⊥b,所以a·b=m-2=0,即m=2,所以b=(2,1),可得a+b=(3,-1),所以cos θ====.
3. ACD 由a=(-1,3),b=(x,2),得a-2b=(-1-2x,-1).由(a-2b)⊥a,得2x+1-3=0,解得x=1.对于A,b=(1,2),故A正确;对于B,2a-b=(-3,4),则|2a-b|==5,故B错误;对于C,设向量a与向量b的夹角是θ,易得|a|=,|b|=,a·b=-1×1+3×2=5,则cos θ===.又0°≤θ≤180°,所以θ=45°,故C正确;对于D,向量a在向量b上的投影向量为b=b=(1,2),故D正确.故选ACD.
4. 因为O为坐标原点,=(1,2),=(-2,-1),且2=,所以P为线段AB的中点,则=(+)=,所以||==.
5. (1) 由题意,得=(2,3)-(-1,-2)=(3,5),=(-2,-1)-(-1,-2)=(-1,1),
所以·=3×(-1)+5×1=2.
(2) 由题意,得-t=(3,5)-t(-2,-1)=(3+2t,5+t),=(2,3).
因为(-t)·=0,
所以2(3+2t)+3(5+t)=0,
解得t=-3.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
