沪科版七下(2024版)10.1.2 垂线及基本事实 教案
文档属性
| 名称 | 沪科版七下(2024版)10.1.2 垂线及基本事实 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 16.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 14:54:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《10.1.2 垂线及基本事实》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《10.1.2 垂线及基本事实》是沪科版七年级下册第10章《相交线、平行线与平移》的第一节第二课时的内容。它是初中几何中“图形与几何”模块的核心内容,承接对顶角知识,进一步深化对直线位置关系的理解。教材通过生活实例(如十字路口、地砖、围棋盘)和动手操作(如折纸、作图)引导学生感知垂线的存在性与唯一性,培养学生用数学眼光观察世界的意识。
学习者分析 七年级学生已具备角、直线相交等基础知识,但对垂线的抽象定义的几何意义理解尚浅。学生能够通过直观操作(如用三角板画垂线)初步感知垂线的特征,但在从具体情境中抽象出几何模型时存在困难,需教师引导。此外,学生空间想象能力参差不齐,部分学生易混淆“垂线”与“垂直线段”的概念,需通过对比分析强化认知。
教学目标 1.理解垂线的定义及掌握垂线的画法。 2.掌握“同一平面内,过一点有且只有一条直线与已知直线垂直”的基本事实,并能运用其解决简单实际问题。 3.感受垂线在生活中的应用价值,体会数学与生活的紧密联系,培养严谨的数学思维和勇于质疑的科学态度。
教学重点 垂线的定义、画法及“同一平面内,过一点有且只有一条直线与已知直线垂直”的基本事实。
教学难点 引导学生从操作活动中抽象出“同一平面内,过一点有且只有一条直线与已知直线垂直”的几何意义,突破从直观感知到逻辑证明的思维瓶颈。
学习活动设计
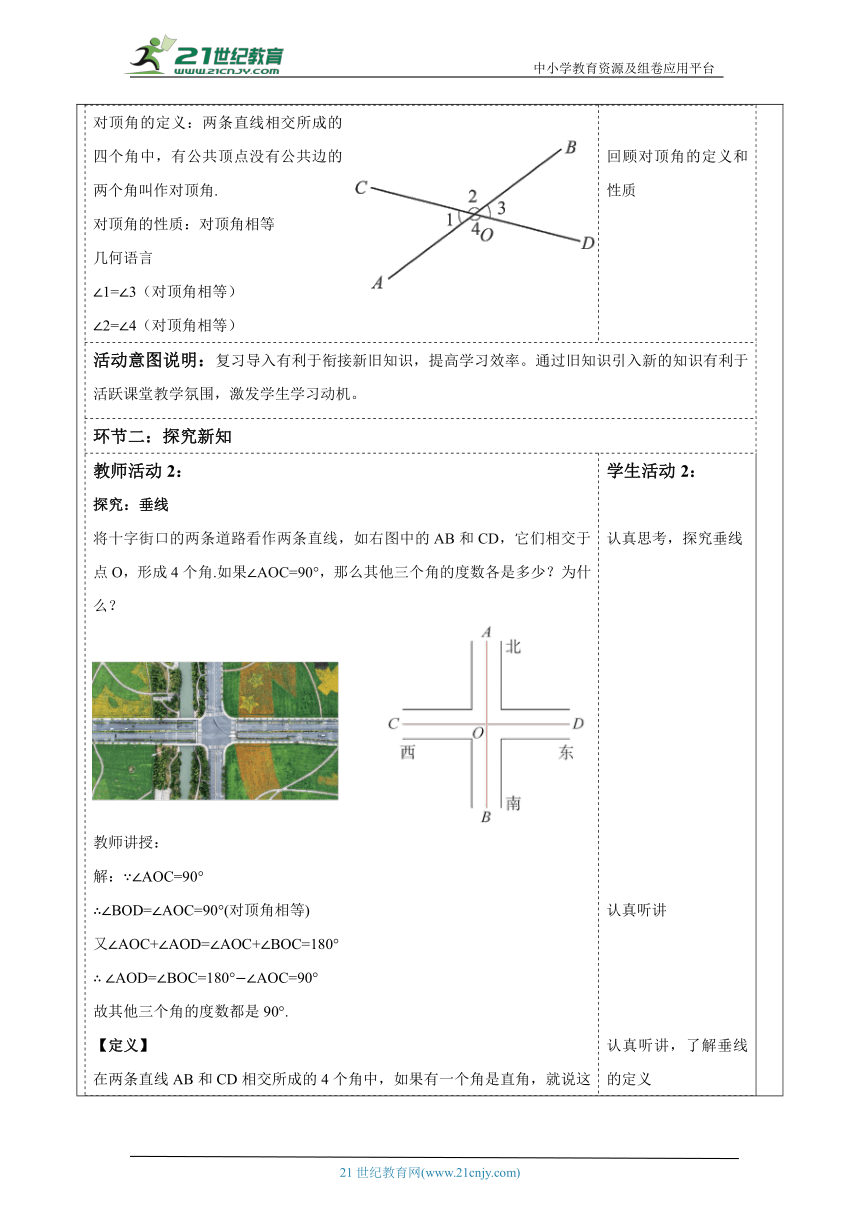
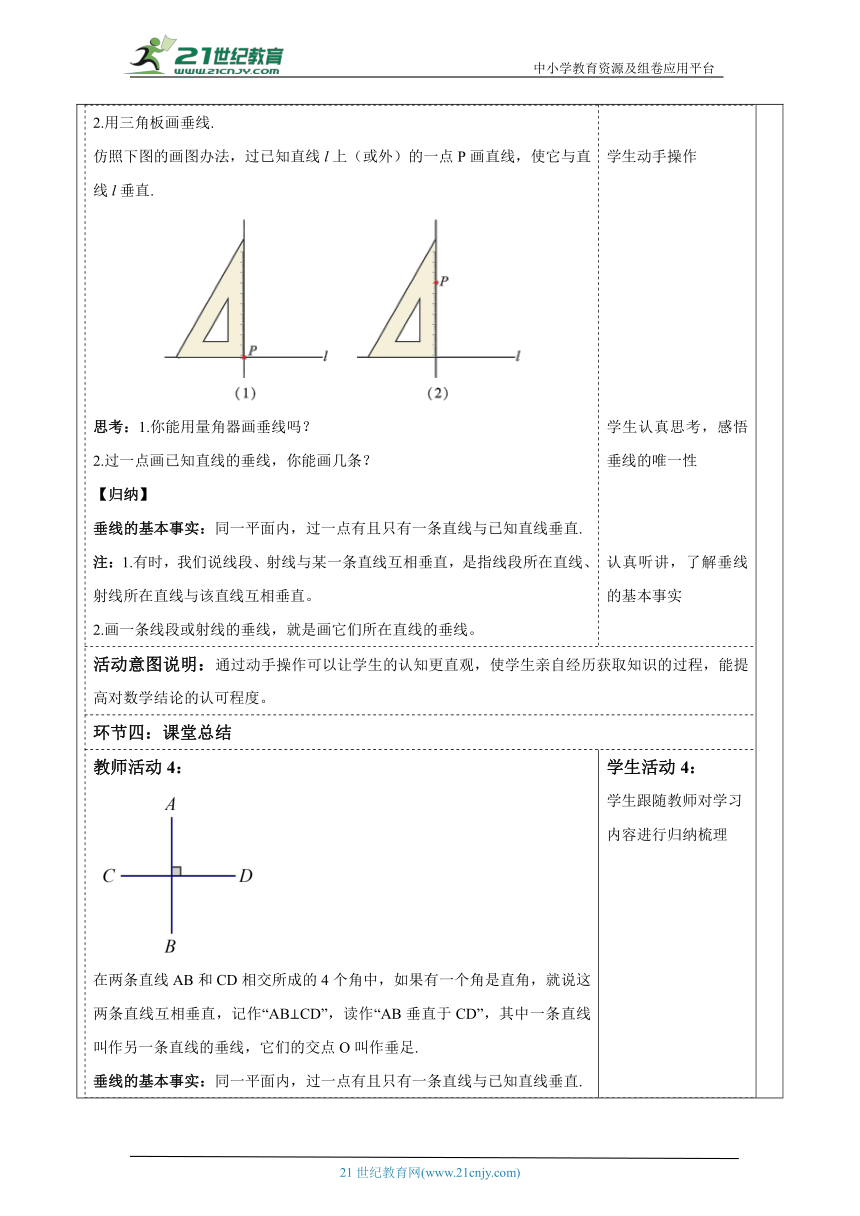
教师活动学生活动环节一:新知导入教师活动1: 教师提问:什么是对顶角?对顶角有什么性质? 对顶角的定义:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角. 对顶角的性质:对顶角相等 几何语言 ∠1=∠3(对顶角相等) ∠2=∠4(对顶角相等)学生活动1: 认真思考,举手回答问题 回顾对顶角的定义和性质活动意图说明:复习导入有利于衔接新旧知识,提高学习效率。通过旧知识引入新的知识有利于活跃课堂教学氛围,激发学生学习动机。环节二:探究新知教师活动2: 探究:垂线 将十字街口的两条道路看作两条直线,如右图中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他三个角的度数各是多少?为什么? 教师讲授: 解:∵∠AOC=90° ∴∠BOD=∠AOC=90°(对顶角相等) 又∠AOC+∠AOD=∠AOC+∠BOC=180° ∴ ∠AOD=∠BOC=180°∠AOC=90° 故其他三个角的度数都是90°. 【定义】 在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足. 【联系生活】 日常生活中两条直线垂直的例子很多,如下图所示的地砖间的缝隙线,围棋盘上的方格线等. 你能再举出一些两条直线互相垂直的例子吗?学生活动2: 认真思考,探究垂线 认真听讲 认真听讲,了解垂线的定义 认真听讲,了解生活中的垂线 活动意图说明:通过生活实例(如十字路口、地砖、围棋盘)引导学生感知垂线,体会到数学与生活处处有联系,培养学生用数学眼光观察世界的意识。环节三:动手操作教师活动3: 探究二:关于垂线的基本事实 操作 1.用折纸方法画垂线. 仿照下图所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线. 2.用三角板画垂线. 仿照下图的画图办法,过已知直线l上(或外)的一点P画直线,使它与直线l垂直. 思考:1.你能用量角器画垂线吗? 2.过一点画已知直线的垂线,你能画几条? 【归纳】 垂线的基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直. 注:1.有时,我们说线段、射线与某一条直线互相垂直,是指线段所在直线、射线所在直线与该直线互相垂直。 2.画一条线段或射线的垂线,就是画它们所在直线的垂线。学生活动3: 学生动手操作 学生动手操作 学生认真思考,感悟垂线的唯一性 认真听讲,了解垂线的基本事实活动意图说明:通过动手操作可以让学生的认知更直观,使学生亲自经历获取知识的过程,能提高对数学结论的认可程度。环节四:课堂总结教师活动4: 在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足. 垂线的基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直.学生活动4: 学生跟随教师对学习内容进行归纳梳理 活动意图说明:对课堂教学进行归纳梳理,给学生一个整体印象,促进学生掌握知识总结规律。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.如图,在同一平面内过点画直线的垂线,能画( ) A.0条 B.1条 C.2条 D.无数条 2.如图,已知直线与直线相交于点O,平分,于点O,,则( ) A. B. C. D. 3.下列各图中,过直线外的点画直线的垂线,三角尺操作正确的是( ) A. B. C. D. 选做题: 4.若A,C是直线l上两点,B,D是直线l外两点,则过点A能画 条直线与l垂直;过点B能画 条直线与l垂直;过C,D两点(填“能画”“不能画”或“不一定能画”) 一条直线与已知直线垂直. 5.如图,,直线都经过点C.若,则的度数为 . 6.如图所示,王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.你能说出这里面的道理吗 . 【综合拓展类作业】 7.如图,P是的边上的一点,点A、O、P都在格点上,在方格纸上按要求画图,并标注相应的字母. (1)过点P画的垂线,垂足为D. (2)过点A画的平行线.
作业设计 【知识技能类作业】 必做题: 1.如图,过直线上一点作,直线经过点,若,则的度数是( ) A. B. C. D. 2.如图,过点P作线段的垂线,垂足在( ) A.线段上 B.线段的延长线上 C.线段的反向延长线上 D.直线外 3.下列说法正确的是 ( ) A.过线段外一点不一定能作出它的垂线 B.过直线m外一点A和直线m上一点B可画一条直线与m垂直 C.只能过直线外一点画一条直线和这条直线垂直 D.过任意一点均可作一条直线的垂线 【综合拓展类作业】 4.如图,直线.相交于点..平分,平分. (1)求的度数: (2)判断射线与之间的位置关系.并说明理由.
教学反思 本节课通过“十字路口”的生活情境导入,结合折纸实验和三角板画垂线操作,有效调动了学生的参与积极性。在探究“同一平面内,过一点有且只有一条直线与已知直线垂直”环节,学生通过折纸和三角板画垂线的方法抽象出基本事实,较好地实现了“做中学”的教学理念,但需进一步优化推理过程的引导策略,促进学生几何思维从经验型向理论型转化。
21世纪教育网(www.21cnjy.com)
分课时教学设计
《10.1.2 垂线及基本事实》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 《10.1.2 垂线及基本事实》是沪科版七年级下册第10章《相交线、平行线与平移》的第一节第二课时的内容。它是初中几何中“图形与几何”模块的核心内容,承接对顶角知识,进一步深化对直线位置关系的理解。教材通过生活实例(如十字路口、地砖、围棋盘)和动手操作(如折纸、作图)引导学生感知垂线的存在性与唯一性,培养学生用数学眼光观察世界的意识。
学习者分析 七年级学生已具备角、直线相交等基础知识,但对垂线的抽象定义的几何意义理解尚浅。学生能够通过直观操作(如用三角板画垂线)初步感知垂线的特征,但在从具体情境中抽象出几何模型时存在困难,需教师引导。此外,学生空间想象能力参差不齐,部分学生易混淆“垂线”与“垂直线段”的概念,需通过对比分析强化认知。
教学目标 1.理解垂线的定义及掌握垂线的画法。 2.掌握“同一平面内,过一点有且只有一条直线与已知直线垂直”的基本事实,并能运用其解决简单实际问题。 3.感受垂线在生活中的应用价值,体会数学与生活的紧密联系,培养严谨的数学思维和勇于质疑的科学态度。
教学重点 垂线的定义、画法及“同一平面内,过一点有且只有一条直线与已知直线垂直”的基本事实。
教学难点 引导学生从操作活动中抽象出“同一平面内,过一点有且只有一条直线与已知直线垂直”的几何意义,突破从直观感知到逻辑证明的思维瓶颈。
学习活动设计
教师活动学生活动环节一:新知导入教师活动1: 教师提问:什么是对顶角?对顶角有什么性质? 对顶角的定义:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角. 对顶角的性质:对顶角相等 几何语言 ∠1=∠3(对顶角相等) ∠2=∠4(对顶角相等)学生活动1: 认真思考,举手回答问题 回顾对顶角的定义和性质活动意图说明:复习导入有利于衔接新旧知识,提高学习效率。通过旧知识引入新的知识有利于活跃课堂教学氛围,激发学生学习动机。环节二:探究新知教师活动2: 探究:垂线 将十字街口的两条道路看作两条直线,如右图中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他三个角的度数各是多少?为什么? 教师讲授: 解:∵∠AOC=90° ∴∠BOD=∠AOC=90°(对顶角相等) 又∠AOC+∠AOD=∠AOC+∠BOC=180° ∴ ∠AOD=∠BOC=180°∠AOC=90° 故其他三个角的度数都是90°. 【定义】 在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足. 【联系生活】 日常生活中两条直线垂直的例子很多,如下图所示的地砖间的缝隙线,围棋盘上的方格线等. 你能再举出一些两条直线互相垂直的例子吗?学生活动2: 认真思考,探究垂线 认真听讲 认真听讲,了解垂线的定义 认真听讲,了解生活中的垂线 活动意图说明:通过生活实例(如十字路口、地砖、围棋盘)引导学生感知垂线,体会到数学与生活处处有联系,培养学生用数学眼光观察世界的意识。环节三:动手操作教师活动3: 探究二:关于垂线的基本事实 操作 1.用折纸方法画垂线. 仿照下图所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线. 2.用三角板画垂线. 仿照下图的画图办法,过已知直线l上(或外)的一点P画直线,使它与直线l垂直. 思考:1.你能用量角器画垂线吗? 2.过一点画已知直线的垂线,你能画几条? 【归纳】 垂线的基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直. 注:1.有时,我们说线段、射线与某一条直线互相垂直,是指线段所在直线、射线所在直线与该直线互相垂直。 2.画一条线段或射线的垂线,就是画它们所在直线的垂线。学生活动3: 学生动手操作 学生动手操作 学生认真思考,感悟垂线的唯一性 认真听讲,了解垂线的基本事实活动意图说明:通过动手操作可以让学生的认知更直观,使学生亲自经历获取知识的过程,能提高对数学结论的认可程度。环节四:课堂总结教师活动4: 在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足. 垂线的基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直.学生活动4: 学生跟随教师对学习内容进行归纳梳理 活动意图说明:对课堂教学进行归纳梳理,给学生一个整体印象,促进学生掌握知识总结规律。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.如图,在同一平面内过点画直线的垂线,能画( ) A.0条 B.1条 C.2条 D.无数条 2.如图,已知直线与直线相交于点O,平分,于点O,,则( ) A. B. C. D. 3.下列各图中,过直线外的点画直线的垂线,三角尺操作正确的是( ) A. B. C. D. 选做题: 4.若A,C是直线l上两点,B,D是直线l外两点,则过点A能画 条直线与l垂直;过点B能画 条直线与l垂直;过C,D两点(填“能画”“不能画”或“不一定能画”) 一条直线与已知直线垂直. 5.如图,,直线都经过点C.若,则的度数为 . 6.如图所示,王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.你能说出这里面的道理吗 . 【综合拓展类作业】 7.如图,P是的边上的一点,点A、O、P都在格点上,在方格纸上按要求画图,并标注相应的字母. (1)过点P画的垂线,垂足为D. (2)过点A画的平行线.
作业设计 【知识技能类作业】 必做题: 1.如图,过直线上一点作,直线经过点,若,则的度数是( ) A. B. C. D. 2.如图,过点P作线段的垂线,垂足在( ) A.线段上 B.线段的延长线上 C.线段的反向延长线上 D.直线外 3.下列说法正确的是 ( ) A.过线段外一点不一定能作出它的垂线 B.过直线m外一点A和直线m上一点B可画一条直线与m垂直 C.只能过直线外一点画一条直线和这条直线垂直 D.过任意一点均可作一条直线的垂线 【综合拓展类作业】 4.如图,直线.相交于点..平分,平分. (1)求的度数: (2)判断射线与之间的位置关系.并说明理由.
教学反思 本节课通过“十字路口”的生活情境导入,结合折纸实验和三角板画垂线操作,有效调动了学生的参与积极性。在探究“同一平面内,过一点有且只有一条直线与已知直线垂直”环节,学生通过折纸和三角板画垂线的方法抽象出基本事实,较好地实现了“做中学”的教学理念,但需进一步优化推理过程的引导策略,促进学生几何思维从经验型向理论型转化。
21世纪教育网(www.21cnjy.com)
