沪科版七下(2024版)10.1.2 垂线及基本事实 课件
文档属性
| 名称 | 沪科版七下(2024版)10.1.2 垂线及基本事实 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 14:54:49 | ||
图片预览




文档简介
(共26张PPT)
第10章 相交线、平行线与平移
10.1.2 垂线及基本事实
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解垂线的定义及掌握垂线的画法。
01
掌握“同一平面内,过一点有且只有一条直线与已知直线垂直”的基本事实,并能运用其解决简单实际问题。
02
感受垂线在生活中的应用价值,体会数学与生活的紧密联系,培养严谨的数学思维和勇于质疑的科学态度。
03
02
新知导入
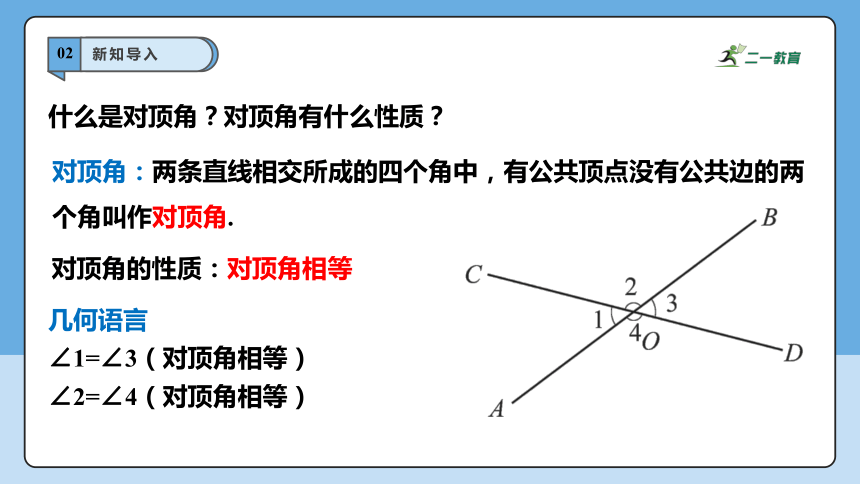
什么是对顶角?对顶角有什么性质?
对顶角:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角.
对顶角的性质:对顶角相等
几何语言
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
02
新知探究
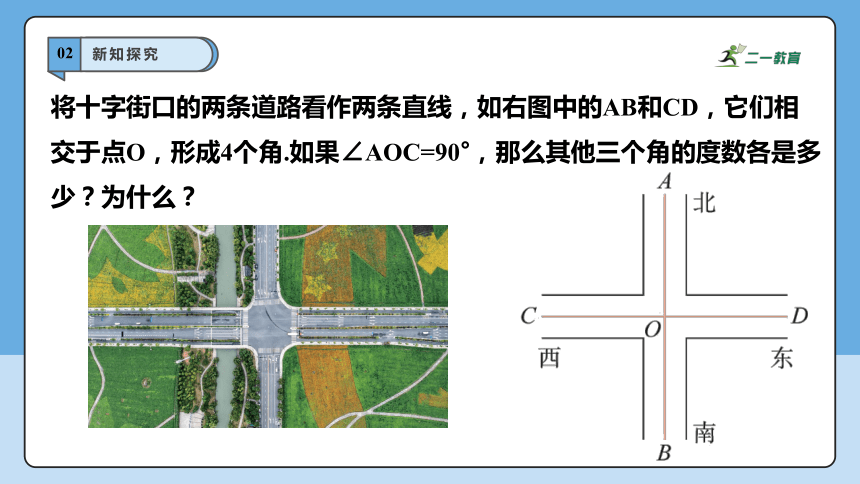
将十字街口的两条道路看作两条直线,如右图中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他三个角的度数各是多少?为什么?
03
新知探究
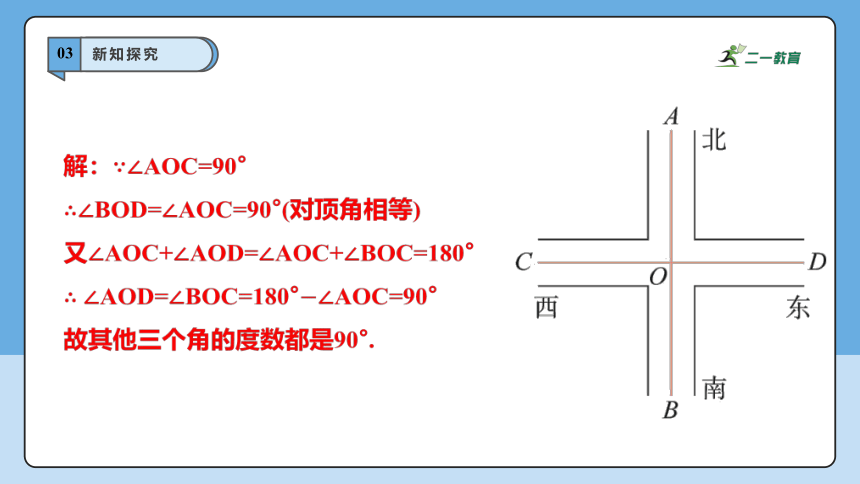
解:∵∠AOC=90°
∴∠BOD=∠AOC=90°(对顶角相等)
又∠AOC+∠AOD=∠AOC+∠BOC=180°
∴ ∠AOD=∠BOC=180°∠AOC=90°
故其他三个角的度数都是90°.
定义
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足.
03
新知探究
你能再举出一些两条直线互相垂直的例子吗?
日常生活中两条直线垂直的例子很多,如下图所示的地砖间的缝隙线,围棋盘上的方格线等.
03
新知探究
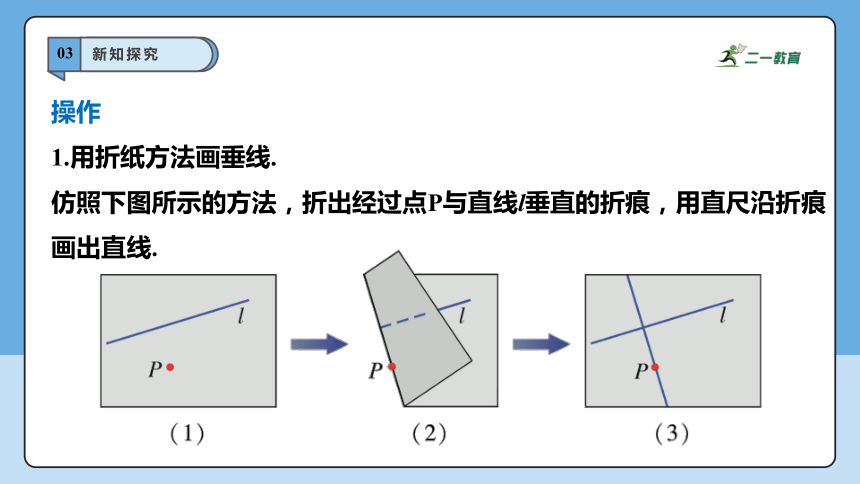
操作
1.用折纸方法画垂线.
仿照下图所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线.
03
新知探究
2.用三角板画垂线.
仿照下图的画图办法,过已知直线l上(或外)的一点P画直线,使它与直线l垂直.
能用量角器画垂线吗?
03
新知探究
过一点画已知直线的垂线,你能画几条?
垂线的基本事实
同一平面内,过一点有且只有一条直线与已知直线垂直.
注:1.有时,我们说线段、射线与某一条直线互相垂直,是指线段所在直线、射线所在直线与该直线互相垂直。
2.画一条线段或射线的垂线,就是画它们所在直线的垂线。
04
课堂练习
【知识技能类作业】必做题:
1.如图,在同一平面内过点A画直线m的垂线,能画( )
A.0条 B.1条 C.2条 D.无数条
B
m
04
课堂练习
【知识技能类作业】必做题:
2.如图,已知直线AB与直线CD相交于点O,OE平分∠BOD,OF⊥CD于点O,∠AOF=4∠BOE,则∠AOC=( )
A.28°
B.30°
C.32°
D.34°
B
04
课堂练习
【知识技能类作业】必做题:
3.下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是( )
C
A
B
C
D
04
课堂练习
【知识技能类作业】选做题:
4.若A,C是直线l上两点,B,D是直线l外两点,则过点A能画 条直线与l垂直;过点B能画 条直线与l垂直;过C,D两点(填“能画”“不能画”或“不一定能画”) 一条直线与已知直线垂直.
5.如图,,直线都经过点C.若,则的度数为 .
1
1
不一定能画
45°
04
课堂练习
6.如图所示,王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.你能说出这里面的道理吗 .
过一点有且只有一条直线垂直于已知直线
04
课堂练习
【综合拓展类作业】
7.如图,P是∠AOB的OB边上的一点,点A、O、P都在格点上,在方格纸上按要求画图,并标注相应的字母.
(1)过点P画OA的垂线,垂足为D.
(2)过点A画OB的平行线AE.
05
课堂小结
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足.
垂线的基本事实
同一平面内,过一点有且只有一条直线与已知直线垂直.
06
作业布置
【知识技能类作业】
1.如图,过直线BC上一点O作AO⊥BC,直线EF经过点O,若∠COF:∠AOF=1:2,则∠AOE的度数是( )
A.110°
B.120°
C.135°
D.150°
B
06
作业布置
2.如图,过点P作线段AB的垂线,垂足在( )
A.线段AB上
B.线段AB的延长线上
C.线段AB的反向延长线上
D.直线AB外
B
06
作业布置
3.下列说法正确的是 ( )
A.过线段外一点不一定能作出它的垂线
B.过直线m外一点A和直线m上一点B可画一条直线与m垂直
C.只能过直线外一点画一条直线和这条直线垂直
D.过任意一点均可作一条直线的垂线
D
06
作业布置
【综合拓展类作业】
4.如图,直线AB.CD相交于点O.∠AOC=28°.OE平分∠AOD,OF平分∠BOD.
(1)求∠BOF的度数:
(2)判断射线OE与OF之间的位置关系.并说明理由.
(1)解:∵∠BOD=∠AOC,∠AOC=28°,
∴∠BOD=28°,
∵OF平分∠BOD,
∴∠BOF=∠BOD= ×28°=14°;
06
作业布置
【综合拓展类作业】
(2)解:垂直,理由如下:
∵∠AOC=28°,
∴∠AOD=180°-∠AOC=180°-28°=152°,
∵OE平分∠AOD,OF平分∠BOD,
∴∠EOD=∠AOD=×152°=76°,∠DOF=∠BOD=×28°=14°,
∴∠EOF=∠EOD+∠DOF=76°+14°=90°,
∴OE⊥OF.
07
板书设计
垂线:
过一点作已知直线的垂线:
基本事实:
10.1.2 垂线及基本事实
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第10章 相交线、平行线与平移
10.1.2 垂线及基本事实
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解垂线的定义及掌握垂线的画法。
01
掌握“同一平面内,过一点有且只有一条直线与已知直线垂直”的基本事实,并能运用其解决简单实际问题。
02
感受垂线在生活中的应用价值,体会数学与生活的紧密联系,培养严谨的数学思维和勇于质疑的科学态度。
03
02
新知导入
什么是对顶角?对顶角有什么性质?
对顶角:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角.
对顶角的性质:对顶角相等
几何语言
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
02
新知探究
将十字街口的两条道路看作两条直线,如右图中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他三个角的度数各是多少?为什么?
03
新知探究
解:∵∠AOC=90°
∴∠BOD=∠AOC=90°(对顶角相等)
又∠AOC+∠AOD=∠AOC+∠BOC=180°
∴ ∠AOD=∠BOC=180°∠AOC=90°
故其他三个角的度数都是90°.
定义
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足.
03
新知探究
你能再举出一些两条直线互相垂直的例子吗?
日常生活中两条直线垂直的例子很多,如下图所示的地砖间的缝隙线,围棋盘上的方格线等.
03
新知探究
操作
1.用折纸方法画垂线.
仿照下图所示的方法,折出经过点P与直线l垂直的折痕,用直尺沿折痕画出直线.
03
新知探究
2.用三角板画垂线.
仿照下图的画图办法,过已知直线l上(或外)的一点P画直线,使它与直线l垂直.
能用量角器画垂线吗?
03
新知探究
过一点画已知直线的垂线,你能画几条?
垂线的基本事实
同一平面内,过一点有且只有一条直线与已知直线垂直.
注:1.有时,我们说线段、射线与某一条直线互相垂直,是指线段所在直线、射线所在直线与该直线互相垂直。
2.画一条线段或射线的垂线,就是画它们所在直线的垂线。
04
课堂练习
【知识技能类作业】必做题:
1.如图,在同一平面内过点A画直线m的垂线,能画( )
A.0条 B.1条 C.2条 D.无数条
B
m
04
课堂练习
【知识技能类作业】必做题:
2.如图,已知直线AB与直线CD相交于点O,OE平分∠BOD,OF⊥CD于点O,∠AOF=4∠BOE,则∠AOC=( )
A.28°
B.30°
C.32°
D.34°
B
04
课堂练习
【知识技能类作业】必做题:
3.下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是( )
C
A
B
C
D
04
课堂练习
【知识技能类作业】选做题:
4.若A,C是直线l上两点,B,D是直线l外两点,则过点A能画 条直线与l垂直;过点B能画 条直线与l垂直;过C,D两点(填“能画”“不能画”或“不一定能画”) 一条直线与已知直线垂直.
5.如图,,直线都经过点C.若,则的度数为 .
1
1
不一定能画
45°
04
课堂练习
6.如图所示,王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.你能说出这里面的道理吗 .
过一点有且只有一条直线垂直于已知直线
04
课堂练习
【综合拓展类作业】
7.如图,P是∠AOB的OB边上的一点,点A、O、P都在格点上,在方格纸上按要求画图,并标注相应的字母.
(1)过点P画OA的垂线,垂足为D.
(2)过点A画OB的平行线AE.
05
课堂小结
在两条直线AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直,记作“AB⊥CD”,读作“AB垂直于CD”,其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足.
垂线的基本事实
同一平面内,过一点有且只有一条直线与已知直线垂直.
06
作业布置
【知识技能类作业】
1.如图,过直线BC上一点O作AO⊥BC,直线EF经过点O,若∠COF:∠AOF=1:2,则∠AOE的度数是( )
A.110°
B.120°
C.135°
D.150°
B
06
作业布置
2.如图,过点P作线段AB的垂线,垂足在( )
A.线段AB上
B.线段AB的延长线上
C.线段AB的反向延长线上
D.直线AB外
B
06
作业布置
3.下列说法正确的是 ( )
A.过线段外一点不一定能作出它的垂线
B.过直线m外一点A和直线m上一点B可画一条直线与m垂直
C.只能过直线外一点画一条直线和这条直线垂直
D.过任意一点均可作一条直线的垂线
D
06
作业布置
【综合拓展类作业】
4.如图,直线AB.CD相交于点O.∠AOC=28°.OE平分∠AOD,OF平分∠BOD.
(1)求∠BOF的度数:
(2)判断射线OE与OF之间的位置关系.并说明理由.
(1)解:∵∠BOD=∠AOC,∠AOC=28°,
∴∠BOD=28°,
∵OF平分∠BOD,
∴∠BOF=∠BOD= ×28°=14°;
06
作业布置
【综合拓展类作业】
(2)解:垂直,理由如下:
∵∠AOC=28°,
∴∠AOD=180°-∠AOC=180°-28°=152°,
∵OE平分∠AOD,OF平分∠BOD,
∴∠EOD=∠AOD=×152°=76°,∠DOF=∠BOD=×28°=14°,
∴∠EOF=∠EOD+∠DOF=76°+14°=90°,
∴OE⊥OF.
07
板书设计
垂线:
过一点作已知直线的垂线:
基本事实:
10.1.2 垂线及基本事实
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
