第二十七章圆同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十七章圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.《九章算术》是我国古代数学经典著作,其中《方田》章给出计算弧田面积所用的经验公式:弧田面积(弦矢矢).弧田(如图所示)由圆弧和其所对弦围成,公式中的“弦”指圆弧所对的弦,“矢”指半径长与圆心O到弦的距离(d)之差.若“弦”为24,d为5,根据上述经验公式计算,该弧田的面积为( )
A.80 B.100 C.104 D.128
2.如图,是⊙O的直径,弦,,若动点M以的速度从C点出发沿着C到A的方向运动,点N以的速度从A点出发沿着A到B的方向运动,当点M到达点A时,点N也随之停止运动,设运动时间为,当是直角三角形时,t的值为( )
A. B.5s C. D.或
3.如图,的弦,为的中点,且,则的半径为( )
A.8 B.6 C.5 D.4
4.如图,小红同学要用纸板制作一个高4cm,底面周长是6πcm的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是( )
A.12πcm2 B.15πcm2 C.18πcm2 D.24πcm2
5.如图所示,C、D为半圆O的三等分点,AB为直径,下列结论:①AD=CD=BC;②∠AOD=∠DOC=∠BOC;③四边形ADCO为菱形,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
6.如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )
A.24° B.26° C.48° D.66°
7.已知一个扇形的面积为,所含的圆心角为,则半径为( )
A.20cm B.24cm C.26cm D.30cm
8.如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是( )
A.1cm B.2cm C.8cm D.2cm或8cm
9.如图,是的弦,半径于点B,且,,则的长为( )
A.1 B.2 C.2.5 D.3
10.有一题目:“已知;点为的外心,,求.”嘉嘉的解答为:画以及它的外接圆,连接,,如图.由,得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的值.”,下列判断正确的是( )
A.淇淇说的对,且的另一个值是115°
B.淇淇说的不对,就得65°
C.嘉嘉求的结果不对,应得50°
D.两人都不对,应有3个不同值
11.如图,在中,弦,,则弦心距的长是( )
A.3 B.4 C.5 D.6
12.如图,是等边的外接圆,点是弧上一动点(不与,重合),下列结论:①;②;③当最长时,;④,其中一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,某传送带的一个转动轮的半径为20cm,当物体从A传送4cm至B时,那么这个转动轮转了 度.(取3.14,结果保留四个有效数字)
14.如图,周长为20cm,,圆是的内切圆,圆的切线与、相交于点、,则的周长为 cm.
15.经过点A且半径为3的圆的圆心的轨迹
16.某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 .
17.如图,电线杆的顶上有一盏高为6 m的路灯,电线杆底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处.若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子BC扫过的面积为 m2.
三、解答题
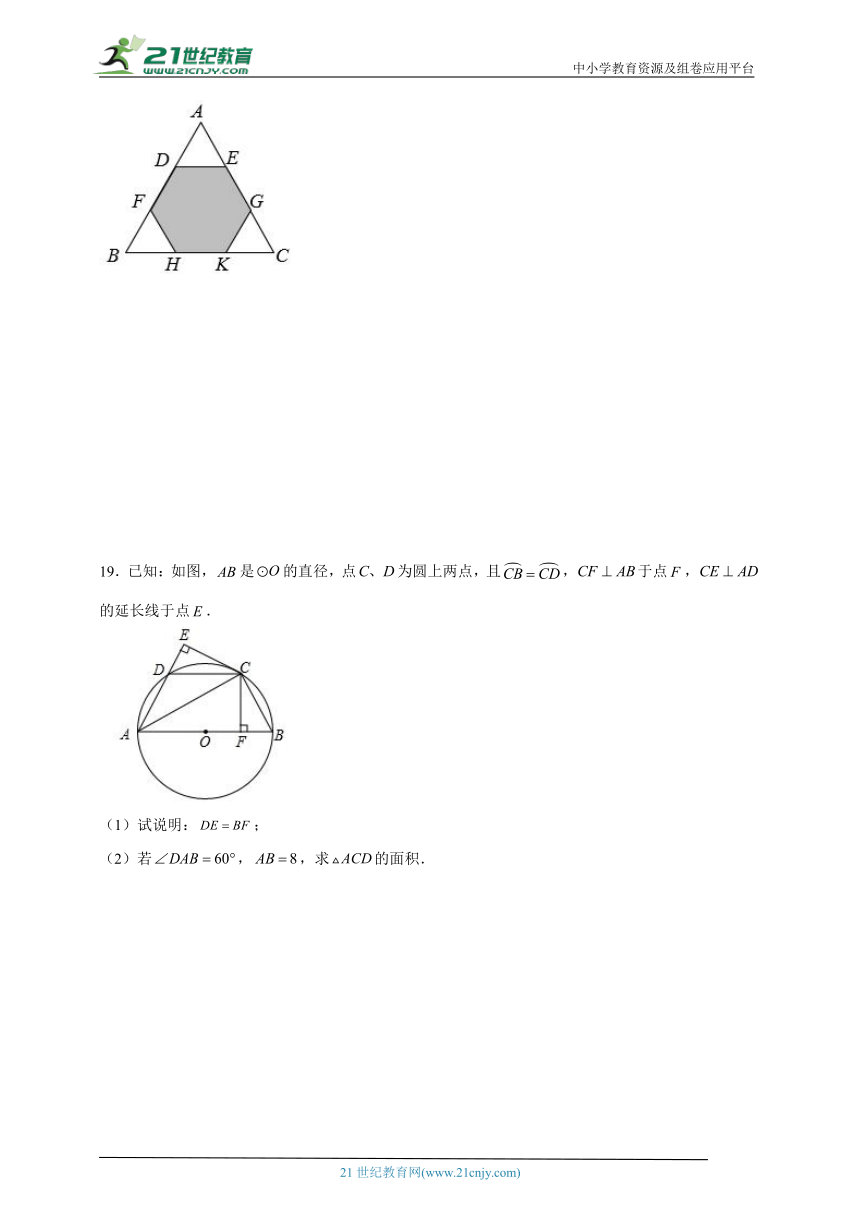
18.如图,把边长为6的正三角形剪去三个三角形得到一个正六边形,求这个正六边形的面积.
19.已知:如图,是的直径,点为圆上两点,且,于点,的延长线于点.
(1)试说明:;
(2)若,,求的面积.
20.如图,在中,直径弦于点E,若,,求的长.
21.已知圆环的大圆半径R=4.56cm,小圆半径r=2.47cm,试用计算器求圆环的面积(结果保留一位小数,π取3.142).
22.如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm,求⊙O的半径.
23.矩形是正多边形吗?菱形呢?正方形呢?为什么?
24.如图,在中,,以为直径的交于点D,切线交于点E.
(1)求证:;
(2)若,,求的长.
《第二十七章圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B A C B D B A
题号 11 12
答案 A C
1.D
【分析】本题考查了弧田面积计算问题,也考查了理解与运算能力.根据题意画出图形,结合图形利用直角三角形的边角关系求出矢和弦的值,代入公式计算求值即可.
【详解】解:如图,过点O作于点C,
由题意可知,
∴,
在中, ,
∴矢,
∴该弧田的面积为,
故选:D.
2.D
【分析】应分两种情况进行讨论:①当时,为直角三角形,根据,可将时间求出;当时,为直角三角形,根据,可将时间求出.
【详解】解:如图,是直径,
.
又,,
根据勾股定理得到.
则,.
当点到达点时,点也随之停止运动,
.
①如图1,
当时,,则
.
故,即,解得.
②如图2,
当时,,
则,即,
解得.
综上所述,当或时,为直角三角形.
故选D.
【点睛】本题考查圆周角定理、相似三角形的性质、直角三角形的性质等知识的综合应用能力.在求时间时应分情况进行讨论,防止漏解.
3.C
【分析】连接,,由和是的半径,则,利用垂径定理可得,,再利用勾股定理即可求解.
【详解】解:连接,,如图所示:
和是的半径,
,
又为的中点,且,
,,
,
在中,,,
,
的半径为:5,
故选C.
【点睛】本题考查了垂径定理、勾股定理,熟练掌握勾股定理及垂径定理,借助辅助线解决问题是解题的关键.
4.B
【详解】∵底面周长是6π,
∴底面圆的半径为3cm,
∵高为4cm,
∴母线长5cm,
∴根据圆锥侧面积=底面周长×母线长,可得S=×6π×5=15πcm2.
故选B.
5.A
【分析】根据“在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相等”仔细找出等量关系即可.
【详解】∵C、D为半圆上三等分点,
∴,
根据在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相等知,AD=CD=BC,∠AOD=∠DOC=∠BOC=60°,
∵AO=OD=OC=OB,
∴△AOD≌△COD≌△COB,
∴△AOD和△COD是等边三角形,
∴OA=AD=DC=OC,
∴四边形ADCO为菱形,
∴三种说法都正确.
故选A.
【点睛】本题利用了在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相等和平角的概念求解.
6.C
【分析】直接利用圆周角求解.
【详解】解:∵点A是的中点,
∴,
∴∠AOB=2∠ADC=2×24°=48°.
故选:C.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
7.B
【分析】设扇形的半径为r,根据扇形的面积公式即可求出r的值.
【详解】解:设扇形的半径为r,
∵扇形的圆心角为150°,它的面积为240πcm2,
∴,
解得r=24.
故选B.
【点睛】本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.
8.D
【详解】试题分析:连接OA,如图:
∵OH⊥AB,AB=8cm,∴AH=4cm,∵OA=OC=5cm,∴由勾股定理可得OH=3cm,∴当直线向下平移到点H与点C重合时,直线与圆相切,∴CH=OC-OH=2cm;同理:当直线向上平移到与圆相切时,平移的距离=5+3=8cm,所以直线在原有位置移动2cm或8cm后与圆相切,故选D.
考点:垂径定理、勾股定理、直线与圆的位置关系.
9.B
【分析】连接,设,在中,用勾股定理求解即可.
【详解】解:连接,如图,
∴,
设,
∵,
∴,
在中,,即,解得:,
∴,
故选:B.
【点睛】本题考查垂径定理,涉及到勾股定理解三角形,灵活运用所学知识是关键.
10.A
【分析】直接利用圆内接四边形的性质结合圆周角定理得出答案.
【详解】解:如图所示:
∵∠BOC=130°,
∴∠A=65°,
∠A还应有另一个不同的值∠A′与∠A互补.
故∠A′=180° 65°=115°.
故选:A.
【点睛】此题主要考查了三角形的外接圆,正确分类讨论是解题关键.
11.A
【分析】由垂径定理得到AC=4,再利用勾股定理,即可求出OC的长度.
【详解】解:根据题意,
∵为弦心距,
∴⊥AB,
∴AC=BC=,
在直角三角形AOC中,由勾股定理,得
.
故选:A.
【点睛】本题考查了垂径定理,以及勾股定理,解题的关键是掌握所学的知识,正确求出OC的长度.
12.C
【分析】根据等边三角形的性质可得,从而得到∠ADB=∠BDC,故①正确;根据点是上一动点,可得不一定等于,故②错误;当最长时,DB为圆O的直径,可得∠BCD=90°,再由是等边的外接圆,可得∠ABD=∠CBD=30°,可得,故③正确;延长DA至点E,使AE=AD,证明△ABE≌△CBD,可得BD=AE,∠ABE=∠DBC,从而得到△BDE是等边三角形,可得到DE=BD,故④正确;即可求解.
【详解】解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∴,
∴∠ADB=∠BDC,故①正确;
∵点是上一动点,
∴不一定等于,
∴DA=DC不一定成立,故②错误;
当最长时,DB为圆O的直径,
∴∠BCD=90°,
∵是等边的外接圆,∠ABC=60°,
∴BD⊥AC,
∴∠ABD=∠CBD=30°,
∴,故③正确;
如图,延长DA至点E,使AE=DC,
∵四边形ABCD为圆O的内接四边形,
∴∠BCD+∠BAD=180°,
∵∠BAE+∠BAD=180°,
∴∠BAE=∠BCD,
∵AB=BC,AE=CD,
∴△ABE≌△CBD,
∴BD=BE,∠ABE=∠DBC,
∴∠ABE+∠ABD=∠DBC+∠ABD=∠ABC=60°,
∴△BDE是等边三角形,
∴DE=BD,
∵DE=AD+AE=AD+CD,
∴,故④正确;
∴正确的有3个.
故选:C.
【点睛】本题主要考查了圆周角定理,三角形的外接圆,圆内接四边形的性质,垂径定理,等边三角形的判定和性质等知识,熟练掌握圆周角定理,三角形的外接圆,圆内接四边形的性质,垂径定理,等边三角形的判定和性质等知识是解题的关键.
13.36°
【分析】根据轮子转过的角度所对的弧长与线段AB的长相等可得.
【详解】解:4 =,
解得n=36°.
故答案是:36°.
【点睛】此题的关键是理解轮子转过的角度所对的弧长与线段AB的长相等,然后利用弧长公式求值即可.
14.
【分析】与的三边分别相切于、、,可得,,,, (cm),可得,即可求解.
【详解】解:如图,与的三边分别相切于、、,
是的内切圆,
的切线与、相交于点、,
,,
,,
周长为20cm,,
(cm),
周长为
().
故答案:.
【点睛】本题主要考查了切线长定理,掌握定理是解题的关键.
15.以A为圆心3为半径的圆
【分析】求圆心的轨迹实际上是求距A点3能画一个什么图形.
【详解】所求圆心的轨迹,就是到A点的距离等于3厘米的点的集合,因此是一个以A为圆心,半径为3的圆.
故答案为:以A为圆心3为半径的圆.
【点睛】此题所求圆心的轨迹,就是到顶点的距离等于定长的点的集合,因此应该是一个圆.
16..
【详解】解:如图,过F作FH⊥OE,连接OG,OM,ON
△OFH是等腰直角三角形,
∴FH=OFsin45°=,AB=,BC=2OE=2
∴矩形ABCD面积=2
∴S空白=2S扇形FOM+2SΔFOG
=
=
∴窗户的透光率=
故答案为:
17.28π
【分析】根据△CBD∽△CAE,即可得到CB=2,AC=8,再根据男孩以6m为半径绕电线杆走一圈,即可得出他在路灯下的影子BC扫过的面积.
【详解】解:如图所示,
∵AE∥BD,
∴△CBD∽△CAE,
,即
解得CB=2,
∴AC=8,
∴男孩以6m为半径绕电线杆走一圈,他在路灯下的影子BC扫过的面积为π×82-π×62=28πm2.
故答案为28π.
【点睛】本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键.
18.
【分析】先求出△ADE是等边三角形,再证明AD=DF=BF=2,即可求出=6.
【详解】解:∵六边形DFHKGE是正六边形,
∴∠EDF=∠DFH=∠FHK=∠KGE=∠GED=120°,DE=DF,
∴∠ADE=∠AED=60°,
∴△ADE是等边三角形,
∴AD=DE=AE,
同理:BH=BF=FH,
∴AD=DF=BF=2,
∴=6=6×=.
【点睛】本题主要考查的是正多边形和圆,熟知等边三角形的性质及正六边形的性质是解题的关键.
19.(1)答案见解析;(2).
【分析】(1)由可知,,;由得出,;由得出;进而可说明.
(2)由,,可知;在中,可得,在中可得;由圆内接四边形的对角互补知,有,在等腰三角形中,,根据可求得的面积.
【详解】解:(1)
,
在和中,
在和中,
(2),
在中
同理在中可得,
又圆内接四边形的对角互补
得
在中
为等腰三角形
的面积为.
【点睛】本题考查了全等三角形的判定与性质;圆内接四边形对角的关系;圆心角、弧、弦的关系等知识点.解题的关键在于判定三角形全等以及三角形的面积公式的表示.
20.8
【分析】本题考查了垂径定理,勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.连接,设,可得,代入数据即可求得的值,从而得到的长.
【详解】如图,连接,设,
则,.
∵直径弦于点E,
,
,
,
,(舍去),
,
.
21.
【分析】本题要求同学们能熟练应用计算器,会用科学计算器进行计算.
【详解】解:圆环的面积,
,
.
故答案为:.
【点睛】本题考查了利用计算器计算有理数的混合运算.解题的关键是掌握保留一位小数就是小数点后有一位小数,也就是精确到十分位.
22.5cm
【分析】首先连接OA,根据垂径定理可得CD⊥AB,AE=4,根据勾股定理求出OA的长度.
【详解】连接OA,CD为直径,且CD平分AB于E,
∴CD⊥AB,AE=AB=4cm,
在Rt△OAE中,
∴⊙O的半径为5cm.
23.矩形、菱形都不是正多边形,只有正方形是正多边形,理由见解析.
【分析】根据正多边形的性质特点即可判断.
【详解】矩形、菱形都不是正多边形,只有正方形是正多边形,
理由如下:因为正多边形不仅各边相等,而且各角也相等,所以正方形是正多边形.
矩形只是角相等,边不一定相等;菱形只是边相等,角不一定相等,故不是正多边形.
【点睛】此题主要考查正多边形的性质辨析,解题的关键是熟知正多边形的性质:正多边形各边相等,各角也相等.
24.(1)见解析
(2)
【分析】(1)连接,根据切线性质,等角对等边,证明.
(2)连接,根据圆的性质,切线的性质,勾股定理解答即可.
本题考查了切线的性质,圆的性质,勾股定理,熟练掌握切线的性质,勾股定理是解题的关键.
【详解】(1)证明:连接,
∵是切线,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
∴.
(2)解:连接.
∵,
∴,
∵是的直径,,
∴是的切线,
∴,
∴,
∵,
∴,
在中,,
∴,
设,在中,,
在中,,
∴,
解得,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十七章圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.《九章算术》是我国古代数学经典著作,其中《方田》章给出计算弧田面积所用的经验公式:弧田面积(弦矢矢).弧田(如图所示)由圆弧和其所对弦围成,公式中的“弦”指圆弧所对的弦,“矢”指半径长与圆心O到弦的距离(d)之差.若“弦”为24,d为5,根据上述经验公式计算,该弧田的面积为( )
A.80 B.100 C.104 D.128
2.如图,是⊙O的直径,弦,,若动点M以的速度从C点出发沿着C到A的方向运动,点N以的速度从A点出发沿着A到B的方向运动,当点M到达点A时,点N也随之停止运动,设运动时间为,当是直角三角形时,t的值为( )
A. B.5s C. D.或
3.如图,的弦,为的中点,且,则的半径为( )
A.8 B.6 C.5 D.4
4.如图,小红同学要用纸板制作一个高4cm,底面周长是6πcm的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是( )
A.12πcm2 B.15πcm2 C.18πcm2 D.24πcm2
5.如图所示,C、D为半圆O的三等分点,AB为直径,下列结论:①AD=CD=BC;②∠AOD=∠DOC=∠BOC;③四边形ADCO为菱形,其中正确的有( )
A.3个 B.2个 C.1个 D.0个
6.如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )
A.24° B.26° C.48° D.66°
7.已知一个扇形的面积为,所含的圆心角为,则半径为( )
A.20cm B.24cm C.26cm D.30cm
8.如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是( )
A.1cm B.2cm C.8cm D.2cm或8cm
9.如图,是的弦,半径于点B,且,,则的长为( )
A.1 B.2 C.2.5 D.3
10.有一题目:“已知;点为的外心,,求.”嘉嘉的解答为:画以及它的外接圆,连接,,如图.由,得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的值.”,下列判断正确的是( )
A.淇淇说的对,且的另一个值是115°
B.淇淇说的不对,就得65°
C.嘉嘉求的结果不对,应得50°
D.两人都不对,应有3个不同值
11.如图,在中,弦,,则弦心距的长是( )
A.3 B.4 C.5 D.6
12.如图,是等边的外接圆,点是弧上一动点(不与,重合),下列结论:①;②;③当最长时,;④,其中一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,某传送带的一个转动轮的半径为20cm,当物体从A传送4cm至B时,那么这个转动轮转了 度.(取3.14,结果保留四个有效数字)
14.如图,周长为20cm,,圆是的内切圆,圆的切线与、相交于点、,则的周长为 cm.
15.经过点A且半径为3的圆的圆心的轨迹
16.某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 .
17.如图,电线杆的顶上有一盏高为6 m的路灯,电线杆底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处.若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子BC扫过的面积为 m2.
三、解答题
18.如图,把边长为6的正三角形剪去三个三角形得到一个正六边形,求这个正六边形的面积.
19.已知:如图,是的直径,点为圆上两点,且,于点,的延长线于点.
(1)试说明:;
(2)若,,求的面积.
20.如图,在中,直径弦于点E,若,,求的长.
21.已知圆环的大圆半径R=4.56cm,小圆半径r=2.47cm,试用计算器求圆环的面积(结果保留一位小数,π取3.142).
22.如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm,求⊙O的半径.
23.矩形是正多边形吗?菱形呢?正方形呢?为什么?
24.如图,在中,,以为直径的交于点D,切线交于点E.
(1)求证:;
(2)若,,求的长.
《第二十七章圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B A C B D B A
题号 11 12
答案 A C
1.D
【分析】本题考查了弧田面积计算问题,也考查了理解与运算能力.根据题意画出图形,结合图形利用直角三角形的边角关系求出矢和弦的值,代入公式计算求值即可.
【详解】解:如图,过点O作于点C,
由题意可知,
∴,
在中, ,
∴矢,
∴该弧田的面积为,
故选:D.
2.D
【分析】应分两种情况进行讨论:①当时,为直角三角形,根据,可将时间求出;当时,为直角三角形,根据,可将时间求出.
【详解】解:如图,是直径,
.
又,,
根据勾股定理得到.
则,.
当点到达点时,点也随之停止运动,
.
①如图1,
当时,,则
.
故,即,解得.
②如图2,
当时,,
则,即,
解得.
综上所述,当或时,为直角三角形.
故选D.
【点睛】本题考查圆周角定理、相似三角形的性质、直角三角形的性质等知识的综合应用能力.在求时间时应分情况进行讨论,防止漏解.
3.C
【分析】连接,,由和是的半径,则,利用垂径定理可得,,再利用勾股定理即可求解.
【详解】解:连接,,如图所示:
和是的半径,
,
又为的中点,且,
,,
,
在中,,,
,
的半径为:5,
故选C.
【点睛】本题考查了垂径定理、勾股定理,熟练掌握勾股定理及垂径定理,借助辅助线解决问题是解题的关键.
4.B
【详解】∵底面周长是6π,
∴底面圆的半径为3cm,
∵高为4cm,
∴母线长5cm,
∴根据圆锥侧面积=底面周长×母线长,可得S=×6π×5=15πcm2.
故选B.
5.A
【分析】根据“在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相等”仔细找出等量关系即可.
【详解】∵C、D为半圆上三等分点,
∴,
根据在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相等知,AD=CD=BC,∠AOD=∠DOC=∠BOC=60°,
∵AO=OD=OC=OB,
∴△AOD≌△COD≌△COB,
∴△AOD和△COD是等边三角形,
∴OA=AD=DC=OC,
∴四边形ADCO为菱形,
∴三种说法都正确.
故选A.
【点睛】本题利用了在同圆或等圆中,等弧对的圆心角相等,等弧对的弦相等和平角的概念求解.
6.C
【分析】直接利用圆周角求解.
【详解】解:∵点A是的中点,
∴,
∴∠AOB=2∠ADC=2×24°=48°.
故选:C.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
7.B
【分析】设扇形的半径为r,根据扇形的面积公式即可求出r的值.
【详解】解:设扇形的半径为r,
∵扇形的圆心角为150°,它的面积为240πcm2,
∴,
解得r=24.
故选B.
【点睛】本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.
8.D
【详解】试题分析:连接OA,如图:
∵OH⊥AB,AB=8cm,∴AH=4cm,∵OA=OC=5cm,∴由勾股定理可得OH=3cm,∴当直线向下平移到点H与点C重合时,直线与圆相切,∴CH=OC-OH=2cm;同理:当直线向上平移到与圆相切时,平移的距离=5+3=8cm,所以直线在原有位置移动2cm或8cm后与圆相切,故选D.
考点:垂径定理、勾股定理、直线与圆的位置关系.
9.B
【分析】连接,设,在中,用勾股定理求解即可.
【详解】解:连接,如图,
∴,
设,
∵,
∴,
在中,,即,解得:,
∴,
故选:B.
【点睛】本题考查垂径定理,涉及到勾股定理解三角形,灵活运用所学知识是关键.
10.A
【分析】直接利用圆内接四边形的性质结合圆周角定理得出答案.
【详解】解:如图所示:
∵∠BOC=130°,
∴∠A=65°,
∠A还应有另一个不同的值∠A′与∠A互补.
故∠A′=180° 65°=115°.
故选:A.
【点睛】此题主要考查了三角形的外接圆,正确分类讨论是解题关键.
11.A
【分析】由垂径定理得到AC=4,再利用勾股定理,即可求出OC的长度.
【详解】解:根据题意,
∵为弦心距,
∴⊥AB,
∴AC=BC=,
在直角三角形AOC中,由勾股定理,得
.
故选:A.
【点睛】本题考查了垂径定理,以及勾股定理,解题的关键是掌握所学的知识,正确求出OC的长度.
12.C
【分析】根据等边三角形的性质可得,从而得到∠ADB=∠BDC,故①正确;根据点是上一动点,可得不一定等于,故②错误;当最长时,DB为圆O的直径,可得∠BCD=90°,再由是等边的外接圆,可得∠ABD=∠CBD=30°,可得,故③正确;延长DA至点E,使AE=AD,证明△ABE≌△CBD,可得BD=AE,∠ABE=∠DBC,从而得到△BDE是等边三角形,可得到DE=BD,故④正确;即可求解.
【详解】解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∴,
∴∠ADB=∠BDC,故①正确;
∵点是上一动点,
∴不一定等于,
∴DA=DC不一定成立,故②错误;
当最长时,DB为圆O的直径,
∴∠BCD=90°,
∵是等边的外接圆,∠ABC=60°,
∴BD⊥AC,
∴∠ABD=∠CBD=30°,
∴,故③正确;
如图,延长DA至点E,使AE=DC,
∵四边形ABCD为圆O的内接四边形,
∴∠BCD+∠BAD=180°,
∵∠BAE+∠BAD=180°,
∴∠BAE=∠BCD,
∵AB=BC,AE=CD,
∴△ABE≌△CBD,
∴BD=BE,∠ABE=∠DBC,
∴∠ABE+∠ABD=∠DBC+∠ABD=∠ABC=60°,
∴△BDE是等边三角形,
∴DE=BD,
∵DE=AD+AE=AD+CD,
∴,故④正确;
∴正确的有3个.
故选:C.
【点睛】本题主要考查了圆周角定理,三角形的外接圆,圆内接四边形的性质,垂径定理,等边三角形的判定和性质等知识,熟练掌握圆周角定理,三角形的外接圆,圆内接四边形的性质,垂径定理,等边三角形的判定和性质等知识是解题的关键.
13.36°
【分析】根据轮子转过的角度所对的弧长与线段AB的长相等可得.
【详解】解:4 =,
解得n=36°.
故答案是:36°.
【点睛】此题的关键是理解轮子转过的角度所对的弧长与线段AB的长相等,然后利用弧长公式求值即可.
14.
【分析】与的三边分别相切于、、,可得,,,, (cm),可得,即可求解.
【详解】解:如图,与的三边分别相切于、、,
是的内切圆,
的切线与、相交于点、,
,,
,,
周长为20cm,,
(cm),
周长为
().
故答案:.
【点睛】本题主要考查了切线长定理,掌握定理是解题的关键.
15.以A为圆心3为半径的圆
【分析】求圆心的轨迹实际上是求距A点3能画一个什么图形.
【详解】所求圆心的轨迹,就是到A点的距离等于3厘米的点的集合,因此是一个以A为圆心,半径为3的圆.
故答案为:以A为圆心3为半径的圆.
【点睛】此题所求圆心的轨迹,就是到顶点的距离等于定长的点的集合,因此应该是一个圆.
16..
【详解】解:如图,过F作FH⊥OE,连接OG,OM,ON
△OFH是等腰直角三角形,
∴FH=OFsin45°=,AB=,BC=2OE=2
∴矩形ABCD面积=2
∴S空白=2S扇形FOM+2SΔFOG
=
=
∴窗户的透光率=
故答案为:
17.28π
【分析】根据△CBD∽△CAE,即可得到CB=2,AC=8,再根据男孩以6m为半径绕电线杆走一圈,即可得出他在路灯下的影子BC扫过的面积.
【详解】解:如图所示,
∵AE∥BD,
∴△CBD∽△CAE,
,即
解得CB=2,
∴AC=8,
∴男孩以6m为半径绕电线杆走一圈,他在路灯下的影子BC扫过的面积为π×82-π×62=28πm2.
故答案为28π.
【点睛】本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键.
18.
【分析】先求出△ADE是等边三角形,再证明AD=DF=BF=2,即可求出=6.
【详解】解:∵六边形DFHKGE是正六边形,
∴∠EDF=∠DFH=∠FHK=∠KGE=∠GED=120°,DE=DF,
∴∠ADE=∠AED=60°,
∴△ADE是等边三角形,
∴AD=DE=AE,
同理:BH=BF=FH,
∴AD=DF=BF=2,
∴=6=6×=.
【点睛】本题主要考查的是正多边形和圆,熟知等边三角形的性质及正六边形的性质是解题的关键.
19.(1)答案见解析;(2).
【分析】(1)由可知,,;由得出,;由得出;进而可说明.
(2)由,,可知;在中,可得,在中可得;由圆内接四边形的对角互补知,有,在等腰三角形中,,根据可求得的面积.
【详解】解:(1)
,
在和中,
在和中,
(2),
在中
同理在中可得,
又圆内接四边形的对角互补
得
在中
为等腰三角形
的面积为.
【点睛】本题考查了全等三角形的判定与性质;圆内接四边形对角的关系;圆心角、弧、弦的关系等知识点.解题的关键在于判定三角形全等以及三角形的面积公式的表示.
20.8
【分析】本题考查了垂径定理,勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.连接,设,可得,代入数据即可求得的值,从而得到的长.
【详解】如图,连接,设,
则,.
∵直径弦于点E,
,
,
,
,(舍去),
,
.
21.
【分析】本题要求同学们能熟练应用计算器,会用科学计算器进行计算.
【详解】解:圆环的面积,
,
.
故答案为:.
【点睛】本题考查了利用计算器计算有理数的混合运算.解题的关键是掌握保留一位小数就是小数点后有一位小数,也就是精确到十分位.
22.5cm
【分析】首先连接OA,根据垂径定理可得CD⊥AB,AE=4,根据勾股定理求出OA的长度.
【详解】连接OA,CD为直径,且CD平分AB于E,
∴CD⊥AB,AE=AB=4cm,
在Rt△OAE中,
∴⊙O的半径为5cm.
23.矩形、菱形都不是正多边形,只有正方形是正多边形,理由见解析.
【分析】根据正多边形的性质特点即可判断.
【详解】矩形、菱形都不是正多边形,只有正方形是正多边形,
理由如下:因为正多边形不仅各边相等,而且各角也相等,所以正方形是正多边形.
矩形只是角相等,边不一定相等;菱形只是边相等,角不一定相等,故不是正多边形.
【点睛】此题主要考查正多边形的性质辨析,解题的关键是熟知正多边形的性质:正多边形各边相等,各角也相等.
24.(1)见解析
(2)
【分析】(1)连接,根据切线性质,等角对等边,证明.
(2)连接,根据圆的性质,切线的性质,勾股定理解答即可.
本题考查了切线的性质,圆的性质,勾股定理,熟练掌握切线的性质,勾股定理是解题的关键.
【详解】(1)证明:连接,
∵是切线,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
∴.
(2)解:连接.
∵,
∴,
∵是的直径,,
∴是的切线,
∴,
∴,
∵,
∴,
在中,,
∴,
设,在中,,
在中,,
∴,
解得,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
