26.3实践与探索同步练习(含解析)
文档属性
| 名称 | 26.3实践与探索同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
26.3实践与探索
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.矩形一边长为x,周长为8,则当矩形面积最大时,x的值为( )
A.4 B.2 C.6 D.5
2.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣(t﹣4)2+20.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3s B.4s C.5s D.6s
3.小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
4.正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )
A. B. C. D.
5.如图,等边三角形ABC中,AB=3,点D在边AB上,且AD=1,点E是边B上的一动点,作射线ED.射线ED绕点E顺时针旋转60°得到射线EF,交AC于点F,则点E从B→C的运动过程中,CF的最大值是( )
A. B.1 C. D.
6.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
7.如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是( )
A.3m B.4m C.5m D.6m
8.某商品现在的售价为每件60元,每星期可销售300件.商场为了清库存,决定让利销售,已知每降价1元,每星期可多销售20件,那么每星期的销售额(元)与降价(元)的函数关系为( )
A. B.
C. D.
9.在平面直角坐标系中,将抛物线 y=(x﹣2)2+1 先向上平移 2 个单位长度,再向左平移3 个单位长度,所得抛物线的解析式为( )
A.y=(x+1)2﹣1 B.y=(x﹣5)2﹣1 C.y=(x+1)2+3 D.y=(x﹣5)2+3
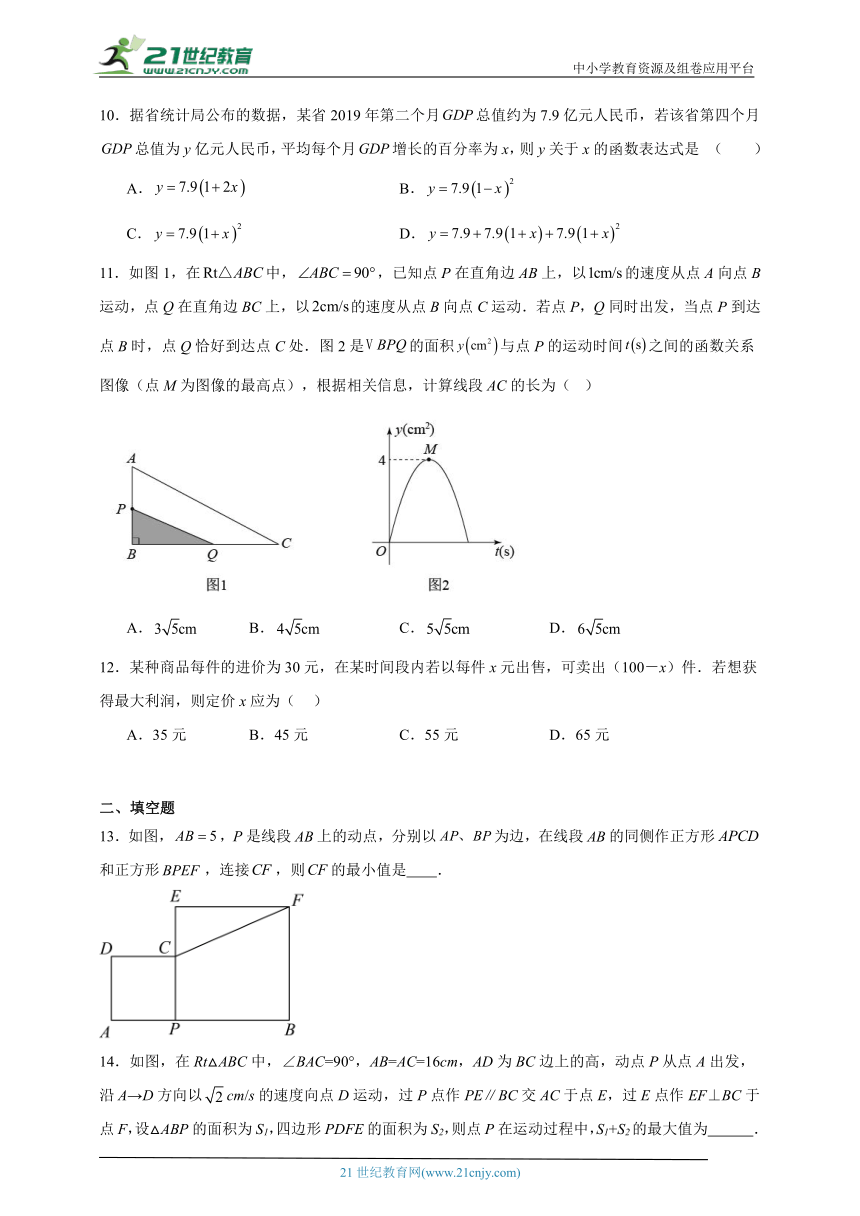
10.据省统计局公布的数据,某省2019年第二个月总值约为7.9亿元人民币,若该省第四个月总值为y亿元人民币,平均每个月增长的百分率为x,则y关于x的函数表达式是 ( )
A. B.
C. D.
11.如图1,在中,,已知点P在直角边AB上,以的速度从点A向点B运动,点Q在直角边BC上,以的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处.图2是的面积与点P的运动时间之间的函数关系图像(点M为图像的最高点),根据相关信息,计算线段AC的长为( )
A. B. C. D.
12.某种商品每件的进价为30元,在某时间段内若以每件x元出售,可卖出(100-x)件.若想获得最大利润,则定价x应为( )
A.35元 B.45元 C.55元 D.65元
二、填空题
13.如图,,P是线段上的动点,分别以为边,在线段的同侧作正方形和正方形,连接,则的最小值是 .
14.如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以cm/s的速度向点D运动,过P点作PE∥BC交AC于点E,过E点作EF⊥BC于点F,设△ABP的面积为S1,四边形PDFE的面积为S2,则点P在运动过程中,S1+S2的最大值为 .
15.如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m.水面下降1m, 水面宽度为多少?水面宽度增加多少?
建立坐标系,设这条抛物线表示的二次函数为 ,
由抛物线过点 ,得到a= ,
所以这条抛物线的解析式为 ,
当水面下降1m时,水面的纵坐标为y= ,
将y= 代入二次函数得,x= ,
∴水面下降1m时,水面的宽度为 m
∴水面的宽度增加了 m
16.要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱如图所示.现以水管与地面交点为原点,原点与水柱落地处所在直线为轴,水管所在直线为轴,建立直角坐标系,喷出的抛物线水柱对应的函数解析式是,则水管长为 .
17.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
三、解答题
18.甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元. 乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;
②月利润=月租车费-月维护费;
③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是_______元;当每个公司租出的汽车为_______辆时,两公司的月利润相等;
(2)求两公司月利润差的最大值;
(3)甲公司热心公益事业,每租出1辆汽车捐出a元给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为17辆时,甲公司剩余的月利润与乙公司月利润之差最大,求a的取值范围.
19.如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
20.已知二次函数图象的顶点坐标为,直线与该二次函数的图象交于A、B两点,其中A点的坐标为,B点在y轴上,P为直线AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,D为直线AB与这个二次函数图象的对称轴的交点.
(1)求m的值及这个二次函数的解析式;
(2)在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;不存在,请说明理由.
(3)抛物线上是否存在点E,使,若存在,请直接写出此时E点的坐标;若不存在,请说明理由
21.某百货商店服装在销售过程中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件,当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?
22.如图,已知二次函数的图象与轴交于两点,点坐标为,与轴交于点,点为抛物线顶点,点为中点.
(1)求二次函数的解析式;
(2)若在直线上方的抛物线上存在点,使得,求点的坐标.
23.一根铝合金型材长为,用它制作一个“日”字形窗户的框架(如图),如果恰好用完整条铝合金型材,那么分别为多少米时,窗户的面积最大?
24.某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) … 30 40 50 60 …
销售量y(万个) … 5 4 3 2 …
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
《26.3实践与探索》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C C C C B C C
题号 11 12
答案 B D
1.B
【分析】根据矩形面积公式列出函数关系式,用配方法化成顶点式求解即可.
【详解】解:由题意得:矩形面积,
所以当x=2时,矩形面积S有最大值4,
故选B.
【点睛】本题考查的是二次函数的应用,根据题意表示出另一边长是根本,将长乘以宽得出面积并配方找最大值是关键.
2.B
【分析】根据顶点式就可以直接求出结论;
【详解】解:∵﹣1<0,
∴当t=4s时,函数有最大值.
即礼炮从升空到引爆需要的时间为4s,
故选:B.
【点睛】本题主要考查了二次函数的应用,掌握二次函数的应用是解题的关键.
3.B
【分析】首先由y=2x2-4x+8求出D点的坐标为(1,6),然后根据AB=4,可知B点的横坐标为x=3,代入y=2x2-4x+8,得到y=14,所以CD=14-6=8,又DE=3,所以可知杯子高度.
【详解】解:,
抛物线顶点的坐标为,
,
点的横坐标为,
把代入,得到,
,
.
故选:B.
【点睛】本题主要考查了二次函数的应用,求出顶点D和点B的坐标是解决问题的关键.
4.C
【分析】由已知得BE=CF=DG=AH=1-x,根据y=S正方形ABCD-S△AEH-S△BEF-S△CFG-S△DGH,求函数关系式,判断函数图象.
【详解】解:依题意,得y=S正方形ABCD-S△AEH-S△BEF-S△CFG-S△DGH=1-4×(1-x)x=2x2-2x+1,
即y=2x2-2x+1(0≤x≤1),抛物线开口向上,对称轴为x=.
故答案选C .
5.C
【分析】根据等边三角形的性质及角的等量代换可得,依据相似三角形的判定和性质可得~,,设,,将各边长代入相似比中可得二次函数,利用二次函数的性质,求其最值即可.
【详解】解:∵为等边三角形,
∴,
在中,
,
由题意旋转,
∴,
∴,
∴,
在与中,
,
,
∴~,
设,,,
∴,
∴,
∴,
当时,
,
∴当,为最大值,
故选:C.
【点睛】题目主要考查等边三角形的性质及动点问题,相似三角形的判定及性质,二次函数的应用,理解题意,根据相似比得出二次函数求最大值是解题关键.
6.C
【分析】利用现有一块长20cm、宽10cm的矩形,将它的四个角各剪去一个边长为xcm的小正方形,则底面长与宽均减少2xcm,表示出无盖的长方体盒子底边的长,进而得出y与x之间的函数关系式.
【详解】解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
【点睛】此题主要考查了根据实际问题列二次函数关系式,表示出长方体盒子底边的长与宽是解题关键.
7.C
【详解】设距水面1m的水平线为x轴,抛物线两端点中点为原点设立平面直角坐标系,
则抛物线左端点为(-5,0),右端点为(5,0),顶点为(0,4),
设抛物线为:,将(5,0)代入可得函数解析式为:;
将y=3代入函数解析式可得:,则两盏景观灯之间的水平距离为5m,故选择C.
【点睛】本题主要考查的就是二次函数的实际应用问题,属于中等难度题目.在解决这个问题的时候,我们首先要确定平面直角坐标系,选择不同的坐标系会对计算产生不同的影响,我们一般情况下要选择顶点在x轴或y轴上,这样计算就会简单好多.实际题目中的数字要转化成坐标系中点的坐标,然后进行计算得出答案.
8.B
【分析】根据让利销售,已知每降价1元,每星期可多销售20件,求得销售量为,根据售价乘以销量得出销售额,据此即可求解.
【详解】解:依题意,每星期的销售额(元)与降价(元)的函数关系为,
故选:B
【点睛】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.
9.C
【分析】根据抛物线平移的口诀解决问题.y轴上平移是,上加下减,x轴上平移是,左加右减
【详解】解:将抛物线 y=(x﹣2)2+1 先向上平移 2 个单位长度,再向左平移 3 个单位长度,得到的抛物线的解析式是将抛物线 y=(x﹣2+3)2+1+2,即:y=(x+1)2+3.
【点睛】抛物线平移的问题是考点,熟练掌握口诀是解决此类问题的关键.是中考的易考点.特别注意的是x轴上平移是易错点.
10.C
【分析】根据平均每个月增长的百分率为,可得第三月的总值为,第四月的总值为,即可解答.
【详解】解:设平均每个月增长的百分率为,
∵第二个月总值约为亿元人民币,
∴第三月的总值为,
∴第四月的总值为,
∴y关于x的函数表达式是:,
故选:C.
【点睛】本题考查了根据实际问题列二次函数关系式,正确理解增长率问题的数量关系是解题的关键.
11.B
【分析】根据题意,得出,,在中,根据面积公式得到的面积与点P的运动时间之间的函数关系,利用顶点式得出当时,有最大值为,从而求出运动时间是,求出,根据勾股定理即可得出结论.
【详解】解:设运动时间,,则,,
在中,,,,则,
当时,有最大值为,
解得,即,
根据的面积与点P的运动时间之间的函数关系可知,
抛物线与轴交于和两点,即运动时间是,
,
在中,,,
根据勾股定理可得,
故选:B.
【点睛】本题考查了几何图形中动点形成的图形面积的函数问题,涉及到三角形面积公式的运用、勾股定理、二次函数的图像与性质等知识点,看懂题意,将几何图形中点的运动情况与函数图像对应起来得到方程是解决问题的关键.
12.D
【分析】设所获得的利润为W,根据利润=(售价-进价)×数量,列出W关于x的二次函数,利用二次函数的性质求解即可.
【详解】解:设所获得的利润为W,
由题意得,
∵,
∴当时,W有最大值1225,
故选D.
【点睛】本题主要考查了二次函数的应用,解题的关键在于能够根据题意列出利润关于售价的二次函数.
13.
【分析】设,,根据正方形的性质和勾股定理列出关于的二次函数关系式,求二次函数的最值即可.本题考查了二次函数的最值.求二次函数的最大(小值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.
【详解】解:依题意,设,,
∵四边形和都是正方形
则.
,
当时,有最小值,且
.
故答案为:
14.72.
【分析】利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后确定最值即可.
【详解】∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8cm,
又∵AP=t,
则S1=AP BD=×8×t=8t,PD=8-t,
∵PE∥BC,
∴△APE∽△ADC,
∴,
∴PE=AP=t,
∴S2=PD PE=(8-t) t,
∴S1+S2=8t+(8-t) t=-2(t-6)2+72.
∴S1+S2的最大值为72,
故答案为72.
【点睛】本题考查了一元二次方程的应用,以及等腰直角三角形的性质,正确表示出S1和S2是关键.
15. (2,-2) -3 -3
【解析】略
16.
【分析】由题意令,得到的值即为水管的长.
【详解】解:在中,
令,得,
水管的长为
故答案为:.
【点睛】本题考查了二次函数的运用,解题的关键是理解水管的长即是时的值.
17.0.5
【分析】根据题意,运用待定系数法,建立适当的函数解析式,代入求值即可解答.
【详解】以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,
由题意可得A(0,2.5),B(2,2.5),C(0.5,1)
设函数解析式为y=ax2+bx+c
把A. B. C三点分别代入得出c=2.5
同时可得4a+2b+c=2.5,0.25a+0.5b+c=1
解得a=2,b= 4,c=2.5.
∴y=2x2 4x+2.5=2(x 1)2+0.5.
∵2>0
∴当x=1时,ymin=0.5米.
18.(1)48000,37;(2)33150元;(3)
【分析】(1)用甲公司未租出的汽车数量算出每辆车的租金,再乘以10,减去维护费用可得甲公司的月利润;设每个公司租出的汽车为x辆,根据月利润相等得到方程,解之即可得到结果;
(2)设两公司的月利润分别为y甲,y乙,月利润差为y,同(1)可得y甲和y乙的表达式,再分甲公司的利润大于乙公司和甲公司的利润小于乙公司两种情况,列出y关于x的表达式,根据二次函数的性质,结合x的范围求出最值,再比较即可;
(3)根据题意得到利润差为,得到对称轴,再根据两公司租出的汽车均为17辆,结合x为整数可得关于a的不等式,即可求出a的范围.
【详解】解:(1)=48000元,
当每个公司租出的汽车为10辆时,甲公司的月利润是48000元;
设每个公司租出的汽车为x辆,
由题意可得:,
解得:x=37或x=-1(舍),
∴当每个公司租出的汽车为37辆时,两公司的月利润相等;
(2)设两公司的月利润分别为y甲,y乙,月利润差为y,
则y甲=,
y乙=,
当甲公司的利润大于乙公司时,0<x<37,
y=y甲-y乙=
=,
当x==18时,利润差最大,且为18050元;
当乙公司的利润大于甲公司时,37<x≤50,
y=y乙-y甲=
=,
∵对称轴为直线x==18,
当x=50时,利润差最大,且为33150元;
综上:两公司月利润差的最大值为33150元;
(3)∵捐款后甲公司剩余的月利润仍高于乙公司月利润,
则利润差为=,
对称轴为直线x=,
∵x只能取整数,且当两公司租出的汽车均为17辆时,月利润之差最大,
∴,
解得:.
【点睛】本题考查了二次函数的实际应用,二次函数的图像和性质,解题时要读懂题意,列出二次函数关系式,尤其(3)中要根据x为整数得到a的不等式.
19.(1)抛物线的函数表达式为y=x2﹣4x+3;(2)△ADB是等腰直角三角形;理由见解析;(3)P(2,﹣3).
【分析】(1)根据抛物线对称轴的定义易求A(1,0),B(3,0).所以1、3是关于x的一元二次方程x2+bx+c=0的两根.由韦达定理易求b、c的值;
(2)先求出顶点D的坐标,再由勾股定理的逆定理证明△ABD是直角三角形,再由对称得AD=BD,进而得△ABD是等腰直角三角形;
(3)连接CA,延长CA与直线x=2交于点P,连接BP,此时P点就是PC﹣PB的值最大的点,求出直线AC的解析式,再求直线AC与直线x=2的交点坐标便可.
【详解】(1)如图,∵AB=2,对称轴为直线x=2.
∴点A的坐标是(1,0),点B的坐标是(3,0).
∵抛物线y=x2+bx+c与x轴交于点A,B,
∴1、3是关于x的一元二次方程x2+bx+c=0的两根.
由韦达定理,
1+3=﹣b,1×3=c,
∴b=﹣4,c=3,
∴抛物线的函数表达式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴D(2,﹣1),
∴AD2+BD2=(2﹣1)2+(﹣1)2+(2﹣3)2+(﹣1)2=4,
∵AB2=22=4,
∴AD2+BD2=AB2,
∴△ADB是直角三角形,
由对称性有AD=BD,
∴△ADB是等腰直角三角形;
(3)连接CA,延长CA与直线x=2交于点P,连接BP,如图2,
∵A、B两点关于直线x=2对称,
∴PB=PA,
∴PC﹣PB=PC﹣PA=AC其值最大(∵另取一点P′,有P′C﹣P′B=P′C﹣P′A<AC),
令x=0,得y=x2﹣4x+3=3,
∴C(0,3),
∵A(1,0),
∴易求直线AC的解析式为:y=﹣3x+3,
当x=2时,y=﹣3x+3=﹣3,
∴P(2,﹣3).
【点睛】考查了二次函数综合题,待定系数法求抛物线的解析式,等腰直角三角形,勾股定理的应用,待定系数法求直线的解析式,解题关键在于作辅助线
20.(1)m=1,y=x2+2x+1;(2)存在,P(-2,3);(3)存在,(-1,0)或(-2,1)或(,)或(,)
【分析】(1)根据顶点坐标(-1,0)设抛物线的解析式为:y=a(x+1)2,把点A(-3,4)分别代入二次函数和一次函数的解析式中可得结论;
(2)先求AB的解析式,根据解析式表示出P、E两点的坐标:设P(x,-x+1),E(x,x2+2x+1),由平行四边形的性质:CD=PE列式可求得x的值,计算点P的坐标;
(3)分两种情况:如图2,点E在AB的下方时,根据三角形面积=铅直高×水平宽,此时的水平宽是3,铅直高是EF,根据解析式表示,由面积=2,代入可求得结论;如图3,点E在AB的上方时,由图2可知,与AB平行且向上平移2个单位的直线EF的解析式为:y=-x+3,该直线与抛物线的交点即是点E,列方程组求出即可.
【详解】解:(1)把A(-3,4)代入y=-x+m得:3+m=4,
m=1,
设抛物线的解析式为:y=a(x+1)2,
把A(-3,4)代入y=a(x+1)2中得:a(-3+1)2=4,
a=1,
∴这个二次函数的解析式为:y=(x+1)2=x2+2x+1;
(2)如图1,当x=0时,y=1,
∴B(0,1),
设直线AB的解析式为:y=kx+b,
把A(-3,4),B(0,1)代入得:,
解得:,
∴直线AB的解析式为:y=-x+1,
当x=-1时,y=1+1=2,
∴D(-1,2),
∴CD=2,
设P(x,-x+1),E(x,x2+2x+1),
∵四边形DCEP是平行四边形,
∴CD=PE,CD∥PE,
∴PE=(-x+1)-(x2+2x+1)=-x2-3x=2,
x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1(舍),x2=-2,
当x=-2时,y=2+1=3,
∴P(-2,3);
(3)存在,
过E作EF∥CD,交AB于F
设F(x,-x+1),E(x,x2+2x+1),
∵S△ABE=×3EF=3
∴EF=2
如图2,点E在AB的下方时,
EF=(-x+1)-(x2+2x+1)=-x2-3x=2,
x1=-1,x2=-2,
当x=-1时,y=0,
当x=-2时,y=1,
此时点E(-1,0)、(-2,1);
如图3,点E在AB的上方时,
由图2可知,与AB平行且向上平移2个单位的直线EF的解析式为:y=-x+3,
则,
解得:或,
∴E(,)或(,),
综上所述,点E的坐标为:(-1,0)或(-2,1)或(,)或(,).
【点睛】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求,本题就是设顶点式来求解析式;对于已知三角形面积的值,确定抛物线上一动点坐标时,常利用确定平行线解析式的方法,再利用两函数的交点来解决问题.
21.每件童装降价15元时,每天销售这种童装的利润最高,最高利润是1250元.
【分析】根据题意可以得到利润与所将价格的关系式,根据二次函数可判断最大利润.
【详解】解:设每件童装降价x元,利润为y元,
,
∴当时,y取得最大值,此时,
即每件童装降价15元时,每天销售这种童装的利润最高,最高利润是1250元.
【点睛】本题考查二次函数的应用,解题的关键是明确题意,列出二次函数解析式,根据二次函数的顶点判断最大利润.
22.(1)
(2)
【分析】()利用待定系数法即可求解;
()求出点坐标,可得是等腰直角三角形,即得,得到, 过点作交抛物线于点,过点作轴于点,可得,得到是等腰直角三角形,即得,设,则,可得,,进而得到,解方程即可求解;
本题考查了待定系数法求二次函数解析式,二次函数的几何应用,等腰直角三角形的判定和性质,掌握二次函数的图象和性质是解题的关键.
【详解】(1)解:把、代入得,
,
解得,
∴二次函数的解析式为;
(2)解:当时,,
解得,,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
如图,过点作交抛物线于点,过点作轴于点,则,
∴,
∴是等腰直角三角形,
∴,
设,则,
∴,,
∴,
解得(不合,舍去) 或,
∴.
23.时,窗户的面积最大
【分析】设为,则,根据矩形的面积求得面积与的函数关系,根据二次函数的性质求解即可求得答案.
【详解】设设为,则,则窗户的面积
当时,取得最大值
即时,窗户的面积最大.
【点睛】本题考查了二次函数的应用,根据题意列出函数解析式是解题的关键.
24.(1) y=x+8
(2) z=x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元
(3)40≤x≤60;销售价格应定为40元/个
【分析】(1)根据数据得出y与x是一次函数关系,进而利用待定系数法求一次函数解析式.
(2)根据z=(x﹣20)y﹣40得出z与x的函数关系式,应用二次函数最值原理求解即可.
(3)首先求出40=(x﹣50)2+50时x的值,从而二次函数的性质根据得出x(元/个)的取值范围,结合一次函数的性质即可求得结果.
【详解】解:(1)根据表格中数据可得出:y与x是一次函数关系,设解析式为:y=ax+b,
则,解得:.
∴函数解析式为:y=x+8.
(2)根据题意得:
z=(x﹣20)y﹣40=(x﹣20)(x+8)﹣40=x2+10x﹣200=(x2﹣100x)﹣200
=[(x﹣50)2﹣2500]﹣200=(x﹣50)2+50,
∵<0,∴x=50,z最大=50.
∴该公司销售这种计算器的净得利润z与销售价格x的函数解析式为z=x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元.
(3)当公司要求净得利润为40万元时,即(x﹣50)2+50=40,解得:x1=40,x2=60.
作函数图象的草图,
通过观察函数y=(x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
而y与x的函数关系式为:y=x+8,y随x的增大而减少,
∴若还需考虑销售量尽可能大,销售价格应定为40元/个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
26.3实践与探索
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.矩形一边长为x,周长为8,则当矩形面积最大时,x的值为( )
A.4 B.2 C.6 D.5
2.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣(t﹣4)2+20.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3s B.4s C.5s D.6s
3.小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
4.正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )
A. B. C. D.
5.如图,等边三角形ABC中,AB=3,点D在边AB上,且AD=1,点E是边B上的一动点,作射线ED.射线ED绕点E顺时针旋转60°得到射线EF,交AC于点F,则点E从B→C的运动过程中,CF的最大值是( )
A. B.1 C. D.
6.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
7.如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是( )
A.3m B.4m C.5m D.6m
8.某商品现在的售价为每件60元,每星期可销售300件.商场为了清库存,决定让利销售,已知每降价1元,每星期可多销售20件,那么每星期的销售额(元)与降价(元)的函数关系为( )
A. B.
C. D.
9.在平面直角坐标系中,将抛物线 y=(x﹣2)2+1 先向上平移 2 个单位长度,再向左平移3 个单位长度,所得抛物线的解析式为( )
A.y=(x+1)2﹣1 B.y=(x﹣5)2﹣1 C.y=(x+1)2+3 D.y=(x﹣5)2+3
10.据省统计局公布的数据,某省2019年第二个月总值约为7.9亿元人民币,若该省第四个月总值为y亿元人民币,平均每个月增长的百分率为x,则y关于x的函数表达式是 ( )
A. B.
C. D.
11.如图1,在中,,已知点P在直角边AB上,以的速度从点A向点B运动,点Q在直角边BC上,以的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处.图2是的面积与点P的运动时间之间的函数关系图像(点M为图像的最高点),根据相关信息,计算线段AC的长为( )
A. B. C. D.
12.某种商品每件的进价为30元,在某时间段内若以每件x元出售,可卖出(100-x)件.若想获得最大利润,则定价x应为( )
A.35元 B.45元 C.55元 D.65元
二、填空题
13.如图,,P是线段上的动点,分别以为边,在线段的同侧作正方形和正方形,连接,则的最小值是 .
14.如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以cm/s的速度向点D运动,过P点作PE∥BC交AC于点E,过E点作EF⊥BC于点F,设△ABP的面积为S1,四边形PDFE的面积为S2,则点P在运动过程中,S1+S2的最大值为 .
15.如图是一座抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m.水面下降1m, 水面宽度为多少?水面宽度增加多少?
建立坐标系,设这条抛物线表示的二次函数为 ,
由抛物线过点 ,得到a= ,
所以这条抛物线的解析式为 ,
当水面下降1m时,水面的纵坐标为y= ,
将y= 代入二次函数得,x= ,
∴水面下降1m时,水面的宽度为 m
∴水面的宽度增加了 m
16.要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱如图所示.现以水管与地面交点为原点,原点与水柱落地处所在直线为轴,水管所在直线为轴,建立直角坐标系,喷出的抛物线水柱对应的函数解析式是,则水管长为 .
17.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
三、解答题
18.甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元. 乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;
②月利润=月租车费-月维护费;
③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为10辆时,甲公司的月利润是_______元;当每个公司租出的汽车为_______辆时,两公司的月利润相等;
(2)求两公司月利润差的最大值;
(3)甲公司热心公益事业,每租出1辆汽车捐出a元给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为17辆时,甲公司剩余的月利润与乙公司月利润之差最大,求a的取值范围.
19.如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
20.已知二次函数图象的顶点坐标为,直线与该二次函数的图象交于A、B两点,其中A点的坐标为,B点在y轴上,P为直线AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,D为直线AB与这个二次函数图象的对称轴的交点.
(1)求m的值及这个二次函数的解析式;
(2)在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;不存在,请说明理由.
(3)抛物线上是否存在点E,使,若存在,请直接写出此时E点的坐标;若不存在,请说明理由
21.某百货商店服装在销售过程中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件,当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?
22.如图,已知二次函数的图象与轴交于两点,点坐标为,与轴交于点,点为抛物线顶点,点为中点.
(1)求二次函数的解析式;
(2)若在直线上方的抛物线上存在点,使得,求点的坐标.
23.一根铝合金型材长为,用它制作一个“日”字形窗户的框架(如图),如果恰好用完整条铝合金型材,那么分别为多少米时,窗户的面积最大?
24.某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) … 30 40 50 60 …
销售量y(万个) … 5 4 3 2 …
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
《26.3实践与探索》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C C C C B C C
题号 11 12
答案 B D
1.B
【分析】根据矩形面积公式列出函数关系式,用配方法化成顶点式求解即可.
【详解】解:由题意得:矩形面积,
所以当x=2时,矩形面积S有最大值4,
故选B.
【点睛】本题考查的是二次函数的应用,根据题意表示出另一边长是根本,将长乘以宽得出面积并配方找最大值是关键.
2.B
【分析】根据顶点式就可以直接求出结论;
【详解】解:∵﹣1<0,
∴当t=4s时,函数有最大值.
即礼炮从升空到引爆需要的时间为4s,
故选:B.
【点睛】本题主要考查了二次函数的应用,掌握二次函数的应用是解题的关键.
3.B
【分析】首先由y=2x2-4x+8求出D点的坐标为(1,6),然后根据AB=4,可知B点的横坐标为x=3,代入y=2x2-4x+8,得到y=14,所以CD=14-6=8,又DE=3,所以可知杯子高度.
【详解】解:,
抛物线顶点的坐标为,
,
点的横坐标为,
把代入,得到,
,
.
故选:B.
【点睛】本题主要考查了二次函数的应用,求出顶点D和点B的坐标是解决问题的关键.
4.C
【分析】由已知得BE=CF=DG=AH=1-x,根据y=S正方形ABCD-S△AEH-S△BEF-S△CFG-S△DGH,求函数关系式,判断函数图象.
【详解】解:依题意,得y=S正方形ABCD-S△AEH-S△BEF-S△CFG-S△DGH=1-4×(1-x)x=2x2-2x+1,
即y=2x2-2x+1(0≤x≤1),抛物线开口向上,对称轴为x=.
故答案选C .
5.C
【分析】根据等边三角形的性质及角的等量代换可得,依据相似三角形的判定和性质可得~,,设,,将各边长代入相似比中可得二次函数,利用二次函数的性质,求其最值即可.
【详解】解:∵为等边三角形,
∴,
在中,
,
由题意旋转,
∴,
∴,
∴,
在与中,
,
,
∴~,
设,,,
∴,
∴,
∴,
当时,
,
∴当,为最大值,
故选:C.
【点睛】题目主要考查等边三角形的性质及动点问题,相似三角形的判定及性质,二次函数的应用,理解题意,根据相似比得出二次函数求最大值是解题关键.
6.C
【分析】利用现有一块长20cm、宽10cm的矩形,将它的四个角各剪去一个边长为xcm的小正方形,则底面长与宽均减少2xcm,表示出无盖的长方体盒子底边的长,进而得出y与x之间的函数关系式.
【详解】解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
【点睛】此题主要考查了根据实际问题列二次函数关系式,表示出长方体盒子底边的长与宽是解题关键.
7.C
【详解】设距水面1m的水平线为x轴,抛物线两端点中点为原点设立平面直角坐标系,
则抛物线左端点为(-5,0),右端点为(5,0),顶点为(0,4),
设抛物线为:,将(5,0)代入可得函数解析式为:;
将y=3代入函数解析式可得:,则两盏景观灯之间的水平距离为5m,故选择C.
【点睛】本题主要考查的就是二次函数的实际应用问题,属于中等难度题目.在解决这个问题的时候,我们首先要确定平面直角坐标系,选择不同的坐标系会对计算产生不同的影响,我们一般情况下要选择顶点在x轴或y轴上,这样计算就会简单好多.实际题目中的数字要转化成坐标系中点的坐标,然后进行计算得出答案.
8.B
【分析】根据让利销售,已知每降价1元,每星期可多销售20件,求得销售量为,根据售价乘以销量得出销售额,据此即可求解.
【详解】解:依题意,每星期的销售额(元)与降价(元)的函数关系为,
故选:B
【点睛】本题考查了二次函数的应用,根据题意列出函数关系式是解题的关键.
9.C
【分析】根据抛物线平移的口诀解决问题.y轴上平移是,上加下减,x轴上平移是,左加右减
【详解】解:将抛物线 y=(x﹣2)2+1 先向上平移 2 个单位长度,再向左平移 3 个单位长度,得到的抛物线的解析式是将抛物线 y=(x﹣2+3)2+1+2,即:y=(x+1)2+3.
【点睛】抛物线平移的问题是考点,熟练掌握口诀是解决此类问题的关键.是中考的易考点.特别注意的是x轴上平移是易错点.
10.C
【分析】根据平均每个月增长的百分率为,可得第三月的总值为,第四月的总值为,即可解答.
【详解】解:设平均每个月增长的百分率为,
∵第二个月总值约为亿元人民币,
∴第三月的总值为,
∴第四月的总值为,
∴y关于x的函数表达式是:,
故选:C.
【点睛】本题考查了根据实际问题列二次函数关系式,正确理解增长率问题的数量关系是解题的关键.
11.B
【分析】根据题意,得出,,在中,根据面积公式得到的面积与点P的运动时间之间的函数关系,利用顶点式得出当时,有最大值为,从而求出运动时间是,求出,根据勾股定理即可得出结论.
【详解】解:设运动时间,,则,,
在中,,,,则,
当时,有最大值为,
解得,即,
根据的面积与点P的运动时间之间的函数关系可知,
抛物线与轴交于和两点,即运动时间是,
,
在中,,,
根据勾股定理可得,
故选:B.
【点睛】本题考查了几何图形中动点形成的图形面积的函数问题,涉及到三角形面积公式的运用、勾股定理、二次函数的图像与性质等知识点,看懂题意,将几何图形中点的运动情况与函数图像对应起来得到方程是解决问题的关键.
12.D
【分析】设所获得的利润为W,根据利润=(售价-进价)×数量,列出W关于x的二次函数,利用二次函数的性质求解即可.
【详解】解:设所获得的利润为W,
由题意得,
∵,
∴当时,W有最大值1225,
故选D.
【点睛】本题主要考查了二次函数的应用,解题的关键在于能够根据题意列出利润关于售价的二次函数.
13.
【分析】设,,根据正方形的性质和勾股定理列出关于的二次函数关系式,求二次函数的最值即可.本题考查了二次函数的最值.求二次函数的最大(小值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.
【详解】解:依题意,设,,
∵四边形和都是正方形
则.
,
当时,有最小值,且
.
故答案为:
14.72.
【分析】利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后确定最值即可.
【详解】∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8cm,
又∵AP=t,
则S1=AP BD=×8×t=8t,PD=8-t,
∵PE∥BC,
∴△APE∽△ADC,
∴,
∴PE=AP=t,
∴S2=PD PE=(8-t) t,
∴S1+S2=8t+(8-t) t=-2(t-6)2+72.
∴S1+S2的最大值为72,
故答案为72.
【点睛】本题考查了一元二次方程的应用,以及等腰直角三角形的性质,正确表示出S1和S2是关键.
15. (2,-2) -3 -3
【解析】略
16.
【分析】由题意令,得到的值即为水管的长.
【详解】解:在中,
令,得,
水管的长为
故答案为:.
【点睛】本题考查了二次函数的运用,解题的关键是理解水管的长即是时的值.
17.0.5
【分析】根据题意,运用待定系数法,建立适当的函数解析式,代入求值即可解答.
【详解】以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,
由题意可得A(0,2.5),B(2,2.5),C(0.5,1)
设函数解析式为y=ax2+bx+c
把A. B. C三点分别代入得出c=2.5
同时可得4a+2b+c=2.5,0.25a+0.5b+c=1
解得a=2,b= 4,c=2.5.
∴y=2x2 4x+2.5=2(x 1)2+0.5.
∵2>0
∴当x=1时,ymin=0.5米.
18.(1)48000,37;(2)33150元;(3)
【分析】(1)用甲公司未租出的汽车数量算出每辆车的租金,再乘以10,减去维护费用可得甲公司的月利润;设每个公司租出的汽车为x辆,根据月利润相等得到方程,解之即可得到结果;
(2)设两公司的月利润分别为y甲,y乙,月利润差为y,同(1)可得y甲和y乙的表达式,再分甲公司的利润大于乙公司和甲公司的利润小于乙公司两种情况,列出y关于x的表达式,根据二次函数的性质,结合x的范围求出最值,再比较即可;
(3)根据题意得到利润差为,得到对称轴,再根据两公司租出的汽车均为17辆,结合x为整数可得关于a的不等式,即可求出a的范围.
【详解】解:(1)=48000元,
当每个公司租出的汽车为10辆时,甲公司的月利润是48000元;
设每个公司租出的汽车为x辆,
由题意可得:,
解得:x=37或x=-1(舍),
∴当每个公司租出的汽车为37辆时,两公司的月利润相等;
(2)设两公司的月利润分别为y甲,y乙,月利润差为y,
则y甲=,
y乙=,
当甲公司的利润大于乙公司时,0<x<37,
y=y甲-y乙=
=,
当x==18时,利润差最大,且为18050元;
当乙公司的利润大于甲公司时,37<x≤50,
y=y乙-y甲=
=,
∵对称轴为直线x==18,
当x=50时,利润差最大,且为33150元;
综上:两公司月利润差的最大值为33150元;
(3)∵捐款后甲公司剩余的月利润仍高于乙公司月利润,
则利润差为=,
对称轴为直线x=,
∵x只能取整数,且当两公司租出的汽车均为17辆时,月利润之差最大,
∴,
解得:.
【点睛】本题考查了二次函数的实际应用,二次函数的图像和性质,解题时要读懂题意,列出二次函数关系式,尤其(3)中要根据x为整数得到a的不等式.
19.(1)抛物线的函数表达式为y=x2﹣4x+3;(2)△ADB是等腰直角三角形;理由见解析;(3)P(2,﹣3).
【分析】(1)根据抛物线对称轴的定义易求A(1,0),B(3,0).所以1、3是关于x的一元二次方程x2+bx+c=0的两根.由韦达定理易求b、c的值;
(2)先求出顶点D的坐标,再由勾股定理的逆定理证明△ABD是直角三角形,再由对称得AD=BD,进而得△ABD是等腰直角三角形;
(3)连接CA,延长CA与直线x=2交于点P,连接BP,此时P点就是PC﹣PB的值最大的点,求出直线AC的解析式,再求直线AC与直线x=2的交点坐标便可.
【详解】(1)如图,∵AB=2,对称轴为直线x=2.
∴点A的坐标是(1,0),点B的坐标是(3,0).
∵抛物线y=x2+bx+c与x轴交于点A,B,
∴1、3是关于x的一元二次方程x2+bx+c=0的两根.
由韦达定理,
1+3=﹣b,1×3=c,
∴b=﹣4,c=3,
∴抛物线的函数表达式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴D(2,﹣1),
∴AD2+BD2=(2﹣1)2+(﹣1)2+(2﹣3)2+(﹣1)2=4,
∵AB2=22=4,
∴AD2+BD2=AB2,
∴△ADB是直角三角形,
由对称性有AD=BD,
∴△ADB是等腰直角三角形;
(3)连接CA,延长CA与直线x=2交于点P,连接BP,如图2,
∵A、B两点关于直线x=2对称,
∴PB=PA,
∴PC﹣PB=PC﹣PA=AC其值最大(∵另取一点P′,有P′C﹣P′B=P′C﹣P′A<AC),
令x=0,得y=x2﹣4x+3=3,
∴C(0,3),
∵A(1,0),
∴易求直线AC的解析式为:y=﹣3x+3,
当x=2时,y=﹣3x+3=﹣3,
∴P(2,﹣3).
【点睛】考查了二次函数综合题,待定系数法求抛物线的解析式,等腰直角三角形,勾股定理的应用,待定系数法求直线的解析式,解题关键在于作辅助线
20.(1)m=1,y=x2+2x+1;(2)存在,P(-2,3);(3)存在,(-1,0)或(-2,1)或(,)或(,)
【分析】(1)根据顶点坐标(-1,0)设抛物线的解析式为:y=a(x+1)2,把点A(-3,4)分别代入二次函数和一次函数的解析式中可得结论;
(2)先求AB的解析式,根据解析式表示出P、E两点的坐标:设P(x,-x+1),E(x,x2+2x+1),由平行四边形的性质:CD=PE列式可求得x的值,计算点P的坐标;
(3)分两种情况:如图2,点E在AB的下方时,根据三角形面积=铅直高×水平宽,此时的水平宽是3,铅直高是EF,根据解析式表示,由面积=2,代入可求得结论;如图3,点E在AB的上方时,由图2可知,与AB平行且向上平移2个单位的直线EF的解析式为:y=-x+3,该直线与抛物线的交点即是点E,列方程组求出即可.
【详解】解:(1)把A(-3,4)代入y=-x+m得:3+m=4,
m=1,
设抛物线的解析式为:y=a(x+1)2,
把A(-3,4)代入y=a(x+1)2中得:a(-3+1)2=4,
a=1,
∴这个二次函数的解析式为:y=(x+1)2=x2+2x+1;
(2)如图1,当x=0时,y=1,
∴B(0,1),
设直线AB的解析式为:y=kx+b,
把A(-3,4),B(0,1)代入得:,
解得:,
∴直线AB的解析式为:y=-x+1,
当x=-1时,y=1+1=2,
∴D(-1,2),
∴CD=2,
设P(x,-x+1),E(x,x2+2x+1),
∵四边形DCEP是平行四边形,
∴CD=PE,CD∥PE,
∴PE=(-x+1)-(x2+2x+1)=-x2-3x=2,
x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1(舍),x2=-2,
当x=-2时,y=2+1=3,
∴P(-2,3);
(3)存在,
过E作EF∥CD,交AB于F
设F(x,-x+1),E(x,x2+2x+1),
∵S△ABE=×3EF=3
∴EF=2
如图2,点E在AB的下方时,
EF=(-x+1)-(x2+2x+1)=-x2-3x=2,
x1=-1,x2=-2,
当x=-1时,y=0,
当x=-2时,y=1,
此时点E(-1,0)、(-2,1);
如图3,点E在AB的上方时,
由图2可知,与AB平行且向上平移2个单位的直线EF的解析式为:y=-x+3,
则,
解得:或,
∴E(,)或(,),
综上所述,点E的坐标为:(-1,0)或(-2,1)或(,)或(,).
【点睛】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求,本题就是设顶点式来求解析式;对于已知三角形面积的值,确定抛物线上一动点坐标时,常利用确定平行线解析式的方法,再利用两函数的交点来解决问题.
21.每件童装降价15元时,每天销售这种童装的利润最高,最高利润是1250元.
【分析】根据题意可以得到利润与所将价格的关系式,根据二次函数可判断最大利润.
【详解】解:设每件童装降价x元,利润为y元,
,
∴当时,y取得最大值,此时,
即每件童装降价15元时,每天销售这种童装的利润最高,最高利润是1250元.
【点睛】本题考查二次函数的应用,解题的关键是明确题意,列出二次函数解析式,根据二次函数的顶点判断最大利润.
22.(1)
(2)
【分析】()利用待定系数法即可求解;
()求出点坐标,可得是等腰直角三角形,即得,得到, 过点作交抛物线于点,过点作轴于点,可得,得到是等腰直角三角形,即得,设,则,可得,,进而得到,解方程即可求解;
本题考查了待定系数法求二次函数解析式,二次函数的几何应用,等腰直角三角形的判定和性质,掌握二次函数的图象和性质是解题的关键.
【详解】(1)解:把、代入得,
,
解得,
∴二次函数的解析式为;
(2)解:当时,,
解得,,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
如图,过点作交抛物线于点,过点作轴于点,则,
∴,
∴是等腰直角三角形,
∴,
设,则,
∴,,
∴,
解得(不合,舍去) 或,
∴.
23.时,窗户的面积最大
【分析】设为,则,根据矩形的面积求得面积与的函数关系,根据二次函数的性质求解即可求得答案.
【详解】设设为,则,则窗户的面积
当时,取得最大值
即时,窗户的面积最大.
【点睛】本题考查了二次函数的应用,根据题意列出函数解析式是解题的关键.
24.(1) y=x+8
(2) z=x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元
(3)40≤x≤60;销售价格应定为40元/个
【分析】(1)根据数据得出y与x是一次函数关系,进而利用待定系数法求一次函数解析式.
(2)根据z=(x﹣20)y﹣40得出z与x的函数关系式,应用二次函数最值原理求解即可.
(3)首先求出40=(x﹣50)2+50时x的值,从而二次函数的性质根据得出x(元/个)的取值范围,结合一次函数的性质即可求得结果.
【详解】解:(1)根据表格中数据可得出:y与x是一次函数关系,设解析式为:y=ax+b,
则,解得:.
∴函数解析式为:y=x+8.
(2)根据题意得:
z=(x﹣20)y﹣40=(x﹣20)(x+8)﹣40=x2+10x﹣200=(x2﹣100x)﹣200
=[(x﹣50)2﹣2500]﹣200=(x﹣50)2+50,
∵<0,∴x=50,z最大=50.
∴该公司销售这种计算器的净得利润z与销售价格x的函数解析式为z=x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元.
(3)当公司要求净得利润为40万元时,即(x﹣50)2+50=40,解得:x1=40,x2=60.
作函数图象的草图,
通过观察函数y=(x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
而y与x的函数关系式为:y=x+8,y随x的增大而减少,
∴若还需考虑销售量尽可能大,销售价格应定为40元/个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
