27.1圆的认识同步练习(含解析)
文档属性
| 名称 | 27.1圆的认识同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1021.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 12:05:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
27.1圆的认识
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正三角形的三个顶点均在上,动点在上,且不与点重合,则的度数为( )
A. B. C. D.
2.在同一个圆中画两条直径,依次连接四个端点得到的四边形是( )
A.菱形 B.等腰梯形 C.正方形 D.矩形
3.在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合”.由此说明( )
A.圆的直径互相平分
B.垂直弦的直径平分弦及弦所对的弧
C.圆是中心对称图形,圆心是它的对称中心
D.圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
4.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
A.40° B.50° C.80° D.100°
5.如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B.3 C.2 D.4
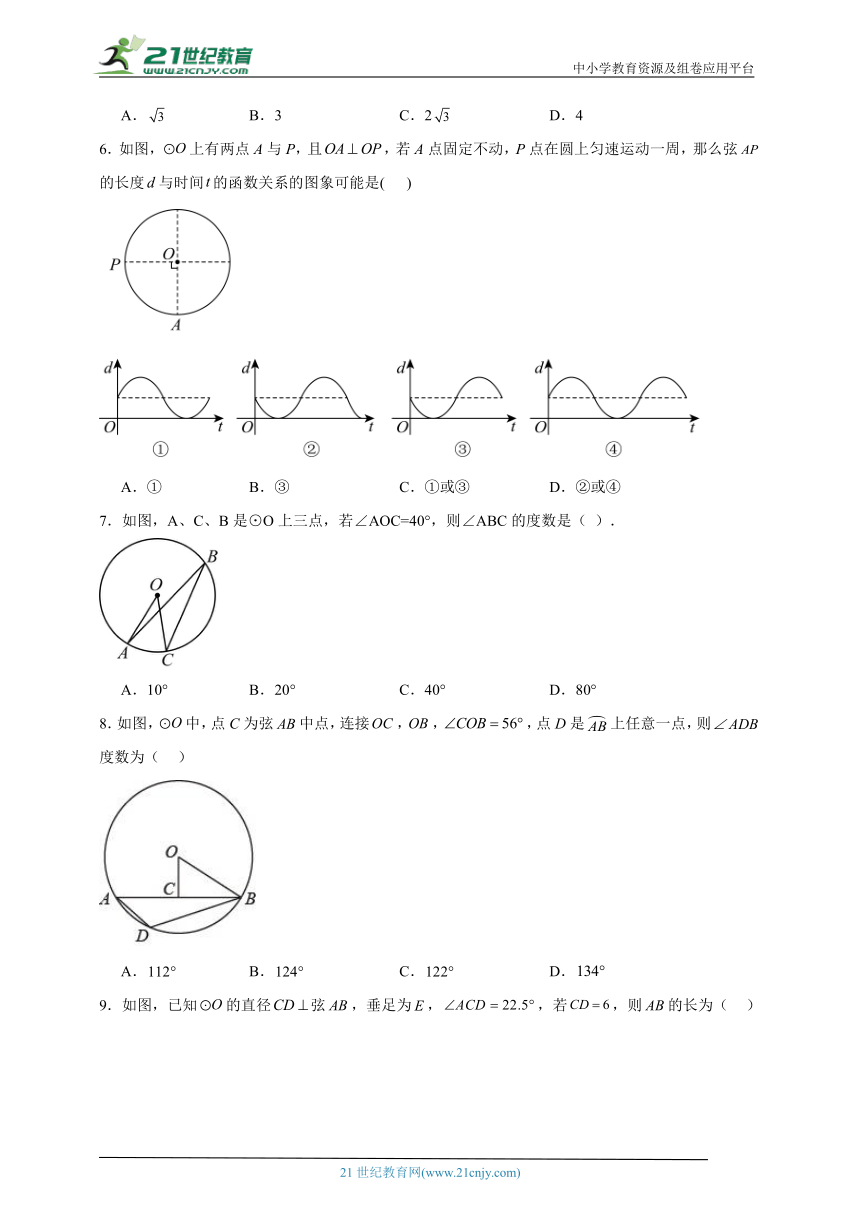
6.如图,上有两点A与P,且,若A点固定不动,P点在圆上匀速运动一周,那么弦的长度与时间的函数关系的图象可能是( )
A.① B.③ C.①或③ D.②或④
7.如图,A、C、B是⊙O上三点,若∠AOC=40°,则∠ABC的度数是( ).
A.10° B.20° C.40° D.80°
8.如图,中,点C为弦中点,连接,,,点D是上任意一点,则度数为( )
A. B. C. D.
9.如图,已知的直径弦,垂足为,,若,则的长为( )
A.4 B. C. D.
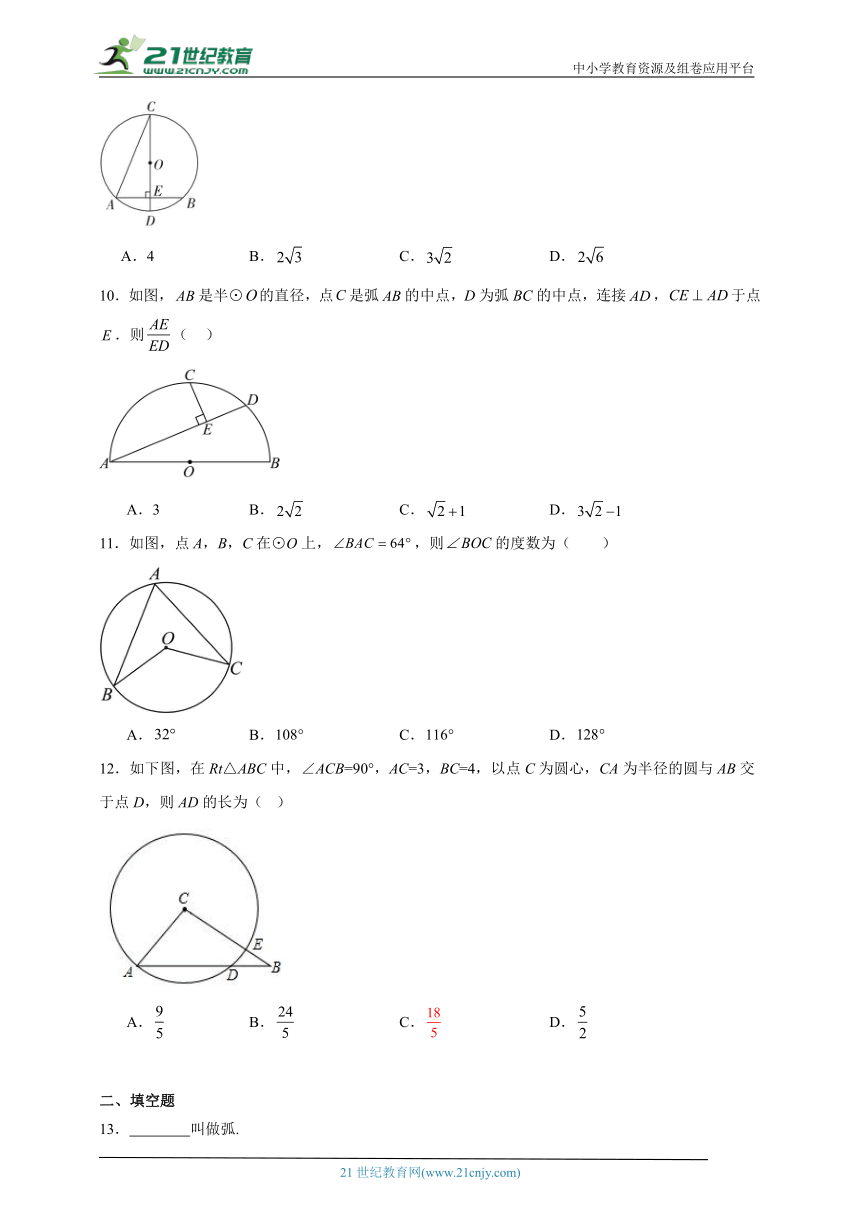
10.如图,是半⊙的直径,点是弧的中点,D为弧BC的中点,连接,于点.则( )
A.3 B. C. D.
11.如图,点A,B,C在⊙O上,,则的度数为( )
A. B. C. D.
12.如下图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
二、填空题
13. 叫做弧.
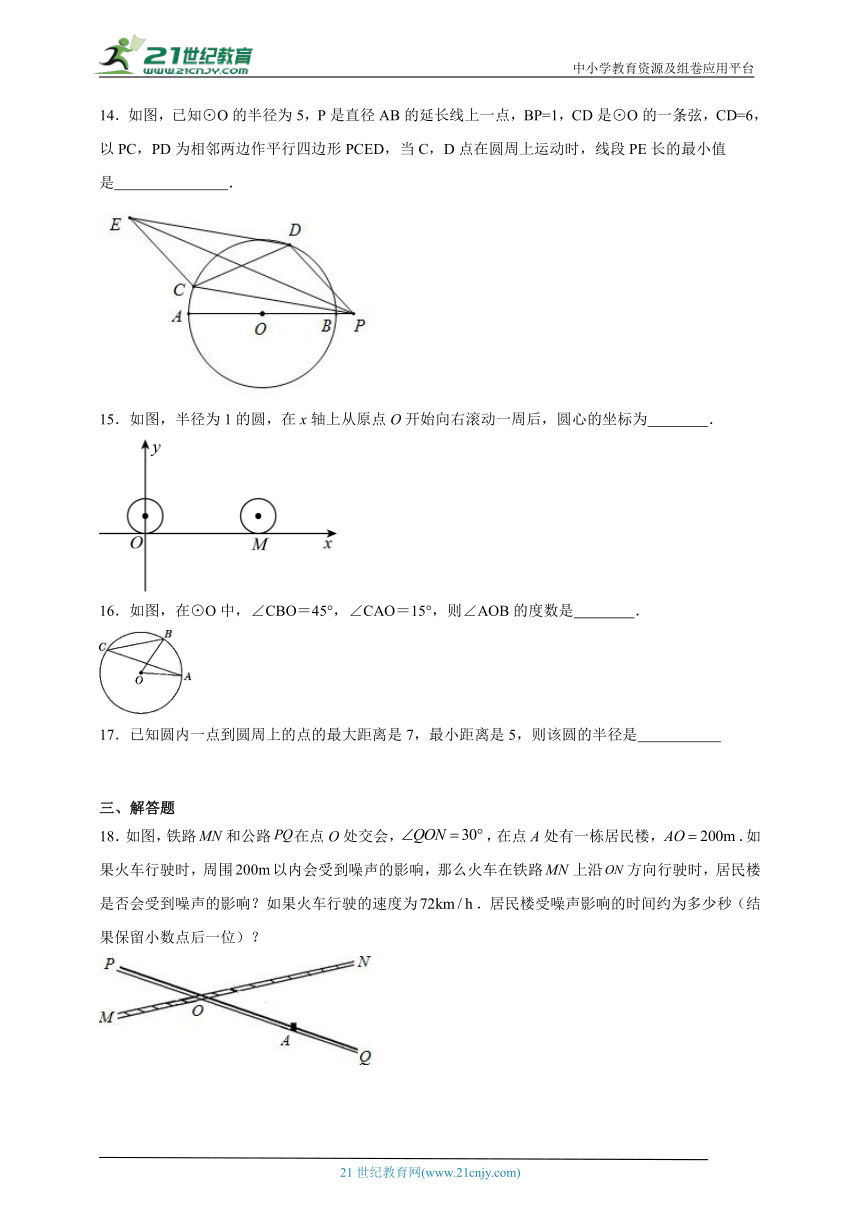
14.如图,已知⊙O的半径为5,P是直径AB的延长线上一点,BP=1,CD是⊙O的一条弦,CD=6,以PC,PD为相邻两边作平行四边形PCED,当C,D点在圆周上运动时,线段PE长的最小值是 .
15.如图,半径为1的圆,在x轴上从原点O开始向右滚动一周后,圆心的坐标为 .
16.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是 .
17.已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是
三、解答题
18.如图,铁路和公路在点O处交会,,在点A处有一栋居民楼,.如果火车行驶时,周围以内会受到噪声的影响,那么火车在铁路上沿方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为.居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
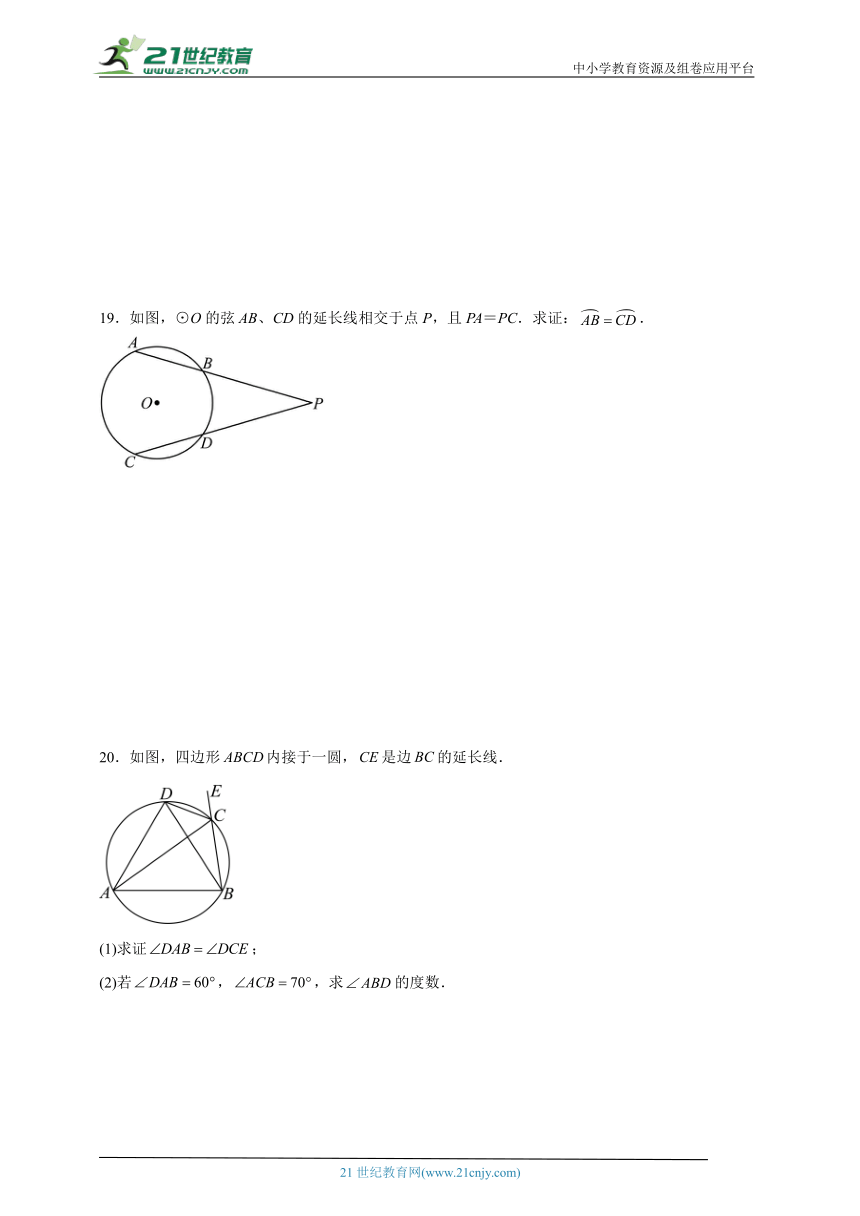
19.如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:.
20.如图,四边形内接于一圆,是边的延长线.
(1)求证;
(2)若,,求的度数.
21.综合与实践
动手操作
利用正方形纸片的折叠开展数学活动.探究体会在正方形折叠过程中,图形与线段的变化及其蕴含的数学思想方法.
如图1,点为正方形的边上的一个动点,,将正方形对折,使点与点重合,点与点重合,折痕为.
思考探索
(1)将正方形展平后沿过点的直线折叠,使点的对应点落在上,折痕为,连接,如图2.
①点在以点为圆心,_________的长为半径的圆上;
②_________;
③为_______三角形,请证明你的结论.
拓展延伸
(2)当时,正方形沿过点的直线(不过点)折叠后,点的对应点落在正方形内部或边上.
①面积的最大值为____________;
②连接,点为的中点,点在上,连接,则的最小值为____________.
22.如图,已知AB是⊙O的直径,.
(1)求的度数;
(2)过点D作,垂足为E,DE的延长线交⊙O于点F.若,求EF的长.
23.下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.
作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
24.已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
《27.1圆的认识》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D B C C B B C C
题号 11 12
答案 D C
1.B
【分析】根据等边三角形的性质求出,根据同弧所对的圆周角相等即可求解.
【详解】解:为正三角形,
,
,
故选:B.
【点睛】本题考查了等边三角形的性质,同弧所对的圆周角相等,解题关键是熟练掌握同弧所对的圆周角相等性质.
2.D
【分析】根据顺次连接圆内两条直径的4个端点,得出四边形的对角线相等且互相平分,即可得出四边形的形状;接下来根据圆的直径所对的圆周角是直角,结合上步得到的结论即可进一步确定四边形形状.
【详解】∵顺次连接圆内两条直径的4个端点,
∴此四边形的对角线相等且互相平分,
∴四边形是平行四边形,
又∵直径所对的圆周角等于90°,
∴所得的四边形一定是矩形.
故选:D.
【点睛】考查圆周角以及矩形的判定,掌握直径所对的圆周角是直角是解题的关键.
3.D
【分析】根据将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合,显然说明了圆的轴对称性.
【详解】解:将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合,由此说明圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
故选:D
【点睛】本题考查了轴对称图形的概念,解题的关键是掌握圆的对称轴为直径所在的直线或过圆心的直线.
4.B
【详解】∵OB=OC,∠OCB=40°,
∴∠BOC=180°-2∠OCB=100°,
∴由圆周角定理可知:∠A=∠BOC=50°.
故选:B.
5.C
【分析】如图,首先证得OA⊥BC;然后由圆周角定理推知∠C=30°,通过解直角△ACD可以求得CD的长度.则BC=2CD.
【详解】解:设AO与BC交于点D.
∵∠AOB=60°,,
∴∠C=∠AOB=30°,
又∵AB=AC,
∴
∴AD⊥BC,
∴BD=CD,
∴在直角△ACD中,CD=AC cos30°=2×=,
∴BC=2CD=2.
故选C.
【点睛】本题考查了圆周角定理,也考查了解直角三角形.题目难度不大.
6.C
【分析】本题考查动点问题的函数图象,根据如果点P向上运动,那么d的距离将逐渐变大;如果点P向下运动,那么d的距离将逐渐变小,两种情况讨论即可
【详解】解:由图中可知:长度d是一开始就存在的,如果点P向上运动,那么d的距离将逐渐变大;当点P运动到和O,A在同一直线上时,d最大,随后开始变小;当运动到点A时,距离d为0,然后继续运动,d开始变大;到点P时,回到原来高度相同的位置.①对,
②点P没有回到原来的位置,应排除.
④回到原来的位置后又继续运动了,应排除.
如果点P向下运动,那么d的距离将逐渐变小,到点A的位置时,距离d为0;继续运动,d的距离将逐渐变大;当点P运动到和O,A在同一直线上时,d最大,随后开始变小,到点P时,回到原来高度相同的位置.③对.
故选C
7.B
【详解】根据同一弧所对的圆周角的度数等于它所对圆心角度数的一半,
所以∠ACB的度数等于∠AOB的一半,
即
故选B
考点:同一弧所对的圆周角与它所对圆心角的关系.
8.B
【分析】连接OA,在上取点E,连接AE,BE,先证明,可得∠AOB=112°,结合圆周角定理和圆内接四边形的性质,即可求解.
【详解】解:连接OA,在上取点E,连接AE,BE,
∵点C为弦中点,
∴OC ⊥AB,即∠ACO=∠BCO=90°,
又∵AC=BC,OC=OC,
∴,
∴∠AOC=,即:∠AOB=112°,
∴∠E=∠AOB=56°,
∵四边形ADBE是的内接四边形,
∴=180°-56°=124°,
故选B.
【点睛】本题主要考查圆周角定理、垂径定理、圆的内接四边形的性质,添加辅助线,构造圆的内接四边形,是解题的关键.
9.C
【分析】连结OA,根据圆周角定理得∠AOD=2∠ACD=45°,由于的直径弦,根据垂径定理得AE=BE,且可判断△OAE为等腰直角三角形,所以AE=OA=,然后利用AB=2AE进行计算.
【详解】解:连结OA,
∵,
∴∠AOD=2∠ACD=45°,
∵的直径弦,
∴AE=BE,
∴△OAE为等腰直角三角形,
∴AE=OAsin45°=OA,
∵CD=6,
∴OA=3,
∴AE=,
∴AB=2AE=.
故选C.
【点睛】本题考查了圆周角定理,垂径定理,等腰直角三角形的性质,特殊角的锐角三角函数等知识.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
10.C
【分析】连接,,,在上取一点,使得,连接.证明,,可得结论.
【详解】解:如图,连接,BC、.
∵是直径,
∴.
∵,
∴.
∴.
∵,
∴.
∵
∴.
∵,
∴.
∴.
∴.
在上取一点,使得,连接.
设,则.
∵,
∴.
∴.
∴.
∴.
故选:C
【点睛】本题考查圆圆周角定理及推论、等腰直角三角形的判定与性质、勾股定理等知识点,熟知上述的定理或推论是解题的基础,根据题目特征,在EA上取点T,构造出两个特殊三角形和是解题的关键.
11.D
【分析】本题考查圆周角定理,根据同弧所对的圆周角是圆心角的一半求解即可.
【详解】解:∵,,
∴,
故选:D.
12.C
【详解】解:如图,过C作CM⊥AB,交AB于点M,
由垂径定理可得M为AD的中点,
∵,且AC=3,BC=4,AB=5,
∴.
在Rt△ACM中,根据勾股定理得:,
∴
(舍去负值).
∴.
故选C.
13.圆上任意两点间的部分
【详解】圆弧的相关概念.
答案为: 圆上任意两点间的部分.
14.4
【分析】连接OC,设CD与PE交于点K,连接OK,根据平行四边形的性质结合垂径定理求出OK的长,在三角形PKO中,根据三角形的三边关系得到线段PK的取值范围,再由,得到结果.
【详解】解:如图,连接OC,设CD与PE交于点K,连接OK,
∵四边形PCED是平行四边形,
∴,,
∴根据垂径定理
在中,,,
∴,
∵,
∴,即,
∵,
∴,
∴线段PE的最小值是4.
故答案是:4.
【点睛】本题考查线段最值问题,解题的关键是掌握平行四边形的性质和圆的垂径定理,再利用三角形三边的数量关系求出线段的取值范围从而得到最小值.
15.
【分析】本题考查圆周长公式,平面直角坐标系坐标表示.根据题意先求出圆周长即可得到本题答案.
【详解】解:∵半径为1的圆,
∴圆周长为:,
∴圆心的坐标为:.
16.60°
【分析】首先连接OC,由OB=OC=OA,∠CBO=45°,∠CAO=15°,根据等边对等角的性质,可求得∠OCB与∠OCA的度数,即可求得∠ACB的度数,又由圆周角定理,求得∠AOB的度数.
【详解】连接OC,
∵OB=OC=OA,∠CBO=45°,∠CAO=15°,
∴∠OCB=∠OBC=45°,∠OCA=∠OAC=15°.
∴∠ACB=∠OCB﹣∠OCA=30°.
∴∠AOB=2∠ACB=60°.
故答案为60°
【点睛】此题考查了圆周角定理以及等腰三角形的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
17.6
【详解】由题意,得
该圆的半径为:. 理由如下.
如图,设圆心为点O,该圆内的点为点P,过点P作直径CD,过点P作弦AB⊥CD.
不妨在圆周上任意取异于点D与点C的两点D1,D2. 连接OD1,OD2,PD1,PD2.
设该圆的半径为r,则OD=OC=OD1=OD2=r.
点P到点D的距离PD=OD-OP=r-OP,点P到点C的距离PC=OC+OP=r+OP.
∴PC>PD.
在△OPD1中,PD1>OD1-OP=r-OP=PD;在△OPD2中,PD2>OD2-OP=r-OP=PD.
∴PD1>PD,PD2>PD,PC>PD.
∴点P到点D的距离PD是点P与圆周上的点的最小距离.
在△OPD1中,PD1∴PD1∴点P到点C的距离PC是点P与圆周上的点的最大距离.
综上所述,对于圆内的一点,它到圆周上的点的最大距离与最小距离之和恰好等于圆的直径,故该圆的半径为上述最大距离与最小距离之和的一半.
故本题应填写:6.
点睛:
本题综合考查了圆的相关性质. 利用三角形三边的关系可以证明:若已知圆内一点到圆周上的点的最大距离和最小距离,则该圆的半径等于上述最大距离与最小距离之和的一半;若已知圆外一点到圆周上的点的最大距离和最小距离,则该圆的半径等于上述最大距离与最小距离之差的一半. 另外,三角形三边的关系是解决平面几何中最值问题的一个重要方法,需要充分理解和掌握.
18.居民楼会受到噪声的影响,17.3s
【分析】过点A作AB⊥MN,利用锐角三角函数的定义求出AB的长与200m相比较即可;过点A作AD=OA=200m,求出OD的长即可得出居民楼受噪音影响的时间.
【详解】解:过点A作AB⊥MN,AB是火车在行驶的过程中,距离居民楼最近的地方,
∵∠QON=30°,AO=200m,
∴AB=OA=200×=100m<200m,
∴居民楼会受到噪音的影响;
∵OA=200m,
∴以A为圆心,OA为半径作圆,交MN于D,
则OA=AD=200(m),
∵AB⊥OD,
∴OB=BD,
∵在Rt△AOB中,OB==100(m),
∴OD=2BO=200(m),
∵火车行驶的速度为72km/h=20m/s,
∴≈17.3(s).
答:居民楼受噪音影响的时间为17.3 s.
【点睛】本题是解直角三角形的应用,主要考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.证明见解析
【分析】连接AC、OA、OB、OC、OD,根据等腰三角形的性质得到∠PAC=∠PCA,根据圆周角定理得到∠BOC=∠AOD,根据圆心角、弧、弦的关系定理证明结论.
【详解】证明:连接AC、OA、OB、OC、OD,
∵PA=PC,
∴∠PAC=∠PCA,
∵∠PAC∠BOC,∠PCA∠AOD,
∴∠BOC=∠AOD,
∴,
∴,即.
【点睛】本题考查的是圆心角、弧、弦的关系定理、圆周角定理,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
20.(1)见解析
(2)
【分析】(1)根据圆内接四边形的性质得到,根据同角的补角相等证明结论;
(2)根据圆周角定理得到,根据三角形内角和定理计算即可.
【详解】(1)证明:四边形内接于圆,
,
,
;
(2)解:,
,
.
【点睛】本题考查的是圆内接四边形的性质、圆周角定理,解题的关键是掌握圆内接四边形的对角互补.
21.(1)①;②;③等边,证明见解析;(2)①3;②.
【分析】(1)①利用圆的基本性质,即可求解;
②根据折叠的性质,利用勾股定理,即可求解;
③利用勾股定理,求得B′D=,即可求解;
(2)①由题意知点B'在以点E为圆心,半径长为2的圆上,△ABB'的面积要最大,只要以AB为底的高最长即可,此时当B'E⊥AB时,△ABB'的面积最大;
②当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,且最小值为EC的长,利用勾股定理即可求解.
【详解】解:(1)根据折叠的性质知:BE=B′E,BC=B′C=3,MA=MB=NC=ND=,
∠B=∠EB′C=90,
①点B′在以点E为圆心,BE的长为半径的圆上;
②B′M=MN- B′N=
=
=;
③B′D=,
∴△DB'C为等边三角形;
故答案为:①BE,②,③等边;
(2)①∵AB=3=3AE,
∴AE=1,BE=2,
故点B'在以点E为圆心,半径长为2的圆上,
∴△ABB'的面积要最大,只要以AB为底的高最长即可,
∴当B'E⊥AB时,△ABB'的面积最大,如图:
△ABB'的面积最大值;
②∵∠AQP=∠AB'E,
∴PQ∥B'E,
∵P为AE的中点,
∴Q为AB'的中点,
∴PQ为△AEB'的中位线,
∴PQ=EB',即EB'=2PQ,
∴B'C+2PQ= B'C+ EB',
当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,
且最小值为EC的长,
∴EC=,
∴B'C+2PQ的最小值为.
故答案为:①;②.
【点睛】本题考查了圆的性质,矩形的性质、图形的折叠、等腰三角形的性质等,有一定的综合性,难度适中,其中(2)①当B'E⊥AB时,△ABB'的面积最大;②当E、B′、C三点共线时,B'C+2PQ取得最小值,是解本题的关键.
22.(1)60°;(2)
【分析】(1)连结,根据同弧所对的圆周角相等得到,然后由直径所对的圆周角是直角得到,根据直角三角形两锐角互余即可求出的度数;
(2)首先根据角所对的直角边是斜边的一半求得,然后根据勾股定理求出BD的长度,利用面积法求出DE的长度,最后根据垂径定理即可求出EF的长度.
【详解】解:(1)如图所示,连结,
∵,
∴,
∵是的直径,
∴,
∴.
(2)∵,,,
∴,
∵,即,
∴,
∵,且是直径,
∴.
【点睛】此题考查了勾股定理,垂径定理的运用,同弧所对的圆周角相等,直径所对的圆周角是直角等知识,解题的关键是连接BD,得到.
23.见详解
【分析】根据直径的性质可得∠ADC=90°,再利用同角的余角相等即可得证.
【详解】证明:∵AC是直径
∴∠ADC=90°(直径所对圆周角为直角)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_∠BCD _=90°,
∴∠BCD=∠A(同角的余角相等).
【点睛】本题考查了直径的性质及同角的余角相等,熟练运用相关性质是解决本题的关键.
24.(1)证明见试题解析;(2)AC=BD,证明见试题解析.
【分析】(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;
(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE-CE=BE-DE,即AC=BD.
【详解】试题解析:
(1)∵AO=OB,OC=OD
∴∠A=∠B,∠OCD=∠ODC
∴∠OCA=∠ODC
∴△ACO≌△ODB
∴∠AOC=∠DOB
(2)过O作OE⊥AB于E
∴AE=EB,CE=ED
∴AC=BD
考点:等边对等角,三角形外角性质,垂径定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.1圆的认识
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正三角形的三个顶点均在上,动点在上,且不与点重合,则的度数为( )
A. B. C. D.
2.在同一个圆中画两条直径,依次连接四个端点得到的四边形是( )
A.菱形 B.等腰梯形 C.正方形 D.矩形
3.在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合”.由此说明( )
A.圆的直径互相平分
B.垂直弦的直径平分弦及弦所对的弧
C.圆是中心对称图形,圆心是它的对称中心
D.圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
4.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
A.40° B.50° C.80° D.100°
5.如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B.3 C.2 D.4
6.如图,上有两点A与P,且,若A点固定不动,P点在圆上匀速运动一周,那么弦的长度与时间的函数关系的图象可能是( )
A.① B.③ C.①或③ D.②或④
7.如图,A、C、B是⊙O上三点,若∠AOC=40°,则∠ABC的度数是( ).
A.10° B.20° C.40° D.80°
8.如图,中,点C为弦中点,连接,,,点D是上任意一点,则度数为( )
A. B. C. D.
9.如图,已知的直径弦,垂足为,,若,则的长为( )
A.4 B. C. D.
10.如图,是半⊙的直径,点是弧的中点,D为弧BC的中点,连接,于点.则( )
A.3 B. C. D.
11.如图,点A,B,C在⊙O上,,则的度数为( )
A. B. C. D.
12.如下图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
二、填空题
13. 叫做弧.
14.如图,已知⊙O的半径为5,P是直径AB的延长线上一点,BP=1,CD是⊙O的一条弦,CD=6,以PC,PD为相邻两边作平行四边形PCED,当C,D点在圆周上运动时,线段PE长的最小值是 .
15.如图,半径为1的圆,在x轴上从原点O开始向右滚动一周后,圆心的坐标为 .
16.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是 .
17.已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是
三、解答题
18.如图,铁路和公路在点O处交会,,在点A处有一栋居民楼,.如果火车行驶时,周围以内会受到噪声的影响,那么火车在铁路上沿方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为.居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
19.如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:.
20.如图,四边形内接于一圆,是边的延长线.
(1)求证;
(2)若,,求的度数.
21.综合与实践
动手操作
利用正方形纸片的折叠开展数学活动.探究体会在正方形折叠过程中,图形与线段的变化及其蕴含的数学思想方法.
如图1,点为正方形的边上的一个动点,,将正方形对折,使点与点重合,点与点重合,折痕为.
思考探索
(1)将正方形展平后沿过点的直线折叠,使点的对应点落在上,折痕为,连接,如图2.
①点在以点为圆心,_________的长为半径的圆上;
②_________;
③为_______三角形,请证明你的结论.
拓展延伸
(2)当时,正方形沿过点的直线(不过点)折叠后,点的对应点落在正方形内部或边上.
①面积的最大值为____________;
②连接,点为的中点,点在上,连接,则的最小值为____________.
22.如图,已知AB是⊙O的直径,.
(1)求的度数;
(2)过点D作,垂足为E,DE的延长线交⊙O于点F.若,求EF的长.
23.下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.
作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
24.已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
《27.1圆的认识》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D B C C B B C C
题号 11 12
答案 D C
1.B
【分析】根据等边三角形的性质求出,根据同弧所对的圆周角相等即可求解.
【详解】解:为正三角形,
,
,
故选:B.
【点睛】本题考查了等边三角形的性质,同弧所对的圆周角相等,解题关键是熟练掌握同弧所对的圆周角相等性质.
2.D
【分析】根据顺次连接圆内两条直径的4个端点,得出四边形的对角线相等且互相平分,即可得出四边形的形状;接下来根据圆的直径所对的圆周角是直角,结合上步得到的结论即可进一步确定四边形形状.
【详解】∵顺次连接圆内两条直径的4个端点,
∴此四边形的对角线相等且互相平分,
∴四边形是平行四边形,
又∵直径所对的圆周角等于90°,
∴所得的四边形一定是矩形.
故选:D.
【点睛】考查圆周角以及矩形的判定,掌握直径所对的圆周角是直角是解题的关键.
3.D
【分析】根据将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合,显然说明了圆的轴对称性.
【详解】解:将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合,由此说明圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
故选:D
【点睛】本题考查了轴对称图形的概念,解题的关键是掌握圆的对称轴为直径所在的直线或过圆心的直线.
4.B
【详解】∵OB=OC,∠OCB=40°,
∴∠BOC=180°-2∠OCB=100°,
∴由圆周角定理可知:∠A=∠BOC=50°.
故选:B.
5.C
【分析】如图,首先证得OA⊥BC;然后由圆周角定理推知∠C=30°,通过解直角△ACD可以求得CD的长度.则BC=2CD.
【详解】解:设AO与BC交于点D.
∵∠AOB=60°,,
∴∠C=∠AOB=30°,
又∵AB=AC,
∴
∴AD⊥BC,
∴BD=CD,
∴在直角△ACD中,CD=AC cos30°=2×=,
∴BC=2CD=2.
故选C.
【点睛】本题考查了圆周角定理,也考查了解直角三角形.题目难度不大.
6.C
【分析】本题考查动点问题的函数图象,根据如果点P向上运动,那么d的距离将逐渐变大;如果点P向下运动,那么d的距离将逐渐变小,两种情况讨论即可
【详解】解:由图中可知:长度d是一开始就存在的,如果点P向上运动,那么d的距离将逐渐变大;当点P运动到和O,A在同一直线上时,d最大,随后开始变小;当运动到点A时,距离d为0,然后继续运动,d开始变大;到点P时,回到原来高度相同的位置.①对,
②点P没有回到原来的位置,应排除.
④回到原来的位置后又继续运动了,应排除.
如果点P向下运动,那么d的距离将逐渐变小,到点A的位置时,距离d为0;继续运动,d的距离将逐渐变大;当点P运动到和O,A在同一直线上时,d最大,随后开始变小,到点P时,回到原来高度相同的位置.③对.
故选C
7.B
【详解】根据同一弧所对的圆周角的度数等于它所对圆心角度数的一半,
所以∠ACB的度数等于∠AOB的一半,
即
故选B
考点:同一弧所对的圆周角与它所对圆心角的关系.
8.B
【分析】连接OA,在上取点E,连接AE,BE,先证明,可得∠AOB=112°,结合圆周角定理和圆内接四边形的性质,即可求解.
【详解】解:连接OA,在上取点E,连接AE,BE,
∵点C为弦中点,
∴OC ⊥AB,即∠ACO=∠BCO=90°,
又∵AC=BC,OC=OC,
∴,
∴∠AOC=,即:∠AOB=112°,
∴∠E=∠AOB=56°,
∵四边形ADBE是的内接四边形,
∴=180°-56°=124°,
故选B.
【点睛】本题主要考查圆周角定理、垂径定理、圆的内接四边形的性质,添加辅助线,构造圆的内接四边形,是解题的关键.
9.C
【分析】连结OA,根据圆周角定理得∠AOD=2∠ACD=45°,由于的直径弦,根据垂径定理得AE=BE,且可判断△OAE为等腰直角三角形,所以AE=OA=,然后利用AB=2AE进行计算.
【详解】解:连结OA,
∵,
∴∠AOD=2∠ACD=45°,
∵的直径弦,
∴AE=BE,
∴△OAE为等腰直角三角形,
∴AE=OAsin45°=OA,
∵CD=6,
∴OA=3,
∴AE=,
∴AB=2AE=.
故选C.
【点睛】本题考查了圆周角定理,垂径定理,等腰直角三角形的性质,特殊角的锐角三角函数等知识.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
10.C
【分析】连接,,,在上取一点,使得,连接.证明,,可得结论.
【详解】解:如图,连接,BC、.
∵是直径,
∴.
∵,
∴.
∴.
∵,
∴.
∵
∴.
∵,
∴.
∴.
∴.
在上取一点,使得,连接.
设,则.
∵,
∴.
∴.
∴.
∴.
故选:C
【点睛】本题考查圆圆周角定理及推论、等腰直角三角形的判定与性质、勾股定理等知识点,熟知上述的定理或推论是解题的基础,根据题目特征,在EA上取点T,构造出两个特殊三角形和是解题的关键.
11.D
【分析】本题考查圆周角定理,根据同弧所对的圆周角是圆心角的一半求解即可.
【详解】解:∵,,
∴,
故选:D.
12.C
【详解】解:如图,过C作CM⊥AB,交AB于点M,
由垂径定理可得M为AD的中点,
∵,且AC=3,BC=4,AB=5,
∴.
在Rt△ACM中,根据勾股定理得:,
∴
(舍去负值).
∴.
故选C.
13.圆上任意两点间的部分
【详解】圆弧的相关概念.
答案为: 圆上任意两点间的部分.
14.4
【分析】连接OC,设CD与PE交于点K,连接OK,根据平行四边形的性质结合垂径定理求出OK的长,在三角形PKO中,根据三角形的三边关系得到线段PK的取值范围,再由,得到结果.
【详解】解:如图,连接OC,设CD与PE交于点K,连接OK,
∵四边形PCED是平行四边形,
∴,,
∴根据垂径定理
在中,,,
∴,
∵,
∴,即,
∵,
∴,
∴线段PE的最小值是4.
故答案是:4.
【点睛】本题考查线段最值问题,解题的关键是掌握平行四边形的性质和圆的垂径定理,再利用三角形三边的数量关系求出线段的取值范围从而得到最小值.
15.
【分析】本题考查圆周长公式,平面直角坐标系坐标表示.根据题意先求出圆周长即可得到本题答案.
【详解】解:∵半径为1的圆,
∴圆周长为:,
∴圆心的坐标为:.
16.60°
【分析】首先连接OC,由OB=OC=OA,∠CBO=45°,∠CAO=15°,根据等边对等角的性质,可求得∠OCB与∠OCA的度数,即可求得∠ACB的度数,又由圆周角定理,求得∠AOB的度数.
【详解】连接OC,
∵OB=OC=OA,∠CBO=45°,∠CAO=15°,
∴∠OCB=∠OBC=45°,∠OCA=∠OAC=15°.
∴∠ACB=∠OCB﹣∠OCA=30°.
∴∠AOB=2∠ACB=60°.
故答案为60°
【点睛】此题考查了圆周角定理以及等腰三角形的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
17.6
【详解】由题意,得
该圆的半径为:. 理由如下.
如图,设圆心为点O,该圆内的点为点P,过点P作直径CD,过点P作弦AB⊥CD.
不妨在圆周上任意取异于点D与点C的两点D1,D2. 连接OD1,OD2,PD1,PD2.
设该圆的半径为r,则OD=OC=OD1=OD2=r.
点P到点D的距离PD=OD-OP=r-OP,点P到点C的距离PC=OC+OP=r+OP.
∴PC>PD.
在△OPD1中,PD1>OD1-OP=r-OP=PD;在△OPD2中,PD2>OD2-OP=r-OP=PD.
∴PD1>PD,PD2>PD,PC>PD.
∴点P到点D的距离PD是点P与圆周上的点的最小距离.
在△OPD1中,PD1
综上所述,对于圆内的一点,它到圆周上的点的最大距离与最小距离之和恰好等于圆的直径,故该圆的半径为上述最大距离与最小距离之和的一半.
故本题应填写:6.
点睛:
本题综合考查了圆的相关性质. 利用三角形三边的关系可以证明:若已知圆内一点到圆周上的点的最大距离和最小距离,则该圆的半径等于上述最大距离与最小距离之和的一半;若已知圆外一点到圆周上的点的最大距离和最小距离,则该圆的半径等于上述最大距离与最小距离之差的一半. 另外,三角形三边的关系是解决平面几何中最值问题的一个重要方法,需要充分理解和掌握.
18.居民楼会受到噪声的影响,17.3s
【分析】过点A作AB⊥MN,利用锐角三角函数的定义求出AB的长与200m相比较即可;过点A作AD=OA=200m,求出OD的长即可得出居民楼受噪音影响的时间.
【详解】解:过点A作AB⊥MN,AB是火车在行驶的过程中,距离居民楼最近的地方,
∵∠QON=30°,AO=200m,
∴AB=OA=200×=100m<200m,
∴居民楼会受到噪音的影响;
∵OA=200m,
∴以A为圆心,OA为半径作圆,交MN于D,
则OA=AD=200(m),
∵AB⊥OD,
∴OB=BD,
∵在Rt△AOB中,OB==100(m),
∴OD=2BO=200(m),
∵火车行驶的速度为72km/h=20m/s,
∴≈17.3(s).
答:居民楼受噪音影响的时间为17.3 s.
【点睛】本题是解直角三角形的应用,主要考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.证明见解析
【分析】连接AC、OA、OB、OC、OD,根据等腰三角形的性质得到∠PAC=∠PCA,根据圆周角定理得到∠BOC=∠AOD,根据圆心角、弧、弦的关系定理证明结论.
【详解】证明:连接AC、OA、OB、OC、OD,
∵PA=PC,
∴∠PAC=∠PCA,
∵∠PAC∠BOC,∠PCA∠AOD,
∴∠BOC=∠AOD,
∴,
∴,即.
【点睛】本题考查的是圆心角、弧、弦的关系定理、圆周角定理,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
20.(1)见解析
(2)
【分析】(1)根据圆内接四边形的性质得到,根据同角的补角相等证明结论;
(2)根据圆周角定理得到,根据三角形内角和定理计算即可.
【详解】(1)证明:四边形内接于圆,
,
,
;
(2)解:,
,
.
【点睛】本题考查的是圆内接四边形的性质、圆周角定理,解题的关键是掌握圆内接四边形的对角互补.
21.(1)①;②;③等边,证明见解析;(2)①3;②.
【分析】(1)①利用圆的基本性质,即可求解;
②根据折叠的性质,利用勾股定理,即可求解;
③利用勾股定理,求得B′D=,即可求解;
(2)①由题意知点B'在以点E为圆心,半径长为2的圆上,△ABB'的面积要最大,只要以AB为底的高最长即可,此时当B'E⊥AB时,△ABB'的面积最大;
②当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,且最小值为EC的长,利用勾股定理即可求解.
【详解】解:(1)根据折叠的性质知:BE=B′E,BC=B′C=3,MA=MB=NC=ND=,
∠B=∠EB′C=90,
①点B′在以点E为圆心,BE的长为半径的圆上;
②B′M=MN- B′N=
=
=;
③B′D=,
∴△DB'C为等边三角形;
故答案为:①BE,②,③等边;
(2)①∵AB=3=3AE,
∴AE=1,BE=2,
故点B'在以点E为圆心,半径长为2的圆上,
∴△ABB'的面积要最大,只要以AB为底的高最长即可,
∴当B'E⊥AB时,△ABB'的面积最大,如图:
△ABB'的面积最大值;
②∵∠AQP=∠AB'E,
∴PQ∥B'E,
∵P为AE的中点,
∴Q为AB'的中点,
∴PQ为△AEB'的中位线,
∴PQ=EB',即EB'=2PQ,
∴B'C+2PQ= B'C+ EB',
当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,
且最小值为EC的长,
∴EC=,
∴B'C+2PQ的最小值为.
故答案为:①;②.
【点睛】本题考查了圆的性质,矩形的性质、图形的折叠、等腰三角形的性质等,有一定的综合性,难度适中,其中(2)①当B'E⊥AB时,△ABB'的面积最大;②当E、B′、C三点共线时,B'C+2PQ取得最小值,是解本题的关键.
22.(1)60°;(2)
【分析】(1)连结,根据同弧所对的圆周角相等得到,然后由直径所对的圆周角是直角得到,根据直角三角形两锐角互余即可求出的度数;
(2)首先根据角所对的直角边是斜边的一半求得,然后根据勾股定理求出BD的长度,利用面积法求出DE的长度,最后根据垂径定理即可求出EF的长度.
【详解】解:(1)如图所示,连结,
∵,
∴,
∵是的直径,
∴,
∴.
(2)∵,,,
∴,
∵,即,
∴,
∵,且是直径,
∴.
【点睛】此题考查了勾股定理,垂径定理的运用,同弧所对的圆周角相等,直径所对的圆周角是直角等知识,解题的关键是连接BD,得到.
23.见详解
【分析】根据直径的性质可得∠ADC=90°,再利用同角的余角相等即可得证.
【详解】证明:∵AC是直径
∴∠ADC=90°(直径所对圆周角为直角)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_∠BCD _=90°,
∴∠BCD=∠A(同角的余角相等).
【点睛】本题考查了直径的性质及同角的余角相等,熟练运用相关性质是解决本题的关键.
24.(1)证明见试题解析;(2)AC=BD,证明见试题解析.
【分析】(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;
(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE-CE=BE-DE,即AC=BD.
【详解】试题解析:
(1)∵AO=OB,OC=OD
∴∠A=∠B,∠OCD=∠ODC
∴∠OCA=∠ODC
∴△ACO≌△ODB
∴∠AOC=∠DOB
(2)过O作OE⊥AB于E
∴AE=EB,CE=ED
∴AC=BD
考点:等边对等角,三角形外角性质,垂径定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
