【期末专项培优】比例高频易错押题卷(含解析)-2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 【期末专项培优】比例高频易错押题卷(含解析)-2024-2025学年六年级下册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 897.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 00:00:00 | ||
图片预览



文档简介
期末专项培优:比例
一.比例的意义和基本性质(共19小题)
1.( )能与:组成比例.
A.3:4 B.4:3 C.3: D.:
2.一个比例的两个内项的积减去两个外项的积,结果是( )
A.0 B.1 C.10 D.无法确定
3.如图,三角形a边上的高为b,c边上的高为d。则下面式子中( )不成立。
A.a:c=b:d B.a:c=d:b C. D.
4.下面每组中的四个数,不能组成比例的是( )
A.2,0.25,3,0.375 B.30,25,6,125
C.,,,
5.能与4:3组成比例的是( )
A. B.3:4 C.8:9
6.下面( )组的两个比不能组成比例。
A.7:8和14:16 B.0.6:0.2和3:1
C.19:110和10:9 D.6:10和9:15
7.在一个比例里,两个外项互为倒数,期中一个内项是,另一个内项是 .
8.如果4x=3y(x、y均不为0),那么x:y= .
9.如果7x=8y(x、y均不为0),那么x:y= : .
10.在一个比例中,两个内项互为倒数,其中一个外项是1.5,另一个外项是 。
11.若一个比例的两个外项互为倒数,其中一个内项是,则另一个内项是 。
12.3、4、9、12这四个数字可以组成比例。如果把“3”作为比例的一个内项,那么这个比例可以是 ;如果把“3”作为比例的一个外项,那么这个比例可以是 。
13.比例是指两个比的相等关系,所以比和比例表示的意义是一样的。 (判断对错)
14.比例是方程. .(判断对错)
15.在一个比例中,两个外项的积与两个内项的积的差为0。 (判断对错)
16.在比例3:5=9:15中,将等号左边比的后项加上20,要使比例成立,等号右边比的后项应加上60。 (判断对错)
17.表示两个比相等的式子叫比例. (判断对错)
18.如果ab(a、b都不为0),那么a:b=8:9。 (判断对错)
19.有一扇通往知识宝藏的大门,门上有三个数,它们分别是2,5,10,请找出第四个数,这个数必须满足下列三个条件:
①这个数要能与原来三个数组成比例;
②这个数是合数;
③这个数是奇数。
这个数是几呢?请写出你的计算过程。
二.正比例和反比例的意义(共3小题)
20.如表所示,当x和y成正比例时,空格里应填 ;当x和y成反比例时,空格里应填 。
x 12
y 6 24
21.如表所示,如果x和y成正比例,那么“?”处应填 。如果x和y成反比例,那么“?”处应填 。
x 3 ?
y 90 150
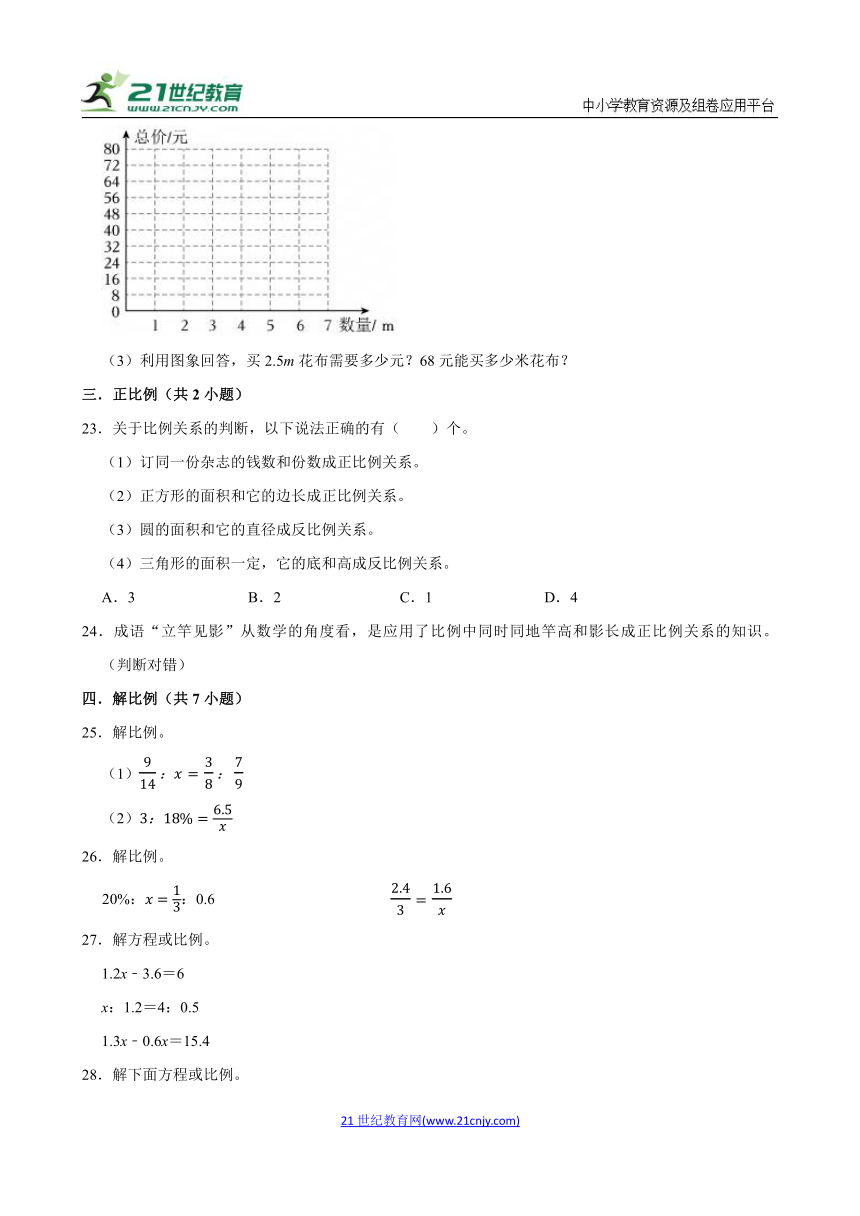
22.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
三.正比例(共2小题)
23.关于比例关系的判断,以下说法正确的有( )个。
(1)订同一份杂志的钱数和份数成正比例关系。
(2)正方形的面积和它的边长成正比例关系。
(3)圆的面积和它的直径成反比例关系。
(4)三角形的面积一定,它的底和高成反比例关系。
A.3 B.2 C.1 D.4
24.成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。 (判断对错)
四.解比例(共7小题)
25.解比例。
(1)
(2)
26.解比例。
20%::0.6
27.解方程或比例。
1.2x﹣3.6=6
x:1.2=4:0.5
1.3x﹣0.6x=15.4
28.解下面方程或比例。
4x+3×0.7=6.5
29.解方程或比例。
30%x+50%x=240
30.解比例。
①0.4:x=0.2:7
②
③
31.解方程。
:x=3:12
x﹣214
五.比例的应用(共8小题)
32.师徒二人同时合作加工一批零件,全部完成一共用了6小时。已知徒弟与师傅加工零件的个数比是3:8,如果师傅平均每小时加工120个零件,那么徒弟平均每小时加工多少个零件?
33.在比例尺是1:1000000的地图上,量的苍南县到杭州距离是3.6厘米。苍南县到杭州的实际距离是多少?
34.一间大厅,用边长为6分米的方砖铺地,需用216块;若改铺边长为4分米的方砖,需要用多少块?(用比例知识解答)
35.500千克稻谷可以碾出大米410千克。照这样计算,现在有这样的稻谷7.5吨,可以碾出多少吨大米?(用比例解)
36.小马骑自行车从家里到书店,前5分钟行了800m。照这样的速度,从家到书店一共用了20分钟。他家和书店相距多少米?(用比例解)
37.某市修一条道路,计划每天修120米,8天可以修完。但因为天气原因,12天才完成任务,实际每天修多少米?(用比例方法解)
38.古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解)
(1)12只羊可以换多少把斧头?
(2)要换9把斧头,需要几只羊?
39.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
六.图形的放大与缩小(共5小题)
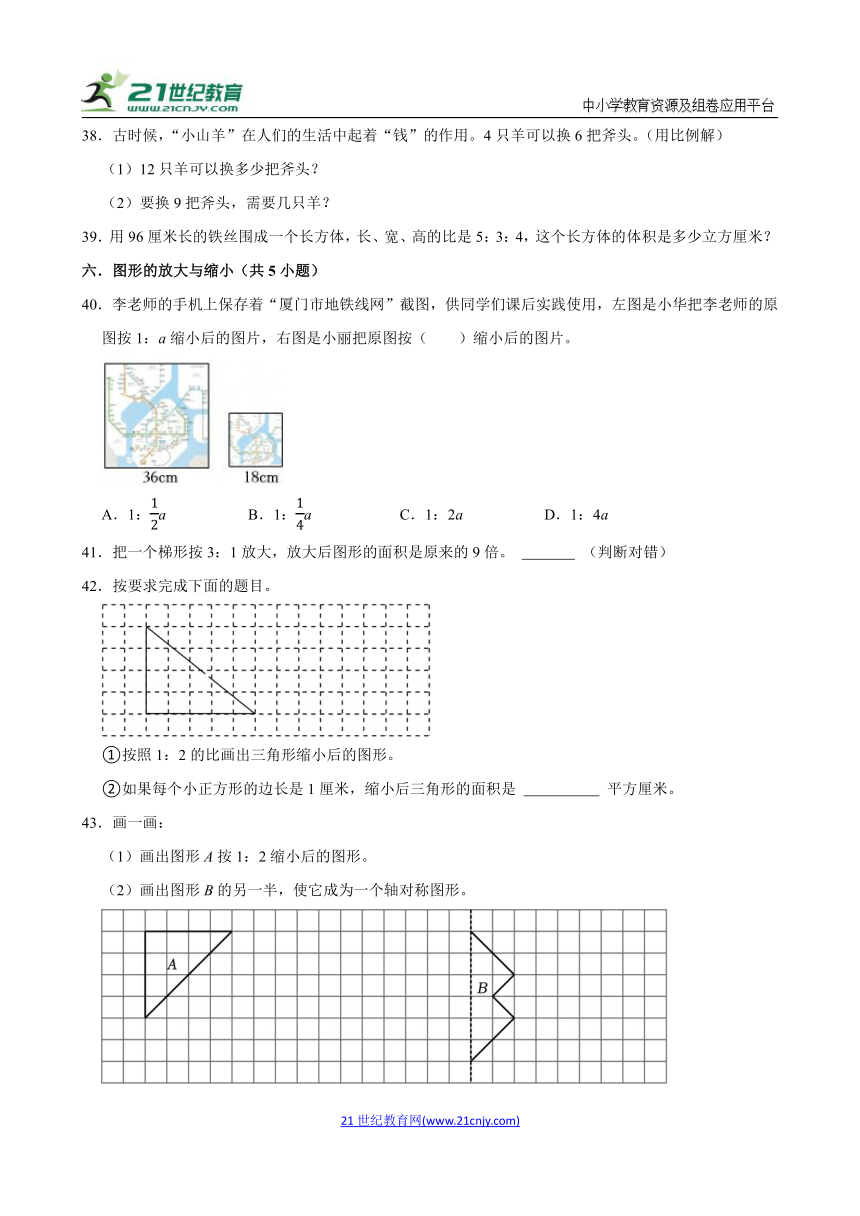
40.李老师的手机上保存着“厦门市地铁线网”截图,供同学们课后实践使用,左图是小华把李老师的原图按1:a缩小后的图片,右图是小丽把原图按( )缩小后的图片。
A.1:a B.1:a C.1:2a D.1:4a
41.把一个梯形按3:1放大,放大后图形的面积是原来的9倍。 (判断对错)
42.按要求完成下面的题目。
①按照1:2的比画出三角形缩小后的图形。
②如果每个小正方形的边长是1厘米,缩小后三角形的面积是 平方厘米。
43.画一画:
(1)画出图形A按1:2缩小后的图形。
(2)画出图形B的另一半,使它成为一个轴对称图形。
44.请把长方形的长和宽都按2:1放大,画出放大后的长方形;请把三角形的各边接1:2缩小,画出缩小后的三角形。
七.比例尺(共16小题)
45.有一张边长为65厘米的正方形图纸,要在上面画长为120米,宽为90米的长方形草坪的平面图,你认为最合适的比例尺是( )
A.1:150 B.1:200 C.1:2000 D.20:1
46.李叔叔是汽轮机厂的工程师,他要将一个长4mm、宽2mm的零件画在一张A3纸(42cm×29.7cm)上,合适的比例尺是( )
A.1:100 B.100:1 C.1:1000 D.1000:1
47.一张地图的比例尺是1:5000000,地图上的1厘米相当于实际距离的( )
A.5000米 B.5000千米 C.50千米 D.500米
48.一幅地图的比例尺是20:1,如果零件图上长5厘米,则实际长( )
A.4厘米 B.100厘米 C.0.25厘米
49.如图是现藏于三星堆博物馆的青铜大立人像,青铜大立人像是现存最高。最完整的青铜立人像,被誉为“世界铜像之王”。在一张比例尺为1:80的图上,这个青铜大立人像的高为( )
A.3.26厘米 B.32.6厘米
C.208.64厘米 D.2.608厘米
50.一种微型零件的实际长度是1mm,画在图纸上长3dm,画图时选用的比例尺是( )
A.1:300 B.1:3 C.300:1 D.3:1
51.一幅地图的线段比例尺是,改成数字比例尺是 ;石家庄到北京的实际距离是330千米,则地图上的距离是 厘米。
52.小玲的妈妈身高1.65m,在一张照片上她的身高是5cm,这张照片的比例尺是 。
53.实际宽度为3m的窗户,在建筑平面图上绘制的宽度为1.5cm,这幅平面图的比例尺为 。
54.在照片上小明的身高是8厘米,他的实际身高是168厘米。这张照片的比例尺是 。
55.一个圆柱形零件的高是5mm,在图纸上的高是2cm,这幅图纸的比例尺是 .
56.在一张图纸上,测得一个零件的长是10cm,已知这个零件实际长度是2mm,这张图纸的比例尺是 。
57.在比例尺是1:20的图纸上画出一种机械配件平面图的角是40°,这个角实际上也是40°。 (判断对错)
58.实际距离为2mm,图上距离为2dm,则比例尺为1:100。 (判断对错)
59.在比例尺是100:1的图纸上,一个长方体零件正面的长是15cm,宽是9cm。这个零件正面的实际面积是多少平方厘米?
60.游泳比赛的泳池是一个长方形,把泳池的长和宽分别缩小到原来的后图形如下.
(1)泳池实际的长和宽各是多少米?
(2)泳池的实际占地面积是多少平方米?
4 比例
参考答案与试题解析
一.比例的意义和基本性质(共19小题)
1.( )能与:组成比例.
A.3:4 B.4:3 C.3: D.:
【答案】A
【分析】表示两个比相等的式子叫作比例,只要比值和:相等比就能和它组成比例,因此下列各选项的比值哪个和:相等,就为正确选项.
【解答】解::3:4;
故选:A.
【点评】本题主要考查了比例的意义.
2.一个比例的两个内项的积减去两个外项的积,结果是( )
A.0 B.1 C.10 D.无法确定
【答案】A
【分析】比例的性质:在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。
【解答】解:一个比例的两个内项的积减去两个外项的积,结果是0。
故选:A。
【点评】本题是比例的性质的应用。
3.如图,三角形a边上的高为b,c边上的高为d。则下面式子中( )不成立。
A.a:c=b:d B.a:c=d:b C. D.
【答案】A
【分析】根据三角形的面积公式:三角的面积=底×高÷2,因为是同一个三角形,所以用对应的底a乘高b除以2等于对应对应的底c和高d除以2,则ab=cd,再根据比例的基本性质把各比例式转化为乘积式,比较得解。
【解答】解:根据ab÷2=cd÷2,可得ab=cd,
A.a:c=b:d,即ad=cb,所以选项A不成立;
B.a:c=d:b,即ab=cd,所以选项B成立;
C.,即ab=cd,所以选项C成立;
D.,即ab=cd,所以选项D成立。
故选:A。
【点评】此题考查了三角形的面积公式及比例基本性质的运用。
4.下面每组中的四个数,不能组成比例的是( )
A.2,0.25,3,0.375 B.30,25,6,125
C.,,,
【答案】C
【分析】根据比例的基本性质:两个外项的及等于两个内项的积,判断即可。
【解答】解:23,所以2,0.25,3,0.375能组成比例;
30×25=6×125,所以30,25,6,125能组成比例;
每组中的四个数,不能组成比例的是,,,。
故选:C。
【点评】本题主要考查比例的意义和基本性质的应用。
5.能与4:3组成比例的是( )
A. B.3:4 C.8:9
【答案】A
【分析】根据比例的意义:表示两个比相等的式子叫做比例;由此依次算出各选项的比值,找出与4:3比值相等的选项组成比例解答即可。
【解答】解:4:3
A.:,所以本选项符合题意;
B.3:4,所以本选项不符合题意;
C.8:9,所以本选项不符合题意。
故选:A。
【点评】本题主要是应用比例的意义解决问题。
6.下面( )组的两个比不能组成比例。
A.7:8和14:16 B.0.6:0.2和3:1
C.19:110和10:9 D.6:10和9:15
【答案】C
【分析】比例的意义:表示两个比相等的式子,叫作比例。
【解答】解:A.14:16=7:8,7:8和14:16能组成比例。
B.0.6:0.2=3:1,0.6:0.2和3:1能组成比例。
C.19:110,10:9,19:110和10:9不能组成比例。
D.6:10,9:15,6:10和9:15能组成比例。
故选:C。
【点评】本题考查了比例的意义。
7.在一个比例里,两个外项互为倒数,期中一个内项是,另一个内项是 .
【答案】见试题解答内容
【分析】依据比例的基本性质,即两内项之积等于两外项之积即可求解.
【解答】解:因为比例的两内项之积等于两外项之积,又因两个外项互为倒数,即两外项之积为1,
所以两内项之积也应为1,即两内项也互为倒数;
又知一个内项为,则另一个内项为;
故答案为:.
【点评】此题主要考查比例的基本性质以及倒数的意义.
8.如果4x=3y(x、y均不为0),那么x:y= 3:4 .
【答案】见试题解答内容
【分析】根据比例的基本性质,如果把x看作比的一个外项,y看作比的一个内项,那么比的另一个外项是4,比的另一个内项是3,构造出比例,然后化简即可.
【解答】解:因为4x=3y(x、y均不为0),
所以x:y=3:4
故答案为:3:4.
【点评】此题主要考查了比例的基本性质的灵活应用.
9.如果7x=8y(x、y均不为0),那么x:y= 8 : 7 .
【答案】见试题解答内容
【分析】逆运用比例的基本性质,即两内项之积等于两外项之积,即可进行解答.
【解答】解:7x=8y(x、y均不为0)
x:y=8:7
故答案为:8,7.
【点评】此题主要考查比例的基本性质的灵活应用.
10.在一个比例中,两个内项互为倒数,其中一个外项是1.5,另一个外项是 。
【答案】。
【分析】互为倒数的两个数的乘积是1;再根据比例的基本性质,内项积等于外项积,则用两个内项的积除以其中一个外项即可求出另一个外项。
【解答】解】1÷1.5
答:则另一个外项是。
故答案为:。
【点评】本题考查比例的基本性质,结合倒数的定义是解题的关键。
11.若一个比例的两个外项互为倒数,其中一个内项是,则另一个内项是 。
【答案】。
【分析】互为倒数的两个数乘积是1。
比例的性质:在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。
【解答】解:1
答:则另一个内项是 。
故答案为:。
【点评】本题考查了倒数的认识及比例的性质。
12.3、4、9、12这四个数字可以组成比例。如果把“3”作为比例的一个内项,那么这个比例可以是 4:3=12:9 ;如果把“3”作为比例的一个外项,那么这个比例可以是 3:4=9:12 。
【答案】4:3=12:9,3:4=9:12。(答案不唯一)
【分析】根据比例的基本性质,两个外项的积等于两个内项的积,组比例即可。
【解答】解:3、4、9、12这四个数字可以组成比例。如果把“3”作为比例的一个内项,那么这个比例可以是4:3=12:9;如果把“3”作为比例的一个外项,那么这个比例可以是3:4=9:12。(答案不唯一)
故答案为:4:3=12:9,3:4=9:12。(答案不唯一)
【点评】本题主要考查比例的基本性质的应用。
13.比例是指两个比的相等关系,所以比和比例表示的意义是一样的。 × (判断对错)
【答案】×
【分析】两个数相除叫作两个数的比。
比例的意义:表示两个比相等的式子,叫作比例。
【解答】解:两个数相除叫作两个数的比。比例是指两个比的相等关系,所以比和比例表示的意义是不一样的。原题说法是错误的。
故答案为:×。
【点评】本题考查了比和比例的意义。
14.比例是方程. × .(判断对错)
【答案】见试题解答内容
【分析】比例:表示两个比相等的式子叫做比例,所以比例中可以没有未知数;而方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等式.由此进行判断.
【解答】解:方程是指含有未知数的等式,而比例是表示两个比相等的式子,比例中可以没有未知数;
故答案为:×.
【点评】本题主要考查了比例与方程的意义和区别.
15.在一个比例中,两个外项的积与两个内项的积的差为0。 √ (判断对错)
【答案】√
【分析】根据比例的基本性质直接判断即可,在比例里,两内项的积等于两外项的积。
【解答】解:根据比例的基本性质可得:在一个比例中,两个外项的积与两个内项的积相等,所以原题说法正确。
故答案为:√。
【点评】此题主要考查比例的基本性质:在比例里,两内项的积等于两外项的积。
16.在比例3:5=9:15中,将等号左边比的后项加上20,要使比例成立,等号右边比的后项应加上60。 √ (判断对错)
【答案】√。
【分析】根据比的基本性质作答即可。
【解答】解:5+20=25
25÷5=5
即:第一个比的后项是5,加上20后为25,相当于后项乘5,比值相应缩小到原来的五分之一。
15×5﹣15
=75﹣15
=60
即:要使比例仍然成立,第二个比的后项也应该同样乘5,即增加60。
故答案为:√。
【点评】本题考查了比例的意义及比的基本性质的理解与应用,解答本题时一定要理解:第一个比的后项乘5,第二个比的后项同样乘5,这样两个比的比值还是相等,比例仍然成立。
17.表示两个比相等的式子叫比例. √ (判断对错)
【答案】√
【分析】比例是表示两个比相等的式子.根据比例的概念直接判断.
【解答】解:比例是表示两个比相等的式子,所以原题说法正确.
故答案为:√.
【点评】此题考查比例的意义:是表示两个比相等的式子.
18.如果ab(a、b都不为0),那么a:b=8:9。 √ (判断对错)
【答案】√
【分析】将a看成比例的两个外项,b看成比例的两个内项,根据比例的基本性质写出比例并化简即可。
【解答】解:根据比例的基本性质可得:如果ab(a、b都不为0),那么a:b:8:9,原说法正确。
故答案为:√。
【点评】本题主要考查比例的基本性质的灵活运用。
19.有一扇通往知识宝藏的大门,门上有三个数,它们分别是2,5,10,请找出第四个数,这个数必须满足下列三个条件:
①这个数要能与原来三个数组成比例;
②这个数是合数;
③这个数是奇数。
这个数是几呢?请写出你的计算过程。
【答案】25。
【分析】在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质;除了1和它本身之外还有其它因数的数叫做合数,奇数是指末尾有0,1,3,5,9的数,据此解答。
【解答】解:25:5=10:2,且25×2=5×10=50,25是奇数也是合数,因此这个数是25。
【点评】本题考查了比例的基本性质的应用及奇数合数的认识。
二.正比例和反比例的意义(共3小题)
20.如表所示,当x和y成正比例时,空格里应填 48 ;当x和y成反比例时,空格里应填 3 。
x 12
y 6 24
【答案】48;3。
【分析】由正、反比例的意义可知:x和y的商一定时,两者成正比例;x和y的积一定时,两者成反比例,据此作答即可。
【解答】解:x:24=12:6
6x=24×12
6x=288
x=288÷6
x=48
24x=12×6
24x=72
x=72÷24
x=3
故答案为:48;3。
【点评】本题考查了正反比例关系的判定问题,解答此类问题时一定要清楚:两种相关联的量,凡是商(比值)一定的,这两种数量就成正比例关系,凡是积一定的,这两种数量就成反比例关系。
21.如表所示,如果x和y成正比例,那么“?”处应填 5 。如果x和y成反比例,那么“?”处应填 1.8 。
x 3 ?
y 90 150
【答案】5;1.8。
【分析】依据题意可知,如果x和y成正比例,90÷3=30,商一定,由此解答本题“?”处应填数,如果x和y成反比例,则xy=270,由此解答本题。
【解答】解:90÷3=30
150÷30=5
3×90=270
270÷150=1.8
则如果x和y成正比例,那么“?”处应填50。如果x和y成反比例,那么“?”处应填1.8。
故答案为:5;1.8。
【点评】本题考查的是正比例、反比例的应用。
22.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示k(一定).
(1)通过计算总价与数量的比值是否一定,来判定总价与数量是否成正比例关系即可.
(2)描点,连线即可.
(3)利用图象看2.5m所对应的图象上的点所对应的总价是多少元即可,然后再看68元所对应的图象上的点所对应的数量是多少米即可.
【解答】解:(1)总价和数量成正比例关系.
因为8(一定),是比值一定,
所以总价和数量成正比例关系.
(2)
由图可知正比例关系的图象是一条射线.
(3)根据图象可知:买2.5m花布需要20元,68元能买米8.5米花布.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.还要学会利用数形结合的思想解决数学问题.
三.正比例(共2小题)
23.关于比例关系的判断,以下说法正确的有( )个。
(1)订同一份杂志的钱数和份数成正比例关系。
(2)正方形的面积和它的边长成正比例关系。
(3)圆的面积和它的直径成反比例关系。
(4)三角形的面积一定,它的底和高成反比例关系。
A.3 B.2 C.1 D.4
【答案】B
【分析】两种相关联的量,如果比值一定,就成正比例关系,如果乘积一定,就成反比例关系;
(1)订同一份杂志时,钱数和份数的比值一定,据此分析;
(2)正方形的面积÷边长=边长,即正方形的面积与它的边长的比值不一定,据此分析;
(3)圆的面积÷直径直径,由此判断;
(4)三角形的底×高=面积×2,由此判断。
【解答】解:(1)订杂志的钱数÷份数=每份的钱数,订同一份杂志时,每份的钱数不变,则订同一份杂志的钱数和份数成正比例关系;
(2)正方形的面积÷边长=边长,因此正方形的面积和它的边长不成正比例关系;
(3)圆的面积和它的直径不成反比例关系;
(4)三角形的底×高=面积×2,则三角形的面积一定时,它的底和高成反比例关系。
综上所述,正确的是(1)(4),共2个。
故选:B。
【点评】本题考查的是正比例和反比例的应用。
24.成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。 √ (判断对错)
【答案】√。
【分析】在同时同地,太阳光线的角度是固定的。根据相似三角形的原理,竿高和影长的比值是一个定值,即竿高和影长成正比例关系。“立竿见影”描述的就是在阳光下竖起一根杆子,立刻就能看到它的影子,从数学角度看,很好地体现了这种同时同地竿高和影长的正比例关系。据此判断。
【解答】解:成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。说法正确。
故答案为:√。
【点评】本题考查了学生对于正比例关系的理解及运用。
四.解比例(共7小题)
25.解比例。
(1)
(2)
【答案】(1)x;(2)x=0.39。
【分析】(1)根据比例的性质,把比例化成普通方程,然后再根据等式的性质求解;
(2)根据比例的性质,把比例化成普通方程,然后再根据等式的性质求解。
【解答】解:(1)
x
x
x
(2)
3x=6.5×18%
3x=1.17
x=0.39
【点评】熟练掌握等式的基本性质以及比例的基本性质是解题的关键,注意等号要对齐。
26.解比例。
20%::0.6
【答案】x=0.36;x=2。
【分析】(1)根据比例的基本性质,把原式化为x=20%×0.6,然后方程的两边同时除以求解;
(2)根据比例的基本性质,把原式化为2.4x=1.6×3,然后方程的两边同时除以2.4求解。
【解答】解:(1)20%::0.6
x=20%×0.6
x20%×0.6
x=0.36
(2)
2.4x=1.6×3
2.4x÷2.4=1.6×3÷2.4
x=2
【点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
27.解方程或比例。
1.2x﹣3.6=6
x:1.2=4:0.5
1.3x﹣0.6x=15.4
【答案】x=8;x=9.6;x=22。
【分析】方程1,等式两边同时加3.6,化简后,再两边同时除以1.2得解。
方程2,先改写成两个外项的乘积等于两个内项的乘积的形式,化简后,再两边同时乘2得解。
方程3,逆用乘法分配律化简后,再两边同时除以0.7得解。
【解答】解:1.2x﹣3.6=6
1.2x﹣3.6+3.6=6+3.6
1.2x=9.6
1.2x÷1.2=9.6÷1.2
x=8
x:1.2=4:0.5
0.5x=1.2×4
0.5x=4.8
2×0.5x=4.8×2
x=9.6
1.3x﹣0.6x=15.4
(1.3﹣0.6)x=15.4
0.7x=15.4
0.7x÷0.7=15.4÷0.7
x=22
【点评】本题考查了解方程、解比例的问题,解答本题一定要熟练掌握两个基本性质:一是等式的基本性质,即等式两边同时加、减、乘或除以一个相同的数(0除外),等式仍然成立;二是比例的基本性质,即两个外项的乘积等于两个内项的乘积。
28.解下面方程或比例。
4x+3×0.7=6.5
【答案】x=54;x=1;x=1.1。
【分析】(1)根据比例的基本性质,把原式化为4x=9×24,然后方程的两边同时除以4求解;
(2)根据比例的基本性质,把原式化为2.5x=5,然后方程的两边同时除以2.5求解;
(3)先计算3×0.7=2.1,根据等式的性质,方程的两边同时减去2.1,然后方程的两边同时除以4求解。
【解答】解:(1)
4x=9×24
4x÷4=9×24÷4
x=54
(2)
2.5x=5
2.5x÷2.5=52.5
x=1
(3)4x+3×0.7=6.5
4x+2.1=6.5
4x+2.1﹣2.1=6.5﹣2.1
4x=4.4
4x÷4=4.4÷4
x=1.1
【点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
29.解方程或比例。
30%x+50%x=240
【答案】x=300;x=0.6;x=108。
【分析】30%x+50%x=240,先计算30%x+50%x=0.8x,然后等式两边同时除以0.8,最后计算求出x的值;
,根据比例的基本性质可得12x=2.4×3,然后等式两边同时除以12,最后计算求出x的值;
,等式两边同时除以,然后计算求出x的值。
【解答】解:30%x+50%x=240
0.8x=240
0.8x÷0.8=240÷0.8
x=300
12x=3×2.4
12x=7.2
12x÷12=7.2÷12
x=0.6
x=108
【点评】解答此题要运用比例的基本性质和等式的基本性质。
30.解比例。
①0.4:x=0.2:7
②
③
【答案】①x=14;②x=1;③x。
【分析】①首先根据比例的基本性质化简,可得:0.2x=0.4×7;然后根据等式的性质,两边同时除以0.2即可;
②首先根据比例的基本性质化简,可得:x;然后根据等式的性质,两边同时乘即可;
③首先根据比例的基本性质化简,可得:4x=0.5×0.6;然后根据等式的性质,两边同时除以4即可。
【解答】解:①0.4:x=0.2:7
0.2x=0.4×7
0.2x=2.8
0.2x÷0.2=2.8÷0.2
x=14
②
x
x
x
x=1
③
4x=0.5×0.6
4x=0.3
4x÷4=0.3÷4
x
【点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用。
31.解方程。
:x=3:12
x﹣214
【答案】x=3;x=27;x=60。
【分析】(1)首先根据比例的基本性质化简,可得3x12,然后根据等式的性质,两边同时除以3即可;
(2)首先根据比例的基本性质化简,可得0.4x=1.2×9,然后根据等式的性质,两边同时除以0.4即可;
(3)首先把x﹣214化成0.3x﹣14=4,然后根据等式的性质,两边同时加上14,最后两边再同时除以0.3即可。
【解答】解:(1):x=3:12
3x12
3x=9
3x÷3=9÷3
x=3
(2)
0.4x=9×1.2
0.4x=10.8
0.4x÷0.4=10.8÷0.4
x=27
(3)
0.3x﹣14=4
0.3x﹣14+14=4+14
0.3x=18
0.3x÷0.3=18÷0.3
x=60
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等,以及解比例问题,注意比例的基本性质的应用。
五.比例的应用(共8小题)
32.师徒二人同时合作加工一批零件,全部完成一共用了6小时。已知徒弟与师傅加工零件的个数比是3:8,如果师傅平均每小时加工120个零件,那么徒弟平均每小时加工多少个零件?
【答案】45个。
【分析】首先根据:工作量=工作效率×工作时间,用师傅平均每小时加工零件的数量乘6,求出师傅6小时加工的零件个数是多少;然后用它乘,求出徒弟6小时加工零件多少个,再求平均每小时加工多少个零件即可。
【解答】解:120×66
=7206
=270÷6
=45(个)
答:徒弟平均每小时加工45个零件。
【点评】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
33.在比例尺是1:1000000的地图上,量的苍南县到杭州距离是3.6厘米。苍南县到杭州的实际距离是多少?
【答案】36千米。
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出上海到杭州的实际距离。
【解答】解:3.63600000(厘米)
3600000厘米=36千米
答:苍南县到杭州的实际距离是36千米。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
34.一间大厅,用边长为6分米的方砖铺地,需用216块;若改铺边长为4分米的方砖,需要用多少块?(用比例知识解答)
【答案】486。
【分析】一间大厅的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即每一块方砖的面积×所需块数=大厅面积(一定),也就是两种相关联的量成反比例,由此设出未知数,列出比例式解答即可。
【解答】解:设需要用x块。
4×4×x=6×6×216
16x=7776
16x÷16=7776÷16
x=486
答:需要486块。
【点评】此题首先利用正反比例的意义判定两种量的关系,再列比例式解答;注意:列比例式时不要把边长当成面积。
35.500千克稻谷可以碾出大米410千克。照这样计算,现在有这样的稻谷7.5吨,可以碾出多少吨大米?(用比例解)
【答案】6.15
【分析】根据出米率一定,列出比例即可。
【解答】解:设可以碾出x吨大米
500:410=7.5:x
500x=3075
x=6.15
答:可以碾出6.15吨大米。
【点评】列出比例,是解答此题的关键。
36.小马骑自行车从家里到书店,前5分钟行了800m。照这样的速度,从家到书店一共用了20分钟。他家和书店相距多少米?(用比例解)
【答案】3200米。
【分析】照这样的速度,说明速度一定,路程和时间成正比例,由此设出未知数,列比例解答即可。
【解答】解:设他家和书店相距x米。
x:20=800:5
5x=16000
x=3200
答:他家和书店相距3200米。
【点评】此题首先判定两种量成正比例,再设出未知数,列出比例式进行解答即可。
37.某市修一条道路,计划每天修120米,8天可以修完。但因为天气原因,12天才完成任务,实际每天修多少米?(用比例方法解)
【答案】80米。
【分析】根据题意知道,总工作量一定,工作时间和工作效率成反比例,由此列式解答即可。
【解答】解:实际每天修x米,
12x=120×8
12x=960
x=80
答:实际每天修80米。
【点评】解答此题的关键是,弄清题意,根据工作效率,工作时间和工作量三者的关系,判断哪两种量成何比例,然后找出对应量,列式解答即可。
38.古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解)
(1)12只羊可以换多少把斧头?
(2)要换9把斧头,需要几只羊?
【答案】(1)18把;
(2)6只。
【分析】(1)设12只羊可以换x把斧头,4与6的比等于12与x的比,据此解答。
(2)设要换9把斧头,需要x只羊,4与6的比等于x与9的比,据此解答。
【解答】解:(1)设12只羊可以换x把斧头。
4:6=12:x
4x=6×12
4x=72
x=18
答:12只羊可以换18把斧头。
(2)设要换9把斧头。
4:6=x:9
6x=4×9
6x=36
x=6
答:需要6只羊。
【点评】本题解题关键是根据比例的意义列出比例式,熟练掌握解比例的方法。
39.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
【答案】480立方厘米。
【分析】用96除以4,求出长方体的长加宽加高的和,再把这个和按5:3:4进行分配,求出长方体的长、宽、高,再根据长方体体积=长×宽×高,即可解答。
【解答】解:96÷4=24(厘米)
2410(厘米)
246(厘米)
248(厘米)
10×6×8
=60×8
=480(立方厘米)
答;这个长方体的体积是480立方厘米。
【点评】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
六.图形的放大与缩小(共5小题)
40.李老师的手机上保存着“厦门市地铁线网”截图,供同学们课后实践使用,左图是小华把李老师的原图按1:a缩小后的图片,右图是小丽把原图按( )缩小后的图片。
A.1:a B.1:a C.1:2a D.1:4a
【答案】C
【分析】根据题意,假设原图的边长是72厘米,结合左图是小华把李老师的原图按1:a缩小后的图片,左图的边长是36厘米,所以左图的边长:原图的边长=36:72=1:a,可知a=2。右图的边长:原图的边长=18:72=1:4,因为a=2,所以右图是小丽把原图按1:2a缩小后的图片。据此解答即可。
【解答】解:假设原图的边长是72厘米,左图的边长:原图的边长=36:72=1:a,可知a=2。右图的边长:原图的边长=18:72=1:4,因为a=2,所以右图是小丽把原图按1:2a缩小后的图片。
答:右图是小丽把原图按1:2a缩小后的图片。
故选:C。
【点评】本题考查了图形的放大和缩小知识,结合题意分析解答即可。
41.把一个梯形按3:1放大,放大后图形的面积是原来的9倍。 √ (判断对错)
【答案】√
【分析】把一个梯形按3:1放大,就是把梯形的上底、下底和高都扩大到原来的3倍,上底和下底的和扩大到原来的3倍,据此解答。
【解答】解:3×3=9
把一个梯形按3:1放大,放大后图形的面积是原来的9倍,原题说法正确。
故答案为:√。
【点评】掌握图形放大的特征是解题的关键。
42.按要求完成下面的题目。
①按照1:2的比画出三角形缩小后的图形。
②如果每个小正方形的边长是1厘米,缩小后三角形的面积是 2.5 平方厘米。
【答案】(1)(2)2.5。
【分析】(1)按1:2的比例画出三角形缩小后的图形,就是把原三角形的三条边都缩小到原来的,据此画图即可;
(2)根据三角形的面积计算公式:S底×高即可计算。
【解答】解:(1)如下图所示:
(2)2.5×2=2.5(cm2)
答:缩小后三角形的面积是2.5平方厘米。
故答案为:2.5。
【点评】本题考查了图形的缩小以及三角形面积的计算。
43.画一画:
(1)画出图形A按1:2缩小后的图形。
(2)画出图形B的另一半,使它成为一个轴对称图形。
【答案】(1)(2)
【分析】(1)根据图形缩小的方法,按1:2缩小,缩小后的图形的每条边都变为原来的,据此画图;
(2)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【解答】解:(1)画出图形A按1:2缩小后的图形。
(2)画出图形B的另一半,使它成为一个轴对称图形。如图:
【点评】本题考查了图形的缩小以及轴对称图形知识,结合题意分析解答即可。
44.请把长方形的长和宽都按2:1放大,画出放大后的长方形;请把三角形的各边接1:2缩小,画出缩小后的三角形。
【答案】
【分析】根据图形放大、缩小的方法,先求出放大2倍后,长方形的长、宽各是多少,再求出缩小2倍后,三角形的底和高各是多少,据此作图即可。
【解答】解:3×2=6
2×2=4
2÷2=1
4÷2=2
作图如下:
【点评】此题考查的目的是理解掌握图形放大与缩小的方法及应用,关键是明确:图形放大或缩小后,图形的形状不变,大小发生了变化。
七.比例尺(共16小题)
45.有一张边长为65厘米的正方形图纸,要在上面画长为120米,宽为90米的长方形草坪的平面图,你认为最合适的比例尺是( )
A.1:150 B.1:200 C.1:2000 D.20:1
【答案】C
【分析】根据“比例尺=图上距离:实际距离”可知“图上距离=实际距离×比例尺”依次代入数值,计算出相对应的图上距离,然后根据实际情况判断所给出的比例尺是否合适。
【解答】解:120米=12000厘米、90米=9000厘米。
A.1200080(厘米)
因为正方形图纸的边长为65厘米,所以比例尺不合适。
B.1200060(厘米)
900045(厘米),
图上长度太长,比例尺不合适。
C.120006(厘米)
90004.5(厘米)
比例尺合适。
D.比例尺是扩大比例尺,不合适。
故选:C。
【点评】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离:实际距离,灵活变形列式解决问题。
46.李叔叔是汽轮机厂的工程师,他要将一个长4mm、宽2mm的零件画在一张A3纸(42cm×29.7cm)上,合适的比例尺是( )
A.1:100 B.100:1 C.1:1000 D.1000:1
【答案】B
【分析】通过题意可知,要用放大比例尺,A和C是缩小比例尺,可以排除,分别求出以B和D为比例尺的图上距离,比较即可。
【解答】解:A.1:100,缩小比例尺,排除;
B.100:1,4×100=400(mm)=40(cm),2×100=200(mm)=20(cm),比例尺合适;
C.1:1000,缩小比例尺,排除;
D.1000:1,4×1000=4000(mm)=400(cm),400>42,比例尺不合适。
故选:B。
【点评】本题考查了比例尺,要把实际距离换算成图上距离。
47.一张地图的比例尺是1:5000000,地图上的1厘米相当于实际距离的( )
A.5000米 B.5000千米 C.50千米 D.500米
【答案】C
【分析】依据比例尺的意义,即图上距离与实际距离的比即为比例尺,即可求解.
【解答】解:因为比例尺1:5000000表示图上距离1厘米代表实际距离5000000厘米,
又因5000000厘米=50千米,
所以比例尺1:5000000表示地图上1厘米的距离相当于地面上50千米的实际距离;
故选:C.
【点评】此题主要考查比例尺的意义,解答时要注意单位的换算.
48.一幅地图的比例尺是20:1,如果零件图上长5厘米,则实际长( )
A.4厘米 B.100厘米 C.0.25厘米
【答案】C
【分析】根据实际距离=图上距离÷比例尺,解答即可。
【解答】解:5÷20=0.25(厘米)
答:实际长0.25厘米。
故选:C。
【点评】本题主要考查了比例尺的意义,要熟练掌握。
49.如图是现藏于三星堆博物馆的青铜大立人像,青铜大立人像是现存最高。最完整的青铜立人像,被誉为“世界铜像之王”。在一张比例尺为1:80的图上,这个青铜大立人像的高为( )
A.3.26厘米 B.32.6厘米
C.208.64厘米 D.2.608厘米
【答案】A
【分析】已知青铜大立人像实际高为2.608米,图纸的比例尺为1:80,根据“图上距离=实际距离×比例尺”,求出这个青铜大立人像在图纸上的高。注意单位的换算:1米=100厘米。
【解答】解:2.608米=260.8厘米
这个青铜大立人像的高为:
260.83.26(厘米)
答:这个青铜大立人像的高为3.26厘米。
故选:A。
【点评】本题考查的是比例尺应用题,掌握“图上距离=实际距离×比例尺”是解答关键。
50.一种微型零件的实际长度是1mm,画在图纸上长3dm,画图时选用的比例尺是( )
A.1:300 B.1:3 C.300:1 D.3:1
【答案】C
【分析】根据比例尺的意义:比例尺=图上距离:实际距离,即可解答,注意单位名数的统一。
【解答】解:1mm=0.1cm;3dm=30cm
30:0.1
=(30×10):(0.1×10)
=300:1
答:一种微型零件的实际长度是1mm,画在图纸上长3dm,画图时选用的比例尺是300:1。
故选:C。
【点评】熟练掌握比例尺的意义是解题的关键。
51.一幅地图的线段比例尺是,改成数字比例尺是 1:3000000 ;石家庄到北京的实际距离是330千米,则地图上的距离是 11 厘米。
【答案】1:3000000;11。
【分析】根据比例尺=图上距离:实际距离,解答此题即可。
【解答】解:30千米=3000000厘米
330÷30=11(厘米)
答:改成数字比例尺是1:3000000;石家庄到北京的实际距离是330千米,则地图上的距离是11厘米。
故答案为:1:3000000;11。
【点评】熟练掌握比例尺的定义,是解答此题的关键。
52.小玲的妈妈身高1.65m,在一张照片上她的身高是5cm,这张照片的比例尺是 1:33 。
【答案】1:33。
【分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:1.65米=165厘米
5厘米:165厘米
=(5÷5)(165÷5)
=1:33
答:这张照片的比例尺是1:33。
故答案为:1:33。
【点评】本题考查了比例尺的意义,比例尺=图上距离:实际距离,注意单位要统一。
53.实际宽度为3m的窗户,在建筑平面图上绘制的宽度为1.5cm,这幅平面图的比例尺为 1:200 。
【答案】1:200。
【分析】读题可知,图上距离为1.5cm,实际距离为3m,据此写出图上距离与实际距离的比,再化简即可。
【解答】解:1.5cm:3m
=1.5cm:300cm
=1.5:300
=(1.5÷1.5):(300÷1.5)
=1:200
答:这幅平面图的比例尺为1:200。
【点评】本题考查了比例尺的意义的应用问题,解答本题时一定要清楚:图上距离与实际距离的比,叫作比例尺;写出图上距离与实际距离的比后,再按式的基本性质化简,得到前项或后项为1的最简整数比即可。
54.在照片上小明的身高是8厘米,他的实际身高是168厘米。这张照片的比例尺是 1:21 。
【答案】1:21。
【分析】因为“图上距离与实际距离的比即为比例尺”,图上距离和实际距离已知,从而可以求得这张照片的比例尺。
【解答】解:8厘米:168厘米=1:21;
答:这张照片的比例尺是1:21.
故答案为:1:21。
【点评】此题主要考查比例尺的意义,即图上距离与实际距离的比即为比例尺,解答时要注意单位统一。
55.一个圆柱形零件的高是5mm,在图纸上的高是2cm,这幅图纸的比例尺是 4:1 .
【答案】见试题解答内容
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺.
【解答】解:因为5毫米=0.5厘米
则2厘米:0.5厘米=4:1
答:这幅图纸的比例尺是4:1.
故答案为:4:1.
【点评】此题主要考查比例尺的计算方法.解答时要注意单位的换算.
56.在一张图纸上,测得一个零件的长是10cm,已知这个零件实际长度是2mm,这张图纸的比例尺是 50:1 。
【答案】50:1。
【分析】比例尺=图上距离:实际距离,再根据比的基本性质:比的前项和后项同时乘或除以一个数(0除外),比值不变,可化简比例尺,进而得出答案。
【解答】解:10厘米=100毫米
100:2=50:1
答:这张图纸的比例尺是50:1。
故答案为:50:1。
【点评】本题主要考查的是比例尺的应用,解题的关键是熟练掌握比例尺的求法,进而得出答案。
57.在比例尺是1:20的图纸上画出一种机械配件平面图的角是40°,这个角实际上也是40°。 √ (判断对错)
【答案】√
【分析】根据图形的放大、缩小的知识可知,图形放大或缩小后,只改变图形的大小,不改变图形的形状。据此判断。
【解答】解:在比例尺是1:20的图纸上画出一种机械配件平面图的角是40°,这个角实际上也是40°。
原题说法正确。
故答案为:√。
【点评】熟练掌握图形的放大与缩小的特征是解题的关键。
58.实际距离为2mm,图上距离为2dm,则比例尺为1:100。 × (判断对错)
【答案】×
【分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:比例尺为2dm:2mm=20cm:0.2cm=100:1
故原题说法错误。
故答案为:×。
【点评】解答此题的关键是掌握比例尺的意义和相关公式。
59.在比例尺是100:1的图纸上,一个长方体零件正面的长是15cm,宽是9cm。这个零件正面的实际面积是多少平方厘米?
【答案】0.0135平方厘米。
【分析】根据实际距离=图上距离÷比例尺,分别求出长方体零件正面的实际长和宽,再根据长方形的面积=长×宽解答。
【解答】解:150.15(厘米)
90.09(厘米)
0.15×0.09=0.0135(平方厘米)
答:这个零件正面的实际面积是0.0135平方厘米。
【点评】熟练掌握实际距离、图上距离、比例尺的关系以及长方形面积的计算方法是解题的关键。
60.游泳比赛的泳池是一个长方形,把泳池的长和宽分别缩小到原来的后图形如下.
(1)泳池实际的长和宽各是多少米?
(2)泳池的实际占地面积是多少平方米?
【答案】见试题解答内容
【分析】(1)根据实际距离=图上距离÷比例尺,可代入数据分别求出实际的长和宽;
(2)用实际的长乘实际的宽可求出实际的占地面积.据此解答.
【解答】解:(1)0.0550(米)
0.02121(米)
答:泳池实际的长是50米,宽是21米.
(2)50×21=1050(平方米)
答:泳池实际占地面积是1050平方米.
【点评】本题重点考查了学生对实际距离=图上距离÷比例尺和长方形面积公式的掌握.
21世纪教育网(www.21cnjy.com)
一.比例的意义和基本性质(共19小题)
1.( )能与:组成比例.
A.3:4 B.4:3 C.3: D.:
2.一个比例的两个内项的积减去两个外项的积,结果是( )
A.0 B.1 C.10 D.无法确定
3.如图,三角形a边上的高为b,c边上的高为d。则下面式子中( )不成立。
A.a:c=b:d B.a:c=d:b C. D.
4.下面每组中的四个数,不能组成比例的是( )
A.2,0.25,3,0.375 B.30,25,6,125
C.,,,
5.能与4:3组成比例的是( )
A. B.3:4 C.8:9
6.下面( )组的两个比不能组成比例。
A.7:8和14:16 B.0.6:0.2和3:1
C.19:110和10:9 D.6:10和9:15
7.在一个比例里,两个外项互为倒数,期中一个内项是,另一个内项是 .
8.如果4x=3y(x、y均不为0),那么x:y= .
9.如果7x=8y(x、y均不为0),那么x:y= : .
10.在一个比例中,两个内项互为倒数,其中一个外项是1.5,另一个外项是 。
11.若一个比例的两个外项互为倒数,其中一个内项是,则另一个内项是 。
12.3、4、9、12这四个数字可以组成比例。如果把“3”作为比例的一个内项,那么这个比例可以是 ;如果把“3”作为比例的一个外项,那么这个比例可以是 。
13.比例是指两个比的相等关系,所以比和比例表示的意义是一样的。 (判断对错)
14.比例是方程. .(判断对错)
15.在一个比例中,两个外项的积与两个内项的积的差为0。 (判断对错)
16.在比例3:5=9:15中,将等号左边比的后项加上20,要使比例成立,等号右边比的后项应加上60。 (判断对错)
17.表示两个比相等的式子叫比例. (判断对错)
18.如果ab(a、b都不为0),那么a:b=8:9。 (判断对错)
19.有一扇通往知识宝藏的大门,门上有三个数,它们分别是2,5,10,请找出第四个数,这个数必须满足下列三个条件:
①这个数要能与原来三个数组成比例;
②这个数是合数;
③这个数是奇数。
这个数是几呢?请写出你的计算过程。
二.正比例和反比例的意义(共3小题)
20.如表所示,当x和y成正比例时,空格里应填 ;当x和y成反比例时,空格里应填 。
x 12
y 6 24
21.如表所示,如果x和y成正比例,那么“?”处应填 。如果x和y成反比例,那么“?”处应填 。
x 3 ?
y 90 150
22.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
三.正比例(共2小题)
23.关于比例关系的判断,以下说法正确的有( )个。
(1)订同一份杂志的钱数和份数成正比例关系。
(2)正方形的面积和它的边长成正比例关系。
(3)圆的面积和它的直径成反比例关系。
(4)三角形的面积一定,它的底和高成反比例关系。
A.3 B.2 C.1 D.4
24.成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。 (判断对错)
四.解比例(共7小题)
25.解比例。
(1)
(2)
26.解比例。
20%::0.6
27.解方程或比例。
1.2x﹣3.6=6
x:1.2=4:0.5
1.3x﹣0.6x=15.4
28.解下面方程或比例。
4x+3×0.7=6.5
29.解方程或比例。
30%x+50%x=240
30.解比例。
①0.4:x=0.2:7
②
③
31.解方程。
:x=3:12
x﹣214
五.比例的应用(共8小题)
32.师徒二人同时合作加工一批零件,全部完成一共用了6小时。已知徒弟与师傅加工零件的个数比是3:8,如果师傅平均每小时加工120个零件,那么徒弟平均每小时加工多少个零件?
33.在比例尺是1:1000000的地图上,量的苍南县到杭州距离是3.6厘米。苍南县到杭州的实际距离是多少?
34.一间大厅,用边长为6分米的方砖铺地,需用216块;若改铺边长为4分米的方砖,需要用多少块?(用比例知识解答)
35.500千克稻谷可以碾出大米410千克。照这样计算,现在有这样的稻谷7.5吨,可以碾出多少吨大米?(用比例解)
36.小马骑自行车从家里到书店,前5分钟行了800m。照这样的速度,从家到书店一共用了20分钟。他家和书店相距多少米?(用比例解)
37.某市修一条道路,计划每天修120米,8天可以修完。但因为天气原因,12天才完成任务,实际每天修多少米?(用比例方法解)
38.古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解)
(1)12只羊可以换多少把斧头?
(2)要换9把斧头,需要几只羊?
39.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
六.图形的放大与缩小(共5小题)
40.李老师的手机上保存着“厦门市地铁线网”截图,供同学们课后实践使用,左图是小华把李老师的原图按1:a缩小后的图片,右图是小丽把原图按( )缩小后的图片。
A.1:a B.1:a C.1:2a D.1:4a
41.把一个梯形按3:1放大,放大后图形的面积是原来的9倍。 (判断对错)
42.按要求完成下面的题目。
①按照1:2的比画出三角形缩小后的图形。
②如果每个小正方形的边长是1厘米,缩小后三角形的面积是 平方厘米。
43.画一画:
(1)画出图形A按1:2缩小后的图形。
(2)画出图形B的另一半,使它成为一个轴对称图形。
44.请把长方形的长和宽都按2:1放大,画出放大后的长方形;请把三角形的各边接1:2缩小,画出缩小后的三角形。
七.比例尺(共16小题)
45.有一张边长为65厘米的正方形图纸,要在上面画长为120米,宽为90米的长方形草坪的平面图,你认为最合适的比例尺是( )
A.1:150 B.1:200 C.1:2000 D.20:1
46.李叔叔是汽轮机厂的工程师,他要将一个长4mm、宽2mm的零件画在一张A3纸(42cm×29.7cm)上,合适的比例尺是( )
A.1:100 B.100:1 C.1:1000 D.1000:1
47.一张地图的比例尺是1:5000000,地图上的1厘米相当于实际距离的( )
A.5000米 B.5000千米 C.50千米 D.500米
48.一幅地图的比例尺是20:1,如果零件图上长5厘米,则实际长( )
A.4厘米 B.100厘米 C.0.25厘米
49.如图是现藏于三星堆博物馆的青铜大立人像,青铜大立人像是现存最高。最完整的青铜立人像,被誉为“世界铜像之王”。在一张比例尺为1:80的图上,这个青铜大立人像的高为( )
A.3.26厘米 B.32.6厘米
C.208.64厘米 D.2.608厘米
50.一种微型零件的实际长度是1mm,画在图纸上长3dm,画图时选用的比例尺是( )
A.1:300 B.1:3 C.300:1 D.3:1
51.一幅地图的线段比例尺是,改成数字比例尺是 ;石家庄到北京的实际距离是330千米,则地图上的距离是 厘米。
52.小玲的妈妈身高1.65m,在一张照片上她的身高是5cm,这张照片的比例尺是 。
53.实际宽度为3m的窗户,在建筑平面图上绘制的宽度为1.5cm,这幅平面图的比例尺为 。
54.在照片上小明的身高是8厘米,他的实际身高是168厘米。这张照片的比例尺是 。
55.一个圆柱形零件的高是5mm,在图纸上的高是2cm,这幅图纸的比例尺是 .
56.在一张图纸上,测得一个零件的长是10cm,已知这个零件实际长度是2mm,这张图纸的比例尺是 。
57.在比例尺是1:20的图纸上画出一种机械配件平面图的角是40°,这个角实际上也是40°。 (判断对错)
58.实际距离为2mm,图上距离为2dm,则比例尺为1:100。 (判断对错)
59.在比例尺是100:1的图纸上,一个长方体零件正面的长是15cm,宽是9cm。这个零件正面的实际面积是多少平方厘米?
60.游泳比赛的泳池是一个长方形,把泳池的长和宽分别缩小到原来的后图形如下.
(1)泳池实际的长和宽各是多少米?
(2)泳池的实际占地面积是多少平方米?
4 比例
参考答案与试题解析
一.比例的意义和基本性质(共19小题)
1.( )能与:组成比例.
A.3:4 B.4:3 C.3: D.:
【答案】A
【分析】表示两个比相等的式子叫作比例,只要比值和:相等比就能和它组成比例,因此下列各选项的比值哪个和:相等,就为正确选项.
【解答】解::3:4;
故选:A.
【点评】本题主要考查了比例的意义.
2.一个比例的两个内项的积减去两个外项的积,结果是( )
A.0 B.1 C.10 D.无法确定
【答案】A
【分析】比例的性质:在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。
【解答】解:一个比例的两个内项的积减去两个外项的积,结果是0。
故选:A。
【点评】本题是比例的性质的应用。
3.如图,三角形a边上的高为b,c边上的高为d。则下面式子中( )不成立。
A.a:c=b:d B.a:c=d:b C. D.
【答案】A
【分析】根据三角形的面积公式:三角的面积=底×高÷2,因为是同一个三角形,所以用对应的底a乘高b除以2等于对应对应的底c和高d除以2,则ab=cd,再根据比例的基本性质把各比例式转化为乘积式,比较得解。
【解答】解:根据ab÷2=cd÷2,可得ab=cd,
A.a:c=b:d,即ad=cb,所以选项A不成立;
B.a:c=d:b,即ab=cd,所以选项B成立;
C.,即ab=cd,所以选项C成立;
D.,即ab=cd,所以选项D成立。
故选:A。
【点评】此题考查了三角形的面积公式及比例基本性质的运用。
4.下面每组中的四个数,不能组成比例的是( )
A.2,0.25,3,0.375 B.30,25,6,125
C.,,,
【答案】C
【分析】根据比例的基本性质:两个外项的及等于两个内项的积,判断即可。
【解答】解:23,所以2,0.25,3,0.375能组成比例;
30×25=6×125,所以30,25,6,125能组成比例;
每组中的四个数,不能组成比例的是,,,。
故选:C。
【点评】本题主要考查比例的意义和基本性质的应用。
5.能与4:3组成比例的是( )
A. B.3:4 C.8:9
【答案】A
【分析】根据比例的意义:表示两个比相等的式子叫做比例;由此依次算出各选项的比值,找出与4:3比值相等的选项组成比例解答即可。
【解答】解:4:3
A.:,所以本选项符合题意;
B.3:4,所以本选项不符合题意;
C.8:9,所以本选项不符合题意。
故选:A。
【点评】本题主要是应用比例的意义解决问题。
6.下面( )组的两个比不能组成比例。
A.7:8和14:16 B.0.6:0.2和3:1
C.19:110和10:9 D.6:10和9:15
【答案】C
【分析】比例的意义:表示两个比相等的式子,叫作比例。
【解答】解:A.14:16=7:8,7:8和14:16能组成比例。
B.0.6:0.2=3:1,0.6:0.2和3:1能组成比例。
C.19:110,10:9,19:110和10:9不能组成比例。
D.6:10,9:15,6:10和9:15能组成比例。
故选:C。
【点评】本题考查了比例的意义。
7.在一个比例里,两个外项互为倒数,期中一个内项是,另一个内项是 .
【答案】见试题解答内容
【分析】依据比例的基本性质,即两内项之积等于两外项之积即可求解.
【解答】解:因为比例的两内项之积等于两外项之积,又因两个外项互为倒数,即两外项之积为1,
所以两内项之积也应为1,即两内项也互为倒数;
又知一个内项为,则另一个内项为;
故答案为:.
【点评】此题主要考查比例的基本性质以及倒数的意义.
8.如果4x=3y(x、y均不为0),那么x:y= 3:4 .
【答案】见试题解答内容
【分析】根据比例的基本性质,如果把x看作比的一个外项,y看作比的一个内项,那么比的另一个外项是4,比的另一个内项是3,构造出比例,然后化简即可.
【解答】解:因为4x=3y(x、y均不为0),
所以x:y=3:4
故答案为:3:4.
【点评】此题主要考查了比例的基本性质的灵活应用.
9.如果7x=8y(x、y均不为0),那么x:y= 8 : 7 .
【答案】见试题解答内容
【分析】逆运用比例的基本性质,即两内项之积等于两外项之积,即可进行解答.
【解答】解:7x=8y(x、y均不为0)
x:y=8:7
故答案为:8,7.
【点评】此题主要考查比例的基本性质的灵活应用.
10.在一个比例中,两个内项互为倒数,其中一个外项是1.5,另一个外项是 。
【答案】。
【分析】互为倒数的两个数的乘积是1;再根据比例的基本性质,内项积等于外项积,则用两个内项的积除以其中一个外项即可求出另一个外项。
【解答】解】1÷1.5
答:则另一个外项是。
故答案为:。
【点评】本题考查比例的基本性质,结合倒数的定义是解题的关键。
11.若一个比例的两个外项互为倒数,其中一个内项是,则另一个内项是 。
【答案】。
【分析】互为倒数的两个数乘积是1。
比例的性质:在比例中,两个外项的积等于两个内项的积,这叫作比例的基本性质。
【解答】解:1
答:则另一个内项是 。
故答案为:。
【点评】本题考查了倒数的认识及比例的性质。
12.3、4、9、12这四个数字可以组成比例。如果把“3”作为比例的一个内项,那么这个比例可以是 4:3=12:9 ;如果把“3”作为比例的一个外项,那么这个比例可以是 3:4=9:12 。
【答案】4:3=12:9,3:4=9:12。(答案不唯一)
【分析】根据比例的基本性质,两个外项的积等于两个内项的积,组比例即可。
【解答】解:3、4、9、12这四个数字可以组成比例。如果把“3”作为比例的一个内项,那么这个比例可以是4:3=12:9;如果把“3”作为比例的一个外项,那么这个比例可以是3:4=9:12。(答案不唯一)
故答案为:4:3=12:9,3:4=9:12。(答案不唯一)
【点评】本题主要考查比例的基本性质的应用。
13.比例是指两个比的相等关系,所以比和比例表示的意义是一样的。 × (判断对错)
【答案】×
【分析】两个数相除叫作两个数的比。
比例的意义:表示两个比相等的式子,叫作比例。
【解答】解:两个数相除叫作两个数的比。比例是指两个比的相等关系,所以比和比例表示的意义是不一样的。原题说法是错误的。
故答案为:×。
【点评】本题考查了比和比例的意义。
14.比例是方程. × .(判断对错)
【答案】见试题解答内容
【分析】比例:表示两个比相等的式子叫做比例,所以比例中可以没有未知数;而方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等式.由此进行判断.
【解答】解:方程是指含有未知数的等式,而比例是表示两个比相等的式子,比例中可以没有未知数;
故答案为:×.
【点评】本题主要考查了比例与方程的意义和区别.
15.在一个比例中,两个外项的积与两个内项的积的差为0。 √ (判断对错)
【答案】√
【分析】根据比例的基本性质直接判断即可,在比例里,两内项的积等于两外项的积。
【解答】解:根据比例的基本性质可得:在一个比例中,两个外项的积与两个内项的积相等,所以原题说法正确。
故答案为:√。
【点评】此题主要考查比例的基本性质:在比例里,两内项的积等于两外项的积。
16.在比例3:5=9:15中,将等号左边比的后项加上20,要使比例成立,等号右边比的后项应加上60。 √ (判断对错)
【答案】√。
【分析】根据比的基本性质作答即可。
【解答】解:5+20=25
25÷5=5
即:第一个比的后项是5,加上20后为25,相当于后项乘5,比值相应缩小到原来的五分之一。
15×5﹣15
=75﹣15
=60
即:要使比例仍然成立,第二个比的后项也应该同样乘5,即增加60。
故答案为:√。
【点评】本题考查了比例的意义及比的基本性质的理解与应用,解答本题时一定要理解:第一个比的后项乘5,第二个比的后项同样乘5,这样两个比的比值还是相等,比例仍然成立。
17.表示两个比相等的式子叫比例. √ (判断对错)
【答案】√
【分析】比例是表示两个比相等的式子.根据比例的概念直接判断.
【解答】解:比例是表示两个比相等的式子,所以原题说法正确.
故答案为:√.
【点评】此题考查比例的意义:是表示两个比相等的式子.
18.如果ab(a、b都不为0),那么a:b=8:9。 √ (判断对错)
【答案】√
【分析】将a看成比例的两个外项,b看成比例的两个内项,根据比例的基本性质写出比例并化简即可。
【解答】解:根据比例的基本性质可得:如果ab(a、b都不为0),那么a:b:8:9,原说法正确。
故答案为:√。
【点评】本题主要考查比例的基本性质的灵活运用。
19.有一扇通往知识宝藏的大门,门上有三个数,它们分别是2,5,10,请找出第四个数,这个数必须满足下列三个条件:
①这个数要能与原来三个数组成比例;
②这个数是合数;
③这个数是奇数。
这个数是几呢?请写出你的计算过程。
【答案】25。
【分析】在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质;除了1和它本身之外还有其它因数的数叫做合数,奇数是指末尾有0,1,3,5,9的数,据此解答。
【解答】解:25:5=10:2,且25×2=5×10=50,25是奇数也是合数,因此这个数是25。
【点评】本题考查了比例的基本性质的应用及奇数合数的认识。
二.正比例和反比例的意义(共3小题)
20.如表所示,当x和y成正比例时,空格里应填 48 ;当x和y成反比例时,空格里应填 3 。
x 12
y 6 24
【答案】48;3。
【分析】由正、反比例的意义可知:x和y的商一定时,两者成正比例;x和y的积一定时,两者成反比例,据此作答即可。
【解答】解:x:24=12:6
6x=24×12
6x=288
x=288÷6
x=48
24x=12×6
24x=72
x=72÷24
x=3
故答案为:48;3。
【点评】本题考查了正反比例关系的判定问题,解答此类问题时一定要清楚:两种相关联的量,凡是商(比值)一定的,这两种数量就成正比例关系,凡是积一定的,这两种数量就成反比例关系。
21.如表所示,如果x和y成正比例,那么“?”处应填 5 。如果x和y成反比例,那么“?”处应填 1.8 。
x 3 ?
y 90 150
【答案】5;1.8。
【分析】依据题意可知,如果x和y成正比例,90÷3=30,商一定,由此解答本题“?”处应填数,如果x和y成反比例,则xy=270,由此解答本题。
【解答】解:90÷3=30
150÷30=5
3×90=270
270÷150=1.8
则如果x和y成正比例,那么“?”处应填50。如果x和y成反比例,那么“?”处应填1.8。
故答案为:5;1.8。
【点评】本题考查的是正比例、反比例的应用。
22.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示k(一定).
(1)通过计算总价与数量的比值是否一定,来判定总价与数量是否成正比例关系即可.
(2)描点,连线即可.
(3)利用图象看2.5m所对应的图象上的点所对应的总价是多少元即可,然后再看68元所对应的图象上的点所对应的数量是多少米即可.
【解答】解:(1)总价和数量成正比例关系.
因为8(一定),是比值一定,
所以总价和数量成正比例关系.
(2)
由图可知正比例关系的图象是一条射线.
(3)根据图象可知:买2.5m花布需要20元,68元能买米8.5米花布.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.还要学会利用数形结合的思想解决数学问题.
三.正比例(共2小题)
23.关于比例关系的判断,以下说法正确的有( )个。
(1)订同一份杂志的钱数和份数成正比例关系。
(2)正方形的面积和它的边长成正比例关系。
(3)圆的面积和它的直径成反比例关系。
(4)三角形的面积一定,它的底和高成反比例关系。
A.3 B.2 C.1 D.4
【答案】B
【分析】两种相关联的量,如果比值一定,就成正比例关系,如果乘积一定,就成反比例关系;
(1)订同一份杂志时,钱数和份数的比值一定,据此分析;
(2)正方形的面积÷边长=边长,即正方形的面积与它的边长的比值不一定,据此分析;
(3)圆的面积÷直径直径,由此判断;
(4)三角形的底×高=面积×2,由此判断。
【解答】解:(1)订杂志的钱数÷份数=每份的钱数,订同一份杂志时,每份的钱数不变,则订同一份杂志的钱数和份数成正比例关系;
(2)正方形的面积÷边长=边长,因此正方形的面积和它的边长不成正比例关系;
(3)圆的面积和它的直径不成反比例关系;
(4)三角形的底×高=面积×2,则三角形的面积一定时,它的底和高成反比例关系。
综上所述,正确的是(1)(4),共2个。
故选:B。
【点评】本题考查的是正比例和反比例的应用。
24.成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。 √ (判断对错)
【答案】√。
【分析】在同时同地,太阳光线的角度是固定的。根据相似三角形的原理,竿高和影长的比值是一个定值,即竿高和影长成正比例关系。“立竿见影”描述的就是在阳光下竖起一根杆子,立刻就能看到它的影子,从数学角度看,很好地体现了这种同时同地竿高和影长的正比例关系。据此判断。
【解答】解:成语“立竿见影”从数学的角度看,是应用了比例中同时同地竿高和影长成正比例关系的知识。说法正确。
故答案为:√。
【点评】本题考查了学生对于正比例关系的理解及运用。
四.解比例(共7小题)
25.解比例。
(1)
(2)
【答案】(1)x;(2)x=0.39。
【分析】(1)根据比例的性质,把比例化成普通方程,然后再根据等式的性质求解;
(2)根据比例的性质,把比例化成普通方程,然后再根据等式的性质求解。
【解答】解:(1)
x
x
x
(2)
3x=6.5×18%
3x=1.17
x=0.39
【点评】熟练掌握等式的基本性质以及比例的基本性质是解题的关键,注意等号要对齐。
26.解比例。
20%::0.6
【答案】x=0.36;x=2。
【分析】(1)根据比例的基本性质,把原式化为x=20%×0.6,然后方程的两边同时除以求解;
(2)根据比例的基本性质,把原式化为2.4x=1.6×3,然后方程的两边同时除以2.4求解。
【解答】解:(1)20%::0.6
x=20%×0.6
x20%×0.6
x=0.36
(2)
2.4x=1.6×3
2.4x÷2.4=1.6×3÷2.4
x=2
【点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
27.解方程或比例。
1.2x﹣3.6=6
x:1.2=4:0.5
1.3x﹣0.6x=15.4
【答案】x=8;x=9.6;x=22。
【分析】方程1,等式两边同时加3.6,化简后,再两边同时除以1.2得解。
方程2,先改写成两个外项的乘积等于两个内项的乘积的形式,化简后,再两边同时乘2得解。
方程3,逆用乘法分配律化简后,再两边同时除以0.7得解。
【解答】解:1.2x﹣3.6=6
1.2x﹣3.6+3.6=6+3.6
1.2x=9.6
1.2x÷1.2=9.6÷1.2
x=8
x:1.2=4:0.5
0.5x=1.2×4
0.5x=4.8
2×0.5x=4.8×2
x=9.6
1.3x﹣0.6x=15.4
(1.3﹣0.6)x=15.4
0.7x=15.4
0.7x÷0.7=15.4÷0.7
x=22
【点评】本题考查了解方程、解比例的问题,解答本题一定要熟练掌握两个基本性质:一是等式的基本性质,即等式两边同时加、减、乘或除以一个相同的数(0除外),等式仍然成立;二是比例的基本性质,即两个外项的乘积等于两个内项的乘积。
28.解下面方程或比例。
4x+3×0.7=6.5
【答案】x=54;x=1;x=1.1。
【分析】(1)根据比例的基本性质,把原式化为4x=9×24,然后方程的两边同时除以4求解;
(2)根据比例的基本性质,把原式化为2.5x=5,然后方程的两边同时除以2.5求解;
(3)先计算3×0.7=2.1,根据等式的性质,方程的两边同时减去2.1,然后方程的两边同时除以4求解。
【解答】解:(1)
4x=9×24
4x÷4=9×24÷4
x=54
(2)
2.5x=5
2.5x÷2.5=52.5
x=1
(3)4x+3×0.7=6.5
4x+2.1=6.5
4x+2.1﹣2.1=6.5﹣2.1
4x=4.4
4x÷4=4.4÷4
x=1.1
【点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
29.解方程或比例。
30%x+50%x=240
【答案】x=300;x=0.6;x=108。
【分析】30%x+50%x=240,先计算30%x+50%x=0.8x,然后等式两边同时除以0.8,最后计算求出x的值;
,根据比例的基本性质可得12x=2.4×3,然后等式两边同时除以12,最后计算求出x的值;
,等式两边同时除以,然后计算求出x的值。
【解答】解:30%x+50%x=240
0.8x=240
0.8x÷0.8=240÷0.8
x=300
12x=3×2.4
12x=7.2
12x÷12=7.2÷12
x=0.6
x=108
【点评】解答此题要运用比例的基本性质和等式的基本性质。
30.解比例。
①0.4:x=0.2:7
②
③
【答案】①x=14;②x=1;③x。
【分析】①首先根据比例的基本性质化简,可得:0.2x=0.4×7;然后根据等式的性质,两边同时除以0.2即可;
②首先根据比例的基本性质化简,可得:x;然后根据等式的性质,两边同时乘即可;
③首先根据比例的基本性质化简,可得:4x=0.5×0.6;然后根据等式的性质,两边同时除以4即可。
【解答】解:①0.4:x=0.2:7
0.2x=0.4×7
0.2x=2.8
0.2x÷0.2=2.8÷0.2
x=14
②
x
x
x
x=1
③
4x=0.5×0.6
4x=0.3
4x÷4=0.3÷4
x
【点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用。
31.解方程。
:x=3:12
x﹣214
【答案】x=3;x=27;x=60。
【分析】(1)首先根据比例的基本性质化简,可得3x12,然后根据等式的性质,两边同时除以3即可;
(2)首先根据比例的基本性质化简,可得0.4x=1.2×9,然后根据等式的性质,两边同时除以0.4即可;
(3)首先把x﹣214化成0.3x﹣14=4,然后根据等式的性质,两边同时加上14,最后两边再同时除以0.3即可。
【解答】解:(1):x=3:12
3x12
3x=9
3x÷3=9÷3
x=3
(2)
0.4x=9×1.2
0.4x=10.8
0.4x÷0.4=10.8÷0.4
x=27
(3)
0.3x﹣14=4
0.3x﹣14+14=4+14
0.3x=18
0.3x÷0.3=18÷0.3
x=60
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等,以及解比例问题,注意比例的基本性质的应用。
五.比例的应用(共8小题)
32.师徒二人同时合作加工一批零件,全部完成一共用了6小时。已知徒弟与师傅加工零件的个数比是3:8,如果师傅平均每小时加工120个零件,那么徒弟平均每小时加工多少个零件?
【答案】45个。
【分析】首先根据:工作量=工作效率×工作时间,用师傅平均每小时加工零件的数量乘6,求出师傅6小时加工的零件个数是多少;然后用它乘,求出徒弟6小时加工零件多少个,再求平均每小时加工多少个零件即可。
【解答】解:120×66
=7206
=270÷6
=45(个)
答:徒弟平均每小时加工45个零件。
【点评】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
33.在比例尺是1:1000000的地图上,量的苍南县到杭州距离是3.6厘米。苍南县到杭州的实际距离是多少?
【答案】36千米。
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出上海到杭州的实际距离。
【解答】解:3.63600000(厘米)
3600000厘米=36千米
答:苍南县到杭州的实际距离是36千米。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
34.一间大厅,用边长为6分米的方砖铺地,需用216块;若改铺边长为4分米的方砖,需要用多少块?(用比例知识解答)
【答案】486。
【分析】一间大厅的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即每一块方砖的面积×所需块数=大厅面积(一定),也就是两种相关联的量成反比例,由此设出未知数,列出比例式解答即可。
【解答】解:设需要用x块。
4×4×x=6×6×216
16x=7776
16x÷16=7776÷16
x=486
答:需要486块。
【点评】此题首先利用正反比例的意义判定两种量的关系,再列比例式解答;注意:列比例式时不要把边长当成面积。
35.500千克稻谷可以碾出大米410千克。照这样计算,现在有这样的稻谷7.5吨,可以碾出多少吨大米?(用比例解)
【答案】6.15
【分析】根据出米率一定,列出比例即可。
【解答】解:设可以碾出x吨大米
500:410=7.5:x
500x=3075
x=6.15
答:可以碾出6.15吨大米。
【点评】列出比例,是解答此题的关键。
36.小马骑自行车从家里到书店,前5分钟行了800m。照这样的速度,从家到书店一共用了20分钟。他家和书店相距多少米?(用比例解)
【答案】3200米。
【分析】照这样的速度,说明速度一定,路程和时间成正比例,由此设出未知数,列比例解答即可。
【解答】解:设他家和书店相距x米。
x:20=800:5
5x=16000
x=3200
答:他家和书店相距3200米。
【点评】此题首先判定两种量成正比例,再设出未知数,列出比例式进行解答即可。
37.某市修一条道路,计划每天修120米,8天可以修完。但因为天气原因,12天才完成任务,实际每天修多少米?(用比例方法解)
【答案】80米。
【分析】根据题意知道,总工作量一定,工作时间和工作效率成反比例,由此列式解答即可。
【解答】解:实际每天修x米,
12x=120×8
12x=960
x=80
答:实际每天修80米。
【点评】解答此题的关键是,弄清题意,根据工作效率,工作时间和工作量三者的关系,判断哪两种量成何比例,然后找出对应量,列式解答即可。
38.古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解)
(1)12只羊可以换多少把斧头?
(2)要换9把斧头,需要几只羊?
【答案】(1)18把;
(2)6只。
【分析】(1)设12只羊可以换x把斧头,4与6的比等于12与x的比,据此解答。
(2)设要换9把斧头,需要x只羊,4与6的比等于x与9的比,据此解答。
【解答】解:(1)设12只羊可以换x把斧头。
4:6=12:x
4x=6×12
4x=72
x=18
答:12只羊可以换18把斧头。
(2)设要换9把斧头。
4:6=x:9
6x=4×9
6x=36
x=6
答:需要6只羊。
【点评】本题解题关键是根据比例的意义列出比例式,熟练掌握解比例的方法。
39.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
【答案】480立方厘米。
【分析】用96除以4,求出长方体的长加宽加高的和,再把这个和按5:3:4进行分配,求出长方体的长、宽、高,再根据长方体体积=长×宽×高,即可解答。
【解答】解:96÷4=24(厘米)
2410(厘米)
246(厘米)
248(厘米)
10×6×8
=60×8
=480(立方厘米)
答;这个长方体的体积是480立方厘米。
【点评】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
六.图形的放大与缩小(共5小题)
40.李老师的手机上保存着“厦门市地铁线网”截图,供同学们课后实践使用,左图是小华把李老师的原图按1:a缩小后的图片,右图是小丽把原图按( )缩小后的图片。
A.1:a B.1:a C.1:2a D.1:4a
【答案】C
【分析】根据题意,假设原图的边长是72厘米,结合左图是小华把李老师的原图按1:a缩小后的图片,左图的边长是36厘米,所以左图的边长:原图的边长=36:72=1:a,可知a=2。右图的边长:原图的边长=18:72=1:4,因为a=2,所以右图是小丽把原图按1:2a缩小后的图片。据此解答即可。
【解答】解:假设原图的边长是72厘米,左图的边长:原图的边长=36:72=1:a,可知a=2。右图的边长:原图的边长=18:72=1:4,因为a=2,所以右图是小丽把原图按1:2a缩小后的图片。
答:右图是小丽把原图按1:2a缩小后的图片。
故选:C。
【点评】本题考查了图形的放大和缩小知识,结合题意分析解答即可。
41.把一个梯形按3:1放大,放大后图形的面积是原来的9倍。 √ (判断对错)
【答案】√
【分析】把一个梯形按3:1放大,就是把梯形的上底、下底和高都扩大到原来的3倍,上底和下底的和扩大到原来的3倍,据此解答。
【解答】解:3×3=9
把一个梯形按3:1放大,放大后图形的面积是原来的9倍,原题说法正确。
故答案为:√。
【点评】掌握图形放大的特征是解题的关键。
42.按要求完成下面的题目。
①按照1:2的比画出三角形缩小后的图形。
②如果每个小正方形的边长是1厘米,缩小后三角形的面积是 2.5 平方厘米。
【答案】(1)(2)2.5。
【分析】(1)按1:2的比例画出三角形缩小后的图形,就是把原三角形的三条边都缩小到原来的,据此画图即可;
(2)根据三角形的面积计算公式:S底×高即可计算。
【解答】解:(1)如下图所示:
(2)2.5×2=2.5(cm2)
答:缩小后三角形的面积是2.5平方厘米。
故答案为:2.5。
【点评】本题考查了图形的缩小以及三角形面积的计算。
43.画一画:
(1)画出图形A按1:2缩小后的图形。
(2)画出图形B的另一半,使它成为一个轴对称图形。
【答案】(1)(2)
【分析】(1)根据图形缩小的方法,按1:2缩小,缩小后的图形的每条边都变为原来的,据此画图;
(2)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【解答】解:(1)画出图形A按1:2缩小后的图形。
(2)画出图形B的另一半,使它成为一个轴对称图形。如图:
【点评】本题考查了图形的缩小以及轴对称图形知识,结合题意分析解答即可。
44.请把长方形的长和宽都按2:1放大,画出放大后的长方形;请把三角形的各边接1:2缩小,画出缩小后的三角形。
【答案】
【分析】根据图形放大、缩小的方法,先求出放大2倍后,长方形的长、宽各是多少,再求出缩小2倍后,三角形的底和高各是多少,据此作图即可。
【解答】解:3×2=6
2×2=4
2÷2=1
4÷2=2
作图如下:
【点评】此题考查的目的是理解掌握图形放大与缩小的方法及应用,关键是明确:图形放大或缩小后,图形的形状不变,大小发生了变化。
七.比例尺(共16小题)
45.有一张边长为65厘米的正方形图纸,要在上面画长为120米,宽为90米的长方形草坪的平面图,你认为最合适的比例尺是( )
A.1:150 B.1:200 C.1:2000 D.20:1
【答案】C
【分析】根据“比例尺=图上距离:实际距离”可知“图上距离=实际距离×比例尺”依次代入数值,计算出相对应的图上距离,然后根据实际情况判断所给出的比例尺是否合适。
【解答】解:120米=12000厘米、90米=9000厘米。
A.1200080(厘米)
因为正方形图纸的边长为65厘米,所以比例尺不合适。
B.1200060(厘米)
900045(厘米),
图上长度太长,比例尺不合适。
C.120006(厘米)
90004.5(厘米)
比例尺合适。
D.比例尺是扩大比例尺,不合适。
故选:C。
【点评】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离:实际距离,灵活变形列式解决问题。
46.李叔叔是汽轮机厂的工程师,他要将一个长4mm、宽2mm的零件画在一张A3纸(42cm×29.7cm)上,合适的比例尺是( )
A.1:100 B.100:1 C.1:1000 D.1000:1
【答案】B
【分析】通过题意可知,要用放大比例尺,A和C是缩小比例尺,可以排除,分别求出以B和D为比例尺的图上距离,比较即可。
【解答】解:A.1:100,缩小比例尺,排除;
B.100:1,4×100=400(mm)=40(cm),2×100=200(mm)=20(cm),比例尺合适;
C.1:1000,缩小比例尺,排除;
D.1000:1,4×1000=4000(mm)=400(cm),400>42,比例尺不合适。
故选:B。
【点评】本题考查了比例尺,要把实际距离换算成图上距离。
47.一张地图的比例尺是1:5000000,地图上的1厘米相当于实际距离的( )
A.5000米 B.5000千米 C.50千米 D.500米
【答案】C
【分析】依据比例尺的意义,即图上距离与实际距离的比即为比例尺,即可求解.
【解答】解:因为比例尺1:5000000表示图上距离1厘米代表实际距离5000000厘米,
又因5000000厘米=50千米,
所以比例尺1:5000000表示地图上1厘米的距离相当于地面上50千米的实际距离;
故选:C.
【点评】此题主要考查比例尺的意义,解答时要注意单位的换算.
48.一幅地图的比例尺是20:1,如果零件图上长5厘米,则实际长( )
A.4厘米 B.100厘米 C.0.25厘米
【答案】C
【分析】根据实际距离=图上距离÷比例尺,解答即可。
【解答】解:5÷20=0.25(厘米)
答:实际长0.25厘米。
故选:C。
【点评】本题主要考查了比例尺的意义,要熟练掌握。
49.如图是现藏于三星堆博物馆的青铜大立人像,青铜大立人像是现存最高。最完整的青铜立人像,被誉为“世界铜像之王”。在一张比例尺为1:80的图上,这个青铜大立人像的高为( )
A.3.26厘米 B.32.6厘米
C.208.64厘米 D.2.608厘米
【答案】A
【分析】已知青铜大立人像实际高为2.608米,图纸的比例尺为1:80,根据“图上距离=实际距离×比例尺”,求出这个青铜大立人像在图纸上的高。注意单位的换算:1米=100厘米。
【解答】解:2.608米=260.8厘米
这个青铜大立人像的高为:
260.83.26(厘米)
答:这个青铜大立人像的高为3.26厘米。
故选:A。
【点评】本题考查的是比例尺应用题,掌握“图上距离=实际距离×比例尺”是解答关键。
50.一种微型零件的实际长度是1mm,画在图纸上长3dm,画图时选用的比例尺是( )
A.1:300 B.1:3 C.300:1 D.3:1
【答案】C
【分析】根据比例尺的意义:比例尺=图上距离:实际距离,即可解答,注意单位名数的统一。
【解答】解:1mm=0.1cm;3dm=30cm
30:0.1
=(30×10):(0.1×10)
=300:1
答:一种微型零件的实际长度是1mm,画在图纸上长3dm,画图时选用的比例尺是300:1。
故选:C。
【点评】熟练掌握比例尺的意义是解题的关键。
51.一幅地图的线段比例尺是,改成数字比例尺是 1:3000000 ;石家庄到北京的实际距离是330千米,则地图上的距离是 11 厘米。
【答案】1:3000000;11。
【分析】根据比例尺=图上距离:实际距离,解答此题即可。
【解答】解:30千米=3000000厘米
330÷30=11(厘米)
答:改成数字比例尺是1:3000000;石家庄到北京的实际距离是330千米,则地图上的距离是11厘米。
故答案为:1:3000000;11。
【点评】熟练掌握比例尺的定义,是解答此题的关键。
52.小玲的妈妈身高1.65m,在一张照片上她的身高是5cm,这张照片的比例尺是 1:33 。
【答案】1:33。
【分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:1.65米=165厘米
5厘米:165厘米
=(5÷5)(165÷5)
=1:33
答:这张照片的比例尺是1:33。
故答案为:1:33。
【点评】本题考查了比例尺的意义,比例尺=图上距离:实际距离,注意单位要统一。
53.实际宽度为3m的窗户,在建筑平面图上绘制的宽度为1.5cm,这幅平面图的比例尺为 1:200 。
【答案】1:200。
【分析】读题可知,图上距离为1.5cm,实际距离为3m,据此写出图上距离与实际距离的比,再化简即可。
【解答】解:1.5cm:3m
=1.5cm:300cm
=1.5:300
=(1.5÷1.5):(300÷1.5)
=1:200
答:这幅平面图的比例尺为1:200。
【点评】本题考查了比例尺的意义的应用问题,解答本题时一定要清楚:图上距离与实际距离的比,叫作比例尺;写出图上距离与实际距离的比后,再按式的基本性质化简,得到前项或后项为1的最简整数比即可。
54.在照片上小明的身高是8厘米,他的实际身高是168厘米。这张照片的比例尺是 1:21 。
【答案】1:21。
【分析】因为“图上距离与实际距离的比即为比例尺”,图上距离和实际距离已知,从而可以求得这张照片的比例尺。
【解答】解:8厘米:168厘米=1:21;
答:这张照片的比例尺是1:21.
故答案为:1:21。
【点评】此题主要考查比例尺的意义,即图上距离与实际距离的比即为比例尺,解答时要注意单位统一。
55.一个圆柱形零件的高是5mm,在图纸上的高是2cm,这幅图纸的比例尺是 4:1 .
【答案】见试题解答内容
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺.
【解答】解:因为5毫米=0.5厘米
则2厘米:0.5厘米=4:1
答:这幅图纸的比例尺是4:1.
故答案为:4:1.
【点评】此题主要考查比例尺的计算方法.解答时要注意单位的换算.
56.在一张图纸上,测得一个零件的长是10cm,已知这个零件实际长度是2mm,这张图纸的比例尺是 50:1 。
【答案】50:1。
【分析】比例尺=图上距离:实际距离,再根据比的基本性质:比的前项和后项同时乘或除以一个数(0除外),比值不变,可化简比例尺,进而得出答案。
【解答】解:10厘米=100毫米
100:2=50:1
答:这张图纸的比例尺是50:1。
故答案为:50:1。
【点评】本题主要考查的是比例尺的应用,解题的关键是熟练掌握比例尺的求法,进而得出答案。
57.在比例尺是1:20的图纸上画出一种机械配件平面图的角是40°,这个角实际上也是40°。 √ (判断对错)
【答案】√
【分析】根据图形的放大、缩小的知识可知,图形放大或缩小后,只改变图形的大小,不改变图形的形状。据此判断。
【解答】解:在比例尺是1:20的图纸上画出一种机械配件平面图的角是40°,这个角实际上也是40°。
原题说法正确。
故答案为:√。
【点评】熟练掌握图形的放大与缩小的特征是解题的关键。
58.实际距离为2mm,图上距离为2dm,则比例尺为1:100。 × (判断对错)
【答案】×
【分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:比例尺为2dm:2mm=20cm:0.2cm=100:1
故原题说法错误。
故答案为:×。
【点评】解答此题的关键是掌握比例尺的意义和相关公式。
59.在比例尺是100:1的图纸上,一个长方体零件正面的长是15cm,宽是9cm。这个零件正面的实际面积是多少平方厘米?
【答案】0.0135平方厘米。
【分析】根据实际距离=图上距离÷比例尺,分别求出长方体零件正面的实际长和宽,再根据长方形的面积=长×宽解答。
【解答】解:150.15(厘米)
90.09(厘米)
0.15×0.09=0.0135(平方厘米)
答:这个零件正面的实际面积是0.0135平方厘米。
【点评】熟练掌握实际距离、图上距离、比例尺的关系以及长方形面积的计算方法是解题的关键。
60.游泳比赛的泳池是一个长方形,把泳池的长和宽分别缩小到原来的后图形如下.
(1)泳池实际的长和宽各是多少米?
(2)泳池的实际占地面积是多少平方米?
【答案】见试题解答内容
【分析】(1)根据实际距离=图上距离÷比例尺,可代入数据分别求出实际的长和宽;
(2)用实际的长乘实际的宽可求出实际的占地面积.据此解答.
【解答】解:(1)0.0550(米)
0.02121(米)
答:泳池实际的长是50米,宽是21米.
(2)50×21=1050(平方米)
答:泳池实际占地面积是1050平方米.
【点评】本题重点考查了学生对实际距离=图上距离÷比例尺和长方形面积公式的掌握.
21世纪教育网(www.21cnjy.com)
