湖北省武汉市2025年中考数学押题预测卷(含答案)
文档属性
| 名称 | 湖北省武汉市2025年中考数学押题预测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 00:00:00 | ||
图片预览




文档简介
2025年中考数学押题预测卷
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1.未来将是一个可以预见的时代.一般指人工智能,它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学.以下是四款常用的人工智能大模型的图标,其中是轴对称图形的是( )
A.B. C. D.
2.下列事件中,属于必然事件的是( )
A.任意画一个三角形,其外角和是
B.打开电视,正在播放跳水比赛
C.经过有交通信号的路口时遇见绿灯
D.若,则
3.榫卯是中国传统建筑的一种结构方式,被誉为“中华民族千年非遗瑰宝”,通过榫和卯的精密配合,实现了构造的稳固性和可持续性,展现了人与自然的和谐关系.如下图是其中一种卯,其俯视图是( )
A. B. C. D.
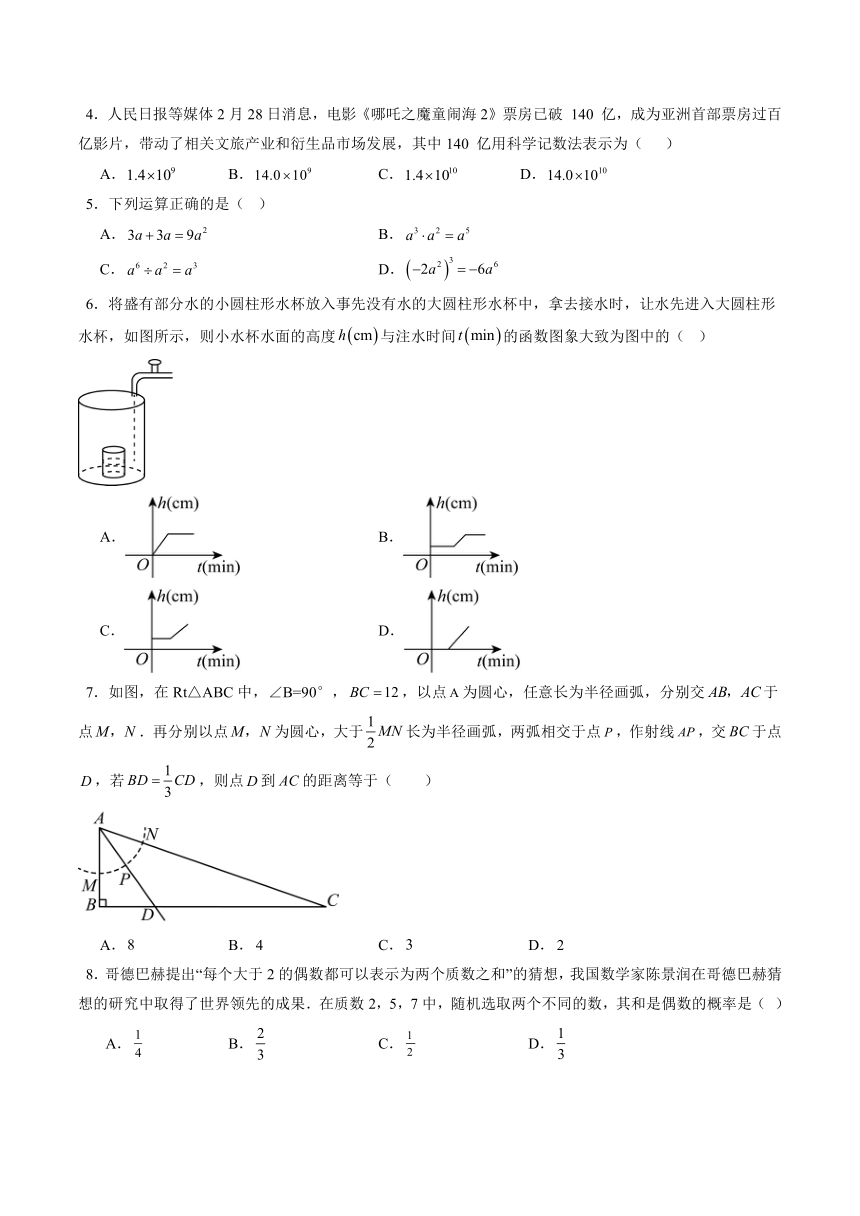
4.人民日报等媒体2月28日消息,电影《哪吒之魔童闹海2》票房已破 140 亿,成为亚洲首部票房过百亿影片,带动了相关文旅产业和衍生品市场发展,其中140 亿用科学记数法表示为( )
A. B. C. D.
5.下列运算正确的是( )
A. B.
C. D.
6.将盛有部分水的小圆柱形水杯放入事先没有水的大圆柱形水杯中,拿去接水时,让水先进入大圆柱形水杯,如图所示,则小水杯水面的高度与注水时间的函数图象大致为图中的( )
A. B.
C. D.
7.如图,在Rt△ABC中,∠B=90°,,以点为圆心,任意长为半径画弧,分别交于点.再分别以点为圆心,大于长为半径画弧,两弧相交于点,作射线,交于点,若,则点到的距离等于( )
A. B. C. D.
8.哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.在质数2,5,7中,随机选取两个不同的数,其和是偶数的概率是( )
A. B. C. D.
9.如图,△ABC内接于,连接,过点C作的切线,交的延长线于点M,,,则的长为( )
A.2 B. C. D.
10.观察规律,运用你观察到的规律解决以下问题:如图,分别过点作轴的垂线,交的图象于点,交直线于点.则的值为( )
A. B. C. D.
第Ⅱ卷
填空题(本大题共6个小题,每小题3分,共18分)
11.《九章算术》中对正负数的概念注有“今两算得失相反,要令正负以名之”.如:粮库把运进30吨粮食记为“”,则“”表示 .
12.已知点、是反比例函数()图象上两点.当时,,则的值可以是 .(写出一个即可)
13.方程的解为 .
14.如图,下左图为《天工开物》记载的用于舂()捣谷物的工具——“碓()”的结构简图,如图为其平面示意图.已知于点B,与水平线l相交于点O,.若,,,则点C到水平线l的距离为 .
15.如图,有一张长方形纸片,其中边的长为2,将长方形沿对角线对折,折叠后得到,点C的对应点为E,与交于点F,再将沿对折,使点E落在长方形纸片的内部点G处,若平分,则的长为 .
16.二次函数的部分图象如图所示,图象过点,对称轴为直线,下列结论:;;(3)若点,点,点在该函数图象上,则;(4)若,则,其中正确的结论的序号是 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明,证明过程或演算步骤)
17.(8分)解不等式组,并写出它的所有正整数解.
18.(8分)如图,AC∥DF,AC=DF.下列三个条件:
①AE=DB;②BC=EF;③∠C=∠F.
请你从①②③中选一个条件,使△ABC≌△DEF.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明△ABC≌△DEF.
19.(8分)年月4日,中国“春节”申遗成功.中国春节文化源远流长,全国各地衍生出纷繁多样的春节习俗.某校为了解学生对春节文化的了解情况,举办了春节文化知识竞赛,现从该校七、八年级学生中各随机抽取名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分为四组:
.,.,.,.,得分在分及以上为优秀),下面给出了部分信息:七年级20名学生的竞赛成绩是:
,,,,,,,,,,,,,,,,,,,.
八年级名学生竞赛成绩在B组的数据是:,,,,,,.
七、八年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
七年级 a
八年级 b
根据以上信息,解答下列问题:
(1)上述图表中的__________, __________, __________;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的春节文化知识竞赛成绩更好?请说明理由;(写出一条理由即可)
(3)该校八年级有学生人,七年级有学生人,估计该校七、八年级学生中中华民族优秀传统文化知识为优秀的学生人数总共有多少人?
20.(8分)如图是由小正方形组成的8×4网格,每个小正方形的顶点叫做格点,△ABC三个顶点均在格点上,仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过四条.
(1)在图(1)中,先画格点D,使得BD⊥AC干E;
(2)在(1)的基础上,在射线BE上画一点E,使得AF=AB;
(3)在图(2)中,先画点P,使点A绕点P逆时针旋转90°得点C,连接BP交AC于G;
(4)在(3)的基础上,将线段BC绕点G旋转180°,画出对应线段MN(点B与点M对应,点C与点N对应).
21.(8分)如图,在△ABC中,∠ABC=90°,点D是BC边上一点,以CD为直径的⊙O与边AC交于点E,连接BE,AB=BE.
(1)求证:BE是⊙O的切线;
(2)若,⊙O的直径为4,求BD的长.
22.(10分)综合与应用
为促进中学生全面发展,培养良好体质,某班同学在“大课间”开展“集体跳绳”运动.跳绳时,绳甩到最高处时的形状是抛物线y=ax2+bx+c的部分图象.以点O为原点建立如图所示的平面直角坐标系,若摇绳的两人之间间距为6米,摇绳时两人手离地面均为米;已知小丽身高1.575米,在距离摇绳者A的水平距离1.5米处,绳子刚好经过她的头顶.
【阅读理解】
(1)求图中抛物线的解析式;(不需要求自变量取值范围)
【问题解决】
(2)体育龙老师身高1.82米,请问他适合参加本次运动吗?说明理由;
(3)若多人进入跳绳区齐跳,且大家身高均为1.7米,要求相邻两人之间间距至少为0.6米,试计算最多可供几人齐跳.
23.(10分)如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AFAE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=4,CE=4,求线段AE的长.
24.(12分)综合与探究:
如图1,抛物线与x轴相交于,两点,与y轴交于点C,连接BC,抛物线顶点为点M.
(1)求抛物线解析式及点M的坐标;
(2)平移直线BC得直线y=mx+n.
①如图2,若直线y=mx+n过点M,交x轴于点D,在x轴上取点,连接EM,求∠DME的度数.
②把抛物线在x轴下方图象沿x轴翻折得到新图象(如图3中的“W”形曲线).当直线y=mx+n与新图象有两个公共点时,请直接写出n的取值范围.
数学·参考答案
第Ⅰ卷
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1 2 3 4 5 6 7 8 9 10
D A D C B B C D A D
第Ⅱ卷
填空题(本大题共6小题,每小题3分,共18分)
11.运出30吨粮食
12.(答案不唯一).
13..
14.
15.
16.(1)(4).
三、解答题(本大题共8个小题,共72分.解答应写出文字说明,证明过程或演算步骤)
17.(8分)
【详解】解:解不等式,得; ……………………2分
解不等式,得. …………………4分
原不等式组的解是, ……………………6分
不等式组的正整数解为1,2,3. ……………………8分
18.(8分)
【详解】(1)解:添加的条件是①或③; ……………………3分
(2)证明:∵AC∥DF,
∴∠A=∠D,
先证明添加的条件①,
∵AE=DB,
∴AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS); ……………………8分
下面证明添加的条件③,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
19.(8分)
【详解】(1)解:七年级20名学生的竞赛成绩中出现次数最多的是,故;
八年级名学生竞赛成绩在组的数据是:,,,,,,共7个数据, 八年级组占,则组人数为:人.剩余组,组共5人,中位数为第位,第位的平均数,则第位,第位在组内:;
,则;
故答案为:,,. ……………………3分
(2)解:八年级成绩更好.
由表中数据可知,七、八年级成绩的平均数相等,而八年级的方差较小,所以八年级的成绩更稳定,成绩更好; ……………………5分
(3)解:人,
计该校七、八年级学生中中华民族优秀传统文化知识为优秀的学生人数总共有人.
……………………8分
20.(8分)
【详解】解:(1)(2)如图(1)所示,(3)(4)如图(2)所示.
……………………8分(每问2分)
21.(8分)
【解答】(1)证明:连接OE,∵AB=BE,
∴∠A=∠AEB,∵OE=OC,∴∠C=∠OEC,∵∠ABC=90°,∴∠A+∠C=90°,
∴∠AEB+∠CEO=90°,∴∠BEO=90°,∵OE是⊙O的半径,
∴BE是⊙O的切线; ……………………4分
(2)解:连接DE,
∵CD为⊙O的直径,∴∠CED=90°,由(1)知,∠BEO=90°,∴∠BED=∠CEO=∠C,
∵∠B=∠B,∴△BDE∽△BEC,∴,∵,∴,∴,
设BD=x,BE=2x,
∴AB=2x,在Rt△ABC中,tan∠ACB,解得x,
故BD的长为. ……………………8分
22.(10分)
【解答】解:(1)∵摇绳的两人之间间距为6米,摇绳时两人手离地面均为米,
∴抛物线的对称轴为直线x=3.
由题意得:抛物线经过点(0,),(1.5,1.575).
∴. 解得:.
∴图中抛物线的解析式为:y=﹣0.1x2+0.6x+0.9; ……………………3分
(2)∵﹣0.1<0,
∴二次函数有最大值1.8. ∵1.8m<1.82m,
∴他不适合参加本次运动; ……………………6分
(3)当y=1.7时. ﹣0.1x2+0.6x+0.9=1.7. (x﹣2)(x﹣4)=0. ∴x1=2,x2=4.
∴4﹣2=2(米).∵相邻两人之间间距至少为0.6米, ∴间距个数为:2÷0.6=3.
∴最多可供4人齐跳.
答:最多可供4人齐跳. ……………………10分
23.(10分)【详解】(1)证明:∵四边形ABFD是平行四边形,∴AB=DF.
在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,
∵AB=AC,∴AC=DF.∵DE=EC,∴AE=EF.
∴△AEF是等腰直角三角形; ……………………3分
(2)证明:连接EF,如图2,
∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DGE=∠ABC=45°,
∴∠EGF=180°﹣∠DGE=135°,EG=ED.∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EGF=∠ADE.∵∠DGC=∠C,∴DG=DC.∵DF=AB=AC,∴GF=AD.
在△EGF和△EDA中,
,∴△EGF≌△EDA(SAS),∴EF=EA,∠GEF=∠AED,∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,∴AFAE; ……………6分
(3)解:当AD=AC=AB时,四边形ABFD是菱形,
设AE交CD于H,依据AD=AC,ED=EC,可得AE垂直平分CD,∵CE=4,
在等腰直角△CDE中,EH=DH=CHCE4=2,在Rt△ACH中,AC=AB=4,
由勾股定理得AH6,
∴AE=AH+EH=8. ……………………10分
24.(12分)
【详解】解:(1)将A,B两点的坐标代入抛物线解析式:
, 解得:a=1,b=3, ∴y=x2﹣3x(x)2﹣1,………3分
∴M(,﹣1); ……………………4分
(2)①设直线BC的解析式为:y=kx,
把B(,0)代入得:0k, 解得:k, ∴直线BC的解析式为:yx,
∴直线BC平移后的解析式为:yx+n,
把点M(,﹣1)代入yx+n,得:﹣1n, 解得:n,
∴直线DM的解析式为:yx, 令y=0,得:x, ∴D(,0),
过点E作EF⊥DM于F,过点M作MH⊥x轴于H,如图:
∴H(,0), ∴MH=1,DH=2, 在Rt△DHM中,DM,
∵E(,0),∴DE, ∵sin∠BDM, ∴EF, ∴DF,
∴FM=DM﹣DF, ∴EF=FM, 又∵EF⊥FM,
∴∠DME=45°; ……………………8分
②把抛物线在x轴下方图象沿x轴翻折得到的新图象,如图:
由平移的性质可知,当直线yx+n在l1和l2之间以及l3上方时,直线与新图象有两个交点,
∵l2的解析式即为直线BC的解析式:yx, ∴n2,
将A(,0)代入直线解析式得:0n1, ∴n1,
翻折后,AB之间的函数解析式为:y=﹣x2+3x,与直线解析式联立得:x2x+n30,
此时,一元二次方程有相同的实数根,∴Δ=()2﹣4(n3)=﹣4n30,
∴n3,
∴当直线y=mx+n与新图象有两个公共点时,n或n.
……………………12分
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1.未来将是一个可以预见的时代.一般指人工智能,它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学.以下是四款常用的人工智能大模型的图标,其中是轴对称图形的是( )
A.B. C. D.
2.下列事件中,属于必然事件的是( )
A.任意画一个三角形,其外角和是
B.打开电视,正在播放跳水比赛
C.经过有交通信号的路口时遇见绿灯
D.若,则
3.榫卯是中国传统建筑的一种结构方式,被誉为“中华民族千年非遗瑰宝”,通过榫和卯的精密配合,实现了构造的稳固性和可持续性,展现了人与自然的和谐关系.如下图是其中一种卯,其俯视图是( )
A. B. C. D.
4.人民日报等媒体2月28日消息,电影《哪吒之魔童闹海2》票房已破 140 亿,成为亚洲首部票房过百亿影片,带动了相关文旅产业和衍生品市场发展,其中140 亿用科学记数法表示为( )
A. B. C. D.
5.下列运算正确的是( )
A. B.
C. D.
6.将盛有部分水的小圆柱形水杯放入事先没有水的大圆柱形水杯中,拿去接水时,让水先进入大圆柱形水杯,如图所示,则小水杯水面的高度与注水时间的函数图象大致为图中的( )
A. B.
C. D.
7.如图,在Rt△ABC中,∠B=90°,,以点为圆心,任意长为半径画弧,分别交于点.再分别以点为圆心,大于长为半径画弧,两弧相交于点,作射线,交于点,若,则点到的距离等于( )
A. B. C. D.
8.哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.在质数2,5,7中,随机选取两个不同的数,其和是偶数的概率是( )
A. B. C. D.
9.如图,△ABC内接于,连接,过点C作的切线,交的延长线于点M,,,则的长为( )
A.2 B. C. D.
10.观察规律,运用你观察到的规律解决以下问题:如图,分别过点作轴的垂线,交的图象于点,交直线于点.则的值为( )
A. B. C. D.
第Ⅱ卷
填空题(本大题共6个小题,每小题3分,共18分)
11.《九章算术》中对正负数的概念注有“今两算得失相反,要令正负以名之”.如:粮库把运进30吨粮食记为“”,则“”表示 .
12.已知点、是反比例函数()图象上两点.当时,,则的值可以是 .(写出一个即可)
13.方程的解为 .
14.如图,下左图为《天工开物》记载的用于舂()捣谷物的工具——“碓()”的结构简图,如图为其平面示意图.已知于点B,与水平线l相交于点O,.若,,,则点C到水平线l的距离为 .
15.如图,有一张长方形纸片,其中边的长为2,将长方形沿对角线对折,折叠后得到,点C的对应点为E,与交于点F,再将沿对折,使点E落在长方形纸片的内部点G处,若平分,则的长为 .
16.二次函数的部分图象如图所示,图象过点,对称轴为直线,下列结论:;;(3)若点,点,点在该函数图象上,则;(4)若,则,其中正确的结论的序号是 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明,证明过程或演算步骤)
17.(8分)解不等式组,并写出它的所有正整数解.
18.(8分)如图,AC∥DF,AC=DF.下列三个条件:
①AE=DB;②BC=EF;③∠C=∠F.
请你从①②③中选一个条件,使△ABC≌△DEF.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明△ABC≌△DEF.
19.(8分)年月4日,中国“春节”申遗成功.中国春节文化源远流长,全国各地衍生出纷繁多样的春节习俗.某校为了解学生对春节文化的了解情况,举办了春节文化知识竞赛,现从该校七、八年级学生中各随机抽取名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分为四组:
.,.,.,.,得分在分及以上为优秀),下面给出了部分信息:七年级20名学生的竞赛成绩是:
,,,,,,,,,,,,,,,,,,,.
八年级名学生竞赛成绩在B组的数据是:,,,,,,.
七、八年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
七年级 a
八年级 b
根据以上信息,解答下列问题:
(1)上述图表中的__________, __________, __________;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的春节文化知识竞赛成绩更好?请说明理由;(写出一条理由即可)
(3)该校八年级有学生人,七年级有学生人,估计该校七、八年级学生中中华民族优秀传统文化知识为优秀的学生人数总共有多少人?
20.(8分)如图是由小正方形组成的8×4网格,每个小正方形的顶点叫做格点,△ABC三个顶点均在格点上,仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过四条.
(1)在图(1)中,先画格点D,使得BD⊥AC干E;
(2)在(1)的基础上,在射线BE上画一点E,使得AF=AB;
(3)在图(2)中,先画点P,使点A绕点P逆时针旋转90°得点C,连接BP交AC于G;
(4)在(3)的基础上,将线段BC绕点G旋转180°,画出对应线段MN(点B与点M对应,点C与点N对应).
21.(8分)如图,在△ABC中,∠ABC=90°,点D是BC边上一点,以CD为直径的⊙O与边AC交于点E,连接BE,AB=BE.
(1)求证:BE是⊙O的切线;
(2)若,⊙O的直径为4,求BD的长.
22.(10分)综合与应用
为促进中学生全面发展,培养良好体质,某班同学在“大课间”开展“集体跳绳”运动.跳绳时,绳甩到最高处时的形状是抛物线y=ax2+bx+c的部分图象.以点O为原点建立如图所示的平面直角坐标系,若摇绳的两人之间间距为6米,摇绳时两人手离地面均为米;已知小丽身高1.575米,在距离摇绳者A的水平距离1.5米处,绳子刚好经过她的头顶.
【阅读理解】
(1)求图中抛物线的解析式;(不需要求自变量取值范围)
【问题解决】
(2)体育龙老师身高1.82米,请问他适合参加本次运动吗?说明理由;
(3)若多人进入跳绳区齐跳,且大家身高均为1.7米,要求相邻两人之间间距至少为0.6米,试计算最多可供几人齐跳.
23.(10分)如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AFAE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=4,CE=4,求线段AE的长.
24.(12分)综合与探究:
如图1,抛物线与x轴相交于,两点,与y轴交于点C,连接BC,抛物线顶点为点M.
(1)求抛物线解析式及点M的坐标;
(2)平移直线BC得直线y=mx+n.
①如图2,若直线y=mx+n过点M,交x轴于点D,在x轴上取点,连接EM,求∠DME的度数.
②把抛物线在x轴下方图象沿x轴翻折得到新图象(如图3中的“W”形曲线).当直线y=mx+n与新图象有两个公共点时,请直接写出n的取值范围.
数学·参考答案
第Ⅰ卷
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1 2 3 4 5 6 7 8 9 10
D A D C B B C D A D
第Ⅱ卷
填空题(本大题共6小题,每小题3分,共18分)
11.运出30吨粮食
12.(答案不唯一).
13..
14.
15.
16.(1)(4).
三、解答题(本大题共8个小题,共72分.解答应写出文字说明,证明过程或演算步骤)
17.(8分)
【详解】解:解不等式,得; ……………………2分
解不等式,得. …………………4分
原不等式组的解是, ……………………6分
不等式组的正整数解为1,2,3. ……………………8分
18.(8分)
【详解】(1)解:添加的条件是①或③; ……………………3分
(2)证明:∵AC∥DF,
∴∠A=∠D,
先证明添加的条件①,
∵AE=DB,
∴AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS); ……………………8分
下面证明添加的条件③,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
19.(8分)
【详解】(1)解:七年级20名学生的竞赛成绩中出现次数最多的是,故;
八年级名学生竞赛成绩在组的数据是:,,,,,,共7个数据, 八年级组占,则组人数为:人.剩余组,组共5人,中位数为第位,第位的平均数,则第位,第位在组内:;
,则;
故答案为:,,. ……………………3分
(2)解:八年级成绩更好.
由表中数据可知,七、八年级成绩的平均数相等,而八年级的方差较小,所以八年级的成绩更稳定,成绩更好; ……………………5分
(3)解:人,
计该校七、八年级学生中中华民族优秀传统文化知识为优秀的学生人数总共有人.
……………………8分
20.(8分)
【详解】解:(1)(2)如图(1)所示,(3)(4)如图(2)所示.
……………………8分(每问2分)
21.(8分)
【解答】(1)证明:连接OE,∵AB=BE,
∴∠A=∠AEB,∵OE=OC,∴∠C=∠OEC,∵∠ABC=90°,∴∠A+∠C=90°,
∴∠AEB+∠CEO=90°,∴∠BEO=90°,∵OE是⊙O的半径,
∴BE是⊙O的切线; ……………………4分
(2)解:连接DE,
∵CD为⊙O的直径,∴∠CED=90°,由(1)知,∠BEO=90°,∴∠BED=∠CEO=∠C,
∵∠B=∠B,∴△BDE∽△BEC,∴,∵,∴,∴,
设BD=x,BE=2x,
∴AB=2x,在Rt△ABC中,tan∠ACB,解得x,
故BD的长为. ……………………8分
22.(10分)
【解答】解:(1)∵摇绳的两人之间间距为6米,摇绳时两人手离地面均为米,
∴抛物线的对称轴为直线x=3.
由题意得:抛物线经过点(0,),(1.5,1.575).
∴. 解得:.
∴图中抛物线的解析式为:y=﹣0.1x2+0.6x+0.9; ……………………3分
(2)∵﹣0.1<0,
∴二次函数有最大值1.8. ∵1.8m<1.82m,
∴他不适合参加本次运动; ……………………6分
(3)当y=1.7时. ﹣0.1x2+0.6x+0.9=1.7. (x﹣2)(x﹣4)=0. ∴x1=2,x2=4.
∴4﹣2=2(米).∵相邻两人之间间距至少为0.6米, ∴间距个数为:2÷0.6=3.
∴最多可供4人齐跳.
答:最多可供4人齐跳. ……………………10分
23.(10分)【详解】(1)证明:∵四边形ABFD是平行四边形,∴AB=DF.
在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,
∵AB=AC,∴AC=DF.∵DE=EC,∴AE=EF.
∴△AEF是等腰直角三角形; ……………………3分
(2)证明:连接EF,如图2,
∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DGE=∠ABC=45°,
∴∠EGF=180°﹣∠DGE=135°,EG=ED.∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EGF=∠ADE.∵∠DGC=∠C,∴DG=DC.∵DF=AB=AC,∴GF=AD.
在△EGF和△EDA中,
,∴△EGF≌△EDA(SAS),∴EF=EA,∠GEF=∠AED,∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,∴AFAE; ……………6分
(3)解:当AD=AC=AB时,四边形ABFD是菱形,
设AE交CD于H,依据AD=AC,ED=EC,可得AE垂直平分CD,∵CE=4,
在等腰直角△CDE中,EH=DH=CHCE4=2,在Rt△ACH中,AC=AB=4,
由勾股定理得AH6,
∴AE=AH+EH=8. ……………………10分
24.(12分)
【详解】解:(1)将A,B两点的坐标代入抛物线解析式:
, 解得:a=1,b=3, ∴y=x2﹣3x(x)2﹣1,………3分
∴M(,﹣1); ……………………4分
(2)①设直线BC的解析式为:y=kx,
把B(,0)代入得:0k, 解得:k, ∴直线BC的解析式为:yx,
∴直线BC平移后的解析式为:yx+n,
把点M(,﹣1)代入yx+n,得:﹣1n, 解得:n,
∴直线DM的解析式为:yx, 令y=0,得:x, ∴D(,0),
过点E作EF⊥DM于F,过点M作MH⊥x轴于H,如图:
∴H(,0), ∴MH=1,DH=2, 在Rt△DHM中,DM,
∵E(,0),∴DE, ∵sin∠BDM, ∴EF, ∴DF,
∴FM=DM﹣DF, ∴EF=FM, 又∵EF⊥FM,
∴∠DME=45°; ……………………8分
②把抛物线在x轴下方图象沿x轴翻折得到的新图象,如图:
由平移的性质可知,当直线yx+n在l1和l2之间以及l3上方时,直线与新图象有两个交点,
∵l2的解析式即为直线BC的解析式:yx, ∴n2,
将A(,0)代入直线解析式得:0n1, ∴n1,
翻折后,AB之间的函数解析式为:y=﹣x2+3x,与直线解析式联立得:x2x+n30,
此时,一元二次方程有相同的实数根,∴Δ=()2﹣4(n3)=﹣4n30,
∴n3,
∴当直线y=mx+n与新图象有两个公共点时,n或n.
……………………12分
同课章节目录
