【期末专项培优】三角形高频易错提高卷(含解析)-2024-2025学年四年级下册数学人教版
文档属性
| 名称 | 【期末专项培优】三角形高频易错提高卷(含解析)-2024-2025学年四年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-09 20:34:17 | ||
图片预览



文档简介
三角形
一.三角形的特性(共7小题)
1.将一根20厘米的细铁丝,剪成3段,拼成一个三角形,以下哪种剪法可以( )
A.8厘米、7厘米、5厘米 B.13厘米、6厘米、1厘米
C.4厘米、9厘米、4厘米 D.10厘米、3厘米、7厘米
2.下面选项中的三条线段能围成(每相邻两条线段的端点相连)三角形的是( )
A. B.
C. D.
3.一个三角形有 条边,一个角有 条边。
4.四月初,乐乐和妈妈一起种了一些黄瓜苗。一天,妈妈用竹竿搭起了很多三角形的黄瓜架,她这样做的原因是三角形具有 。
5.在中有3个三角形。
6.把一根长10厘米的吸管剪成3段(每段都是整厘米),围成一个三角形。能围成多少个不同的三角形,它们的每条边长度分别是多少厘米?
7.有5根小棒,长度分别是3厘米、3厘米、3厘米、4厘米、6厘米,可以摆成几种不同的三角形?请你列举出来.
二.三角形的分类(共19小题)
8.一个三角形最大的内角是120°,这个三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形
9.一个等腰三角形的一个底角与顶角的度数相等,这个三角形是( )三角形。
A.直角 B.钝角 C.等边
10.如图所示,一张三角形的纸片被撕去了一个角,原来这张三角形纸片的形状是( )三角形的。
A.锐角 B.直角 C.钝角 D.等腰
11.在三角形ABC中,∠A﹣∠C=∠B,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形
12.一个三角形中的最小角是46°,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
13.下面( )不是按角分类。
A.直角三角形 B.钝角三角形
C.等边三角形 D.锐角三角形
14.一个三角形中有两个内角的和等于90°,这个三角形( )是直角三角形。
A.一定 B.可能 C.不一定 D.不可能
15.分一分,分成两类。
第一类:
第二类:
16.如图是一块三角形玻璃打碎后留下的碎片,它原来是一个 三角形。
17.如果一个三角形中有两个锐角的度数之和大于90°,那么按角分,这个三角形是 三角形。
18.在一个三角形中三个内角的关系是:∠1+∠2=∠3,那么可以判断这是一个 角三角形。
19.如图,三角形中的三个内角都相等,则∠1= °;按角分,这是一个 三角形;按边分,这个是一个 三角形。
20.只有2个锐角的三角形可能是钝角三角形。
21.当三角形中两个内角的和小于第三个角时,这个三角形一定是钝角三角形。
22.一个三角形,三个内角的度数比是3:7:10,三个内角各是多少度?这是一个什么三角形?
23.一个四边形如何变成三角形呢?
小明想到了一种方法,连接对点(如图所示),此时分成两个三角形。
(1)其中一个为等边三角形,一边长为2cm,请问其它两条边长和三个角分别为多少?
(2)另一个三角形中,已知最大角的度数是最小角的3倍,另外一个角的度数是最小角的2倍,你知道这个三角形每个角的度数吗?它是什么三角形?
24.在方格纸上分别画一个钝角三角形、等腰直角三角形和梯形。
25.认一认、画一画:画出每个图形中所指定的底边上高。
26.以线段AB为底,画一个高为3厘米的直角三角形。(图中每个小方格的边长是1cm)
三.三角形的内角和(共22小题)
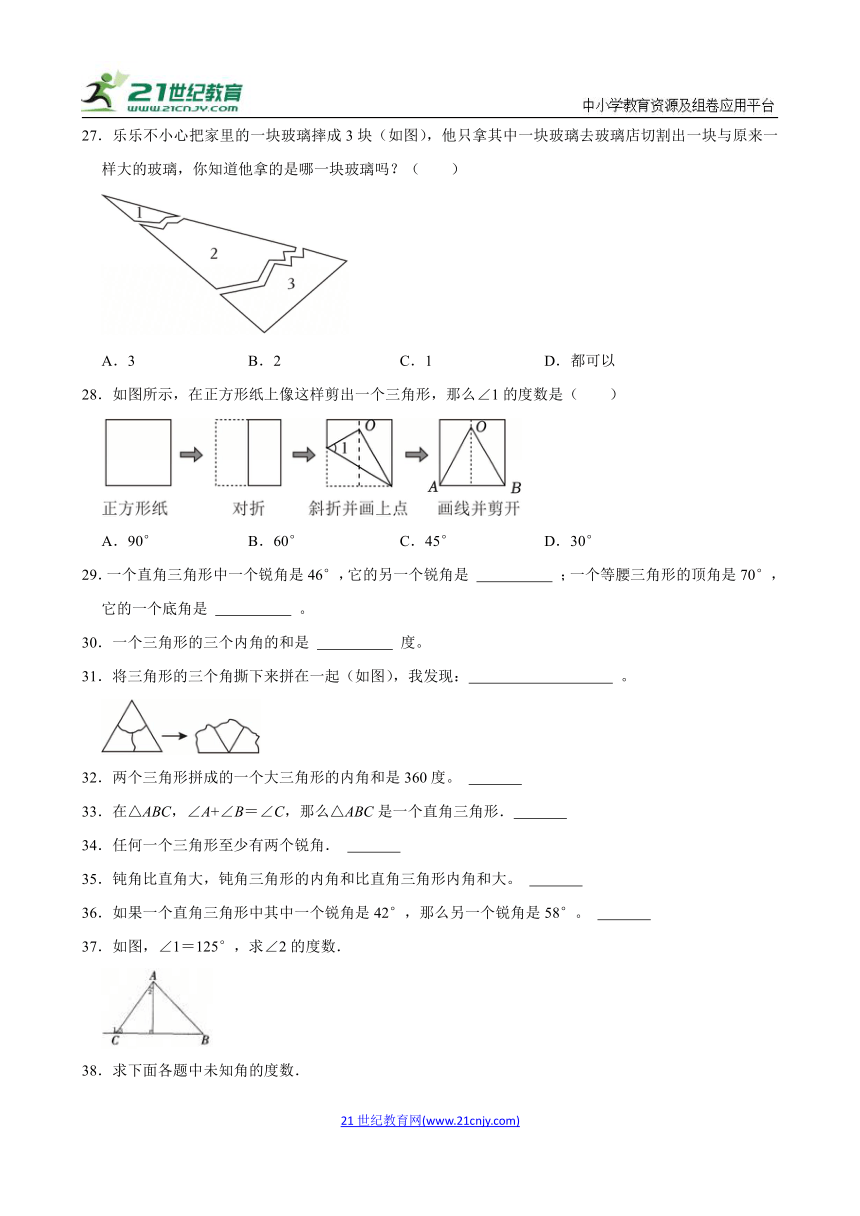
27.乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
28.如图所示,在正方形纸上像这样剪出一个三角形,那么∠1的度数是( )
A.90° B.60° C.45° D.30°
29.一个直角三角形中一个锐角是46°,它的另一个锐角是 ;一个等腰三角形的顶角是70°,它的一个底角是 。
30.一个三角形的三个内角的和是 度。
31.将三角形的三个角撕下来拼在一起(如图),我发现: 。
32.两个三角形拼成的一个大三角形的内角和是360度。
33.在△ABC,∠A+∠B=∠C,那么△ABC是一个直角三角形.
34.任何一个三角形至少有两个锐角.
35.钝角比直角大,钝角三角形的内角和比直角三角形内角和大。
36.如果一个直角三角形中其中一个锐角是42°,那么另一个锐角是58°。
37.如图,∠1=125°,求∠2的度数.
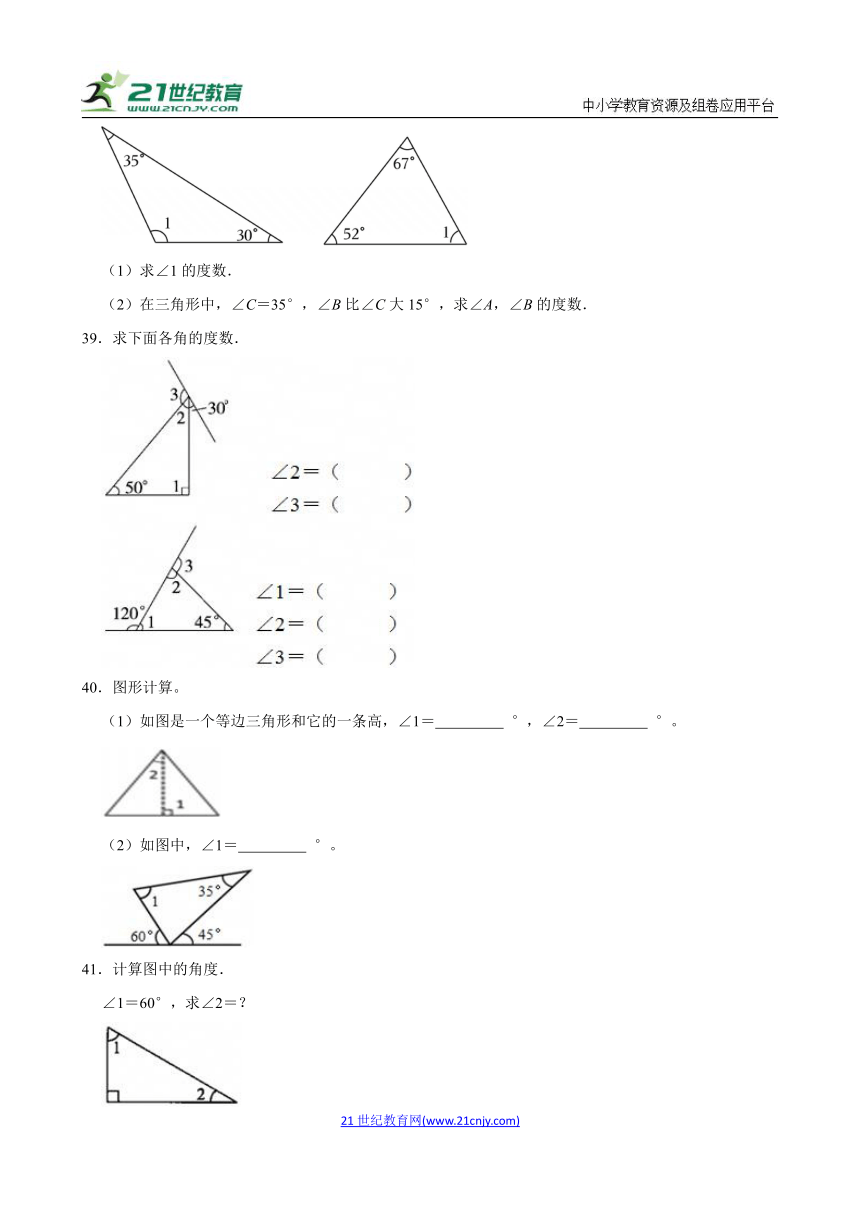
38.求下面各题中未知角的度数.
(1)求∠1的度数.
(2)在三角形中,∠C=35°,∠B比∠C大15°,求∠A,∠B的度数.
39.求下面各角的度数.
40.图形计算。
(1)如图是一个等边三角形和它的一条高,∠1= °,∠2= °。
(2)如图中,∠1= °。
41.计算图中的角度.
∠1=60°,求∠2=?
42.如图,∠1=145°,∠2=40°,求∠3,∠4的度数.
43.算一算,填一填.
∠B= .
44.公园的花坛分别种了红、黄、白、蓝四种花(如图)。
45.等腰三角形的一个角是100度,求另两个角是多少度?
46.张云同学要制作一个等腰三角形的学具,这个等腰三角形的一个内角必须是68°,请你想一想,另外两个内角分别是多少度?(用两种思路分别解答)
47.一个直角三角形,其中一个锐角是30°,另一个锐角是多少度?
48.劳动课上,第三小组的同学一起制作了一个等腰三角形形状的风筝,它的顶角是110°,另外的两个角是多少度呢?
四.三角形的稳定性(共1小题)
49.自行车的车身结构做成了三角形的形状,是利用了 。
五.三角形边的关系(共11小题)
50.下面的线段中,能围成三角形的是( )
A.3cm,4cm,7cm B.2cm,4cm,4cm
C.5cm,6cm,12cm D.8cm,2cm,6cm
51.下面能组成三角形的一组线段长度是( )
A.1cm,4cm,3cm B.5cm,7cm,11cm
C.2cm,3cm,6cm
52.一个三角形的两边分别长5厘米、8厘米,第三边可能是( )
A.3 B.14 C.10 D.13
53.从学校到少年宫有三条路线,最近的是 号线路,
用以前学过的知识解释是 ,
用三角形的知识解释是 。
54.用长度分别为11cm,6cm和 cm的小棒一定能围成一个三角形。
55.用三根小棒围成一个三角形,其中两根小棒的长度分别为6厘米和15厘米,则第三根小棒的长度最长是 厘米。(填整厘米数)
56.淘气用3dm和7dm的两种木条做一个等腰三角形画框,它的周长是13dm或17dm。
57.用2分米、3分米、8分米长的三根小棒恰好能围成一个三角形。
58.淘气的姐姐身高1.72米,体重52千克,腿长约95厘米。淘气说他姐姐走一步能迈2米,对于这种说法,你相信吗?请从数学角度解释理由。
59.有4根小棒,第一根长2.5厘米,第二根长3.05厘米,第三根长4.16厘米,第四根长10.2厘米。
请选择3根小棒组成一个三角形,并计算这个三角形的周长。
60.一个三角形的两条边分别是7厘米和13厘米,那么第三条边的长最短是多少厘米?最长是多少厘米?(取整厘米数)
5 三角形
参考答案与试题解析
一.三角形的特性(共7小题)
1.将一根20厘米的细铁丝,剪成3段,拼成一个三角形,以下哪种剪法可以( )
A.8厘米、7厘米、5厘米 B.13厘米、6厘米、1厘米
C.4厘米、9厘米、4厘米 D.10厘米、3厘米、7厘米
【答案】A
【分析】根据三角形的特性:任意两边之和大于第三边,三角形的任意两边的差一定小于第三边;进行依次分析即可.
【解答】解:A、7+5>8,所以本组小棒能围成三角形;
B、6+1<13,所以本组小棒不能围成三角形;
C、4+4<9,所以本组小棒不能围成三角形;
D、3+7=10,所以本组小棒不能围成三角形;
故选:A.
【点评】此题是考查三角形的特性,应灵活掌握和运用.
2.下面选项中的三条线段能围成(每相邻两条线段的端点相连)三角形的是( )
A. B.
C. D.
【答案】A
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:A.两边之和大于第三边,能围成三角形;
B.两边之和小于第三边,不能围成三角形;
C.两边之和小于第三边,不能围成三角形;
D.两边之和等于第三边,不能围成三角形。
故选:A。
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可。
3.一个三角形有 3 条边,一个角有 2 条边。
【答案】3;2。
【分析】不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫作三角形。这三条线段叫作三角形的边;
具有公共端点的两条射线组成的图形叫作角。这个公共端点叫作角的顶点,这两条射线叫作角的两条边。据此解答。
【解答】解:一个三角形有3条边,一个角有2条边。
故答案为:3;2。
【点评】本题考查了三角形和角的认识。
4.四月初,乐乐和妈妈一起种了一些黄瓜苗。一天,妈妈用竹竿搭起了很多三角形的黄瓜架,她这样做的原因是三角形具有 稳定性 。
【答案】稳定性。
【分析】根据三角形具有稳定性解答。
【解答】解:四月初,乐乐和妈妈一起种了一些黄瓜苗。一天,妈妈用竹竿搭起了很多三角形的黄瓜架,她这样做的原因是三角形具有稳定性。
故答案为:稳定性。
【点评】本题考查三角形稳定性的实际应用;三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得。
5.在中有3个三角形。 √
【答案】√
【分析】三角形有3条边,3个角,据此数出三角形的数量即可解答。
【解答】解:在中有3个三角形。说法正确。
故答案为:√。
【点评】本题考查了三角形的认识。
6.把一根长10厘米的吸管剪成3段(每段都是整厘米),围成一个三角形。能围成多少个不同的三角形,它们的每条边长度分别是多少厘米?
【答案】2;4厘米、4厘米、2厘米;4厘米、3厘米、3厘米。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:10÷2=5(厘米)
所以每边都要小于5厘米;
4+4+2=10
4+3+3=10
答:能围成2个不同的三角形,它们的每条边长度分别是4厘米、4厘米、2厘米;4厘米、3厘米、3厘米。
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可。
7.有5根小棒,长度分别是3厘米、3厘米、3厘米、4厘米、6厘米,可以摆成几种不同的三角形?请你列举出来.
【答案】见试题解答内容
【分析】根据三角形边的特征,在三角形中任意两边之和大于第三边,由此解答.
【解答】解:根据分析知,共有以下情况,
①3厘米,3厘米,3厘米;
②3厘米,3厘米,4厘米;
③3厘米,4厘米,6厘米;
答:一共可以拼成3个不同的三角形.
【点评】此题主要根据三角形的任意两边之和大于第三边解决问题.
二.三角形的分类(共19小题)
8.一个三角形最大的内角是120°,这个三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形
【答案】A
【分析】依据钝角的意义,即大于90°,小于180°的角叫做钝角,以及三角形的分类方法,即可进行选择.
【解答】解:因为120°的角是钝角,
且有一个角是钝角的三角形是钝角三角形;
故选:A.
【点评】此题主要考查钝角的意义,以及三角形的分类方法.
9.一个等腰三角形的一个底角与顶角的度数相等,这个三角形是( )三角形。
A.直角 B.钝角 C.等边
【答案】C
【分析】在三角形中,内角和等于180°。在等腰三角形中,两底角相等。据此解答。
【解答】解:在等腰三角形中,两底角相等。而这个底角刚好与顶角的度数相等,所以三个内角都相等,它们的度数是:180°÷3=60°。所以这个三角形是等边三角形。
故选:C。
【点评】解答此题的关键是:先通过计算出三个角的度数,然后根据三角形的角分类,进行判断即可。
10.如图所示,一张三角形的纸片被撕去了一个角,原来这张三角形纸片的形状是( )三角形的。
A.锐角 B.直角 C.钝角 D.等腰
【答案】C
【分析】根据三角形内角和为180°以及图中的两个内角度数,即可求出撕去角的度数,再根据三角形的分类方法即可判断。
【解答】解:180°﹣110°﹣45°=25°
答:原来这张三角形纸片的形状是钝角三角形的。
故选:C。
【点评】此题考查了三角形的内角和定理:三角形的内角和等于180°,同时考查了三角形的按角分类知识,结合题意分析解答即可。
11.在三角形ABC中,∠A﹣∠C=∠B,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形
【答案】B
【分析】三角形ABC的三个内角和是180°,又因为∠A﹣∠C=∠B;所以∠A=∠B+∠C,所以∠A=180°÷2=90°,进一步判断三角形ABC是直角三角形。
【解答】解:因为∠A+∠B+∠C=180°,∠A﹣∠C=∠B;所以∠A=∠B+∠C,即∠A=180°÷2=90°,三角形ABC的三个角中,有一个是直角,是直角三角形。
故选:B。
【点评】此题考查三角形内角和为180°和三角形的分类(按角分)。
12.一个三角形中的最小角是46°,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
【答案】B
【分析】三角形的内角和是180°,因为三角形中最小的角是46°,假设第二小的角也是46°,所以最大的角最大为:180°﹣46°﹣46°=88°;根据锐角三角形的含义:三个角都是锐角的三角形,是锐角三角形;进而判断即可。
【解答】解:因为三角形中最小的角是46°,假设第二小的角也是46°,所以最大的角最大为:
180°﹣46°﹣46°
=134°﹣46°
=88°
由于三角形的三个角都是锐角,所以是锐角三角形。
故选:B。
【点评】解答此题的关键:先进行假设,进而根据三角形的内角和是180°,求出最大的角的度数,进而根据三角形的分类进行解答。
13.下面( )不是按角分类。
A.直角三角形 B.钝角三角形
C.等边三角形 D.锐角三角形
【答案】C
【分析】最大角是直角的三角形是直角三角形,最大角是钝角的三角形是钝角三角形,最大角是锐角的三角形是锐角三角形。三条边都相等的三角形是等边三角形,两条边相等的三角形是等腰三角形。
【解答】解:直角三角形、钝角三角形、锐角三角形都是按角分,等边三角形是按边分。
故选:C。
【点评】本题考查了角的分类特征。
14.一个三角形中有两个内角的和等于90°,这个三角形( )是直角三角形。
A.一定 B.可能 C.不一定 D.不可能
【答案】A
【分析】三角形的3个内角的和是180度,利用180度减去两个内角的和等于90°求出第三个角,再根据锐角三角形:最大角小于90°;直角三角形:最大角等于90°;钝角三角形:最大角大于90°判断。
【解答】解:180°﹣90°=90°
90°是直角,因此这个三角形一定是直角三角形。
故选:A。
【点评】本题考查了三角形按角分类的方法及三角形内角和的应用。
15.分一分,分成两类。
第一类: ①④
第二类: ②③⑤⑥
【答案】①④;②③⑤⑥。
【分析】根据图示可以分成第一类:三角形内有个小三角形,第二类:三角形内有个小圆。
【解答】解:第一类:①④;
第二类:②③⑤⑥。
故答案为:①④;②③⑤⑥。
【点评】本题考查了物体的分类。
16.如图是一块三角形玻璃打碎后留下的碎片,它原来是一个 钝角 三角形。
【答案】钝角。
【分析】因为三角形的内角度数和是180°,根据图中的两个内角度数可求打碎的一个角的度数,再根据三角形的分类即可作出判断。
【解答】解:因为180°﹣30°﹣40°=110°;所以这是一个钝角三角形。
故答案为:钝角。
【点评】本题主要考查了三角形的内角和定理及三角形的分类,解题的关键是求出玻璃碎处角的度数。
17.如果一个三角形中有两个锐角的度数之和大于90°,那么按角分,这个三角形是 锐角 三角形。
【答案】锐角。
【分析】三角形按角分分为锐角三角形、直角三角形、钝角三角形。三个角都是锐角的三角形是锐角三角形,有一个直角的三角形是直角三角形,有一个钝角的三角形是钝角三角形。
【解答】解:三角形内角和是 180°,180° 减去一个大于 90° 的角,差一定是一个小于 90°的角,大于0°小于90°的角是锐角,三个角都是锐角的三角形是锐角三角形,所以这个三角形是一个锐角三角形。
故答案为:锐角。
【点评】解答此题用到的知识点:(1)三角形的内角和是180度;(2)三角形的分类。
18.在一个三角形中三个内角的关系是:∠1+∠2=∠3,那么可以判断这是一个 直 角三角形。
【答案】直。
【分析】根据角对三角形分类的方法:三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形,结合三角形的内角和是180°,在一个三角形中三个内角的关系是:∠1+∠2=∠3,可知∠3=180°÷2=90°,所以这是一个直角三角形。据此解答即可。
【解答】解:因为∠1+∠2=∠3,所以∠3=180°÷2=90°。
答:这是一个直角三角形。
故答案为:直。
【点评】本题考查了三角形的分类知识,结合三角形的内角和知识解答即可。
19.如图,三角形中的三个内角都相等,则∠1= 60 °;按角分,这是一个 锐角 三角形;按边分,这个是一个 等边 三角形。
【答案】60,锐角,等边。
【分析】这个三角形中,三个内角都相等且它们的和是180°。可以用除法算出一个角的度数;三个角都是锐角的三角形是锐角三角形;三条边都相等的三角形是等边三角形。据此解答。
【解答】解:180°÷3=60°,即∠1=60°。
答:这个三角形的∠1=60°;按角分,这是一个锐角三角形;按边分,这个是一个等边三角形。
故答案为:60,锐角,等边。
【点评】本题考查了三角形的内角和以及分类知识,结合题意分析解答即可。
20.只有2个锐角的三角形可能是钝角三角形。 √
【答案】√
【分析】不管是什么三角形,最少有2个锐角,据此解答。
【解答】解:有两个角是锐角的三角形可能是钝角三角形,原题说法正确。
故答案为:√。
【点评】本题考查了三角形的按角分类的方法。
21.当三角形中两个内角的和小于第三个角时,这个三角形一定是钝角三角形。 √
【答案】√
【分析】根据三角形的内角和等于180度,如果其中两个内角之和小于第三个内角,说明第三个内角大于90度,根据钝角三角形的含义:有一个角是钝角的三角形是钝角三角形,可知:这个三角形是钝角三角形。
【解答】解:三角形的三角内角和等于180度,如果其中两个内角之和小于第三个内角,说明第三个内角大于90度,因此这个三角形是钝角三角形。
故答案为:√。
【点评】解答此题用到的知识点:(1)三角形的内角和是180度;(2)钝角三角形的含义。
22.一个三角形,三个内角的度数比是3:7:10,三个内角各是多少度?这是一个什么三角形?
【答案】27°,63°,90°,直角三角形。
【分析】根据三角形的内角和是180°,三角形的内角和永远是180度,把180度的角按3:7:10进行比例分配即可,根据最大角的度数判断三角形的种类即可。
【解答】解:180°27°
180°63°
180°90°
最大的角90°是一个直角,因此这是一个直角三角形。
答:三个内角各是27°,63°,90°,这是一个直角三角形。
【点评】此题考查了三角形的内角和定理以及三角形的分类,三角形按角分类有锐角三角形、直角三角形、钝角三角形。
23.一个四边形如何变成三角形呢?
小明想到了一种方法,连接对点(如图所示),此时分成两个三角形。
(1)其中一个为等边三角形,一边长为2cm,请问其它两条边长和三个角分别为多少?
(2)另一个三角形中,已知最大角的度数是最小角的3倍,另外一个角的度数是最小角的2倍,你知道这个三角形每个角的度数吗?它是什么三角形?
【答案】2厘米,2厘米,60°,60°,60°;30°,60°,90°,直角三角形。
【分析】(1)等边三角形的三条边相等,三个角相等,都是60度,据此解答;
(2)假设最小的角是1,那么最大的角就是3,较大的角就是2,由三角形内角和是180°÷(3+2+1)求出最小的角,即可求出另外两个角的度数,根据最大的角的度数判断是什么三角形即可。
【解答】解:(1)等边三角形三条边都是2厘米,三个角都是60°;
(2)180°÷(3+2+1)
=180°÷6
=30°
30°×2=60°
30°×3=90°
由最大的角是90度是直角可以判断这个三角形是直角三角形。
答:这个三角形的三个角的度数分别是30°,60°,90°,这是一个直角三角形。
故答案为:2厘米,2厘米,60°,60°,60°;30°,60°,90°,直角三角形。
【点评】本题主要考查了等边三角形的特点及三角形的内角和以及直角三角形的特征。
24.在方格纸上分别画一个钝角三角形、等腰直角三角形和梯形。
【答案】(答案不唯一)
【分析】根据梯形、等腰直角三角形、钝角三角形的特征,梯形只有一组对边平行,平行的一组对边叫做梯形的上底和下底,不平行的两条边叫做梯形的腰;等腰直角三角形的特征是有一个角是直角且两条直角边相等;有一个角是钝角的三角形叫钝角三角形,据此解答即可。
【解答】解:
(答案不唯一)
【点评】此题考查的目的是理解掌握梯形、等腰直角三角形、钝角三角形的特征,以及它们的画法。
25.认一认、画一画:画出每个图形中所指定的底边上高。
【答案】
【分析】从图中标出底边所对应的边上取一点,(三角形取顶点)利用直角三角板的一条直角边与标有底边的一边对齐,沿另一条直角边过取的点作底边的垂线即可。
【解答】解:如图:
【点评】本题考查了三角形、平行四边形及梯形高的画法。
26.以线段AB为底,画一个高为3厘米的直角三角形。(图中每个小方格的边长是1cm)
【答案】
【分析】根据直角三角形的特征和画法,直角三角形有一个角是直角,让其中的一条直角边为3厘米即可。
【解答】解:如图:
【点评】本题考查了直角三角形的画法知识,结合题意分析解答即可。
三.三角形的内角和(共22小题)
27.乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
【答案】A
【分析】三角形的内角和是180°,已知三角形的一条边的长度和这条边上的两个角的度数即可求出另一个角的度数与另外两条边的长度。据此解答。
【解答】解:由分析得:乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,我知道他拿的是第3块玻璃。
故选:A。
【点评】此题考查的目的是理解掌握三角形的特征及应用,三角形内角和及应用。
28.如图所示,在正方形纸上像这样剪出一个三角形,那么∠1的度数是( )
A.90° B.60° C.45° D.30°
【答案】B
【分析】根据等边三角形的特点可知,等边三角形的各个内角都是60°。
【解答】解:如上图所示,在正方形纸上像这样剪出一个三角形,那么∠1的度数是60°。
故选:B。
【点评】本题主要考查图形的折叠,关键是知道等边三角形是如何得出的。
29.一个直角三角形中一个锐角是46°,它的另一个锐角是 44° ;一个等腰三角形的顶角是70°,它的一个底角是 55° 。
【答案】44°;55°。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:180°﹣90°﹣46°=44°
(180°﹣70°)÷2
=110°÷2
=55°
答:一个直角三角形中一个锐角是46°,它的另一个锐角是44°;一个等腰三角形的顶角是70°,它的一个底角是55°。
故答案为:44°;55°。
【点评】熟练掌握三角形的内角和知识和等腰三角形的性质,是解答此题的关键。
30.一个三角形的三个内角的和是 180 度。
【答案】180。
【分析】根据数学常识可知一个三角形的三个内角的和是180°。据此解答即可。
【解答】解:一个三角形的三个内角的和是180度。
故答案为:180。
【点评】本题考查三角形内角和的认识。
31.将三角形的三个角撕下来拼在一起(如图),我发现: 三角形的内角和是180° 。
【答案】三角形的内角和是180°。
【分析】根据平角的意义,平角是180°,将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形的内角和是180°。据此解答。
【解答】解:将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形三个内角的和是180°。
故答案为:三角形的内角和是180°。
【点评】此题考查的目的是理解掌握三角形内角和的推算方法及应用,平角的意义及应用。
32.两个三角形拼成的一个大三角形的内角和是360度。 ×
【答案】×。
【分析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答。
【解答】解:两个三角形拼成的一个大三角形的内角和是180°,故原题说法错误。
故答案为:×。
【点评】解答此题的主要依据是:三角形的内角和是180度。
33.在△ABC,∠A+∠B=∠C,那么△ABC是一个直角三角形. √
【答案】见试题解答内容
【分析】根据在△ABC中,∠A+∠B=∠C,∠A+∠B+∠C=180°可求出∠C的度数,进而得出结论.
【解答】解:因为在△ABC中,∠A+∠B=∠C,∠A+∠B+∠C=180°,
所以2∠C=180°,解得∠C=90°,、
所以△ABC是直角三角形.
故答案为:√.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
34.任何一个三角形至少有两个锐角. √
【答案】√
【分析】根据三角形的内角和可知,一个三角形中若有两个直角或钝角,就超过180°,由此可以做出判断.
【解答】解:因为三角形的内角和是180°,一个三角形中若有两个直角或钝角,就超过180°,就够不成一个三角形了,
所以一个三角形,至少应有两个锐角是正确的.
故答案为:√.
【点评】此题主要考查三角形的分类以及三角形的内角和.
35.钝角比直角大,钝角三角形的内角和比直角三角形内角和大。 ×
【答案】×
【分析】根据三角形的内角和等于180°,解答此题即可。
【解答】解:钝角比直角大,钝角三角形的内角和与直角三角形内角和一样大。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握三角形的内角和定理,是解答此题的关键。
36.如果一个直角三角形中其中一个锐角是42°,那么另一个锐角是58°。 ×
【答案】×
【分析】根据三角形的内角和是180°,用三角形的内角和180度减去两个已知角的度数,就是第三个角的度数,据此解答。
【解答】解:180﹣90﹣42
=90﹣42
=48(度)
答:另一个锐角是48°。
所以,如果一个直角三角形中其中一个锐角是42°,那么另一个锐角是58°,错误。
故答案为:×。
【点评】本题考查了三角形内角和定理,关键是掌握三角形内角和为180度。
37.如图,∠1=125°,求∠2的度数.
【答案】见试题解答内容
【分析】
∠1与∠ACB组成的角为平角,即∠1+∠ACD=180°,∠1的度数已知,据此即可求出∠ACD的度数.在三角形ACD中,∠ACD的度数前面已求出,∠ADC为直角(90°),根据三角形的内角和定理,三角形三个内角之和为180°即可求出∠2的度数.
【解答】解:如图:
因为∠1+∠ACD=180°,∠1=125°
所以∠ACD=180°﹣125°=55°
因为∠2+ACD+∠ADC=180°,ACD=55°,∠ADC=90°
所以∠2=180°﹣90°﹣55°=35°
答:∠2是35°.
【点评】解答此题应用的知识点有平角的意义、直角的意义、三角形内角和定理.
38.求下面各题中未知角的度数.
(1)求∠1的度数.
(2)在三角形中,∠C=35°,∠B比∠C大15°,求∠A,∠B的度数.
【答案】见试题解答内容
【分析】(1)根据三角形的内角和是180°,用180°减去两个已知角的度数就等于未知角的度数.
(2)根据三角形的内角和是180°,在三角形中,∠C=35°,∠B比∠C大15°,∠B=35°+15°=50°,所以∠A=180°﹣35°﹣50°=95°
【解答】解:(1)180°﹣30°﹣35°
=150°﹣35°
=115°
答:∠1的度数是115度.
180°﹣67°﹣52°
=113°﹣52°
=61°
答:∠1的度数是61度.
(2)∠B=35°+15°=50°
∠A=180°﹣35°﹣50°=95°
答:∠A是95度,∠B的度数是50度.
【点评】本题考查的是三角形内角和是180度的运用,用180度减去已知角的度数就等于未知角的度数.
39.求下面各角的度数.
【答案】见试题解答内容
【分析】(1)根据三角形内角和定理:三角形内角和是180°,根据已知两个角的度数,求∠2:180°﹣50°﹣90°=40°;根据平角的意义,求∠3:180°﹣30°﹣40°=110°.
(2)根据平角的意义,先求∠1:180°﹣120°=60°;利用三角形内角和定理,求∠2:180°﹣60°﹣45°=75°;∠3=180°﹣75°=105°.
【解答】解:(1)∠2=180°﹣50°﹣90°=40°
∠3=180°﹣30°﹣40°=110°
(2)∠1=180°﹣120°=60°
∠2=180°﹣60°﹣45°=75°
∠3=180°﹣75°=105°
如图:
【点评】本题考查了三角形内角和定理,关键是掌握三角形内角和为180度.
40.图形计算。
(1)如图是一个等边三角形和它的一条高,∠1= 90 °,∠2= 30 °。
(2)如图中,∠1= 70 °。
【答案】(1)90;30;
(2)70。
【分析】根据三角形的内角和等于180°和等边三角形的性质,解答此题即可。
【解答】解:(1)∠2=60÷2=30(度)
∠1=180﹣30﹣60=90(度)
(2)∠1=180﹣(180﹣60﹣45)﹣35
=180﹣75﹣35
=70(度)
故答案为:90;30;70。
【点评】熟练掌握三角形的内角和知识和等边三角形的性质,是解答此题的关键。
41.计算图中的角度.
∠1=60°,求∠2=?
【答案】见试题解答内容
【分析】由图知这是一个直角三角形,∠2的度数等于90度减去∠1的度数,据此解答.
【解答】解:∠2=90°﹣∠1
=90°﹣60°
=30°
答:∠2等于30度.
【点评】本题主要考查了三角形的内角和等于180度和直角三角形的性质等相关知识.
42.如图,∠1=145°,∠2=40°,求∠3,∠4的度数.
【答案】见试题解答内容
【分析】用180°减去∠1的度数等于∠3的度数,再用180°减去∠2和∠3即可求出∠4的度数,据此解答.
【解答】解:∠3=180°﹣∠1
=180°﹣145°
=35°
∠4=180°﹣∠2﹣∠3
=180°﹣40°﹣35°
=105°
答:∠3的度数是35°,∠4的度数是105°.
【点评】解答本题的关键是掌握三角形的内角和等于180°,平角等于180°.
43.算一算,填一填.
∠B= 52° .
【答案】52°.
【分析】直角三角形中,有一个角是直角90°,已知∠C=38°,则∠B=180°﹣90°﹣38°,据此解答.
【解答】解:180°﹣90°﹣38°
=90°﹣38°
=52°
故答案为:52°.
【点评】解答本题的关键是熟练掌握三角形的内角和等于180°.
44.公园的花坛分别种了红、黄、白、蓝四种花(如图)。
【答案】47°。
【分析】运用平角等于180°求出∠2;再运用三角形的内角和是180°求出∠1。
【解答】解:
∠2=180°﹣110°=70°
∠1=180°﹣63°﹣70°=47°
答:∠1是47°。
【点评】本题考查了平角及内角和的意义及应用。
45.等腰三角形的一个角是100度,求另两个角是多少度?
【答案】40°、40°。
【分析】一个角是100度,属于钝角,一个三角形内只能有一个,因此它是顶角。根据三角形的内角和是180°以及等边对等角,分别减去其余两个内角即可求出第三个角的度数。
【解答】解:(180°﹣100°)÷2
=80°÷2
=40°
答:另两个角都是40°。
【点评】本题考查了三角形内角和定理,属于基础题,关键是掌握三角形内角和为180度。
46.张云同学要制作一个等腰三角形的学具,这个等腰三角形的一个内角必须是68°,请你想一想,另外两个内角分别是多少度?(用两种思路分别解答)
【答案】56°、56°或68°、44°。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:如果顶角是68°。
(180°﹣68°)÷2
=112°÷2
=56°
如果底角是68°。
180°﹣68°×2
=180°﹣136°
=44°
答:另外两个内角分别是56°、56°或68°、44°。
【点评】熟练掌握三角形的内角和知识和等腰三角形的性质,是解答此题的关键。
47.一个直角三角形,其中一个锐角是30°,另一个锐角是多少度?
【答案】60°。
【分析】因为三角形的内角和是180度,其中直角三角形中有一个角是直角,给出的直角三角形中一个锐角是30度,用内角和分别减去90度和30度,即可求出另一个锐角的度数。
【解答】解:180°﹣90°﹣30°=60°
答:另一个锐角是60°。
【点评】正确利用直角三角形的性质,明确三角形的内角和是180度,是解此题的关键。
48.劳动课上,第三小组的同学一起制作了一个等腰三角形形状的风筝,它的顶角是110°,另外的两个角是多少度呢?
【答案】35度。
【分析】根据等腰三角形的两个底角相等,解答此题即可。
【解答】解:(180°﹣110°)÷2
=70°÷2
=35°
答:另外的两个角是35度。
【点评】熟练掌握等腰三角形的性质,是解答此题的关键。
四.三角形的稳定性(共1小题)
49.自行车的车身结构做成了三角形的形状,是利用了 三角形的稳定性 。
【答案】见试题解答内容
【分析】三角形具有稳定性,生活中很多物品的设计都利用这一特性设计的。
【解答】解:自行车的车身结构做成了三角形的形状,是利用了三角形的稳定性。
故答案为:三角形的稳定性。
【点评】本题考查了三角形的稳定性的应用。
五.三角形边的关系(共11小题)
50.下面的线段中,能围成三角形的是( )
A.3cm,4cm,7cm B.2cm,4cm,4cm
C.5cm,6cm,12cm D.8cm,2cm,6cm
【答案】B
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:A.3+4=7,不能围成三角形;
B.2+4>4,可以围成三角形;
C.5+6<12,不能围成三角形;
D.2+6=8,不能围成三角形。
故选:B。
【点评】本题考查了三角形的三边关系的应用。
51.下面能组成三角形的一组线段长度是( )
A.1cm,4cm,3cm B.5cm,7cm,11cm
C.2cm,3cm,6cm
【答案】B
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:A.1+3=4,所以1cm,4cm,3cm不能围成三角形;
B.5+7>11,11﹣7<5,所以5cm,7cm,11cm 能围成三角形;
C.2+3<6,所以2cm,3cm,6cm 不能围成三角形。
故选:B。
【点评】本题考查了三角形的三边关系的应用,结合题意分析解答即可。
52.一个三角形的两边分别长5厘米、8厘米,第三边可能是( )
A.3 B.14 C.10 D.13
【答案】C
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:8﹣5<第三边<8+5,
所以:3<第三边<13,即另一条边的长应在3~13厘米之间(不包括3厘米和13厘米);
另一条也是整数,可能是4,5,6,7,8,9,10,11,12厘米。
故选:C。
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可。
53.从学校到少年宫有三条路线,最近的是 ② 号线路,
用以前学过的知识解释是 两点之间,线段最短 ,
用三角形的知识解释是 两边之和大于第三边 。
【答案】②,两点之间,线段最短,两边之和大于第三边。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:通过观察图示发现从学校到少年宫有三条路线,最近的是②号线路,用以前学过的知识解释是:两点之间,线段最短,用三角形的知识解释是:两边之和大于第三边。
故答案为:②,两点之间,线段最短,两边之和大于第三边。
【点评】本题考查了三角形的三边关系的应用。
54.用长度分别为11cm,6cm和 6 cm的小棒一定能围成一个三角形。
【答案】6。(答案不唯一)
【分析】任意三角形的两边之和都大于第三边,两边之差必须小于第三边,据此计算解答。
【解答】解:6+6>11,因此用长度分别为11cm,6cm和6cm的小棒一定能围成一个三角形。
故答案为:6。(答案不唯一)
【点评】本题考查了三角形的三边关系。
55.用三根小棒围成一个三角形,其中两根小棒的长度分别为6厘米和15厘米,则第三根小棒的长度最长是 20 厘米。(填整厘米数)
【答案】20。
【分析】根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。用三根小棒围成一个三角形,已知三角形其中两根小棒的长度分别为6厘米和15厘米,则第三根小棒的长度最长小于两边之和,大于两边之差,据此解答即可。
【解答】解:6+15=21(厘米)
21﹣1=20(厘米)
答:第三根小棒的长度最长是20厘米。
故答案为:20。
【点评】此题考查三角形边的关系。任意两边之和大于第三边,任意两边之差小于第三边。
56.淘气用3dm和7dm的两种木条做一个等腰三角形画框,它的周长是13dm或17dm。 ×
【答案】×。
【分析】根据三角形的三边关系:两边之和大于第三边,可知:3+3=6dm;6<7;所以3dm的木条不能作腰,所以围成的等腰三角形的腰是7dm,底是3dm,由此即可求出这个三角形的周长。
【解答】解:根据分析可知,淘气用3dm和7dm的两种木条做一个等腰三角形画框,三边长是7dm,7dm,3dm,所以它的周长是7+7+3=14+3=17dm,本题说法错误。
故答案为:×。
【点评】此题考查了三角形的周长计算方法以及等腰三角形的两条腰相等的性质,关键是根据三角形的三边关系确定这个等腰三角形的腰与底的长度。
57.用2分米、3分米、8分米长的三根小棒恰好能围成一个三角形。 ×
【答案】×
【分析】根据三角形中三边的关系进行分析即可判断正误。
【解答】解:三角形中,任意两边之和大于第三边,任意两边之差小于第三边,
2+3=5(分米)
5<8,所以用2分米、3分米、8分米长的三根小棒不能围成三角形,即原题说法错误。
故答案为:×。
【点评】此题考查三角形的三边关系。三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
58.淘气的姐姐身高1.72米,体重52千克,腿长约95厘米。淘气说他姐姐走一步能迈2米,对于这种说法,你相信吗?请从数学角度解释理由。
【答案】不可信。因为95厘米+95厘米=190厘米,2米=200厘米,190厘米<200厘米,不符合三角形的任意两边之和大于第三边,所以淘气说他姐姐走一步能迈2米这种说法是不可信的。
【分析】依据三角形的任意两边之和大于第三边,腿长约95厘米,走一步两腿和地面形成一个三角形,两腿的长度和要大于一步的距离,据此解答即可。
【解答】解:95厘米+95厘米=190厘米,2米=200厘米,190厘米<200厘米,不符合三角形的任意两边之和大于第三边,所以淘气说他姐姐走一步能迈2米这种说法是不可信的。
【点评】此题主要考查了三角形的三条边的关系,结合题意分析解答即可。
59.有4根小棒,第一根长2.5厘米,第二根长3.05厘米,第三根长4.16厘米,第四根长10.2厘米。
请选择3根小棒组成一个三角形,并计算这个三角形的周长。
【答案】9.71厘米。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:2.5+3.05>4.16,所以第一根长2.5厘米,第二根长3.05厘米,第三根长4.16厘米可以围成三角形。
周长:2.5+3.05+4.16
=5.55+4.16
=9.71(厘米)
答:三角形的周长是9.71厘米。
【点评】本题考查了三角形的三边关系的应用。
60.一个三角形的两条边分别是7厘米和13厘米,那么第三条边的长最短是多少厘米?最长是多少厘米?(取整厘米数)
【答案】7厘米,19厘米。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:根据三角形的特性可知:(13﹣7)厘米<第三边<(13+7)厘米,
所以:6厘米<第三边<20厘米,
因为要求取整厘米数,
所以第三条边最长是19厘米,最短是7厘米。
答:第三条边最长是19厘米,最短是7厘米。
【点评】解答此题的关键是根据三角形的特性进行分析、解答。
21世纪教育网(www.21cnjy.com)
一.三角形的特性(共7小题)
1.将一根20厘米的细铁丝,剪成3段,拼成一个三角形,以下哪种剪法可以( )
A.8厘米、7厘米、5厘米 B.13厘米、6厘米、1厘米
C.4厘米、9厘米、4厘米 D.10厘米、3厘米、7厘米
2.下面选项中的三条线段能围成(每相邻两条线段的端点相连)三角形的是( )
A. B.
C. D.
3.一个三角形有 条边,一个角有 条边。
4.四月初,乐乐和妈妈一起种了一些黄瓜苗。一天,妈妈用竹竿搭起了很多三角形的黄瓜架,她这样做的原因是三角形具有 。
5.在中有3个三角形。
6.把一根长10厘米的吸管剪成3段(每段都是整厘米),围成一个三角形。能围成多少个不同的三角形,它们的每条边长度分别是多少厘米?
7.有5根小棒,长度分别是3厘米、3厘米、3厘米、4厘米、6厘米,可以摆成几种不同的三角形?请你列举出来.
二.三角形的分类(共19小题)
8.一个三角形最大的内角是120°,这个三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形
9.一个等腰三角形的一个底角与顶角的度数相等,这个三角形是( )三角形。
A.直角 B.钝角 C.等边
10.如图所示,一张三角形的纸片被撕去了一个角,原来这张三角形纸片的形状是( )三角形的。
A.锐角 B.直角 C.钝角 D.等腰
11.在三角形ABC中,∠A﹣∠C=∠B,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形
12.一个三角形中的最小角是46°,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
13.下面( )不是按角分类。
A.直角三角形 B.钝角三角形
C.等边三角形 D.锐角三角形
14.一个三角形中有两个内角的和等于90°,这个三角形( )是直角三角形。
A.一定 B.可能 C.不一定 D.不可能
15.分一分,分成两类。
第一类:
第二类:
16.如图是一块三角形玻璃打碎后留下的碎片,它原来是一个 三角形。
17.如果一个三角形中有两个锐角的度数之和大于90°,那么按角分,这个三角形是 三角形。
18.在一个三角形中三个内角的关系是:∠1+∠2=∠3,那么可以判断这是一个 角三角形。
19.如图,三角形中的三个内角都相等,则∠1= °;按角分,这是一个 三角形;按边分,这个是一个 三角形。
20.只有2个锐角的三角形可能是钝角三角形。
21.当三角形中两个内角的和小于第三个角时,这个三角形一定是钝角三角形。
22.一个三角形,三个内角的度数比是3:7:10,三个内角各是多少度?这是一个什么三角形?
23.一个四边形如何变成三角形呢?
小明想到了一种方法,连接对点(如图所示),此时分成两个三角形。
(1)其中一个为等边三角形,一边长为2cm,请问其它两条边长和三个角分别为多少?
(2)另一个三角形中,已知最大角的度数是最小角的3倍,另外一个角的度数是最小角的2倍,你知道这个三角形每个角的度数吗?它是什么三角形?
24.在方格纸上分别画一个钝角三角形、等腰直角三角形和梯形。
25.认一认、画一画:画出每个图形中所指定的底边上高。
26.以线段AB为底,画一个高为3厘米的直角三角形。(图中每个小方格的边长是1cm)
三.三角形的内角和(共22小题)
27.乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
28.如图所示,在正方形纸上像这样剪出一个三角形,那么∠1的度数是( )
A.90° B.60° C.45° D.30°
29.一个直角三角形中一个锐角是46°,它的另一个锐角是 ;一个等腰三角形的顶角是70°,它的一个底角是 。
30.一个三角形的三个内角的和是 度。
31.将三角形的三个角撕下来拼在一起(如图),我发现: 。
32.两个三角形拼成的一个大三角形的内角和是360度。
33.在△ABC,∠A+∠B=∠C,那么△ABC是一个直角三角形.
34.任何一个三角形至少有两个锐角.
35.钝角比直角大,钝角三角形的内角和比直角三角形内角和大。
36.如果一个直角三角形中其中一个锐角是42°,那么另一个锐角是58°。
37.如图,∠1=125°,求∠2的度数.
38.求下面各题中未知角的度数.
(1)求∠1的度数.
(2)在三角形中,∠C=35°,∠B比∠C大15°,求∠A,∠B的度数.
39.求下面各角的度数.
40.图形计算。
(1)如图是一个等边三角形和它的一条高,∠1= °,∠2= °。
(2)如图中,∠1= °。
41.计算图中的角度.
∠1=60°,求∠2=?
42.如图,∠1=145°,∠2=40°,求∠3,∠4的度数.
43.算一算,填一填.
∠B= .
44.公园的花坛分别种了红、黄、白、蓝四种花(如图)。
45.等腰三角形的一个角是100度,求另两个角是多少度?
46.张云同学要制作一个等腰三角形的学具,这个等腰三角形的一个内角必须是68°,请你想一想,另外两个内角分别是多少度?(用两种思路分别解答)
47.一个直角三角形,其中一个锐角是30°,另一个锐角是多少度?
48.劳动课上,第三小组的同学一起制作了一个等腰三角形形状的风筝,它的顶角是110°,另外的两个角是多少度呢?
四.三角形的稳定性(共1小题)
49.自行车的车身结构做成了三角形的形状,是利用了 。
五.三角形边的关系(共11小题)
50.下面的线段中,能围成三角形的是( )
A.3cm,4cm,7cm B.2cm,4cm,4cm
C.5cm,6cm,12cm D.8cm,2cm,6cm
51.下面能组成三角形的一组线段长度是( )
A.1cm,4cm,3cm B.5cm,7cm,11cm
C.2cm,3cm,6cm
52.一个三角形的两边分别长5厘米、8厘米,第三边可能是( )
A.3 B.14 C.10 D.13
53.从学校到少年宫有三条路线,最近的是 号线路,
用以前学过的知识解释是 ,
用三角形的知识解释是 。
54.用长度分别为11cm,6cm和 cm的小棒一定能围成一个三角形。
55.用三根小棒围成一个三角形,其中两根小棒的长度分别为6厘米和15厘米,则第三根小棒的长度最长是 厘米。(填整厘米数)
56.淘气用3dm和7dm的两种木条做一个等腰三角形画框,它的周长是13dm或17dm。
57.用2分米、3分米、8分米长的三根小棒恰好能围成一个三角形。
58.淘气的姐姐身高1.72米,体重52千克,腿长约95厘米。淘气说他姐姐走一步能迈2米,对于这种说法,你相信吗?请从数学角度解释理由。
59.有4根小棒,第一根长2.5厘米,第二根长3.05厘米,第三根长4.16厘米,第四根长10.2厘米。
请选择3根小棒组成一个三角形,并计算这个三角形的周长。
60.一个三角形的两条边分别是7厘米和13厘米,那么第三条边的长最短是多少厘米?最长是多少厘米?(取整厘米数)
5 三角形
参考答案与试题解析
一.三角形的特性(共7小题)
1.将一根20厘米的细铁丝,剪成3段,拼成一个三角形,以下哪种剪法可以( )
A.8厘米、7厘米、5厘米 B.13厘米、6厘米、1厘米
C.4厘米、9厘米、4厘米 D.10厘米、3厘米、7厘米
【答案】A
【分析】根据三角形的特性:任意两边之和大于第三边,三角形的任意两边的差一定小于第三边;进行依次分析即可.
【解答】解:A、7+5>8,所以本组小棒能围成三角形;
B、6+1<13,所以本组小棒不能围成三角形;
C、4+4<9,所以本组小棒不能围成三角形;
D、3+7=10,所以本组小棒不能围成三角形;
故选:A.
【点评】此题是考查三角形的特性,应灵活掌握和运用.
2.下面选项中的三条线段能围成(每相邻两条线段的端点相连)三角形的是( )
A. B.
C. D.
【答案】A
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:A.两边之和大于第三边,能围成三角形;
B.两边之和小于第三边,不能围成三角形;
C.两边之和小于第三边,不能围成三角形;
D.两边之和等于第三边,不能围成三角形。
故选:A。
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可。
3.一个三角形有 3 条边,一个角有 2 条边。
【答案】3;2。
【分析】不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫作三角形。这三条线段叫作三角形的边;
具有公共端点的两条射线组成的图形叫作角。这个公共端点叫作角的顶点,这两条射线叫作角的两条边。据此解答。
【解答】解:一个三角形有3条边,一个角有2条边。
故答案为:3;2。
【点评】本题考查了三角形和角的认识。
4.四月初,乐乐和妈妈一起种了一些黄瓜苗。一天,妈妈用竹竿搭起了很多三角形的黄瓜架,她这样做的原因是三角形具有 稳定性 。
【答案】稳定性。
【分析】根据三角形具有稳定性解答。
【解答】解:四月初,乐乐和妈妈一起种了一些黄瓜苗。一天,妈妈用竹竿搭起了很多三角形的黄瓜架,她这样做的原因是三角形具有稳定性。
故答案为:稳定性。
【点评】本题考查三角形稳定性的实际应用;三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得。
5.在中有3个三角形。 √
【答案】√
【分析】三角形有3条边,3个角,据此数出三角形的数量即可解答。
【解答】解:在中有3个三角形。说法正确。
故答案为:√。
【点评】本题考查了三角形的认识。
6.把一根长10厘米的吸管剪成3段(每段都是整厘米),围成一个三角形。能围成多少个不同的三角形,它们的每条边长度分别是多少厘米?
【答案】2;4厘米、4厘米、2厘米;4厘米、3厘米、3厘米。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:10÷2=5(厘米)
所以每边都要小于5厘米;
4+4+2=10
4+3+3=10
答:能围成2个不同的三角形,它们的每条边长度分别是4厘米、4厘米、2厘米;4厘米、3厘米、3厘米。
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可。
7.有5根小棒,长度分别是3厘米、3厘米、3厘米、4厘米、6厘米,可以摆成几种不同的三角形?请你列举出来.
【答案】见试题解答内容
【分析】根据三角形边的特征,在三角形中任意两边之和大于第三边,由此解答.
【解答】解:根据分析知,共有以下情况,
①3厘米,3厘米,3厘米;
②3厘米,3厘米,4厘米;
③3厘米,4厘米,6厘米;
答:一共可以拼成3个不同的三角形.
【点评】此题主要根据三角形的任意两边之和大于第三边解决问题.
二.三角形的分类(共19小题)
8.一个三角形最大的内角是120°,这个三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形
【答案】A
【分析】依据钝角的意义,即大于90°,小于180°的角叫做钝角,以及三角形的分类方法,即可进行选择.
【解答】解:因为120°的角是钝角,
且有一个角是钝角的三角形是钝角三角形;
故选:A.
【点评】此题主要考查钝角的意义,以及三角形的分类方法.
9.一个等腰三角形的一个底角与顶角的度数相等,这个三角形是( )三角形。
A.直角 B.钝角 C.等边
【答案】C
【分析】在三角形中,内角和等于180°。在等腰三角形中,两底角相等。据此解答。
【解答】解:在等腰三角形中,两底角相等。而这个底角刚好与顶角的度数相等,所以三个内角都相等,它们的度数是:180°÷3=60°。所以这个三角形是等边三角形。
故选:C。
【点评】解答此题的关键是:先通过计算出三个角的度数,然后根据三角形的角分类,进行判断即可。
10.如图所示,一张三角形的纸片被撕去了一个角,原来这张三角形纸片的形状是( )三角形的。
A.锐角 B.直角 C.钝角 D.等腰
【答案】C
【分析】根据三角形内角和为180°以及图中的两个内角度数,即可求出撕去角的度数,再根据三角形的分类方法即可判断。
【解答】解:180°﹣110°﹣45°=25°
答:原来这张三角形纸片的形状是钝角三角形的。
故选:C。
【点评】此题考查了三角形的内角和定理:三角形的内角和等于180°,同时考查了三角形的按角分类知识,结合题意分析解答即可。
11.在三角形ABC中,∠A﹣∠C=∠B,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形
【答案】B
【分析】三角形ABC的三个内角和是180°,又因为∠A﹣∠C=∠B;所以∠A=∠B+∠C,所以∠A=180°÷2=90°,进一步判断三角形ABC是直角三角形。
【解答】解:因为∠A+∠B+∠C=180°,∠A﹣∠C=∠B;所以∠A=∠B+∠C,即∠A=180°÷2=90°,三角形ABC的三个角中,有一个是直角,是直角三角形。
故选:B。
【点评】此题考查三角形内角和为180°和三角形的分类(按角分)。
12.一个三角形中的最小角是46°,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
【答案】B
【分析】三角形的内角和是180°,因为三角形中最小的角是46°,假设第二小的角也是46°,所以最大的角最大为:180°﹣46°﹣46°=88°;根据锐角三角形的含义:三个角都是锐角的三角形,是锐角三角形;进而判断即可。
【解答】解:因为三角形中最小的角是46°,假设第二小的角也是46°,所以最大的角最大为:
180°﹣46°﹣46°
=134°﹣46°
=88°
由于三角形的三个角都是锐角,所以是锐角三角形。
故选:B。
【点评】解答此题的关键:先进行假设,进而根据三角形的内角和是180°,求出最大的角的度数,进而根据三角形的分类进行解答。
13.下面( )不是按角分类。
A.直角三角形 B.钝角三角形
C.等边三角形 D.锐角三角形
【答案】C
【分析】最大角是直角的三角形是直角三角形,最大角是钝角的三角形是钝角三角形,最大角是锐角的三角形是锐角三角形。三条边都相等的三角形是等边三角形,两条边相等的三角形是等腰三角形。
【解答】解:直角三角形、钝角三角形、锐角三角形都是按角分,等边三角形是按边分。
故选:C。
【点评】本题考查了角的分类特征。
14.一个三角形中有两个内角的和等于90°,这个三角形( )是直角三角形。
A.一定 B.可能 C.不一定 D.不可能
【答案】A
【分析】三角形的3个内角的和是180度,利用180度减去两个内角的和等于90°求出第三个角,再根据锐角三角形:最大角小于90°;直角三角形:最大角等于90°;钝角三角形:最大角大于90°判断。
【解答】解:180°﹣90°=90°
90°是直角,因此这个三角形一定是直角三角形。
故选:A。
【点评】本题考查了三角形按角分类的方法及三角形内角和的应用。
15.分一分,分成两类。
第一类: ①④
第二类: ②③⑤⑥
【答案】①④;②③⑤⑥。
【分析】根据图示可以分成第一类:三角形内有个小三角形,第二类:三角形内有个小圆。
【解答】解:第一类:①④;
第二类:②③⑤⑥。
故答案为:①④;②③⑤⑥。
【点评】本题考查了物体的分类。
16.如图是一块三角形玻璃打碎后留下的碎片,它原来是一个 钝角 三角形。
【答案】钝角。
【分析】因为三角形的内角度数和是180°,根据图中的两个内角度数可求打碎的一个角的度数,再根据三角形的分类即可作出判断。
【解答】解:因为180°﹣30°﹣40°=110°;所以这是一个钝角三角形。
故答案为:钝角。
【点评】本题主要考查了三角形的内角和定理及三角形的分类,解题的关键是求出玻璃碎处角的度数。
17.如果一个三角形中有两个锐角的度数之和大于90°,那么按角分,这个三角形是 锐角 三角形。
【答案】锐角。
【分析】三角形按角分分为锐角三角形、直角三角形、钝角三角形。三个角都是锐角的三角形是锐角三角形,有一个直角的三角形是直角三角形,有一个钝角的三角形是钝角三角形。
【解答】解:三角形内角和是 180°,180° 减去一个大于 90° 的角,差一定是一个小于 90°的角,大于0°小于90°的角是锐角,三个角都是锐角的三角形是锐角三角形,所以这个三角形是一个锐角三角形。
故答案为:锐角。
【点评】解答此题用到的知识点:(1)三角形的内角和是180度;(2)三角形的分类。
18.在一个三角形中三个内角的关系是:∠1+∠2=∠3,那么可以判断这是一个 直 角三角形。
【答案】直。
【分析】根据角对三角形分类的方法:三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形,结合三角形的内角和是180°,在一个三角形中三个内角的关系是:∠1+∠2=∠3,可知∠3=180°÷2=90°,所以这是一个直角三角形。据此解答即可。
【解答】解:因为∠1+∠2=∠3,所以∠3=180°÷2=90°。
答:这是一个直角三角形。
故答案为:直。
【点评】本题考查了三角形的分类知识,结合三角形的内角和知识解答即可。
19.如图,三角形中的三个内角都相等,则∠1= 60 °;按角分,这是一个 锐角 三角形;按边分,这个是一个 等边 三角形。
【答案】60,锐角,等边。
【分析】这个三角形中,三个内角都相等且它们的和是180°。可以用除法算出一个角的度数;三个角都是锐角的三角形是锐角三角形;三条边都相等的三角形是等边三角形。据此解答。
【解答】解:180°÷3=60°,即∠1=60°。
答:这个三角形的∠1=60°;按角分,这是一个锐角三角形;按边分,这个是一个等边三角形。
故答案为:60,锐角,等边。
【点评】本题考查了三角形的内角和以及分类知识,结合题意分析解答即可。
20.只有2个锐角的三角形可能是钝角三角形。 √
【答案】√
【分析】不管是什么三角形,最少有2个锐角,据此解答。
【解答】解:有两个角是锐角的三角形可能是钝角三角形,原题说法正确。
故答案为:√。
【点评】本题考查了三角形的按角分类的方法。
21.当三角形中两个内角的和小于第三个角时,这个三角形一定是钝角三角形。 √
【答案】√
【分析】根据三角形的内角和等于180度,如果其中两个内角之和小于第三个内角,说明第三个内角大于90度,根据钝角三角形的含义:有一个角是钝角的三角形是钝角三角形,可知:这个三角形是钝角三角形。
【解答】解:三角形的三角内角和等于180度,如果其中两个内角之和小于第三个内角,说明第三个内角大于90度,因此这个三角形是钝角三角形。
故答案为:√。
【点评】解答此题用到的知识点:(1)三角形的内角和是180度;(2)钝角三角形的含义。
22.一个三角形,三个内角的度数比是3:7:10,三个内角各是多少度?这是一个什么三角形?
【答案】27°,63°,90°,直角三角形。
【分析】根据三角形的内角和是180°,三角形的内角和永远是180度,把180度的角按3:7:10进行比例分配即可,根据最大角的度数判断三角形的种类即可。
【解答】解:180°27°
180°63°
180°90°
最大的角90°是一个直角,因此这是一个直角三角形。
答:三个内角各是27°,63°,90°,这是一个直角三角形。
【点评】此题考查了三角形的内角和定理以及三角形的分类,三角形按角分类有锐角三角形、直角三角形、钝角三角形。
23.一个四边形如何变成三角形呢?
小明想到了一种方法,连接对点(如图所示),此时分成两个三角形。
(1)其中一个为等边三角形,一边长为2cm,请问其它两条边长和三个角分别为多少?
(2)另一个三角形中,已知最大角的度数是最小角的3倍,另外一个角的度数是最小角的2倍,你知道这个三角形每个角的度数吗?它是什么三角形?
【答案】2厘米,2厘米,60°,60°,60°;30°,60°,90°,直角三角形。
【分析】(1)等边三角形的三条边相等,三个角相等,都是60度,据此解答;
(2)假设最小的角是1,那么最大的角就是3,较大的角就是2,由三角形内角和是180°÷(3+2+1)求出最小的角,即可求出另外两个角的度数,根据最大的角的度数判断是什么三角形即可。
【解答】解:(1)等边三角形三条边都是2厘米,三个角都是60°;
(2)180°÷(3+2+1)
=180°÷6
=30°
30°×2=60°
30°×3=90°
由最大的角是90度是直角可以判断这个三角形是直角三角形。
答:这个三角形的三个角的度数分别是30°,60°,90°,这是一个直角三角形。
故答案为:2厘米,2厘米,60°,60°,60°;30°,60°,90°,直角三角形。
【点评】本题主要考查了等边三角形的特点及三角形的内角和以及直角三角形的特征。
24.在方格纸上分别画一个钝角三角形、等腰直角三角形和梯形。
【答案】(答案不唯一)
【分析】根据梯形、等腰直角三角形、钝角三角形的特征,梯形只有一组对边平行,平行的一组对边叫做梯形的上底和下底,不平行的两条边叫做梯形的腰;等腰直角三角形的特征是有一个角是直角且两条直角边相等;有一个角是钝角的三角形叫钝角三角形,据此解答即可。
【解答】解:
(答案不唯一)
【点评】此题考查的目的是理解掌握梯形、等腰直角三角形、钝角三角形的特征,以及它们的画法。
25.认一认、画一画:画出每个图形中所指定的底边上高。
【答案】
【分析】从图中标出底边所对应的边上取一点,(三角形取顶点)利用直角三角板的一条直角边与标有底边的一边对齐,沿另一条直角边过取的点作底边的垂线即可。
【解答】解:如图:
【点评】本题考查了三角形、平行四边形及梯形高的画法。
26.以线段AB为底,画一个高为3厘米的直角三角形。(图中每个小方格的边长是1cm)
【答案】
【分析】根据直角三角形的特征和画法,直角三角形有一个角是直角,让其中的一条直角边为3厘米即可。
【解答】解:如图:
【点评】本题考查了直角三角形的画法知识,结合题意分析解答即可。
三.三角形的内角和(共22小题)
27.乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,你知道他拿的是哪一块玻璃吗?( )
A.3 B.2 C.1 D.都可以
【答案】A
【分析】三角形的内角和是180°,已知三角形的一条边的长度和这条边上的两个角的度数即可求出另一个角的度数与另外两条边的长度。据此解答。
【解答】解:由分析得:乐乐不小心把家里的一块玻璃摔成3块(如图),他只拿其中一块玻璃去玻璃店切割出一块与原来一样大的玻璃,我知道他拿的是第3块玻璃。
故选:A。
【点评】此题考查的目的是理解掌握三角形的特征及应用,三角形内角和及应用。
28.如图所示,在正方形纸上像这样剪出一个三角形,那么∠1的度数是( )
A.90° B.60° C.45° D.30°
【答案】B
【分析】根据等边三角形的特点可知,等边三角形的各个内角都是60°。
【解答】解:如上图所示,在正方形纸上像这样剪出一个三角形,那么∠1的度数是60°。
故选:B。
【点评】本题主要考查图形的折叠,关键是知道等边三角形是如何得出的。
29.一个直角三角形中一个锐角是46°,它的另一个锐角是 44° ;一个等腰三角形的顶角是70°,它的一个底角是 55° 。
【答案】44°;55°。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:180°﹣90°﹣46°=44°
(180°﹣70°)÷2
=110°÷2
=55°
答:一个直角三角形中一个锐角是46°,它的另一个锐角是44°;一个等腰三角形的顶角是70°,它的一个底角是55°。
故答案为:44°;55°。
【点评】熟练掌握三角形的内角和知识和等腰三角形的性质,是解答此题的关键。
30.一个三角形的三个内角的和是 180 度。
【答案】180。
【分析】根据数学常识可知一个三角形的三个内角的和是180°。据此解答即可。
【解答】解:一个三角形的三个内角的和是180度。
故答案为:180。
【点评】本题考查三角形内角和的认识。
31.将三角形的三个角撕下来拼在一起(如图),我发现: 三角形的内角和是180° 。
【答案】三角形的内角和是180°。
【分析】根据平角的意义,平角是180°,将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形的内角和是180°。据此解答。
【解答】解:将三角形的三个角撕下来拼在一起,正好拼成一个平角,所以三角形三个内角的和是180°。
故答案为:三角形的内角和是180°。
【点评】此题考查的目的是理解掌握三角形内角和的推算方法及应用,平角的意义及应用。
32.两个三角形拼成的一个大三角形的内角和是360度。 ×
【答案】×。
【分析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答。
【解答】解:两个三角形拼成的一个大三角形的内角和是180°,故原题说法错误。
故答案为:×。
【点评】解答此题的主要依据是:三角形的内角和是180度。
33.在△ABC,∠A+∠B=∠C,那么△ABC是一个直角三角形. √
【答案】见试题解答内容
【分析】根据在△ABC中,∠A+∠B=∠C,∠A+∠B+∠C=180°可求出∠C的度数,进而得出结论.
【解答】解:因为在△ABC中,∠A+∠B=∠C,∠A+∠B+∠C=180°,
所以2∠C=180°,解得∠C=90°,、
所以△ABC是直角三角形.
故答案为:√.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
34.任何一个三角形至少有两个锐角. √
【答案】√
【分析】根据三角形的内角和可知,一个三角形中若有两个直角或钝角,就超过180°,由此可以做出判断.
【解答】解:因为三角形的内角和是180°,一个三角形中若有两个直角或钝角,就超过180°,就够不成一个三角形了,
所以一个三角形,至少应有两个锐角是正确的.
故答案为:√.
【点评】此题主要考查三角形的分类以及三角形的内角和.
35.钝角比直角大,钝角三角形的内角和比直角三角形内角和大。 ×
【答案】×
【分析】根据三角形的内角和等于180°,解答此题即可。
【解答】解:钝角比直角大,钝角三角形的内角和与直角三角形内角和一样大。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握三角形的内角和定理,是解答此题的关键。
36.如果一个直角三角形中其中一个锐角是42°,那么另一个锐角是58°。 ×
【答案】×
【分析】根据三角形的内角和是180°,用三角形的内角和180度减去两个已知角的度数,就是第三个角的度数,据此解答。
【解答】解:180﹣90﹣42
=90﹣42
=48(度)
答:另一个锐角是48°。
所以,如果一个直角三角形中其中一个锐角是42°,那么另一个锐角是58°,错误。
故答案为:×。
【点评】本题考查了三角形内角和定理,关键是掌握三角形内角和为180度。
37.如图,∠1=125°,求∠2的度数.
【答案】见试题解答内容
【分析】
∠1与∠ACB组成的角为平角,即∠1+∠ACD=180°,∠1的度数已知,据此即可求出∠ACD的度数.在三角形ACD中,∠ACD的度数前面已求出,∠ADC为直角(90°),根据三角形的内角和定理,三角形三个内角之和为180°即可求出∠2的度数.
【解答】解:如图:
因为∠1+∠ACD=180°,∠1=125°
所以∠ACD=180°﹣125°=55°
因为∠2+ACD+∠ADC=180°,ACD=55°,∠ADC=90°
所以∠2=180°﹣90°﹣55°=35°
答:∠2是35°.
【点评】解答此题应用的知识点有平角的意义、直角的意义、三角形内角和定理.
38.求下面各题中未知角的度数.
(1)求∠1的度数.
(2)在三角形中,∠C=35°,∠B比∠C大15°,求∠A,∠B的度数.
【答案】见试题解答内容
【分析】(1)根据三角形的内角和是180°,用180°减去两个已知角的度数就等于未知角的度数.
(2)根据三角形的内角和是180°,在三角形中,∠C=35°,∠B比∠C大15°,∠B=35°+15°=50°,所以∠A=180°﹣35°﹣50°=95°
【解答】解:(1)180°﹣30°﹣35°
=150°﹣35°
=115°
答:∠1的度数是115度.
180°﹣67°﹣52°
=113°﹣52°
=61°
答:∠1的度数是61度.
(2)∠B=35°+15°=50°
∠A=180°﹣35°﹣50°=95°
答:∠A是95度,∠B的度数是50度.
【点评】本题考查的是三角形内角和是180度的运用,用180度减去已知角的度数就等于未知角的度数.
39.求下面各角的度数.
【答案】见试题解答内容
【分析】(1)根据三角形内角和定理:三角形内角和是180°,根据已知两个角的度数,求∠2:180°﹣50°﹣90°=40°;根据平角的意义,求∠3:180°﹣30°﹣40°=110°.
(2)根据平角的意义,先求∠1:180°﹣120°=60°;利用三角形内角和定理,求∠2:180°﹣60°﹣45°=75°;∠3=180°﹣75°=105°.
【解答】解:(1)∠2=180°﹣50°﹣90°=40°
∠3=180°﹣30°﹣40°=110°
(2)∠1=180°﹣120°=60°
∠2=180°﹣60°﹣45°=75°
∠3=180°﹣75°=105°
如图:
【点评】本题考查了三角形内角和定理,关键是掌握三角形内角和为180度.
40.图形计算。
(1)如图是一个等边三角形和它的一条高,∠1= 90 °,∠2= 30 °。
(2)如图中,∠1= 70 °。
【答案】(1)90;30;
(2)70。
【分析】根据三角形的内角和等于180°和等边三角形的性质,解答此题即可。
【解答】解:(1)∠2=60÷2=30(度)
∠1=180﹣30﹣60=90(度)
(2)∠1=180﹣(180﹣60﹣45)﹣35
=180﹣75﹣35
=70(度)
故答案为:90;30;70。
【点评】熟练掌握三角形的内角和知识和等边三角形的性质,是解答此题的关键。
41.计算图中的角度.
∠1=60°,求∠2=?
【答案】见试题解答内容
【分析】由图知这是一个直角三角形,∠2的度数等于90度减去∠1的度数,据此解答.
【解答】解:∠2=90°﹣∠1
=90°﹣60°
=30°
答:∠2等于30度.
【点评】本题主要考查了三角形的内角和等于180度和直角三角形的性质等相关知识.
42.如图,∠1=145°,∠2=40°,求∠3,∠4的度数.
【答案】见试题解答内容
【分析】用180°减去∠1的度数等于∠3的度数,再用180°减去∠2和∠3即可求出∠4的度数,据此解答.
【解答】解:∠3=180°﹣∠1
=180°﹣145°
=35°
∠4=180°﹣∠2﹣∠3
=180°﹣40°﹣35°
=105°
答:∠3的度数是35°,∠4的度数是105°.
【点评】解答本题的关键是掌握三角形的内角和等于180°,平角等于180°.
43.算一算,填一填.
∠B= 52° .
【答案】52°.
【分析】直角三角形中,有一个角是直角90°,已知∠C=38°,则∠B=180°﹣90°﹣38°,据此解答.
【解答】解:180°﹣90°﹣38°
=90°﹣38°
=52°
故答案为:52°.
【点评】解答本题的关键是熟练掌握三角形的内角和等于180°.
44.公园的花坛分别种了红、黄、白、蓝四种花(如图)。
【答案】47°。
【分析】运用平角等于180°求出∠2;再运用三角形的内角和是180°求出∠1。
【解答】解:
∠2=180°﹣110°=70°
∠1=180°﹣63°﹣70°=47°
答:∠1是47°。
【点评】本题考查了平角及内角和的意义及应用。
45.等腰三角形的一个角是100度,求另两个角是多少度?
【答案】40°、40°。
【分析】一个角是100度,属于钝角,一个三角形内只能有一个,因此它是顶角。根据三角形的内角和是180°以及等边对等角,分别减去其余两个内角即可求出第三个角的度数。
【解答】解:(180°﹣100°)÷2
=80°÷2
=40°
答:另两个角都是40°。
【点评】本题考查了三角形内角和定理,属于基础题,关键是掌握三角形内角和为180度。
46.张云同学要制作一个等腰三角形的学具,这个等腰三角形的一个内角必须是68°,请你想一想,另外两个内角分别是多少度?(用两种思路分别解答)
【答案】56°、56°或68°、44°。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:如果顶角是68°。
(180°﹣68°)÷2
=112°÷2
=56°
如果底角是68°。
180°﹣68°×2
=180°﹣136°
=44°
答:另外两个内角分别是56°、56°或68°、44°。
【点评】熟练掌握三角形的内角和知识和等腰三角形的性质,是解答此题的关键。
47.一个直角三角形,其中一个锐角是30°,另一个锐角是多少度?
【答案】60°。
【分析】因为三角形的内角和是180度,其中直角三角形中有一个角是直角,给出的直角三角形中一个锐角是30度,用内角和分别减去90度和30度,即可求出另一个锐角的度数。
【解答】解:180°﹣90°﹣30°=60°
答:另一个锐角是60°。
【点评】正确利用直角三角形的性质,明确三角形的内角和是180度,是解此题的关键。
48.劳动课上,第三小组的同学一起制作了一个等腰三角形形状的风筝,它的顶角是110°,另外的两个角是多少度呢?
【答案】35度。
【分析】根据等腰三角形的两个底角相等,解答此题即可。
【解答】解:(180°﹣110°)÷2
=70°÷2
=35°
答:另外的两个角是35度。
【点评】熟练掌握等腰三角形的性质,是解答此题的关键。
四.三角形的稳定性(共1小题)
49.自行车的车身结构做成了三角形的形状,是利用了 三角形的稳定性 。
【答案】见试题解答内容
【分析】三角形具有稳定性,生活中很多物品的设计都利用这一特性设计的。
【解答】解:自行车的车身结构做成了三角形的形状,是利用了三角形的稳定性。
故答案为:三角形的稳定性。
【点评】本题考查了三角形的稳定性的应用。
五.三角形边的关系(共11小题)
50.下面的线段中,能围成三角形的是( )
A.3cm,4cm,7cm B.2cm,4cm,4cm
C.5cm,6cm,12cm D.8cm,2cm,6cm
【答案】B
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:A.3+4=7,不能围成三角形;
B.2+4>4,可以围成三角形;
C.5+6<12,不能围成三角形;
D.2+6=8,不能围成三角形。
故选:B。
【点评】本题考查了三角形的三边关系的应用。
51.下面能组成三角形的一组线段长度是( )
A.1cm,4cm,3cm B.5cm,7cm,11cm
C.2cm,3cm,6cm
【答案】B
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:A.1+3=4,所以1cm,4cm,3cm不能围成三角形;
B.5+7>11,11﹣7<5,所以5cm,7cm,11cm 能围成三角形;
C.2+3<6,所以2cm,3cm,6cm 不能围成三角形。
故选:B。
【点评】本题考查了三角形的三边关系的应用,结合题意分析解答即可。
52.一个三角形的两边分别长5厘米、8厘米,第三边可能是( )
A.3 B.14 C.10 D.13
【答案】C
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:8﹣5<第三边<8+5,
所以:3<第三边<13,即另一条边的长应在3~13厘米之间(不包括3厘米和13厘米);
另一条也是整数,可能是4,5,6,7,8,9,10,11,12厘米。
故选:C。
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可。
53.从学校到少年宫有三条路线,最近的是 ② 号线路,
用以前学过的知识解释是 两点之间,线段最短 ,
用三角形的知识解释是 两边之和大于第三边 。
【答案】②,两点之间,线段最短,两边之和大于第三边。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:通过观察图示发现从学校到少年宫有三条路线,最近的是②号线路,用以前学过的知识解释是:两点之间,线段最短,用三角形的知识解释是:两边之和大于第三边。
故答案为:②,两点之间,线段最短,两边之和大于第三边。
【点评】本题考查了三角形的三边关系的应用。
54.用长度分别为11cm,6cm和 6 cm的小棒一定能围成一个三角形。
【答案】6。(答案不唯一)
【分析】任意三角形的两边之和都大于第三边,两边之差必须小于第三边,据此计算解答。
【解答】解:6+6>11,因此用长度分别为11cm,6cm和6cm的小棒一定能围成一个三角形。
故答案为:6。(答案不唯一)
【点评】本题考查了三角形的三边关系。
55.用三根小棒围成一个三角形,其中两根小棒的长度分别为6厘米和15厘米,则第三根小棒的长度最长是 20 厘米。(填整厘米数)
【答案】20。
【分析】根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。用三根小棒围成一个三角形,已知三角形其中两根小棒的长度分别为6厘米和15厘米,则第三根小棒的长度最长小于两边之和,大于两边之差,据此解答即可。
【解答】解:6+15=21(厘米)
21﹣1=20(厘米)
答:第三根小棒的长度最长是20厘米。
故答案为:20。
【点评】此题考查三角形边的关系。任意两边之和大于第三边,任意两边之差小于第三边。
56.淘气用3dm和7dm的两种木条做一个等腰三角形画框,它的周长是13dm或17dm。 ×
【答案】×。
【分析】根据三角形的三边关系:两边之和大于第三边,可知:3+3=6dm;6<7;所以3dm的木条不能作腰,所以围成的等腰三角形的腰是7dm,底是3dm,由此即可求出这个三角形的周长。
【解答】解:根据分析可知,淘气用3dm和7dm的两种木条做一个等腰三角形画框,三边长是7dm,7dm,3dm,所以它的周长是7+7+3=14+3=17dm,本题说法错误。
故答案为:×。
【点评】此题考查了三角形的周长计算方法以及等腰三角形的两条腰相等的性质,关键是根据三角形的三边关系确定这个等腰三角形的腰与底的长度。
57.用2分米、3分米、8分米长的三根小棒恰好能围成一个三角形。 ×
【答案】×
【分析】根据三角形中三边的关系进行分析即可判断正误。
【解答】解:三角形中,任意两边之和大于第三边,任意两边之差小于第三边,
2+3=5(分米)
5<8,所以用2分米、3分米、8分米长的三根小棒不能围成三角形,即原题说法错误。
故答案为:×。
【点评】此题考查三角形的三边关系。三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
58.淘气的姐姐身高1.72米,体重52千克,腿长约95厘米。淘气说他姐姐走一步能迈2米,对于这种说法,你相信吗?请从数学角度解释理由。
【答案】不可信。因为95厘米+95厘米=190厘米,2米=200厘米,190厘米<200厘米,不符合三角形的任意两边之和大于第三边,所以淘气说他姐姐走一步能迈2米这种说法是不可信的。
【分析】依据三角形的任意两边之和大于第三边,腿长约95厘米,走一步两腿和地面形成一个三角形,两腿的长度和要大于一步的距离,据此解答即可。
【解答】解:95厘米+95厘米=190厘米,2米=200厘米,190厘米<200厘米,不符合三角形的任意两边之和大于第三边,所以淘气说他姐姐走一步能迈2米这种说法是不可信的。
【点评】此题主要考查了三角形的三条边的关系,结合题意分析解答即可。
59.有4根小棒,第一根长2.5厘米,第二根长3.05厘米,第三根长4.16厘米,第四根长10.2厘米。
请选择3根小棒组成一个三角形,并计算这个三角形的周长。
【答案】9.71厘米。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:2.5+3.05>4.16,所以第一根长2.5厘米,第二根长3.05厘米,第三根长4.16厘米可以围成三角形。
周长:2.5+3.05+4.16
=5.55+4.16
=9.71(厘米)
答:三角形的周长是9.71厘米。
【点评】本题考查了三角形的三边关系的应用。
60.一个三角形的两条边分别是7厘米和13厘米,那么第三条边的长最短是多少厘米?最长是多少厘米?(取整厘米数)
【答案】7厘米,19厘米。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:根据三角形的特性可知:(13﹣7)厘米<第三边<(13+7)厘米,
所以:6厘米<第三边<20厘米,
因为要求取整厘米数,
所以第三条边最长是19厘米,最短是7厘米。
答:第三条边最长是19厘米,最短是7厘米。
【点评】解答此题的关键是根据三角形的特性进行分析、解答。
21世纪教育网(www.21cnjy.com)
