2025年九年级数学中考前冲刺提分训练卷(含答案)
文档属性
| 名称 | 2025年九年级数学中考前冲刺提分训练卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 399.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 21:25:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考前冲刺提分训练卷
一、单选题
1.(2024七下·滕州月考)下列四个说法:
①射线和射线是同一条射线;
②若点B为线段的中点,则;
③锐角和钝角互补;
④一个角的补角一定大于这个角.
其中正确说法的个数是( ).
A.0个 B.1个 C.2个 D.3个
2.(2024七下·凉州月考)如图,∠B+∠DCB=180°,AC平分∠DAB,且∠D∶∠DAC=5∶2,则∠D的度数是( )
A.100° B.105° C.110° D.120°
3.(2023八上·玉林期中)小芳有两根长度为和的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择的木条长度为( )
A. B. C. D.
4.(2024·新城模拟)如图,为等腰直角三角形,,直线交于点E,.若,则的度数为( )
A. B. C. D.
5.(2025八下·龙马潭开学考)下列计算正确的是( )
A. B. C. D.
6.(2025八下·东莞期中)下列计算结果正确的是( )
A. B. C. D.
7.(2024七下·资中期末)一个长方形周长为28,若它的长减少2,宽增加2,就变成了一个正方形,那么该长方形的面积为( )
A.45 B.48 C.40 D.49
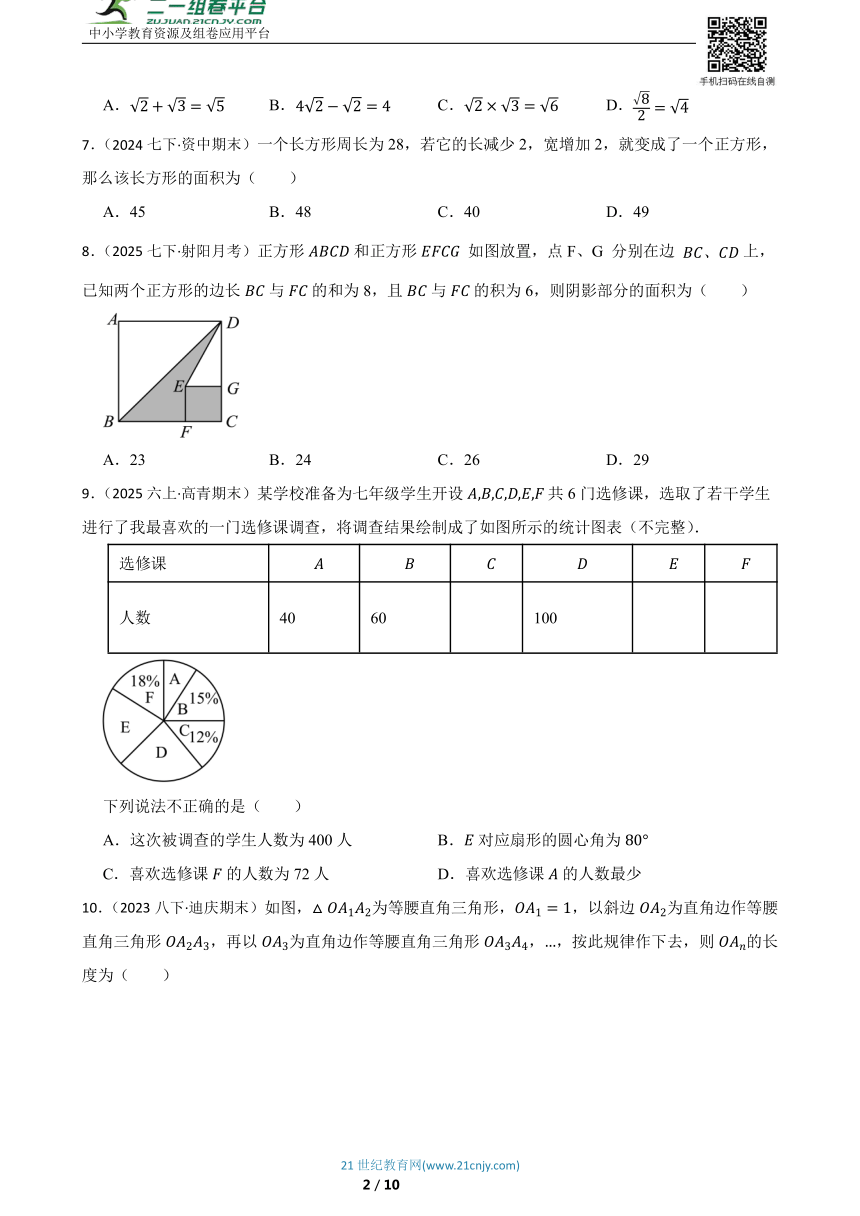
8.(2025七下·射阳月考)正方形和正方形 如图放置,点F、G 分别在边 上,已知两个正方形的边长与的和为8,且与的积为6,则阴影部分的面积为( )
A.23 B.24 C.26 D.29
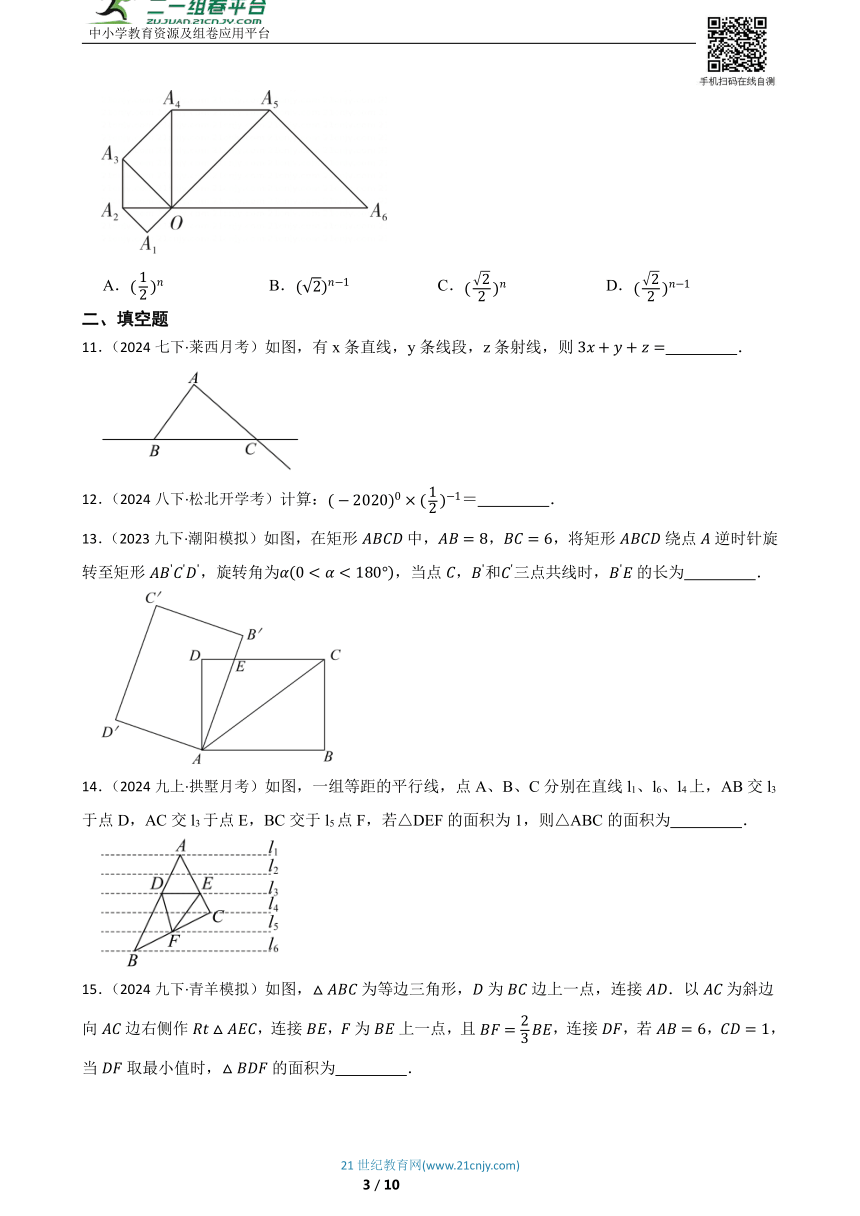
9.(2025六上·高青期末)某学校准备为七年级学生开设共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课
人数 40 60
100
下列说法不正确的是( )
A.这次被调查的学生人数为400人 B.对应扇形的圆心角为
C.喜欢选修课的人数为72人 D.喜欢选修课的人数最少
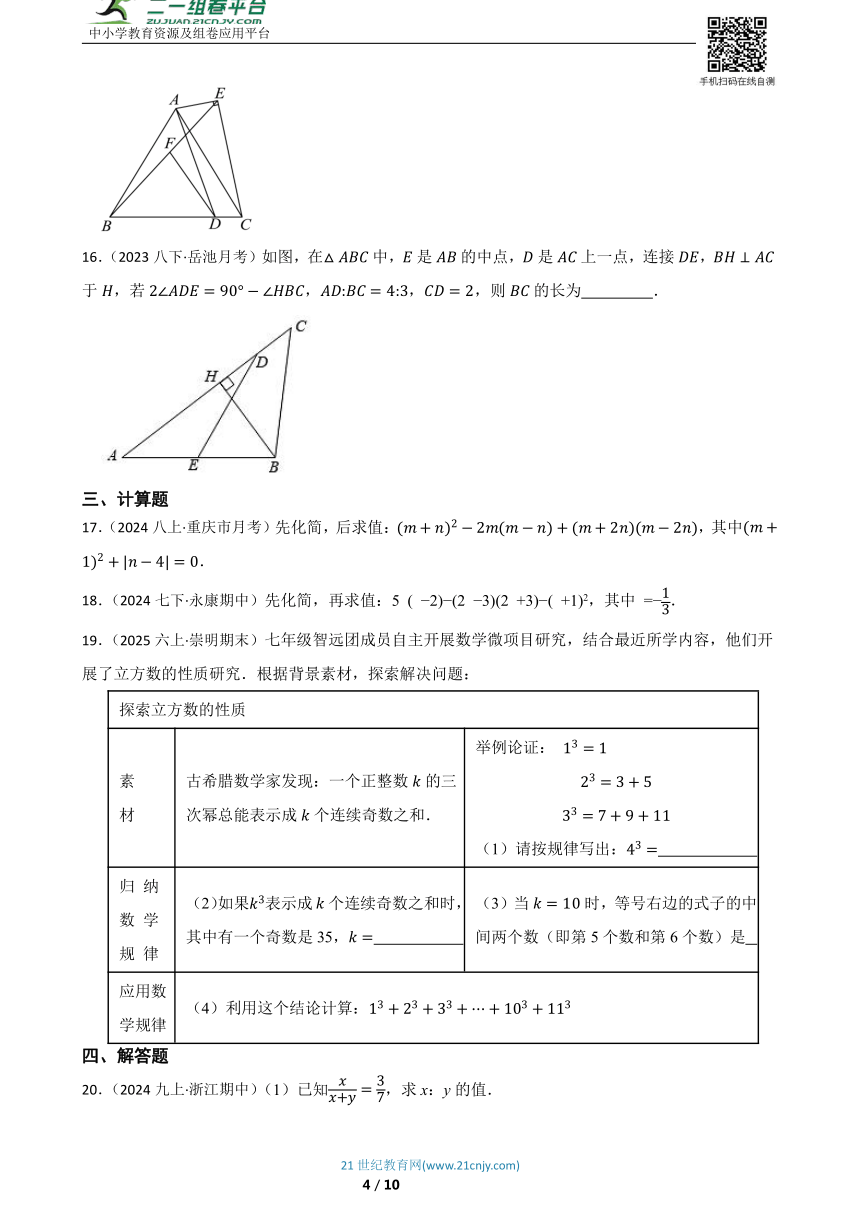
10.(2023八下·迪庆期末)如图,为等腰直角三角形,,以斜边为直角边作等腰直角三角形,再以为直角边作等腰直角三角形,,按此规律作下去,则的长度为( )
A. B. C. D.
二、填空题
11.(2024七下·莱西月考)如图,有x条直线,y条线段,z条射线,则 .
12.(2024八下·松北开学考)计算:= .
13.(2023九下·潮阳模拟)如图,在矩形中,,,将矩形绕点逆时针旋转至矩形,旋转角为,当点,和三点共线时,的长为 .
14.(2024九上·拱墅月考)如图,一组等距的平行线,点A、B、C分别在直线l1、l6、l4上,AB交l3于点D,AC交l3于点E,BC交于l5点F,若△DEF的面积为1,则△ABC的面积为 .
15.(2024九下·青羊模拟)如图,为等边三角形,为边上一点,连接.以为斜边向边右侧作,连接,为上一点,且,连接,若,,当取最小值时,的面积为 .
16.(2023八下·岳池月考)如图,在中,是的中点,是上一点,连接,于,若,,,则的长为 .
三、计算题
17.(2024八上·重庆市月考)先化简,后求值:,其中.
18.(2024七下·永康期中)先化简,再求值:5 ( 2) (2 3)(2 +3) ( +1)2,其中 = .
19.(2025六上·崇明期末)七年级智远团成员自主开展数学微项目研究,结合最近所学内容,他们开展了立方数的性质研究.根据背景素材,探索解决问题:
探索立方数的性质
素 材 古希腊数学家发现:一个正整数的三次幂总能表示成个连续奇数之和. 举例论证: (1)请按规律写出:
归 纳 数 学 规 律 (2)如果表示成个连续奇数之和时,其中有一个奇数是35, (3)当时,等号右边的式子的中间两个数(即第5个数和第6个数)是
应用数学规律 (4)利用这个结论计算:
四、解答题
20.(2024九上·浙江期中)(1)已知,求x:y的值.
(2)已知线段a=2,b=8,求线段a,b的比例中项.
21.(2023八上·甘州期中)已知点Q与关于x轴对称,一个一次函数的图象经过点Q,且与y轴的交点M与原点距离为5,求这个一次函数的解析式.
22.(2024七下·横州期中)图1展示了光线反射定律:EF是平面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角.
(1)在图1中,证明:;
(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知,判断AB与BC的位置关系,并说明理由;
(3)图3是潜望镜工作原理示意图,AB,CD是放置其中的两面平面镜.若进入潜望镜的光线m和离开潜望镜的光线n是平行的,判断AB与CD的位置关系,并说明理由.
23.(2022八下·南海月考)已知函数y1=﹣x+3,y2=2x﹣4.
(1)若y1<y2,求x的取值范围;
(2)若点P(m,n)是函数y1与y2图象的交点,求32m2+16mn+2n2的值;
(3)若关于x的不等式组的解集为﹣1<x<1.求(a+1)(b﹣1)的值.
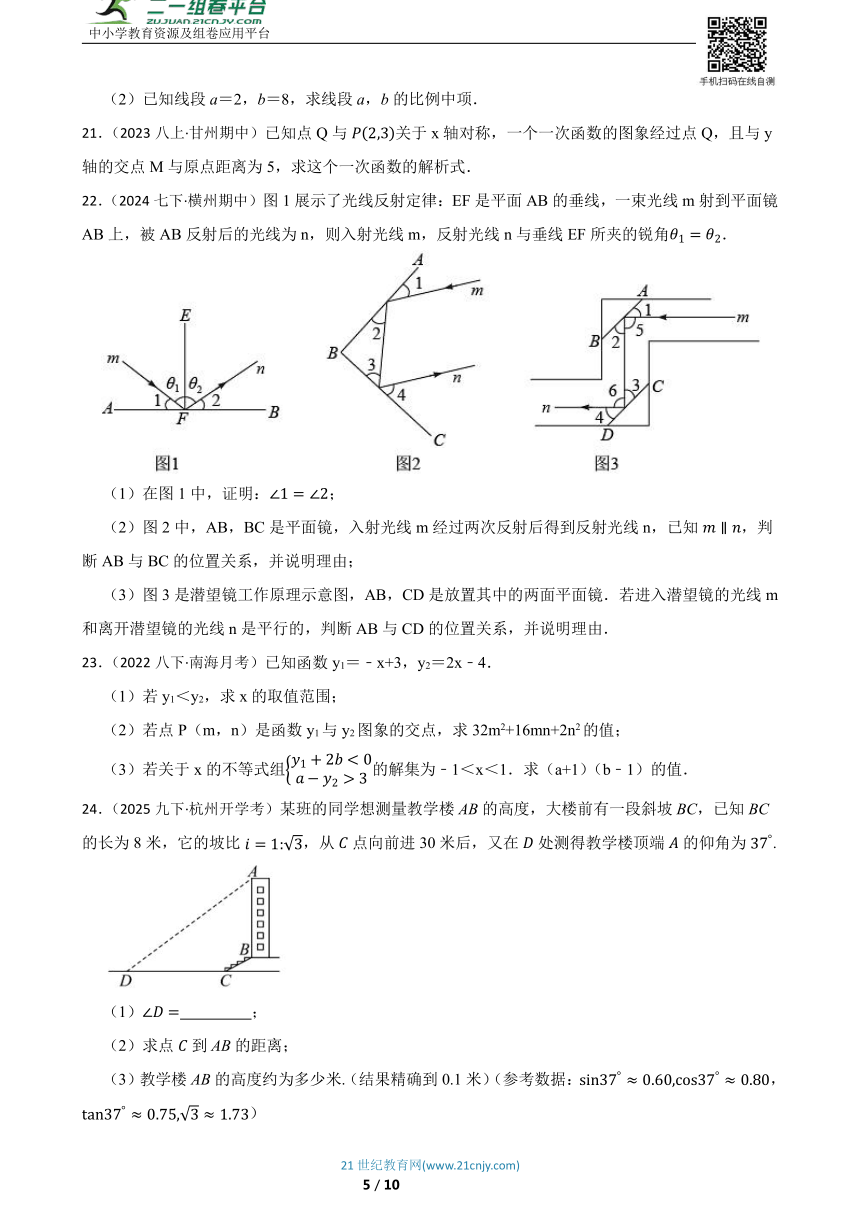
24.(2025九下·杭州开学考)某班的同学想测量教学楼AB的高度,大楼前有一段斜坡BC,已知BC的长为8米,它的坡比,从点向前进30米后,又在处测得教学楼顶端的仰角为.
(1) ;
(2)求点到AB的距离;
(3)教学楼AB的高度约为多少米.(结果精确到0.1米)(参考数据:,)
25.(2024七下·马尾期末)在平面直角坐标系中,已知点,.将点A向下平移个单位,B点先向右平移4个单位,再向下平移个单位,分别得到点,.
(1)若与坐标轴平行,则m与n的数量关系是 ;
(2)分别过,作y轴的垂线,垂足分别为M,N,且.
①求四边形的面积;
②连接,,,线段交x轴于点C,若OC将三角形的面积分成的两部分,求点C的坐标.
答案解析部分
1.【答案】B
【知识点】直线、射线、线段;余角、补角及其性质;线段的中点
2.【答案】A
【知识点】平行线的判定与性质;角平分线的性质
3.【答案】D
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质
5.【答案】B
【知识点】同底数幂的乘法;合并同类项法则及应用;积的乘方运算;幂的乘方运算
6.【答案】C
【知识点】二次根式的性质与化简;二次根式的乘除法;二次根式的加减法
7.【答案】A
【知识点】一元一次方程的实际应用-几何问题
8.【答案】A
【知识点】完全平方公式及运用;完全平方公式的几何背景
9.【答案】B
【知识点】扇形统计图
10.【答案】B
【知识点】勾股定理的应用
11.【答案】
【知识点】求代数式的值-直接代入求值;线段的计数问题
12.【答案】2
【知识点】零指数幂;负整数指数幂
13.【答案】
【知识点】勾股定理;矩形的性质;旋转的性质
14.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
15.【答案】
【知识点】等边三角形的性质;勾股定理;相似三角形的判定与性质;解直角三角形
16.【答案】6
【知识点】三角形的外角性质;三角形全等及其性质;等腰三角形的性质
17.【答案】,
【知识点】多项式乘多项式;完全平方公式及运用
18.【答案】解:5 ( 2) (2 3)(2 +3) ( +1)2
=5a2-10a-(4a2-9)-(a2+2a+1)
=5a2-10a-4a2+9-a2-2a-1
=-12a+8
当时,
【知识点】利用整式的混合运算化简求值
19.【答案】(1);(2)6 ;(3)99,101;(4)4356
【知识点】探索数与式的规律;一元一次方程的实际应用-数字、日历、年龄问题
20.【答案】(1)解:∵,
∴7x=3x+3y,
∴4x=3y,
∴x:y=3:4
(2)解:设c为线段 a,b的比例中项,
则c2=ab,
即c2=16,
由于 c>0,
故c=4.
【知识点】比例的性质;比例中项
21.【答案】一次函数解析式为或
【知识点】待定系数法求一次函数解析式;坐标与图形变化﹣对称
22.【答案】(1)解:∵EF是平面AB的垂线,∴∠AFE=∠BFE=90°,
∵,
∴;
(2)解:AB⊥BC,理由如下:∵入射光线m经过两次反射后得到反射光线n,
∴,,
∵,
∴,
∴,
∴,
∴,
(3)解:AB∥CD,理由如下:∵进入潜望镜的光线m和离开潜望镜的光线n是平行的,
∴,,,
∴,
∵,,
∴,
∴AB∥CD.
【知识点】平行线的判定与性质;三角形内角和定理;余角
23.【答案】(1);(2)200;(3)-6
【知识点】解一元一次不等式组;一次函数与不等式(组)的关系
24.【答案】(1)
(2)解:如图,延长AB交DC延长线于点F,则∠BFC=90°,
在Rt△BCF中,,
∴,
设BF=k米,则米,
∴(米),
又∵BC=8米,
∴2k=8,
解得:k=4,
∴(米)
(3)解:由(2)得,BF=4米,米,
∴米,
在Rt△ADF中,,
∴(米),
∴AB=AF-BF≈23.7(米),
∴教学楼AB的高度约为23.7米
【知识点】解直角三角形的实际应用﹣坡度坡角问题
25.【答案】(1)
(2)①四边形的面积;②点C的坐标为或
【知识点】点的坐标;坐标与图形变化﹣平移
21世纪教育网(www.21cnjy.com)
10 / 10
2025年九年级数学中考前冲刺提分训练卷
一、单选题
1.(2024七下·滕州月考)下列四个说法:
①射线和射线是同一条射线;
②若点B为线段的中点,则;
③锐角和钝角互补;
④一个角的补角一定大于这个角.
其中正确说法的个数是( ).
A.0个 B.1个 C.2个 D.3个
2.(2024七下·凉州月考)如图,∠B+∠DCB=180°,AC平分∠DAB,且∠D∶∠DAC=5∶2,则∠D的度数是( )
A.100° B.105° C.110° D.120°
3.(2023八上·玉林期中)小芳有两根长度为和的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择的木条长度为( )
A. B. C. D.
4.(2024·新城模拟)如图,为等腰直角三角形,,直线交于点E,.若,则的度数为( )
A. B. C. D.
5.(2025八下·龙马潭开学考)下列计算正确的是( )
A. B. C. D.
6.(2025八下·东莞期中)下列计算结果正确的是( )
A. B. C. D.
7.(2024七下·资中期末)一个长方形周长为28,若它的长减少2,宽增加2,就变成了一个正方形,那么该长方形的面积为( )
A.45 B.48 C.40 D.49
8.(2025七下·射阳月考)正方形和正方形 如图放置,点F、G 分别在边 上,已知两个正方形的边长与的和为8,且与的积为6,则阴影部分的面积为( )
A.23 B.24 C.26 D.29
9.(2025六上·高青期末)某学校准备为七年级学生开设共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课
人数 40 60
100
下列说法不正确的是( )
A.这次被调查的学生人数为400人 B.对应扇形的圆心角为
C.喜欢选修课的人数为72人 D.喜欢选修课的人数最少
10.(2023八下·迪庆期末)如图,为等腰直角三角形,,以斜边为直角边作等腰直角三角形,再以为直角边作等腰直角三角形,,按此规律作下去,则的长度为( )
A. B. C. D.
二、填空题
11.(2024七下·莱西月考)如图,有x条直线,y条线段,z条射线,则 .
12.(2024八下·松北开学考)计算:= .
13.(2023九下·潮阳模拟)如图,在矩形中,,,将矩形绕点逆时针旋转至矩形,旋转角为,当点,和三点共线时,的长为 .
14.(2024九上·拱墅月考)如图,一组等距的平行线,点A、B、C分别在直线l1、l6、l4上,AB交l3于点D,AC交l3于点E,BC交于l5点F,若△DEF的面积为1,则△ABC的面积为 .
15.(2024九下·青羊模拟)如图,为等边三角形,为边上一点,连接.以为斜边向边右侧作,连接,为上一点,且,连接,若,,当取最小值时,的面积为 .
16.(2023八下·岳池月考)如图,在中,是的中点,是上一点,连接,于,若,,,则的长为 .
三、计算题
17.(2024八上·重庆市月考)先化简,后求值:,其中.
18.(2024七下·永康期中)先化简,再求值:5 ( 2) (2 3)(2 +3) ( +1)2,其中 = .
19.(2025六上·崇明期末)七年级智远团成员自主开展数学微项目研究,结合最近所学内容,他们开展了立方数的性质研究.根据背景素材,探索解决问题:
探索立方数的性质
素 材 古希腊数学家发现:一个正整数的三次幂总能表示成个连续奇数之和. 举例论证: (1)请按规律写出:
归 纳 数 学 规 律 (2)如果表示成个连续奇数之和时,其中有一个奇数是35, (3)当时,等号右边的式子的中间两个数(即第5个数和第6个数)是
应用数学规律 (4)利用这个结论计算:
四、解答题
20.(2024九上·浙江期中)(1)已知,求x:y的值.
(2)已知线段a=2,b=8,求线段a,b的比例中项.
21.(2023八上·甘州期中)已知点Q与关于x轴对称,一个一次函数的图象经过点Q,且与y轴的交点M与原点距离为5,求这个一次函数的解析式.
22.(2024七下·横州期中)图1展示了光线反射定律:EF是平面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角.
(1)在图1中,证明:;
(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知,判断AB与BC的位置关系,并说明理由;
(3)图3是潜望镜工作原理示意图,AB,CD是放置其中的两面平面镜.若进入潜望镜的光线m和离开潜望镜的光线n是平行的,判断AB与CD的位置关系,并说明理由.
23.(2022八下·南海月考)已知函数y1=﹣x+3,y2=2x﹣4.
(1)若y1<y2,求x的取值范围;
(2)若点P(m,n)是函数y1与y2图象的交点,求32m2+16mn+2n2的值;
(3)若关于x的不等式组的解集为﹣1<x<1.求(a+1)(b﹣1)的值.
24.(2025九下·杭州开学考)某班的同学想测量教学楼AB的高度,大楼前有一段斜坡BC,已知BC的长为8米,它的坡比,从点向前进30米后,又在处测得教学楼顶端的仰角为.
(1) ;
(2)求点到AB的距离;
(3)教学楼AB的高度约为多少米.(结果精确到0.1米)(参考数据:,)
25.(2024七下·马尾期末)在平面直角坐标系中,已知点,.将点A向下平移个单位,B点先向右平移4个单位,再向下平移个单位,分别得到点,.
(1)若与坐标轴平行,则m与n的数量关系是 ;
(2)分别过,作y轴的垂线,垂足分别为M,N,且.
①求四边形的面积;
②连接,,,线段交x轴于点C,若OC将三角形的面积分成的两部分,求点C的坐标.
答案解析部分
1.【答案】B
【知识点】直线、射线、线段;余角、补角及其性质;线段的中点
2.【答案】A
【知识点】平行线的判定与性质;角平分线的性质
3.【答案】D
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质
5.【答案】B
【知识点】同底数幂的乘法;合并同类项法则及应用;积的乘方运算;幂的乘方运算
6.【答案】C
【知识点】二次根式的性质与化简;二次根式的乘除法;二次根式的加减法
7.【答案】A
【知识点】一元一次方程的实际应用-几何问题
8.【答案】A
【知识点】完全平方公式及运用;完全平方公式的几何背景
9.【答案】B
【知识点】扇形统计图
10.【答案】B
【知识点】勾股定理的应用
11.【答案】
【知识点】求代数式的值-直接代入求值;线段的计数问题
12.【答案】2
【知识点】零指数幂;负整数指数幂
13.【答案】
【知识点】勾股定理;矩形的性质;旋转的性质
14.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
15.【答案】
【知识点】等边三角形的性质;勾股定理;相似三角形的判定与性质;解直角三角形
16.【答案】6
【知识点】三角形的外角性质;三角形全等及其性质;等腰三角形的性质
17.【答案】,
【知识点】多项式乘多项式;完全平方公式及运用
18.【答案】解:5 ( 2) (2 3)(2 +3) ( +1)2
=5a2-10a-(4a2-9)-(a2+2a+1)
=5a2-10a-4a2+9-a2-2a-1
=-12a+8
当时,
【知识点】利用整式的混合运算化简求值
19.【答案】(1);(2)6 ;(3)99,101;(4)4356
【知识点】探索数与式的规律;一元一次方程的实际应用-数字、日历、年龄问题
20.【答案】(1)解:∵,
∴7x=3x+3y,
∴4x=3y,
∴x:y=3:4
(2)解:设c为线段 a,b的比例中项,
则c2=ab,
即c2=16,
由于 c>0,
故c=4.
【知识点】比例的性质;比例中项
21.【答案】一次函数解析式为或
【知识点】待定系数法求一次函数解析式;坐标与图形变化﹣对称
22.【答案】(1)解:∵EF是平面AB的垂线,∴∠AFE=∠BFE=90°,
∵,
∴;
(2)解:AB⊥BC,理由如下:∵入射光线m经过两次反射后得到反射光线n,
∴,,
∵,
∴,
∴,
∴,
∴,
(3)解:AB∥CD,理由如下:∵进入潜望镜的光线m和离开潜望镜的光线n是平行的,
∴,,,
∴,
∵,,
∴,
∴AB∥CD.
【知识点】平行线的判定与性质;三角形内角和定理;余角
23.【答案】(1);(2)200;(3)-6
【知识点】解一元一次不等式组;一次函数与不等式(组)的关系
24.【答案】(1)
(2)解:如图,延长AB交DC延长线于点F,则∠BFC=90°,
在Rt△BCF中,,
∴,
设BF=k米,则米,
∴(米),
又∵BC=8米,
∴2k=8,
解得:k=4,
∴(米)
(3)解:由(2)得,BF=4米,米,
∴米,
在Rt△ADF中,,
∴(米),
∴AB=AF-BF≈23.7(米),
∴教学楼AB的高度约为23.7米
【知识点】解直角三角形的实际应用﹣坡度坡角问题
25.【答案】(1)
(2)①四边形的面积;②点C的坐标为或
【知识点】点的坐标;坐标与图形变化﹣平移
21世纪教育网(www.21cnjy.com)
10 / 10
同课章节目录
