小升初解决问题专项训练:探索规律(含解析)-2024-2025学年数学六年级下册人教版
文档属性
| 名称 | 小升初解决问题专项训练:探索规律(含解析)-2024-2025学年数学六年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 687.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 09:47:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
小升初解决问题专项训练:探索规律-2024-2025学年数学六年
1.一个球被人从32米高的地方扔下,它落到地面后,反弹的高度是下落高度的一半,这个球在它第三次到达地面时,一共经过了多长的距离?
2.用小棒按照如下方式摆图形,摆一个八边形需要8根小棒。观察规律。
(1)根据规律,怎样摆出4个八边形,把你的想法画在方框内。
(2)照这样画下去,想一想,摆7个八边形需要( )根小棒,如果想摆n个八边形需要( )根小棒。
3.用火柴棒按照如图的方法摆正方形(每条边只摆1根火柴棒)。
……
(1)观察如图并填表。
正方形个数 1 2 3 4 … n
火柴棒根数 ( ) ( ) ( ) ( ) … ( )
(2)如果用了25根火柴棒,一共摆了多少个正方形?写出你的思考过程。
4.甲乙丙丁四位学生围成一圈依序循环报数,规定:
(1)甲、乙、丙、丁首次报出的数依次为1,2,3,4,接着甲报5,乙报6……按此规律,后一位同学报出的数比前一位同学报出的数大1,当报到的数是50时,报数结束;
(2)若报出的数为3的倍数,则报该数的同学需拍手一次。
在此过程中,请你计算甲同学需拍手的次数为多少?
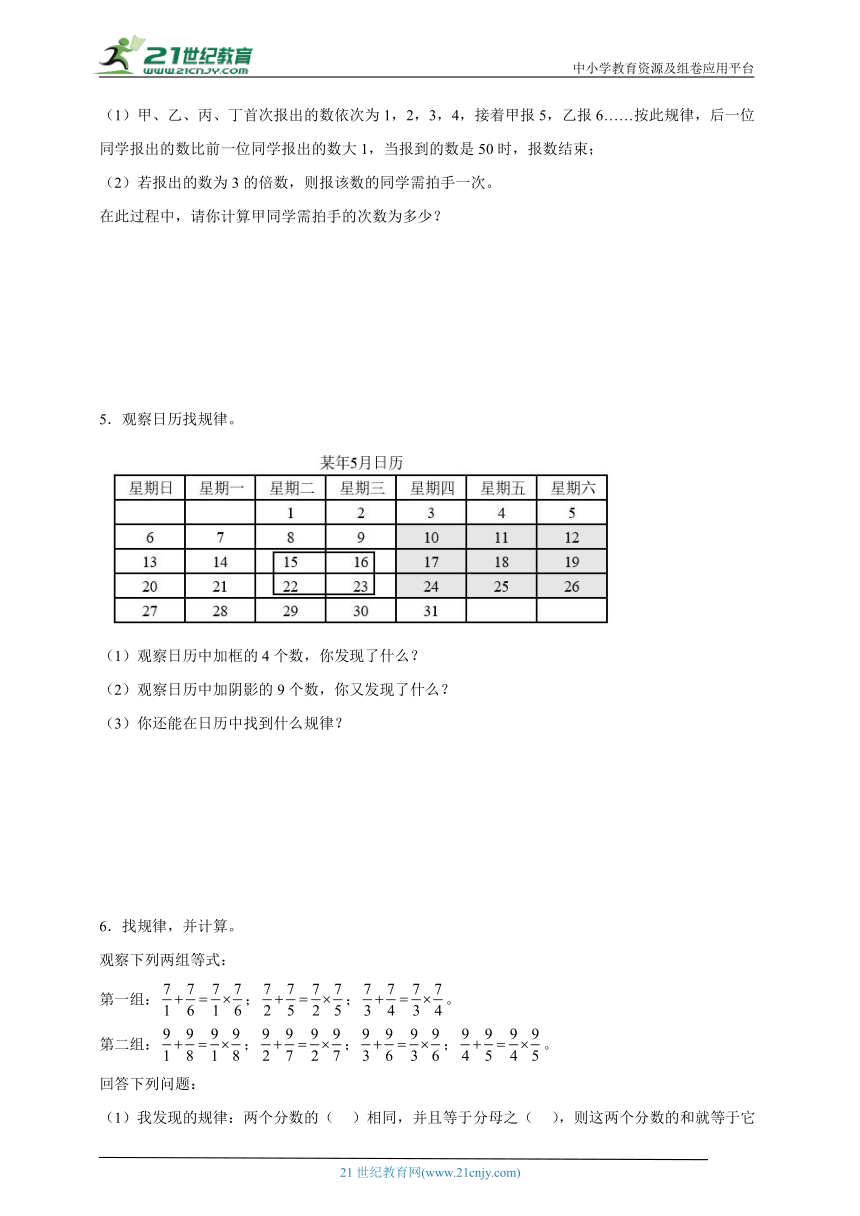
5.观察日历找规律。
(1)观察日历中加框的4个数,你发现了什么?
(2)观察日历中加阴影的9个数,你又发现了什么?
(3)你还能在日历中找到什么规律?
6.找规律,并计算。
观察下列两组等式:
第一组:;;。
第二组:;;;。
回答下列问题:
(1)我发现的规律:两个分数的( )相同,并且等于分母之( ),则这两个分数的和就等于它们的积。
(2)根据这个规律计算:
①;
②若,则正整数m等于( )。
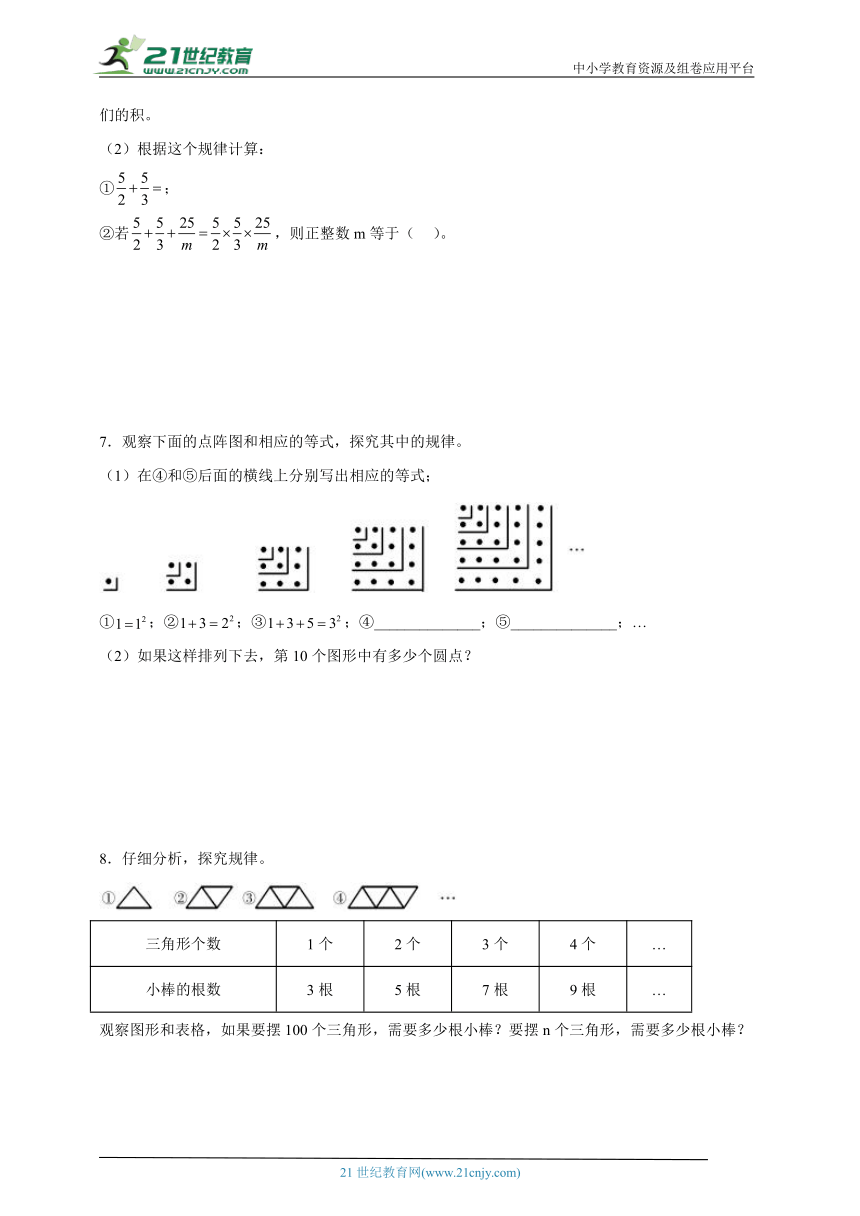
7.观察下面的点阵图和相应的等式,探究其中的规律。
(1)在④和⑤后面的横线上分别写出相应的等式;
①;②;③;④______________;⑤______________;…
(2)如果这样排列下去,第10个图形中有多少个圆点?
8.仔细分析,探究规律。
三角形个数 1个 2个 3个 4个 …
小棒的根数 3根 5根 7根 9根 …
观察图形和表格,如果要摆100个三角形,需要多少根小棒?要摆n个三角形,需要多少根小棒?
9.如图,一张方桌可以坐4人,两张方桌可以坐6人,3张方桌可以坐8人,22张方桌可以坐多少人?坐18人需要几张方桌?
10.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有多少个菱形?第幅图中有多少个菱形?
11.如下图,铺一个空心的大正方形需要8块小方砖,铺2个需要13块小方砖,铺3个空心的大正方形需要18块小方砖。
(1)想一想,按照上面的方法继续铺,铺5个空心的大正方形需要( )块小方砖。
(2)第n个空心的大正方形需要多少块小方砖?
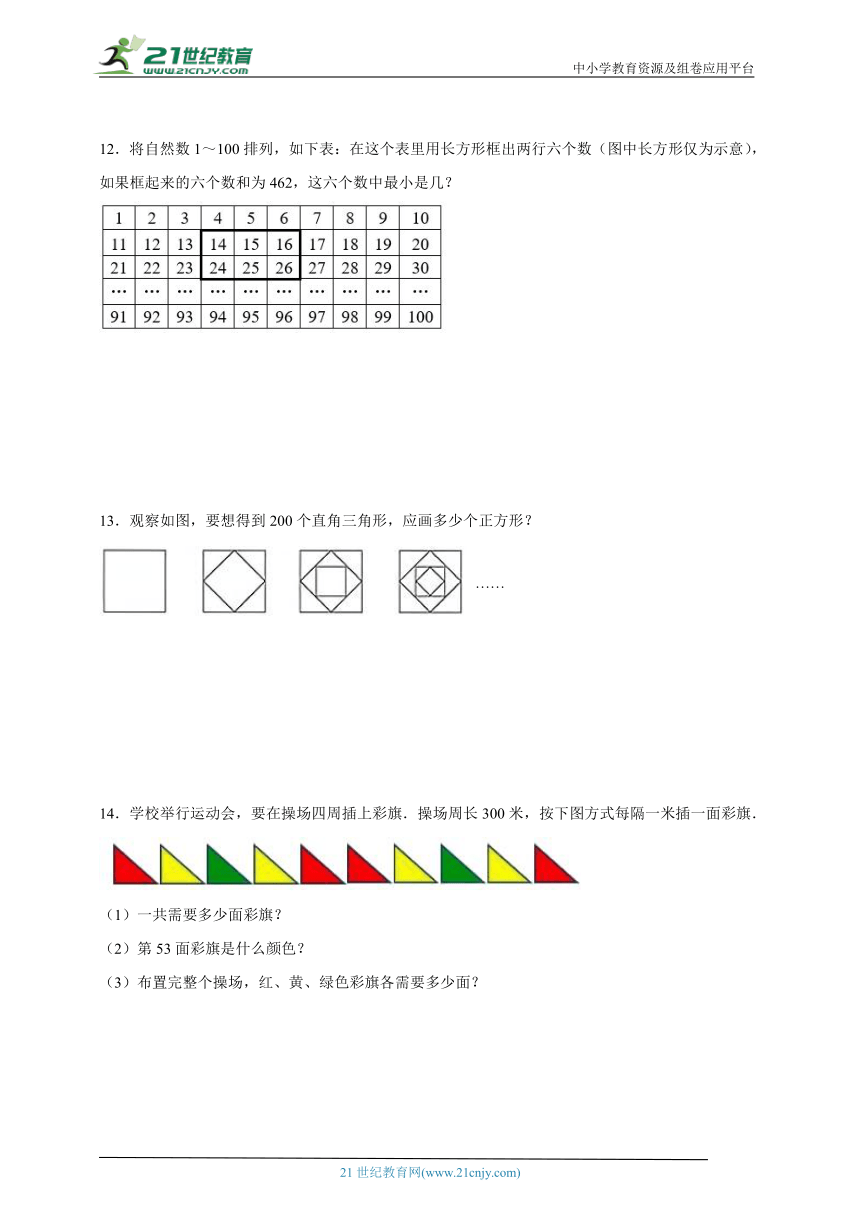
12.将自然数1~100排列,如下表:在这个表里用长方形框出两行六个数(图中长方形仅为示意),如果框起来的六个数和为462,这六个数中最小是几?
13.观察如图,要想得到200个直角三角形,应画多少个正方形?
……
14.学校举行运动会,要在操场四周插上彩旗.操场周长300米,按下图方式每隔一米插一面彩旗.
(1)一共需要多少面彩旗?
(2)第53面彩旗是什么颜色?
(3)布置完整个操场,红、黄、绿色彩旗各需要多少面?
15.用边长为1厘米的小正方形拼长方形,如下图,图1的周长是4,图2的周长是6,图3的周长是8。
(1)你发现第几幅图和周长之间有什么关系吗?把你的发现写出来。
(2)你的发现对吗?请画出图4和图5验证一下。
(3)按照上面的规律,图20的图形周长是多少?请把你的思考过程写出来。
16.车甫为了参加速算比赛,做了一些练习题,以下是其中几道:
23×11=253 46×11=506 31×11=341
58×11=638 45×11=495 69×11=759
(1)车甫通过观察以上算式及其结果后发现,一个两位数与11相乘所得的积有如下规律:首尾( ),中间( ),满十向前一位( )。
①进一 ②不变 ③相加 ④相减
(2)通过上面发现的规律,你能直接写出下面算式的结果吗?
52×11=( );
11×63=( );
77×11=( )。
17.先阅读理解,再解决问题。
有这样一组有规律的算式:
第1层:;
第2层:;
第3层:;
第4层:;
第5层:;
……
(1)我发现:每一层的第1个数,都正好等于( ),像第7层的第1个数是( )。
(2)我发现:每层右边的数的个数等于( ),如第7层右边一共有( )个数。
(3)请你列式计算出第7层等号左边数的和。
18.(1)先计算下面各题,然后找出规律。
(2)应用上面的规律,直接写出下面式子的得数。
19.阅读与解答。
宋朝数学家杨辉在公元1261年著书《详解九章算法》,下面这幅图就是其中著名的“杨辉三角”。1654年,欧洲的帕斯卡也发现这一规律,所以这个图又叫做“帕斯卡三角形”,但是帕斯卡的发现比杨辉要迟393年。
“杨辉三角”最外斜列的数都是1,其它数字都是肩上两个数之和。
(1)下面分别取自“杨辉三角”中的一部分,请你根据上面的规律把缺失的数补充完整。
(2)请观察每一横行所有数之和,你发现了什么规律?
我发现________________________________________运用规律,算一算第10行所有数之和是( )。
(3)“杨辉三角”最外斜列数都是相同的,如果改变最外斜列数,继续按照“杨辉三角”的规律创造属于自己的“新杨辉三角”(如下图)。
?代表的数是( ),此时最外斜列数是( )。
20.有24个同学站成一排做游戏,头上分别戴上编号1,2,3…24的帽子,他们从左往右按1,2,1,2…依次报数,凡报到1的同学退出游戏,剩下的同学又从左往右继续按1,2,1,2…依次报数,如此进行下去。
(1)当还剩下最后一人时,这个同学的帽子编号是几号呢?
(2)如果有80个同学做这样的游戏,当剩下最后一人时,这个同学的帽子编号又是几号呢?有何规律?
21.有2000个数,按照下列的方法排列成五列。
请问2000应写在第几列?
《小升初解决问题专项训练:探索规律-2024-2025学年数学六年级下册人教版》参考答案
1.80米
【分析】一个球被人从32米高的地方扔下,它落到地面经过了32米,反弹经过了(32÷2)米,再次落下又经过了(32÷2)米;再次反弹经过了(32÷2÷2)米,落下又经过了(32÷2÷2)米。这时它第三次到达地面,把所有经过的距离相加即可解答。
【详解】32+32÷2×2+32÷2÷2×2
=32+32+16
=80(米)
答:一共经过了80米的距离。
【点睛】根据题意,求出球每次下落和反弹的高度是解题的关键。
2.(1)见详解
(2)50;1+7n
【分析】(1)摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,15=1+2×7,摆3个八边形需要22根小棒,22=1+3×7, 摆n个八边形需要的小棒数为:(1+7n)根,据此解答即可。
【详解】(1)如图所示:
(2)摆7个八边形需要小棒的根数为:
1+7n=1+7×7
=1+49
=50
则摆7个八边形需要50根小棒,如果想摆n个八边形需要(1+7n)根小棒。
【点睛】本题主要考查数.与形结合的规律,发现每多1个八边形就多7根小棒是解本题的关键。
3.(1)如表:
正方形个数 1 2 3 4 … n
火柴棒根数 4 7 10 13 … 3n+1
(2)8个;思考过程见详解
【分析】(1)根据图中的正方形个数与需的火柴根数可知,从第二个图形开始,每多一个小正方形,就多3根小棒,据此找规律填表;
(2)按(1)找出的规律,计算出用25根火柴棒摆成的小正方形个数即可。
【详解】(1)
正方形个数 1 2 3 4 … n
火柴棒根数 4 7 10 13 … 3n+1
(2)解:设一共摆了n个正方形。
3n+1=25
3n+1-1=25-1
3n=24
3n÷3=24÷3
n=8
答:一共摆了8个正方形。
【点睛】解答本题的关键是找准摆成的小正方形的个数与需要的小棒根数之间的关系。
4.4次
【分析】4个数是一个周期,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数格周期多n个,也就是余数是n,那么结果为下一个周期里的第n个;如果不是从第一个开始循环,可以从总量例减掉不是循环的个数后,再继续计算。据此确定甲报数的次数。
根据报数规律得出甲共报数13次,分别为1,5,9,13,17,21,25,29,33,37,41,45,49,即可得出报出的数为3的倍数的个数,即可得出答案。3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
【详解】……
甲共报数(次
分别为:1、5、9、13、17、21、25、29、33、37、41、45、49
在此过程中,甲同学需报到:9,21,33,45这4个数时,应拍手4次。
【点睛】此题主要考查了数字规律,得出甲的报数次数以及分别报数的数据是解决问题的关键。
5.(1)如果左上的数字为x,则右上为x+1,左下为:x+7,右下为:x+8。
(2)方框中9个数的和是中间数的9倍。
(3)表格每一列的数字从上到下依次增加7;每行中相邻的两个数字相差1。
【分析】(1)根据所给日历,利用日历中各数之间的关系,发现规律:如果左上的数字为x,则右上为x+1,左下为:x+7,右下为:x+8。
(2)根据所给日历,利用日历中的各数的关系,发现:中间的数为y,左面的数是y-1,右面是y+1,上面是y-7,下面是y+7,左上是y-8,右上是y-6;左下是y+6,右下是y+8,据此解答。
(3)根据表格找出正确的规律即可。每一列的数字从上到下依次增加7;每行中相邻的两个数字相差1。
【详解】(1)利用日历中各数之间的关系,发现规律:
如果左上的数字为x,则右上为x+1,左下为:x+7,右下为:x+8。
(2)10+11+12+17+18+19+24+25+26
=33+54+75
=162
=18×9
答:方框中9个数的和是中间数的9倍。
(3)我发现:表格每一列的数字从上到下依次增加7;每行中相邻的两个数字相差1。
【点睛】本题考查了数表中的规律,月历卡中不同的和的情况要一行一行的找,再相加进行解答。
6.(1)分子,和
(2)①
②19
【分析】(1)观察算式可知,若两个分数的分子相同,且分母之和等于分子,所以这两个分数的和等于它们的积;
(2)①根据(1)中发现的规律进行计算即可;
②根据规律可知=,然后根据发现的规律求出m的值即可。
【详解】(1)我发现的规律:两个分数的分子相同,并且等于分母之和,则这两个分数的和就等于它们的积。
(2)①
②
=
=
所以6+m=25
m=19
【点睛】本题考查算式的变化规律,发现规律,利用规律是解题的关键。
7.(1);;
(2)100个
【分析】(1)根据所给图形即可得到所填的式子;
(2)从题意分析可得,从1开始的连续奇数之和等于数个数的平方,用n表示第n个图形以及数的个数,对应的等式规律为:1+3+5+…+(2n 1)=n2,根据找出的规律可得第10个图形对应的等式。
【详解】(1);
(2)1+3+5+7+9+11+13+15+17+19
=102
=100
答:如果这样排列下去,第10个图形中有100个圆点。
【点睛】此题考查了规律型:数字的变化类,找出题中的规律是解本题的关键。
8.201根;(2n+1)根
【分析】搭第一个图形需要3根小棒,结合图形,发现:后边每多一个图形,则多用2根小棒。据此解答。
【详解】搭第100个图形,需要小棒:
3+2×(100 1)
=3+198
=201(根)
则要搭n个三角形时,需要小棒:
3+2(n 1)=(2n+1)根
答:摆100个三角形,需要201根小棒,要摆n个三角形,需要(2n+1)根小棒。
【点睛】此题考查了数与形问题,要能够从图形中发现规律。
9.46人; 8张
【分析】观察摆放的桌子,不难发现:在1张桌子坐4人的基础上,多1张桌子,多2人.则有n张桌子时,有4+2(n-1)=2n+2人;由此即可计算当n=22时,求出2n+2的值;当2n+2=18人时,求得桌子张数n的值。
【详解】第一张桌子可以坐4人;
拼2张桌子可以坐4+2×1=6人;
拼3张桌子可以坐4+2×2=8人;
故n张桌子拼在一起可以坐4+2(n-1)=2n+2。
当n=22时,
2n+2
=2×22+2
=46(人)
当2n+2=18时,n=8。
【点睛】此题考查了平面图形的规律变化,解答此题关键是观察图形,分析、归纳并发现其中的规律,并应用规律解决问题。
10.7个;(2n-1)个
【分析】根据图意,第1幅图中有1个菱形,第二个图中有3=2×2-1,第三个图中有5=2×3-1,第4幅图有7=2×4-1,以此类推,则第n个图中,有(2n-1)个菱形。注意分析菱形的个数与第几个图形的对应关系。
【详解】由分析可知:
则第4幅图中有:
2×4-1
=8-1
=7(个)
则第n个图中,有(2n-1)个菱形。
【点睛】此题考查的是找规律,关键是通过归纳与总结,得到其中的规律并运用规律。
11.(1)28;
(2)5n+3
【分析】看图,铺一个大正方形需要1×5+3=8(块)小方砖,铺两个需要2×5+3=13(块)小方砖,铺三个需要3×5+3=18(块)小方砖。所以,铺五个需要5×5+3=28(块)小方砖,铺n个需要(n×5+3)块小方砖。据此解题。
【详解】(1)5×5+3
=25+3
=28(块)
所以,铺5个空心的大正方形需要28块小方砖。
(2)n×5+3=5n+3
答:第n个空心的大正方形需要(5n+3)块小方砖。
【点睛】本题考查了用字母表示数,有一定逻辑推理和抽象概括能力是解题的关键。
12.71
【分析】从图上看,每行10个数,从左向右依次递增,长方形框起来的六个数,最小的数是上行最左边的数,设它是x,则其它数是x+1,x+2,下行的数对应的是x+10,x+11,x+12;加起来和为462,列出方程即可得出答案。
【详解】解:设这六个数中最小是x。
x+x+1+x+2+x+10+x+11+x+12=462
6x+36=462
6x=462-36
6x=426
x=426÷6
x=71
答:这六个数中最小是71。
【点睛】此题考查了数表中的规律,应通过认真观察找出数与数之间规律,方可快速列出方程解答。
13.51个
【分析】第1个正方体中有0个直角三角形;第2个正方体中有4个直角三角形;第3个正方体中有8个直角三角形;第4个正方体中有12个直角三角形。由此得出规律,三角形的个数都是4的倍数,然后得出假设第n个正方体,就有(n-1)×4个直角三角形。
【详解】根据图中的数据可得:1个正方形有0个三角形,可以写成(1-1)×4个;
2个正方形有4个三角形,可以写成(2-1)×4个;
3个正方形有8个三角形,可以写成(3-1)×4个;
4个正方形有12个三角形,可以写成(4-1)×4个;
所以当正方形的个数为a时,三角形的个数可以写成:(a-1)×4个;
设需要画a个正方形才得到200个直角三角形,则根据上面的结论可得:
(a-1)×4=200
a-1=200÷4
a-1=50
a=51
答:应画51个正方形。
【点睛】本题的关键是根据图形发现规律:第1个正方体就有0×4个直角三角形;第2个正方体就有(2-1)×4个直角三角形,然后以此类推。
14.(1)300面;(2)绿色;(3)红色120面,黄色120面,绿色60面
【分析】对于(1)题,封闭线路上的植树问题的数量关系:株数=全长÷株距,代入数据计算即可;
对于(2)题,首先明确彩旗排列顺序:红色、黄色、绿色、黄色、红色,即5面彩旗是一个周期,再用53除以5根据求得的余数即可解答;
对于(3)题,首先明确5面彩旗是一个周期,一个周期中红旗是2面、黄旗是2面,绿旗是1面,再用彩旗的总数量300除以一个周期中彩旗的面数5,求出有几个周期,再用一个周期中每种颜色旗乘周期个数即可解答.
【详解】(1)300÷1=300(面)
答:一共需要300面彩旗.
(2)由彩旗排列顺序可得:5面彩旗是一个周期,这5面彩旗排列顺序是红色、黄色、绿色、黄色、红色,53÷5=10(个)……3(面),余数3是下一个周期的第3面,第3面是绿色的.
答:第53面彩旗是绿颜色.
(3)300÷5=60(个),红色:2×60=120(面),黄色:2×60=120(面);绿色:1×60=60(面).
答:红色彩旗120面,黄色彩旗120面,绿色彩旗60面.
15.(1)第几幅图加1的和再乘2是它的周长。
(2)对;
(3)42厘米
【详解】(1)第几幅图加1的和再乘2是它的周长。
(2
(3)图20是第20幅图,所以周长是
(20+1)× 2
=21×2
=42(厘米)
答:周长是42厘米。
16.(1) ② ③ ①
(2) 572 693 847
【分析】(1)通过观察,从给定的算式中找出两位数与11相乘的积的规律;
(2)根据发现的规律去解答后面的算式。
【详解】(1)观察 23×11=253,这里23的首位2和末尾3在积的首位和末尾,所以首尾不变选②。
再看积的中间数字5,是23的首位2和末尾3相加得到的2+3=5,所以中间相加,选③。
对于46×11=506,4+6=10,积的中间是0,并且向百位进了1,所以满十向前一位进一,选①。
(2)对于 52×11,按照规律,首位是5,末尾是2,中间是5+2=7,所以结果是572。
对于11×63,首位是6,末尾是3,中间是6+3=9,结果是693。
对于77×11,首位是7,末尾是7,中间是7+7=14,满十进一,所以结果是847。
17.(1)层数的平方;49;
(2)层数;7;
(3)420
【分析】(1)观察算式,第1、2、3、4层的第1个数分别是1、4、9、16,也就是12、22、32、42,据此得出每一层的第1个数的规律,并按此规律得出第7层的第1个数是几。
(2)观察算式,第1、2、3、4层的右边的数的个数分别是1、2、3、4个,据此得出每层右边的数的个数的规律,并按此规律得出第7层右边数的个数。
(3)结合上面两题的规律,写出第7层的算式,并计算出得数。
【详解】(1)第1层的第1个数是1,1=12;
第2层的第1个数是4,4=22;
第3层的第1个数是9,9=32;
第4层的第1个数是16,16=42;
……
第7层的第1个数是72=49。
我发现:每一层的第1个数,都正好等于层数的平方,像第7层的第1个数是49。
(2)我发现:每层右边的数的个数等于层数,如第7层右边一共有7个数。
(3)第7层:49+50+51+52+53+54+55+56=57+58+59+60+61+62+63=420
答:第7层等号左边数的和是420。
18.(1);;;规律见详解
(2)
【分析】(1)异分母分数相加减,先通分成分母相同的分数,再按照同分母分数相加减的方法进行计算。据此可得:,,。
观察这三个式子可以发现:加数的分子都是1,分母从2开始连续乘2,而=1-,=1-,=1-,则式子的结果都等于1减去最后一个加数的差。
(2)由(1)可知,这个式子的得数等于1减去的差。据此解答。
【详解】(1)
=
=
=
=
=
=
规律:当加数的分子都是1,分母从2开始连续乘2时,式子的结果等于1减去最后一个加数的差。
(2)
=1-
=
19.(1)28;56;45
(2)后一横行所有数的和是前一横行所有数的和的2倍;512
(3)27;9
【分析】(1)根据题意,上面两个数字的和是下面一个数字,用上面两个数字相加即可求出下面的数字;用下面的数字减去上面其中的一个数字,即可求出另一个数字。
(2)先分别计算出每一横行所有数之和,找出其中的规律后,算出第10行所有数之和即可。
(3)根据题意,27是第三横行左边两个数相加的结果,所求的数是第三横行右边两个数相加的结果,最外斜列数都相同且中间的数一样,则所求的数也是27;第二横行的两个数相加得到第三横行中间的数,且第二横行的两个数和第三横行左右两个数一样,则第三横行中间的数是左边数即最外斜列数的2倍,相加为27,用27÷3即可求出此时最外斜列数是多少。
【详解】(1)7+21=28
84-28=56
165-120=45
(2)第一横行:1
第二横行:1+1=2
第三横行:1+2+1=3+1=4
第四横行:1+3+3+1=4+3+1=7+1=8
第五横行:1+4+6+4+1=5+6+4+1=11+4+1=15+1=16
1×2=2,2×2=4,4×2=8,8×2=16
第六横行:16×2=32
第七横行:32×2=64
第八横行:64×2=128
第九横行:128×2=256
第十横行:256×2=512
我发现后一横行所有数的和是前一横行所有数的和的2倍。第10行所有数之和是512。
(3)27÷3=9
?代表的数是27,此时最外斜列数是9。
【点睛】本题主要注意找到数与数之间的规律,通过加法或减法求出要求的数。
20.(1)16号
(2)64号;规律见详解
【分析】(1)根据题意,可以画图找到答案,先写出1~24的编号,每次把报1的编号划掉,看最后剩下一名同学的编号是几,并从中找到规律。
(2)由上一题发现规律,剩下1人所需淘汰的次数为n时,这个同学的编号是2n;据此求出80个同学做这样的游戏,当剩下最后一人时的编号。
【详解】(1)如图:
第一次:24人剩12人
第二次:12人剩6人
第三次:6人剩3人
第四次:3人剩1人
24=16
答:当还剩下最后一人时,这个同学的帽子编号是16号。
(2)第一次:80人剩40人
第二次:40人剩20人
第三次:20人剩10人
第四次:10人剩5人
第五次:5人剩2人
第六次:2人剩1人
26=64
答:这个同学的帽子编号是64号。规律:最后一个同学的编号是2n的编号(n为剩下1人所需淘汰的次数)。
21.第三列
【分析】观察图形可知:除去第一行,其它各行的排列都是有规律的,也就是八个数字一组,每四个数字为一行,前四个数字分别占居一二三四列的位置,后四个数字分别占居二三四五列。所以本题需要用有余数除法来解决,先计算2000-5=1995,再用1995除以8,看余数是多少即可判断出2000应写在哪一列。
【详解】
=1995÷8
=249……3
2000应写在第三列。
答:2000应写在第三列。
【点睛】先找出这个数阵周期性的规律,再根据规律求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初解决问题专项训练:探索规律-2024-2025学年数学六年
1.一个球被人从32米高的地方扔下,它落到地面后,反弹的高度是下落高度的一半,这个球在它第三次到达地面时,一共经过了多长的距离?
2.用小棒按照如下方式摆图形,摆一个八边形需要8根小棒。观察规律。
(1)根据规律,怎样摆出4个八边形,把你的想法画在方框内。
(2)照这样画下去,想一想,摆7个八边形需要( )根小棒,如果想摆n个八边形需要( )根小棒。
3.用火柴棒按照如图的方法摆正方形(每条边只摆1根火柴棒)。
……
(1)观察如图并填表。
正方形个数 1 2 3 4 … n
火柴棒根数 ( ) ( ) ( ) ( ) … ( )
(2)如果用了25根火柴棒,一共摆了多少个正方形?写出你的思考过程。
4.甲乙丙丁四位学生围成一圈依序循环报数,规定:
(1)甲、乙、丙、丁首次报出的数依次为1,2,3,4,接着甲报5,乙报6……按此规律,后一位同学报出的数比前一位同学报出的数大1,当报到的数是50时,报数结束;
(2)若报出的数为3的倍数,则报该数的同学需拍手一次。
在此过程中,请你计算甲同学需拍手的次数为多少?
5.观察日历找规律。
(1)观察日历中加框的4个数,你发现了什么?
(2)观察日历中加阴影的9个数,你又发现了什么?
(3)你还能在日历中找到什么规律?
6.找规律,并计算。
观察下列两组等式:
第一组:;;。
第二组:;;;。
回答下列问题:
(1)我发现的规律:两个分数的( )相同,并且等于分母之( ),则这两个分数的和就等于它们的积。
(2)根据这个规律计算:
①;
②若,则正整数m等于( )。
7.观察下面的点阵图和相应的等式,探究其中的规律。
(1)在④和⑤后面的横线上分别写出相应的等式;
①;②;③;④______________;⑤______________;…
(2)如果这样排列下去,第10个图形中有多少个圆点?
8.仔细分析,探究规律。
三角形个数 1个 2个 3个 4个 …
小棒的根数 3根 5根 7根 9根 …
观察图形和表格,如果要摆100个三角形,需要多少根小棒?要摆n个三角形,需要多少根小棒?
9.如图,一张方桌可以坐4人,两张方桌可以坐6人,3张方桌可以坐8人,22张方桌可以坐多少人?坐18人需要几张方桌?
10.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有多少个菱形?第幅图中有多少个菱形?
11.如下图,铺一个空心的大正方形需要8块小方砖,铺2个需要13块小方砖,铺3个空心的大正方形需要18块小方砖。
(1)想一想,按照上面的方法继续铺,铺5个空心的大正方形需要( )块小方砖。
(2)第n个空心的大正方形需要多少块小方砖?
12.将自然数1~100排列,如下表:在这个表里用长方形框出两行六个数(图中长方形仅为示意),如果框起来的六个数和为462,这六个数中最小是几?
13.观察如图,要想得到200个直角三角形,应画多少个正方形?
……
14.学校举行运动会,要在操场四周插上彩旗.操场周长300米,按下图方式每隔一米插一面彩旗.
(1)一共需要多少面彩旗?
(2)第53面彩旗是什么颜色?
(3)布置完整个操场,红、黄、绿色彩旗各需要多少面?
15.用边长为1厘米的小正方形拼长方形,如下图,图1的周长是4,图2的周长是6,图3的周长是8。
(1)你发现第几幅图和周长之间有什么关系吗?把你的发现写出来。
(2)你的发现对吗?请画出图4和图5验证一下。
(3)按照上面的规律,图20的图形周长是多少?请把你的思考过程写出来。
16.车甫为了参加速算比赛,做了一些练习题,以下是其中几道:
23×11=253 46×11=506 31×11=341
58×11=638 45×11=495 69×11=759
(1)车甫通过观察以上算式及其结果后发现,一个两位数与11相乘所得的积有如下规律:首尾( ),中间( ),满十向前一位( )。
①进一 ②不变 ③相加 ④相减
(2)通过上面发现的规律,你能直接写出下面算式的结果吗?
52×11=( );
11×63=( );
77×11=( )。
17.先阅读理解,再解决问题。
有这样一组有规律的算式:
第1层:;
第2层:;
第3层:;
第4层:;
第5层:;
……
(1)我发现:每一层的第1个数,都正好等于( ),像第7层的第1个数是( )。
(2)我发现:每层右边的数的个数等于( ),如第7层右边一共有( )个数。
(3)请你列式计算出第7层等号左边数的和。
18.(1)先计算下面各题,然后找出规律。
(2)应用上面的规律,直接写出下面式子的得数。
19.阅读与解答。
宋朝数学家杨辉在公元1261年著书《详解九章算法》,下面这幅图就是其中著名的“杨辉三角”。1654年,欧洲的帕斯卡也发现这一规律,所以这个图又叫做“帕斯卡三角形”,但是帕斯卡的发现比杨辉要迟393年。
“杨辉三角”最外斜列的数都是1,其它数字都是肩上两个数之和。
(1)下面分别取自“杨辉三角”中的一部分,请你根据上面的规律把缺失的数补充完整。
(2)请观察每一横行所有数之和,你发现了什么规律?
我发现________________________________________运用规律,算一算第10行所有数之和是( )。
(3)“杨辉三角”最外斜列数都是相同的,如果改变最外斜列数,继续按照“杨辉三角”的规律创造属于自己的“新杨辉三角”(如下图)。
?代表的数是( ),此时最外斜列数是( )。
20.有24个同学站成一排做游戏,头上分别戴上编号1,2,3…24的帽子,他们从左往右按1,2,1,2…依次报数,凡报到1的同学退出游戏,剩下的同学又从左往右继续按1,2,1,2…依次报数,如此进行下去。
(1)当还剩下最后一人时,这个同学的帽子编号是几号呢?
(2)如果有80个同学做这样的游戏,当剩下最后一人时,这个同学的帽子编号又是几号呢?有何规律?
21.有2000个数,按照下列的方法排列成五列。
请问2000应写在第几列?
《小升初解决问题专项训练:探索规律-2024-2025学年数学六年级下册人教版》参考答案
1.80米
【分析】一个球被人从32米高的地方扔下,它落到地面经过了32米,反弹经过了(32÷2)米,再次落下又经过了(32÷2)米;再次反弹经过了(32÷2÷2)米,落下又经过了(32÷2÷2)米。这时它第三次到达地面,把所有经过的距离相加即可解答。
【详解】32+32÷2×2+32÷2÷2×2
=32+32+16
=80(米)
答:一共经过了80米的距离。
【点睛】根据题意,求出球每次下落和反弹的高度是解题的关键。
2.(1)见详解
(2)50;1+7n
【分析】(1)摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,15=1+2×7,摆3个八边形需要22根小棒,22=1+3×7, 摆n个八边形需要的小棒数为:(1+7n)根,据此解答即可。
【详解】(1)如图所示:
(2)摆7个八边形需要小棒的根数为:
1+7n=1+7×7
=1+49
=50
则摆7个八边形需要50根小棒,如果想摆n个八边形需要(1+7n)根小棒。
【点睛】本题主要考查数.与形结合的规律,发现每多1个八边形就多7根小棒是解本题的关键。
3.(1)如表:
正方形个数 1 2 3 4 … n
火柴棒根数 4 7 10 13 … 3n+1
(2)8个;思考过程见详解
【分析】(1)根据图中的正方形个数与需的火柴根数可知,从第二个图形开始,每多一个小正方形,就多3根小棒,据此找规律填表;
(2)按(1)找出的规律,计算出用25根火柴棒摆成的小正方形个数即可。
【详解】(1)
正方形个数 1 2 3 4 … n
火柴棒根数 4 7 10 13 … 3n+1
(2)解:设一共摆了n个正方形。
3n+1=25
3n+1-1=25-1
3n=24
3n÷3=24÷3
n=8
答:一共摆了8个正方形。
【点睛】解答本题的关键是找准摆成的小正方形的个数与需要的小棒根数之间的关系。
4.4次
【分析】4个数是一个周期,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数格周期多n个,也就是余数是n,那么结果为下一个周期里的第n个;如果不是从第一个开始循环,可以从总量例减掉不是循环的个数后,再继续计算。据此确定甲报数的次数。
根据报数规律得出甲共报数13次,分别为1,5,9,13,17,21,25,29,33,37,41,45,49,即可得出报出的数为3的倍数的个数,即可得出答案。3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
【详解】……
甲共报数(次
分别为:1、5、9、13、17、21、25、29、33、37、41、45、49
在此过程中,甲同学需报到:9,21,33,45这4个数时,应拍手4次。
【点睛】此题主要考查了数字规律,得出甲的报数次数以及分别报数的数据是解决问题的关键。
5.(1)如果左上的数字为x,则右上为x+1,左下为:x+7,右下为:x+8。
(2)方框中9个数的和是中间数的9倍。
(3)表格每一列的数字从上到下依次增加7;每行中相邻的两个数字相差1。
【分析】(1)根据所给日历,利用日历中各数之间的关系,发现规律:如果左上的数字为x,则右上为x+1,左下为:x+7,右下为:x+8。
(2)根据所给日历,利用日历中的各数的关系,发现:中间的数为y,左面的数是y-1,右面是y+1,上面是y-7,下面是y+7,左上是y-8,右上是y-6;左下是y+6,右下是y+8,据此解答。
(3)根据表格找出正确的规律即可。每一列的数字从上到下依次增加7;每行中相邻的两个数字相差1。
【详解】(1)利用日历中各数之间的关系,发现规律:
如果左上的数字为x,则右上为x+1,左下为:x+7,右下为:x+8。
(2)10+11+12+17+18+19+24+25+26
=33+54+75
=162
=18×9
答:方框中9个数的和是中间数的9倍。
(3)我发现:表格每一列的数字从上到下依次增加7;每行中相邻的两个数字相差1。
【点睛】本题考查了数表中的规律,月历卡中不同的和的情况要一行一行的找,再相加进行解答。
6.(1)分子,和
(2)①
②19
【分析】(1)观察算式可知,若两个分数的分子相同,且分母之和等于分子,所以这两个分数的和等于它们的积;
(2)①根据(1)中发现的规律进行计算即可;
②根据规律可知=,然后根据发现的规律求出m的值即可。
【详解】(1)我发现的规律:两个分数的分子相同,并且等于分母之和,则这两个分数的和就等于它们的积。
(2)①
②
=
=
所以6+m=25
m=19
【点睛】本题考查算式的变化规律,发现规律,利用规律是解题的关键。
7.(1);;
(2)100个
【分析】(1)根据所给图形即可得到所填的式子;
(2)从题意分析可得,从1开始的连续奇数之和等于数个数的平方,用n表示第n个图形以及数的个数,对应的等式规律为:1+3+5+…+(2n 1)=n2,根据找出的规律可得第10个图形对应的等式。
【详解】(1);
(2)1+3+5+7+9+11+13+15+17+19
=102
=100
答:如果这样排列下去,第10个图形中有100个圆点。
【点睛】此题考查了规律型:数字的变化类,找出题中的规律是解本题的关键。
8.201根;(2n+1)根
【分析】搭第一个图形需要3根小棒,结合图形,发现:后边每多一个图形,则多用2根小棒。据此解答。
【详解】搭第100个图形,需要小棒:
3+2×(100 1)
=3+198
=201(根)
则要搭n个三角形时,需要小棒:
3+2(n 1)=(2n+1)根
答:摆100个三角形,需要201根小棒,要摆n个三角形,需要(2n+1)根小棒。
【点睛】此题考查了数与形问题,要能够从图形中发现规律。
9.46人; 8张
【分析】观察摆放的桌子,不难发现:在1张桌子坐4人的基础上,多1张桌子,多2人.则有n张桌子时,有4+2(n-1)=2n+2人;由此即可计算当n=22时,求出2n+2的值;当2n+2=18人时,求得桌子张数n的值。
【详解】第一张桌子可以坐4人;
拼2张桌子可以坐4+2×1=6人;
拼3张桌子可以坐4+2×2=8人;
故n张桌子拼在一起可以坐4+2(n-1)=2n+2。
当n=22时,
2n+2
=2×22+2
=46(人)
当2n+2=18时,n=8。
【点睛】此题考查了平面图形的规律变化,解答此题关键是观察图形,分析、归纳并发现其中的规律,并应用规律解决问题。
10.7个;(2n-1)个
【分析】根据图意,第1幅图中有1个菱形,第二个图中有3=2×2-1,第三个图中有5=2×3-1,第4幅图有7=2×4-1,以此类推,则第n个图中,有(2n-1)个菱形。注意分析菱形的个数与第几个图形的对应关系。
【详解】由分析可知:
则第4幅图中有:
2×4-1
=8-1
=7(个)
则第n个图中,有(2n-1)个菱形。
【点睛】此题考查的是找规律,关键是通过归纳与总结,得到其中的规律并运用规律。
11.(1)28;
(2)5n+3
【分析】看图,铺一个大正方形需要1×5+3=8(块)小方砖,铺两个需要2×5+3=13(块)小方砖,铺三个需要3×5+3=18(块)小方砖。所以,铺五个需要5×5+3=28(块)小方砖,铺n个需要(n×5+3)块小方砖。据此解题。
【详解】(1)5×5+3
=25+3
=28(块)
所以,铺5个空心的大正方形需要28块小方砖。
(2)n×5+3=5n+3
答:第n个空心的大正方形需要(5n+3)块小方砖。
【点睛】本题考查了用字母表示数,有一定逻辑推理和抽象概括能力是解题的关键。
12.71
【分析】从图上看,每行10个数,从左向右依次递增,长方形框起来的六个数,最小的数是上行最左边的数,设它是x,则其它数是x+1,x+2,下行的数对应的是x+10,x+11,x+12;加起来和为462,列出方程即可得出答案。
【详解】解:设这六个数中最小是x。
x+x+1+x+2+x+10+x+11+x+12=462
6x+36=462
6x=462-36
6x=426
x=426÷6
x=71
答:这六个数中最小是71。
【点睛】此题考查了数表中的规律,应通过认真观察找出数与数之间规律,方可快速列出方程解答。
13.51个
【分析】第1个正方体中有0个直角三角形;第2个正方体中有4个直角三角形;第3个正方体中有8个直角三角形;第4个正方体中有12个直角三角形。由此得出规律,三角形的个数都是4的倍数,然后得出假设第n个正方体,就有(n-1)×4个直角三角形。
【详解】根据图中的数据可得:1个正方形有0个三角形,可以写成(1-1)×4个;
2个正方形有4个三角形,可以写成(2-1)×4个;
3个正方形有8个三角形,可以写成(3-1)×4个;
4个正方形有12个三角形,可以写成(4-1)×4个;
所以当正方形的个数为a时,三角形的个数可以写成:(a-1)×4个;
设需要画a个正方形才得到200个直角三角形,则根据上面的结论可得:
(a-1)×4=200
a-1=200÷4
a-1=50
a=51
答:应画51个正方形。
【点睛】本题的关键是根据图形发现规律:第1个正方体就有0×4个直角三角形;第2个正方体就有(2-1)×4个直角三角形,然后以此类推。
14.(1)300面;(2)绿色;(3)红色120面,黄色120面,绿色60面
【分析】对于(1)题,封闭线路上的植树问题的数量关系:株数=全长÷株距,代入数据计算即可;
对于(2)题,首先明确彩旗排列顺序:红色、黄色、绿色、黄色、红色,即5面彩旗是一个周期,再用53除以5根据求得的余数即可解答;
对于(3)题,首先明确5面彩旗是一个周期,一个周期中红旗是2面、黄旗是2面,绿旗是1面,再用彩旗的总数量300除以一个周期中彩旗的面数5,求出有几个周期,再用一个周期中每种颜色旗乘周期个数即可解答.
【详解】(1)300÷1=300(面)
答:一共需要300面彩旗.
(2)由彩旗排列顺序可得:5面彩旗是一个周期,这5面彩旗排列顺序是红色、黄色、绿色、黄色、红色,53÷5=10(个)……3(面),余数3是下一个周期的第3面,第3面是绿色的.
答:第53面彩旗是绿颜色.
(3)300÷5=60(个),红色:2×60=120(面),黄色:2×60=120(面);绿色:1×60=60(面).
答:红色彩旗120面,黄色彩旗120面,绿色彩旗60面.
15.(1)第几幅图加1的和再乘2是它的周长。
(2)对;
(3)42厘米
【详解】(1)第几幅图加1的和再乘2是它的周长。
(2
(3)图20是第20幅图,所以周长是
(20+1)× 2
=21×2
=42(厘米)
答:周长是42厘米。
16.(1) ② ③ ①
(2) 572 693 847
【分析】(1)通过观察,从给定的算式中找出两位数与11相乘的积的规律;
(2)根据发现的规律去解答后面的算式。
【详解】(1)观察 23×11=253,这里23的首位2和末尾3在积的首位和末尾,所以首尾不变选②。
再看积的中间数字5,是23的首位2和末尾3相加得到的2+3=5,所以中间相加,选③。
对于46×11=506,4+6=10,积的中间是0,并且向百位进了1,所以满十向前一位进一,选①。
(2)对于 52×11,按照规律,首位是5,末尾是2,中间是5+2=7,所以结果是572。
对于11×63,首位是6,末尾是3,中间是6+3=9,结果是693。
对于77×11,首位是7,末尾是7,中间是7+7=14,满十进一,所以结果是847。
17.(1)层数的平方;49;
(2)层数;7;
(3)420
【分析】(1)观察算式,第1、2、3、4层的第1个数分别是1、4、9、16,也就是12、22、32、42,据此得出每一层的第1个数的规律,并按此规律得出第7层的第1个数是几。
(2)观察算式,第1、2、3、4层的右边的数的个数分别是1、2、3、4个,据此得出每层右边的数的个数的规律,并按此规律得出第7层右边数的个数。
(3)结合上面两题的规律,写出第7层的算式,并计算出得数。
【详解】(1)第1层的第1个数是1,1=12;
第2层的第1个数是4,4=22;
第3层的第1个数是9,9=32;
第4层的第1个数是16,16=42;
……
第7层的第1个数是72=49。
我发现:每一层的第1个数,都正好等于层数的平方,像第7层的第1个数是49。
(2)我发现:每层右边的数的个数等于层数,如第7层右边一共有7个数。
(3)第7层:49+50+51+52+53+54+55+56=57+58+59+60+61+62+63=420
答:第7层等号左边数的和是420。
18.(1);;;规律见详解
(2)
【分析】(1)异分母分数相加减,先通分成分母相同的分数,再按照同分母分数相加减的方法进行计算。据此可得:,,。
观察这三个式子可以发现:加数的分子都是1,分母从2开始连续乘2,而=1-,=1-,=1-,则式子的结果都等于1减去最后一个加数的差。
(2)由(1)可知,这个式子的得数等于1减去的差。据此解答。
【详解】(1)
=
=
=
=
=
=
规律:当加数的分子都是1,分母从2开始连续乘2时,式子的结果等于1减去最后一个加数的差。
(2)
=1-
=
19.(1)28;56;45
(2)后一横行所有数的和是前一横行所有数的和的2倍;512
(3)27;9
【分析】(1)根据题意,上面两个数字的和是下面一个数字,用上面两个数字相加即可求出下面的数字;用下面的数字减去上面其中的一个数字,即可求出另一个数字。
(2)先分别计算出每一横行所有数之和,找出其中的规律后,算出第10行所有数之和即可。
(3)根据题意,27是第三横行左边两个数相加的结果,所求的数是第三横行右边两个数相加的结果,最外斜列数都相同且中间的数一样,则所求的数也是27;第二横行的两个数相加得到第三横行中间的数,且第二横行的两个数和第三横行左右两个数一样,则第三横行中间的数是左边数即最外斜列数的2倍,相加为27,用27÷3即可求出此时最外斜列数是多少。
【详解】(1)7+21=28
84-28=56
165-120=45
(2)第一横行:1
第二横行:1+1=2
第三横行:1+2+1=3+1=4
第四横行:1+3+3+1=4+3+1=7+1=8
第五横行:1+4+6+4+1=5+6+4+1=11+4+1=15+1=16
1×2=2,2×2=4,4×2=8,8×2=16
第六横行:16×2=32
第七横行:32×2=64
第八横行:64×2=128
第九横行:128×2=256
第十横行:256×2=512
我发现后一横行所有数的和是前一横行所有数的和的2倍。第10行所有数之和是512。
(3)27÷3=9
?代表的数是27,此时最外斜列数是9。
【点睛】本题主要注意找到数与数之间的规律,通过加法或减法求出要求的数。
20.(1)16号
(2)64号;规律见详解
【分析】(1)根据题意,可以画图找到答案,先写出1~24的编号,每次把报1的编号划掉,看最后剩下一名同学的编号是几,并从中找到规律。
(2)由上一题发现规律,剩下1人所需淘汰的次数为n时,这个同学的编号是2n;据此求出80个同学做这样的游戏,当剩下最后一人时的编号。
【详解】(1)如图:
第一次:24人剩12人
第二次:12人剩6人
第三次:6人剩3人
第四次:3人剩1人
24=16
答:当还剩下最后一人时,这个同学的帽子编号是16号。
(2)第一次:80人剩40人
第二次:40人剩20人
第三次:20人剩10人
第四次:10人剩5人
第五次:5人剩2人
第六次:2人剩1人
26=64
答:这个同学的帽子编号是64号。规律:最后一个同学的编号是2n的编号(n为剩下1人所需淘汰的次数)。
21.第三列
【分析】观察图形可知:除去第一行,其它各行的排列都是有规律的,也就是八个数字一组,每四个数字为一行,前四个数字分别占居一二三四列的位置,后四个数字分别占居二三四五列。所以本题需要用有余数除法来解决,先计算2000-5=1995,再用1995除以8,看余数是多少即可判断出2000应写在哪一列。
【详解】
=1995÷8
=249……3
2000应写在第三列。
答:2000应写在第三列。
【点睛】先找出这个数阵周期性的规律,再根据规律求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
