小升初分班考模拟测试卷(含解析)-2024-2025学年数学六年级下册北师大版
文档属性
| 名称 | 小升初分班考模拟测试卷(含解析)-2024-2025学年数学六年级下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 678.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考模拟测试卷-2024-2025学年数学六年级下册北师大版
一、选择题
1.不计算,判断下面的算式,得数正确的是( )。
A. B. C. D.
2.在,0.26, ,24%这四个数中,( )最大。
A. B.0.26 C. D.24%
3.一个小数,十位上的数字m,个位上的数字是0,十分位上的数字是n,根据每个数位上的计数单位,这个小数用含有字母的式子表示是( )。
A.m+0.1n B.m+n C.10m+n D.10m+0.1n
4.一批货物,第一次运走总量的20%,第二次运走余下货物的25%,两次运走货物的质量相比,( )。
A.第一次运走的多 B.第二次运走的多
C.两次一样多 D.无法比较
5.实验课上,四个小组分别调制了一杯蜂蜜水,最甜的是( )。
A.一组,用20克蜂蜜配成200克蜂蜜水。
B.二组,水的质量是蜂蜜的11倍。
C.三组,蜂蜜占蜂蜜水的12%。
D.四组,蜂蜜与水的质量比是1∶10。
二、填空题
6.某开发商按照分期付款的形式售房,张明家购买了一套现价为12万元的新房,购房时需首付(第一年)款3万元,从第二年起,以后每年应付房款5000元与上一年剩余欠款的利息之和。已知剩余欠款的年利率为,第( )年张明家需要交房款5200元。
7.已知,则的整数部分是( )。
8.古希腊毕达哥拉斯学派信奉“万物皆数”,将“数”排列成三角形、正方形等美丽的图形。如下图,排列成三角形的数叫作三角形数。照这样排列下去,第8个图形所表示的数是( )。
9.新龟兔赛跑故事里说,比赛开始后,跑在前面的兔子中途看到树荫,便设闹钟睡了一小觉。它醒来后发现乌龟跑到它前面一点,便飞速追赶,最后在乌龟前面到达终点,图( )描述了这个过程。第二次,小乌龟觉得仅凭自己的能力,再努力跑步也追不上兔子,便决定借助滑板赢得比赛,乌龟利用滑板再次跟兔子比赛,最终取得了胜利,图( )描述了这个过程。
10.如图,这是老师调查的六年级学生参加数学兴趣活动小组的情况统计图(每人只参加一项)。
(1)如果参加“数独”小组的有36人,六年级参加数学兴趣活动小组的一共有 ( )人。
(2)参加“七巧板”小组的人数比参加“数独”小组的多( )人。
11.如图,涂色部分是三角形和圆的重叠部分。已知涂色部分占圆面积的,又占三角形面积的,三角形面积是圆面积的( ),如果圆和三角形的面积之和是54cm2,圆的面积比三角形的面积大( )cm2。
12.《九章算术》中记载着一种求圆环面积的方法:“并中外周而半之,以径乘之为积步”。意思是:圆环面积=(内圆周长十外圆周长)÷2×径,径的长度是外圆半径与内圆半径的差。按照这样的计算公式,下图圆环的面积列式为( )。
13.为庆祝2024年建国75周年,某地准备建设观光塔和喷水池。如图,如果在地图上量得观光塔和喷水池图上距离是3厘米,喷水池在观光塔( )偏( )45°方向,实际距离是( )米。
14.2024年9月23日至10月6日,中国网球公开赛在北京国家网球中心举行,男子单打共32位选手,第一轮是分组循环赛,4人一组,组内每两位球员之间要进行一场比赛,每一小组内要比赛( )场;第一轮总共要比赛( )场。
15.一种树苗的成活率在80%-90%之间(包括80%和90%),要想保证成活棵数不少于360棵,至少要栽( )棵这种树苗。
三、判断题
16.2+3=5,2+5=7,所以两个质数的和一定是奇数。( )
17.a÷b=6……6,将a、b同时扩大到原来的10倍,则商不变,余数也不变。( )
18.(、均不为0),则>。( )
19.在同一平面内的两条直线,它们的位置关系不相交就是平行。( )
20.某地天气预报说:“明天的降水概率是10%”。根据这个预报,明天下雨的可能性小。( )
四、计算题
21.直接写出得数。
27+73= 78-0.8= 32÷0.01=
22.计算下面各题,能简算的要简算。
23.求未知数x。
(1) (2)
五、作图题
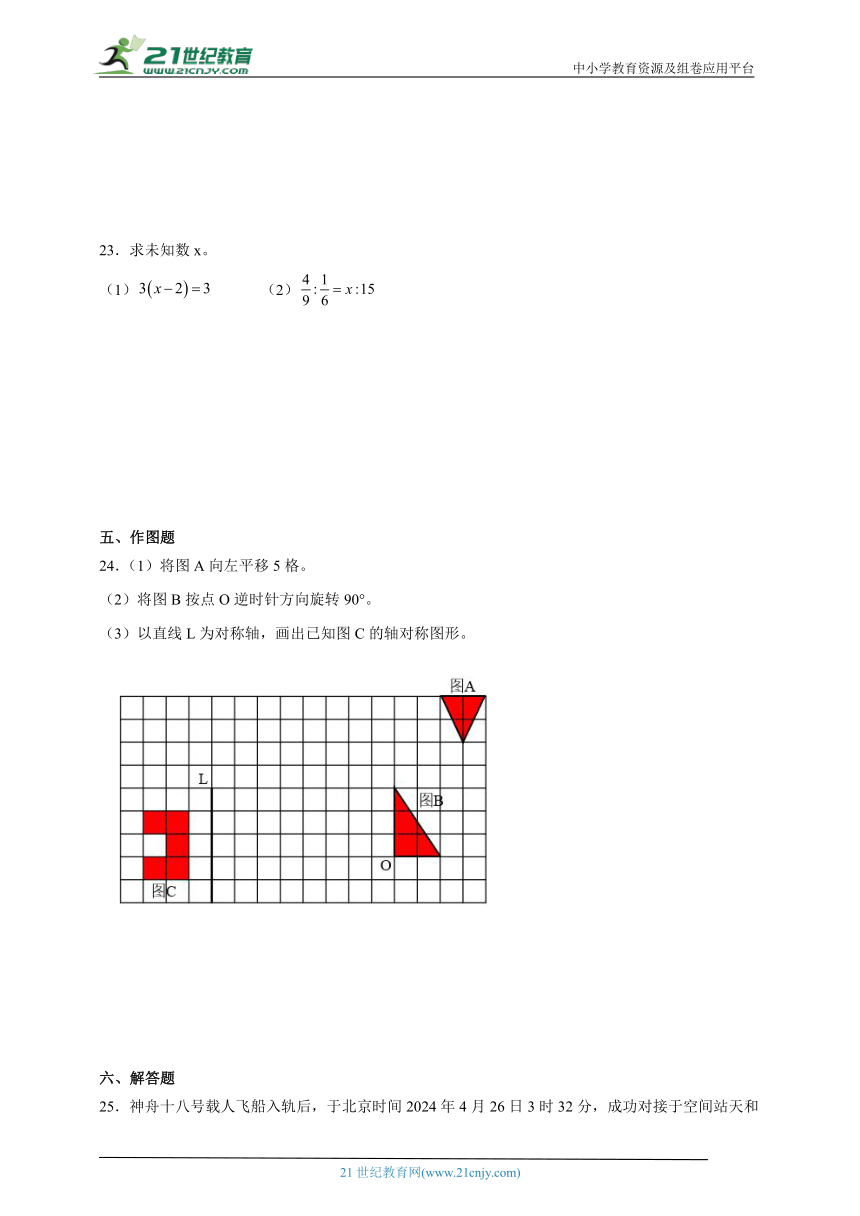
24.(1)将图A向左平移5格。
(2)将图B按点O逆时针方向旋转90°。
(3)以直线L为对称轴,画出已知图C的轴对称图形。
六、解答题
25.神舟十八号载人飞船入轨后,于北京时间2024年4月26日3时32分,成功对接于空间站天和核心舱径向端口。这是一个激动人心的时刻,6名宇航员在太空中举行了一次特别的“会师”,他们决定用一张合影来纪念这一历史性事件。某照相馆为宇航员们提供了一个特别的服务套餐,包括冲洗胶片和照片打印。套餐的基础费用是15元,这个费用包括了冲洗胶片和提供2张照片。如果宇航员们需要额外加印照片,照相馆每加印一张照片收取的费用是基础费用的。如果想要每位宇航员都得到一张照片,一共要支付多少钱?
26.两地间的路程是500千米,甲、乙两辆汽车同时从两地开出,相向而行,经过4小时相遇,甲车每小时行65千米,乙车每小时行多少千米?(先写出等量关系,再列方程解答)
27.六(2)班同学血型情况加图。该班有50人,O型血的人数占全班人数的百分之几?比A型血的人数多多少人?
28.陀螺在我国最少有四、五千年的历史,是民间最早的娱乐工具之一。小刚有一个底面直径是6厘米的木制陀螺(如图),这个陀螺的体积是多少立方厘米?
29.妈妈把150000元存入中国工商银行,定期2年,年利率是2.25%。到期后妈妈所获得的利息能买一台7000元的笔记本电脑吗?你是怎么想的?请说明理由。
30.红星口罩厂接到一批订单,原计划10天完成任务,由于急需口罩,工人们加班加点生产,实际每天生产了4.5万只,结果8天就完成了任务,原计划每天生产口罩多少万只?(用比例知识解答)
31.在奥运会比赛中,“铁人三项”是将游泳、自行车和跑步这三项运动结合起来的比赛项目。其中游泳此赛的距离是最短的,占三项比赛全程的,自行车和跑步这两项比赛的距离一共是50千米。“铁人三项”比赛的全程是多少千米?
32.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 0 1 2 3 4 5 6 …
路程/ 0 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗?
(3)列车运行2.5分时,行驶的路程是多少?
《小升初分班考模拟测试卷-2024-2025学年数学六年级下册北师大版》参考答案
题号 1 2 3 4 5
答案 B C D C C
1.B
【分析】观察各选项中的算式,这四个算式都是整数乘法,可以利用整数乘法的估算方法排除选项A和D,再根据选项B和C算式中的因数特点,积的末尾不可能有0排除选项C,所以得数正确的一组62×31=1922。
【详解】因为62×31≈60×30=1800,62×31的积比1800大,估算结果与2852相差太远,所以排除选项A和D,又因为相乘的两因数62和31末尾没有0,所以它两的积末尾不会有0,所以排除选项C,所以不计算,得数正确的一组是62×31=1922。
故答案为:B
2.C
【分析】将分数和百分数都化成小数,再比较。分数化小数,直接用分子÷分母;百分数化小数,去掉百分号,小数点向左移动两位即可。
【详解】=1÷4=0.25、=4÷15≈0.267、24%=0.24,>0.26>>24%
在,0.26, ,24%这四个数中,最大。
故答案为:C
3.D
【分析】一个一位小数,十位上的数字是m,表示m个10;个位上的数字是0,表示0个一;十分位上的数字是n,表示n个0.1,据此用含字母的式子表示这个数。
【详解】m×10+0+n×0.1
=10m+0.1n
所以这个小数用含有字母的式子表示是(10m+0.1n)。
故答案为:D
4.C
【分析】以总量为单位“1”,第一次运走总量的20%,还余下总量的1-20%=80%,第二次运走余下货物的25%,即第二次运走80%的25%,即运走总量的80%×25%=20%。据此比较判断即可。
【详解】(1-20%)×25%
=80%×25%
=20%
第一次运走总量的20%,第二次也运走总量的20%,两次运走货物一样多。
故答案为:C
5.C
【分析】根据含糖率=含糖质量÷总质量×100%,据此计算各选项的含糖率,再比较,含糖率最高的就是最甜的。
【详解】A.一组,用20克蜂蜜配成200克蜂蜜水,那么含糖率是:20÷200×100%=10%;
B.二组,水的质量是蜂蜜的11倍,把蜂蜜的质量看作1,则水的质量是11,那么含糖率是:1÷(1+11)×100%≈8.33%;
C.三组,蜂蜜占蜂蜜水的12%,那么含糖率是12%;
D.四组,蜂蜜与水的质量比是1∶10,那么含糖率是:1÷(1+10)×100%≈9.09%。
因为12%>10%>9.09%>8.33%,所以最甜的是三组。
故答案为:C
6.10
【分析】本题可以采用列方程来解决。先设第x年张明家需要交房款5200元。则可知这一年的剩余欠款金额数为:。再根据以后每年应付房款5000元与上一年剩余欠款的利息之和为5200元列出方程,即可解答。
【详解】解:设第x年张明家需要交房款5200元。
答:第10年张明家需要交房款5200元。
7.100
【分析】观察发现,可以先将所有的分数看作,则和一定小于20个;
同理,将所有的分数的看作,则和一定大于20个。
再分别算出的值,找出取值范围后得出整数部分。
【详解】
则的整数部分是100。
8.36
【分析】根据题意,第一个图形有1个点,表示1;第二个图形有3个点,表示3,可以写成:1+2=3;第三个图形有6个点,表示6,可以写成:1+2+3=6;第四个图形有10个点,表示10,可以写成:1+2+3+4=10;由此可知,第n个图形有(1+2+3++n)个点,表示(1+2+3++n),由此当n=8时,把8代入算式计算即可。
【详解】根据分析可知,第n个图形有(1+2+3++n)个点。
当n=8时,表示的数是:
1+2+3+4+5+6+7+8=36
古希腊毕达哥拉斯学派信奉“万物皆数”,将“数”排列成三角形、正方形等美丽的图形。如下图,排列成三角形的数叫作三角形数。照这样排列下去,第8个图形所表示的数是36。
9. A C
【分析】比赛中途兔子睡了一小觉,这时时间在增加,距离终点的路程不变,最后兔子在乌龟前面到达终点,说明比乌龟到达终点用的时间短,兔子胜;第二次,乌龟利用滑板再次跟兔子比赛,兔子没有睡觉,最终乌龟取得了胜利,它比兔子用的时间短。
图A表示兔子的折线中途时间在增加,但距离终点的路程不变,说明它在睡觉,而最终兔子取得胜利;图B乌龟和兔子同时到达终点;图C乌龟和兔子都没有休息,但同一时间,乌龟距离终点更近,说明它的速度更快,最终乌龟胜利;图D兔子睡了一觉,最终乌龟胜利。
【详解】通过分析可得:新龟兔赛跑故事里说,比赛开始后,跑在前面的兔子中途看到树荫,便设闹钟睡了一小觉。它醒来后发现乌龟跑到它前面一点,便飞速追赶,最后在乌龟前面到达终点,图A描述了这个过程。第二次,小乌龟觉得仅凭自己的能力,再努力跑步也追不上兔子,便决定借助滑板赢得比赛,乌龟利用滑板再次跟兔子比赛,最终取得了胜利,图C描述了这个过程。
10.(1)200
(2)12
【分析】(1)根据扇形统计图,把参加兴趣活动小组的总人数看作单位“1”,用单位“1”连续减去折纸、七巧板、五子棋人数所占的百分比,得到参加“数独”人数所占的百分比是18%,即总人数的18%是36人,已知一个数的百分之几是多少求这个数用除法,则用参加“数独”的人数除以参加“数独”所占的百分比,即可求出参加兴趣小组的总人数;
(2)用参加“七巧板”人数比参加“数独”人数多占的百分比乘总人数,即可求出参加“七巧板”小组的人数比参加“数独”小组多的人数。
【详解】(1)1-22%-24%-36%=18%
36÷18%=200(人)
则六年级参加数学兴趣活动小组的一共有200人。
(2)200×(24%-18%)
=200×6%
=12(人)
则参加“七巧板”小组的人数比参加“数独”小组的多12人。
11. 6
【分析】可以设涂色部分的面积是1,涂色部分占圆面积的,单位“1”是圆的面积,单位“1”未知,用除法,用1÷即可求出圆的面积;涂色部分还占三角形面积的,单位“1”是三角形的面积,单位“1”未知,用除法,即1÷求出三角形的面积,再用三角形的面积除以圆的面积即可求出三角形面积是圆面积的几分之几;
由于第一问求出三角形面积是圆面积的几分之几,分子相当于三角形的份数,分母相当于圆的份数,总份数的面积是54cm2,用54除以总份数求出1份量,再用一份量乘圆的面积份数与三角形面积的份数差即可求解。
【详解】可以设涂色部分面积是1。
圆的面积:1÷=1×5=5
三角形的面积:1÷=1×4=4
三角形面积是圆面积的4÷5=
54÷(4+5)×(5-4)
=54÷9×1
=6×1
=6(cm2)
涂色部分是三角形和圆的重叠部分。已知涂色部分占圆面积的,又占三角形面积的,三角形面积是圆面积的,如果圆和三角形的面积之和是54cm2,圆的面积比三角形的面积大6cm2。
12.(2×3.14×4+2×3.14×7)÷2×(7-4)
【分析】根据题意,圆环面积=(内圆周长十外圆周长)÷2×径,从图中可知,内圆的半径是4cm,外圆的半径是7cm;根据圆的周长公式C=2πr,径的长度是外圆半径与内圆半径的差,把数据代入圆环的面积公式中,据此列出算式。
【详解】内圆周长列式为:2×3.14×4
外圆周长列式为:2×3.14×7
圆环的面积列式为:(2×3.14×4+2×3.14×7)÷2×(7-4)。
13. 北 西 60
【分析】根据实际距离=图上距离÷比例尺,求出观光塔到喷水池的实际距离;再根据地图上方向的规定“上北下南,左西右东”,以观光塔为观察点,确定出喷水池的位置。
【详解】3÷
=3×2000
=6000(厘米)
6000厘米=60米
90°-45°=45°
喷水池在观光塔的北偏西45°(或西偏北45°)方向,实际距离是60米。
为庆祝2024年建国75周年,某地准备建设观光塔和喷水池。如图,如果在地图上量得观光塔和喷水池图上距离是3厘米,喷水池在观光塔的北偏西45°方向,实际距离是60米。
14. 6 48
【分析】4人一组,32人一共分成了8组。每一组内4人,两人进行比赛,组内第1个人分别要和第2、第3、第4人比赛,要比3场;组内第2个人分别要和第3、第4人比赛,要比2场,第3个人要和第4个人比1场,一共要比1+2+3=6场。所以8组一共有8×6=48场比赛。
【详解】1+2+3=6(场)
8×6=48(场)
所以每一小组内要比赛6场,第一轮一共有48场比赛。
15.450
【分析】根据成活率=成活棵数÷栽树总数的逆运算,用成活棵数除以成活率可得栽树总数,因成活率在80%-90%之间(包括80%和90%),要保证成功栽活360棵,就要用成活率最低的80%计算。据此解答。
【详解】(棵)
一种树苗的成活率在80%-90%之间(包括80%和90%),要想保证成活棵数不少于360棵,至少要栽450棵这种树苗。
16.×
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数;整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;举例说明。
【详解】例如:3和5是质数
3+5=8,8是偶数
5和7是质数
5+7=12,12是偶数
所以两个质数的和不一定是奇数,原题说法错误。
故答案为:×
17.×
【分析】商不变的规律,被除数和除数乘同一个不为0的数,商不变。
当被除数和除数同时扩大相同的倍数时,商不变,余数也扩大相同的倍数,据此判断即可。
【详解】a÷b=6……6
根据商不变的规律可知,将a、b同时扩大到原来的10倍,即a、b同时乘10,则商不变,余数也要乘10,即余数也要扩大到原来的10倍。
原题说法错误。
故答案为:×
18.√
【分析】根据一个乘数,等于积除以另一个乘数,假设×=×=1,分别求出a、b的值,然后比较即可解答。
【详解】假设×=×=1。
×=1
=1÷=1×==
×=1
=1÷=1×==
,所以>。
则(、均不为0),则>。故原说法正确。
故答案为:√
19.√
【分析】在同一平面内,直线间的关系有相交和平行。相交线:两条直线交于一点或是两条直线的延长线交于一点,我们称这两条直线相交,垂直是相交中的一种特殊情况。平行线:在同一平面内,不相交的两直线叫做平行线,它们的关系叫互相平行。
【详解】由分析可知:在同一平面内的两条直线,它们的位置关系不相交就是平行。
如图:
所以原题说法正确。
故答案为:√
20.√
【分析】降水概率10%表示明天下雨的可能性较小。在概率中,0%代表不可能发生,100%代表必然发生。10%属于较低的概率,通常认为可能性小。据此判断。
【详解】根据分析可知,“降水概率是10%”意味着明天下雨的可能性小。原题干说法正确。
故答案为:√
21.100;77.2;3200;0.03;
;0.001;a;36
【详解】略
22.10;6
【分析】,根据带符号搬家,将算式变为,然后根据括号的应用以及减法的性质,将算式变为进行简算即可;
,先把除法化为乘法,然后根据乘法分配律,将算式变为进行简算即可。
【详解】
23.(1);(2)
【分析】(1)根据等式的性质,方程两边同时除以3,再同时加上2即可;
(2)根据比例的基本性质,把式子转化为,再化简方程,最后根据等式的性质,方程两边同时除以即可。
【详解】(1)
解:3(x-2)÷3=3÷3
x-2=1
x-2+2=1+2
x=3
(2)
解:
24.(1)(2)(3)见详解
【分析】(1)根据平移的特征,将图A的各顶点分别向左平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图B按点O逆时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)补全轴对称图形的方法:找出图C的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)(2)(3)
【点睛】此题主要考查作轴对称图形、图形的平移和图形的旋转,掌握其作图方法是解答题目的关键。
25.27元
【分析】有6名宇航员,每人都得到一张照片,一共需要6张。拍照要付15元同时送2张照片,所以还需要加印4张照片。“照相馆每加印一张照片收取的费用是基础费用的”,基础费用是单位“1”,单位“1”已知,用分数乘法计算出加印一张照片的费用,进而计算出加印4张照片的费用,再加上基础费用就是一共要支付的钱数,据此解答即可。
【详解】宇航员有6人,基础费用已包含2张照片,所以还需加印4张。
加印费用:15××4=3×4=12(元)
总费用:15+12=27(元)
答:一共要支付27元。
26.(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程;60千米
【分析】找出等量关系,即(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程,据此设乙车每小时行x千米,列方程解答即可。
【详解】解:设乙车每小时行x千米。
答:乙车每小时行60千米。
【点睛】明确题中的等量关系是解题的关键。
27.40%;6人
【分析】把该班总人数看作单位“1”,用减法计算即可得O型血的人数占全班人数的百分之几;用该班的总人数分别乘O型血的人数和A型血的人数占总人数的百分率,再相减即可。
【详解】1-24%-28%-8%
=76%-28%-8%
=40%
50×40%-50×28%
=20-14
=6(人)
答:O型血的人数占全班人数的40%,O型血的人数比A型血的人数多6人。
【点睛】此题主要考查的是如何从扇形统计图中获取信息,然后再根据信息进行计算的能力。
28.113.04立方厘米
【分析】由题干可知,圆柱和圆锥是等底的,求圆柱和圆锥的体积之和就是陀螺的体积。分别利用圆柱和圆锥的体积公式求解即可。
【详解】3.14×(6÷2)2×3+×3.14×(6÷2)2×3
=3.14×32×3+×3×3.14×32
=3.14×9×3+3.14×9
=84.78+28.26
=113.04(立方厘米)
答:这个陀螺的体积是113.04立方厘米。
【点睛】此题考查的是圆柱和圆锥的体积公式的应用,熟记公式是解题关键。
29.不能,理由见解析
【分析】要求到期后妈妈所获得的利息能否买一台7000元的笔记本电脑,先根据利息的计算公式,求出利息,再与7000元比较,即可作出判断。
【详解】150000×2.25%×2=6750(元)
因为6750元<7000元,所以不能买一台7000元的笔记本电脑。
答:到期后妈妈所获得的利息不能买一台7000元的笔记本电脑。
【点睛】解答本题的关键是掌握利息的计算公式,即利息=本金×利率×时间。
30.3.6万只
【分析】由题意可知:这批订单所需口罩的总数量是一定的,即每天生产的口罩数量与生产时间的乘积是一定的,则每天生产的口罩数量与生产时间成反比例,据此即可列比例求解。
【详解】解:设原计划每天生产口罩x万只。
10×x=4.5×8
10x=36
x=36÷10
x=3.6
答:原计划每天生产口罩3.6万只。
【点睛】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
31.千米
【分析】把“铁人三项”比赛的全程看作单位“1”,其中游泳此赛的距离占三项比赛全程的,那么自行车和跑步这两项比赛的距离50千米占比赛全程的(1-),单位“1”未知,根据分数除法的意义求出“铁人三项”比赛的全程。
【详解】50÷(1-)
=50÷
=50×
=(千米)
答:“铁人三项”比赛的全程是千米。
32.(1)图见详解
(2)在
(3)17.5千米
【分析】(1)结合表格中的数据,先在图中的横轴上找到时间,再在纵轴上找到对应的路程,横轴和纵轴交叉的点就在该时间对应行驶的路程,据此在图中描出各点。
(2)连接各点,得出它们是否在一条直线上。
(3)因为磁悬浮列车匀速行驶,已知行驶1分的路程是7千米,据此得出磁悬浮列车的速度;再根据“路程=速度×时间”求出列车运行2.5分时行驶的路程。
【详解】(1)描出表中的各点,如下图。
(2)连接各点,它们在一条直线上。
如下图:
(3)7÷1=7(千米/分)
7×2.5=17.5(千米)
答:列车运行2.5分时,行驶的路程是17.5千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考模拟测试卷-2024-2025学年数学六年级下册北师大版
一、选择题
1.不计算,判断下面的算式,得数正确的是( )。
A. B. C. D.
2.在,0.26, ,24%这四个数中,( )最大。
A. B.0.26 C. D.24%
3.一个小数,十位上的数字m,个位上的数字是0,十分位上的数字是n,根据每个数位上的计数单位,这个小数用含有字母的式子表示是( )。
A.m+0.1n B.m+n C.10m+n D.10m+0.1n
4.一批货物,第一次运走总量的20%,第二次运走余下货物的25%,两次运走货物的质量相比,( )。
A.第一次运走的多 B.第二次运走的多
C.两次一样多 D.无法比较
5.实验课上,四个小组分别调制了一杯蜂蜜水,最甜的是( )。
A.一组,用20克蜂蜜配成200克蜂蜜水。
B.二组,水的质量是蜂蜜的11倍。
C.三组,蜂蜜占蜂蜜水的12%。
D.四组,蜂蜜与水的质量比是1∶10。
二、填空题
6.某开发商按照分期付款的形式售房,张明家购买了一套现价为12万元的新房,购房时需首付(第一年)款3万元,从第二年起,以后每年应付房款5000元与上一年剩余欠款的利息之和。已知剩余欠款的年利率为,第( )年张明家需要交房款5200元。
7.已知,则的整数部分是( )。
8.古希腊毕达哥拉斯学派信奉“万物皆数”,将“数”排列成三角形、正方形等美丽的图形。如下图,排列成三角形的数叫作三角形数。照这样排列下去,第8个图形所表示的数是( )。
9.新龟兔赛跑故事里说,比赛开始后,跑在前面的兔子中途看到树荫,便设闹钟睡了一小觉。它醒来后发现乌龟跑到它前面一点,便飞速追赶,最后在乌龟前面到达终点,图( )描述了这个过程。第二次,小乌龟觉得仅凭自己的能力,再努力跑步也追不上兔子,便决定借助滑板赢得比赛,乌龟利用滑板再次跟兔子比赛,最终取得了胜利,图( )描述了这个过程。
10.如图,这是老师调查的六年级学生参加数学兴趣活动小组的情况统计图(每人只参加一项)。
(1)如果参加“数独”小组的有36人,六年级参加数学兴趣活动小组的一共有 ( )人。
(2)参加“七巧板”小组的人数比参加“数独”小组的多( )人。
11.如图,涂色部分是三角形和圆的重叠部分。已知涂色部分占圆面积的,又占三角形面积的,三角形面积是圆面积的( ),如果圆和三角形的面积之和是54cm2,圆的面积比三角形的面积大( )cm2。
12.《九章算术》中记载着一种求圆环面积的方法:“并中外周而半之,以径乘之为积步”。意思是:圆环面积=(内圆周长十外圆周长)÷2×径,径的长度是外圆半径与内圆半径的差。按照这样的计算公式,下图圆环的面积列式为( )。
13.为庆祝2024年建国75周年,某地准备建设观光塔和喷水池。如图,如果在地图上量得观光塔和喷水池图上距离是3厘米,喷水池在观光塔( )偏( )45°方向,实际距离是( )米。
14.2024年9月23日至10月6日,中国网球公开赛在北京国家网球中心举行,男子单打共32位选手,第一轮是分组循环赛,4人一组,组内每两位球员之间要进行一场比赛,每一小组内要比赛( )场;第一轮总共要比赛( )场。
15.一种树苗的成活率在80%-90%之间(包括80%和90%),要想保证成活棵数不少于360棵,至少要栽( )棵这种树苗。
三、判断题
16.2+3=5,2+5=7,所以两个质数的和一定是奇数。( )
17.a÷b=6……6,将a、b同时扩大到原来的10倍,则商不变,余数也不变。( )
18.(、均不为0),则>。( )
19.在同一平面内的两条直线,它们的位置关系不相交就是平行。( )
20.某地天气预报说:“明天的降水概率是10%”。根据这个预报,明天下雨的可能性小。( )
四、计算题
21.直接写出得数。
27+73= 78-0.8= 32÷0.01=
22.计算下面各题,能简算的要简算。
23.求未知数x。
(1) (2)
五、作图题
24.(1)将图A向左平移5格。
(2)将图B按点O逆时针方向旋转90°。
(3)以直线L为对称轴,画出已知图C的轴对称图形。
六、解答题
25.神舟十八号载人飞船入轨后,于北京时间2024年4月26日3时32分,成功对接于空间站天和核心舱径向端口。这是一个激动人心的时刻,6名宇航员在太空中举行了一次特别的“会师”,他们决定用一张合影来纪念这一历史性事件。某照相馆为宇航员们提供了一个特别的服务套餐,包括冲洗胶片和照片打印。套餐的基础费用是15元,这个费用包括了冲洗胶片和提供2张照片。如果宇航员们需要额外加印照片,照相馆每加印一张照片收取的费用是基础费用的。如果想要每位宇航员都得到一张照片,一共要支付多少钱?
26.两地间的路程是500千米,甲、乙两辆汽车同时从两地开出,相向而行,经过4小时相遇,甲车每小时行65千米,乙车每小时行多少千米?(先写出等量关系,再列方程解答)
27.六(2)班同学血型情况加图。该班有50人,O型血的人数占全班人数的百分之几?比A型血的人数多多少人?
28.陀螺在我国最少有四、五千年的历史,是民间最早的娱乐工具之一。小刚有一个底面直径是6厘米的木制陀螺(如图),这个陀螺的体积是多少立方厘米?
29.妈妈把150000元存入中国工商银行,定期2年,年利率是2.25%。到期后妈妈所获得的利息能买一台7000元的笔记本电脑吗?你是怎么想的?请说明理由。
30.红星口罩厂接到一批订单,原计划10天完成任务,由于急需口罩,工人们加班加点生产,实际每天生产了4.5万只,结果8天就完成了任务,原计划每天生产口罩多少万只?(用比例知识解答)
31.在奥运会比赛中,“铁人三项”是将游泳、自行车和跑步这三项运动结合起来的比赛项目。其中游泳此赛的距离是最短的,占三项比赛全程的,自行车和跑步这两项比赛的距离一共是50千米。“铁人三项”比赛的全程是多少千米?
32.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 0 1 2 3 4 5 6 …
路程/ 0 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗?
(3)列车运行2.5分时,行驶的路程是多少?
《小升初分班考模拟测试卷-2024-2025学年数学六年级下册北师大版》参考答案
题号 1 2 3 4 5
答案 B C D C C
1.B
【分析】观察各选项中的算式,这四个算式都是整数乘法,可以利用整数乘法的估算方法排除选项A和D,再根据选项B和C算式中的因数特点,积的末尾不可能有0排除选项C,所以得数正确的一组62×31=1922。
【详解】因为62×31≈60×30=1800,62×31的积比1800大,估算结果与2852相差太远,所以排除选项A和D,又因为相乘的两因数62和31末尾没有0,所以它两的积末尾不会有0,所以排除选项C,所以不计算,得数正确的一组是62×31=1922。
故答案为:B
2.C
【分析】将分数和百分数都化成小数,再比较。分数化小数,直接用分子÷分母;百分数化小数,去掉百分号,小数点向左移动两位即可。
【详解】=1÷4=0.25、=4÷15≈0.267、24%=0.24,>0.26>>24%
在,0.26, ,24%这四个数中,最大。
故答案为:C
3.D
【分析】一个一位小数,十位上的数字是m,表示m个10;个位上的数字是0,表示0个一;十分位上的数字是n,表示n个0.1,据此用含字母的式子表示这个数。
【详解】m×10+0+n×0.1
=10m+0.1n
所以这个小数用含有字母的式子表示是(10m+0.1n)。
故答案为:D
4.C
【分析】以总量为单位“1”,第一次运走总量的20%,还余下总量的1-20%=80%,第二次运走余下货物的25%,即第二次运走80%的25%,即运走总量的80%×25%=20%。据此比较判断即可。
【详解】(1-20%)×25%
=80%×25%
=20%
第一次运走总量的20%,第二次也运走总量的20%,两次运走货物一样多。
故答案为:C
5.C
【分析】根据含糖率=含糖质量÷总质量×100%,据此计算各选项的含糖率,再比较,含糖率最高的就是最甜的。
【详解】A.一组,用20克蜂蜜配成200克蜂蜜水,那么含糖率是:20÷200×100%=10%;
B.二组,水的质量是蜂蜜的11倍,把蜂蜜的质量看作1,则水的质量是11,那么含糖率是:1÷(1+11)×100%≈8.33%;
C.三组,蜂蜜占蜂蜜水的12%,那么含糖率是12%;
D.四组,蜂蜜与水的质量比是1∶10,那么含糖率是:1÷(1+10)×100%≈9.09%。
因为12%>10%>9.09%>8.33%,所以最甜的是三组。
故答案为:C
6.10
【分析】本题可以采用列方程来解决。先设第x年张明家需要交房款5200元。则可知这一年的剩余欠款金额数为:。再根据以后每年应付房款5000元与上一年剩余欠款的利息之和为5200元列出方程,即可解答。
【详解】解:设第x年张明家需要交房款5200元。
答:第10年张明家需要交房款5200元。
7.100
【分析】观察发现,可以先将所有的分数看作,则和一定小于20个;
同理,将所有的分数的看作,则和一定大于20个。
再分别算出的值,找出取值范围后得出整数部分。
【详解】
则的整数部分是100。
8.36
【分析】根据题意,第一个图形有1个点,表示1;第二个图形有3个点,表示3,可以写成:1+2=3;第三个图形有6个点,表示6,可以写成:1+2+3=6;第四个图形有10个点,表示10,可以写成:1+2+3+4=10;由此可知,第n个图形有(1+2+3++n)个点,表示(1+2+3++n),由此当n=8时,把8代入算式计算即可。
【详解】根据分析可知,第n个图形有(1+2+3++n)个点。
当n=8时,表示的数是:
1+2+3+4+5+6+7+8=36
古希腊毕达哥拉斯学派信奉“万物皆数”,将“数”排列成三角形、正方形等美丽的图形。如下图,排列成三角形的数叫作三角形数。照这样排列下去,第8个图形所表示的数是36。
9. A C
【分析】比赛中途兔子睡了一小觉,这时时间在增加,距离终点的路程不变,最后兔子在乌龟前面到达终点,说明比乌龟到达终点用的时间短,兔子胜;第二次,乌龟利用滑板再次跟兔子比赛,兔子没有睡觉,最终乌龟取得了胜利,它比兔子用的时间短。
图A表示兔子的折线中途时间在增加,但距离终点的路程不变,说明它在睡觉,而最终兔子取得胜利;图B乌龟和兔子同时到达终点;图C乌龟和兔子都没有休息,但同一时间,乌龟距离终点更近,说明它的速度更快,最终乌龟胜利;图D兔子睡了一觉,最终乌龟胜利。
【详解】通过分析可得:新龟兔赛跑故事里说,比赛开始后,跑在前面的兔子中途看到树荫,便设闹钟睡了一小觉。它醒来后发现乌龟跑到它前面一点,便飞速追赶,最后在乌龟前面到达终点,图A描述了这个过程。第二次,小乌龟觉得仅凭自己的能力,再努力跑步也追不上兔子,便决定借助滑板赢得比赛,乌龟利用滑板再次跟兔子比赛,最终取得了胜利,图C描述了这个过程。
10.(1)200
(2)12
【分析】(1)根据扇形统计图,把参加兴趣活动小组的总人数看作单位“1”,用单位“1”连续减去折纸、七巧板、五子棋人数所占的百分比,得到参加“数独”人数所占的百分比是18%,即总人数的18%是36人,已知一个数的百分之几是多少求这个数用除法,则用参加“数独”的人数除以参加“数独”所占的百分比,即可求出参加兴趣小组的总人数;
(2)用参加“七巧板”人数比参加“数独”人数多占的百分比乘总人数,即可求出参加“七巧板”小组的人数比参加“数独”小组多的人数。
【详解】(1)1-22%-24%-36%=18%
36÷18%=200(人)
则六年级参加数学兴趣活动小组的一共有200人。
(2)200×(24%-18%)
=200×6%
=12(人)
则参加“七巧板”小组的人数比参加“数独”小组的多12人。
11. 6
【分析】可以设涂色部分的面积是1,涂色部分占圆面积的,单位“1”是圆的面积,单位“1”未知,用除法,用1÷即可求出圆的面积;涂色部分还占三角形面积的,单位“1”是三角形的面积,单位“1”未知,用除法,即1÷求出三角形的面积,再用三角形的面积除以圆的面积即可求出三角形面积是圆面积的几分之几;
由于第一问求出三角形面积是圆面积的几分之几,分子相当于三角形的份数,分母相当于圆的份数,总份数的面积是54cm2,用54除以总份数求出1份量,再用一份量乘圆的面积份数与三角形面积的份数差即可求解。
【详解】可以设涂色部分面积是1。
圆的面积:1÷=1×5=5
三角形的面积:1÷=1×4=4
三角形面积是圆面积的4÷5=
54÷(4+5)×(5-4)
=54÷9×1
=6×1
=6(cm2)
涂色部分是三角形和圆的重叠部分。已知涂色部分占圆面积的,又占三角形面积的,三角形面积是圆面积的,如果圆和三角形的面积之和是54cm2,圆的面积比三角形的面积大6cm2。
12.(2×3.14×4+2×3.14×7)÷2×(7-4)
【分析】根据题意,圆环面积=(内圆周长十外圆周长)÷2×径,从图中可知,内圆的半径是4cm,外圆的半径是7cm;根据圆的周长公式C=2πr,径的长度是外圆半径与内圆半径的差,把数据代入圆环的面积公式中,据此列出算式。
【详解】内圆周长列式为:2×3.14×4
外圆周长列式为:2×3.14×7
圆环的面积列式为:(2×3.14×4+2×3.14×7)÷2×(7-4)。
13. 北 西 60
【分析】根据实际距离=图上距离÷比例尺,求出观光塔到喷水池的实际距离;再根据地图上方向的规定“上北下南,左西右东”,以观光塔为观察点,确定出喷水池的位置。
【详解】3÷
=3×2000
=6000(厘米)
6000厘米=60米
90°-45°=45°
喷水池在观光塔的北偏西45°(或西偏北45°)方向,实际距离是60米。
为庆祝2024年建国75周年,某地准备建设观光塔和喷水池。如图,如果在地图上量得观光塔和喷水池图上距离是3厘米,喷水池在观光塔的北偏西45°方向,实际距离是60米。
14. 6 48
【分析】4人一组,32人一共分成了8组。每一组内4人,两人进行比赛,组内第1个人分别要和第2、第3、第4人比赛,要比3场;组内第2个人分别要和第3、第4人比赛,要比2场,第3个人要和第4个人比1场,一共要比1+2+3=6场。所以8组一共有8×6=48场比赛。
【详解】1+2+3=6(场)
8×6=48(场)
所以每一小组内要比赛6场,第一轮一共有48场比赛。
15.450
【分析】根据成活率=成活棵数÷栽树总数的逆运算,用成活棵数除以成活率可得栽树总数,因成活率在80%-90%之间(包括80%和90%),要保证成功栽活360棵,就要用成活率最低的80%计算。据此解答。
【详解】(棵)
一种树苗的成活率在80%-90%之间(包括80%和90%),要想保证成活棵数不少于360棵,至少要栽450棵这种树苗。
16.×
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数;一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数;整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;举例说明。
【详解】例如:3和5是质数
3+5=8,8是偶数
5和7是质数
5+7=12,12是偶数
所以两个质数的和不一定是奇数,原题说法错误。
故答案为:×
17.×
【分析】商不变的规律,被除数和除数乘同一个不为0的数,商不变。
当被除数和除数同时扩大相同的倍数时,商不变,余数也扩大相同的倍数,据此判断即可。
【详解】a÷b=6……6
根据商不变的规律可知,将a、b同时扩大到原来的10倍,即a、b同时乘10,则商不变,余数也要乘10,即余数也要扩大到原来的10倍。
原题说法错误。
故答案为:×
18.√
【分析】根据一个乘数,等于积除以另一个乘数,假设×=×=1,分别求出a、b的值,然后比较即可解答。
【详解】假设×=×=1。
×=1
=1÷=1×==
×=1
=1÷=1×==
,所以>。
则(、均不为0),则>。故原说法正确。
故答案为:√
19.√
【分析】在同一平面内,直线间的关系有相交和平行。相交线:两条直线交于一点或是两条直线的延长线交于一点,我们称这两条直线相交,垂直是相交中的一种特殊情况。平行线:在同一平面内,不相交的两直线叫做平行线,它们的关系叫互相平行。
【详解】由分析可知:在同一平面内的两条直线,它们的位置关系不相交就是平行。
如图:
所以原题说法正确。
故答案为:√
20.√
【分析】降水概率10%表示明天下雨的可能性较小。在概率中,0%代表不可能发生,100%代表必然发生。10%属于较低的概率,通常认为可能性小。据此判断。
【详解】根据分析可知,“降水概率是10%”意味着明天下雨的可能性小。原题干说法正确。
故答案为:√
21.100;77.2;3200;0.03;
;0.001;a;36
【详解】略
22.10;6
【分析】,根据带符号搬家,将算式变为,然后根据括号的应用以及减法的性质,将算式变为进行简算即可;
,先把除法化为乘法,然后根据乘法分配律,将算式变为进行简算即可。
【详解】
23.(1);(2)
【分析】(1)根据等式的性质,方程两边同时除以3,再同时加上2即可;
(2)根据比例的基本性质,把式子转化为,再化简方程,最后根据等式的性质,方程两边同时除以即可。
【详解】(1)
解:3(x-2)÷3=3÷3
x-2=1
x-2+2=1+2
x=3
(2)
解:
24.(1)(2)(3)见详解
【分析】(1)根据平移的特征,将图A的各顶点分别向左平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图B按点O逆时针方向旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)补全轴对称图形的方法:找出图C的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)(2)(3)
【点睛】此题主要考查作轴对称图形、图形的平移和图形的旋转,掌握其作图方法是解答题目的关键。
25.27元
【分析】有6名宇航员,每人都得到一张照片,一共需要6张。拍照要付15元同时送2张照片,所以还需要加印4张照片。“照相馆每加印一张照片收取的费用是基础费用的”,基础费用是单位“1”,单位“1”已知,用分数乘法计算出加印一张照片的费用,进而计算出加印4张照片的费用,再加上基础费用就是一共要支付的钱数,据此解答即可。
【详解】宇航员有6人,基础费用已包含2张照片,所以还需加印4张。
加印费用:15××4=3×4=12(元)
总费用:15+12=27(元)
答:一共要支付27元。
26.(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程;60千米
【分析】找出等量关系,即(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程,据此设乙车每小时行x千米,列方程解答即可。
【详解】解:设乙车每小时行x千米。
答:乙车每小时行60千米。
【点睛】明确题中的等量关系是解题的关键。
27.40%;6人
【分析】把该班总人数看作单位“1”,用减法计算即可得O型血的人数占全班人数的百分之几;用该班的总人数分别乘O型血的人数和A型血的人数占总人数的百分率,再相减即可。
【详解】1-24%-28%-8%
=76%-28%-8%
=40%
50×40%-50×28%
=20-14
=6(人)
答:O型血的人数占全班人数的40%,O型血的人数比A型血的人数多6人。
【点睛】此题主要考查的是如何从扇形统计图中获取信息,然后再根据信息进行计算的能力。
28.113.04立方厘米
【分析】由题干可知,圆柱和圆锥是等底的,求圆柱和圆锥的体积之和就是陀螺的体积。分别利用圆柱和圆锥的体积公式求解即可。
【详解】3.14×(6÷2)2×3+×3.14×(6÷2)2×3
=3.14×32×3+×3×3.14×32
=3.14×9×3+3.14×9
=84.78+28.26
=113.04(立方厘米)
答:这个陀螺的体积是113.04立方厘米。
【点睛】此题考查的是圆柱和圆锥的体积公式的应用,熟记公式是解题关键。
29.不能,理由见解析
【分析】要求到期后妈妈所获得的利息能否买一台7000元的笔记本电脑,先根据利息的计算公式,求出利息,再与7000元比较,即可作出判断。
【详解】150000×2.25%×2=6750(元)
因为6750元<7000元,所以不能买一台7000元的笔记本电脑。
答:到期后妈妈所获得的利息不能买一台7000元的笔记本电脑。
【点睛】解答本题的关键是掌握利息的计算公式,即利息=本金×利率×时间。
30.3.6万只
【分析】由题意可知:这批订单所需口罩的总数量是一定的,即每天生产的口罩数量与生产时间的乘积是一定的,则每天生产的口罩数量与生产时间成反比例,据此即可列比例求解。
【详解】解:设原计划每天生产口罩x万只。
10×x=4.5×8
10x=36
x=36÷10
x=3.6
答:原计划每天生产口罩3.6万只。
【点睛】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
31.千米
【分析】把“铁人三项”比赛的全程看作单位“1”,其中游泳此赛的距离占三项比赛全程的,那么自行车和跑步这两项比赛的距离50千米占比赛全程的(1-),单位“1”未知,根据分数除法的意义求出“铁人三项”比赛的全程。
【详解】50÷(1-)
=50÷
=50×
=(千米)
答:“铁人三项”比赛的全程是千米。
32.(1)图见详解
(2)在
(3)17.5千米
【分析】(1)结合表格中的数据,先在图中的横轴上找到时间,再在纵轴上找到对应的路程,横轴和纵轴交叉的点就在该时间对应行驶的路程,据此在图中描出各点。
(2)连接各点,得出它们是否在一条直线上。
(3)因为磁悬浮列车匀速行驶,已知行驶1分的路程是7千米,据此得出磁悬浮列车的速度;再根据“路程=速度×时间”求出列车运行2.5分时行驶的路程。
【详解】(1)描出表中的各点,如下图。
(2)连接各点,它们在一条直线上。
如下图:
(3)7÷1=7(千米/分)
7×2.5=17.5(千米)
答:列车运行2.5分时,行驶的路程是17.5千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
