专项2 填空题2 (天津中考真题+中考模拟)(含答案) —2025年中考数学冲刺中考模拟真题速递(天津专用)
文档属性
| 名称 | 专项2 填空题2 (天津中考真题+中考模拟)(含答案) —2025年中考数学冲刺中考模拟真题速递(天津专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 545.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 00:00:00 | ||
图片预览




文档简介
2025年中考数学冲刺中考模拟真题速递(天津专用)
专项2 填空题2 (天津中考真题+中考模拟)
一、填空题
1.(2024·天津)若正比例函数(是常数,)的图象经过第一、第三象限,则的值可以是 (写出一个即可).
2.(2024·天津) 如图,在每个小正方形的边长为1的网格中,点均在格点上.
(1)线段的长为 ;
(2)点在水平网格线上,过点作圆,经过圆与水平网格线的交点作切线,分别与的延长线相交于点中,点在边上,点在边上,点在边上.请用无刻度的直尺,在如图所示的网格中,画出点,使的周长最短,并简要说明点的位置是如何找到的(不要求证明).
3.(2024九下·天津市模拟)如图,正方形的边长为4,点E是边的中点,,交正方形外角的平分线于点F.
(1)的面积为 ;
(2)若M是的中点,连接,则的长为 .
4.(2024九下·天津市模拟)一个不透明的袋子里装有13个球,其中有6个黑球和7个白球,这些球除颜色外无其他差别.从袋中随机取出一个球,则它是黑球的概率为 .
5.(2024九下·天津市模拟)若将直线向下平移2个单位长度后经过点,则的值为 .
6.(2024九下·天津市模拟)有一个运算程序,可以使:(为常数)时,得,,现在已知,那么 .
7.(2024九下·天津市模拟)如图,在中,,分别为,的中点,点F在线段上,且.若,,则的长为 .
8.(2024九下·河西模拟)如图,在四边形中,,,连接对角线AC、BD,,,若为的中点,为的中点,连接.
(Ⅰ)四边形的面积为 .
(Ⅱ)的长为 .
9.(2024九下·河西模拟)若点在一次函数的图象上,则这个点可以是 (任意写出一个具体的点即可),
10.(2024九下·河西模拟)不透明袋子中装有6个球,其中有1个粉色球和5个蓝色球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是蓝色球的概率为 .
11.(2024九下·河西模拟)计算的结果为 .
12.(2024九下·河东模拟)如图,E为平行四边形外一点,且满足,,,.
(Ⅰ)平行四边形的面积为 ;
(Ⅱ)若点M,N分别在线段,上,连接,当时,连接,,的最小值为 .
13.(2024九下·河东模拟)一次函数的图象向上平移3个单位后,经过点关于原点的对称点,则m的值为 .
14.(2024九下·河东模拟)计算的结果为 .
15.(2024九下·河北模拟)如图, 正方形的边长为,作以为底的等腰三角形,
(1)的面积为 ;
(2)若,分别为,的中点,为的中点,射线,相交于点, 则的长为 .
16.(2024九下·河北模拟)已知直线向下平移个单位后经过点,则值为 .
17.(2024九下·河北模拟)不透明的袋子中装有个球,其中有个红球,个绿球,个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,则它是绿球的概率为 .
18.(2024九下·和平模拟)如图,正方形的边长为4,点在边上,,作等腰直角三角形.
(1)的长为 .
(2)若为AF的中点,连接DM,则DM的长为 .
19.(2024九下·和平模拟)若直线(a为常数)经过点,则它与轴的交点坐标为 .
20.(2024九下·和平模拟)计算的结果为 .
21.(2024九下·和平模拟)不透明袋子中装有个球,其中有个红球、个黑球,这些球除颜色外无其他差别.从袋子中随机取出个球,则它是黑球的概率是 .
22.(2024九下·南开模拟)计算的结果是 .
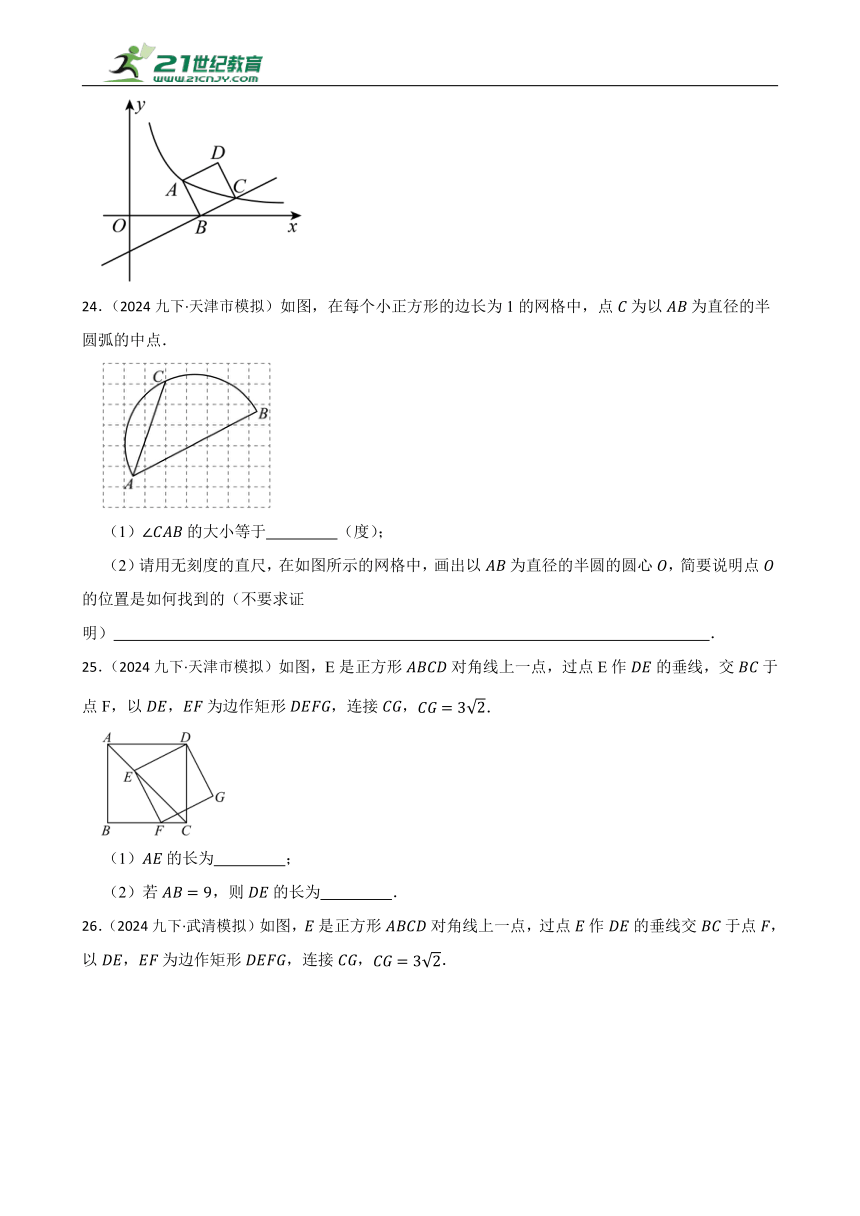
23.(2024九下·天津市模拟)如图,正方形的顶点在轴上,点A和点C在反比例函数图象上,若直线的函数表达式为,则的值为 .
24.(2024九下·天津市模拟)如图,在每个小正方形的边长为1的网格中,点为以为直径的半圆弧的中点.
(1)的大小等于 (度);
(2)请用无刻度的直尺,在如图所示的网格中,画出以为直径的半圆的圆心,简要说明点的位置是如何找到的(不要求证明) .
25.(2024九下·天津市模拟)如图,E是正方形对角线上一点,过点E作的垂线,交于点F,以,为边作矩形,连接,
(1)的长为 ;
(2)若,则的长为 .
26.(2024九下·武清模拟)如图,是正方形对角线上一点,过点作的垂线交于点,以,为边作矩形,连接,.
(1)的长为 ;
(2)若,则的长为 .
27.(2024九下·天津市模拟)写出一个过点且随的增大而增大的一次函数解析式 .(写出一个即可)
28.(2024九下·天津市模拟)计算的结果等于 .
29.(2024九下·河东模拟)如图,在中,,,点在外,连接,过点作,交于点,连接,若,则
(Ⅰ)线段的长等于;
(Ⅱ)的面积为.
30.(2024九下·河东模拟)一次函数的图像向下平移个单位后经过点,则的值为.
31.(2024九下·河东模拟)计算的结果为.
32.(2024九下·河东模拟)一个不透明的袋子里装有2个绿球、3个黑球和6个红球,它们除颜色外其余相同,从袋中任意摸出一个球为绿球的概率为.
33.(2024九下·南开模拟)如图,在等腰中,,过点C作,连接,交于点,点为中点,连接,,若,则.
34.(2024九下·南开模拟)直线与x轴交于点,与y轴交于点,将直线沿y轴向下平移2个单位长度得到直线l,则直线l的解析式为.
35.(2024九下·南开模拟)计算的结果为.
36.(2024九下·南开模拟)计算的结果是.
37.(2024九下·河北模拟)如图,在边长为6的正方形中,点M为的中点,点E在上,,等腰三角形中,.
(1)的面积为 ;
(2)若N为的中点,则的值为 .
38.(2024九下·天津市模拟)不透明袋子中装有9个球,其中有2个红球、7个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .
39.(2024九下·津南模拟)如图,点M为正方形边上一动点,,将点M绕点P顺时针旋转到点N,若分别为中点,则的最小值为 .
40.(2024九下·津南模拟)用“筝形”和“镖形”两种不同的瓷砖铺设成如图所示的地面,则“筝形”瓷砖中的内角 °.
41.(2024九下·津南模拟) .
42.(2024九下·和平模拟)如图,已知半圆的直径长为2,点为中点,为上任意一点,与相交于点.
(1) (度);
(2)的最小值为 .
43.(2024九下·和平模拟)已知点,在反比例函数的图象上.如果,则,的大小关系为: .
44.(2024九下·和平模拟)不透明袋子中装有9个球,其中有3个黄球、6个红球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是黄球的概率为 .
45.(2024九下·西青模拟)计算的结果是 .
46.(2024九下·天津市模拟)= .
47.(2024九下·滨海模拟)如图,在每个小正方形的边长为1的网格中,等边三角形内接于圆,且顶点A,B均在格点上.
(1)线段的长为 ;
(2)圆与格线交于点,点为线段上一动点,当取得最小值时,请利用无刻度的直尺,在如图所示的网格中,画出点,并简要说明点的位置是如何找到的(不要求证明) .
48.(2024·红桥模拟)如图, 在矩形中,,, 以点B为圆心,适当长为半径画弧,分别交,于点E,F,再分别以点E,F为圆心, 大于 长为半径画弧(弧所在圆的半径相等),两弧相交于点P,作射线,过点C作的垂线分别交,于点M,N,垂足为O,则的长为 .
49.(2024·红桥模拟)一个不透明的袋子里装有个球,其中有个红球,个白球,这些球除颜色外其它均相同.现从中随机摸出一个球,则摸出的球是白球的概率为 .
50.(2024九下·滨海模拟)不透明袋子中装有9个球,其中有7个绿球、2个白球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是绿球的概率是 .
答案解析部分
1.1(答案不唯一)
∵正比例函数的图象经过第一、第三象限,
∴k>0,
故答案为:1(答案不唯一).
利用一次函数的图象与系数的关系判断出k>0,再求解即可.
2.(1)
(2)解:如图,根据题意,切点为M;连接ME并延长,与网格线相交于点M1;取圆与网格线的交点D和格点H,连接DH并延长,与网格线相交于点M2;连接M1M2,分别与AB ,AC相交于点N,P,则点M,N,P即为所求.
解:(1)AG2=12+12=2,
∴AG=;
故答案为:;
(1)根据勾股定理即可得出结论;
(2)作点M关于AB,AC的对称点M1和M2,连接M1M2,与ABAC相较于点NP,△PMN的周长=线段M1M2的长度,等腰三角形AM1M2的腰长为AM,当AM的值最小时,M1M2的值最小,此时M是切点,由此作图即可。
3.12;
4.
5.1
6.
7.
8.40;
9.(答案不唯一)
10.
11.
12.;
13.
14.
15.;
16.
17.
18.;
19.
20.
21.
22.
23.6
24.;取圆上两个格点,,再作的垂直平分线与的交点即为圆心
25.;
26.;
27.(答案不唯一)
28.
29.2,5
30.
31.18
32.
33.5
34.
35.
36.
37.;
38.
39.
40.144
41.
42.;
43.
44.
45.4
46.-6
47.;设与网格交点为,连接、,与交于点,连接,交圆于点,连接,交于,则点即为所求.
48.
49.
50.
解:∵袋子中共有9个小球,其中绿球有7个,
∴摸出一个球是绿球的概率是,
故答案为:.
利用概率公式求解即可。
专项2 填空题2 (天津中考真题+中考模拟)
一、填空题
1.(2024·天津)若正比例函数(是常数,)的图象经过第一、第三象限,则的值可以是 (写出一个即可).
2.(2024·天津) 如图,在每个小正方形的边长为1的网格中,点均在格点上.
(1)线段的长为 ;
(2)点在水平网格线上,过点作圆,经过圆与水平网格线的交点作切线,分别与的延长线相交于点中,点在边上,点在边上,点在边上.请用无刻度的直尺,在如图所示的网格中,画出点,使的周长最短,并简要说明点的位置是如何找到的(不要求证明).
3.(2024九下·天津市模拟)如图,正方形的边长为4,点E是边的中点,,交正方形外角的平分线于点F.
(1)的面积为 ;
(2)若M是的中点,连接,则的长为 .
4.(2024九下·天津市模拟)一个不透明的袋子里装有13个球,其中有6个黑球和7个白球,这些球除颜色外无其他差别.从袋中随机取出一个球,则它是黑球的概率为 .
5.(2024九下·天津市模拟)若将直线向下平移2个单位长度后经过点,则的值为 .
6.(2024九下·天津市模拟)有一个运算程序,可以使:(为常数)时,得,,现在已知,那么 .
7.(2024九下·天津市模拟)如图,在中,,分别为,的中点,点F在线段上,且.若,,则的长为 .
8.(2024九下·河西模拟)如图,在四边形中,,,连接对角线AC、BD,,,若为的中点,为的中点,连接.
(Ⅰ)四边形的面积为 .
(Ⅱ)的长为 .
9.(2024九下·河西模拟)若点在一次函数的图象上,则这个点可以是 (任意写出一个具体的点即可),
10.(2024九下·河西模拟)不透明袋子中装有6个球,其中有1个粉色球和5个蓝色球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是蓝色球的概率为 .
11.(2024九下·河西模拟)计算的结果为 .
12.(2024九下·河东模拟)如图,E为平行四边形外一点,且满足,,,.
(Ⅰ)平行四边形的面积为 ;
(Ⅱ)若点M,N分别在线段,上,连接,当时,连接,,的最小值为 .
13.(2024九下·河东模拟)一次函数的图象向上平移3个单位后,经过点关于原点的对称点,则m的值为 .
14.(2024九下·河东模拟)计算的结果为 .
15.(2024九下·河北模拟)如图, 正方形的边长为,作以为底的等腰三角形,
(1)的面积为 ;
(2)若,分别为,的中点,为的中点,射线,相交于点, 则的长为 .
16.(2024九下·河北模拟)已知直线向下平移个单位后经过点,则值为 .
17.(2024九下·河北模拟)不透明的袋子中装有个球,其中有个红球,个绿球,个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,则它是绿球的概率为 .
18.(2024九下·和平模拟)如图,正方形的边长为4,点在边上,,作等腰直角三角形.
(1)的长为 .
(2)若为AF的中点,连接DM,则DM的长为 .
19.(2024九下·和平模拟)若直线(a为常数)经过点,则它与轴的交点坐标为 .
20.(2024九下·和平模拟)计算的结果为 .
21.(2024九下·和平模拟)不透明袋子中装有个球,其中有个红球、个黑球,这些球除颜色外无其他差别.从袋子中随机取出个球,则它是黑球的概率是 .
22.(2024九下·南开模拟)计算的结果是 .
23.(2024九下·天津市模拟)如图,正方形的顶点在轴上,点A和点C在反比例函数图象上,若直线的函数表达式为,则的值为 .
24.(2024九下·天津市模拟)如图,在每个小正方形的边长为1的网格中,点为以为直径的半圆弧的中点.
(1)的大小等于 (度);
(2)请用无刻度的直尺,在如图所示的网格中,画出以为直径的半圆的圆心,简要说明点的位置是如何找到的(不要求证明) .
25.(2024九下·天津市模拟)如图,E是正方形对角线上一点,过点E作的垂线,交于点F,以,为边作矩形,连接,
(1)的长为 ;
(2)若,则的长为 .
26.(2024九下·武清模拟)如图,是正方形对角线上一点,过点作的垂线交于点,以,为边作矩形,连接,.
(1)的长为 ;
(2)若,则的长为 .
27.(2024九下·天津市模拟)写出一个过点且随的增大而增大的一次函数解析式 .(写出一个即可)
28.(2024九下·天津市模拟)计算的结果等于 .
29.(2024九下·河东模拟)如图,在中,,,点在外,连接,过点作,交于点,连接,若,则
(Ⅰ)线段的长等于;
(Ⅱ)的面积为.
30.(2024九下·河东模拟)一次函数的图像向下平移个单位后经过点,则的值为.
31.(2024九下·河东模拟)计算的结果为.
32.(2024九下·河东模拟)一个不透明的袋子里装有2个绿球、3个黑球和6个红球,它们除颜色外其余相同,从袋中任意摸出一个球为绿球的概率为.
33.(2024九下·南开模拟)如图,在等腰中,,过点C作,连接,交于点,点为中点,连接,,若,则.
34.(2024九下·南开模拟)直线与x轴交于点,与y轴交于点,将直线沿y轴向下平移2个单位长度得到直线l,则直线l的解析式为.
35.(2024九下·南开模拟)计算的结果为.
36.(2024九下·南开模拟)计算的结果是.
37.(2024九下·河北模拟)如图,在边长为6的正方形中,点M为的中点,点E在上,,等腰三角形中,.
(1)的面积为 ;
(2)若N为的中点,则的值为 .
38.(2024九下·天津市模拟)不透明袋子中装有9个球,其中有2个红球、7个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .
39.(2024九下·津南模拟)如图,点M为正方形边上一动点,,将点M绕点P顺时针旋转到点N,若分别为中点,则的最小值为 .
40.(2024九下·津南模拟)用“筝形”和“镖形”两种不同的瓷砖铺设成如图所示的地面,则“筝形”瓷砖中的内角 °.
41.(2024九下·津南模拟) .
42.(2024九下·和平模拟)如图,已知半圆的直径长为2,点为中点,为上任意一点,与相交于点.
(1) (度);
(2)的最小值为 .
43.(2024九下·和平模拟)已知点,在反比例函数的图象上.如果,则,的大小关系为: .
44.(2024九下·和平模拟)不透明袋子中装有9个球,其中有3个黄球、6个红球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是黄球的概率为 .
45.(2024九下·西青模拟)计算的结果是 .
46.(2024九下·天津市模拟)= .
47.(2024九下·滨海模拟)如图,在每个小正方形的边长为1的网格中,等边三角形内接于圆,且顶点A,B均在格点上.
(1)线段的长为 ;
(2)圆与格线交于点,点为线段上一动点,当取得最小值时,请利用无刻度的直尺,在如图所示的网格中,画出点,并简要说明点的位置是如何找到的(不要求证明) .
48.(2024·红桥模拟)如图, 在矩形中,,, 以点B为圆心,适当长为半径画弧,分别交,于点E,F,再分别以点E,F为圆心, 大于 长为半径画弧(弧所在圆的半径相等),两弧相交于点P,作射线,过点C作的垂线分别交,于点M,N,垂足为O,则的长为 .
49.(2024·红桥模拟)一个不透明的袋子里装有个球,其中有个红球,个白球,这些球除颜色外其它均相同.现从中随机摸出一个球,则摸出的球是白球的概率为 .
50.(2024九下·滨海模拟)不透明袋子中装有9个球,其中有7个绿球、2个白球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是绿球的概率是 .
答案解析部分
1.1(答案不唯一)
∵正比例函数的图象经过第一、第三象限,
∴k>0,
故答案为:1(答案不唯一).
利用一次函数的图象与系数的关系判断出k>0,再求解即可.
2.(1)
(2)解:如图,根据题意,切点为M;连接ME并延长,与网格线相交于点M1;取圆与网格线的交点D和格点H,连接DH并延长,与网格线相交于点M2;连接M1M2,分别与AB ,AC相交于点N,P,则点M,N,P即为所求.
解:(1)AG2=12+12=2,
∴AG=;
故答案为:;
(1)根据勾股定理即可得出结论;
(2)作点M关于AB,AC的对称点M1和M2,连接M1M2,与ABAC相较于点NP,△PMN的周长=线段M1M2的长度,等腰三角形AM1M2的腰长为AM,当AM的值最小时,M1M2的值最小,此时M是切点,由此作图即可。
3.12;
4.
5.1
6.
7.
8.40;
9.(答案不唯一)
10.
11.
12.;
13.
14.
15.;
16.
17.
18.;
19.
20.
21.
22.
23.6
24.;取圆上两个格点,,再作的垂直平分线与的交点即为圆心
25.;
26.;
27.(答案不唯一)
28.
29.2,5
30.
31.18
32.
33.5
34.
35.
36.
37.;
38.
39.
40.144
41.
42.;
43.
44.
45.4
46.-6
47.;设与网格交点为,连接、,与交于点,连接,交圆于点,连接,交于,则点即为所求.
48.
49.
50.
解:∵袋子中共有9个小球,其中绿球有7个,
∴摸出一个球是绿球的概率是,
故答案为:.
利用概率公式求解即可。
同课章节目录
