专项3 解答题1(天津中考真题+中考模拟)(含答案) —2025年中考数学冲刺中考模拟真题速递(天津专用)
文档属性
| 名称 | 专项3 解答题1(天津中考真题+中考模拟)(含答案) —2025年中考数学冲刺中考模拟真题速递(天津专用) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 05:46:04 | ||
图片预览



文档简介
2025年中考数学冲刺中考模拟真题速递(天津专用)
专项3 解答题1(天津中考真题+中考模拟)
一、解答题
1.(2024·天津) 已知抛物线的顶点为,且,对称轴与轴相交于点,点在抛物线上,为坐标原点.
(1)当时,求该抛物线顶点的坐标;
(2)当时,求的值;
(3)若是抛物线上的点,且点在第四象限,,点在线段上,点在线段上,,当取得最小值为时,求的值.
2.(2024·天津) 将一个平行四边形纸片放置在平面直角坐标系中,点,点,点在第一象限,且.
(1)填空:如图①,点的坐标为 ,点的坐标为 ;
(2)若为轴的正半轴上一动点,过点作直线轴,沿直线折叠该纸片,折叠后点的对应点落在轴的正半轴上,点的对应点为.设.
①如图②,若直线与边相交于点,当折叠后四边形与重叠部分为五边形时,与相交于点.试用含有的式子表示线段的长,并直接写出的取值范围;
②设折叠后重叠部分的面积为,当时,求的取值范围(直接写出结果即可).
3.(2024九下·和平模拟)已知学生宿舍、超市、体育场依次在同一条直线上,超市离宿舍0.6km,体育场离学生宿舍1.2km.张强从宿舍出发,先用了20min匀速步行去超市,在超市购买一些水和食物后,用了10min匀速跑步到达体育场,锻炼了半小时后匀速骑车返回宿舍,下面图中x表示时间,y表示离宿舍的距离.图象反映了这个过程中张强离宿舍的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张强离开宿舍的时间/min 10 20 35 70
张强离宿舍的距离/km 0.6
②填空:张强从超市到体育场的速度为 km/min;
③当0≤x≤40时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(2)同宿舍的李明比张强晚5min从学生宿舍出发直接匀速步行前往体育场,却比张强早15min 到达体育场.李明在去体育场的途中遇到张强时离宿舍的距离是多少 (直接写出结果即可)
4.(2024九下·武清模拟)已知抛物线(为常数,)与轴相交于,两点(点在点的左侧),与轴相交于点.
(1)若点的坐标为,求该抛物线的顶点坐标;
(2)当时,求的值;
(3)若点为轴上方对称轴右侧抛物线上的一个动点,为轴正半轴上的一点,过点作抛物线对称轴的垂线,垂足为,连接,当的最小值为17时,求的值.
5.(2024九下·武清模拟)将一个直角三角形纸片放置在平面直角坐标系中,其中,点,点,过边上的动点 (不与点重合)作交于点.设.
(1)如图①,当时,点的坐标为_______,点的坐标为_______;
(2)沿着PQ折叠该纸片,点的对应点为.设折叠后的与的重叠部分的面积为.
①如图②,若折叠后的与的重叠部分为四边形,交于点,交于点,试用含有的式子表示,并直接写出的取值范围;
②当时,求的值(直接写出结果即可).
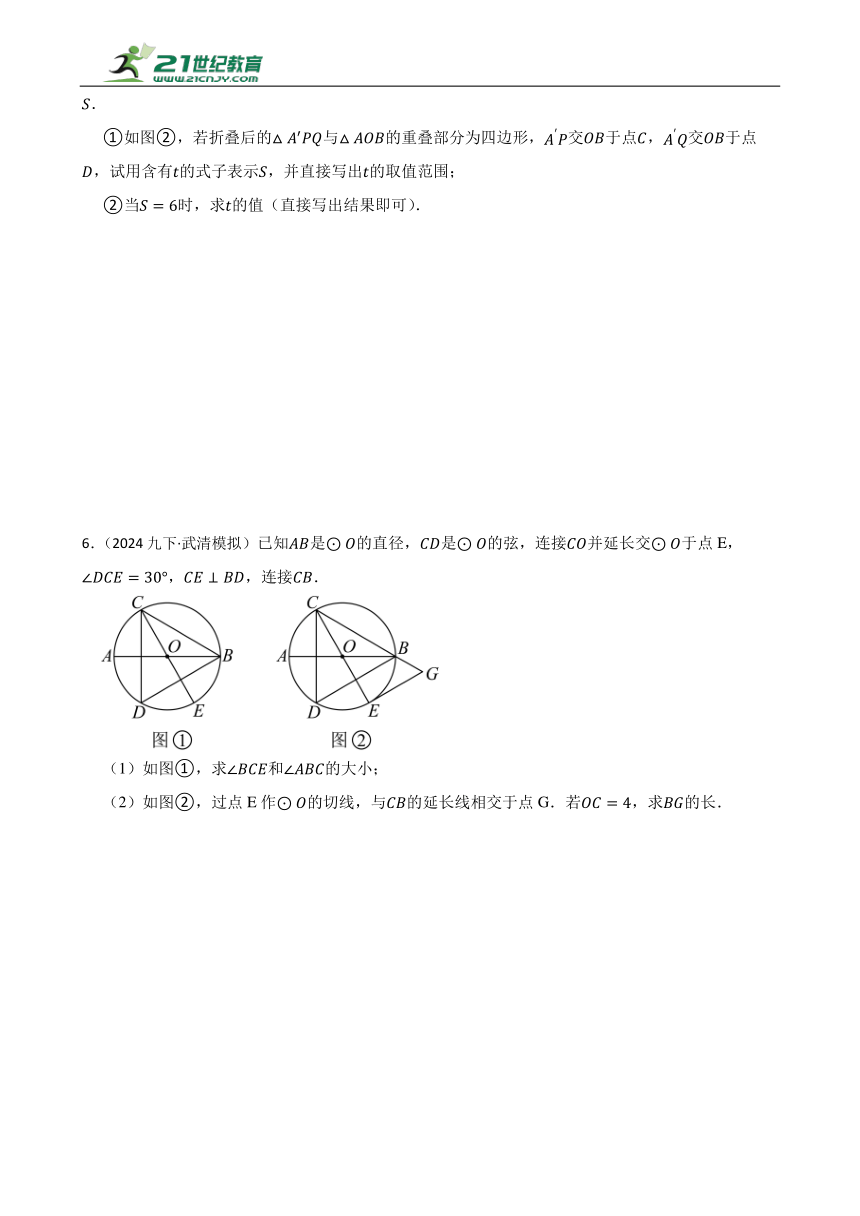
6.(2024九下·武清模拟)已知是的直径,是的弦,连接并延长交于点E,,,连接.
(1)如图①,求和的大小;
(2)如图②,过点E作的切线,与的延长线相交于点G.若,求的长.
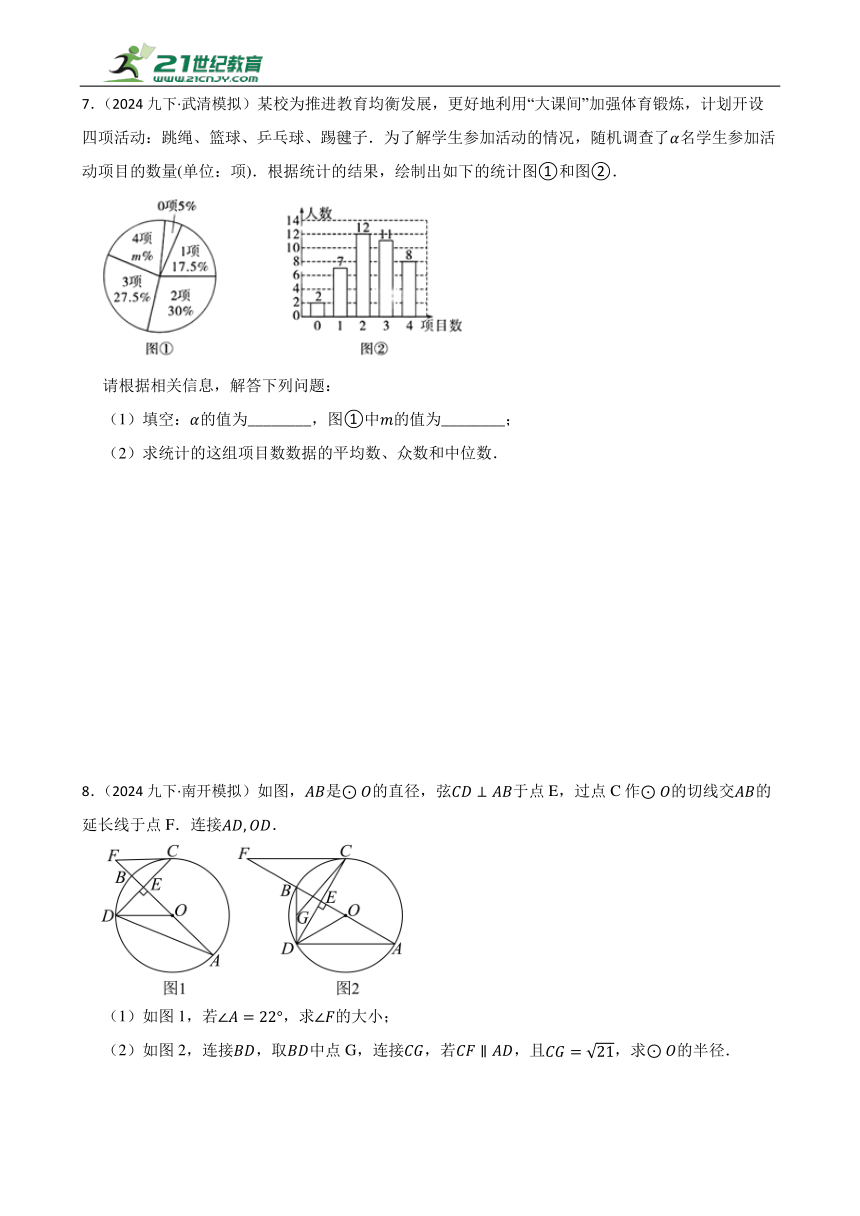
7.(2024九下·武清模拟)某校为推进教育均衡发展,更好地利用“大课间”加强体育锻炼,计划开设四项活动:跳绳、篮球、乒乓球、踢毽子.为了解学生参加活动的情况,随机调查了名学生参加活动项目的数量(单位:项).根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:的值为________,图①中的值为________;
(2)求统计的这组项目数数据的平均数、众数和中位数.
8.(2024九下·南开模拟)如图,是的直径,弦于点E,过点C作的切线交的延长线于点F.连接.
(1)如图1,若,求的大小;
(2)如图2,连接,取中点G,连接,若,且,求的半径.
9.(2024九下·南开模拟)某部门为了解工人的生产能力情况,进行了抽样调查,随机抽取了a名工人每人每天加工零件的件数(单位:件),绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为__________,图①中的m值为__________;
(2)求统计的这组工人加工零件数据的平均数、众数和中位数.
10.(2024九下·天津市模拟)在平面直角坐标系中,O为原点,是直角三角形,,,点,射线上有一个动点C,线段上有一个动点D,沿直线折叠,点B对应点为,轴.
(1)如图①,若点落x轴上,求点C的坐标;
(2)设.
①如图②,折叠后的与重叠部分为四边形,和分别与x轴交于P,Q两点,试用含t的式子表示的长,并直接写出t的取值范围;
②若与重叠部分的面积S,当时,求S的取值范围.(直接写出结果即可)
11.(2024九下·天津市模拟)已知小明家、书店、森林公园依次在同一条直线上,书店离家, 森林公园离家.小明从家里出发,匀速骑行后到达书店,在书店停留后,匀速骑行9分钟到达森林公园:在森林公园游玩一段时间,然后返回家中.给出的图象反映了这个过程中小明离家的距离与时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
小明离开家的时间 10 20 49 79 112
小明离家的距离 2.75
5
(2)填空:
① a的值为
②小明从家出发前往书店的骑行速度为 ;
③当 时,请直接写出小明离家的距离 y 关于时间x 的函数解析式.
(3)小明从森林公园出发回家时,爸爸从家开车出发匀速行驶前往森林公园,已知爸爸的速度为0.8km/min,当小明与爸爸相遇时,求小明离开家的时间.(直接写出结果)
12.(2024九下·天津市模拟)已知四边形内接于,为的直径,,连接.
(1)如图①,若D 为弧的中点,求,求和的大小:
(2)如图②,若,C为弧的中点,过点作的切线与弦的延长线相交于点E,求 的长.
13.(2024九下·红桥模拟)如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A,过点P(1,m)作直线PB⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B、C不重合),连接CB、CP,
(I)当m=3时,求点A的坐标及BC的长;
(II)当m>1时,连接CA,若CA⊥CP,求m的值;
(III)过点P作PE⊥PC,且PE=PC,当点E落在坐标轴上时,求m的值,并确定相对应的点E的坐标.
14.(2024九下·红桥模拟)在平面直角坐标系中,点,点,将绕点B顺时针旋转,得,点A,O旋转后的对应点为,,记旋转角为.
(1)填空:如图①,当时,点的坐标为______,点的坐标为______;
(2)如图②,当时,求点的坐标;
(3)连接,设线段的中点为M,连接,求线段的长的最小值(直接写出结果即可).
15.(2024九下·红桥模拟)在△ABC中,,以边AB上一点O为圆心,OA为半径的圈与BC相切于点D,分别交AB,AC于点E,F
(I)如图①,连接AD,若,求∠B的大小;
(Ⅱ)如图②,若点F为的中点,的半径为2,求AB的长.
16.(2024九下·红桥模拟)为了解某校男生在体能测试的引体向上项目的情况,随机调查了a名男生引体向上项目的测试成绩(单位:次),根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为______,图①中m的值为______;
(2)求统计的这组测试成绩数据的平均数、众数和中位数.
17.(2024九下·河西模拟)已知抛物线(为常数)与轴相交于两点(点在点的左侧),与轴负半轴交于点.
(1)当时,求抛物线的顶点坐标;
(2)若有点是轴上一点,连接,点是的中点,连接.
当点的坐标为,且时,求的值;
当的最小值是时,求的值.
18.(2024九下·河西模拟)将一个矩形纸片放置在平面直角坐标系中,点,点,点,点在边上(点不与点,重合),折叠该纸片,使折痕所在的直线经过点,并与轴的正半轴相交于点,且,点的对应点落在第一象限.设.
(1)如图①,当时,的大小为______,点的坐标为______;
(2)如图②,若折叠后重合部分为四边形,点的对应点为,且在直线的下方,与边相交于点,折痕与边相交于点,试用含有的式子表示的长,并直接写出的取值范围;
(3)当,求折叠后重合部分面积的取值范围.
19.(2024九下·河西模拟)如图,甲、乙两座建筑物的水平距离为,从甲的顶部处测得乙的顶部处的俯角为,测得底部处的俯角为,求甲、乙建筑物的高度和(结果取整数).参考数据:,.
20.(2024九下·河西模拟)在中,延长直径至点,以为一边的等腰三角形,,底边与交于点,直线是的切线,交于点.
(1)如图①,当时,求和的大小;
(2)如图②,当且直线恰与相切.若,求的长.
21.(2024九下·和平模拟)已知抛物线(a,b,c为常数,)经过坐标原点,顶点P的坐标为,与x轴的另一个交点为A.
(1)求抛物线解析式和点A的坐标;
(2)抛物线上有一点D,过点D作直线的垂线,垂足为点E,,求点D的坐标;
(3)抛物线的对称轴与x轴相交于点F,点G是点F关于点P的对称点,点Q是x轴下方抛物线上的动点.若过点Q的直线l;(,为常数,)与抛物线只有一个公共点,且分别与线段相交于点H,K,求的值.
22.(2024九下·和平模拟)将一个直角三角形纸片放置在平面直角坐标系中,,,,D为边的中点,连接,点E,F分别为,的中点.
(1)填空:如图①,点D的坐标为 ,点F的坐标为 ;
(2)将矩形沿水平方向向右平移,得到矩形,点E,F,G,H的对应点分别为,,,,当点与点B重合时停止移动.设,矩形与重叠部分的面积记为S.
①如图②, 当边与相交于点M,边与相交于点N,且矩形与重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围;
②当时,求S的取值范围(直接写出结果即可).
23.(2024九下·和平模拟)在一次中学生田径运动会上,根据参加男子跳高初赛的名运动员的成绩(单位:),绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:的值为 ,图①中的值为 ;
(2)求统计的这组运动员初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定人进入复赛,请直接写出初赛成绩为的运动员能否进入复赛.
24.(2024九下·宝坻模拟)在平面直角坐标系中,为原点,的顶点,,点是线段上一动点(点不与点重合),过作交于点,将沿翻折,使点落在轴的点处.
(1)如图①,当点与点重合时,求点的坐标;
(2)设,与重叠部分的面积为.
①如图②,当重叠部分为四边形时,试用含的式子表示,并直接写出的取值范围;
②当时,求的取值范围(直接写出结果即可).
25.(2024九下·宝坻模拟)已知是的直径,是的弦.
(1)如图①,若为的中点,,求和的大小;
(2)如图②,过点作的切线交延长线于点,连接,若是的直径,,,求的长.
答案解析部分
1.(1)解:,得.又,
该抛物线的解析式为.
,
该抛物线顶点的坐标为.
(2)解:过点作轴,垂足为,则.
在Rt中,由,.解得(舍).
点的坐标为.
,即.
抛物线的对称轴为.
对称轴与轴相交于点,则.
在Rt中,由,
.解得.
由,得该抛物线顶点的坐标为.
该抛物线的解析式为.
点在该抛物线上,有.
.
(3)解:过点作轴,垂足为,则.
在Rt中,.
过点作轴,垂足为,则.
又
.得点的坐标为.
在Rt中,,,即.
根据题意,,得.
在的外部,作,且,连接GF,
得.
.有.
当满足条件的点落在线段GM上时,取得最小值,即.
在Rt中,,
.得.
.解得(舍).
点的坐标为,点的坐标为.
点都在抛物线上,
得.
.
(1)先求得a,b的值,再配成顶点坐标,即可求解;
(2)过点作轴,垂足为H,在Rt中,根据勾股定理可求得m=,在Rt中,根据勾股定理可求得求得PD=,得出抛物线的顶点坐标为(1,-),再利用待定系数求解即可;
(3)过点作轴,过点作轴,垂足为,证,即可得出N为.在Rt中,根据勾股定理。可得出,在的外部,作,且,证,得到,当满足条件的点落在线段GM上时,取得最小值,求得点的坐标为,再利用待定系数法求解即可.
2.(1);
(2)解:①t的取值范围是.
②.
解:(1)过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,
∵,
∴OD=AE=1,CD=BE=,
∴OE=OA+AE=4,
∴点C的坐标为(1,),点D(4,);
故第1空答案为(1,);第2空答案为:D(4,);
(2)①由折叠知,∠OO'C'=∠AOC=60°,O'P=OP=1,则OO'=2t.
∵点A(3,0),得OA=3.
∴AO'=OO'-OA=2t-3.
∵四边形OABC为平行四边形,
∴AB=OC=2,AB∥OC.得∠O'AB=∠AOC=60°.
∴△AO'E为等边三角形.有AE=AO'=2t-3.
∵BE=AB-AE,即BE=2-(2t-3)=5-2t,
∴BE=-2t+5,其中t的取值范围是.
②如图,过点C作CH⊥OA于点H,由(1)得:C(1,),∠COA=60°,
∴tan60°=,
∴,
∴MP=,
当时,S=,
∵>0,
∴抛物线开口向上,且对称轴为直线t=0,
∴在时,S随着t的增大而增大,
∴;
当时,如图:
S=,
∴,S随着t的增大而增大,
∴在t=时,S=,
在t=1时,S=,
∴当时,;
当时,过点E作EN⊥x轴于点N,如图:
由(1)得:△EO'A是等边三角形,EN⊥AO,
∴AN=,
∴tan60°=,
∴EN=,
∴S=
=
=,
∵-<0,
∴抛物线开口向下,在t=时,S有最大值,
S=,
∴在时,丨2-丨=丨2-丨,
∴S=,
∴当时,;
当时,如图:
S==,
∵-<0,S随t的增大而减小,
∴当时,把t=和t=时,分别代入解析式S=,可得:S=,
S=,
∴当时,.
综上可得:.
(1)过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,根据含30°锐角的直角三角形的性质,即可得出答案;
(2)①(2)①由折叠知,∠OO'C'=∠AOC=60°,O'P=OP=t,则OO'=2t,结合平行四边形的性质,可得出△AO'E为等边三角形,从而得出AE=AO'=2t-3,进而根据BE=AB-AE,即可得出BE=5-2t,然后根据当点O'与点A重合和点O'与点B重合,分别求得OP的长度,即可得出t的取值范围;
②根据不同情况分别进行讨论:当时,S=,可得;当时,S,可得:;当时,S=,可得:;当时,S=,可得:。综上即可得出s的取值范围。
3.(1)①0.3,0.9,1.2;②0.06;③
(2)0.3km
4.(1)
(2)
(3)
5.(1),
(2)①;②当时,的值为或
6.(1),;
(2).
7.(1),
(2),,
8.(1)
(2)
9.(1)20,25
(2)平均数为124,众数为130,中位数为125
10.(1)
(2)①;②
11.(1)2.75;5;4.4
(2)①40;②0.275;③
(3)
12.(1),
(2)
13.(I)4;(II) (III)(2,0)或(0,4)
14.(1),
(2)
(3)
15.(1)∠B=40°;(2)AB= 6.
16.(1)40,25
(2)平均数为15.8次,众数为15次,中位数为16次
17.(1)
(2);
18.(1);
(2),
(3)
19.甲建筑物的高度约为,乙建筑物的高度约为.
20.(1),
(2)
21.(1),
(2),
(3)
22.(1),
(2)①
②
23.(1);
(2)平均数是,众数是m,中位数是m
(3)能
24.(1)
(2)①
②或
25.(1),
(2)
专项3 解答题1(天津中考真题+中考模拟)
一、解答题
1.(2024·天津) 已知抛物线的顶点为,且,对称轴与轴相交于点,点在抛物线上,为坐标原点.
(1)当时,求该抛物线顶点的坐标;
(2)当时,求的值;
(3)若是抛物线上的点,且点在第四象限,,点在线段上,点在线段上,,当取得最小值为时,求的值.
2.(2024·天津) 将一个平行四边形纸片放置在平面直角坐标系中,点,点,点在第一象限,且.
(1)填空:如图①,点的坐标为 ,点的坐标为 ;
(2)若为轴的正半轴上一动点,过点作直线轴,沿直线折叠该纸片,折叠后点的对应点落在轴的正半轴上,点的对应点为.设.
①如图②,若直线与边相交于点,当折叠后四边形与重叠部分为五边形时,与相交于点.试用含有的式子表示线段的长,并直接写出的取值范围;
②设折叠后重叠部分的面积为,当时,求的取值范围(直接写出结果即可).
3.(2024九下·和平模拟)已知学生宿舍、超市、体育场依次在同一条直线上,超市离宿舍0.6km,体育场离学生宿舍1.2km.张强从宿舍出发,先用了20min匀速步行去超市,在超市购买一些水和食物后,用了10min匀速跑步到达体育场,锻炼了半小时后匀速骑车返回宿舍,下面图中x表示时间,y表示离宿舍的距离.图象反映了这个过程中张强离宿舍的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张强离开宿舍的时间/min 10 20 35 70
张强离宿舍的距离/km 0.6
②填空:张强从超市到体育场的速度为 km/min;
③当0≤x≤40时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(2)同宿舍的李明比张强晚5min从学生宿舍出发直接匀速步行前往体育场,却比张强早15min 到达体育场.李明在去体育场的途中遇到张强时离宿舍的距离是多少 (直接写出结果即可)
4.(2024九下·武清模拟)已知抛物线(为常数,)与轴相交于,两点(点在点的左侧),与轴相交于点.
(1)若点的坐标为,求该抛物线的顶点坐标;
(2)当时,求的值;
(3)若点为轴上方对称轴右侧抛物线上的一个动点,为轴正半轴上的一点,过点作抛物线对称轴的垂线,垂足为,连接,当的最小值为17时,求的值.
5.(2024九下·武清模拟)将一个直角三角形纸片放置在平面直角坐标系中,其中,点,点,过边上的动点 (不与点重合)作交于点.设.
(1)如图①,当时,点的坐标为_______,点的坐标为_______;
(2)沿着PQ折叠该纸片,点的对应点为.设折叠后的与的重叠部分的面积为.
①如图②,若折叠后的与的重叠部分为四边形,交于点,交于点,试用含有的式子表示,并直接写出的取值范围;
②当时,求的值(直接写出结果即可).
6.(2024九下·武清模拟)已知是的直径,是的弦,连接并延长交于点E,,,连接.
(1)如图①,求和的大小;
(2)如图②,过点E作的切线,与的延长线相交于点G.若,求的长.
7.(2024九下·武清模拟)某校为推进教育均衡发展,更好地利用“大课间”加强体育锻炼,计划开设四项活动:跳绳、篮球、乒乓球、踢毽子.为了解学生参加活动的情况,随机调查了名学生参加活动项目的数量(单位:项).根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:的值为________,图①中的值为________;
(2)求统计的这组项目数数据的平均数、众数和中位数.
8.(2024九下·南开模拟)如图,是的直径,弦于点E,过点C作的切线交的延长线于点F.连接.
(1)如图1,若,求的大小;
(2)如图2,连接,取中点G,连接,若,且,求的半径.
9.(2024九下·南开模拟)某部门为了解工人的生产能力情况,进行了抽样调查,随机抽取了a名工人每人每天加工零件的件数(单位:件),绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为__________,图①中的m值为__________;
(2)求统计的这组工人加工零件数据的平均数、众数和中位数.
10.(2024九下·天津市模拟)在平面直角坐标系中,O为原点,是直角三角形,,,点,射线上有一个动点C,线段上有一个动点D,沿直线折叠,点B对应点为,轴.
(1)如图①,若点落x轴上,求点C的坐标;
(2)设.
①如图②,折叠后的与重叠部分为四边形,和分别与x轴交于P,Q两点,试用含t的式子表示的长,并直接写出t的取值范围;
②若与重叠部分的面积S,当时,求S的取值范围.(直接写出结果即可)
11.(2024九下·天津市模拟)已知小明家、书店、森林公园依次在同一条直线上,书店离家, 森林公园离家.小明从家里出发,匀速骑行后到达书店,在书店停留后,匀速骑行9分钟到达森林公园:在森林公园游玩一段时间,然后返回家中.给出的图象反映了这个过程中小明离家的距离与时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)填表:
小明离开家的时间 10 20 49 79 112
小明离家的距离 2.75
5
(2)填空:
① a的值为
②小明从家出发前往书店的骑行速度为 ;
③当 时,请直接写出小明离家的距离 y 关于时间x 的函数解析式.
(3)小明从森林公园出发回家时,爸爸从家开车出发匀速行驶前往森林公园,已知爸爸的速度为0.8km/min,当小明与爸爸相遇时,求小明离开家的时间.(直接写出结果)
12.(2024九下·天津市模拟)已知四边形内接于,为的直径,,连接.
(1)如图①,若D 为弧的中点,求,求和的大小:
(2)如图②,若,C为弧的中点,过点作的切线与弦的延长线相交于点E,求 的长.
13.(2024九下·红桥模拟)如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A,过点P(1,m)作直线PB⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B、C不重合),连接CB、CP,
(I)当m=3时,求点A的坐标及BC的长;
(II)当m>1时,连接CA,若CA⊥CP,求m的值;
(III)过点P作PE⊥PC,且PE=PC,当点E落在坐标轴上时,求m的值,并确定相对应的点E的坐标.
14.(2024九下·红桥模拟)在平面直角坐标系中,点,点,将绕点B顺时针旋转,得,点A,O旋转后的对应点为,,记旋转角为.
(1)填空:如图①,当时,点的坐标为______,点的坐标为______;
(2)如图②,当时,求点的坐标;
(3)连接,设线段的中点为M,连接,求线段的长的最小值(直接写出结果即可).
15.(2024九下·红桥模拟)在△ABC中,,以边AB上一点O为圆心,OA为半径的圈与BC相切于点D,分别交AB,AC于点E,F
(I)如图①,连接AD,若,求∠B的大小;
(Ⅱ)如图②,若点F为的中点,的半径为2,求AB的长.
16.(2024九下·红桥模拟)为了解某校男生在体能测试的引体向上项目的情况,随机调查了a名男生引体向上项目的测试成绩(单位:次),根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为______,图①中m的值为______;
(2)求统计的这组测试成绩数据的平均数、众数和中位数.
17.(2024九下·河西模拟)已知抛物线(为常数)与轴相交于两点(点在点的左侧),与轴负半轴交于点.
(1)当时,求抛物线的顶点坐标;
(2)若有点是轴上一点,连接,点是的中点,连接.
当点的坐标为,且时,求的值;
当的最小值是时,求的值.
18.(2024九下·河西模拟)将一个矩形纸片放置在平面直角坐标系中,点,点,点,点在边上(点不与点,重合),折叠该纸片,使折痕所在的直线经过点,并与轴的正半轴相交于点,且,点的对应点落在第一象限.设.
(1)如图①,当时,的大小为______,点的坐标为______;
(2)如图②,若折叠后重合部分为四边形,点的对应点为,且在直线的下方,与边相交于点,折痕与边相交于点,试用含有的式子表示的长,并直接写出的取值范围;
(3)当,求折叠后重合部分面积的取值范围.
19.(2024九下·河西模拟)如图,甲、乙两座建筑物的水平距离为,从甲的顶部处测得乙的顶部处的俯角为,测得底部处的俯角为,求甲、乙建筑物的高度和(结果取整数).参考数据:,.
20.(2024九下·河西模拟)在中,延长直径至点,以为一边的等腰三角形,,底边与交于点,直线是的切线,交于点.
(1)如图①,当时,求和的大小;
(2)如图②,当且直线恰与相切.若,求的长.
21.(2024九下·和平模拟)已知抛物线(a,b,c为常数,)经过坐标原点,顶点P的坐标为,与x轴的另一个交点为A.
(1)求抛物线解析式和点A的坐标;
(2)抛物线上有一点D,过点D作直线的垂线,垂足为点E,,求点D的坐标;
(3)抛物线的对称轴与x轴相交于点F,点G是点F关于点P的对称点,点Q是x轴下方抛物线上的动点.若过点Q的直线l;(,为常数,)与抛物线只有一个公共点,且分别与线段相交于点H,K,求的值.
22.(2024九下·和平模拟)将一个直角三角形纸片放置在平面直角坐标系中,,,,D为边的中点,连接,点E,F分别为,的中点.
(1)填空:如图①,点D的坐标为 ,点F的坐标为 ;
(2)将矩形沿水平方向向右平移,得到矩形,点E,F,G,H的对应点分别为,,,,当点与点B重合时停止移动.设,矩形与重叠部分的面积记为S.
①如图②, 当边与相交于点M,边与相交于点N,且矩形与重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围;
②当时,求S的取值范围(直接写出结果即可).
23.(2024九下·和平模拟)在一次中学生田径运动会上,根据参加男子跳高初赛的名运动员的成绩(单位:),绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:的值为 ,图①中的值为 ;
(2)求统计的这组运动员初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定人进入复赛,请直接写出初赛成绩为的运动员能否进入复赛.
24.(2024九下·宝坻模拟)在平面直角坐标系中,为原点,的顶点,,点是线段上一动点(点不与点重合),过作交于点,将沿翻折,使点落在轴的点处.
(1)如图①,当点与点重合时,求点的坐标;
(2)设,与重叠部分的面积为.
①如图②,当重叠部分为四边形时,试用含的式子表示,并直接写出的取值范围;
②当时,求的取值范围(直接写出结果即可).
25.(2024九下·宝坻模拟)已知是的直径,是的弦.
(1)如图①,若为的中点,,求和的大小;
(2)如图②,过点作的切线交延长线于点,连接,若是的直径,,,求的长.
答案解析部分
1.(1)解:,得.又,
该抛物线的解析式为.
,
该抛物线顶点的坐标为.
(2)解:过点作轴,垂足为,则.
在Rt中,由,.解得(舍).
点的坐标为.
,即.
抛物线的对称轴为.
对称轴与轴相交于点,则.
在Rt中,由,
.解得.
由,得该抛物线顶点的坐标为.
该抛物线的解析式为.
点在该抛物线上,有.
.
(3)解:过点作轴,垂足为,则.
在Rt中,.
过点作轴,垂足为,则.
又
.得点的坐标为.
在Rt中,,,即.
根据题意,,得.
在的外部,作,且,连接GF,
得.
.有.
当满足条件的点落在线段GM上时,取得最小值,即.
在Rt中,,
.得.
.解得(舍).
点的坐标为,点的坐标为.
点都在抛物线上,
得.
.
(1)先求得a,b的值,再配成顶点坐标,即可求解;
(2)过点作轴,垂足为H,在Rt中,根据勾股定理可求得m=,在Rt中,根据勾股定理可求得求得PD=,得出抛物线的顶点坐标为(1,-),再利用待定系数求解即可;
(3)过点作轴,过点作轴,垂足为,证,即可得出N为.在Rt中,根据勾股定理。可得出,在的外部,作,且,证,得到,当满足条件的点落在线段GM上时,取得最小值,求得点的坐标为,再利用待定系数法求解即可.
2.(1);
(2)解:①t的取值范围是.
②.
解:(1)过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,
∵,
∴OD=AE=1,CD=BE=,
∴OE=OA+AE=4,
∴点C的坐标为(1,),点D(4,);
故第1空答案为(1,);第2空答案为:D(4,);
(2)①由折叠知,∠OO'C'=∠AOC=60°,O'P=OP=1,则OO'=2t.
∵点A(3,0),得OA=3.
∴AO'=OO'-OA=2t-3.
∵四边形OABC为平行四边形,
∴AB=OC=2,AB∥OC.得∠O'AB=∠AOC=60°.
∴△AO'E为等边三角形.有AE=AO'=2t-3.
∵BE=AB-AE,即BE=2-(2t-3)=5-2t,
∴BE=-2t+5,其中t的取值范围是.
②如图,过点C作CH⊥OA于点H,由(1)得:C(1,),∠COA=60°,
∴tan60°=,
∴,
∴MP=,
当时,S=,
∵>0,
∴抛物线开口向上,且对称轴为直线t=0,
∴在时,S随着t的增大而增大,
∴;
当时,如图:
S=,
∴,S随着t的增大而增大,
∴在t=时,S=,
在t=1时,S=,
∴当时,;
当时,过点E作EN⊥x轴于点N,如图:
由(1)得:△EO'A是等边三角形,EN⊥AO,
∴AN=,
∴tan60°=,
∴EN=,
∴S=
=
=,
∵-<0,
∴抛物线开口向下,在t=时,S有最大值,
S=,
∴在时,丨2-丨=丨2-丨,
∴S=,
∴当时,;
当时,如图:
S==,
∵-<0,S随t的增大而减小,
∴当时,把t=和t=时,分别代入解析式S=,可得:S=,
S=,
∴当时,.
综上可得:.
(1)过点C作CD⊥x轴于点D,过点B作BE⊥x轴于点E,根据含30°锐角的直角三角形的性质,即可得出答案;
(2)①(2)①由折叠知,∠OO'C'=∠AOC=60°,O'P=OP=t,则OO'=2t,结合平行四边形的性质,可得出△AO'E为等边三角形,从而得出AE=AO'=2t-3,进而根据BE=AB-AE,即可得出BE=5-2t,然后根据当点O'与点A重合和点O'与点B重合,分别求得OP的长度,即可得出t的取值范围;
②根据不同情况分别进行讨论:当时,S=,可得;当时,S,可得:;当时,S=,可得:;当时,S=,可得:。综上即可得出s的取值范围。
3.(1)①0.3,0.9,1.2;②0.06;③
(2)0.3km
4.(1)
(2)
(3)
5.(1),
(2)①;②当时,的值为或
6.(1),;
(2).
7.(1),
(2),,
8.(1)
(2)
9.(1)20,25
(2)平均数为124,众数为130,中位数为125
10.(1)
(2)①;②
11.(1)2.75;5;4.4
(2)①40;②0.275;③
(3)
12.(1),
(2)
13.(I)4;(II) (III)(2,0)或(0,4)
14.(1),
(2)
(3)
15.(1)∠B=40°;(2)AB= 6.
16.(1)40,25
(2)平均数为15.8次,众数为15次,中位数为16次
17.(1)
(2);
18.(1);
(2),
(3)
19.甲建筑物的高度约为,乙建筑物的高度约为.
20.(1),
(2)
21.(1),
(2),
(3)
22.(1),
(2)①
②
23.(1);
(2)平均数是,众数是m,中位数是m
(3)能
24.(1)
(2)①
②或
25.(1),
(2)
同课章节目录
