专项3 解答题2 (天津中考真题+中考模拟)(含答案) —2025年中考数学冲刺中考模拟真题速递(天津专用)
文档属性
| 名称 | 专项3 解答题2 (天津中考真题+中考模拟)(含答案) —2025年中考数学冲刺中考模拟真题速递(天津专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 892.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 05:50:36 | ||
图片预览



文档简介
2025年中考数学冲刺中考模拟真题速递(天津专用)
专项3 解答题2 (天津中考真题+中考模拟)
一、解答题
1.(2024·天津) 已知张华的家、画社、文化广场依次在同一条直线上,画社离家,文化广场离家.张华从家出发,先匀速骑行了到画社,在画社停留了,之后匀速骑行了到文化广场,在文化广场停留后,再匀速步行了返回家.下面图中表示时间,表示离家的距离.图象反映了这个过程中张华离家的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张华离开家的时间 1 4 13 30
张华离家的距离
②填空:张华从文化广场返回家的速度为 ▲ ;
③当时,请直接写出张华离家的距离关于时间的函数解析式;
(2)当张华离开家时,他的爸爸也从家出发匀速步行了直接到达了文化广场,那么从画社到文化广场的途中两人相遇时离家的距离是多少?(直接写出结果即可)
2.(2024·天津) 为了解某校八年级学生每周参加科学教育的时间(单位:),随机调查了该校八年级名学生,根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:的值为 ,图①中的值为 ,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为 和 ;
(2)求统计的这组学生每周参加科学教育的时间数据的平均数;
(3)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是的人数约为多少?
3.(2024·天津) 解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为 .
4.(2024九下·红桥模拟)已知抛物线(,为常数,)经过点和点,与轴相交于点,为抛物线上横坐标为的点.
(1)求该抛物线的解析式;
(2)当时,过点作轴的垂线与相交于点,若,求点的坐标;
(3)为线段的中点,当时,求点的坐标.
5.(2024九下·清水模拟)已知,,E在线段延长线上,平分.连接,若.
(1)若,求的度数;
(2)若,探究与的位置关系,并说明理由.
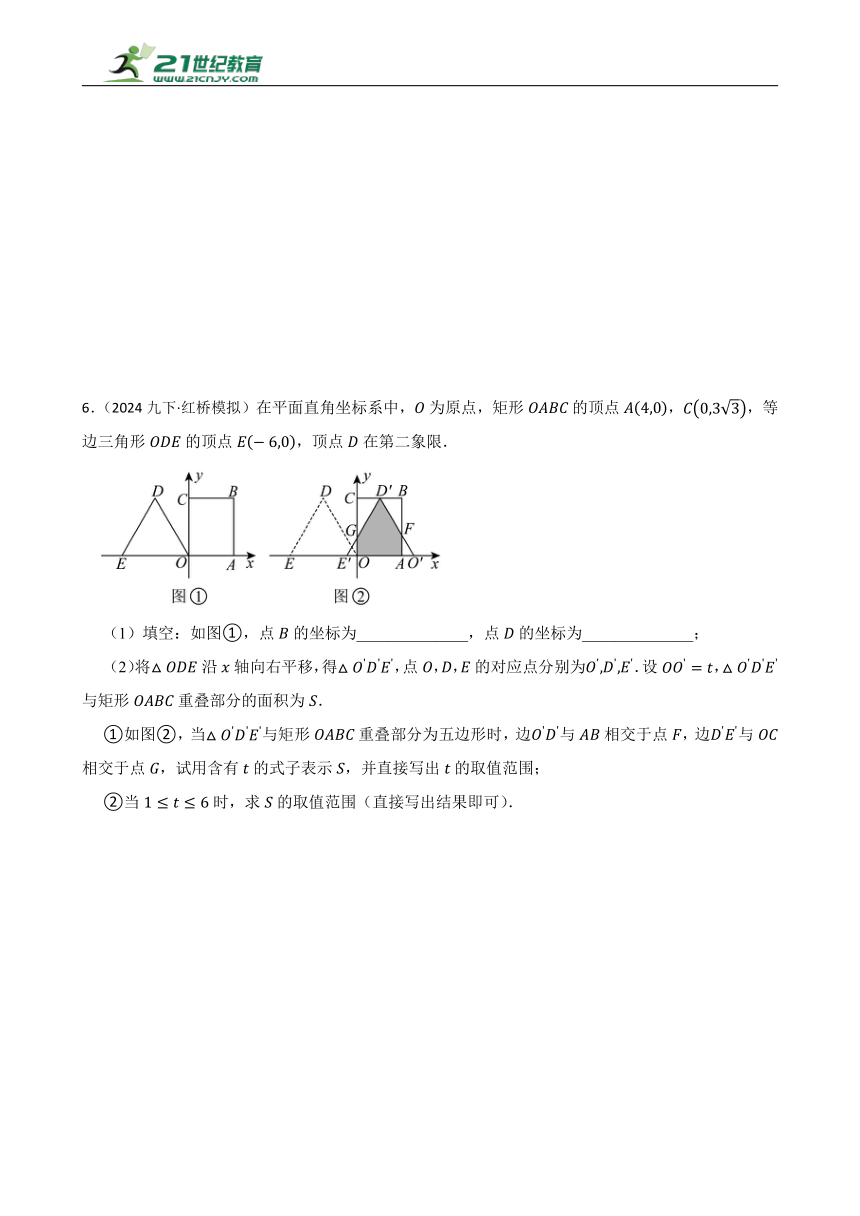
6.(2024九下·红桥模拟)在平面直角坐标系中,为原点,矩形的顶点,,等边三角形的顶点,顶点在第二象限.
(1)填空:如图①,点的坐标为______________,点的坐标为______________;
(2)将沿轴向右平移,得,点,,的对应点分别为.设,与矩形重叠部分的面积为.
①如图②,当与矩形重叠部分为五边形时,边与相交于点,边与相交于点,试用含有的式子表示,并直接写出的取值范围;
②当时,求的取值范围(直接写出结果即可).
7.(2024九下·红桥模拟)以为直径的分别与的边相交于点D,E,平分.
(1)如图①,连接,若,求的大小;
(2)如图②,过点E作的切线,与的延长线相交于点F,与相交于点G.若,求的长.
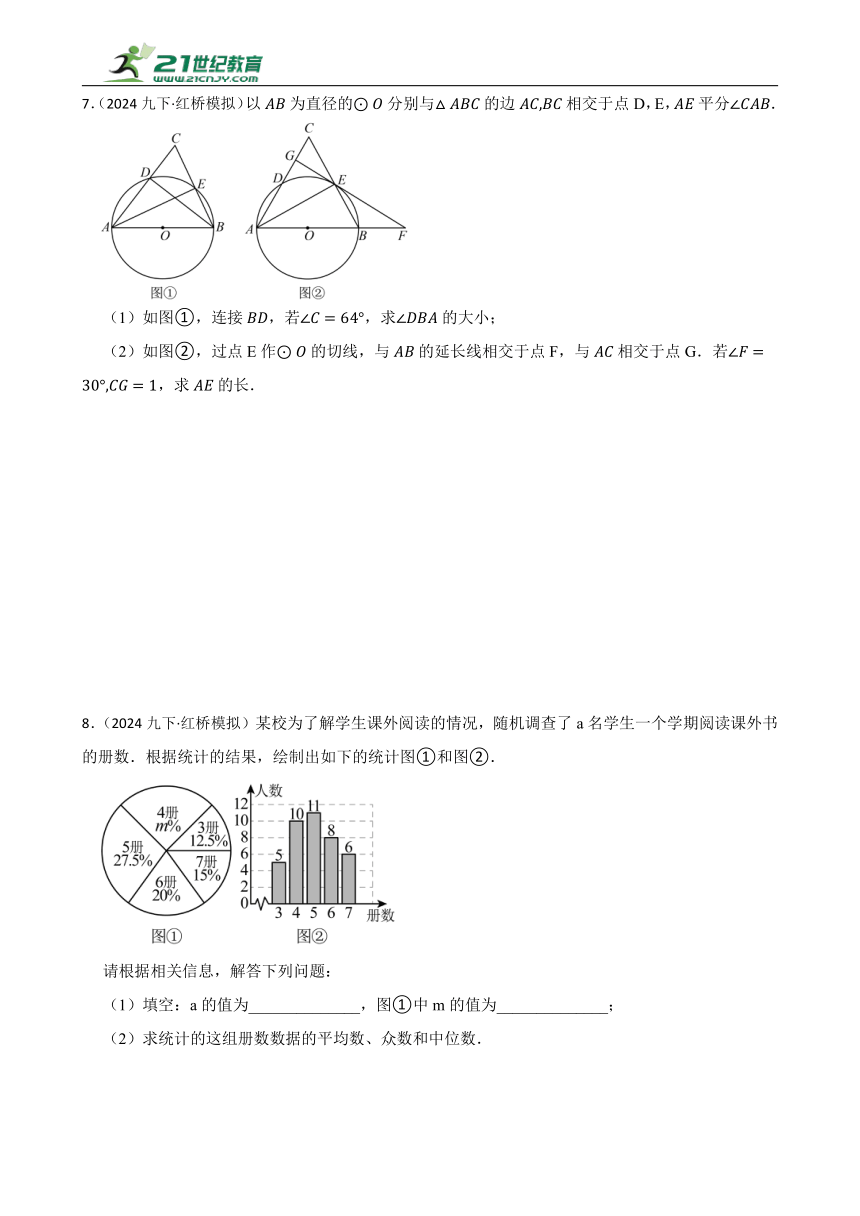
8.(2024九下·红桥模拟)某校为了解学生课外阅读的情况,随机调查了a名学生一个学期阅读课外书的册数.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为______________,图①中m的值为______________;
(2)求统计的这组册数数据的平均数、众数和中位数.
9.(2024九下·南开模拟)已知抛物线(其中a,b,c为常数,,)与x轴交于A,B两点(其中点A在点B的左侧),与y轴相交于点C,且点A坐标为.点在抛物线上,连接,过抛物线的顶点E作直线,交抛物线于点P,设点P的横坐标为m.
(1)若时,求抛物线的解析式及点E的坐标;
(2)若,求a,m的值;
(3)过点P作轴交直线于点Q,连接,恰有轴,求a,m的值(直接写出结果即可).
10.(2024九下·南开模拟)如图1,将一个矩形纸片放置在平面直角坐标系中,点,点,点,点D在边上(点D不与点O,C重合),折叠该纸片,使折痕所在的直线经过点D,并与直线相交于点F,且,点C的对应点为﹒设.
(1)如图2,当折痕经过点B时,求t的值和点的坐标;
(2)若折叠后的图形为四边形,点B的对应点为,与边相交于点G,,分别与x轴相交于点H,I,设折叠后四边形与矩形重合部分的面积为S.
①如图3,当折叠后四边形与矩形重合部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围;
②当时,直接写出S的取值范围.
11.(2024九下·南开模拟)已知,的半径为.在中,,,点在上.
(1)如图,的顶点在上,,分别交于,两点,连接,.求的大小和的长;
(2)如图,的顶点在外,且边与相切于点,边与相交于点,连接,,求和的长.
12.(2024九下·南开模拟)在一次中学生田径运动会上,根据参加男子跳高初赛的a名运动员的成绩(单位:m),绘制出了如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)填空:a的值为________,图①中的m值为________;
(2)求统计的这组男子跳高初赛运动员成绩的数据的平均数、众数和中位数.
13.(2024九下·滨海模拟)已知抛物线(,,为常数,),对称轴为直线,与轴交于点和点,与轴交于点,且,连接.
(1)求抛物线解析式;
(2)点为直线下方抛物线上一点,过点作轴于点,交直线于点,过点作交直线于点,若,求点坐标;
(3)点是抛物线的顶点,将抛物线沿着射线平移,点的对应点为,过点作轴于点,在平移的过程中,是否存在以为腰的等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
14.(2024九下·滨海模拟)在平面直角坐标系中,为原点,矩形的顶点,分别在轴,轴的正半轴上,顶点.是等腰直角三角形,,点,点在轴的负半轴上.将沿轴向右平移,得到,点,,的对应点分别为,,.
(1)如图①,当经过点时,求点的坐标;
(2)设,与矩形重叠部分的面积为;
①如图②,当与矩形重叠部分为五边形时,与相交于点,分别与,交于点,,试用含有的式子表示,并直接写出的取值范围;
②请直接写出满足的所有的值______.
15.(2024九下·滨海模拟)在中,是的直径,弦垂直于,垂足为点,过点作的切线交的延长线于点.
(1)如图①,若,求;
(2)如图②,若,,是的中点,连接,求的长.
16.(2024九下·滨海模拟)某校为了解学生参加社区活动的情况,随机调查了部分学生,对他们参加社区活动的天数进行了统计.根据统计的结果,绘制出如下统计图和图.请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为______,图中的值为______;
(2)求统计的这组学生活动天数数据的平均数、众数和中位数.
17.(2024九下·天津市模拟)在平面直角坐标系中,О为原点,顶点,,点C是线段上一动点(点C不与点O,B重合),过C作交于点D,将沿翻折,使点B落在x轴的点E处.
(1)如图①,当点E与点О重合时,求点D的坐标;
(2)设,与重叠部分的面积为S.
①如图②,当重叠部分为四边形时,试用含t的式子表示S,并直接写出t的取值范围;
②当时,求t的取值范围(直接写出结果即可).
18.(2024九下·天津市模拟)已知是的直径,是的弦.
(1)如图①,若为的中点,,求和的大小;
(2)如图②,过点作的切线交延长线于点,连接,若是的直径,,,求的长.
19.(2024九下·天津市模拟)已知抛物线(为常数,)与轴交于两点,与轴交于点,点的坐标是,点的坐标为.
(1)求的值及抛物线顶点坐标;
(2)点关于轴对称点为为线段上的一个动点,连接.
①当最短时,求点的坐标;
②若为线段上一点,且,连接,当的值最小时,求的长.
20.(2024九下·河西模拟)已知学生宿舍、体育场、文具店依次在同一条直线上,张强从宿舍出发跑步去体育场,在体育场锻炼一阵后又到文具店买笔,然后散步返回宿舍.下面的图象反映了在这个过程中张强离宿舍的距离y(单位:)与时间x(单位:)之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张强离开宿舍的时间/ 1 10 30 55
张强离宿舍的距离/
1.2
②填空:张强从文具店回到家的平均速度为______;
③当时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(2)当张强离开体育场时,同宿舍的李明也从体育场出发匀速步行直接回宿舍,如果李明的速度为,那么他在回宿舍的途中遇到张强时离宿舍的距离是多少?(直接写出结果即可)
21.(2024九下·河西模拟)在中,直径垂直于弦,垂足为E,连接,,,
(1)如图①,若,求和的大小;
(2)如图②,过点C作的切线交AB的延长线于点F.若,,求此圆半径的长.
22.(2024九下·河东模拟)已知抛物线(a,b,c为常数).
(1)若直线l:是抛物线的对称轴,且.
①求抛物线与x轴的交点坐标;
②在平面直角坐标系中,点,点,若动点P在直线下方的抛物线上,连结、,当面积最大时,求点P坐标;
(2)若,抛物线过点,与y轴交于点C,将点B绕点顺时针旋转(旋转角小于)得到点,当点恰好落在抛物线上,且满足时,求n的值.
答案解析部分
1.(1)①0.15,0.6,1.5;
②0.075;
③当0≤4时,y=0.15x;
当4<x≤19时,y=0.6;
当19<x≤25时,y=0.15x-2.25.
(2)爸爸步行的速度为:1.5÷20=0.075,张华的速度为:0.6÷4=0.15,设离家的距离为y,
则,解得:y=1.05.
答:两人相遇时离家的距离是 1.05km
解:(1)①根据点(4,0.6)可得出当0≤x≤4时,y=,
∴当x=1时,y=;
由图象知当x=13时,y=0.6;当x=30时,y=1.5;
故①中表格答案依次为:0.15;0.6;1.5;
②由图象知:返回家所用时间为:51-31=20,
∴ 张华从文化广场返回家的速度为 :1.5÷20=0.075(km/min)
故②的答案为:0.075;
③当0≤x≤4时,设y=kx,
把(4,0.6)代入y=kx中,可得:k=0.15,
即:0≤x≤4时,设y=0.15x;
当4<x≤19时,y=0.6;
当19<x≤25时,设y=k1x+b,
把(19,0.6)和(25,1.5)代入y=k1x+b中,可得:k1=0.15,b=-2.25,
所以当19<x≤25时:y=0.15x-2.25;
(1)①根据表格数据首先可得出当0≤x≤4时,y=,然后可求得当x=1时的函数值Y=0.15;在结合函数图象知当X=13时,函数值为0.6,x=30时,函数值为1.5,即可完成填表;
②由图象知:返回家所用时间为:51-31=20,路程为1.5,即可计算得出张华从文化广场返回家的速度;
③分段函数:当0≤x≤4时,设y=kx,把(4,0.6)代入y=kx中,可得y=0.15x;当4<x≤19时,y=0.6;当19<x≤25时,设y=k1x+b,把(19,0.6)和(25,1.5)代入y=k1x+b中,可得y=0.15x-2.25;
(2)爸爸步行的速度为:1.5÷20=0.075,张华的速度为:0.6÷4=0.15,设离家的距离为y,根据相遇时张华比爸爸多用8min,即可得出方程,解方程即可得出答案。
2.(1)50;34;8;8
(2)观察条形统计图,
这组数据的平均数是8.36.
(3)∵在所抽取的样本中,每周参加科学教育的时间是9h的学生占30%,
∴根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是9h的学生占30%,有500×30%=150.
∴估计该校八年级学生每周参加科学教育的时间是9h的人数约为150.
(1)a=3+7+17+15+8=50;m=;众数为:8;中位数为:;
故第1空答案为:50;第2空答案为:34;第3空答案为:8;第4空答案为:8.
(1)根据各组数据即可得出a的值;根据频率的计算方法,即可得出m的值;根据众数,中位数的定义即可得出3空,4空的答案;
(2)根据平均数的定义即可得出答案;
(3)首先根据样本求得八年级学生每周参加科学教育的时间是 的频率为30%。然后用样本估计总体,用八年级总人数500×30%,即可得出答案。
3.(1)
(2)
(3)
(4)
(1)2x+1≤3,
2x≤2,
∴x≤1;
故答案为:x≤1;
(2)3x-1≥x-7,
3x-x≥-7+1,
∴2x≥-6,
∴x≥-3;
故答案为:x≥-3;
(4)由(3)可知原不等式组的解集为:-3≤x≤1.
(1)解不等式①即可得出答案;
(2)解不等式②即可得出答案;
(3)在同一数轴上分别正确表示①和②的解集;
(4)根据(3),找出公共部分,即可得出答案。
4.(1)
(2)
(3)的坐标为或或或
5.(1)解:∵,
∴设,,
即,
∵,
∴,
∵平分,
∴,
∵,
∴,,
又∵,,
∴,
∴,
∴.
(2)解:,理由如下:
∵,,
∴,
∵平分,
∴,
∵,
∴,
∵,,
∴,
又∵,
∴,
∴.
(1)设,,即,再根据直线平行性质可得,根据角平分线定义可得,再根据直线平行性质可得,,建立方程,解方程即可求出答案.
(2)根据直线平行性质可得,根据角平分线定义可得,再根据直线平行性质可得,根据角之间的关系可得,再根据直线平行性质即可求出答案.
6.(1),
(2)①;②
7.(1)
(2)
8.(1)40,25
(2)这组册数数据的平均数为5、众数为5,中位数为5
9.(1)抛物线解析式为,点E的坐标为;
(2),m的值为;
(3),
10.(1);点的坐标为;
(2)①;;②.
11.(1),;
(2);.
12.(1)15,20;
(2)这组数据的平均数为1.68,众数为1.70,中位数为1.70
13.(1);
(2);
(3)存在,.
14.(1)
(2)①;②或
15.(1)
(2)
16.(1),;
(2)平均数为,众数为,中位数为.;
17.(1)
(2)①,;②或或
18.(1),;
(2)
19.(1),抛物线顶点坐标为;
(2)①点的坐标;②.
20.(1)①0.12,1.2,0.6;
②0.03;.
③
(2)
21.(1);
(2)半径为4
22.(1)①②当面积最大时,此时
(2)
专项3 解答题2 (天津中考真题+中考模拟)
一、解答题
1.(2024·天津) 已知张华的家、画社、文化广场依次在同一条直线上,画社离家,文化广场离家.张华从家出发,先匀速骑行了到画社,在画社停留了,之后匀速骑行了到文化广场,在文化广场停留后,再匀速步行了返回家.下面图中表示时间,表示离家的距离.图象反映了这个过程中张华离家的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张华离开家的时间 1 4 13 30
张华离家的距离
②填空:张华从文化广场返回家的速度为 ▲ ;
③当时,请直接写出张华离家的距离关于时间的函数解析式;
(2)当张华离开家时,他的爸爸也从家出发匀速步行了直接到达了文化广场,那么从画社到文化广场的途中两人相遇时离家的距离是多少?(直接写出结果即可)
2.(2024·天津) 为了解某校八年级学生每周参加科学教育的时间(单位:),随机调查了该校八年级名学生,根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:的值为 ,图①中的值为 ,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为 和 ;
(2)求统计的这组学生每周参加科学教育的时间数据的平均数;
(3)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是的人数约为多少?
3.(2024·天津) 解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为 .
4.(2024九下·红桥模拟)已知抛物线(,为常数,)经过点和点,与轴相交于点,为抛物线上横坐标为的点.
(1)求该抛物线的解析式;
(2)当时,过点作轴的垂线与相交于点,若,求点的坐标;
(3)为线段的中点,当时,求点的坐标.
5.(2024九下·清水模拟)已知,,E在线段延长线上,平分.连接,若.
(1)若,求的度数;
(2)若,探究与的位置关系,并说明理由.
6.(2024九下·红桥模拟)在平面直角坐标系中,为原点,矩形的顶点,,等边三角形的顶点,顶点在第二象限.
(1)填空:如图①,点的坐标为______________,点的坐标为______________;
(2)将沿轴向右平移,得,点,,的对应点分别为.设,与矩形重叠部分的面积为.
①如图②,当与矩形重叠部分为五边形时,边与相交于点,边与相交于点,试用含有的式子表示,并直接写出的取值范围;
②当时,求的取值范围(直接写出结果即可).
7.(2024九下·红桥模拟)以为直径的分别与的边相交于点D,E,平分.
(1)如图①,连接,若,求的大小;
(2)如图②,过点E作的切线,与的延长线相交于点F,与相交于点G.若,求的长.
8.(2024九下·红桥模拟)某校为了解学生课外阅读的情况,随机调查了a名学生一个学期阅读课外书的册数.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)填空:a的值为______________,图①中m的值为______________;
(2)求统计的这组册数数据的平均数、众数和中位数.
9.(2024九下·南开模拟)已知抛物线(其中a,b,c为常数,,)与x轴交于A,B两点(其中点A在点B的左侧),与y轴相交于点C,且点A坐标为.点在抛物线上,连接,过抛物线的顶点E作直线,交抛物线于点P,设点P的横坐标为m.
(1)若时,求抛物线的解析式及点E的坐标;
(2)若,求a,m的值;
(3)过点P作轴交直线于点Q,连接,恰有轴,求a,m的值(直接写出结果即可).
10.(2024九下·南开模拟)如图1,将一个矩形纸片放置在平面直角坐标系中,点,点,点,点D在边上(点D不与点O,C重合),折叠该纸片,使折痕所在的直线经过点D,并与直线相交于点F,且,点C的对应点为﹒设.
(1)如图2,当折痕经过点B时,求t的值和点的坐标;
(2)若折叠后的图形为四边形,点B的对应点为,与边相交于点G,,分别与x轴相交于点H,I,设折叠后四边形与矩形重合部分的面积为S.
①如图3,当折叠后四边形与矩形重合部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围;
②当时,直接写出S的取值范围.
11.(2024九下·南开模拟)已知,的半径为.在中,,,点在上.
(1)如图,的顶点在上,,分别交于,两点,连接,.求的大小和的长;
(2)如图,的顶点在外,且边与相切于点,边与相交于点,连接,,求和的长.
12.(2024九下·南开模拟)在一次中学生田径运动会上,根据参加男子跳高初赛的a名运动员的成绩(单位:m),绘制出了如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)填空:a的值为________,图①中的m值为________;
(2)求统计的这组男子跳高初赛运动员成绩的数据的平均数、众数和中位数.
13.(2024九下·滨海模拟)已知抛物线(,,为常数,),对称轴为直线,与轴交于点和点,与轴交于点,且,连接.
(1)求抛物线解析式;
(2)点为直线下方抛物线上一点,过点作轴于点,交直线于点,过点作交直线于点,若,求点坐标;
(3)点是抛物线的顶点,将抛物线沿着射线平移,点的对应点为,过点作轴于点,在平移的过程中,是否存在以为腰的等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
14.(2024九下·滨海模拟)在平面直角坐标系中,为原点,矩形的顶点,分别在轴,轴的正半轴上,顶点.是等腰直角三角形,,点,点在轴的负半轴上.将沿轴向右平移,得到,点,,的对应点分别为,,.
(1)如图①,当经过点时,求点的坐标;
(2)设,与矩形重叠部分的面积为;
①如图②,当与矩形重叠部分为五边形时,与相交于点,分别与,交于点,,试用含有的式子表示,并直接写出的取值范围;
②请直接写出满足的所有的值______.
15.(2024九下·滨海模拟)在中,是的直径,弦垂直于,垂足为点,过点作的切线交的延长线于点.
(1)如图①,若,求;
(2)如图②,若,,是的中点,连接,求的长.
16.(2024九下·滨海模拟)某校为了解学生参加社区活动的情况,随机调查了部分学生,对他们参加社区活动的天数进行了统计.根据统计的结果,绘制出如下统计图和图.请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为______,图中的值为______;
(2)求统计的这组学生活动天数数据的平均数、众数和中位数.
17.(2024九下·天津市模拟)在平面直角坐标系中,О为原点,顶点,,点C是线段上一动点(点C不与点O,B重合),过C作交于点D,将沿翻折,使点B落在x轴的点E处.
(1)如图①,当点E与点О重合时,求点D的坐标;
(2)设,与重叠部分的面积为S.
①如图②,当重叠部分为四边形时,试用含t的式子表示S,并直接写出t的取值范围;
②当时,求t的取值范围(直接写出结果即可).
18.(2024九下·天津市模拟)已知是的直径,是的弦.
(1)如图①,若为的中点,,求和的大小;
(2)如图②,过点作的切线交延长线于点,连接,若是的直径,,,求的长.
19.(2024九下·天津市模拟)已知抛物线(为常数,)与轴交于两点,与轴交于点,点的坐标是,点的坐标为.
(1)求的值及抛物线顶点坐标;
(2)点关于轴对称点为为线段上的一个动点,连接.
①当最短时,求点的坐标;
②若为线段上一点,且,连接,当的值最小时,求的长.
20.(2024九下·河西模拟)已知学生宿舍、体育场、文具店依次在同一条直线上,张强从宿舍出发跑步去体育场,在体育场锻炼一阵后又到文具店买笔,然后散步返回宿舍.下面的图象反映了在这个过程中张强离宿舍的距离y(单位:)与时间x(单位:)之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
张强离开宿舍的时间/ 1 10 30 55
张强离宿舍的距离/
1.2
②填空:张强从文具店回到家的平均速度为______;
③当时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(2)当张强离开体育场时,同宿舍的李明也从体育场出发匀速步行直接回宿舍,如果李明的速度为,那么他在回宿舍的途中遇到张强时离宿舍的距离是多少?(直接写出结果即可)
21.(2024九下·河西模拟)在中,直径垂直于弦,垂足为E,连接,,,
(1)如图①,若,求和的大小;
(2)如图②,过点C作的切线交AB的延长线于点F.若,,求此圆半径的长.
22.(2024九下·河东模拟)已知抛物线(a,b,c为常数).
(1)若直线l:是抛物线的对称轴,且.
①求抛物线与x轴的交点坐标;
②在平面直角坐标系中,点,点,若动点P在直线下方的抛物线上,连结、,当面积最大时,求点P坐标;
(2)若,抛物线过点,与y轴交于点C,将点B绕点顺时针旋转(旋转角小于)得到点,当点恰好落在抛物线上,且满足时,求n的值.
答案解析部分
1.(1)①0.15,0.6,1.5;
②0.075;
③当0≤4时,y=0.15x;
当4<x≤19时,y=0.6;
当19<x≤25时,y=0.15x-2.25.
(2)爸爸步行的速度为:1.5÷20=0.075,张华的速度为:0.6÷4=0.15,设离家的距离为y,
则,解得:y=1.05.
答:两人相遇时离家的距离是 1.05km
解:(1)①根据点(4,0.6)可得出当0≤x≤4时,y=,
∴当x=1时,y=;
由图象知当x=13时,y=0.6;当x=30时,y=1.5;
故①中表格答案依次为:0.15;0.6;1.5;
②由图象知:返回家所用时间为:51-31=20,
∴ 张华从文化广场返回家的速度为 :1.5÷20=0.075(km/min)
故②的答案为:0.075;
③当0≤x≤4时,设y=kx,
把(4,0.6)代入y=kx中,可得:k=0.15,
即:0≤x≤4时,设y=0.15x;
当4<x≤19时,y=0.6;
当19<x≤25时,设y=k1x+b,
把(19,0.6)和(25,1.5)代入y=k1x+b中,可得:k1=0.15,b=-2.25,
所以当19<x≤25时:y=0.15x-2.25;
(1)①根据表格数据首先可得出当0≤x≤4时,y=,然后可求得当x=1时的函数值Y=0.15;在结合函数图象知当X=13时,函数值为0.6,x=30时,函数值为1.5,即可完成填表;
②由图象知:返回家所用时间为:51-31=20,路程为1.5,即可计算得出张华从文化广场返回家的速度;
③分段函数:当0≤x≤4时,设y=kx,把(4,0.6)代入y=kx中,可得y=0.15x;当4<x≤19时,y=0.6;当19<x≤25时,设y=k1x+b,把(19,0.6)和(25,1.5)代入y=k1x+b中,可得y=0.15x-2.25;
(2)爸爸步行的速度为:1.5÷20=0.075,张华的速度为:0.6÷4=0.15,设离家的距离为y,根据相遇时张华比爸爸多用8min,即可得出方程,解方程即可得出答案。
2.(1)50;34;8;8
(2)观察条形统计图,
这组数据的平均数是8.36.
(3)∵在所抽取的样本中,每周参加科学教育的时间是9h的学生占30%,
∴根据样本数据,估计该校八年级学生500人中,每周参加科学教育的时间是9h的学生占30%,有500×30%=150.
∴估计该校八年级学生每周参加科学教育的时间是9h的人数约为150.
(1)a=3+7+17+15+8=50;m=;众数为:8;中位数为:;
故第1空答案为:50;第2空答案为:34;第3空答案为:8;第4空答案为:8.
(1)根据各组数据即可得出a的值;根据频率的计算方法,即可得出m的值;根据众数,中位数的定义即可得出3空,4空的答案;
(2)根据平均数的定义即可得出答案;
(3)首先根据样本求得八年级学生每周参加科学教育的时间是 的频率为30%。然后用样本估计总体,用八年级总人数500×30%,即可得出答案。
3.(1)
(2)
(3)
(4)
(1)2x+1≤3,
2x≤2,
∴x≤1;
故答案为:x≤1;
(2)3x-1≥x-7,
3x-x≥-7+1,
∴2x≥-6,
∴x≥-3;
故答案为:x≥-3;
(4)由(3)可知原不等式组的解集为:-3≤x≤1.
(1)解不等式①即可得出答案;
(2)解不等式②即可得出答案;
(3)在同一数轴上分别正确表示①和②的解集;
(4)根据(3),找出公共部分,即可得出答案。
4.(1)
(2)
(3)的坐标为或或或
5.(1)解:∵,
∴设,,
即,
∵,
∴,
∵平分,
∴,
∵,
∴,,
又∵,,
∴,
∴,
∴.
(2)解:,理由如下:
∵,,
∴,
∵平分,
∴,
∵,
∴,
∵,,
∴,
又∵,
∴,
∴.
(1)设,,即,再根据直线平行性质可得,根据角平分线定义可得,再根据直线平行性质可得,,建立方程,解方程即可求出答案.
(2)根据直线平行性质可得,根据角平分线定义可得,再根据直线平行性质可得,根据角之间的关系可得,再根据直线平行性质即可求出答案.
6.(1),
(2)①;②
7.(1)
(2)
8.(1)40,25
(2)这组册数数据的平均数为5、众数为5,中位数为5
9.(1)抛物线解析式为,点E的坐标为;
(2),m的值为;
(3),
10.(1);点的坐标为;
(2)①;;②.
11.(1),;
(2);.
12.(1)15,20;
(2)这组数据的平均数为1.68,众数为1.70,中位数为1.70
13.(1);
(2);
(3)存在,.
14.(1)
(2)①;②或
15.(1)
(2)
16.(1),;
(2)平均数为,众数为,中位数为.;
17.(1)
(2)①,;②或或
18.(1),;
(2)
19.(1),抛物线顶点坐标为;
(2)①点的坐标;②.
20.(1)①0.12,1.2,0.6;
②0.03;.
③
(2)
21.(1);
(2)半径为4
22.(1)①②当面积最大时,此时
(2)
同课章节目录
