2024-2025学年小升初数学备考真题分类汇编(湖南地区专版)专题3 计算题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(湖南地区专版)专题3 计算题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 65.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 10:05:37 | ||
图片预览



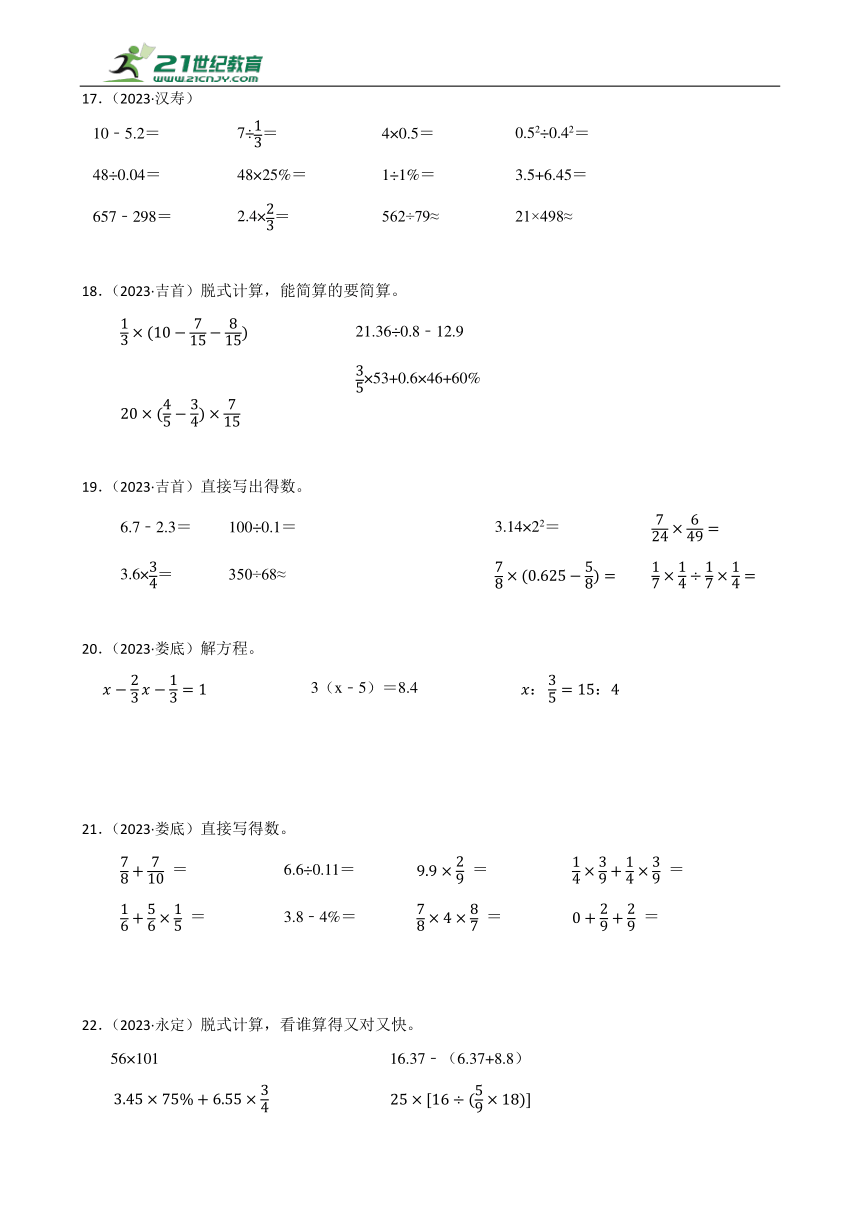

文档简介
2024-2025学年小升初数学备考真题分类汇编(湖南地区专版)
专题3 计算题
一、计算题
1.(2024·蓝山)求未知数x。
15:x=0.6: x+80%=40
2.(2024·岳阳)解方程或比例。
①x+0.4÷=60 ②
3.(2024·安化)求未知数x。
7.2x﹣5.4x=25.2 13x+17=108 =
4.(2024·安化)估算。
803﹣208≈ 24×398≈ 6298÷9≈
732÷89≈ 503×4≈
5.(2024·安化)直接写得数。
5.6×100= 4.5÷10= 2.5×4= 0.32×25=
2.8×0.5= 0.47+0.63= 16.8÷0.4= 2.4×5=
1÷18= 2.8÷0.5=
6.(2024·蒸湘)解方程。
3.2x﹣4×3=52 x:1.2=3:4 2x+3×0.9=24.7
7.(2024·蒸湘)直接写出得数。
4×0.625= 8-0.75-= ×8.1= +=
3.7×99+3.7= 12.5×8÷12.5×8= ÷2= 1.05÷0.5=
8.(2024·汨罗)计算。
9.(2024·蓝山)计算下面各题,能简算的要简算。
×+÷ 0.9×999+0.9
25%×÷ 9+(-0.75)÷
10.(2024·蓝山)直接写出得数。
×0.9= 18÷0.8= += ×÷×=
1.9﹣7%= 122÷4= 6﹣-0.4= 631÷89%≈
11.(2024·岳阳)直接写出得数。
4.8÷24= 1.4÷70%= ×8= (+)×30=
6.9+7= ×6.3= 49.01÷7≈ =
12.(2024·云安)计算,能简算的要简算。
13.(2024·蒸湘)脱式计算,能简算的要简算。
(+-)×72 1.75×30%+1.75×0.7
19÷[(+)÷] 3.14×43+7.2×31.4﹣150×0.314
14.(2023·芙蓉)解方程。
15.(2023·芙蓉)直接写得数。
16.(2023·汉寿)计算下面各题,能简算的要简算。
4×0.8×2.5×12.5 60×
15.28﹣3.99﹣9.01 10.7﹣2.9×0.2÷0.58
17.(2023·汉寿)
10﹣5.2= 7÷= 4×0.5= 0.52÷0.42=
48÷0.04= 48×25%= 1÷1%= 3.5+6.45=
657﹣298= 2.4×= 562÷79≈ 21×498≈
18.(2023·吉首)脱式计算,能简算的要简算。
21.36÷0.8﹣12.9
×53+0.6×46+60%
19.(2023·吉首)直接写出得数。
6.7﹣2.3= 100÷0.1= 3.14×22=
3.6×= 350÷68≈
20.(2023·娄底)解方程。
3(x﹣5)=8.4
21.(2023·娄底)直接写得数。
= 6.6÷0.11= = =
= 3.8﹣4%= = =
22.(2023·永定)脱式计算,看谁算得又对又快。
56×101 16.37﹣(6.37+8.8)
23.(2023·炎陵)解方程(比例)。
①4x÷ =6
②160%x+4.5×20%=8.9
③1.8:x=27:60
24.(2023·炎陵)直接写出得数。
2.3+5.7= 12.2﹣0.5= 140×0.3= 401﹣198=
3600÷12= + = ﹣ = ×240=
÷ = 25%×5.6÷ =
25.(2023·岳阳)直接写出得数
15﹣8.6= 88×62.5%= (0.18+0.9)÷9=
÷7= + = ﹣ ×0=
答案解析部分
1.
15:x=0.6:
解:0.6x=15×
0.6x=
x=÷0.6
x= x+80%=40
解:x=40-80%
x=39.2
x=39.2÷
x=196
比例的基本性质:在比例里,两个内项积等于两个外项积。依据比例的基本性质解比例;
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先应用等式的性质1,等式两边同时减去80%,然后应用等式的性质2,等式的两边同时除以计算出结果。
2.
①x+0.4÷=60
解: x+6=60
x+6﹣6=60﹣6
x=63 ②
解:x=4×0.6
x=2.4÷
x=28
等式的性质1:等式两边同时加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边同时乘一个数,或同时除以一个不是0的数,两边仍然相等。
比例的基本性质:在比例里,两个内项的积等于两个外项的积。
①先计算方程左边的部分,然后把方程两边同时减去6,再同时除以即可求出x的值;
②根据比例的基本性质把比例写成两个內项积等于两个外项积的形式,然后根据等式的性质求出未知数的值。
3.
解:
解:
解:
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个,或除以同一个不为0的数,左右两边仍然相等;
比例的基本性质:比例的外项积等于其内项积。
第一题运用等式的性质2解方程;
第二题运用等式的性质1和等式的性质2解方程;
第三题运用比例的基本性质和等式的性质2解方程。
4.
803﹣208≈600 24×398≈10000 6298÷9≈700
732÷89≈8 503×4≈2000
估算是一种常用的数学技巧,用于快速得到一个数值的近似值。在进行估算时,我们通常会将数值四舍五入到最接近的十、百、千等数位,以便进行简单的计算。对于本题中的各个小问,我们将根据具体的数值,采用四舍五入的方法进行估算,并给出最终的近似值。通过估算,我们得到了各个算式的近似值。需要注意的是,估算的结果是一个近似值,可能与实际计算结果略有出入。然而,在许多实际情境中,估算能够帮助我们快速得到一个合理的答案,这对于提高解题效率和解决实际问题具有重要意义。
5.
5.6×100=560 4.5÷10=0.45 2.5×4=10 0.32×25=8
2.8×0.5=1.4 0.47+0.63=1.1 16.8÷0.4=42 2.4×5=12
1÷18= 2.8÷0.5=5.6
本题主要考查小数的四则运算,包括乘法、除法、加法,以及小数点移动的问题。解题关键在于熟练掌握小数运算的基本法则。在计算小数乘除法时,要注意小数点的位置,乘法时先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;除法时,根据除数中小数点的位置,调整被除数和除数的小数点位置,使之成为整数除法,再进行计算。此外,计算小数加减法时,确保小数点对齐,然后按整数加减法的计算方法进行计算。
6.解:3.2x-4×3=52
3.2x=12+52
3.2x=64
x=64÷3.2
x=20
x:1.2=3:4
解:4x=1.2×3
4x=3.6
x=3.6÷4
x=0.9
2x+3×0.9=24.7
解:2x+2.7=24.7
2x=24.7-2.7
2x=22
x=22÷2
x=11
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先算4×3=12,然后应用等式的性质1,等式两边同时加上52,然后再应用等式的性质2,等式两边同时除以3.2;
比例的基本性质:在比例里,两个内项积等于两个外项积,应用比例的基本性质解比例;
先计算3×0.9=2.7,然后应用等式的性质1,等式两边同时减去2.7,再应用等式的性质2,等式两边同时除以2,计算出结果。
7.
4×0.625=2.5 8-0.75-=7 ×8.1=0.9 +=
3.7×99+3.7=370 12.5×8÷12.5×8=64 ÷2= 1.05÷0.5=2.1
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母;
异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的除法进行计算。
8.解:
=(+-1)×
=5×
=11
=++
=+
=
乘法分配律=a×-b+a×c=a×(b+c);
在没有小括号,只有加减法的计算中,要按照顺序从左往右依次计算。
9.
解:×+÷
=(+)×
=1×
= 0.9×999+0.9
=(999+1)×0.9
=1000×0.9
=900
25%×÷
=(25%÷)×
=1×
= 9+(-0.75)÷
=9+(-)×28
=9+×28-×28
=9+24-21
=33-21
=12
应用乘法分配律,先计算(+)=1,然后再乘;
应用乘法分配律,先计算(999+1)=1000,然后再乘0.9;
先计算(25%÷)=1,然后再乘;
先把除以变成乘28,然后应用乘法分配律,括号里面的数分别与28相乘,再把所得的积相加减。
10.
×0.9=0.7 18÷0.8=22.5 += ×÷×=
1.9-7%=1.83 122÷4=36 6--0.4=5 631÷89%≈700
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
11.
4.8÷24=0.2 1.4÷70%=2 ×8=1 (+)×30=11
6.9+7=13.9 ×6.3=3.6 49.01÷7≈7 =
计算小数加减乘除时注意小数点的位置;计算分数乘法时能约分的要先约分再乘;计算分数除法时把除法转化成乘法计算;混合运算先确定运算顺序再计算;含有百分数的把百分数化成小数或分数计算。
12.解:18×(+-)
=18×+18×-18×
=3+6-9
=9-9
=0
6.5+6.5×7+6.5×2
=6.5×(1+7+2)
=6.5×10
=65
=×+×
=×(+)
=×1
=
=[+×-×]÷
=[-×]÷
=[×(1-)]÷
=×
=
0,65,,
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,用字母表示为:a(b+c)=ab+ac;
第1题:通过观察发现括号外面的数都能与括号里面的每一个数进约分,所以利用乘法分配律会计算简便;
第2题:因为有相同因数6.5,所以可以利用乘法分配律使计算简便;
第3题:通过观察发现可以将×改写成×,这样就有相同因数,可以利用乘法分配律的逆运用使计算简便;
第4题:通过观察发现括号里面可以先使用乘法分配律去掉括号,先计算出×的积与的和后,又发现有相同因数,可以再次使用乘法分配律的逆运用加上括号会使计算简便。
13.解:(+-)×72
=×72+×72-×72
=56+60-18
=116-18
=98
1.75×30%+1.75×0.7
=(30%+0.7)×1.75
=1×1.75
=1.75
19÷[(+)÷]
=19÷[÷]
=19÷
=10
3.14×43+7.2×31.4-150×0.314
=(43+72-15)×3.14
=100×3.14
=314
应用乘法分配律,括号里面的数分别与括号外面的数相乘,再把所得的积相加减;
应用乘法分配律,先计算(30%+0.7)=1,然后再乘1.75;
分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
应用乘法分配律,先计算(43+72-15)=100,然后再乘3.14。
14.
解:
x=3
解:0.4x+
0.4x=
0.4x÷0.4=÷0.4
x=
解:
x=2
第一题,等式两边先同时加上,再同时除以即可;第二题,40%=0.4,等式两边同时减去,再同时除以0.4即可;第三题,等式左边化简得到,再同时除以即可。
15.
3.5 1
分数与小数相乘,把分子与小数相乘,再除以分母即可;含有百分数的计算,现将百分数转化成分数,再进行计算;除以一个分数等于乘这个分数的倒数;不含括号的四则混合运算,先算乘除法,再算加减法;分数乘分数,分母与分母相乘的积作分母,分子与分子相乘的积作分子,能约分的要约分。
16.解:
4×0.8×2.5×12.5
=4×2.5×(0.8×12.5)
=10×10
=100 60×
=60×+60×-60×
=10+24-16
=34-16
=18
15.28-3.99-9.01
=15.28-(3.99+9.01)
=15.28-13
=2.28 10.7﹣2.9×0.2÷0.58
=10.7-0.58÷0.58
=10.7-1
=9.7
第一题,利用乘法交换律和乘法结合律简便计算;第二题,利用乘法分配律简便计算;第三题,连续减去两个数等于减去这两个数的和;第四题,按照四则混合运算顺序,先算乘法,再算除法,最后算减法。
17.
10-5.2=4.8 7÷=21 4×0.5=2 0.52÷0.42=
48÷0.04=1200 48×25%=12 1÷1%=100 3.5+6.45=9.95
657-298=359 2.4×=1.6 562÷79≈7 21×498≈10000
小数加减法要注意相同数位相加减;除以一个数等于乘这个数的倒数;小数乘法与整数乘法计算方法相同,最后看因数中一共有几位小数,就在结果的末尾往左数出几位点上小数点,小数末尾的0可以去掉;除数是小数的除法,向右移动除数的小数点使其变成整数,再根据商不变的性质将被除数的小数点向右移动相同的数位,再进行计算,商的小数点与被除数移动后的小数点对齐;百分数的计算,可以先将百分数转化成分数或小数再进行计算;小数与分数相乘,分母不变,只把小数与分子相乘,能约分的要约分。
18.解:
=3 21.36÷0.8﹣12.9
=26.7-12.9
=13.8
= ×53+0.6×46+60%
=0.6×53+0.6×46+0.6
=0.6×(53+46+1)
=0.6×100
=60
混合运算顺序:从左往右计算,先算乘除,再算加减;有括号的先算括号里面的,先算小括号再算中括号。
第一题:利用连减的性质,把改写成,再按运算顺序进行计算;
第二题:按运算顺序进行计算;
第三题:利用乘法分配律,把改写成,再运算顺序计算;
第四题:先把分数、百分数统一化成小数0.6,再利用乘法分配律把×53+0.6×46+60%改写成0.6×53+0.6×46+0.6,最后按运算顺序进行计算。
19.
6.7﹣2.3=4.4 100÷0.1=1000 3.14×22=12.56
3.6×=2.7 350÷68≈5 0
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
20.
解: x- =1
x=1+
x=
x×3= ×3
x=4
3(x-5)=8.4
解:3(x-5)÷3=8.4÷3
x-5=2.8
x=2.8+5
x=7.8
解:4x= ×15
4x=9
x=9÷4
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
综合应用等式的性质解方程;
综合应用等式的性质解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质解比例。
21.
= 6.6÷0.11=60 =2.2 =
= 3.8-4%=3.76 =4 =
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
22.解:56×101
=56×(100+1)
=56×100+56
=5600+56
=5656
16.37﹣(6.37+8.8)
=16.37﹣6.37﹣8.8
=10﹣8.8
=1.2
3.45×75%+6.55×
=0.75×(3.45+6.55)
=0.75×10
=7.5
25×[16÷(×18)]
=25×[16÷10]
=25×1.6
=40
观察数据可知,先把101分成(100+1),再利用乘法分配律简算;
观察数据可知,此题应用减法的性质,一个数减去两个数的和,等于连续减去这两个数,据此计算简便;
观察数据可知,此题应用乘法分配律简算;
观察算式可知,算式中有中括号和小括号,先算中括号里面的小括号里的乘法,再计算中括号里面的除法,最后计算中括号外面的乘法,据此顺序解答。
23.① 4x÷ =6
解:4x÷ × =6×
4x=
4x÷4= ÷4
x=
②160%x+4.5×20%=8.9
解: 160%x+0.9=8.9
160%x+0.9﹣0.9=8.9﹣0.9
1.6x=8
1.6x÷1.6=8÷1.6
x=5
③ 1.8:x=27:60
解: 27x=1.8×60
27x=108
27x÷27=108÷27
x=4
解方程的依据是等式的性质:等式的两边同时加减乘除相同的数(0除外),等式仍然成立,据此解答;
解比例的依据是比例的基本性质:在比例里,两外项之积等于两内项之积,据此解答。
24.
2.3+5.7=8 12.2﹣0.5=11.7 140×0.3=42 401﹣198=203
3600÷12=300 + = ﹣ = ×240=200
÷ = 25%×5.6÷ =2
计算小数加减法时,先把小数点对齐,也就是相同数位对齐,然后再按照整数加减法的计算法则进行计算,据此解答;
小数乘法法则:先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足,注意:计算的结果,如果小数末尾有0的,根据小数的基本性质,在小数的末尾去掉零,小数的大小不变;
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的法则进行计算,计算结果能约分的要约成最简分数;
分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此解答;
百分数与分数、小数混合运算,可以把百分数化成小数,再计算。
25.
15﹣8.6=6.4 88×62.5%=55 (0.18+0.9)÷9=0.12
÷7= + = - ×0=
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
专题3 计算题
一、计算题
1.(2024·蓝山)求未知数x。
15:x=0.6: x+80%=40
2.(2024·岳阳)解方程或比例。
①x+0.4÷=60 ②
3.(2024·安化)求未知数x。
7.2x﹣5.4x=25.2 13x+17=108 =
4.(2024·安化)估算。
803﹣208≈ 24×398≈ 6298÷9≈
732÷89≈ 503×4≈
5.(2024·安化)直接写得数。
5.6×100= 4.5÷10= 2.5×4= 0.32×25=
2.8×0.5= 0.47+0.63= 16.8÷0.4= 2.4×5=
1÷18= 2.8÷0.5=
6.(2024·蒸湘)解方程。
3.2x﹣4×3=52 x:1.2=3:4 2x+3×0.9=24.7
7.(2024·蒸湘)直接写出得数。
4×0.625= 8-0.75-= ×8.1= +=
3.7×99+3.7= 12.5×8÷12.5×8= ÷2= 1.05÷0.5=
8.(2024·汨罗)计算。
9.(2024·蓝山)计算下面各题,能简算的要简算。
×+÷ 0.9×999+0.9
25%×÷ 9+(-0.75)÷
10.(2024·蓝山)直接写出得数。
×0.9= 18÷0.8= += ×÷×=
1.9﹣7%= 122÷4= 6﹣-0.4= 631÷89%≈
11.(2024·岳阳)直接写出得数。
4.8÷24= 1.4÷70%= ×8= (+)×30=
6.9+7= ×6.3= 49.01÷7≈ =
12.(2024·云安)计算,能简算的要简算。
13.(2024·蒸湘)脱式计算,能简算的要简算。
(+-)×72 1.75×30%+1.75×0.7
19÷[(+)÷] 3.14×43+7.2×31.4﹣150×0.314
14.(2023·芙蓉)解方程。
15.(2023·芙蓉)直接写得数。
16.(2023·汉寿)计算下面各题,能简算的要简算。
4×0.8×2.5×12.5 60×
15.28﹣3.99﹣9.01 10.7﹣2.9×0.2÷0.58
17.(2023·汉寿)
10﹣5.2= 7÷= 4×0.5= 0.52÷0.42=
48÷0.04= 48×25%= 1÷1%= 3.5+6.45=
657﹣298= 2.4×= 562÷79≈ 21×498≈
18.(2023·吉首)脱式计算,能简算的要简算。
21.36÷0.8﹣12.9
×53+0.6×46+60%
19.(2023·吉首)直接写出得数。
6.7﹣2.3= 100÷0.1= 3.14×22=
3.6×= 350÷68≈
20.(2023·娄底)解方程。
3(x﹣5)=8.4
21.(2023·娄底)直接写得数。
= 6.6÷0.11= = =
= 3.8﹣4%= = =
22.(2023·永定)脱式计算,看谁算得又对又快。
56×101 16.37﹣(6.37+8.8)
23.(2023·炎陵)解方程(比例)。
①4x÷ =6
②160%x+4.5×20%=8.9
③1.8:x=27:60
24.(2023·炎陵)直接写出得数。
2.3+5.7= 12.2﹣0.5= 140×0.3= 401﹣198=
3600÷12= + = ﹣ = ×240=
÷ = 25%×5.6÷ =
25.(2023·岳阳)直接写出得数
15﹣8.6= 88×62.5%= (0.18+0.9)÷9=
÷7= + = ﹣ ×0=
答案解析部分
1.
15:x=0.6:
解:0.6x=15×
0.6x=
x=÷0.6
x= x+80%=40
解:x=40-80%
x=39.2
x=39.2÷
x=196
比例的基本性质:在比例里,两个内项积等于两个外项积。依据比例的基本性质解比例;
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先应用等式的性质1,等式两边同时减去80%,然后应用等式的性质2,等式的两边同时除以计算出结果。
2.
①x+0.4÷=60
解: x+6=60
x+6﹣6=60﹣6
x=63 ②
解:x=4×0.6
x=2.4÷
x=28
等式的性质1:等式两边同时加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边同时乘一个数,或同时除以一个不是0的数,两边仍然相等。
比例的基本性质:在比例里,两个内项的积等于两个外项的积。
①先计算方程左边的部分,然后把方程两边同时减去6,再同时除以即可求出x的值;
②根据比例的基本性质把比例写成两个內项积等于两个外项积的形式,然后根据等式的性质求出未知数的值。
3.
解:
解:
解:
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个,或除以同一个不为0的数,左右两边仍然相等;
比例的基本性质:比例的外项积等于其内项积。
第一题运用等式的性质2解方程;
第二题运用等式的性质1和等式的性质2解方程;
第三题运用比例的基本性质和等式的性质2解方程。
4.
803﹣208≈600 24×398≈10000 6298÷9≈700
732÷89≈8 503×4≈2000
估算是一种常用的数学技巧,用于快速得到一个数值的近似值。在进行估算时,我们通常会将数值四舍五入到最接近的十、百、千等数位,以便进行简单的计算。对于本题中的各个小问,我们将根据具体的数值,采用四舍五入的方法进行估算,并给出最终的近似值。通过估算,我们得到了各个算式的近似值。需要注意的是,估算的结果是一个近似值,可能与实际计算结果略有出入。然而,在许多实际情境中,估算能够帮助我们快速得到一个合理的答案,这对于提高解题效率和解决实际问题具有重要意义。
5.
5.6×100=560 4.5÷10=0.45 2.5×4=10 0.32×25=8
2.8×0.5=1.4 0.47+0.63=1.1 16.8÷0.4=42 2.4×5=12
1÷18= 2.8÷0.5=5.6
本题主要考查小数的四则运算,包括乘法、除法、加法,以及小数点移动的问题。解题关键在于熟练掌握小数运算的基本法则。在计算小数乘除法时,要注意小数点的位置,乘法时先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;除法时,根据除数中小数点的位置,调整被除数和除数的小数点位置,使之成为整数除法,再进行计算。此外,计算小数加减法时,确保小数点对齐,然后按整数加减法的计算方法进行计算。
6.解:3.2x-4×3=52
3.2x=12+52
3.2x=64
x=64÷3.2
x=20
x:1.2=3:4
解:4x=1.2×3
4x=3.6
x=3.6÷4
x=0.9
2x+3×0.9=24.7
解:2x+2.7=24.7
2x=24.7-2.7
2x=22
x=22÷2
x=11
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
先算4×3=12,然后应用等式的性质1,等式两边同时加上52,然后再应用等式的性质2,等式两边同时除以3.2;
比例的基本性质:在比例里,两个内项积等于两个外项积,应用比例的基本性质解比例;
先计算3×0.9=2.7,然后应用等式的性质1,等式两边同时减去2.7,再应用等式的性质2,等式两边同时除以2,计算出结果。
7.
4×0.625=2.5 8-0.75-=7 ×8.1=0.9 +=
3.7×99+3.7=370 12.5×8÷12.5×8=64 ÷2= 1.05÷0.5=2.1
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母;
异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的除法进行计算。
8.解:
=(+-1)×
=5×
=11
=++
=+
=
乘法分配律=a×-b+a×c=a×(b+c);
在没有小括号,只有加减法的计算中,要按照顺序从左往右依次计算。
9.
解:×+÷
=(+)×
=1×
= 0.9×999+0.9
=(999+1)×0.9
=1000×0.9
=900
25%×÷
=(25%÷)×
=1×
= 9+(-0.75)÷
=9+(-)×28
=9+×28-×28
=9+24-21
=33-21
=12
应用乘法分配律,先计算(+)=1,然后再乘;
应用乘法分配律,先计算(999+1)=1000,然后再乘0.9;
先计算(25%÷)=1,然后再乘;
先把除以变成乘28,然后应用乘法分配律,括号里面的数分别与28相乘,再把所得的积相加减。
10.
×0.9=0.7 18÷0.8=22.5 += ×÷×=
1.9-7%=1.83 122÷4=36 6--0.4=5 631÷89%≈700
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
11.
4.8÷24=0.2 1.4÷70%=2 ×8=1 (+)×30=11
6.9+7=13.9 ×6.3=3.6 49.01÷7≈7 =
计算小数加减乘除时注意小数点的位置;计算分数乘法时能约分的要先约分再乘;计算分数除法时把除法转化成乘法计算;混合运算先确定运算顺序再计算;含有百分数的把百分数化成小数或分数计算。
12.解:18×(+-)
=18×+18×-18×
=3+6-9
=9-9
=0
6.5+6.5×7+6.5×2
=6.5×(1+7+2)
=6.5×10
=65
=×+×
=×(+)
=×1
=
=[+×-×]÷
=[-×]÷
=[×(1-)]÷
=×
=
0,65,,
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,用字母表示为:a(b+c)=ab+ac;
第1题:通过观察发现括号外面的数都能与括号里面的每一个数进约分,所以利用乘法分配律会计算简便;
第2题:因为有相同因数6.5,所以可以利用乘法分配律使计算简便;
第3题:通过观察发现可以将×改写成×,这样就有相同因数,可以利用乘法分配律的逆运用使计算简便;
第4题:通过观察发现括号里面可以先使用乘法分配律去掉括号,先计算出×的积与的和后,又发现有相同因数,可以再次使用乘法分配律的逆运用加上括号会使计算简便。
13.解:(+-)×72
=×72+×72-×72
=56+60-18
=116-18
=98
1.75×30%+1.75×0.7
=(30%+0.7)×1.75
=1×1.75
=1.75
19÷[(+)÷]
=19÷[÷]
=19÷
=10
3.14×43+7.2×31.4-150×0.314
=(43+72-15)×3.14
=100×3.14
=314
应用乘法分配律,括号里面的数分别与括号外面的数相乘,再把所得的积相加减;
应用乘法分配律,先计算(30%+0.7)=1,然后再乘1.75;
分数四则混合运算,如果有括号先算小括号里面的,再算中括号里面的,最后算括号外面的;如果没有括号,先算乘除,再算加减;只含有同一级运算,按照从左到右的顺序计算;
应用乘法分配律,先计算(43+72-15)=100,然后再乘3.14。
14.
解:
x=3
解:0.4x+
0.4x=
0.4x÷0.4=÷0.4
x=
解:
x=2
第一题,等式两边先同时加上,再同时除以即可;第二题,40%=0.4,等式两边同时减去,再同时除以0.4即可;第三题,等式左边化简得到,再同时除以即可。
15.
3.5 1
分数与小数相乘,把分子与小数相乘,再除以分母即可;含有百分数的计算,现将百分数转化成分数,再进行计算;除以一个分数等于乘这个分数的倒数;不含括号的四则混合运算,先算乘除法,再算加减法;分数乘分数,分母与分母相乘的积作分母,分子与分子相乘的积作分子,能约分的要约分。
16.解:
4×0.8×2.5×12.5
=4×2.5×(0.8×12.5)
=10×10
=100 60×
=60×+60×-60×
=10+24-16
=34-16
=18
15.28-3.99-9.01
=15.28-(3.99+9.01)
=15.28-13
=2.28 10.7﹣2.9×0.2÷0.58
=10.7-0.58÷0.58
=10.7-1
=9.7
第一题,利用乘法交换律和乘法结合律简便计算;第二题,利用乘法分配律简便计算;第三题,连续减去两个数等于减去这两个数的和;第四题,按照四则混合运算顺序,先算乘法,再算除法,最后算减法。
17.
10-5.2=4.8 7÷=21 4×0.5=2 0.52÷0.42=
48÷0.04=1200 48×25%=12 1÷1%=100 3.5+6.45=9.95
657-298=359 2.4×=1.6 562÷79≈7 21×498≈10000
小数加减法要注意相同数位相加减;除以一个数等于乘这个数的倒数;小数乘法与整数乘法计算方法相同,最后看因数中一共有几位小数,就在结果的末尾往左数出几位点上小数点,小数末尾的0可以去掉;除数是小数的除法,向右移动除数的小数点使其变成整数,再根据商不变的性质将被除数的小数点向右移动相同的数位,再进行计算,商的小数点与被除数移动后的小数点对齐;百分数的计算,可以先将百分数转化成分数或小数再进行计算;小数与分数相乘,分母不变,只把小数与分子相乘,能约分的要约分。
18.解:
=3 21.36÷0.8﹣12.9
=26.7-12.9
=13.8
= ×53+0.6×46+60%
=0.6×53+0.6×46+0.6
=0.6×(53+46+1)
=0.6×100
=60
混合运算顺序:从左往右计算,先算乘除,再算加减;有括号的先算括号里面的,先算小括号再算中括号。
第一题:利用连减的性质,把改写成,再按运算顺序进行计算;
第二题:按运算顺序进行计算;
第三题:利用乘法分配律,把改写成,再运算顺序计算;
第四题:先把分数、百分数统一化成小数0.6,再利用乘法分配律把×53+0.6×46+60%改写成0.6×53+0.6×46+0.6,最后按运算顺序进行计算。
19.
6.7﹣2.3=4.4 100÷0.1=1000 3.14×22=12.56
3.6×=2.7 350÷68≈5 0
一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
20.
解: x- =1
x=1+
x=
x×3= ×3
x=4
3(x-5)=8.4
解:3(x-5)÷3=8.4÷3
x-5=2.8
x=2.8+5
x=7.8
解:4x= ×15
4x=9
x=9÷4
x=
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
综合应用等式的性质解方程;
综合应用等式的性质解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质解比例。
21.
= 6.6÷0.11=60 =2.2 =
= 3.8-4%=3.76 =4 =
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
22.解:56×101
=56×(100+1)
=56×100+56
=5600+56
=5656
16.37﹣(6.37+8.8)
=16.37﹣6.37﹣8.8
=10﹣8.8
=1.2
3.45×75%+6.55×
=0.75×(3.45+6.55)
=0.75×10
=7.5
25×[16÷(×18)]
=25×[16÷10]
=25×1.6
=40
观察数据可知,先把101分成(100+1),再利用乘法分配律简算;
观察数据可知,此题应用减法的性质,一个数减去两个数的和,等于连续减去这两个数,据此计算简便;
观察数据可知,此题应用乘法分配律简算;
观察算式可知,算式中有中括号和小括号,先算中括号里面的小括号里的乘法,再计算中括号里面的除法,最后计算中括号外面的乘法,据此顺序解答。
23.① 4x÷ =6
解:4x÷ × =6×
4x=
4x÷4= ÷4
x=
②160%x+4.5×20%=8.9
解: 160%x+0.9=8.9
160%x+0.9﹣0.9=8.9﹣0.9
1.6x=8
1.6x÷1.6=8÷1.6
x=5
③ 1.8:x=27:60
解: 27x=1.8×60
27x=108
27x÷27=108÷27
x=4
解方程的依据是等式的性质:等式的两边同时加减乘除相同的数(0除外),等式仍然成立,据此解答;
解比例的依据是比例的基本性质:在比例里,两外项之积等于两内项之积,据此解答。
24.
2.3+5.7=8 12.2﹣0.5=11.7 140×0.3=42 401﹣198=203
3600÷12=300 + = ﹣ = ×240=200
÷ = 25%×5.6÷ =2
计算小数加减法时,先把小数点对齐,也就是相同数位对齐,然后再按照整数加减法的计算法则进行计算,据此解答;
小数乘法法则:先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足,注意:计算的结果,如果小数末尾有0的,根据小数的基本性质,在小数的末尾去掉零,小数的大小不变;
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的法则进行计算,计算结果能约分的要约成最简分数;
分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此解答;
百分数与分数、小数混合运算,可以把百分数化成小数,再计算。
25.
15﹣8.6=6.4 88×62.5%=55 (0.18+0.9)÷9=0.12
÷7= + = - ×0=
含有百分数的计算,把百分数化成分数或小数,然后再计算;一个非0的数除以一个分数,等于这个数乘它的倒数;分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
同课章节目录
