2024-2025学年小升初数学备考真题分类汇编(江西地区专版)专题3 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(江西地区专版)专题3 填空题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览




文档简介
2024-2025学年小升初数学备考真题分类汇编(江西地区专版)
专题3 填空题
一、填空题
1.(2024·袁州)正方形的周长和边长成 比例。(在横线里写上“正”“反”“不成”)
2.(2024·修水)1200平方米= 公顷
0.45时= 分
3.(2024·铅山)一个圆锥形土堆,底面半径是4m,高是3m,把这堆土铺在一个底面半径为5m的圆柱形坑里,能铺 米的厚度。
4.(2024·袁州)修路队要修1000米长的公路,每天修a米,5天修了 米;当a=128时,还剩 米没修。
5.(2024·袁州) 0.4小时:40分钟的比值是 ,化简成最简单的整数比是 。
6.(2024·铅山)一个九位数亿位上是5,百万位上是最大的一位数,十万位上是最小的质数,万位上是最小的奇数,其余各位上都是0,这个数写作 ,读作 ,改写成用“万”作单位的数是 ,精确到亿位是 。
7.(2024·铅山)爸爸和小军要去商场各买一双鞋,已知鞋的尺码中“码”和“厘米”之间的换算关系是b=2a﹣10(b表示码数,a表示厘米数)。小军今年的脚长22.5厘米,他要穿 码的鞋,爸爸平常要穿43码鞋,他的脚长为 厘米。
8.(2024·都昌)如图,第①个图中有1个小三角形,第②个图中有4个小三角形,第⑤个图形中有 个小三角形;第n个图形中有 个小三角形。
9.(2024·都昌)已知,b﹣a=10,则a= ,b= 。
10.(2023·青山湖)如图是图图未完成的一张表格,如果A与B成正比例关系,则“?”处为 ;如果A与B成反比例关系,则“?”处为 。
A 10 5
B 6 ?
11.(2024·都昌)把化成最简整数比是 ;的比值是 。
12.(2024·都昌)修一条路,已经修了90米,还剩270米没修,已经修了这条路的 ,再修 米,就修了这条路的50%。
13.(2023·青山湖)一个几何体从上面看到的形状如图,如果用5个小正方体摆,共有 种不同的摆法。
14.(2024·都昌)把75cm长的彩带平均分成5段,每段长 cm,每段占全长的 。
15.(2024·都昌)无限循环小数0.33453345……的小数点后第15位上的数字是 ,第30位上的数字是 。
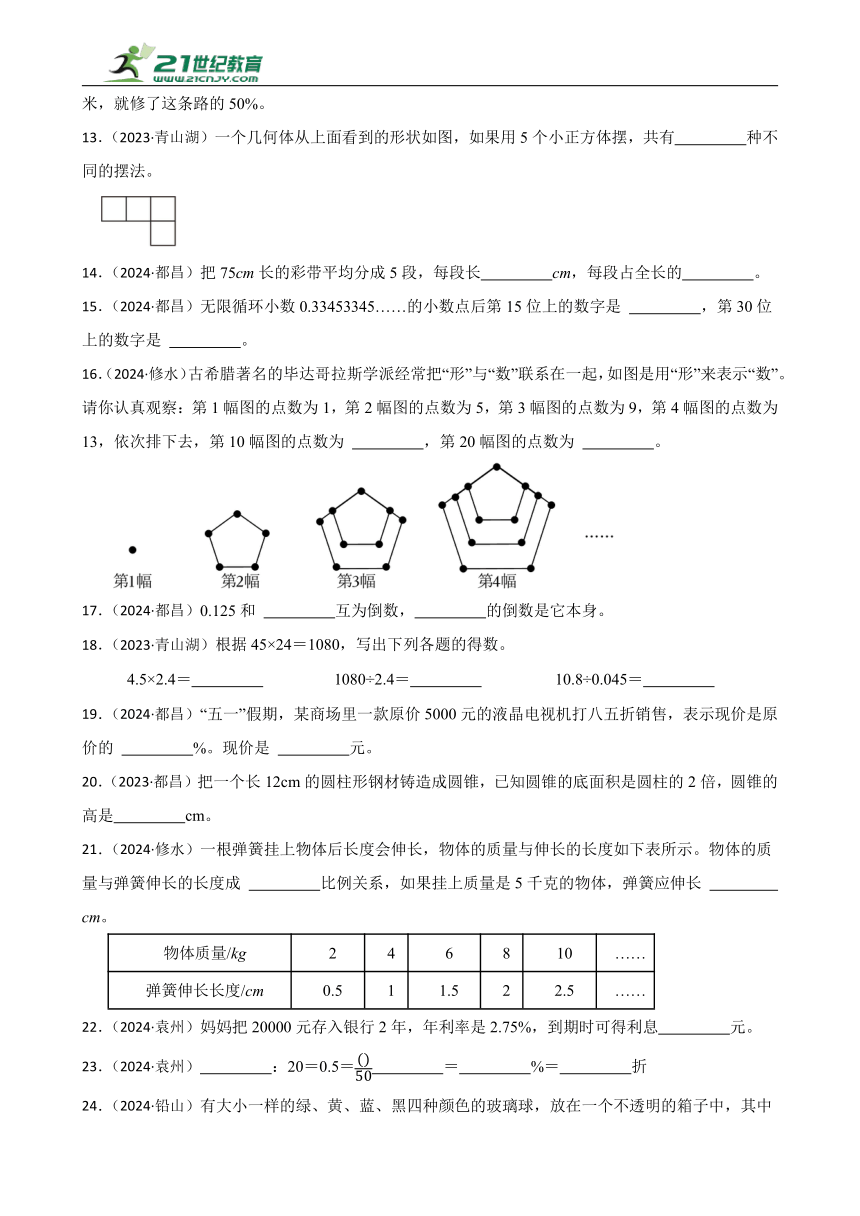
16.(2024·修水)古希腊著名的毕达哥拉斯学派经常把“形”与“数”联系在一起,如图是用“形”来表示“数”。请你认真观察:第1幅图的点数为1,第2幅图的点数为5,第3幅图的点数为9,第4幅图的点数为13,依次排下去,第10幅图的点数为 ,第20幅图的点数为 。
17.(2024·都昌)0.125和 互为倒数, 的倒数是它本身。
18.(2023·青山湖)根据45×24=1080,写出下列各题的得数。
4.5×2.4= 1080÷2.4= 10.8÷0.045=
19.(2024·都昌)“五一”假期,某商场里一款原价5000元的液晶电视机打八五折销售,表示现价是原价的 %。现价是 元。
20.(2023·都昌)把一个长12cm的圆柱形钢材铸造成圆锥,已知圆锥的底面积是圆柱的2倍,圆锥的高是 cm。
21.(2024·修水)一根弹簧挂上物体后长度会伸长,物体的质量与伸长的长度如下表所示。物体的质量与弹簧伸长的长度成 比例关系,如果挂上质量是5千克的物体,弹簧应伸长 cm。
物体质量/kg 2 4 6 8 10 ……
弹簧伸长长度/cm 0.5 1 1.5 2 2.5 ……
22.(2024·袁州)妈妈把20000元存入银行2年,年利率是2.75%,到期时可得利息 元。
23.(2024·袁州) :20=0.5= = %= 折
24.(2024·铅山)有大小一样的绿、黄、蓝、黑四种颜色的玻璃球,放在一个不透明的箱子中,其中绿球有5个、黄球有8个、蓝球有6个、黑球有10个。至少摸出 个球才能保证一定有4种颜色不同的小球;如果从中摸出一个球,那么摸到绿球、黄球或篮球的可能性比摸到黑球的可能性 。(填“大”或“小”)
25.(2024·修水)三角形三内角和的度数是 ,平行四边形的内角和是 。
26.(2024·修水)如图直线上点A表示的数是 ,点B表示的数是 。
27.(2024·修水) 地球离太阳的距离约是149600000千米,把横线上的数改写成用“亿”作单位的数是 千米,保留两位小数是 千米。
28.(2023·都昌)一件衣服原价320元,现按“每满100元减20元”的优惠销售,则实际价格为 元,与“打八折”相比,购买时, 的优惠方式更合算。
29.(2024·都昌)地球赤道周长为 四千零七万五千七百米,这个数写作 ,省略万位后面的尾数大约是 万。
30.(2024·遂川)根据第七次全国人口普查结果、登记的大陆31个省、自治区、直辖市和现役军人的人口共1411778724人,横线上的数读作 ,改写成用“万”作单位的数是 万,用“四舍五入”法省略亿位后面的尾数约是 亿。
31.(2024·铅山)如图,一块黑六边形配6块白六边形;两块黑六边形可以配10块白六边形。照这样排列,8块黑六边形需要 块白六边形;106块白六边形需要 块黑六边形。
32.(2024·铅山)体育老师对某班进行仰卧起坐的测试,以一分钟做22个为达标,超过的个数用正数表示,不足的个数用负数表示。老师记录了其中5个男生的成绩,分别为:﹣3、﹣2、0、2、3。这5个男生的达标率是 %,他们一共做了 个仰卧起坐。
33.(2024·修水)一个圆形车轮的周长是125.6厘米,它的直径是 厘米,半径是 厘米.
34.(2024·铅山)林林借助一个盛满水的圆柱形大量杯测量一个小铁球的体积,他先把一个棱长为2cm的正方体铁块浸没在大量杯中,用小量杯接住溢出的水,量得水面高2.5cm,接着将大量杯重新装满水,他又把小铁球浸没在当中,溢出的水使小量杯水面又上升了2cm。这个小铁球的体积是 cm3。
35.(2024·铅山) x和y成比例关系,其中的两组相对应的值如下表。
①如果a=8,x与y成 比例;
②如果x与y成反比例,a= 。
x 10 20 ……
y 4 a ……
36.(2024·都昌)5小时24分= 小时
2.05千克= 千克 克
37.(2024·修水)袋子里有同样的黄球和白球各5个,要保证摸出的球一定有2个颜色相同,最少要摸出 个;要保证摸出的球一定有两个颜色不同,至少要摸出 个。
38.(2024·铅山)在一幅地图上,公园和科技馆之间的距离是18cm,而两地之间的实际距离是72km,这幅地图的比例尺是 。把一个底为6cm,高为4cm的三角形按3:1放大,得到的图形的面积是 cm2。
39.(2024·铅山)蒋老师买一副眼镜原价是680元,现在打八五折销售,便宜了 元。
40.(2024·铅山)王叔叔文具店5月份营业额中应缴纳营业税的部分为4500元,需要按3%的税率缴纳营业税,这个月他应缴的营业税为 元。
41.(2024·铅山)如果甲数的等于乙数的(甲、乙两数均不为0),那么甲数:乙数= : 。
42.(2023·青山湖)方方用一个正方体木料削了一个最大的圆锥,从上面看的图形如图①所示,从前面看到的图形如图②所示。(如图中每个小正方形的边长是1cm)
(1)这个圆锥的底面半径是 cm,高是 cm;
(2)这个圆锥的体积是 cm3。
43.(2023·青山湖)用小棒摆三角形(如图),摆6个这样的三角形需要 根小棒;摆n个这样的三角形需要 根小棒。
44.(2023·青山湖)甲数是乙数的 ,乙数是丙数的80%。甲数是丙数的 。
45.(2023·青山湖)据统计,截至2023年3月19日,贺岁档电影《满江红》综合票房达4538725800元。横线上的数读作 ,将它改写成用“亿”作单位并保留两位小数约是 亿元。
46.(2023·都昌)小红周末在家帮妈妈做家务,用洗衣机洗衣服要用25分钟,扫地10分钟,擦桌子用了6分钟,晾衣服用了5分钟。她做完这些家务至少要用 分钟。
47.(2023·都昌)一根钢管长0.5米,重 吨,平均每米重 吨,平均每吨长 米。
48.(2023·都昌)45比50少 %, 比20多40%。
49.(2023·都昌)甲数的与乙数的相等,则甲数是乙数的 ,如果两数的和是230,那么乙数是 。
50.(2023·都昌)一个三位小数用“四舍五入”法取近似值是3.20,这个三位小数最大是 ,最小是 。
答案解析部分
1.正
解:因为正方形的周长÷边长=4(一定),所以正方形的周长和边长成正比例。
故答案为:正。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
2.0.12;27
解:1200÷10000=0.12(公顷)
0.45×60=27(分)。
故答案为:0.12;27。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
3.0.64
解:(3.14×42×3÷3)÷(3.14×52)
=3.14×16÷3.15÷25
=16÷25
=0.64(米)。
故答案为:0.64。
能铺的厚度=(圆锥底面半径2×π×高÷3)÷(π×圆柱底面半径2)。
4.5a;360
解:a×5=5a(米),
所以还剩(1000-5a)米,
当a=128时,1000-5a=1000-5×128=360(米);
故答案为:5a;360。
本题主要考查的是用字母表示数以及代数表达式的求值。题目给出了修路队每天修路的长度(用a表示),可以计算5天内总共修了5a米路,进而求出还剩(1000-5a)米未修,当a取特定值(128米)时,即可求出剩余未修的路长。
5.;3:5
解:0.4×60=24(分),
,,
故答案为:;3:5。
本题考查了学生对时间单位转换和比值计算的理解和掌握。需要将所有的时间单位统一,选择分钟作为统一的时间单位,求出两个时间的比值,并将其化简为最简单的整数比。
6.509210000;五亿零九百二十一万;50921万;5亿
解:这个数写作:509210000;读作: 五亿零九百二十一万 ;
509210000÷10000=50921万
509210000≈5亿。
故答案为:509210000; 五亿零九百二十一万;50921万;5亿。
亿以上的数的写法,先看这个数有几级,再从最高级写起,哪个数位上一个单位也没有,就在那个数位上写0。亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零。
改写成用“万”作单位的数,小数点向左移动4位,再在后面加上一个“万”字;改写成用“亿”作单位的数,小数点向左移动8位,再在后面加上一个“亿”字。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
7.35;26.5
解:2×22.5-10
=45-10
=35(码)
(43+10)÷2
=53÷2
=26.5(厘米)。
故答案为:35;26.5。
小军要穿的码数=小军今年的脚长×2-10;爸爸的脚长厘米数=(爸爸穿的码数+10)÷2。
8.25;n2
解:5×5=25(个)
n×n=n2。
故答案为:25;n2。
第n个图形中有小三角形的个数=n2个。
9.25;35
解:a:b=,则a=b
b-a=10
b-b= 10
b= 10
b=10÷
b=35
a=35-10=25。
故答案为:25;35。
由a:b=,得到a=b,然后代入b-a=10,求出b=35,a=35-10=25。
10.3;12
解:第一问:6:10=,?处为:5×=3;
第二问:10×6÷5=12。
故答案为:3;12。
第一问:A与B成正比例关系,所以A与B相对应的两个数的比值一定,所以求出B与A的比值,用5乘这个比值即可求出?处的数字;
第二问:A与B成反比例,所以A与B相对应的数的乘积一定,因此用A、B相对应的两个数的乘积除以5即可求出?处的数字。
11.1:2;
解:0.9:=(0.9×10):(1.8×10)=1:2;
:=÷=。
故答案为:1:2;。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。依据比的基本性质化简比;
求比值=比的前项÷比的后项。
12.;90
解:90÷(90+270)
=90÷360
=
(90+270)÷2-90
=180-90
=90(米)。
故答案为:;90。
已经修了这条路的分率=已经修的米数÷(已经修的米数+还剩下没有修的米数),修这条路的50%还需要再修的米数=(已经修的米数+还剩下没有修的米数)÷2-已经修的米数。
13.4
解:下层后排摆3个,前排靠右1个。剩下的1个无论摆在哪个正方体上面都可以,所以共有4种不同的摆法。
故答案为:4。
根据从上面观察到的图形可以判断下层摆的个数及位置。因为从上面观察到的图形不变,所以最后一个正方体一定在某个正方体的上面。
14.15;
解:75÷5=15(厘米)
1÷5=。
故答案为:15;。
每段的长度=彩带的总长度÷平均分的段数;每段占全长的分率=1 ÷平均分的段数。
15.4;3
解:15÷4=3(组)······3(个),小数点后第15位上的数字是4;
30÷4=7(组)······2(个),第30位上的数字是3。
故答案为:4;3。
这个循环小数的循环节是3345,按照“3345”4个数字为一组循环,小数点后第15位上的数字循环了3组,剩余3个,则是4;第30位上的数字循环了7组,剩余2个,则是3。
16.37;77
解:4×(10-1)+1
=36+1
=37
4×(20-1)+1
=76+1
=77。
故答案为:37;77。
第n幅图有点数的个数=4×(n-1)+1。
17.8;1
解:1÷0.125=8
1÷1=1。
故答案为:8;1。
求一个数(0除外)的倒数=1÷这个数;1的倒数还是它本身。
18.10.8;450;240
45×24=1080
4.5×2.4=10.8;1080÷2.4=450;10.8÷0.045=240。
故答案为:10.8;450;240。
根据两个因数中小数的位数确定乘积中小数的位数。计算除法时可以把被除数或除数转化成整数,再根据乘法算式确定商。
19.85;4250
解:打八五折销售,表示现价是原价的85%;
5000×85%=4250(元)。
故答案为:85;4250。
打八五折销售,表示现价是原价的85%;现价=原价×折扣。
20.18
解:设圆柱的底面积为S,
12S÷÷2S
=36S÷2S
=18(厘米)
故答案为:18。
根据圆柱的体积公式:V=Sh,圆锥的体积公式:V=Sh,设圆柱的底面积为S,则圆锥的底面积为2S,把数据代入公式解答。
21.正;1.25
解:2÷0.5=4÷1=6÷1.5=4(一定),物体的质量与弹簧伸长的长度成正比例;
5÷4=1.25(厘米)。
故答案为:正;1.25。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
如果挂上质量是5千克的物体,弹簧应伸长的长度=物体的质量÷4。
22.1100
解:20000×2.75%×2=1100(元),
故答案为:1100。
本题的关键在于正确使用整存整取的计息公式,使用整存整取的计息公式:利息 = 本金 × 年利率 × 存期,代入即可求得利息。
23.10;25;50;五
解:20×0.5=10
0.5×50=25
0.5=50%=五折
所以10:20=0.5==50%=五折。
故答案为:10;25;50;五。
比的前项=比值×比的后项;分子=分母×分数值;小数化成百分数,把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折。
24.25;小
解:10+8+6+1=25(个)
5<6<8<10,如果从中摸出一个球,那么摸到绿球、黄球或篮球的可能性比摸到黑球的可能性小。
故答案为:25;小。
最坏的情况下黑球、黄球、蓝球全部摸完,再摸一个球,保证一定有4种颜色不同的小球;
因为数黑球的数量最多,则如果从中摸出一个球,那么摸到绿球、黄球或篮球的可能性比摸到黑球的可能性小。
25.180°;360°
解:三角形三内角和的度数是180°,平行四边形内角和是:
(4-2)×180°
=2×180°
=360°。
故答案为:180°;360°。
三角形三内角和是180°,平行四边形内角和=(n-2)×180°。
26.-3;4
解:点A表示的数在0左边3个单位的地方,是-3,点B表示的数在0右边4个单位的地方,是4。
故答案为:-3;4。
正数在0的右侧,负数在0的左侧,在几个单位的地方就是几。
27.1.496亿;1.50亿
解:149600000÷100000000=1.496亿;
1.496亿≈1.50亿。
故答案为:1.496亿;1.50亿。
改写成用“亿”作单位的数,小数点向左移动8位,再在后面加上一个“亿”字。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
28.260;打八折
解:320-(20×3)
=320-60
=260(元)
320×80%
=320×0.8
=256(元)
260>256
故答案为:260;打八折。
一件衣服原价320元,现按“每满100元减20元”的优惠销售,则应减去的价格为(20×3)=60元,用原价-60即可算出实际价格;打八折也就是:现价=原价×80%,计算出现价;二者进行比较即可。
29.40075700;4008
解:四千零七万五千七百写作:40075700;
40075700≈4008万。
故答案为:40075700;4008。
亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
30.十四亿一千一百七十七万八千七百二十四;141177.8724;14
解: 1411778724读作十四亿一千一百七十七万八千七百二十四,改写成用“万”作单位的数是141177.8724,用“四舍五入”法省略亿位后面的尾数约是14 亿 。
故答案为:十四亿一千一百七十七万八千七百二十四;141177.8724;14。
整数的读法:从高位到低位,一级一级地读。读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零;
在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。改写后的数是原数的准确数。1411778724改写成以万做单位的数是141177.8724万;
省略“亿”后面的尾数是四舍五入到亿位,就是把亿位后的千万位上的数字进行四舍五入,再在数的后面写上“亿”字。
31.34;26
解:8×4+2=34(块)
(106-2)÷4
=104÷4
=26(块)。
故答案为:34;26。
n块黑六边形需要白六边形的块数=(4n+2);106块白六边形需要黑六边形的块数=(106-2)÷4。
32.60;110
解:3÷5=60%
(-3-2+5+22)×5
=22×5
=110(个)。
故答案为:60;110。
这5个男生的达标率=达标的人数÷总人数;他们一共做仰卧起坐的个数= (-3-2+5+22)×人数。
33.40;20
解:125.6÷3.14=40(厘米)
40÷2=20(厘米)。
故答案为:40;20。
这个圆形车轮的直径=周长÷π,半径=直径÷2。
34.6.4
解:23÷2.5×2
=3.2×2
=6.4(立方厘米)。
故答案为:6.4。
根据题目描述,我们首先需要明确正方体铁块和小铁球浸入水中时水面上升的原理。水面上升的体积等于物体排开水的体积,因此,通过计算正方体铁块排开水的体积,可以求得圆柱形大量杯的底面积。然后,利用这个底面积和小铁球浸入水中后水面上升的高度,可以求得小铁球的体积。
35.正;2
解:①10÷4=20÷8=2.5(一定),x与y成正比例;
②10×4÷20
=40÷20
=2。
故答案为:正;2。
①判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
②如果x与y成反比例,a=10×4÷20。
36.5.4;2;50
解:5+24÷60
=5+0.4
=5.4(小时);
(2.05-2)×1000
=0.05×1000
=50(克),所以2.05千克=2千克50克。
故答案为:5.4;2;50。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
37.3;6
解:2+1=3(个)
5+1=6(个)。
故答案为:3;6。
最坏的情况两个都是同色的,再摸一个,就保证摸出的球一定有2个颜色相同;最坏的情况6个都是同色的,再摸一个,要保证摸出的球一定有两个颜色不同,至少要摸出6个。
38.1:400000;108
解:18÷(72×100000)
=18:7200000
=1:400000
(6×3)×(4×3)÷2
=18×12÷2
=216÷2
=108(平方厘米)。
故答案为:1:400000;108。
先单位换算,这幅地图的比例尺=图上距离:实际距离;得到图形的面积=(原来三角形的底×3)×(原来三角形的高×3)÷2。
39.102
解:680×(1-85%)
=680×15%
=102(元)。
故答案为:102。
便宜的钱数=这副眼镜的原价×(1-折扣)。
40.135
解:4500×3%=135(元)。
故答案为:135。
这个月他应缴的营业税金额=应缴纳营业税部分的金额×税率。
41.7;10
解:甲数:乙数=:=7:10。
故答案为:7;10。
比例的基本性质:在比例里,两个内项积等于两个外项积。据此写出甲数:乙数=:=7:10。
42.(1)3;6
(2)56.52
解:(1)这个圆锥的底面半径是3cm,高是6cm;
(2)3.14×32×6×
=3.14×18
=56.52(cm3)
故答案为:(1)3;6;(2)56.52。
(1)圆锥的底面是圆形,根据图①判断底面半径;圆锥的侧面观察是一个三角形,三角形底边上的高就是圆锥的高,根据图②确定高;
(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
43.13;(2n+1)
解:摆6个这样的三角形:2×6+1=13(根);摆n个这样的三角形需要(2n+1)根小棒。
故答案为:13;(2n+1)。
观察已知图形可知:小棒的根数=2×三角形个数+1,根据规律计算并用含有n的式子表示这个规律即可。
44.44%
解:1×80%×=×≈44%
故答案为:44%。(答案不唯一)
把丙数看作单位“1”,用1乘80%表示出乙数;用乙数乘即可求出甲数是丙数的几分之几或百分之几。
45.四十五亿三千八百七十二万五千八百;45.39
解:4538725800读作:四十五亿三千八百七十二万五千八百;4538725800≈45.39亿。
故答案为:四十五亿三千八百七十二万五千八百;45.39。
读数时从高位到低位一级一级往下读,亿级和万级的数都按照个级的读法来读,只是要在后面加上“亿”或“万”,每级末尾的0都不读,其它数位上一个0或连续几个0都只读一个零。在亿位后面点上小数点,根据千分位数字四舍五入保留两位小数,在后面加上亿字即可改写成用亿作单位的数。
46.30
解:25分+5分=30(分)
故答案为:30。
洗衣机洗衣服的同时可以扫地和擦桌子,用洗衣服的时间加晾衣服的时间,即为做这些家务至少要用的时间。
47.;10
解:÷0.5=×2=(吨);
0.5÷=0.520=10(米);
故答案为:;10。
求平均每米重多少吨=重量÷长度;求平均每吨长多少米=长度÷重量,据此解答即可。
48.10;28
解:(50-45)÷50
=5÷50
=0.1
=10%
20×(1+40%)
=20×1.4
=28
故答案为:10;28。
求一个数比另一个数多(少)百分之几:(大数-小数)÷单位“1”的量;
求比一个数多百分之几的数:这个数×(1+百分之几)。
49.;140
解:根据题意: 甲数的与乙数的相等 ,假设它们的结果都为1;
甲=乙=1,则甲=,乙=;
÷==;
甲数是乙数的;
230÷(9+14)
=230÷23
=10
14×10=140
故答案为:;140。
根据题意,假设它们的结果都为1,分别算出甲、乙数,然后用甲数除以乙数即可求出甲数的乙数的几分之几;用230除以甲和乙的总分数,求出一份是多少,再乘以乙的份数即可求出乙数是多少。
50.3.204;3.195
解:近似值是3.20的三位小数,最大是3.204,最小是3.195;
故答案为:3.204;3.195。
3.20是一个三位小数的近似数,“四舍”得到的3.20最大是3.204,“五入”得到的3.20最小是3.195.
专题3 填空题
一、填空题
1.(2024·袁州)正方形的周长和边长成 比例。(在横线里写上“正”“反”“不成”)
2.(2024·修水)1200平方米= 公顷
0.45时= 分
3.(2024·铅山)一个圆锥形土堆,底面半径是4m,高是3m,把这堆土铺在一个底面半径为5m的圆柱形坑里,能铺 米的厚度。
4.(2024·袁州)修路队要修1000米长的公路,每天修a米,5天修了 米;当a=128时,还剩 米没修。
5.(2024·袁州) 0.4小时:40分钟的比值是 ,化简成最简单的整数比是 。
6.(2024·铅山)一个九位数亿位上是5,百万位上是最大的一位数,十万位上是最小的质数,万位上是最小的奇数,其余各位上都是0,这个数写作 ,读作 ,改写成用“万”作单位的数是 ,精确到亿位是 。
7.(2024·铅山)爸爸和小军要去商场各买一双鞋,已知鞋的尺码中“码”和“厘米”之间的换算关系是b=2a﹣10(b表示码数,a表示厘米数)。小军今年的脚长22.5厘米,他要穿 码的鞋,爸爸平常要穿43码鞋,他的脚长为 厘米。
8.(2024·都昌)如图,第①个图中有1个小三角形,第②个图中有4个小三角形,第⑤个图形中有 个小三角形;第n个图形中有 个小三角形。
9.(2024·都昌)已知,b﹣a=10,则a= ,b= 。
10.(2023·青山湖)如图是图图未完成的一张表格,如果A与B成正比例关系,则“?”处为 ;如果A与B成反比例关系,则“?”处为 。
A 10 5
B 6 ?
11.(2024·都昌)把化成最简整数比是 ;的比值是 。
12.(2024·都昌)修一条路,已经修了90米,还剩270米没修,已经修了这条路的 ,再修 米,就修了这条路的50%。
13.(2023·青山湖)一个几何体从上面看到的形状如图,如果用5个小正方体摆,共有 种不同的摆法。
14.(2024·都昌)把75cm长的彩带平均分成5段,每段长 cm,每段占全长的 。
15.(2024·都昌)无限循环小数0.33453345……的小数点后第15位上的数字是 ,第30位上的数字是 。
16.(2024·修水)古希腊著名的毕达哥拉斯学派经常把“形”与“数”联系在一起,如图是用“形”来表示“数”。请你认真观察:第1幅图的点数为1,第2幅图的点数为5,第3幅图的点数为9,第4幅图的点数为13,依次排下去,第10幅图的点数为 ,第20幅图的点数为 。
17.(2024·都昌)0.125和 互为倒数, 的倒数是它本身。
18.(2023·青山湖)根据45×24=1080,写出下列各题的得数。
4.5×2.4= 1080÷2.4= 10.8÷0.045=
19.(2024·都昌)“五一”假期,某商场里一款原价5000元的液晶电视机打八五折销售,表示现价是原价的 %。现价是 元。
20.(2023·都昌)把一个长12cm的圆柱形钢材铸造成圆锥,已知圆锥的底面积是圆柱的2倍,圆锥的高是 cm。
21.(2024·修水)一根弹簧挂上物体后长度会伸长,物体的质量与伸长的长度如下表所示。物体的质量与弹簧伸长的长度成 比例关系,如果挂上质量是5千克的物体,弹簧应伸长 cm。
物体质量/kg 2 4 6 8 10 ……
弹簧伸长长度/cm 0.5 1 1.5 2 2.5 ……
22.(2024·袁州)妈妈把20000元存入银行2年,年利率是2.75%,到期时可得利息 元。
23.(2024·袁州) :20=0.5= = %= 折
24.(2024·铅山)有大小一样的绿、黄、蓝、黑四种颜色的玻璃球,放在一个不透明的箱子中,其中绿球有5个、黄球有8个、蓝球有6个、黑球有10个。至少摸出 个球才能保证一定有4种颜色不同的小球;如果从中摸出一个球,那么摸到绿球、黄球或篮球的可能性比摸到黑球的可能性 。(填“大”或“小”)
25.(2024·修水)三角形三内角和的度数是 ,平行四边形的内角和是 。
26.(2024·修水)如图直线上点A表示的数是 ,点B表示的数是 。
27.(2024·修水) 地球离太阳的距离约是149600000千米,把横线上的数改写成用“亿”作单位的数是 千米,保留两位小数是 千米。
28.(2023·都昌)一件衣服原价320元,现按“每满100元减20元”的优惠销售,则实际价格为 元,与“打八折”相比,购买时, 的优惠方式更合算。
29.(2024·都昌)地球赤道周长为 四千零七万五千七百米,这个数写作 ,省略万位后面的尾数大约是 万。
30.(2024·遂川)根据第七次全国人口普查结果、登记的大陆31个省、自治区、直辖市和现役军人的人口共1411778724人,横线上的数读作 ,改写成用“万”作单位的数是 万,用“四舍五入”法省略亿位后面的尾数约是 亿。
31.(2024·铅山)如图,一块黑六边形配6块白六边形;两块黑六边形可以配10块白六边形。照这样排列,8块黑六边形需要 块白六边形;106块白六边形需要 块黑六边形。
32.(2024·铅山)体育老师对某班进行仰卧起坐的测试,以一分钟做22个为达标,超过的个数用正数表示,不足的个数用负数表示。老师记录了其中5个男生的成绩,分别为:﹣3、﹣2、0、2、3。这5个男生的达标率是 %,他们一共做了 个仰卧起坐。
33.(2024·修水)一个圆形车轮的周长是125.6厘米,它的直径是 厘米,半径是 厘米.
34.(2024·铅山)林林借助一个盛满水的圆柱形大量杯测量一个小铁球的体积,他先把一个棱长为2cm的正方体铁块浸没在大量杯中,用小量杯接住溢出的水,量得水面高2.5cm,接着将大量杯重新装满水,他又把小铁球浸没在当中,溢出的水使小量杯水面又上升了2cm。这个小铁球的体积是 cm3。
35.(2024·铅山) x和y成比例关系,其中的两组相对应的值如下表。
①如果a=8,x与y成 比例;
②如果x与y成反比例,a= 。
x 10 20 ……
y 4 a ……
36.(2024·都昌)5小时24分= 小时
2.05千克= 千克 克
37.(2024·修水)袋子里有同样的黄球和白球各5个,要保证摸出的球一定有2个颜色相同,最少要摸出 个;要保证摸出的球一定有两个颜色不同,至少要摸出 个。
38.(2024·铅山)在一幅地图上,公园和科技馆之间的距离是18cm,而两地之间的实际距离是72km,这幅地图的比例尺是 。把一个底为6cm,高为4cm的三角形按3:1放大,得到的图形的面积是 cm2。
39.(2024·铅山)蒋老师买一副眼镜原价是680元,现在打八五折销售,便宜了 元。
40.(2024·铅山)王叔叔文具店5月份营业额中应缴纳营业税的部分为4500元,需要按3%的税率缴纳营业税,这个月他应缴的营业税为 元。
41.(2024·铅山)如果甲数的等于乙数的(甲、乙两数均不为0),那么甲数:乙数= : 。
42.(2023·青山湖)方方用一个正方体木料削了一个最大的圆锥,从上面看的图形如图①所示,从前面看到的图形如图②所示。(如图中每个小正方形的边长是1cm)
(1)这个圆锥的底面半径是 cm,高是 cm;
(2)这个圆锥的体积是 cm3。
43.(2023·青山湖)用小棒摆三角形(如图),摆6个这样的三角形需要 根小棒;摆n个这样的三角形需要 根小棒。
44.(2023·青山湖)甲数是乙数的 ,乙数是丙数的80%。甲数是丙数的 。
45.(2023·青山湖)据统计,截至2023年3月19日,贺岁档电影《满江红》综合票房达4538725800元。横线上的数读作 ,将它改写成用“亿”作单位并保留两位小数约是 亿元。
46.(2023·都昌)小红周末在家帮妈妈做家务,用洗衣机洗衣服要用25分钟,扫地10分钟,擦桌子用了6分钟,晾衣服用了5分钟。她做完这些家务至少要用 分钟。
47.(2023·都昌)一根钢管长0.5米,重 吨,平均每米重 吨,平均每吨长 米。
48.(2023·都昌)45比50少 %, 比20多40%。
49.(2023·都昌)甲数的与乙数的相等,则甲数是乙数的 ,如果两数的和是230,那么乙数是 。
50.(2023·都昌)一个三位小数用“四舍五入”法取近似值是3.20,这个三位小数最大是 ,最小是 。
答案解析部分
1.正
解:因为正方形的周长÷边长=4(一定),所以正方形的周长和边长成正比例。
故答案为:正。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
2.0.12;27
解:1200÷10000=0.12(公顷)
0.45×60=27(分)。
故答案为:0.12;27。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
3.0.64
解:(3.14×42×3÷3)÷(3.14×52)
=3.14×16÷3.15÷25
=16÷25
=0.64(米)。
故答案为:0.64。
能铺的厚度=(圆锥底面半径2×π×高÷3)÷(π×圆柱底面半径2)。
4.5a;360
解:a×5=5a(米),
所以还剩(1000-5a)米,
当a=128时,1000-5a=1000-5×128=360(米);
故答案为:5a;360。
本题主要考查的是用字母表示数以及代数表达式的求值。题目给出了修路队每天修路的长度(用a表示),可以计算5天内总共修了5a米路,进而求出还剩(1000-5a)米未修,当a取特定值(128米)时,即可求出剩余未修的路长。
5.;3:5
解:0.4×60=24(分),
,,
故答案为:;3:5。
本题考查了学生对时间单位转换和比值计算的理解和掌握。需要将所有的时间单位统一,选择分钟作为统一的时间单位,求出两个时间的比值,并将其化简为最简单的整数比。
6.509210000;五亿零九百二十一万;50921万;5亿
解:这个数写作:509210000;读作: 五亿零九百二十一万 ;
509210000÷10000=50921万
509210000≈5亿。
故答案为:509210000; 五亿零九百二十一万;50921万;5亿。
亿以上的数的写法,先看这个数有几级,再从最高级写起,哪个数位上一个单位也没有,就在那个数位上写0。亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零。
改写成用“万”作单位的数,小数点向左移动4位,再在后面加上一个“万”字;改写成用“亿”作单位的数,小数点向左移动8位,再在后面加上一个“亿”字。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
7.35;26.5
解:2×22.5-10
=45-10
=35(码)
(43+10)÷2
=53÷2
=26.5(厘米)。
故答案为:35;26.5。
小军要穿的码数=小军今年的脚长×2-10;爸爸的脚长厘米数=(爸爸穿的码数+10)÷2。
8.25;n2
解:5×5=25(个)
n×n=n2。
故答案为:25;n2。
第n个图形中有小三角形的个数=n2个。
9.25;35
解:a:b=,则a=b
b-a=10
b-b= 10
b= 10
b=10÷
b=35
a=35-10=25。
故答案为:25;35。
由a:b=,得到a=b,然后代入b-a=10,求出b=35,a=35-10=25。
10.3;12
解:第一问:6:10=,?处为:5×=3;
第二问:10×6÷5=12。
故答案为:3;12。
第一问:A与B成正比例关系,所以A与B相对应的两个数的比值一定,所以求出B与A的比值,用5乘这个比值即可求出?处的数字;
第二问:A与B成反比例,所以A与B相对应的数的乘积一定,因此用A、B相对应的两个数的乘积除以5即可求出?处的数字。
11.1:2;
解:0.9:=(0.9×10):(1.8×10)=1:2;
:=÷=。
故答案为:1:2;。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。依据比的基本性质化简比;
求比值=比的前项÷比的后项。
12.;90
解:90÷(90+270)
=90÷360
=
(90+270)÷2-90
=180-90
=90(米)。
故答案为:;90。
已经修了这条路的分率=已经修的米数÷(已经修的米数+还剩下没有修的米数),修这条路的50%还需要再修的米数=(已经修的米数+还剩下没有修的米数)÷2-已经修的米数。
13.4
解:下层后排摆3个,前排靠右1个。剩下的1个无论摆在哪个正方体上面都可以,所以共有4种不同的摆法。
故答案为:4。
根据从上面观察到的图形可以判断下层摆的个数及位置。因为从上面观察到的图形不变,所以最后一个正方体一定在某个正方体的上面。
14.15;
解:75÷5=15(厘米)
1÷5=。
故答案为:15;。
每段的长度=彩带的总长度÷平均分的段数;每段占全长的分率=1 ÷平均分的段数。
15.4;3
解:15÷4=3(组)······3(个),小数点后第15位上的数字是4;
30÷4=7(组)······2(个),第30位上的数字是3。
故答案为:4;3。
这个循环小数的循环节是3345,按照“3345”4个数字为一组循环,小数点后第15位上的数字循环了3组,剩余3个,则是4;第30位上的数字循环了7组,剩余2个,则是3。
16.37;77
解:4×(10-1)+1
=36+1
=37
4×(20-1)+1
=76+1
=77。
故答案为:37;77。
第n幅图有点数的个数=4×(n-1)+1。
17.8;1
解:1÷0.125=8
1÷1=1。
故答案为:8;1。
求一个数(0除外)的倒数=1÷这个数;1的倒数还是它本身。
18.10.8;450;240
45×24=1080
4.5×2.4=10.8;1080÷2.4=450;10.8÷0.045=240。
故答案为:10.8;450;240。
根据两个因数中小数的位数确定乘积中小数的位数。计算除法时可以把被除数或除数转化成整数,再根据乘法算式确定商。
19.85;4250
解:打八五折销售,表示现价是原价的85%;
5000×85%=4250(元)。
故答案为:85;4250。
打八五折销售,表示现价是原价的85%;现价=原价×折扣。
20.18
解:设圆柱的底面积为S,
12S÷÷2S
=36S÷2S
=18(厘米)
故答案为:18。
根据圆柱的体积公式:V=Sh,圆锥的体积公式:V=Sh,设圆柱的底面积为S,则圆锥的底面积为2S,把数据代入公式解答。
21.正;1.25
解:2÷0.5=4÷1=6÷1.5=4(一定),物体的质量与弹簧伸长的长度成正比例;
5÷4=1.25(厘米)。
故答案为:正;1.25。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
如果挂上质量是5千克的物体,弹簧应伸长的长度=物体的质量÷4。
22.1100
解:20000×2.75%×2=1100(元),
故答案为:1100。
本题的关键在于正确使用整存整取的计息公式,使用整存整取的计息公式:利息 = 本金 × 年利率 × 存期,代入即可求得利息。
23.10;25;50;五
解:20×0.5=10
0.5×50=25
0.5=50%=五折
所以10:20=0.5==50%=五折。
故答案为:10;25;50;五。
比的前项=比值×比的后项;分子=分母×分数值;小数化成百分数,把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折。
24.25;小
解:10+8+6+1=25(个)
5<6<8<10,如果从中摸出一个球,那么摸到绿球、黄球或篮球的可能性比摸到黑球的可能性小。
故答案为:25;小。
最坏的情况下黑球、黄球、蓝球全部摸完,再摸一个球,保证一定有4种颜色不同的小球;
因为数黑球的数量最多,则如果从中摸出一个球,那么摸到绿球、黄球或篮球的可能性比摸到黑球的可能性小。
25.180°;360°
解:三角形三内角和的度数是180°,平行四边形内角和是:
(4-2)×180°
=2×180°
=360°。
故答案为:180°;360°。
三角形三内角和是180°,平行四边形内角和=(n-2)×180°。
26.-3;4
解:点A表示的数在0左边3个单位的地方,是-3,点B表示的数在0右边4个单位的地方,是4。
故答案为:-3;4。
正数在0的右侧,负数在0的左侧,在几个单位的地方就是几。
27.1.496亿;1.50亿
解:149600000÷100000000=1.496亿;
1.496亿≈1.50亿。
故答案为:1.496亿;1.50亿。
改写成用“亿”作单位的数,小数点向左移动8位,再在后面加上一个“亿”字。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
28.260;打八折
解:320-(20×3)
=320-60
=260(元)
320×80%
=320×0.8
=256(元)
260>256
故答案为:260;打八折。
一件衣服原价320元,现按“每满100元减20元”的优惠销售,则应减去的价格为(20×3)=60元,用原价-60即可算出实际价格;打八折也就是:现价=原价×80%,计算出现价;二者进行比较即可。
29.40075700;4008
解:四千零七万五千七百写作:40075700;
40075700≈4008万。
故答案为:40075700;4008。
亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零。
用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
30.十四亿一千一百七十七万八千七百二十四;141177.8724;14
解: 1411778724读作十四亿一千一百七十七万八千七百二十四,改写成用“万”作单位的数是141177.8724,用“四舍五入”法省略亿位后面的尾数约是14 亿 。
故答案为:十四亿一千一百七十七万八千七百二十四;141177.8724;14。
整数的读法:从高位到低位,一级一级地读。读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零;
在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。改写后的数是原数的准确数。1411778724改写成以万做单位的数是141177.8724万;
省略“亿”后面的尾数是四舍五入到亿位,就是把亿位后的千万位上的数字进行四舍五入,再在数的后面写上“亿”字。
31.34;26
解:8×4+2=34(块)
(106-2)÷4
=104÷4
=26(块)。
故答案为:34;26。
n块黑六边形需要白六边形的块数=(4n+2);106块白六边形需要黑六边形的块数=(106-2)÷4。
32.60;110
解:3÷5=60%
(-3-2+5+22)×5
=22×5
=110(个)。
故答案为:60;110。
这5个男生的达标率=达标的人数÷总人数;他们一共做仰卧起坐的个数= (-3-2+5+22)×人数。
33.40;20
解:125.6÷3.14=40(厘米)
40÷2=20(厘米)。
故答案为:40;20。
这个圆形车轮的直径=周长÷π,半径=直径÷2。
34.6.4
解:23÷2.5×2
=3.2×2
=6.4(立方厘米)。
故答案为:6.4。
根据题目描述,我们首先需要明确正方体铁块和小铁球浸入水中时水面上升的原理。水面上升的体积等于物体排开水的体积,因此,通过计算正方体铁块排开水的体积,可以求得圆柱形大量杯的底面积。然后,利用这个底面积和小铁球浸入水中后水面上升的高度,可以求得小铁球的体积。
35.正;2
解:①10÷4=20÷8=2.5(一定),x与y成正比例;
②10×4÷20
=40÷20
=2。
故答案为:正;2。
①判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
②如果x与y成反比例,a=10×4÷20。
36.5.4;2;50
解:5+24÷60
=5+0.4
=5.4(小时);
(2.05-2)×1000
=0.05×1000
=50(克),所以2.05千克=2千克50克。
故答案为:5.4;2;50。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
37.3;6
解:2+1=3(个)
5+1=6(个)。
故答案为:3;6。
最坏的情况两个都是同色的,再摸一个,就保证摸出的球一定有2个颜色相同;最坏的情况6个都是同色的,再摸一个,要保证摸出的球一定有两个颜色不同,至少要摸出6个。
38.1:400000;108
解:18÷(72×100000)
=18:7200000
=1:400000
(6×3)×(4×3)÷2
=18×12÷2
=216÷2
=108(平方厘米)。
故答案为:1:400000;108。
先单位换算,这幅地图的比例尺=图上距离:实际距离;得到图形的面积=(原来三角形的底×3)×(原来三角形的高×3)÷2。
39.102
解:680×(1-85%)
=680×15%
=102(元)。
故答案为:102。
便宜的钱数=这副眼镜的原价×(1-折扣)。
40.135
解:4500×3%=135(元)。
故答案为:135。
这个月他应缴的营业税金额=应缴纳营业税部分的金额×税率。
41.7;10
解:甲数:乙数=:=7:10。
故答案为:7;10。
比例的基本性质:在比例里,两个内项积等于两个外项积。据此写出甲数:乙数=:=7:10。
42.(1)3;6
(2)56.52
解:(1)这个圆锥的底面半径是3cm,高是6cm;
(2)3.14×32×6×
=3.14×18
=56.52(cm3)
故答案为:(1)3;6;(2)56.52。
(1)圆锥的底面是圆形,根据图①判断底面半径;圆锥的侧面观察是一个三角形,三角形底边上的高就是圆锥的高,根据图②确定高;
(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
43.13;(2n+1)
解:摆6个这样的三角形:2×6+1=13(根);摆n个这样的三角形需要(2n+1)根小棒。
故答案为:13;(2n+1)。
观察已知图形可知:小棒的根数=2×三角形个数+1,根据规律计算并用含有n的式子表示这个规律即可。
44.44%
解:1×80%×=×≈44%
故答案为:44%。(答案不唯一)
把丙数看作单位“1”,用1乘80%表示出乙数;用乙数乘即可求出甲数是丙数的几分之几或百分之几。
45.四十五亿三千八百七十二万五千八百;45.39
解:4538725800读作:四十五亿三千八百七十二万五千八百;4538725800≈45.39亿。
故答案为:四十五亿三千八百七十二万五千八百;45.39。
读数时从高位到低位一级一级往下读,亿级和万级的数都按照个级的读法来读,只是要在后面加上“亿”或“万”,每级末尾的0都不读,其它数位上一个0或连续几个0都只读一个零。在亿位后面点上小数点,根据千分位数字四舍五入保留两位小数,在后面加上亿字即可改写成用亿作单位的数。
46.30
解:25分+5分=30(分)
故答案为:30。
洗衣机洗衣服的同时可以扫地和擦桌子,用洗衣服的时间加晾衣服的时间,即为做这些家务至少要用的时间。
47.;10
解:÷0.5=×2=(吨);
0.5÷=0.520=10(米);
故答案为:;10。
求平均每米重多少吨=重量÷长度;求平均每吨长多少米=长度÷重量,据此解答即可。
48.10;28
解:(50-45)÷50
=5÷50
=0.1
=10%
20×(1+40%)
=20×1.4
=28
故答案为:10;28。
求一个数比另一个数多(少)百分之几:(大数-小数)÷单位“1”的量;
求比一个数多百分之几的数:这个数×(1+百分之几)。
49.;140
解:根据题意: 甲数的与乙数的相等 ,假设它们的结果都为1;
甲=乙=1,则甲=,乙=;
÷==;
甲数是乙数的;
230÷(9+14)
=230÷23
=10
14×10=140
故答案为:;140。
根据题意,假设它们的结果都为1,分别算出甲、乙数,然后用甲数除以乙数即可求出甲数的乙数的几分之几;用230除以甲和乙的总分数,求出一份是多少,再乘以乙的份数即可求出乙数是多少。
50.3.204;3.195
解:近似值是3.20的三位小数,最大是3.204,最小是3.195;
故答案为:3.204;3.195。
3.20是一个三位小数的近似数,“四舍”得到的3.20最大是3.204,“五入”得到的3.20最小是3.195.
同课章节目录
