2024-2025学年小升初数学备考真题分类汇编(江西地区专版)专题5 解决问题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(江西地区专版)专题5 解决问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 309.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 10:09:50 | ||
图片预览



文档简介
2024-2025学年小升初数学备考真题分类汇编(江西地区专版)
专题5 解决问题
一、解决问题
1.(2024·袁州)甲、乙两车分别从A、B两地同时相对开出,当甲车行了全程的时,乙车行了36千米,当甲车到达B地时乙车行了全程的。A、B两地相距多少千米?
2.(2024·余干) 2023年的植树节主题是“共建绿色生态,共享美丽家园”。培文小学六年级三个班去植树,他们的任务分配如下:六⑴班要植三个班植树总棵数的40%,六⑵班和六⑶班植树的棵数比是4:3。当六⑴班植树200棵时,正好完成三个班植树总棵数的,那么六⑶班要植树多少棵?
3.(2024·余干)芸芸的妈妈每天都开车送她上学,一天共计行驶20km,按每行驶1km花费0.6元计算,一个月需要花费多少钱?为了响应国家绿色出行的号召,芸芸改乘公共汽车上学,如果乘坐公共汽车每天只需要8元,那么一个月能节省多少钱?(一个月上学按22天计算)
4.(2024·瑞昌)端午节是我国的传统节日之一。育才小学民俗社团为了调查全校学生对端午节文化习俗的了解情况,设计了一份调查问卷。根据问卷的结果,他们把全校学生对端午节文化习俗了解的程度分为四档:A——很了解,B——比较了解,C——了解较少,D——不了解,并将统计结果绘制成下面的统计图。
(1)本次一共调查了多少人?其中对端午节文化习俗“很了解”的人数占总人数的百分之几?
(2)将条形统计图补充完整。
5.(2024·瑞昌)如下图是一个无盖的长方体玻璃容器,水面的高度是8cm。
(1)做这个容器一共用了多少平方厘米的玻璃?
(2)把一个底面半径为4cm的圆锥形铅锤完全浸入水中,水面高度上升了0.628cm,这个铅锤的高是多少?
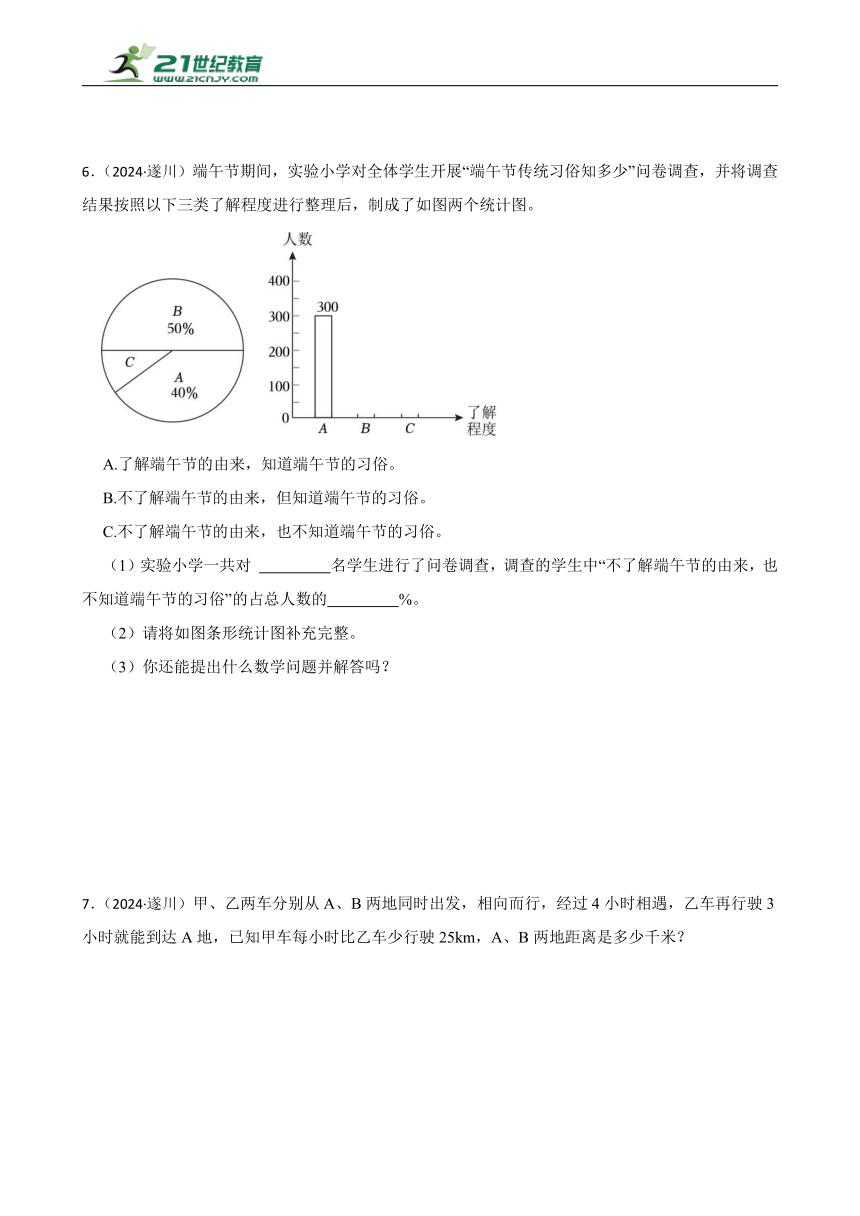
6.(2024·遂川)端午节期间,实验小学对全体学生开展“端午节传统习俗知多少”问卷调查,并将调查结果按照以下三类了解程度进行整理后,制成了如图两个统计图。
A.了解端午节的由来,知道端午节的习俗。
B.不了解端午节的由来,但知道端午节的习俗。
C.不了解端午节的由来,也不知道端午节的习俗。
(1)实验小学一共对 名学生进行了问卷调查,调查的学生中“不了解端午节的由来,也不知道端午节的习俗”的占总人数的 %。
(2)请将如图条形统计图补充完整。
(3)你还能提出什么数学问题并解答吗?
7.(2024·遂川)甲、乙两车分别从A、B两地同时出发,相向而行,经过4小时相遇,乙车再行驶3小时就能到达A地,已知甲车每小时比乙车少行驶25km,A、B两地距离是多少千米?
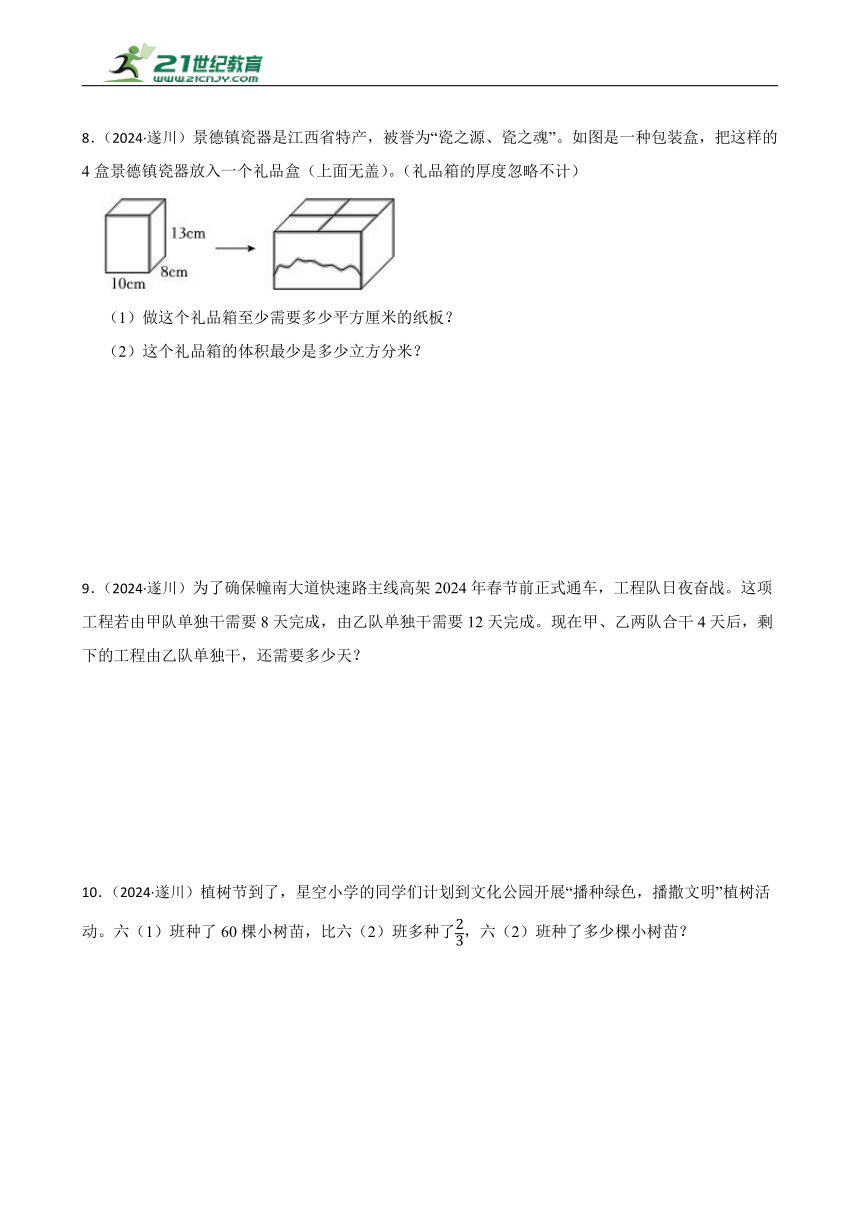
8.(2024·遂川)景德镇瓷器是江西省特产,被誉为“瓷之源、瓷之魂”。如图是一种包装盒,把这样的4盒景德镇瓷器放入一个礼品盒(上面无盖)。(礼品箱的厚度忽略不计)
(1)做这个礼品箱至少需要多少平方厘米的纸板?
(2)这个礼品箱的体积最少是多少立方分米?
9.(2024·遂川)为了确保幢南大道快速路主线高架2024年春节前正式通车,工程队日夜奋战。这项工程若由甲队单独干需要8天完成,由乙队单独干需要12天完成。现在甲、乙两队合干4天后,剩下的工程由乙队单独干,还需要多少天?
10.(2024·遂川)植树节到了,星空小学的同学们计划到文化公园开展“播种绿色,播撒文明”植树活动。六(1)班种了60棵小树苗,比六(2)班多种了,六(2)班种了多少棵小树苗?
11.(2024·遂川)实验小学举行“六一儿童节”文艺表演、请你算一算,三个方阵分别有多少人?
12.(2024·遂川)某仓库要运送一批货物,用6辆相同的货车每天一共可以运货84吨。现在计划增加4辆同样的货车,现在每天共运货多少?
13.(2024·都昌)2024年4月25日20时59分,搭载神舟十八号载人飞船的长征二号F遥十八运载火箭在酒泉卫星发射中心点火发射,约10分钟后,神舟十八号载人飞船与火箭成功分离,进入预定轨道,发射取得成功。长征二号F运载火箭全长58.34米,起飞质量479.7吨,芯级直径3.35米,其中芯一级长约21米,芯二级长约15.4米,4个助推器的直径各为2.25米,长约16.1米。整流罩最大直径3.8米,逃逸塔高约8米。可将8吨有效载荷送入近地点200千米,远地点350千米的椭圆轨道。
(1)长征二号F运载火箭一二级芯的总长度约占火箭全长的百分之几?(按整米数计算,得数百分号前保留一位小数)
(2)长征二号F运载火箭芯一级为圆柱形,它的侧面积约是多少平方米?(得数保留π)
14.(2024·都昌)一批零件,张师傅单独做要6天,李师傅单独做要9天,两人同做三天后,这批零件还剩下几分之几没有完成?
15.(2024·都昌)客车从甲城开往乙城要6小时,小轿车沿同一路线从乙城开往甲城要4小时。两车同时从甲乙两城相对开出,几小时后相遇?
16.(2024·都昌)“六一”儿童节,阳光小学举行了联欢晚会。参加表演的男生有200人,比女生少。
(1)请用线段图表示出题中的数量关系。
(2)参加表演的女生有多少人?
17.(2024·都昌)南昌西站到北京西站之间的高速铁路大约长1404km。一趟高铁列车早上7:20从南昌西站出发匀速行驶,10:50途经郑州东站,13:20到达北京西站(途中经停时间忽略不计)。南昌西站到郑州东站的高速铁路大约有多长?(用比例解)
18.(2024·都昌)某小学组织六年级学生进行体能测试。第一天测试了六年级总人数的,第二天测试了六年级总人数的24%,第二天比第一天多测试了25人,该校六年级一共有多少学生?
19.(2024·修水)为落实“双减”政策,促进学生德、智、体、美、劳全面发展,引导学生养成热爱劳动的习惯,光明小学开展了丰富多彩的劳动教育实践活动。劳动实践活动有四个项目,分别是农耕劳动、厨艺坊、木艺坊和编织坊。学校规定所有学生都要参加劳动实践活动,每位学生只能选择其中一个劳动实践活动项目。如图是光明小学六年级学生参加劳动实践活动情况的统计图。请结合统计图,完成下面的问题。
(1)光明小学六年级学生一共有多少人?
(2)参加“编织坊”的六年级学生人数比参加“农耕劳动”的多百分之几?
(3)请把条形统计图补充完整。(此小问不写计算过程,把条形统计图补充完整即可)
20.(2024·修水)如图是两个互相啮(niè)合的齿轮,它们在同一时间内转动时,大齿轮和小齿转过的总齿数是相同的。大齿轮有40个齿,小齿轮有24个齿。如果大齿轮分钟转120圈,小齿轮每分钟转多少圈?
21.(2024·修水)用96厘米长的铁丝围成一个直角三角形,这个三角形的三条边长度的比是3:4:5。这个三角形的面积是多少平方厘米?
22.(2023·宜春)聪聪来到景区的纪念品商店准备购买一本纪念册,据了解商店以每本4.5元的价格进的一批纪念册,开始出售时营业员把单价搞错了,按每本4元的零售价卖出了全部的,接着把剩下的以每本6元卖出,当全部卖出时,还能获利630元。那么这批纪念册共有多少本?
23.(2023·青山湖)4月23日是世界读书日,在这一天,启航小学新买来800本图书,把这些图书的40%放在了图书馆,剩下的书按3:4:5分给了四、五、六年级。六年级分到了多少本书?
24.(2023·青山湖)周日,阳阳家要进行房屋大扫除。阳阳单独做要60分钟做完,爸爸单独做要40分钟做完,妈妈单独做要30分钟做完。如果阳阳全家一起合作,需要多少分钟才能完成大扫除的任务?
25.(2023·都昌)如图中左边是一种玻璃酒杯,杯口内直径4cm,总深12cm,圆柱部分高7.5cm。把酒杯装满水倒入右边的茶杯,能倒满吗?
26.(2023·都昌)某市政府决定对A区沿河两岸在房子进行重新装饰。这项工程甲单独做要12天完成,乙对单独做要8天完成,现乙队单独做3天,剩下在由甲乙两队合作完成,甲乙要合作几天才能完成全部工程?
27.(2023·都昌)在比例尺是1:5000000的地图上,量得A、B两地相距6cm,如果甲、乙两辆汽车同时从AB两地相对开出,2小时后相遇,这时甲乙两车所行路程比是3:2。甲、乙两车的速度各是多少?
28.(2023·都昌)某修路队要修一段公路,每天修4.5km,20天可以修完,如果每天多修1.5km,多少天可以修完?(用比例解)
29.(2023·宜春)到达景区时,看到成人票:98元/张,学生票:78元/张;但为庆祝“六一”推出三种结算方式:现金支付、手机软件支付、银行卡支付。现金支付:每满100元减20元;手机软件支付:随机减免的方式;银行卡支付:直接按八五折支付。妈妈结算时选用了手机软件支付的方式,结果随机减免了68.8元。在这次购票过程中,妈妈选用的结算方式是最划算的吗?请用计算说明。
30.(2023·宜春)聪聪和爸爸妈妈还有爷爷奶奶8:30从家开车出发,10:00时发现已经行了120千米,照这样计算,他们还需几小时可以到达景区?(用比例知识解答)
答案解析部分
1.解:36÷(×)
=36÷
=180(千米)
答:A、B两地相距180千米。
本题主要考查了分数四则复合应用题,解题的关键是正确找出看作单位“1”及36千米对应的分率。当甲车到达B地时,乙车行了全程的,即乙车速度是甲车的,根据分数乘法的意义可知,当甲行了全程的时,乙车行了全程的,又当甲行了全程的时,乙车行了36千米,即这36千米是全程的,根据分数乘法的意义,用这36千米除以其占全程的分率,即得两地相距多少千米。
2.解:200÷=700(棵)
700×(1﹣40%)=420(棵)
420×=180(棵)
答:六⑶班要植树180棵。
首先,根据题目信息知道六(1)班植树数占总植树数的40%,并且六(1)班已经植了200棵树,这代表了总植树数的2/7。可以通过这些信息计算出总植树数。接着知道六(2)班和六(3)班的植树数之比为4:3,可以利用这个比例和已知的总植树数来计算六(3)班应植树的数量。
3.解:20×0.6×22
=12×22
=264(元)
8×22=176(元)
264﹣176=88(元)
答:一个月(按22天计算)需要花费264元,一个月大约能节省88元。
本题主要考察的是费用计算和比较。题目中给出了两种出行方式的费用计算方式,一是开车,一是乘公共汽车。开车的费用根据行驶的公里数和每公里的费用计算,而乘坐公共汽车的费用是固定的每天费用乘以天数。我们需分别计算出两种出行方式的月费用,并求出费用差额。
4.(1)解:160÷40%=400(人)
140÷400×100%=35%
答:本次一共调查了400人,其中对端午节文化习俗“很了解”的人数占总人数的35%。
(2)解:400-140-160-20=80(人)。
(1)本次一共调查的人数=B项的人数÷所占的百分率;其中对端午节文化习俗“很了解”的人数占总人数的百分率=A的人数÷总人数;
(2)C项的人数=总人数-其余各项分别的人数,依据计算的数据画出直条,并且标上数据。
5.(1)解:16×10+16×12×2+10×12×2
=160+384+240
=784(平方厘米)
答:做这个容器一共用了785平方厘米的玻璃。
(2)解:16×10×0.628÷÷(3.14×42)
=160×0.628×3÷(3.14×16)
=301.44÷50.24
=6(厘米)
答:这个圆锥的高是6厘米。
(1)做这个容器一共用玻璃的面积=长×宽+长×高×2+宽×高×2;
(2)这个圆锥的高=长方体的长×宽×上升水面的高度÷÷圆锥的底面积。
6.(1)750;10
(2)解:750×50%=375(人)
750×10%=75(人)
条形统计图如下:
(3)解:调查的学生中“不了解端午节的由来,但知道端午节的习俗”和“不了解端午节的由来,也不知道端午节的习俗”的一共有多少人?(答案不唯一)
375+75=450(人)
答:调查的学生中“不了解端午节的由来,但知道端午节的习俗”和“不了解端午节的由来,也不知道端午节的习俗”的一共有450人。
(1)300÷40%=750(名);
1-40%-50%=10%。
故答案为:(1)750;10。
(1)观察两个统计图,获取数据,得到”了解端午节的由来,知道端午节的习俗“人数为300人,占参加问卷的学生总人数的40%,用除法即可求出参加问卷的学生总人数;观察扇形统计图,用整体”1“减去其余两个占比,即可求出“不了解端午节的由来,也不知道端午节的习俗”的占总人数的百分之几;
(2)由第(1)小题得到参加问卷的学生总人数为750人,“ 不了解端午节的由来,也不知道端午节的习俗 ”人数占比10%,观察统计图,可知 ”不了解端午节的由来,但知道端午节的习俗“人数占比50% ,根据公式”不了解端午节的由来,但知道端午节的习俗“人数=总人数×对应百分比, “ 不了解端午节的由来,也不知道端午节的习俗 ”人数=总人数×对应百分比,代入数据求出对应人数,再补全条形统计图即可;
(3)答案不唯一,合理即可。
7.解:4+3=7(小时)
设甲车每小时行驶x千米,则乙车每小时行驶(x+25)千米。
4(x+x+25)=7(x+25)
4(2x+25)=7x+175
8x+100=7x+175
8x﹣7x=175﹣100
x=75
75+25=100(千米/时)
100×7=700(千米)
答:A、B两地距离是700千米。
设甲车行驶速度为每小时x千米,根据”甲车每小时比乙车少行驶25km“得到乙车每小时行驶(x+25)千米,然后根据公式“路程=速度×时间,得到甲乙两车相遇时行驶的总路程为4(x+x+25)千米,乙车行驶的总路程(A、B两地距离)为7(x+25),然后根据数量关系”甲乙两车相遇时行驶的总路程=乙车行驶的总路程“列出方程 4(x+x+25)=7(x+25) ,解方程求出甲车行驶速度,最后代入7(x+25)求解即可。
8.(1)解:(10×2)×(8×2)+(10×2)×13×2+(8×2)×13×2
=20×16+20×13×2+16×13×2
=320+520+416
=1256(平方厘米)
答:做这个礼品箱至少需要1256平方厘米的纸板。
(2)解:(10×2)×(8×2)×13
=20×16×13
=320×13
=4160(立方厘米)
4160立方厘米=4.16立方分米
答:这个礼品箱的体积最少是4.16立方分米。
(1)由于这个礼品箱无盖,所以需要纸板的面积=这个长方体的一个底面和4个侧面的总面积,根据长方体的表面积公式解答;
(2)长方体的体积=长×宽×高,把数据代入公式解答。
9.解:[1﹣()×4]÷
=
=2(天)
答:还需要2天。
把这项工程的总工作量看作单位“1”,根据“工作效率=总工作量÷工作时间”,分别求出两队的工作效率,甲、乙两队合干的工作量=(甲队的工作效率+乙队的工作效率)×合干天数,总工作量-甲、乙两队合干的工作量=剩下的工作量,剩下的工作量÷乙队的工作效率=乙队单独干还需要的天数。
10.解:60÷(1+)
=60÷
=60×
=36(棵)
答:六(2)班种了36棵小树苗。
已知一个数比另一个数多几分之几,求另一个数,用除法计算。将六(2)班种的小树苗的棵数看作单位“1”,六(1)班种的小树苗的棵数÷(1+六(1)班比六(2)班多种的分率)=六(2)班种的小树苗的棵数。
11.解:400×=150(人)
400﹣150=250(人)
250×=50(人)
250×=200(人)
答:彩旗方阵有150人,爱心方阵200人,花环方阵50人。
根据题意,用六年级的总人数乘,求出彩旗方阵的人数;用六年级的总人数减去彩旗方阵的人数,求出剩下的学生人数;把剩下的学生人数按4:1进行分配,爱心方阵占剩下学生人数的,花环方阵占剩下学生人数的,用剩下的学生人数分别乘爱心方阵和花环方阵占剩下学生人数的几分之几,即可求出爱心方阵和花环方阵的人数。
12.解:(84÷6)×(6+4)
=14×10
=140(吨)
答:现在每天共运货140吨。
首先用6辆相同的货车每天一共运货的数量除以6求出一辆货车每天运货的数量,再用求得的结果乘(6+4)即可求出现在每天共运货的数量。
13.(1)解:(21+15)÷58
=36÷58
≈0.621
=62.1%
答:长征二号F运载火箭一二级芯的总长度占火箭全长的62.1%。
(2)解:π×3.35×21
=35π×21
=70.35π(平方米)
答:它的侧面积约是70.35π平方米。
(1)长征二号F运载火箭一二级芯的总长度占火箭全长的百分率=(芯一级大约长度+芯二级大约的长度)÷长征二号F运载火箭的全长;
(2)它的侧面积=π×直径×高。
14.解:1-[(+)×3]
=1-[×3]
=1-
=
答:这批零件还剩没有完成。
这批零件还剩下没有完成的分率=1-(张师傅的工作效率+李师傅的工作效率)×工作时间。
15.解:1÷(+)
=1÷
=2.4(小时)
答:两车同时从甲乙两城相对开出,2.4小时后相遇。
两车同时从甲乙两城相对开出后的相遇时间=路程÷速度和。
16.(1)解:
(2)解:
=200÷
=250(人)
答:参加表演的女生有250人。
参加表演的女生人数=参加表演的男生人数÷(1-少的分率)。
17.解:10时50分-7时20分=3时30分
3时30分=3.5时
13时20分-7时20分=6时
设南昌西站到郑州东站的高速铁路大约有xkm。
1404:6=x:3.5
6x=4914
x=819
答:南昌西站到郑州东站的高速铁路大约有819km。
设南昌西站到郑州东站的高速铁路大约有xkm。依据南昌西站到北京西站之间的高速铁路大约的长度:时间=南昌西站到郑州东站的高速铁路大约的时间:3.5,列比例,解比例。
18.解:25÷(24%-)
=25÷4%
=625(名)
答:该校六年级一共有625名学生。
该校六年级一共有学生的人数=第二天比第一天多测试的人数÷( 第二天测试占六年级总人数的百分率- 第一天测试占六年级总人数的百分率 ) 。
19.(1)解:70÷35%=200(人)
答:光明小学六年级学生一共有200人。
(2)解:(60-40)÷40
=20÷40
=0.5
=50%
答:参加“编织坊”的六年级学生人数比参加“农耕劳动”的多50%。
(3)解:200-70-60-40=30(人)
(1)光明小学六年级学生一共的人数=厨艺坊的人数÷所占的百分率;
(2)参加“编织坊”的六年级学生人数比参加“农耕劳动”多的分率=(参加“编织坊”的人数-参加“农耕劳动”的人数)÷参加“农耕劳动”的人数;
(3)木艺坊的人数=总人数-其余各项分别的人数,然后画出直条,并且标上数据。
20.解:设小齿轮每分钟转x圈。
40×120=24x
24x=4800
x=200
答:小齿轮每分钟转200圈。
设小齿轮每分钟转x圈。依据大齿轮的个数×大齿轮平均每分钟转的圈数=小齿轮的个数×小齿轮平均每分钟转的圈数,列比例,解比例。
21.解:96÷(3+4+5)
=96÷12
=8(厘米)
(8×3)×(8×4)÷2
=24×32÷2
=384(平方厘米)
答:这个三角形的面积是384平方厘米。
这个三角形的面积=底×高÷2;底、高分别=三角形的周长÷总份数×各自分别占的份数。
22.解:假设这批书有x本。
x×4+[(1-)x×6﹣4.5x=630
x×4+x×6﹣4.5x=630
x+x﹣4.5x=630
x﹣4.5x=630
5.25x-4.5x=630
0.75x=630
x=840
答:这批纪念册共有840本。
设这批书有x本,总的进价是4.5x元,以每本4元的零售价卖出了全部的,则卖出的钱数为(x4)元,以每本6元的价格卖的钱数为元,根据按4元卖的钱数+按6元卖的钱数-进价=获利钱数,即可列方程解答。
23.解:800×(1﹣40%)
=800×0.6
=480(本)
480×
=480×
=200(本)
答:六年级分到了200本书。
剩下的图书占总数的(1-40%),根据分数乘法的意义先求出剩下的本数。六年级分到的占剩下本数的,根据分数乘法的意义求出六年级分到的本数即可。
24.解:1÷( + + )
=1÷
= (分钟)
答:如果阳阳全家一起合作,需要 分钟才能完成大扫除的任务。
把这次任务看作单位“1”,用1除以每人完成需要的时间,分别表示出每人的工作效率。用1除以三人的工作效率和即可求出合作完成需要的时间。
25.解:酒杯内水的体积:
3.14×(4÷2)2×(12﹣7.5)× +3.14×(6÷2)2×7.5
=3.14×4×4.5× +3.14×4×7.5
=3.14×4×1.5+3.14×4×7.5
=3.14×4×(1.5+7.5)
=3.14×36
=113.04(立方厘米)
茶杯内的水深:
113.04÷[3.14×(6÷2)2]
=113.04÷[3.14×9]
=113.04÷28.26
=4(厘米)
4厘米<5厘米
答:不能倒满。
酒杯的体积=圆柱部分体积+圆锥部分体积。再根据圆柱的体积公式算出右图茶杯的水深,二者比较即可。
26.解:(1﹣3× )÷( + )
= ÷
=3(天)
答:甲乙要合作3天才能完成全部工程。
先算出乙队3天做了这项工程的多少,把这项工程看作单位“1”,剩下的工程=1-已做的。最后用剩下的工程÷(甲的工效+乙的工效),即可解答。
27.解:6÷ =30000000(厘米)
30000000厘米=300千米
300÷2=150(千米)
150× =90(千米/时)
150× =60(千米/时)
答:甲车的速度是90千米/时,乙车的速度是60千米/时。
根据实际距离=图上距离÷比例尺,先算出实际距离。再根据:速度=路程÷实际,算出甲乙两车的速度和,最后根据按比分配的方法,分别算出甲、乙的速度。
28.解:设x天可以修完。
(4.5+1.5)x=4.5×20
6x=90
x=15
答:15天可修完。
根据题意可知: 每天修的长度×天数=总长度(一定),每天修的长度与天数成反比例,根据反比例的意义列比例解答。
29.解:现金支付:
98×4+78-4×20
=470-80
=390(元)
手机软件支付:
98×4+78-68.8
=470-68.8
=401.2(元)
银行卡支付:
(98×4+78)×0.85
=470×0.85
=399.5(元)
401.2>399.5>390
所以,妈妈选用的结算方式不是最划算的。
答:妈妈选用的结算方式不是最划算的。
依次算出三种结算方式所付的钱。现金支付的总价=成人票单价×数量+儿童票的单价-减免的钱数;手机软件支付的总价=成人票单价×数量+儿童票的单价-减免的钱数;银行卡支付的总价=(成人票单价×数量+儿童票的单价)×折扣,然后比较大小。
30.解:10时-8时30分=1时30分=1.5(小时)
设他们需要x小时到达。
120:1.5=200:x
120x=200×1.5
x=300÷120
x=2.5
2.5-1.5=1(小时)
答:他们还需要1小时到达。
根据比例的知识,速度不变,路程和时间成正比例,列出方程。计算出总时间,再减去已用时间,即可得到还需要的时间。
专题5 解决问题
一、解决问题
1.(2024·袁州)甲、乙两车分别从A、B两地同时相对开出,当甲车行了全程的时,乙车行了36千米,当甲车到达B地时乙车行了全程的。A、B两地相距多少千米?
2.(2024·余干) 2023年的植树节主题是“共建绿色生态,共享美丽家园”。培文小学六年级三个班去植树,他们的任务分配如下:六⑴班要植三个班植树总棵数的40%,六⑵班和六⑶班植树的棵数比是4:3。当六⑴班植树200棵时,正好完成三个班植树总棵数的,那么六⑶班要植树多少棵?
3.(2024·余干)芸芸的妈妈每天都开车送她上学,一天共计行驶20km,按每行驶1km花费0.6元计算,一个月需要花费多少钱?为了响应国家绿色出行的号召,芸芸改乘公共汽车上学,如果乘坐公共汽车每天只需要8元,那么一个月能节省多少钱?(一个月上学按22天计算)
4.(2024·瑞昌)端午节是我国的传统节日之一。育才小学民俗社团为了调查全校学生对端午节文化习俗的了解情况,设计了一份调查问卷。根据问卷的结果,他们把全校学生对端午节文化习俗了解的程度分为四档:A——很了解,B——比较了解,C——了解较少,D——不了解,并将统计结果绘制成下面的统计图。
(1)本次一共调查了多少人?其中对端午节文化习俗“很了解”的人数占总人数的百分之几?
(2)将条形统计图补充完整。
5.(2024·瑞昌)如下图是一个无盖的长方体玻璃容器,水面的高度是8cm。
(1)做这个容器一共用了多少平方厘米的玻璃?
(2)把一个底面半径为4cm的圆锥形铅锤完全浸入水中,水面高度上升了0.628cm,这个铅锤的高是多少?
6.(2024·遂川)端午节期间,实验小学对全体学生开展“端午节传统习俗知多少”问卷调查,并将调查结果按照以下三类了解程度进行整理后,制成了如图两个统计图。
A.了解端午节的由来,知道端午节的习俗。
B.不了解端午节的由来,但知道端午节的习俗。
C.不了解端午节的由来,也不知道端午节的习俗。
(1)实验小学一共对 名学生进行了问卷调查,调查的学生中“不了解端午节的由来,也不知道端午节的习俗”的占总人数的 %。
(2)请将如图条形统计图补充完整。
(3)你还能提出什么数学问题并解答吗?
7.(2024·遂川)甲、乙两车分别从A、B两地同时出发,相向而行,经过4小时相遇,乙车再行驶3小时就能到达A地,已知甲车每小时比乙车少行驶25km,A、B两地距离是多少千米?
8.(2024·遂川)景德镇瓷器是江西省特产,被誉为“瓷之源、瓷之魂”。如图是一种包装盒,把这样的4盒景德镇瓷器放入一个礼品盒(上面无盖)。(礼品箱的厚度忽略不计)
(1)做这个礼品箱至少需要多少平方厘米的纸板?
(2)这个礼品箱的体积最少是多少立方分米?
9.(2024·遂川)为了确保幢南大道快速路主线高架2024年春节前正式通车,工程队日夜奋战。这项工程若由甲队单独干需要8天完成,由乙队单独干需要12天完成。现在甲、乙两队合干4天后,剩下的工程由乙队单独干,还需要多少天?
10.(2024·遂川)植树节到了,星空小学的同学们计划到文化公园开展“播种绿色,播撒文明”植树活动。六(1)班种了60棵小树苗,比六(2)班多种了,六(2)班种了多少棵小树苗?
11.(2024·遂川)实验小学举行“六一儿童节”文艺表演、请你算一算,三个方阵分别有多少人?
12.(2024·遂川)某仓库要运送一批货物,用6辆相同的货车每天一共可以运货84吨。现在计划增加4辆同样的货车,现在每天共运货多少?
13.(2024·都昌)2024年4月25日20时59分,搭载神舟十八号载人飞船的长征二号F遥十八运载火箭在酒泉卫星发射中心点火发射,约10分钟后,神舟十八号载人飞船与火箭成功分离,进入预定轨道,发射取得成功。长征二号F运载火箭全长58.34米,起飞质量479.7吨,芯级直径3.35米,其中芯一级长约21米,芯二级长约15.4米,4个助推器的直径各为2.25米,长约16.1米。整流罩最大直径3.8米,逃逸塔高约8米。可将8吨有效载荷送入近地点200千米,远地点350千米的椭圆轨道。
(1)长征二号F运载火箭一二级芯的总长度约占火箭全长的百分之几?(按整米数计算,得数百分号前保留一位小数)
(2)长征二号F运载火箭芯一级为圆柱形,它的侧面积约是多少平方米?(得数保留π)
14.(2024·都昌)一批零件,张师傅单独做要6天,李师傅单独做要9天,两人同做三天后,这批零件还剩下几分之几没有完成?
15.(2024·都昌)客车从甲城开往乙城要6小时,小轿车沿同一路线从乙城开往甲城要4小时。两车同时从甲乙两城相对开出,几小时后相遇?
16.(2024·都昌)“六一”儿童节,阳光小学举行了联欢晚会。参加表演的男生有200人,比女生少。
(1)请用线段图表示出题中的数量关系。
(2)参加表演的女生有多少人?
17.(2024·都昌)南昌西站到北京西站之间的高速铁路大约长1404km。一趟高铁列车早上7:20从南昌西站出发匀速行驶,10:50途经郑州东站,13:20到达北京西站(途中经停时间忽略不计)。南昌西站到郑州东站的高速铁路大约有多长?(用比例解)
18.(2024·都昌)某小学组织六年级学生进行体能测试。第一天测试了六年级总人数的,第二天测试了六年级总人数的24%,第二天比第一天多测试了25人,该校六年级一共有多少学生?
19.(2024·修水)为落实“双减”政策,促进学生德、智、体、美、劳全面发展,引导学生养成热爱劳动的习惯,光明小学开展了丰富多彩的劳动教育实践活动。劳动实践活动有四个项目,分别是农耕劳动、厨艺坊、木艺坊和编织坊。学校规定所有学生都要参加劳动实践活动,每位学生只能选择其中一个劳动实践活动项目。如图是光明小学六年级学生参加劳动实践活动情况的统计图。请结合统计图,完成下面的问题。
(1)光明小学六年级学生一共有多少人?
(2)参加“编织坊”的六年级学生人数比参加“农耕劳动”的多百分之几?
(3)请把条形统计图补充完整。(此小问不写计算过程,把条形统计图补充完整即可)
20.(2024·修水)如图是两个互相啮(niè)合的齿轮,它们在同一时间内转动时,大齿轮和小齿转过的总齿数是相同的。大齿轮有40个齿,小齿轮有24个齿。如果大齿轮分钟转120圈,小齿轮每分钟转多少圈?
21.(2024·修水)用96厘米长的铁丝围成一个直角三角形,这个三角形的三条边长度的比是3:4:5。这个三角形的面积是多少平方厘米?
22.(2023·宜春)聪聪来到景区的纪念品商店准备购买一本纪念册,据了解商店以每本4.5元的价格进的一批纪念册,开始出售时营业员把单价搞错了,按每本4元的零售价卖出了全部的,接着把剩下的以每本6元卖出,当全部卖出时,还能获利630元。那么这批纪念册共有多少本?
23.(2023·青山湖)4月23日是世界读书日,在这一天,启航小学新买来800本图书,把这些图书的40%放在了图书馆,剩下的书按3:4:5分给了四、五、六年级。六年级分到了多少本书?
24.(2023·青山湖)周日,阳阳家要进行房屋大扫除。阳阳单独做要60分钟做完,爸爸单独做要40分钟做完,妈妈单独做要30分钟做完。如果阳阳全家一起合作,需要多少分钟才能完成大扫除的任务?
25.(2023·都昌)如图中左边是一种玻璃酒杯,杯口内直径4cm,总深12cm,圆柱部分高7.5cm。把酒杯装满水倒入右边的茶杯,能倒满吗?
26.(2023·都昌)某市政府决定对A区沿河两岸在房子进行重新装饰。这项工程甲单独做要12天完成,乙对单独做要8天完成,现乙队单独做3天,剩下在由甲乙两队合作完成,甲乙要合作几天才能完成全部工程?
27.(2023·都昌)在比例尺是1:5000000的地图上,量得A、B两地相距6cm,如果甲、乙两辆汽车同时从AB两地相对开出,2小时后相遇,这时甲乙两车所行路程比是3:2。甲、乙两车的速度各是多少?
28.(2023·都昌)某修路队要修一段公路,每天修4.5km,20天可以修完,如果每天多修1.5km,多少天可以修完?(用比例解)
29.(2023·宜春)到达景区时,看到成人票:98元/张,学生票:78元/张;但为庆祝“六一”推出三种结算方式:现金支付、手机软件支付、银行卡支付。现金支付:每满100元减20元;手机软件支付:随机减免的方式;银行卡支付:直接按八五折支付。妈妈结算时选用了手机软件支付的方式,结果随机减免了68.8元。在这次购票过程中,妈妈选用的结算方式是最划算的吗?请用计算说明。
30.(2023·宜春)聪聪和爸爸妈妈还有爷爷奶奶8:30从家开车出发,10:00时发现已经行了120千米,照这样计算,他们还需几小时可以到达景区?(用比例知识解答)
答案解析部分
1.解:36÷(×)
=36÷
=180(千米)
答:A、B两地相距180千米。
本题主要考查了分数四则复合应用题,解题的关键是正确找出看作单位“1”及36千米对应的分率。当甲车到达B地时,乙车行了全程的,即乙车速度是甲车的,根据分数乘法的意义可知,当甲行了全程的时,乙车行了全程的,又当甲行了全程的时,乙车行了36千米,即这36千米是全程的,根据分数乘法的意义,用这36千米除以其占全程的分率,即得两地相距多少千米。
2.解:200÷=700(棵)
700×(1﹣40%)=420(棵)
420×=180(棵)
答:六⑶班要植树180棵。
首先,根据题目信息知道六(1)班植树数占总植树数的40%,并且六(1)班已经植了200棵树,这代表了总植树数的2/7。可以通过这些信息计算出总植树数。接着知道六(2)班和六(3)班的植树数之比为4:3,可以利用这个比例和已知的总植树数来计算六(3)班应植树的数量。
3.解:20×0.6×22
=12×22
=264(元)
8×22=176(元)
264﹣176=88(元)
答:一个月(按22天计算)需要花费264元,一个月大约能节省88元。
本题主要考察的是费用计算和比较。题目中给出了两种出行方式的费用计算方式,一是开车,一是乘公共汽车。开车的费用根据行驶的公里数和每公里的费用计算,而乘坐公共汽车的费用是固定的每天费用乘以天数。我们需分别计算出两种出行方式的月费用,并求出费用差额。
4.(1)解:160÷40%=400(人)
140÷400×100%=35%
答:本次一共调查了400人,其中对端午节文化习俗“很了解”的人数占总人数的35%。
(2)解:400-140-160-20=80(人)。
(1)本次一共调查的人数=B项的人数÷所占的百分率;其中对端午节文化习俗“很了解”的人数占总人数的百分率=A的人数÷总人数;
(2)C项的人数=总人数-其余各项分别的人数,依据计算的数据画出直条,并且标上数据。
5.(1)解:16×10+16×12×2+10×12×2
=160+384+240
=784(平方厘米)
答:做这个容器一共用了785平方厘米的玻璃。
(2)解:16×10×0.628÷÷(3.14×42)
=160×0.628×3÷(3.14×16)
=301.44÷50.24
=6(厘米)
答:这个圆锥的高是6厘米。
(1)做这个容器一共用玻璃的面积=长×宽+长×高×2+宽×高×2;
(2)这个圆锥的高=长方体的长×宽×上升水面的高度÷÷圆锥的底面积。
6.(1)750;10
(2)解:750×50%=375(人)
750×10%=75(人)
条形统计图如下:
(3)解:调查的学生中“不了解端午节的由来,但知道端午节的习俗”和“不了解端午节的由来,也不知道端午节的习俗”的一共有多少人?(答案不唯一)
375+75=450(人)
答:调查的学生中“不了解端午节的由来,但知道端午节的习俗”和“不了解端午节的由来,也不知道端午节的习俗”的一共有450人。
(1)300÷40%=750(名);
1-40%-50%=10%。
故答案为:(1)750;10。
(1)观察两个统计图,获取数据,得到”了解端午节的由来,知道端午节的习俗“人数为300人,占参加问卷的学生总人数的40%,用除法即可求出参加问卷的学生总人数;观察扇形统计图,用整体”1“减去其余两个占比,即可求出“不了解端午节的由来,也不知道端午节的习俗”的占总人数的百分之几;
(2)由第(1)小题得到参加问卷的学生总人数为750人,“ 不了解端午节的由来,也不知道端午节的习俗 ”人数占比10%,观察统计图,可知 ”不了解端午节的由来,但知道端午节的习俗“人数占比50% ,根据公式”不了解端午节的由来,但知道端午节的习俗“人数=总人数×对应百分比, “ 不了解端午节的由来,也不知道端午节的习俗 ”人数=总人数×对应百分比,代入数据求出对应人数,再补全条形统计图即可;
(3)答案不唯一,合理即可。
7.解:4+3=7(小时)
设甲车每小时行驶x千米,则乙车每小时行驶(x+25)千米。
4(x+x+25)=7(x+25)
4(2x+25)=7x+175
8x+100=7x+175
8x﹣7x=175﹣100
x=75
75+25=100(千米/时)
100×7=700(千米)
答:A、B两地距离是700千米。
设甲车行驶速度为每小时x千米,根据”甲车每小时比乙车少行驶25km“得到乙车每小时行驶(x+25)千米,然后根据公式“路程=速度×时间,得到甲乙两车相遇时行驶的总路程为4(x+x+25)千米,乙车行驶的总路程(A、B两地距离)为7(x+25),然后根据数量关系”甲乙两车相遇时行驶的总路程=乙车行驶的总路程“列出方程 4(x+x+25)=7(x+25) ,解方程求出甲车行驶速度,最后代入7(x+25)求解即可。
8.(1)解:(10×2)×(8×2)+(10×2)×13×2+(8×2)×13×2
=20×16+20×13×2+16×13×2
=320+520+416
=1256(平方厘米)
答:做这个礼品箱至少需要1256平方厘米的纸板。
(2)解:(10×2)×(8×2)×13
=20×16×13
=320×13
=4160(立方厘米)
4160立方厘米=4.16立方分米
答:这个礼品箱的体积最少是4.16立方分米。
(1)由于这个礼品箱无盖,所以需要纸板的面积=这个长方体的一个底面和4个侧面的总面积,根据长方体的表面积公式解答;
(2)长方体的体积=长×宽×高,把数据代入公式解答。
9.解:[1﹣()×4]÷
=
=2(天)
答:还需要2天。
把这项工程的总工作量看作单位“1”,根据“工作效率=总工作量÷工作时间”,分别求出两队的工作效率,甲、乙两队合干的工作量=(甲队的工作效率+乙队的工作效率)×合干天数,总工作量-甲、乙两队合干的工作量=剩下的工作量,剩下的工作量÷乙队的工作效率=乙队单独干还需要的天数。
10.解:60÷(1+)
=60÷
=60×
=36(棵)
答:六(2)班种了36棵小树苗。
已知一个数比另一个数多几分之几,求另一个数,用除法计算。将六(2)班种的小树苗的棵数看作单位“1”,六(1)班种的小树苗的棵数÷(1+六(1)班比六(2)班多种的分率)=六(2)班种的小树苗的棵数。
11.解:400×=150(人)
400﹣150=250(人)
250×=50(人)
250×=200(人)
答:彩旗方阵有150人,爱心方阵200人,花环方阵50人。
根据题意,用六年级的总人数乘,求出彩旗方阵的人数;用六年级的总人数减去彩旗方阵的人数,求出剩下的学生人数;把剩下的学生人数按4:1进行分配,爱心方阵占剩下学生人数的,花环方阵占剩下学生人数的,用剩下的学生人数分别乘爱心方阵和花环方阵占剩下学生人数的几分之几,即可求出爱心方阵和花环方阵的人数。
12.解:(84÷6)×(6+4)
=14×10
=140(吨)
答:现在每天共运货140吨。
首先用6辆相同的货车每天一共运货的数量除以6求出一辆货车每天运货的数量,再用求得的结果乘(6+4)即可求出现在每天共运货的数量。
13.(1)解:(21+15)÷58
=36÷58
≈0.621
=62.1%
答:长征二号F运载火箭一二级芯的总长度占火箭全长的62.1%。
(2)解:π×3.35×21
=35π×21
=70.35π(平方米)
答:它的侧面积约是70.35π平方米。
(1)长征二号F运载火箭一二级芯的总长度占火箭全长的百分率=(芯一级大约长度+芯二级大约的长度)÷长征二号F运载火箭的全长;
(2)它的侧面积=π×直径×高。
14.解:1-[(+)×3]
=1-[×3]
=1-
=
答:这批零件还剩没有完成。
这批零件还剩下没有完成的分率=1-(张师傅的工作效率+李师傅的工作效率)×工作时间。
15.解:1÷(+)
=1÷
=2.4(小时)
答:两车同时从甲乙两城相对开出,2.4小时后相遇。
两车同时从甲乙两城相对开出后的相遇时间=路程÷速度和。
16.(1)解:
(2)解:
=200÷
=250(人)
答:参加表演的女生有250人。
参加表演的女生人数=参加表演的男生人数÷(1-少的分率)。
17.解:10时50分-7时20分=3时30分
3时30分=3.5时
13时20分-7时20分=6时
设南昌西站到郑州东站的高速铁路大约有xkm。
1404:6=x:3.5
6x=4914
x=819
答:南昌西站到郑州东站的高速铁路大约有819km。
设南昌西站到郑州东站的高速铁路大约有xkm。依据南昌西站到北京西站之间的高速铁路大约的长度:时间=南昌西站到郑州东站的高速铁路大约的时间:3.5,列比例,解比例。
18.解:25÷(24%-)
=25÷4%
=625(名)
答:该校六年级一共有625名学生。
该校六年级一共有学生的人数=第二天比第一天多测试的人数÷( 第二天测试占六年级总人数的百分率- 第一天测试占六年级总人数的百分率 ) 。
19.(1)解:70÷35%=200(人)
答:光明小学六年级学生一共有200人。
(2)解:(60-40)÷40
=20÷40
=0.5
=50%
答:参加“编织坊”的六年级学生人数比参加“农耕劳动”的多50%。
(3)解:200-70-60-40=30(人)
(1)光明小学六年级学生一共的人数=厨艺坊的人数÷所占的百分率;
(2)参加“编织坊”的六年级学生人数比参加“农耕劳动”多的分率=(参加“编织坊”的人数-参加“农耕劳动”的人数)÷参加“农耕劳动”的人数;
(3)木艺坊的人数=总人数-其余各项分别的人数,然后画出直条,并且标上数据。
20.解:设小齿轮每分钟转x圈。
40×120=24x
24x=4800
x=200
答:小齿轮每分钟转200圈。
设小齿轮每分钟转x圈。依据大齿轮的个数×大齿轮平均每分钟转的圈数=小齿轮的个数×小齿轮平均每分钟转的圈数,列比例,解比例。
21.解:96÷(3+4+5)
=96÷12
=8(厘米)
(8×3)×(8×4)÷2
=24×32÷2
=384(平方厘米)
答:这个三角形的面积是384平方厘米。
这个三角形的面积=底×高÷2;底、高分别=三角形的周长÷总份数×各自分别占的份数。
22.解:假设这批书有x本。
x×4+[(1-)x×6﹣4.5x=630
x×4+x×6﹣4.5x=630
x+x﹣4.5x=630
x﹣4.5x=630
5.25x-4.5x=630
0.75x=630
x=840
答:这批纪念册共有840本。
设这批书有x本,总的进价是4.5x元,以每本4元的零售价卖出了全部的,则卖出的钱数为(x4)元,以每本6元的价格卖的钱数为元,根据按4元卖的钱数+按6元卖的钱数-进价=获利钱数,即可列方程解答。
23.解:800×(1﹣40%)
=800×0.6
=480(本)
480×
=480×
=200(本)
答:六年级分到了200本书。
剩下的图书占总数的(1-40%),根据分数乘法的意义先求出剩下的本数。六年级分到的占剩下本数的,根据分数乘法的意义求出六年级分到的本数即可。
24.解:1÷( + + )
=1÷
= (分钟)
答:如果阳阳全家一起合作,需要 分钟才能完成大扫除的任务。
把这次任务看作单位“1”,用1除以每人完成需要的时间,分别表示出每人的工作效率。用1除以三人的工作效率和即可求出合作完成需要的时间。
25.解:酒杯内水的体积:
3.14×(4÷2)2×(12﹣7.5)× +3.14×(6÷2)2×7.5
=3.14×4×4.5× +3.14×4×7.5
=3.14×4×1.5+3.14×4×7.5
=3.14×4×(1.5+7.5)
=3.14×36
=113.04(立方厘米)
茶杯内的水深:
113.04÷[3.14×(6÷2)2]
=113.04÷[3.14×9]
=113.04÷28.26
=4(厘米)
4厘米<5厘米
答:不能倒满。
酒杯的体积=圆柱部分体积+圆锥部分体积。再根据圆柱的体积公式算出右图茶杯的水深,二者比较即可。
26.解:(1﹣3× )÷( + )
= ÷
=3(天)
答:甲乙要合作3天才能完成全部工程。
先算出乙队3天做了这项工程的多少,把这项工程看作单位“1”,剩下的工程=1-已做的。最后用剩下的工程÷(甲的工效+乙的工效),即可解答。
27.解:6÷ =30000000(厘米)
30000000厘米=300千米
300÷2=150(千米)
150× =90(千米/时)
150× =60(千米/时)
答:甲车的速度是90千米/时,乙车的速度是60千米/时。
根据实际距离=图上距离÷比例尺,先算出实际距离。再根据:速度=路程÷实际,算出甲乙两车的速度和,最后根据按比分配的方法,分别算出甲、乙的速度。
28.解:设x天可以修完。
(4.5+1.5)x=4.5×20
6x=90
x=15
答:15天可修完。
根据题意可知: 每天修的长度×天数=总长度(一定),每天修的长度与天数成反比例,根据反比例的意义列比例解答。
29.解:现金支付:
98×4+78-4×20
=470-80
=390(元)
手机软件支付:
98×4+78-68.8
=470-68.8
=401.2(元)
银行卡支付:
(98×4+78)×0.85
=470×0.85
=399.5(元)
401.2>399.5>390
所以,妈妈选用的结算方式不是最划算的。
答:妈妈选用的结算方式不是最划算的。
依次算出三种结算方式所付的钱。现金支付的总价=成人票单价×数量+儿童票的单价-减免的钱数;手机软件支付的总价=成人票单价×数量+儿童票的单价-减免的钱数;银行卡支付的总价=(成人票单价×数量+儿童票的单价)×折扣,然后比较大小。
30.解:10时-8时30分=1时30分=1.5(小时)
设他们需要x小时到达。
120:1.5=200:x
120x=200×1.5
x=300÷120
x=2.5
2.5-1.5=1(小时)
答:他们还需要1小时到达。
根据比例的知识,速度不变,路程和时间成正比例,列出方程。计算出总时间,再减去已用时间,即可得到还需要的时间。
同课章节目录
