2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题1 选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题1 选择题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 366.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 10:09:27 | ||
图片预览




文档简介
2024-2025学年小升初数学备考真题分类汇编(山东地区专版)
专题1 选择题
一、单选题
1.(2024·枣庄)在比例中,两内项的积是最小的合数,其中一个外项是0.8,另一个外项是( )
A.5 B.1.6 C.10
2.(2023·章丘)下列单位换算,正确的是( )
A.0.6平方千米=600公顷 B.45分钟=0.45小时
C.7吨50千克=7.05吨 D.80dm3= m3
3.(2024·枣庄)我们用竖式计算14×12时,用到的运算定律是( )
A.加法交换律 B.乘法结合律 C.乘法分配律
4.(2024·枣庄)在长方形、正方形、圆、扇形、等腰梯形、等边三角形中,只有1条对称轴的图形有( )个。
A.2个 B.1个 C.3个
5.(2023·罗庄)下列判断正确的选项是( )
A.2是质数中唯一的偶数 B.假分数的倒数一定是真分数
C.a (a>1)所有的因数都小于a D.所有的数分为正数和负数
6.(2023·章丘)有甲、乙两根绳子,甲绳减去 ,乙绳减去 米,两根绳子都剩下2米,比较两根绳子原来的长度,正确的是( )
A.甲比乙长 B.乙比甲长
C.两根绳子一样长 D.无法比较
7.(2023·武城)下列各图中,能表示出两个量成正比例关系的是( )
A. B.
C. D.
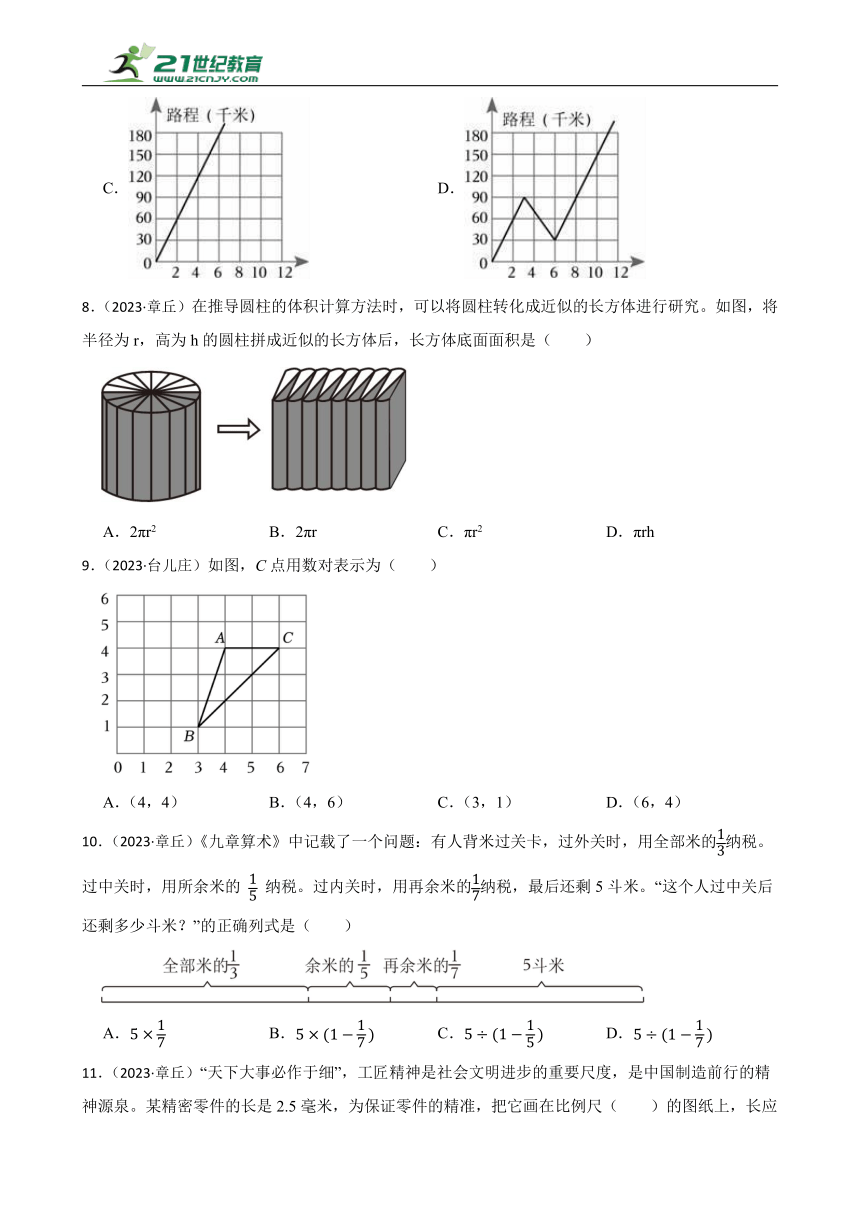
8.(2023·章丘)在推导圆柱的体积计算方法时,可以将圆柱转化成近似的长方体进行研究。如图,将半径为r,高为h的圆柱拼成近似的长方体后,长方体底面面积是( )
A.2πr2 B.2πr C.πr2 D.πrh
9.(2023·台儿庄)如图,C点用数对表示为( )
A.(4,4) B.(4,6) C.(3,1) D.(6,4)
10.(2023·章丘)《九章算术》中记载了一个问题:有人背米过关卡,过外关时,用全部米的纳税。过中关时,用所余米的 纳税。过内关时,用再余米的纳税,最后还剩5斗米。“这个人过中关后还剩多少斗米?”的正确列式是( )
A. B. C. D.
11.(2023·章丘)“天下大事必作于细”,工匠精神是社会文明进步的重要尺度,是中国制造前行的精神源泉。某精密零件的长是2.5毫米,为保证零件的精准,把它画在比例尺( )的图纸上,长应画5厘米。
A.1:20 B.20:1 C.1:200 D.200:1
12.(2023·章丘)小学阶段学的很多数学知识之间有着密切联系。下面不能正确表示它们之间关系的是( )
A. B.
C. D.
13.(2023·章丘)抛两颗骰子,出现点数和为8的可能性比和为7的可能性( )
A.大 B.小 C.相同 D.无法比较
14.(2023·章丘)圆周率是圆的周长与直径的比值,人类对圆周率的研究历史悠久。我国古代数学著作《周髀算经》中就有“周三径一”的记载,东晋时期数学家刘徽用“割圆术”求得圆周率的近似值是3.14,到了南北朝时期数学家祖冲之求得了圆周率的7位小数精确值。如果如图中线段AF表示一个圆的周长,那么这个圆的直径可能是( )
A.AB B.AC C.AD D.CE
15.(2023·章丘)反映儿童牛奶中各营养成分的含量选用( )统计图更好一些。
儿童牛奶营养成分表
名称 水分 蛋白质 脂肪 乳糖 矿物质 其他
百分比 87% 3.3% 3.5% 5% 0.75% 0.45%
A.扇形 B.条形 C.折线 D.都可以
16.(2023·章丘)用一块长25.12cm,宽18.84cm的长方形铁片和两块半径是( )cm的圆形铁片正好可以做一个圆柱形容器。
A.2 B.3 C.6 D.8
17.(2023·章丘)如图,折成一个正方体后,与“建”字相对的字是( )
A.构 B.谐 C.社 D.会
18.(2023·武城)下面说法中正确的有( )个。
①长方形、正方形和平行四边形的面积都可以理解成“底×高”计算。
②钟面上,从12走到3,分针绕中心点旋转了90°。
③商品打“七五折”出售就是降价75%出售。
④甲、乙两人分一箱苹果,若按照1:2或2:4分配,两种分法乙得到的苹果一样多。
A.1 B.2 C.3
19.(2023·章丘)大于 小于 的分数有( )个;大于0.3小于0.4的二位小数有( )个。
A.无数;无数 B.无数;9个 C.1;9 D.0;无数
20.(2023·武城)有两根绳子,如果第一根用去全长的,第二根用去全长的,两根绳子剩下的长度相等,( )绳子较长。
A.第二根 B.第一根 C.无法判断
21.(2023·武城)如图中,一个小正方体的体积是1立方厘米,长宽高不变,要把如图的图形补成一个完整的立方体,补上的那部分的体积是( )立方厘米。
A.14 B.34 C.48
22.(2023·台儿庄)欢欢从甲地走向乙地,前20分钟走了全程的30%,接下来的20分钟走了剩下路程的50%,前20分钟的速度比接下来的20分钟的速度( )
A.慢 B.快 C.一样 D.无法比较
23.(2023·台儿庄)下面说法错误的是( )
A.3与4、6、8能组成比例
B.2010年是平年
C.所有的比例尺的前项都是1
D.抛一次硬币,落地后可能正面朝上
24.(2023·台儿庄)糖与水的比是1:4,糖占糖水的( )
A.25% B.20% C.40% D.80%
25.(2023·台儿庄)x=6是下面方程( )的解
A.24÷x=6 B.5x=35 C.4x+5=29 D.4x÷8=6
26.(2023·武城)六(3)班的老师组织学生去距学校5千米的科技馆参观,从学校出发,乘车0.5小时后到达,在科技馆参观1小时后,出馆休息0.5小时,然后乘车0.5小时返回学校。下面( )图正确描述了同学们的行程过程。
A.
B.
C.
27.(2023·武城)将标有1、2、3、4、5的五张形状相同的数字卡片放在一个口袋里,每次任意摸出一张,摸后放回,下列哪种说法是正确的?( )
A.摸到合数的可能性是40%。
B.摸到“3”的可能性是20%。
C.摸到质数的可能性是80%。
28.(2023·武城)观察如图,根据左面方格中数字排列的规律,右面方格空白处填( )
A.3 B.4 C.5
29.(2023·武城)历亭路小学统计了六年级学生最喜欢的课外活动人数,为了直观地看出各类活动人数的多少,要将各项数据制作成统计图,用( )最合适。
A.条形统计图 B.折线统计图 C.扇形统计图
30.(2023·武城)2023年春节,小军共收到长辈的祝福压岁钱5000元,根据他的理财计划,他打算用这笔资金在他上高中时买学习资料,他把钱存入银行,定期3年,年利率为3.25%,求到期后小军可从银行取出多少元,正确列式为( )
A.5000×3×3.25%
B.5000+5000×3.25%
C.5000×3×3.25%+5000
31.(2023·武城)我国古代名著《墨经》中有这样的记载:“圆,一中同长也。”这句话中的“一中”指( )
A.圆有无数条半径
B.圆有一个圆心
C.同一个圆中半径相等
32.(2023·五莲)用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
33.(2023·五莲)10以内的质数有( )个。
A.5 B.3 C.4 D.6
34.(2023·五莲)下列选项中能用2a+4表示的是( )
A.长方形的面积 B.长方形的周长
C.线段的总长度 D.长方形的周长
35.(2023·五莲)一张圆形纸片至少要对折( )次,才能找到它的圆心。
A.1 B.2 C.3 D.4
36.(2023·五莲)两个小朋友在玩摸球的游戏,袋子里有32个白球、8个红球、10个篮球任意摸出一个球,摸出( )球的可能性大
A.白 B.红 C.蓝 D.无法确定
37.(2023·齐河)一个圆柱型无盖水桶,底面积是8平方分米,高5分米,在水桶的侧面上有一个洞,洞的位置距离下底2分米,如图,这个水桶现在最多可以盛( )升水。(桶壁厚度忽略不计)
A.40 B.16 C.24 D.28
38.(2023·齐河)一个圆柱形蛋糕盒(如图),量得底面周长是0.8米,高是0.2米,侧面接头处重合1厘米(即0.01米),把侧面从接头处展开后是一个长方形。它的侧面共用了多少平方米的纸板?下面答案正确的是( )
A.0.16 B.0.18 C.0.36 D.0.162
39.(2023·齐河)下面( )图,和正好拼成一个棱长为2的大正方体。(每个小正方体的棱长为1)
A. B. C. D.
40.(2023·齐河)下面各题中的两个量成正比例的是( )
A.单价一定,数量和总价
B.路程一定,行驶的速度和行驶的时间
C.圆的面积与它的半径
D.从甲地到乙地,已经走的路程和剩下的路程
41.(2023·齐河)在一幅比例尺是1:500000的地图上,量得A、B两地的距离是6.8厘米,如果把甲、乙两地画在比例尺为1:250000的新地图上,则甲、乙两地在新地图上的距离是多少厘米?( )
A.34 B.13.6 C.3.4 D.1.36
42.(2023·齐河)等底等高的圆柱和圆锥的体积相差18.6立方厘米,则圆柱的体积是( )立方厘米。
A.9.3 B.18.6 C.27.9 D.37.2
43.(2023·齐河)用三根同样长的铁丝分别围成平行四边形、正方形、长方形三个不同的图形,三个图形的面积相比,( )
A.平行四边形面积最大 B.正方形面积最大
C.长方形面积最大 D.三个图形的面积相等
44.(2023·齐河)南极大陆记录的最低温度是﹣89.6℃,北极最低温度记录大约是﹣70℃左右,我国最北方漠河的最低温度记录是﹣53℃,珠穆朗玛峰峰顶的最低气温记录是零下60℃左右。这四个地方记录的最低温度相比,最低的是( )
A.南极大陆 B.北极
C.漠河 D.珠穆朗玛峰峰顶
45.(2023·齐河)李倩和张萌的家相距a米。星期天,李倩骑自行车去张萌家做客,她每分钟骑行b米。t分钟后,还未到张萌家,离张萌家还有多少米?( )
A.(a﹣b)t B.a﹣bt C.b﹣at D.at﹣bt
46.(2023·齐河)下面的分数不能用百分数表示的是( )
A.小芳用半小时做了全部作业的
B.妹妹喝了一杯牛奶的
C.合唱队的人数比军乐队的人数多
D.一张纸的长比宽多分米
47.(2023·德州)一件稿件,甲 小时打完。乙 小时打完,甲、乙的工作效率比是( )
A. : B.3:2 C. : D.2:3
48.(2023·德州)一根绳子第一次剪去 米,第二次剪去全长的 ,剪下的这两段绳子( )
A.一样长 B.第一段长 C.第二段长 D.无法确定
49.(2023·德州) 的分母加上14,要使分数的大小不变,分子应( )
A.加上14 B.扩大到原来的2倍 C.加上6
50.(2023·德州)两个不同质数的积一定是( )
A.奇数 B.偶数 C.质数 D.合数
答案解析部分
1.A
解:4÷0.8=5
故答案为:A。
分析题干,两内项的积是最小的合数,故得到内项积=4,又已知一个外项是0.8,根据比例的基本性质:内项积等于外项积,得到另一个外项=内项积÷一个外项,代入数据计算即可。
2.C
解:选项A中,0.6×100=60,所以0.6平方千米=60公顷,单位换算错误;
选项B中,45÷60=0.75,所以45分钟=0.75小时,单位换算错误;
选项C中,7+50÷1000=7.05,所以7吨50千克=7.05吨,单位换算正确;
选项D中,80÷1000=,所以80dm3=m3,单位换算错误;
故答案为:C。
根据1平方千米=100公顷、1小时=60分钟、1吨=1000千克、1立方米=1000立方分米进行单位换算,选择正确的即可。
3.C
解:
故答案为:C。
用竖式计算14×12时,首先计算的是14×2,然后计算的是14×10,最后将两部分相加得到结果。
4.A
解:长方形有2条对称轴
正方形有4条对称轴
圆有无数条对称轴
扇形有1条对称轴
等腰梯形有1条对称轴
等边三角形有3条对称轴
故答案为:A。
对称轴是指使几何图形成轴对称或旋转对称的直线,据此判断即可。
5.A
解:A选项,2是质数中唯一的偶数,原选项说法正确;
B选项,假分数的倒数不一定是真分数,原选项说法错误;
C选项,a(a>1)所有的因数小于等于a,原选项说法错误;
D选项,所有的数分为正数、负数和0,原选项说法错误。
故答案为:A。
一个数,如果只有1和它本身两个因数,这样的数叫做质数。
一个整数的倒数就是这个整数分之一。假分数的倒数也可能是假分数,如是假分数,它的倒数是1;
一个数可以表示成两个自然数的乘积,那么这两个自然数都是它的因数。一个数最大的因数是它本身;
0既不是负数也不是正数。
6.A
解:甲绳:2÷(1-)
=2÷
=(米)
乙绳:2+=(米)
因为>,所以甲绳原来的长度比乙绳原来的长度长。
故答案为:A。
甲绳减去,是把甲绳原来长度看作单位“1”,那么甲绳剩下的长度就是原来长度的1-,用剩下的长度除以1-就可以求出甲绳原来的长度;乙绳减去米,剩下2米,那么将剪去的长度与剩下的长度相加就可以求出乙绳原来的长度;最后将两根绳子原来的长度进行比较即可。
7.C
解:正比例图像是从(0,0)出发的无限延伸的射线;
故答案为:C。
正比例图像是从(0,0)出发的无限延伸的射线,这条线上所有对应的两个量的比值都相等,据此判断。
8.C
解:长方体底面长:2πr÷2=πr;
长方体地面面积:πr×r=πr2;
所以长方体地面面积是πr2。
故答案为:C。
由图可知,长方体底面的长是圆柱底面周长的一半,长方体底面的宽是圆柱底面半径,代入到长方形面积=长×宽即可解答。
9.D
解:C点在第6列,第4行,所以C点用数对表示是(6,4);
故答案为:D。
数对中,第一个数表示列,第二个数表示行;据此解答。
10.D
解:余下米的是5斗米,余下的米为:5÷(1-)
故答案为:D。
由题意可知,最后剩的5斗米是过中关后剩的米的1-,也就是把过中关后剩的米看作单位“1”,按照对应量÷对应率=单位“1”进行列式即可。
11.D
解:5厘米=50毫米
50:2.5=200:1
所以该图纸的比例尺是200:1。
故答案为:D。
首先进行统一单位,再根据比例尺=图上距离:实际距离代入数值进行计算即可。
12.A
解:选项A中,长方形属于特殊的平行四边形,但是梯形不属于平行四边形,所以该选项表示错误;
选项B中,三角形按照角可以划分为锐角三角形、直角三角形、钝角三角形,所以该选项表示正确;
选项C中,方程也是等式的一种,所以该选项表示正确;
选项D中,一个数的最大因数是它本身,最小倍数也是它本身,所以a既是a的因数也是a的倍数,该选项表示正确;
故答案为:A。
根据四边形的分类、三角形的分类、等式以及因数与倍数的关系进行解答。
13.B
解:和为8的情况:2和6、3和5、4和4、5和3、6和2共5种情况;
和为7的情况:1和6、2和5、3和4、4和3、5和2、6和1共6种情况;
因为6>5,所以出现点数和为8的可能性比和为7的可能性小。
故答案为:B。
已知骰子上的数字为1~6,分别列举出和为8与和为7时的所以情况进行解答。
14.B
解:直径大约是圆周长的,所以线段AF表示一个圆的周长时,圆的直径可能是AC。
故答案为:B。
圆周长=直径×π,即圆的周长是直径的π倍,由于π的近似值是3.14,所以当AF表示一个圆的周长时,直径的长度大约是AF的,由此解答。
15.A
解:选项A中,扇形统计图可以反应部分与整体之间的关系;
选项B中,条形统计图能够使人一眼看出各个数据的大小;
选项C中,折线统计图不仅可以表示数量的多少,还可以显示数据的变化趋势;
因为统计表中的数据是牛奶中各营养成分占牛奶总量的百分比,也就是需要用统计图反应部分与整体之间的关系,所以用扇形统计图合适。
故答案为:A。
由统计表可知,需要用统计图反应牛奶中各营养成分与牛奶总量之间的关系,由此解答。
16.B
解:长为底面周长:25.12÷3.14÷2=4(cm);
宽为底面周长:18.84÷3.14÷2=3(cm)
所以该长方形铁片和半径为3cm或者4cm的圆形铁片都可以做一个圆柱形容器。
故答案为:B。
根据圆周长=半径×2×π,得到半径=圆周长÷2÷π。有两种方法做成圆柱容器,第一种,以长方形的长做圆柱的底面周长;第二种,以长方形的宽做圆柱的底面周长;分别代入数值进行计算即可。
17.C
解:以“和”字为正方体底面折成正方体如图:
由图可知,与“和”字相对的是“会”字;与“建”字相对的是“社”字;与“构”字相对的是“谐”字。
故答案为:C。
该展开图属于正方体展开图的“1-4-1”型,以“和”字为正方体底面折成正方体,则“构”字在正方体的背面,“建”字在正方体的左面,“谐”字在正方体的前面,“社”字在正方体的右面,“会”字在正方体的上面,由此解答。
18.C
解:①长方形、正方形都是特殊的平行四边形,所以求它们的面积都可以理解成“底×高”计算,说法正确;
②钟面上一大格表示30°,从12到3走了3大格,即转了30°×3=90°,说法正确;
③商品打“七五折”出售就是按原价的75%出售,说法错误;
④1:2=(1×2):(2×2)=2:4,因此,两种分法乙得到的苹果一样多说法正确;
故答案为:C。
①长方形、正方形都是特殊的平行四边形;②钟面上每个大格对应30°;③打几折就是按原价的百分之几十出售;④比的基本性质:比的前项和后项同时乘或除以同一个数(不为0),比值不变;据此解答。
19.B
解:====;====;
大于小于的分数是,大于小于的分数是、,所以大于小于的分数有无数个。
大于0.3小于0.4的两位小数有:0.31、0.32、0.33、0.34、0.35、0.36、0.37、0.38、0.39一共9个。
故答案为:B。
本题将和化为同分母分数,就可以找到这两个分数之间的分数;用列举法写出0.3到0.4之间的两位小数,即在0.3后面的百分位上添数;由此解答。
20.A
解:第一根剩下原来的1-=,第二根剩下原来的1-=;<,所以第二根绳子较长。
故答案为:A。
求一个数的几分之几,用乘法计算;两根绳子剩下的长度相等,即第一根长度×(1-)=第二根长度×(1-),比较剩下的分率,剩下的分率越小,表示原来的绳子越长,据此解答。
21.B
解:完整立方体体积:4×4×3=48(立方厘米);
现有体积:1+3+10=14(立方厘米);
补上部分体积:48-14=34(立方厘米);
故答案为:B。
该图形补成的完整的立方体的长和宽都是由4个小正方体组成,高是由3个小立方体组成,计算出完整的立方体的体积后再减去现有的立方体体积即可解答;长方体体积=长×宽×高,现有的小立方体上层有1个小正方体,中间层有3个小正方体,下层有10个小正方体,将三层小正方体个数相加就是现有图形体积;据此解答。
22.A
前20分钟:30%;
接下来20分钟:(1-30%)×50%
=70%×50%
=35%;
20%<35%,所以前20分钟的速度比接下来20分钟的速度慢。
故答案为:A。
时间相同,比较两次所走的路程即可,路程越长,速度越快;把全程看作单位“1”,前2分钟走了全程30%;接下来的20分钟走了全程的(1-30%)×50%;据此解答。
23.C
解:选项A:3÷4=,6÷8=,所以3:4=6:8,该说法正确;
选项B:2010÷4=502……2,所以2010年是平年,该说法正确;
选项C:图上距离较大,实际距离较小时,比例尺写成后项是1的形式,该说法错误;
选项D:抛一次硬币,落地后可能正面朝上也可能反面朝上,该说法正确;
故答案为:C。
能组成比例的两组比的比值相等;非整百年份能被4整除就是闰年,不能被4整除就是平年;比例尺=图上距离:实际距离,当图上距离较大,实际距离较小时,比例尺写成后项是1的形式;抛一枚硬币只有正面朝上或反面朝上两种情况;据此解答。
24.B
解:1÷(1+4)
=1÷5
=20%;
故答案为:B。
糖与水的比是1:4,把糖看作1份,那么水就是这样的4份;含糖率=糖的份数÷糖水的份数,据此解答。
25.C
解:选项A:24÷x=6
24÷x×x=6×x
24=6x
6x÷6=24÷6
x=4;
选项B:5x=35
5x÷5=35÷5
x=7;
选项C:4x+5=29
4x+5-5=29-5
4x=24
4x÷4=24÷4
x=6;
选项D:4x÷8=6
4x÷8×8=6×8
4x=48
4x÷4=48÷4
x=12;
故答案为:C。
等式的基本性质1:等式两边同时加减同一个数,等式仍成立;等式的基本性质2:等式两边同时乘或除以同一个数(不为0),等式仍成立;根据等式的基本性质求出各个选项的解即可。
26.B
解:能正确描述同学们的行程过程;
故答案为:B。
由题意可知,0~0.5小时之间路程随时间增加而增加,0.5小时时路程是5千米,0.5~2小时之间路程不变,2~2.5小时之间路程随时间增加而减少,在2.5小时时路程是0千米;据此解答。
27.B
解:选项A:摸到合数的可能性是1÷5=20%,说法错误;
选项B:摸到“3”的可能性是1÷5=20%,说法正确;
选项C:摸到质数的可能性是3÷5=60%,说法错误;
故答案为:B。
1、2、3、4、5中合数有4,质数有2、3、5;摸到合数的可能性=合数张数÷总张数,摸到“3”的可能性=1÷总张数,摸到质数的可能性=质数张数÷总张数;据此解答。
28.A
解:右面方格空白处与2相加得到5,所以空白处的数是5-2=3;
故答案为:A。
从左面方格可以发现规律:第一行是后两个数相乘是前一个数,第二行和第三行都是后两个数相加得到前一个数,第一列是后两个数相乘是前一个数,第二列和第三列都是后两个数相加得到前一个数,据此解答。
29.A
解:为了直观地看出各类活动人数的多少,用条形统计图合适;
故答案为:A。
条形统计图:能清楚地看出数量的多少;折线统计图:不仅能看出数量的多少,还能反应数量的增减变化;扇形统计图:表示部分与整体之间的关系;据此选择合适的统计图。
30.C
解:利息:5000×3×3.25%;
到期后取回的钱:5000×3×3.25%+5000;
故答案为:C。
利息=本金×利率×存期,求出利息再加上本金,就是到期后取回的钱;据此解答。
31.C
解:“圆,一中同长也。”这句话中的“一中”指同一个圆中半径相等;
故答案为:C。
根据圆的特征:连接圆心到圆上任意一点的距离,叫做半径,在同圆中,所有的半径都相等,据此解答。
32.D
解:第n个图形需要小木棒的数量:6+3×(n-1)
6+3×(8-1)
=6+3×7
=6+21
=27(根)
故答案为:D。
第1个图形需要6根小木棒,第2个图形需要6+3根小木棒,第3个图形需要6+3×2根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要6+3×(n-1)根小木棒,最后将n=8代入即可。
33.C
解:10以内的质数有2,3,5,7
故答案为:C。
一个非零自然数,如果只有1和它本身两个因数,那么这样的数叫作质数;一个非零自然数,如果除了1和它本身还有别的因数,那么这样的数叫作合数,1既不是质数也不是合数,据此解答。
34.B
解:A:S=(4+2)a=6a
B:C=(2+a)×2=2a+4
C:L=2+a+4=6+a
D:C=(a+4)×2=2a+8
故答案为:B。
长方形周长等于长与宽和的2倍,面积等于长×宽,据此列式整理再与题干比较。
35.B
一张圆形纸片至少要对折2次,才能找到它的圆心
故答案为:B。
两条线相交确定一个点,据此解答即可。
36.A
解:32个>10个>8个
故答案为:A。
在一个袋子里面一共有三种颜色的球,由于白球的数量最多,红球的数量最少,所以同种颜色多的球摸到的可能性大,同种颜色少的球摸到的可能性小。
37.D
解:8×2+8×(5-2)÷2
=16+12
=28(立方分米)
故答案为:D。
由图可知,最多可以盛水的体积=底面积是8平方分米、高是2分米的圆柱体积+底面积是8平方分米、高是(5-2)分米的圆柱体积的一半;圆柱体积=底面积×高;据此解答。
38.D
解:(0.8+0.01)×0.2
=0.81×0.2
=0.162(平方米)
故答案为:D。
侧面展开的长方形的长等于圆柱的底面周长+0.01米,宽等于圆柱的高,再根据长方形面积=长×宽代入数值解答。
39.A
解:根据图形的拼组可知,和正好拼成一个棱长为2的大正方体。
故答案为:A。
要想拼成一个大正方体,还需要4个小正方体,据此解答。
40.A
解:选项A:=单价(一定),比值一定,总价和数量成正比例关系;
选项B:行驶的速度×行驶的时间=路程(一定),乘积一定,行驶的速度和行驶的时间成反比例;
选项C:=半径×π,比值不是一定值,所以圆面积和它的半径不成比例;
选项D:已走的路程+剩下的路程=全部路程,所以已经走的路程和剩下的路程不成比例。
故答案为:A。
两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,那么这两种量成正比例;据此解答。
41.B
解:6.8÷=3400000(厘米);
3400000×=13.6(厘米)。
故答案为:B。
用比例尺是1:500000的图上距离除以该比例尺求出A、B两地的实际距离;再用实际距离乘新地图上的比例尺即可求出新地图上的图上距离。
42.C
解:18.6÷(1-)
=18.6÷
=27.9(立方厘米)
故答案为:C。
圆锥的体积是与它等底等高的圆柱体积的,即等底等高的圆锥比圆柱的体积少(1-);已知一个数的几分之几是多少,求这个数,用除法计算。
43.B
解:平行四边形面积=底×高,长方形面积=长×宽,假设平行四边形的底边与长方形的长相等,那么平行四边形的高一定比小于长方形的宽,因此,平行四边形的面积一定小于长方形的面积;
假设长方形的长+宽=正方形的边长+边长=8,长方形的长是5,宽是3,面积就是5×3=15;正方形的边长就是4,面积是4×4=16;所以长方形面积小于正方形面积。综上所述,正方形面积最大。
故答案为:B。
周长一定,平行四边形的底边+邻边=长方形的长+宽=正方形的边长+边长;平行四边形的高一定比邻边短,平行四边形面积=底×高,长方形面积=长×宽,假设平行四边形的底边与长方形的长相等,那么平行四边形的高一定比小于长方形的宽,因此,平行四边形的面积一定小于长方形的面积;再假设长方形的长+宽=正方形的边长+边长=8,分别计算出长方形面积和正方形面积,再比较即可。
44.A
解:-53℃<-60℃<-70℃<-89.6℃,所以温度最低的是南极大陆。
故答案为:A。
这四个地方的气温都是负数,负数比较大小要看负号后面的数字,数字越大的反而越小;据此解答。
45.B
解:李倩骑行t分钟,骑行了bt米,离张萌家还有(a-bt)米。
故答案为:B。
路程=速度×时间,用总距离减去李倩骑行的路程即可解答。
46.D
解:选项A:全部作业看作单位“1”,半小时做的作业占全部作业的,也就是75%;
选项B:一杯牛奶看作单位“1”,妹妹喝了一杯牛奶的,也就是50%;
选项C:军乐队的人数看作单位“1”,合唱队的人数比军乐队的人数多,也就是多66.67%;
选项D:长比宽多分米,表示的具体的数量,不能用百分数表示。
故答案为:D。
百分数表示一个数是另一个数的百分之几,百分数没有的单位;据此解答。
47.D
解:甲、乙的工作时间比是: : =3:2 ;
甲、乙的工作效率比是2:3 。
故答案为:D。
工作量一定,工作效率的比和工作时间的比刚好相反,据此解答。
48.C
解:第二次剪去全长的 ,比全长的一半还多;
不管绳子长多少米,第一次剪去的长度都小于绳子长的一半;
所以剪下的这两段绳子第二段长 。
故答案为:C。
绳子的原长看做单位1,第二次剪去的长度超过一半,第一次剪去的长度不足一半,据此可以判断,剪的第二段长。
49.C
解:分母加上14,就是分母增加了2倍,要使分数的大小不变,分子应增加2倍,3的2倍是6。
故答案为:C。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
50.D
解:两个不同质数相乘,积的因数有1、这两个质数、这两个质数的积;
据此可以看出,两个不同质数的积一定是合数。
故答案为:D。
一个数,除了1和它本身还有别的因数,这样的数叫做合数。
专题1 选择题
一、单选题
1.(2024·枣庄)在比例中,两内项的积是最小的合数,其中一个外项是0.8,另一个外项是( )
A.5 B.1.6 C.10
2.(2023·章丘)下列单位换算,正确的是( )
A.0.6平方千米=600公顷 B.45分钟=0.45小时
C.7吨50千克=7.05吨 D.80dm3= m3
3.(2024·枣庄)我们用竖式计算14×12时,用到的运算定律是( )
A.加法交换律 B.乘法结合律 C.乘法分配律
4.(2024·枣庄)在长方形、正方形、圆、扇形、等腰梯形、等边三角形中,只有1条对称轴的图形有( )个。
A.2个 B.1个 C.3个
5.(2023·罗庄)下列判断正确的选项是( )
A.2是质数中唯一的偶数 B.假分数的倒数一定是真分数
C.a (a>1)所有的因数都小于a D.所有的数分为正数和负数
6.(2023·章丘)有甲、乙两根绳子,甲绳减去 ,乙绳减去 米,两根绳子都剩下2米,比较两根绳子原来的长度,正确的是( )
A.甲比乙长 B.乙比甲长
C.两根绳子一样长 D.无法比较
7.(2023·武城)下列各图中,能表示出两个量成正比例关系的是( )
A. B.
C. D.
8.(2023·章丘)在推导圆柱的体积计算方法时,可以将圆柱转化成近似的长方体进行研究。如图,将半径为r,高为h的圆柱拼成近似的长方体后,长方体底面面积是( )
A.2πr2 B.2πr C.πr2 D.πrh
9.(2023·台儿庄)如图,C点用数对表示为( )
A.(4,4) B.(4,6) C.(3,1) D.(6,4)
10.(2023·章丘)《九章算术》中记载了一个问题:有人背米过关卡,过外关时,用全部米的纳税。过中关时,用所余米的 纳税。过内关时,用再余米的纳税,最后还剩5斗米。“这个人过中关后还剩多少斗米?”的正确列式是( )
A. B. C. D.
11.(2023·章丘)“天下大事必作于细”,工匠精神是社会文明进步的重要尺度,是中国制造前行的精神源泉。某精密零件的长是2.5毫米,为保证零件的精准,把它画在比例尺( )的图纸上,长应画5厘米。
A.1:20 B.20:1 C.1:200 D.200:1
12.(2023·章丘)小学阶段学的很多数学知识之间有着密切联系。下面不能正确表示它们之间关系的是( )
A. B.
C. D.
13.(2023·章丘)抛两颗骰子,出现点数和为8的可能性比和为7的可能性( )
A.大 B.小 C.相同 D.无法比较
14.(2023·章丘)圆周率是圆的周长与直径的比值,人类对圆周率的研究历史悠久。我国古代数学著作《周髀算经》中就有“周三径一”的记载,东晋时期数学家刘徽用“割圆术”求得圆周率的近似值是3.14,到了南北朝时期数学家祖冲之求得了圆周率的7位小数精确值。如果如图中线段AF表示一个圆的周长,那么这个圆的直径可能是( )
A.AB B.AC C.AD D.CE
15.(2023·章丘)反映儿童牛奶中各营养成分的含量选用( )统计图更好一些。
儿童牛奶营养成分表
名称 水分 蛋白质 脂肪 乳糖 矿物质 其他
百分比 87% 3.3% 3.5% 5% 0.75% 0.45%
A.扇形 B.条形 C.折线 D.都可以
16.(2023·章丘)用一块长25.12cm,宽18.84cm的长方形铁片和两块半径是( )cm的圆形铁片正好可以做一个圆柱形容器。
A.2 B.3 C.6 D.8
17.(2023·章丘)如图,折成一个正方体后,与“建”字相对的字是( )
A.构 B.谐 C.社 D.会
18.(2023·武城)下面说法中正确的有( )个。
①长方形、正方形和平行四边形的面积都可以理解成“底×高”计算。
②钟面上,从12走到3,分针绕中心点旋转了90°。
③商品打“七五折”出售就是降价75%出售。
④甲、乙两人分一箱苹果,若按照1:2或2:4分配,两种分法乙得到的苹果一样多。
A.1 B.2 C.3
19.(2023·章丘)大于 小于 的分数有( )个;大于0.3小于0.4的二位小数有( )个。
A.无数;无数 B.无数;9个 C.1;9 D.0;无数
20.(2023·武城)有两根绳子,如果第一根用去全长的,第二根用去全长的,两根绳子剩下的长度相等,( )绳子较长。
A.第二根 B.第一根 C.无法判断
21.(2023·武城)如图中,一个小正方体的体积是1立方厘米,长宽高不变,要把如图的图形补成一个完整的立方体,补上的那部分的体积是( )立方厘米。
A.14 B.34 C.48
22.(2023·台儿庄)欢欢从甲地走向乙地,前20分钟走了全程的30%,接下来的20分钟走了剩下路程的50%,前20分钟的速度比接下来的20分钟的速度( )
A.慢 B.快 C.一样 D.无法比较
23.(2023·台儿庄)下面说法错误的是( )
A.3与4、6、8能组成比例
B.2010年是平年
C.所有的比例尺的前项都是1
D.抛一次硬币,落地后可能正面朝上
24.(2023·台儿庄)糖与水的比是1:4,糖占糖水的( )
A.25% B.20% C.40% D.80%
25.(2023·台儿庄)x=6是下面方程( )的解
A.24÷x=6 B.5x=35 C.4x+5=29 D.4x÷8=6
26.(2023·武城)六(3)班的老师组织学生去距学校5千米的科技馆参观,从学校出发,乘车0.5小时后到达,在科技馆参观1小时后,出馆休息0.5小时,然后乘车0.5小时返回学校。下面( )图正确描述了同学们的行程过程。
A.
B.
C.
27.(2023·武城)将标有1、2、3、4、5的五张形状相同的数字卡片放在一个口袋里,每次任意摸出一张,摸后放回,下列哪种说法是正确的?( )
A.摸到合数的可能性是40%。
B.摸到“3”的可能性是20%。
C.摸到质数的可能性是80%。
28.(2023·武城)观察如图,根据左面方格中数字排列的规律,右面方格空白处填( )
A.3 B.4 C.5
29.(2023·武城)历亭路小学统计了六年级学生最喜欢的课外活动人数,为了直观地看出各类活动人数的多少,要将各项数据制作成统计图,用( )最合适。
A.条形统计图 B.折线统计图 C.扇形统计图
30.(2023·武城)2023年春节,小军共收到长辈的祝福压岁钱5000元,根据他的理财计划,他打算用这笔资金在他上高中时买学习资料,他把钱存入银行,定期3年,年利率为3.25%,求到期后小军可从银行取出多少元,正确列式为( )
A.5000×3×3.25%
B.5000+5000×3.25%
C.5000×3×3.25%+5000
31.(2023·武城)我国古代名著《墨经》中有这样的记载:“圆,一中同长也。”这句话中的“一中”指( )
A.圆有无数条半径
B.圆有一个圆心
C.同一个圆中半径相等
32.(2023·五莲)用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
33.(2023·五莲)10以内的质数有( )个。
A.5 B.3 C.4 D.6
34.(2023·五莲)下列选项中能用2a+4表示的是( )
A.长方形的面积 B.长方形的周长
C.线段的总长度 D.长方形的周长
35.(2023·五莲)一张圆形纸片至少要对折( )次,才能找到它的圆心。
A.1 B.2 C.3 D.4
36.(2023·五莲)两个小朋友在玩摸球的游戏,袋子里有32个白球、8个红球、10个篮球任意摸出一个球,摸出( )球的可能性大
A.白 B.红 C.蓝 D.无法确定
37.(2023·齐河)一个圆柱型无盖水桶,底面积是8平方分米,高5分米,在水桶的侧面上有一个洞,洞的位置距离下底2分米,如图,这个水桶现在最多可以盛( )升水。(桶壁厚度忽略不计)
A.40 B.16 C.24 D.28
38.(2023·齐河)一个圆柱形蛋糕盒(如图),量得底面周长是0.8米,高是0.2米,侧面接头处重合1厘米(即0.01米),把侧面从接头处展开后是一个长方形。它的侧面共用了多少平方米的纸板?下面答案正确的是( )
A.0.16 B.0.18 C.0.36 D.0.162
39.(2023·齐河)下面( )图,和正好拼成一个棱长为2的大正方体。(每个小正方体的棱长为1)
A. B. C. D.
40.(2023·齐河)下面各题中的两个量成正比例的是( )
A.单价一定,数量和总价
B.路程一定,行驶的速度和行驶的时间
C.圆的面积与它的半径
D.从甲地到乙地,已经走的路程和剩下的路程
41.(2023·齐河)在一幅比例尺是1:500000的地图上,量得A、B两地的距离是6.8厘米,如果把甲、乙两地画在比例尺为1:250000的新地图上,则甲、乙两地在新地图上的距离是多少厘米?( )
A.34 B.13.6 C.3.4 D.1.36
42.(2023·齐河)等底等高的圆柱和圆锥的体积相差18.6立方厘米,则圆柱的体积是( )立方厘米。
A.9.3 B.18.6 C.27.9 D.37.2
43.(2023·齐河)用三根同样长的铁丝分别围成平行四边形、正方形、长方形三个不同的图形,三个图形的面积相比,( )
A.平行四边形面积最大 B.正方形面积最大
C.长方形面积最大 D.三个图形的面积相等
44.(2023·齐河)南极大陆记录的最低温度是﹣89.6℃,北极最低温度记录大约是﹣70℃左右,我国最北方漠河的最低温度记录是﹣53℃,珠穆朗玛峰峰顶的最低气温记录是零下60℃左右。这四个地方记录的最低温度相比,最低的是( )
A.南极大陆 B.北极
C.漠河 D.珠穆朗玛峰峰顶
45.(2023·齐河)李倩和张萌的家相距a米。星期天,李倩骑自行车去张萌家做客,她每分钟骑行b米。t分钟后,还未到张萌家,离张萌家还有多少米?( )
A.(a﹣b)t B.a﹣bt C.b﹣at D.at﹣bt
46.(2023·齐河)下面的分数不能用百分数表示的是( )
A.小芳用半小时做了全部作业的
B.妹妹喝了一杯牛奶的
C.合唱队的人数比军乐队的人数多
D.一张纸的长比宽多分米
47.(2023·德州)一件稿件,甲 小时打完。乙 小时打完,甲、乙的工作效率比是( )
A. : B.3:2 C. : D.2:3
48.(2023·德州)一根绳子第一次剪去 米,第二次剪去全长的 ,剪下的这两段绳子( )
A.一样长 B.第一段长 C.第二段长 D.无法确定
49.(2023·德州) 的分母加上14,要使分数的大小不变,分子应( )
A.加上14 B.扩大到原来的2倍 C.加上6
50.(2023·德州)两个不同质数的积一定是( )
A.奇数 B.偶数 C.质数 D.合数
答案解析部分
1.A
解:4÷0.8=5
故答案为:A。
分析题干,两内项的积是最小的合数,故得到内项积=4,又已知一个外项是0.8,根据比例的基本性质:内项积等于外项积,得到另一个外项=内项积÷一个外项,代入数据计算即可。
2.C
解:选项A中,0.6×100=60,所以0.6平方千米=60公顷,单位换算错误;
选项B中,45÷60=0.75,所以45分钟=0.75小时,单位换算错误;
选项C中,7+50÷1000=7.05,所以7吨50千克=7.05吨,单位换算正确;
选项D中,80÷1000=,所以80dm3=m3,单位换算错误;
故答案为:C。
根据1平方千米=100公顷、1小时=60分钟、1吨=1000千克、1立方米=1000立方分米进行单位换算,选择正确的即可。
3.C
解:
故答案为:C。
用竖式计算14×12时,首先计算的是14×2,然后计算的是14×10,最后将两部分相加得到结果。
4.A
解:长方形有2条对称轴
正方形有4条对称轴
圆有无数条对称轴
扇形有1条对称轴
等腰梯形有1条对称轴
等边三角形有3条对称轴
故答案为:A。
对称轴是指使几何图形成轴对称或旋转对称的直线,据此判断即可。
5.A
解:A选项,2是质数中唯一的偶数,原选项说法正确;
B选项,假分数的倒数不一定是真分数,原选项说法错误;
C选项,a(a>1)所有的因数小于等于a,原选项说法错误;
D选项,所有的数分为正数、负数和0,原选项说法错误。
故答案为:A。
一个数,如果只有1和它本身两个因数,这样的数叫做质数。
一个整数的倒数就是这个整数分之一。假分数的倒数也可能是假分数,如是假分数,它的倒数是1;
一个数可以表示成两个自然数的乘积,那么这两个自然数都是它的因数。一个数最大的因数是它本身;
0既不是负数也不是正数。
6.A
解:甲绳:2÷(1-)
=2÷
=(米)
乙绳:2+=(米)
因为>,所以甲绳原来的长度比乙绳原来的长度长。
故答案为:A。
甲绳减去,是把甲绳原来长度看作单位“1”,那么甲绳剩下的长度就是原来长度的1-,用剩下的长度除以1-就可以求出甲绳原来的长度;乙绳减去米,剩下2米,那么将剪去的长度与剩下的长度相加就可以求出乙绳原来的长度;最后将两根绳子原来的长度进行比较即可。
7.C
解:正比例图像是从(0,0)出发的无限延伸的射线;
故答案为:C。
正比例图像是从(0,0)出发的无限延伸的射线,这条线上所有对应的两个量的比值都相等,据此判断。
8.C
解:长方体底面长:2πr÷2=πr;
长方体地面面积:πr×r=πr2;
所以长方体地面面积是πr2。
故答案为:C。
由图可知,长方体底面的长是圆柱底面周长的一半,长方体底面的宽是圆柱底面半径,代入到长方形面积=长×宽即可解答。
9.D
解:C点在第6列,第4行,所以C点用数对表示是(6,4);
故答案为:D。
数对中,第一个数表示列,第二个数表示行;据此解答。
10.D
解:余下米的是5斗米,余下的米为:5÷(1-)
故答案为:D。
由题意可知,最后剩的5斗米是过中关后剩的米的1-,也就是把过中关后剩的米看作单位“1”,按照对应量÷对应率=单位“1”进行列式即可。
11.D
解:5厘米=50毫米
50:2.5=200:1
所以该图纸的比例尺是200:1。
故答案为:D。
首先进行统一单位,再根据比例尺=图上距离:实际距离代入数值进行计算即可。
12.A
解:选项A中,长方形属于特殊的平行四边形,但是梯形不属于平行四边形,所以该选项表示错误;
选项B中,三角形按照角可以划分为锐角三角形、直角三角形、钝角三角形,所以该选项表示正确;
选项C中,方程也是等式的一种,所以该选项表示正确;
选项D中,一个数的最大因数是它本身,最小倍数也是它本身,所以a既是a的因数也是a的倍数,该选项表示正确;
故答案为:A。
根据四边形的分类、三角形的分类、等式以及因数与倍数的关系进行解答。
13.B
解:和为8的情况:2和6、3和5、4和4、5和3、6和2共5种情况;
和为7的情况:1和6、2和5、3和4、4和3、5和2、6和1共6种情况;
因为6>5,所以出现点数和为8的可能性比和为7的可能性小。
故答案为:B。
已知骰子上的数字为1~6,分别列举出和为8与和为7时的所以情况进行解答。
14.B
解:直径大约是圆周长的,所以线段AF表示一个圆的周长时,圆的直径可能是AC。
故答案为:B。
圆周长=直径×π,即圆的周长是直径的π倍,由于π的近似值是3.14,所以当AF表示一个圆的周长时,直径的长度大约是AF的,由此解答。
15.A
解:选项A中,扇形统计图可以反应部分与整体之间的关系;
选项B中,条形统计图能够使人一眼看出各个数据的大小;
选项C中,折线统计图不仅可以表示数量的多少,还可以显示数据的变化趋势;
因为统计表中的数据是牛奶中各营养成分占牛奶总量的百分比,也就是需要用统计图反应部分与整体之间的关系,所以用扇形统计图合适。
故答案为:A。
由统计表可知,需要用统计图反应牛奶中各营养成分与牛奶总量之间的关系,由此解答。
16.B
解:长为底面周长:25.12÷3.14÷2=4(cm);
宽为底面周长:18.84÷3.14÷2=3(cm)
所以该长方形铁片和半径为3cm或者4cm的圆形铁片都可以做一个圆柱形容器。
故答案为:B。
根据圆周长=半径×2×π,得到半径=圆周长÷2÷π。有两种方法做成圆柱容器,第一种,以长方形的长做圆柱的底面周长;第二种,以长方形的宽做圆柱的底面周长;分别代入数值进行计算即可。
17.C
解:以“和”字为正方体底面折成正方体如图:
由图可知,与“和”字相对的是“会”字;与“建”字相对的是“社”字;与“构”字相对的是“谐”字。
故答案为:C。
该展开图属于正方体展开图的“1-4-1”型,以“和”字为正方体底面折成正方体,则“构”字在正方体的背面,“建”字在正方体的左面,“谐”字在正方体的前面,“社”字在正方体的右面,“会”字在正方体的上面,由此解答。
18.C
解:①长方形、正方形都是特殊的平行四边形,所以求它们的面积都可以理解成“底×高”计算,说法正确;
②钟面上一大格表示30°,从12到3走了3大格,即转了30°×3=90°,说法正确;
③商品打“七五折”出售就是按原价的75%出售,说法错误;
④1:2=(1×2):(2×2)=2:4,因此,两种分法乙得到的苹果一样多说法正确;
故答案为:C。
①长方形、正方形都是特殊的平行四边形;②钟面上每个大格对应30°;③打几折就是按原价的百分之几十出售;④比的基本性质:比的前项和后项同时乘或除以同一个数(不为0),比值不变;据此解答。
19.B
解:====;====;
大于小于的分数是,大于小于的分数是、,所以大于小于的分数有无数个。
大于0.3小于0.4的两位小数有:0.31、0.32、0.33、0.34、0.35、0.36、0.37、0.38、0.39一共9个。
故答案为:B。
本题将和化为同分母分数,就可以找到这两个分数之间的分数;用列举法写出0.3到0.4之间的两位小数,即在0.3后面的百分位上添数;由此解答。
20.A
解:第一根剩下原来的1-=,第二根剩下原来的1-=;<,所以第二根绳子较长。
故答案为:A。
求一个数的几分之几,用乘法计算;两根绳子剩下的长度相等,即第一根长度×(1-)=第二根长度×(1-),比较剩下的分率,剩下的分率越小,表示原来的绳子越长,据此解答。
21.B
解:完整立方体体积:4×4×3=48(立方厘米);
现有体积:1+3+10=14(立方厘米);
补上部分体积:48-14=34(立方厘米);
故答案为:B。
该图形补成的完整的立方体的长和宽都是由4个小正方体组成,高是由3个小立方体组成,计算出完整的立方体的体积后再减去现有的立方体体积即可解答;长方体体积=长×宽×高,现有的小立方体上层有1个小正方体,中间层有3个小正方体,下层有10个小正方体,将三层小正方体个数相加就是现有图形体积;据此解答。
22.A
前20分钟:30%;
接下来20分钟:(1-30%)×50%
=70%×50%
=35%;
20%<35%,所以前20分钟的速度比接下来20分钟的速度慢。
故答案为:A。
时间相同,比较两次所走的路程即可,路程越长,速度越快;把全程看作单位“1”,前2分钟走了全程30%;接下来的20分钟走了全程的(1-30%)×50%;据此解答。
23.C
解:选项A:3÷4=,6÷8=,所以3:4=6:8,该说法正确;
选项B:2010÷4=502……2,所以2010年是平年,该说法正确;
选项C:图上距离较大,实际距离较小时,比例尺写成后项是1的形式,该说法错误;
选项D:抛一次硬币,落地后可能正面朝上也可能反面朝上,该说法正确;
故答案为:C。
能组成比例的两组比的比值相等;非整百年份能被4整除就是闰年,不能被4整除就是平年;比例尺=图上距离:实际距离,当图上距离较大,实际距离较小时,比例尺写成后项是1的形式;抛一枚硬币只有正面朝上或反面朝上两种情况;据此解答。
24.B
解:1÷(1+4)
=1÷5
=20%;
故答案为:B。
糖与水的比是1:4,把糖看作1份,那么水就是这样的4份;含糖率=糖的份数÷糖水的份数,据此解答。
25.C
解:选项A:24÷x=6
24÷x×x=6×x
24=6x
6x÷6=24÷6
x=4;
选项B:5x=35
5x÷5=35÷5
x=7;
选项C:4x+5=29
4x+5-5=29-5
4x=24
4x÷4=24÷4
x=6;
选项D:4x÷8=6
4x÷8×8=6×8
4x=48
4x÷4=48÷4
x=12;
故答案为:C。
等式的基本性质1:等式两边同时加减同一个数,等式仍成立;等式的基本性质2:等式两边同时乘或除以同一个数(不为0),等式仍成立;根据等式的基本性质求出各个选项的解即可。
26.B
解:能正确描述同学们的行程过程;
故答案为:B。
由题意可知,0~0.5小时之间路程随时间增加而增加,0.5小时时路程是5千米,0.5~2小时之间路程不变,2~2.5小时之间路程随时间增加而减少,在2.5小时时路程是0千米;据此解答。
27.B
解:选项A:摸到合数的可能性是1÷5=20%,说法错误;
选项B:摸到“3”的可能性是1÷5=20%,说法正确;
选项C:摸到质数的可能性是3÷5=60%,说法错误;
故答案为:B。
1、2、3、4、5中合数有4,质数有2、3、5;摸到合数的可能性=合数张数÷总张数,摸到“3”的可能性=1÷总张数,摸到质数的可能性=质数张数÷总张数;据此解答。
28.A
解:右面方格空白处与2相加得到5,所以空白处的数是5-2=3;
故答案为:A。
从左面方格可以发现规律:第一行是后两个数相乘是前一个数,第二行和第三行都是后两个数相加得到前一个数,第一列是后两个数相乘是前一个数,第二列和第三列都是后两个数相加得到前一个数,据此解答。
29.A
解:为了直观地看出各类活动人数的多少,用条形统计图合适;
故答案为:A。
条形统计图:能清楚地看出数量的多少;折线统计图:不仅能看出数量的多少,还能反应数量的增减变化;扇形统计图:表示部分与整体之间的关系;据此选择合适的统计图。
30.C
解:利息:5000×3×3.25%;
到期后取回的钱:5000×3×3.25%+5000;
故答案为:C。
利息=本金×利率×存期,求出利息再加上本金,就是到期后取回的钱;据此解答。
31.C
解:“圆,一中同长也。”这句话中的“一中”指同一个圆中半径相等;
故答案为:C。
根据圆的特征:连接圆心到圆上任意一点的距离,叫做半径,在同圆中,所有的半径都相等,据此解答。
32.D
解:第n个图形需要小木棒的数量:6+3×(n-1)
6+3×(8-1)
=6+3×7
=6+21
=27(根)
故答案为:D。
第1个图形需要6根小木棒,第2个图形需要6+3根小木棒,第3个图形需要6+3×2根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要6+3×(n-1)根小木棒,最后将n=8代入即可。
33.C
解:10以内的质数有2,3,5,7
故答案为:C。
一个非零自然数,如果只有1和它本身两个因数,那么这样的数叫作质数;一个非零自然数,如果除了1和它本身还有别的因数,那么这样的数叫作合数,1既不是质数也不是合数,据此解答。
34.B
解:A:S=(4+2)a=6a
B:C=(2+a)×2=2a+4
C:L=2+a+4=6+a
D:C=(a+4)×2=2a+8
故答案为:B。
长方形周长等于长与宽和的2倍,面积等于长×宽,据此列式整理再与题干比较。
35.B
一张圆形纸片至少要对折2次,才能找到它的圆心
故答案为:B。
两条线相交确定一个点,据此解答即可。
36.A
解:32个>10个>8个
故答案为:A。
在一个袋子里面一共有三种颜色的球,由于白球的数量最多,红球的数量最少,所以同种颜色多的球摸到的可能性大,同种颜色少的球摸到的可能性小。
37.D
解:8×2+8×(5-2)÷2
=16+12
=28(立方分米)
故答案为:D。
由图可知,最多可以盛水的体积=底面积是8平方分米、高是2分米的圆柱体积+底面积是8平方分米、高是(5-2)分米的圆柱体积的一半;圆柱体积=底面积×高;据此解答。
38.D
解:(0.8+0.01)×0.2
=0.81×0.2
=0.162(平方米)
故答案为:D。
侧面展开的长方形的长等于圆柱的底面周长+0.01米,宽等于圆柱的高,再根据长方形面积=长×宽代入数值解答。
39.A
解:根据图形的拼组可知,和正好拼成一个棱长为2的大正方体。
故答案为:A。
要想拼成一个大正方体,还需要4个小正方体,据此解答。
40.A
解:选项A:=单价(一定),比值一定,总价和数量成正比例关系;
选项B:行驶的速度×行驶的时间=路程(一定),乘积一定,行驶的速度和行驶的时间成反比例;
选项C:=半径×π,比值不是一定值,所以圆面积和它的半径不成比例;
选项D:已走的路程+剩下的路程=全部路程,所以已经走的路程和剩下的路程不成比例。
故答案为:A。
两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,那么这两种量成正比例;据此解答。
41.B
解:6.8÷=3400000(厘米);
3400000×=13.6(厘米)。
故答案为:B。
用比例尺是1:500000的图上距离除以该比例尺求出A、B两地的实际距离;再用实际距离乘新地图上的比例尺即可求出新地图上的图上距离。
42.C
解:18.6÷(1-)
=18.6÷
=27.9(立方厘米)
故答案为:C。
圆锥的体积是与它等底等高的圆柱体积的,即等底等高的圆锥比圆柱的体积少(1-);已知一个数的几分之几是多少,求这个数,用除法计算。
43.B
解:平行四边形面积=底×高,长方形面积=长×宽,假设平行四边形的底边与长方形的长相等,那么平行四边形的高一定比小于长方形的宽,因此,平行四边形的面积一定小于长方形的面积;
假设长方形的长+宽=正方形的边长+边长=8,长方形的长是5,宽是3,面积就是5×3=15;正方形的边长就是4,面积是4×4=16;所以长方形面积小于正方形面积。综上所述,正方形面积最大。
故答案为:B。
周长一定,平行四边形的底边+邻边=长方形的长+宽=正方形的边长+边长;平行四边形的高一定比邻边短,平行四边形面积=底×高,长方形面积=长×宽,假设平行四边形的底边与长方形的长相等,那么平行四边形的高一定比小于长方形的宽,因此,平行四边形的面积一定小于长方形的面积;再假设长方形的长+宽=正方形的边长+边长=8,分别计算出长方形面积和正方形面积,再比较即可。
44.A
解:-53℃<-60℃<-70℃<-89.6℃,所以温度最低的是南极大陆。
故答案为:A。
这四个地方的气温都是负数,负数比较大小要看负号后面的数字,数字越大的反而越小;据此解答。
45.B
解:李倩骑行t分钟,骑行了bt米,离张萌家还有(a-bt)米。
故答案为:B。
路程=速度×时间,用总距离减去李倩骑行的路程即可解答。
46.D
解:选项A:全部作业看作单位“1”,半小时做的作业占全部作业的,也就是75%;
选项B:一杯牛奶看作单位“1”,妹妹喝了一杯牛奶的,也就是50%;
选项C:军乐队的人数看作单位“1”,合唱队的人数比军乐队的人数多,也就是多66.67%;
选项D:长比宽多分米,表示的具体的数量,不能用百分数表示。
故答案为:D。
百分数表示一个数是另一个数的百分之几,百分数没有的单位;据此解答。
47.D
解:甲、乙的工作时间比是: : =3:2 ;
甲、乙的工作效率比是2:3 。
故答案为:D。
工作量一定,工作效率的比和工作时间的比刚好相反,据此解答。
48.C
解:第二次剪去全长的 ,比全长的一半还多;
不管绳子长多少米,第一次剪去的长度都小于绳子长的一半;
所以剪下的这两段绳子第二段长 。
故答案为:C。
绳子的原长看做单位1,第二次剪去的长度超过一半,第一次剪去的长度不足一半,据此可以判断,剪的第二段长。
49.C
解:分母加上14,就是分母增加了2倍,要使分数的大小不变,分子应增加2倍,3的2倍是6。
故答案为:C。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
50.D
解:两个不同质数相乘,积的因数有1、这两个质数、这两个质数的积;
据此可以看出,两个不同质数的积一定是合数。
故答案为:D。
一个数,除了1和它本身还有别的因数,这样的数叫做合数。
同课章节目录
