2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题4 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题4 填空题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 243.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 10:11:06 | ||
图片预览




文档简介
2024-2025学年小升初数学备考真题分类汇编(山东地区专版)
专题4 填空题
一、填空题
1.(2024·岳阳)如图,一个顶角为40°的等腰三角形纸片,剪去顶角后,得到一个四边形。则∠1+∠2= 。
2.(2024·枣庄)如图四个正方形中,阴影部分与空白部分的面积比是 。
3.(2024·枣庄)三角形内角和180°,四边形内角和是 °,试着画图分析,五边形内角和是 °,……n边形内角和是 °。
4.(2024·枣庄)从24的因数中选出四个因数,组成两个比的比值都是4的比例是 。
5.(2024·五莲模拟) 一个圆柱和一个圆锥底面积与体积分别相等,圆柱高1.2米,圆锥高是 米。
6.(2024·枣庄)把两个完全相同的正方体拼成一个长方体,拼成的长方体的表面积是100cm2,原来每个正方体的表面积是 cm2。
7.(2024·枣庄)一个圆柱形零件,高是5cm,与它等底等体积的圆锥形高是 cm。
8.(2024·枣庄)2m:300cm化成最简整数比是 ,比值是 。
9.(2024·五莲模拟)某商场搞促销活动,“买三送一”相当于打 折。
10.(2024·枣庄)0.7的计数单位是 ,它有 个这样的计数单位。
11.(2024·枣庄)=24: = %= 折= 成。
12.(2024·五莲模拟) 一个长方体的棱长和是240厘米,长、宽、高的比是3:2:1,长方体的体积是 立方厘米,合 立方分米。
13.(2023·兖州)如果甲数比乙数多20%,那么甲数与乙数最简单的整数比是 .
14.(2023·东昌府)5G技术具有更高速率、更大连接、更低时延的特性,用5G下载的时间约是4G的 。用4G下载一部电影需要5分钟,如果用5G下载只需 秒。
15.(2023·章丘)下面各图是由棱长是1厘米的正方体拼成的,根据前三个图形的排列规律,第五个图形的表面积是 平方厘米,第n个图形的表面积是 平方厘米。
16.(2023·章丘)2 的计数单位是 ,再添加 个这样的计数单位就是12和15的最大公因数。
17.(2023·章丘)一箱苹果有50多个,如果把这箱苹果每6个装一盒,还剩余4个,如果每8个装一盒,也剩余4个,这箱苹果共 个。
18.(2023·章丘)在方格纸上画一个平行四边形,其中三个顶点的位置分别是(3,4)(8,4)(4,6)那么第四个顶点的位置是 。
19.(2023·章丘)某校共2650名学生,这些学生中至少 人是在同一天过生日。
20.(2023·章丘)一个四位数6□7□能同时被2、3、5整除,这个四位数最大是 。
21.(2023·章丘)已知 (a、b均不为0),则a:b= ,a与b成 比例关系。
22.(2023·章丘)请你从30的因数中选择两个质数和两个合数组成一个比例: 。
23.(2023·台儿庄)420克大豆榨油52克,大豆与油的质量比是 ,比值是 。
24.(2023·台儿庄)一个数,亿位上的数字是4,千万位上的数字是9,百万位和百位上的数字都是7,其余各位上的数字是0,这个数写作 ,省略“亿位”后面的尾数约是 。
25.(2023·台儿庄)在﹣6,﹣,9.3,0,﹣5.4,60中,正数有 ,负数有 。
26.(2023·台儿庄)16世纪末法国数学家韦达是第一个系统使用字母表示数的人,被称为“代数之父”。请解决问题:端午节,小红包8个粽子用了a克糯米,平均每个粽子用糯米 克;当a=400时,平均每个粽子用糯米 克。
27.(2023·台儿庄)长方形有 条对称轴;一个长方形的长是8厘米,宽是6厘米,面积是 平方厘米。
28.(2023·台儿庄)0.69里有 个0.01; 个是。
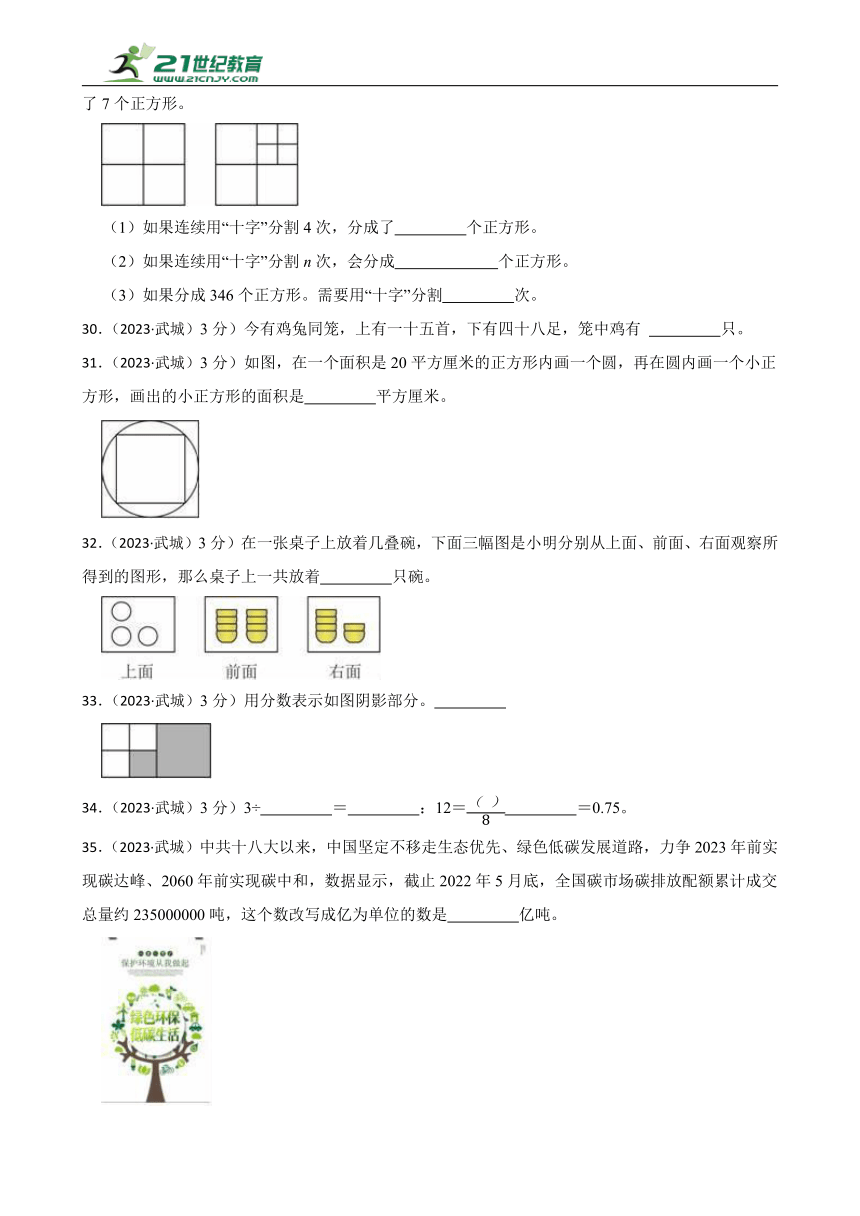
29.(2023·武城)如图所示,用“十字”分割正方形。分割一次,分成了4个正方形,分割两次,分成了7个正方形。
(1)如果连续用“十字”分割4次,分成了 个正方形。
(2)如果连续用“十字”分割n次,会分成 个正方形。
(3)如果分成346个正方形。需要用“十字”分割 次。
30.(2023·武城)3分)今有鸡兔同笼,上有一十五首,下有四十八足,笼中鸡有 只。
31.(2023·武城)3分)如图,在一个面积是20平方厘米的正方形内画一个圆,再在圆内画一个小正方形,画出的小正方形的面积是 平方厘米。
32.(2023·武城)3分)在一张桌子上放着几叠碗,下面三幅图是小明分别从上面、前面、右面观察所得到的图形,那么桌子上一共放着 只碗。
33.(2023·武城)3分)用分数表示如图阴影部分。
34.(2023·武城)3分)3÷ = :12= =0.75。
35.(2023·武城)中共十八大以来,中国坚定不移走生态优先、绿色低碳发展道路,力争2023年前实现碳达峰、2060年前实现碳中和,数据显示,截止2022年5月底,全国碳市场碳排放配额累计成交总量约235000000吨,这个数改写成亿为单位的数是 亿吨。
36.(2023·五莲)如图所示,把底面半径为4分米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加40平方分米,这个圆柱的高是 分米,圆柱的体积是 立方分米。
37.(2023·五莲)用一张长15厘米、宽10厘米的长方形纸片围成一个圆柱,那么这个圆柱的侧面积是 。
38.(2023·五莲)有一个半径为20m的半圆形菜园,要在菜园的周围围上栅栏,需要 米长的栅栏。
39.(2023·五莲)一张零件图纸的比例尺为20:1,在图纸上量得某一零件的长度为40厘米,这个零件的实际长度为 厘米。
40.(2023·五莲)在没有余数的除法里,除数一定,被除数和商成 比例。
41.(2023·五莲)2023年5月30日,景海鹏、朱杨柱、桂海潮3名航天员乘坐“神舟十六号”载人飞船于9时31分发射升空,当日18时22分航天员入驻“天宫”,整个过程历行 小时 分。
42.(2023·五莲)小红参加数学竞赛,共10道题,做对一道得10分,做错一道扣2分,小红每一道题都做了,结果得了64分,她做对了 道题,小红做题的正确率是 %。
43.(2023·五莲)两根绳子,一根长60米,一根长96米,要把这两根绳子剪成同样长的小段,每段最长 米。
44.(2023·五莲)在4.5、﹣3、0、﹣1.5、中, 是正数, 是负数, 既不是正数也不是负数。
45.(2023·五莲) =4:5=20÷ = 成= %
46.(2023·齐河)如图中的数值比例尺表示图中的1厘米是实际距离 千米,济南到威海的图上直线距离是6厘米,实际距离是 千米。“济南一德州”两地实际距离约是128千米,在地图上的距离是 厘米。
47.(2023·德州)一个长方体、一个圆柱体和一个圆锥体,它们的底面积和体积分别相等,如果长方体的高是12厘米,那么圆柱体的高是 厘米,圆锥体的高是 厘米。
48.(2023·德州)把一块长80米、宽60米的长方形菜地画在比例尺是1:2000的图纸上,图上面积是 .
49.(2023·德州)比80多20%的数是 ;80比 少20%
答案解析部分
1.220°
∠1+∠2=360°-(180°-40°)=360°-140°=220°。
故答案为:220°。
∠1+∠2=两个平角-(三角形内角和-顶角)。
2.3:5
解:(2+1):(2×2+1)=3:5
故答案为:3:5。
观察图形,因为一个正方形可以分成两个完全一样的三角形,由此可知:阴影部分可以看作三个三角形,空白部分可以看作五个三角形,根据比的意义解答即可。
3.360;540;(n﹣2)×180
解:四边形的内角和(正方形)=2×180°=360°
五边形的内角和=3×180°=540°
n边形的内角和=(n-2)×180°
故答案为:360,540,(n-2)×180。
已知三角形内角和是180°,根据正方形的特征及性质,正方形的内角和就是两个三角形的内角和,所以四边形的内角和就是2×180°=360°;五边形的内角和就是三个三角形的内角和,所以四边形的内角和就是3×180°=540°;n边形的内角和就是(n-2)个三角形的内角和,所以四边形的内角和就是(n-2)×180°。
4.4:1=8:2
解:24的因数有1,2,3,4,6,8,12,24
4÷1=48÷2=4
故比例是4:1=8:2
故答案为:4:1=8:2。
因数 ,也称约数、因子、除子,用于描述整数之间存在的整除关系。具体来说,如果整数n可以被另一个非零整数m整除,且商为整数,那么我们称m是n的一个因数。首先找出24的所有因数,然后根据除法计算并找到两个比值都是4的比组成比例即可。
5.3.6
解:圆锥高度=圆柱高度×3
=1.2×3
=3.6(米);
故答案为:3.6。
等底面积等高的圆柱的体积是圆锥的3倍,当圆柱和圆锥的体积以及底面积相等时,圆锥的高应该是圆柱高的3倍,据此求解。
6.60
解:100÷10×6
=10×6
=60(cm2)
故答案为:60。
两个完全相同的正方体拼成一个长方体,减少了两个面的面积,原来两个正方体一共是12个面,拼成长方体后为12-10=2(个)面,每个面的面积为100÷10=10(cm2),再乘以一个正方体的6个面,即可求出正方体的表面积。
7.15
解:5×3=15(cm)
故答案为:15。
已知“圆柱体积=底面积×高”“圆锥体积=底面积×高÷3”,故可得到等底等体积的圆锥的高是圆柱高的3倍,据此解答即可。
8.2:3;
解:2m:300cm
=200cm:300cm
=2:3
=
故答案为:2:3,。
根据“1m=100cm”得到原比=200cm:300cm,根据比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,将前项和后项同时除以100,得到最简整数比为2:3,再通过除法计算出比值即可。
9.七五
解:设每件价格为1元,
3÷4=0.75=75%=七五折;
故答案为:七五。
设每件价格为1元,即买四件商品只需要支付三件商品的金额,现价÷原价即可求出折扣。
10.0.1;7
解:0.7÷0.1=7
故答案为:0.1,7。
小数计数单位即分位上的最小量,故0.7的计数单位为0.1,欲求有几个这样的计数单位,用0.7除以0.1计算即可。
11.30;80;八;八
解:24÷=30
=80%=八折=八成
故答案为:30,80,八,八。
比的后项=前项÷比值,故得到第一个空为24÷=30;等于4除以5,得到商为0.8,将小数点向右移动两位,加上百分号得到80%即为第二空;80%即八折,同样也是八成。
12.6000;6
解:240 ÷ 4 = 60(厘米),
3+2+1=6,
长=60×=30(厘米),
宽=60×=20(厘米),
高=60×=10(厘米),
30 × 20 × 10= 6000(立方厘米)=6(立方分米);
故答案为:6000;6。
首先用棱长总和除以4得到一组长宽高的总和,然后根据比例关系,将总和分配到长、宽、高上,长方体体积 = 长 × 宽 × 高,将得到的长、宽、高值代入体积公式中,1立方分米=1000立方厘米,据此求解。
13.6:5
解:(1+20%):1
=1.2:1
=(1.2×10):(1×10)
=12:10
=(12÷2):(10÷2)
=6:5
故答案为:6:5。
把乙数看作单位“1”,甲数=1+20%,然后写出甲和乙的比,再运用比的基本性质化简比。
14.3
解:5分钟=300秒,300×=3(秒)。
故答案为:3。
把5分钟换算成300秒,根据分数乘法的意义用4G下载的时间乘即可求出用5G下载需要的时间。
15.22;(4n+2)
解:1×1=1(平方厘米)
图1:1×6=6(平方厘米)
图2:2×6-(2-1)×2=10(平方厘米)
图3:3×6-(3-1)×2=14(平方厘米)
图5:5×6-(5-1)×2=22(平方厘米)
图n:n×6-(n-1)×2=4n+2(平方厘米)
所以第五个图形的表面积是22平方厘米,第n个图形的表面积是(4n+2)平方厘米。
故答案为:22;4n+2。
由图可知,每个图形的表面积由小正方形面积组成,每个小正方形的面积是1平方厘米。图1表面积是由6个小正方形组成,图2表面积是由2×6-(2-1)×2个小正方形组成,图3表面积是由3×6-(3-1)×2个小正方形组成……所以第五个图形表面积是由5×6-(5-1)×2个小正方形组成,第n个图形表面积是由n×6-(n-1)×2个小正方形组成,代入解答即可。
16.;4
解:的分母是9,所以它的计数单位是;
分解质因数:12=2×2×3,15=3×5,所以12和15的最大公因数是3。
3-=-=
所以再添加4个这样的计数单位就是12和15的最大公因数。
故答案为:;4。
第一问:这个分数的分母是几,计数单位就是几分之一;第二问:用分解质因数法找到12和15的最小公因数,再减去这个分数,得到的分数,分子是几,就是几个计数单位。
17.52
解:分解质因数6=2×3,8=2×2×2,所以6和8的最小公倍数是2×2×2×3=24
因为24×2+4=52,24×3+4=76,所以这箱苹果共52个
故答案为:52。
每6个装一盒和每8个装一盒都剩余4个,也就是这箱苹果拿出4个后是6和8的公倍数。首先用分解质因数方法求出6和8的最小公倍数,再找到最小公倍数的倍数加上4在50到60之间的数即可解答。
18.(9,6)
解:8-3=5,4+5=9,所以第四个顶点的位置是 (9,6) 。
故答案为: (9,6) 。
首先根据数对画出三个顶点的位置如图:
顶点(3,4)和顶点(8,4)在同一行,那么这两个顶点间的距离就是8-3=5,因为平行四边形对边平行且相等,所以第四个顶点和顶点(4,6)也在同一行,且距离也是5,由此解答。
19.8
解:2650÷365=7(人)95(人),7+1=8(人)
2650÷366=7(人)88(人),7+1=8(人)
所以这些学生中至少8人是在同一天过生日。
故答案为:8。
需要分情况讨论,当是平年的时候,一年有365天,那么用总人数除以365得到的商就是同一天过生日的人数,余下的人无论在哪天过生日,这一天当中都至少有商+1人在同一天过生日。同样的,当是闰年的时候,一年有366天,计算方法同理。
20.6870
解:因为能被2和5同时整除,所以这个四位数是6□70;
6+7+0=13,要想这个四位数能被3整除,所以百位上可以是2、5、8;
百位上是8时,这个四位数最大,最大是6870。
故答案为:6870。
能被2和5同时整除的数特点是:个位上是0;能被3整除的数的特点是:各个数位上的数字相加的和能被3整除;由此解答。
21.3:4;正
解:因为3a=b,所以a:b=:3=3:4;
a:b=3:4=,比值一定,所以a与b成正比例关系。
故答案为:3:4;正。
两种相关联的量,一种量变化,另一种量也随之变化,如果表示这两种量的数值的比值一定,则这两种量成正比例关系。在比例中,两个外项积等于两个内项积,由此解答。
22.2:3=10:15(答案不唯一)
解:30的因数:1、2、3、5、6、10、15、30;
质数有:2、3、5;
合数有:6、10、15、30;
可组成比例: 2:3=10:15 (答案不唯一);
故答案为:2:3=10:15 (答案不唯一)。
首先列举出30的因数,再从中找到质数和合数,最后根据组成比例的两个比的比值相等进行解答(答案不唯一)。
23.105:13;
解:大豆与油的质量比是:420:52
=(420÷4):(52÷4)
=105:13;
比值是:105÷13=;
故答案为:105:13;。
大豆与油的质量比=大豆质量:油的质量,再根据比的基本性质:比的前项和后项同时乘或除以同一个数(不为0),比值不变,化简比;比值=比的前项÷比的后项。
24.497000700;5亿
解:这个数写作497000700;省略“亿”位后的尾数约是5亿;
故答案为:497000700;5亿。
哪一个数位上是几就在哪一位上写几,据此写出此数;省略“亿”位后的尾数,要看千万位上的数,千万位上的数大于等于5,就向亿位进1,亿位后的数舍去,并在末尾添一个“亿”字;千万位上的数小于5,直接舍去,并在末尾添一个“亿”字。
25.9.3,60;-6,-,-5.4
解:正数有:9.3,60;负数有:-6,-,-5.4。
故答案为:9.3,60;-6,-,-5.4。
大于0的数是正数,小于0的数是负数;据此解答。
26.(a÷8);50
解:平均每个粽子:(a÷8)克;
a=400时,平均每个粽子:400÷8=50(克);
故答案为:(a÷8);50。
平均分用除法计算,即用糯米总质量除以粽子个数即可求出平均每个粽子需要的糯米质量;据此解答。
27.2;48
解:如图:
长方形有2条对称轴;
面积是:8×6=48(平方厘米);
故答案为:2;48。
平面内,一个图形沿一条直线对折,对折后的两部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是它的对称轴;长方形面积=长×宽,据此解答。
28.69;3
解:0.69里面有69个0.01,;3个是。
故答案为:69;3。
0.69写成分数形式是,计数单位是,也就是0.01;的计数单位是,分子是几就表示有几个这样的计数单位。
29.(1)13
(2)(3n+1)
(3)115
解:(1)4+3+3+3
=7+6
=13(个);
(2)4+3(n-1)
=4+3n-4
=3n+1(个);
(3)(346-1)÷3
=345÷3
=115(次);
故答案为:(1)13;(2)(3n+1);(3)115。
(1)分割一次,分成4个正方形,分割两次,分成(4+3)个正方形,那么分割三次,分成4+3+3)个正方形,分割四次,分成了(4+3+3+3)个正方形;(2)可以发现分割分割n次可以分成[4+3(n-1)]个正方形;(3)[4+3(n-1)]=346,据此求出n即可。
30.6
(15×4-48)÷(4-2)
=(60-48)÷2
=12÷2
=6(只)
故答案为:6。
假设全是兔,则一共有(15×4)只脚,比实际多了(15×4-48)只脚,而每只兔比每只鸡多(4-2)只脚,用假设比实际多的脚数除以每只兔比每只鸡多的脚数即可求出鸡的只数;据此解答。
31.10
解:设这个圆的半径为r厘米,则大正方形的边长就是2r,
根据大正方形的面积是20平方厘米可得:2rX2r=20,整理可得:r2=5;
小正方形的面积是:2r×2r÷2=10(平方厘米)
故答案为:10。
正方形内最大的圆的直径等于这个正方形的边长,设这个圆的半径为r厘米,则正方形的边长就是2r,根据正方形的面积是20平方厘米可得:2r×2r=20,整理可得:r2=5,把它代入到圆的面积公式中即可求出这个最大圆的面积。在圆中所画最大正方形的对角线就等于圆的直径,圆的面积已知,可以求出半径平方的值,小正方形的对角线等于圆的直径,则小正方形的面积为对角线的平方的一半,也就能求出正方形的面积,据此解答即可。
32.10
解:4+4+2=10(只);
故答案为:10。
从观察到的三幅图可知,前面有2摞,每摞有4只碗,后面有1摞,这1摞有2只碗,据此解答。
33.
解:把单位“1”平均分成8份,阴影部分占其中的5份,用分数表示是;
故答案为:。
该图是把长方形面积看作单位“1”,把它平均分成8份,阴影部分占其中的5份,据此解答。
34.4;9;6
解:3÷0.75=4,所以3÷4=0.75;
12×0.75=9,所以9:12=0.75;
8×0.75=6,所以=0.75;
故答案为:4;9;6。
除数=被除数÷商;比的前项=比的后项×比值;分子=分母×分数值;据此解答。
35.2.35
解:235000000吨=2.35亿吨;
故答案为:2.35。
改写成亿为单位的数,就在亿位上数的右下角点上小数点,小数末尾的0省略,并在末尾添一个“亿”字;据此解答。
36.5;251.2
解:40÷2÷4=5(分米)
3.14×42×5
=3.14×16×5
=50.24×5
=251.2(立方分米)
故答案为:5,251.2。
由图可知,近似长方体的长相当于圆柱底面周长的一半,近似长方体的宽相当于圆柱的底面半径,近似长方体的高相当于圆柱的高,近似长方体的表面积比圆柱的表面积多两个侧面的面积,先根据增加部分面积求出圆柱的高,再利用“V圆柱=πr2h”求出这个圆柱的体积,据此解答。
37.150平方厘米
解:15×10=150(平方厘米)
故答案为:150平方厘米。
圆柱的表面积可以看做是两个圆的面积和一个长方形(或正方形)的面积,所以这个长方形围成的圆柱的侧面积就是这个长方形的面积,利用长方形的面积计算公式,长方形面积=长×宽,直接代入数据计算即可。
38.102.8
解:2×3.14×20÷2+20×2
=6.28×10+40
=62.8+40
=102.8(m)
故答案为:102.8。
半圆的周长=圆的周长的一半+一条直径的长度,先利用“C圆=2πr”表示出圆周长的一半,再加上一条直径的长度即可。
39.2
解:40÷20=2(厘米)
故答案为:2。
已知比例尺=图上距离:实际距离,则实际距离=图上距离÷比例尺,据此解答。
40.正
解:被除数÷除数=商
被除数÷商=除数
故答案为:正。
两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫作正比例关系,据此解答。
41.8;51
解:18时22分-9时31分=8小时51分
故答案为:8,51。
用结束的时刻减去开始的时刻即可;分不够减时则向时借“1”,即60分。
42.7;70
解:(10×10-64)÷(10+2)
=36÷12
=3(道)
10-3=7(道)
7÷10×100%=70%
故答案为:7,70。
分析题干,假设10道题全做对,则得10×10=100(分),这样就少得100-64=36(分),错一题比对一题少10+2=12(分),也就是做错36÷12=3(道)题,进而得出做对题的数量;再用做对题的数量除以总数量,乘以100%即可求解。
43.12
解:(60,96)=12
故答案为:12。
两根绳子,一根长60米,一根长96米,要把这两根绳子剪成同样长的小段,每段最长为60米和96米的最大公因数;60=1×60=2×30=3×20=4×15=5×12=6×10,96=1×96=2×48=3×32=4×24=6×16=8×12,进而得出60和96的最大公因数为12,故每段最长是12米。
44.4.5,;﹣3,-1.5;0
解:4.5、是正数,-3、-1.5是负数,0既不是正数也不是负数
故答案为:4.5,,-3,-1.5,0。
大于0的数为正数,小于0的数为负数,负数前有负号“-”,0既不是正数也不是负数。
45.32;25;八;80
解:4:5=0.8=八成=80%
40×0.8=32
20÷0.8=25
故答案为:32,25,八,80。
已知所有值都为4:5=0.8,分子=分母×比值;除数=被除数÷商;小数化为百分数:将小数点向右移动2位,再加上百分号即可。
46.80;480;1.6
解:图中1厘米表示实际距离:1÷=8000000(厘米)=80千米;
济南到威海实际距离:6÷=48000000(厘米)=480千米;
济南到德州图上距离:128千米=12800000厘米,12800000×=1.6(厘米);
故答案为:80;480;1.6。
实际距离与图上距离及比例尺的关系是:实际距离=图上距离÷比例尺;据此解答。
47.12;36
解:底面积和体积相等的长方体、圆柱体和圆锥体,
长方体的高=圆柱体的高=12厘米,
圆锥体的高是圆柱体高的3倍,是12×3=36(厘米)。
故答案为:12;36。
长方体体积=底面积×高、圆柱体体积=底面积×高,圆锥体体积=底面积×高÷3。
48.12平方厘米
解:80米=8000厘米,60米=6000厘米,
8000×=4(厘米),6000×=3(厘米),
图上面积是4×3=12(平方厘米)。
故答案为:12平方厘米。
图上距离=实际距离×比例尺,据此求出长方形图上的长和宽,图上的长×图上的宽=图上的面积。
49.96;100
解:80×(1+20%)=80×1.2=96;
80÷(1-20%)=80÷0.8=100。
故答案为:96;100。
求比一个数多百分之几的数是多少用乘法,列式为:这个数×(1+多的百分之几)=所求的数;已知一个数比另一个数少百分之几,求另一个数,方法是:一个数÷(1-少的百分之几)。
专题4 填空题
一、填空题
1.(2024·岳阳)如图,一个顶角为40°的等腰三角形纸片,剪去顶角后,得到一个四边形。则∠1+∠2= 。
2.(2024·枣庄)如图四个正方形中,阴影部分与空白部分的面积比是 。
3.(2024·枣庄)三角形内角和180°,四边形内角和是 °,试着画图分析,五边形内角和是 °,……n边形内角和是 °。
4.(2024·枣庄)从24的因数中选出四个因数,组成两个比的比值都是4的比例是 。
5.(2024·五莲模拟) 一个圆柱和一个圆锥底面积与体积分别相等,圆柱高1.2米,圆锥高是 米。
6.(2024·枣庄)把两个完全相同的正方体拼成一个长方体,拼成的长方体的表面积是100cm2,原来每个正方体的表面积是 cm2。
7.(2024·枣庄)一个圆柱形零件,高是5cm,与它等底等体积的圆锥形高是 cm。
8.(2024·枣庄)2m:300cm化成最简整数比是 ,比值是 。
9.(2024·五莲模拟)某商场搞促销活动,“买三送一”相当于打 折。
10.(2024·枣庄)0.7的计数单位是 ,它有 个这样的计数单位。
11.(2024·枣庄)=24: = %= 折= 成。
12.(2024·五莲模拟) 一个长方体的棱长和是240厘米,长、宽、高的比是3:2:1,长方体的体积是 立方厘米,合 立方分米。
13.(2023·兖州)如果甲数比乙数多20%,那么甲数与乙数最简单的整数比是 .
14.(2023·东昌府)5G技术具有更高速率、更大连接、更低时延的特性,用5G下载的时间约是4G的 。用4G下载一部电影需要5分钟,如果用5G下载只需 秒。
15.(2023·章丘)下面各图是由棱长是1厘米的正方体拼成的,根据前三个图形的排列规律,第五个图形的表面积是 平方厘米,第n个图形的表面积是 平方厘米。
16.(2023·章丘)2 的计数单位是 ,再添加 个这样的计数单位就是12和15的最大公因数。
17.(2023·章丘)一箱苹果有50多个,如果把这箱苹果每6个装一盒,还剩余4个,如果每8个装一盒,也剩余4个,这箱苹果共 个。
18.(2023·章丘)在方格纸上画一个平行四边形,其中三个顶点的位置分别是(3,4)(8,4)(4,6)那么第四个顶点的位置是 。
19.(2023·章丘)某校共2650名学生,这些学生中至少 人是在同一天过生日。
20.(2023·章丘)一个四位数6□7□能同时被2、3、5整除,这个四位数最大是 。
21.(2023·章丘)已知 (a、b均不为0),则a:b= ,a与b成 比例关系。
22.(2023·章丘)请你从30的因数中选择两个质数和两个合数组成一个比例: 。
23.(2023·台儿庄)420克大豆榨油52克,大豆与油的质量比是 ,比值是 。
24.(2023·台儿庄)一个数,亿位上的数字是4,千万位上的数字是9,百万位和百位上的数字都是7,其余各位上的数字是0,这个数写作 ,省略“亿位”后面的尾数约是 。
25.(2023·台儿庄)在﹣6,﹣,9.3,0,﹣5.4,60中,正数有 ,负数有 。
26.(2023·台儿庄)16世纪末法国数学家韦达是第一个系统使用字母表示数的人,被称为“代数之父”。请解决问题:端午节,小红包8个粽子用了a克糯米,平均每个粽子用糯米 克;当a=400时,平均每个粽子用糯米 克。
27.(2023·台儿庄)长方形有 条对称轴;一个长方形的长是8厘米,宽是6厘米,面积是 平方厘米。
28.(2023·台儿庄)0.69里有 个0.01; 个是。
29.(2023·武城)如图所示,用“十字”分割正方形。分割一次,分成了4个正方形,分割两次,分成了7个正方形。
(1)如果连续用“十字”分割4次,分成了 个正方形。
(2)如果连续用“十字”分割n次,会分成 个正方形。
(3)如果分成346个正方形。需要用“十字”分割 次。
30.(2023·武城)3分)今有鸡兔同笼,上有一十五首,下有四十八足,笼中鸡有 只。
31.(2023·武城)3分)如图,在一个面积是20平方厘米的正方形内画一个圆,再在圆内画一个小正方形,画出的小正方形的面积是 平方厘米。
32.(2023·武城)3分)在一张桌子上放着几叠碗,下面三幅图是小明分别从上面、前面、右面观察所得到的图形,那么桌子上一共放着 只碗。
33.(2023·武城)3分)用分数表示如图阴影部分。
34.(2023·武城)3分)3÷ = :12= =0.75。
35.(2023·武城)中共十八大以来,中国坚定不移走生态优先、绿色低碳发展道路,力争2023年前实现碳达峰、2060年前实现碳中和,数据显示,截止2022年5月底,全国碳市场碳排放配额累计成交总量约235000000吨,这个数改写成亿为单位的数是 亿吨。
36.(2023·五莲)如图所示,把底面半径为4分米的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加40平方分米,这个圆柱的高是 分米,圆柱的体积是 立方分米。
37.(2023·五莲)用一张长15厘米、宽10厘米的长方形纸片围成一个圆柱,那么这个圆柱的侧面积是 。
38.(2023·五莲)有一个半径为20m的半圆形菜园,要在菜园的周围围上栅栏,需要 米长的栅栏。
39.(2023·五莲)一张零件图纸的比例尺为20:1,在图纸上量得某一零件的长度为40厘米,这个零件的实际长度为 厘米。
40.(2023·五莲)在没有余数的除法里,除数一定,被除数和商成 比例。
41.(2023·五莲)2023年5月30日,景海鹏、朱杨柱、桂海潮3名航天员乘坐“神舟十六号”载人飞船于9时31分发射升空,当日18时22分航天员入驻“天宫”,整个过程历行 小时 分。
42.(2023·五莲)小红参加数学竞赛,共10道题,做对一道得10分,做错一道扣2分,小红每一道题都做了,结果得了64分,她做对了 道题,小红做题的正确率是 %。
43.(2023·五莲)两根绳子,一根长60米,一根长96米,要把这两根绳子剪成同样长的小段,每段最长 米。
44.(2023·五莲)在4.5、﹣3、0、﹣1.5、中, 是正数, 是负数, 既不是正数也不是负数。
45.(2023·五莲) =4:5=20÷ = 成= %
46.(2023·齐河)如图中的数值比例尺表示图中的1厘米是实际距离 千米,济南到威海的图上直线距离是6厘米,实际距离是 千米。“济南一德州”两地实际距离约是128千米,在地图上的距离是 厘米。
47.(2023·德州)一个长方体、一个圆柱体和一个圆锥体,它们的底面积和体积分别相等,如果长方体的高是12厘米,那么圆柱体的高是 厘米,圆锥体的高是 厘米。
48.(2023·德州)把一块长80米、宽60米的长方形菜地画在比例尺是1:2000的图纸上,图上面积是 .
49.(2023·德州)比80多20%的数是 ;80比 少20%
答案解析部分
1.220°
∠1+∠2=360°-(180°-40°)=360°-140°=220°。
故答案为:220°。
∠1+∠2=两个平角-(三角形内角和-顶角)。
2.3:5
解:(2+1):(2×2+1)=3:5
故答案为:3:5。
观察图形,因为一个正方形可以分成两个完全一样的三角形,由此可知:阴影部分可以看作三个三角形,空白部分可以看作五个三角形,根据比的意义解答即可。
3.360;540;(n﹣2)×180
解:四边形的内角和(正方形)=2×180°=360°
五边形的内角和=3×180°=540°
n边形的内角和=(n-2)×180°
故答案为:360,540,(n-2)×180。
已知三角形内角和是180°,根据正方形的特征及性质,正方形的内角和就是两个三角形的内角和,所以四边形的内角和就是2×180°=360°;五边形的内角和就是三个三角形的内角和,所以四边形的内角和就是3×180°=540°;n边形的内角和就是(n-2)个三角形的内角和,所以四边形的内角和就是(n-2)×180°。
4.4:1=8:2
解:24的因数有1,2,3,4,6,8,12,24
4÷1=48÷2=4
故比例是4:1=8:2
故答案为:4:1=8:2。
因数 ,也称约数、因子、除子,用于描述整数之间存在的整除关系。具体来说,如果整数n可以被另一个非零整数m整除,且商为整数,那么我们称m是n的一个因数。首先找出24的所有因数,然后根据除法计算并找到两个比值都是4的比组成比例即可。
5.3.6
解:圆锥高度=圆柱高度×3
=1.2×3
=3.6(米);
故答案为:3.6。
等底面积等高的圆柱的体积是圆锥的3倍,当圆柱和圆锥的体积以及底面积相等时,圆锥的高应该是圆柱高的3倍,据此求解。
6.60
解:100÷10×6
=10×6
=60(cm2)
故答案为:60。
两个完全相同的正方体拼成一个长方体,减少了两个面的面积,原来两个正方体一共是12个面,拼成长方体后为12-10=2(个)面,每个面的面积为100÷10=10(cm2),再乘以一个正方体的6个面,即可求出正方体的表面积。
7.15
解:5×3=15(cm)
故答案为:15。
已知“圆柱体积=底面积×高”“圆锥体积=底面积×高÷3”,故可得到等底等体积的圆锥的高是圆柱高的3倍,据此解答即可。
8.2:3;
解:2m:300cm
=200cm:300cm
=2:3
=
故答案为:2:3,。
根据“1m=100cm”得到原比=200cm:300cm,根据比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,将前项和后项同时除以100,得到最简整数比为2:3,再通过除法计算出比值即可。
9.七五
解:设每件价格为1元,
3÷4=0.75=75%=七五折;
故答案为:七五。
设每件价格为1元,即买四件商品只需要支付三件商品的金额,现价÷原价即可求出折扣。
10.0.1;7
解:0.7÷0.1=7
故答案为:0.1,7。
小数计数单位即分位上的最小量,故0.7的计数单位为0.1,欲求有几个这样的计数单位,用0.7除以0.1计算即可。
11.30;80;八;八
解:24÷=30
=80%=八折=八成
故答案为:30,80,八,八。
比的后项=前项÷比值,故得到第一个空为24÷=30;等于4除以5,得到商为0.8,将小数点向右移动两位,加上百分号得到80%即为第二空;80%即八折,同样也是八成。
12.6000;6
解:240 ÷ 4 = 60(厘米),
3+2+1=6,
长=60×=30(厘米),
宽=60×=20(厘米),
高=60×=10(厘米),
30 × 20 × 10= 6000(立方厘米)=6(立方分米);
故答案为:6000;6。
首先用棱长总和除以4得到一组长宽高的总和,然后根据比例关系,将总和分配到长、宽、高上,长方体体积 = 长 × 宽 × 高,将得到的长、宽、高值代入体积公式中,1立方分米=1000立方厘米,据此求解。
13.6:5
解:(1+20%):1
=1.2:1
=(1.2×10):(1×10)
=12:10
=(12÷2):(10÷2)
=6:5
故答案为:6:5。
把乙数看作单位“1”,甲数=1+20%,然后写出甲和乙的比,再运用比的基本性质化简比。
14.3
解:5分钟=300秒,300×=3(秒)。
故答案为:3。
把5分钟换算成300秒,根据分数乘法的意义用4G下载的时间乘即可求出用5G下载需要的时间。
15.22;(4n+2)
解:1×1=1(平方厘米)
图1:1×6=6(平方厘米)
图2:2×6-(2-1)×2=10(平方厘米)
图3:3×6-(3-1)×2=14(平方厘米)
图5:5×6-(5-1)×2=22(平方厘米)
图n:n×6-(n-1)×2=4n+2(平方厘米)
所以第五个图形的表面积是22平方厘米,第n个图形的表面积是(4n+2)平方厘米。
故答案为:22;4n+2。
由图可知,每个图形的表面积由小正方形面积组成,每个小正方形的面积是1平方厘米。图1表面积是由6个小正方形组成,图2表面积是由2×6-(2-1)×2个小正方形组成,图3表面积是由3×6-(3-1)×2个小正方形组成……所以第五个图形表面积是由5×6-(5-1)×2个小正方形组成,第n个图形表面积是由n×6-(n-1)×2个小正方形组成,代入解答即可。
16.;4
解:的分母是9,所以它的计数单位是;
分解质因数:12=2×2×3,15=3×5,所以12和15的最大公因数是3。
3-=-=
所以再添加4个这样的计数单位就是12和15的最大公因数。
故答案为:;4。
第一问:这个分数的分母是几,计数单位就是几分之一;第二问:用分解质因数法找到12和15的最小公因数,再减去这个分数,得到的分数,分子是几,就是几个计数单位。
17.52
解:分解质因数6=2×3,8=2×2×2,所以6和8的最小公倍数是2×2×2×3=24
因为24×2+4=52,24×3+4=76,所以这箱苹果共52个
故答案为:52。
每6个装一盒和每8个装一盒都剩余4个,也就是这箱苹果拿出4个后是6和8的公倍数。首先用分解质因数方法求出6和8的最小公倍数,再找到最小公倍数的倍数加上4在50到60之间的数即可解答。
18.(9,6)
解:8-3=5,4+5=9,所以第四个顶点的位置是 (9,6) 。
故答案为: (9,6) 。
首先根据数对画出三个顶点的位置如图:
顶点(3,4)和顶点(8,4)在同一行,那么这两个顶点间的距离就是8-3=5,因为平行四边形对边平行且相等,所以第四个顶点和顶点(4,6)也在同一行,且距离也是5,由此解答。
19.8
解:2650÷365=7(人)95(人),7+1=8(人)
2650÷366=7(人)88(人),7+1=8(人)
所以这些学生中至少8人是在同一天过生日。
故答案为:8。
需要分情况讨论,当是平年的时候,一年有365天,那么用总人数除以365得到的商就是同一天过生日的人数,余下的人无论在哪天过生日,这一天当中都至少有商+1人在同一天过生日。同样的,当是闰年的时候,一年有366天,计算方法同理。
20.6870
解:因为能被2和5同时整除,所以这个四位数是6□70;
6+7+0=13,要想这个四位数能被3整除,所以百位上可以是2、5、8;
百位上是8时,这个四位数最大,最大是6870。
故答案为:6870。
能被2和5同时整除的数特点是:个位上是0;能被3整除的数的特点是:各个数位上的数字相加的和能被3整除;由此解答。
21.3:4;正
解:因为3a=b,所以a:b=:3=3:4;
a:b=3:4=,比值一定,所以a与b成正比例关系。
故答案为:3:4;正。
两种相关联的量,一种量变化,另一种量也随之变化,如果表示这两种量的数值的比值一定,则这两种量成正比例关系。在比例中,两个外项积等于两个内项积,由此解答。
22.2:3=10:15(答案不唯一)
解:30的因数:1、2、3、5、6、10、15、30;
质数有:2、3、5;
合数有:6、10、15、30;
可组成比例: 2:3=10:15 (答案不唯一);
故答案为:2:3=10:15 (答案不唯一)。
首先列举出30的因数,再从中找到质数和合数,最后根据组成比例的两个比的比值相等进行解答(答案不唯一)。
23.105:13;
解:大豆与油的质量比是:420:52
=(420÷4):(52÷4)
=105:13;
比值是:105÷13=;
故答案为:105:13;。
大豆与油的质量比=大豆质量:油的质量,再根据比的基本性质:比的前项和后项同时乘或除以同一个数(不为0),比值不变,化简比;比值=比的前项÷比的后项。
24.497000700;5亿
解:这个数写作497000700;省略“亿”位后的尾数约是5亿;
故答案为:497000700;5亿。
哪一个数位上是几就在哪一位上写几,据此写出此数;省略“亿”位后的尾数,要看千万位上的数,千万位上的数大于等于5,就向亿位进1,亿位后的数舍去,并在末尾添一个“亿”字;千万位上的数小于5,直接舍去,并在末尾添一个“亿”字。
25.9.3,60;-6,-,-5.4
解:正数有:9.3,60;负数有:-6,-,-5.4。
故答案为:9.3,60;-6,-,-5.4。
大于0的数是正数,小于0的数是负数;据此解答。
26.(a÷8);50
解:平均每个粽子:(a÷8)克;
a=400时,平均每个粽子:400÷8=50(克);
故答案为:(a÷8);50。
平均分用除法计算,即用糯米总质量除以粽子个数即可求出平均每个粽子需要的糯米质量;据此解答。
27.2;48
解:如图:
长方形有2条对称轴;
面积是:8×6=48(平方厘米);
故答案为:2;48。
平面内,一个图形沿一条直线对折,对折后的两部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是它的对称轴;长方形面积=长×宽,据此解答。
28.69;3
解:0.69里面有69个0.01,;3个是。
故答案为:69;3。
0.69写成分数形式是,计数单位是,也就是0.01;的计数单位是,分子是几就表示有几个这样的计数单位。
29.(1)13
(2)(3n+1)
(3)115
解:(1)4+3+3+3
=7+6
=13(个);
(2)4+3(n-1)
=4+3n-4
=3n+1(个);
(3)(346-1)÷3
=345÷3
=115(次);
故答案为:(1)13;(2)(3n+1);(3)115。
(1)分割一次,分成4个正方形,分割两次,分成(4+3)个正方形,那么分割三次,分成4+3+3)个正方形,分割四次,分成了(4+3+3+3)个正方形;(2)可以发现分割分割n次可以分成[4+3(n-1)]个正方形;(3)[4+3(n-1)]=346,据此求出n即可。
30.6
(15×4-48)÷(4-2)
=(60-48)÷2
=12÷2
=6(只)
故答案为:6。
假设全是兔,则一共有(15×4)只脚,比实际多了(15×4-48)只脚,而每只兔比每只鸡多(4-2)只脚,用假设比实际多的脚数除以每只兔比每只鸡多的脚数即可求出鸡的只数;据此解答。
31.10
解:设这个圆的半径为r厘米,则大正方形的边长就是2r,
根据大正方形的面积是20平方厘米可得:2rX2r=20,整理可得:r2=5;
小正方形的面积是:2r×2r÷2=10(平方厘米)
故答案为:10。
正方形内最大的圆的直径等于这个正方形的边长,设这个圆的半径为r厘米,则正方形的边长就是2r,根据正方形的面积是20平方厘米可得:2r×2r=20,整理可得:r2=5,把它代入到圆的面积公式中即可求出这个最大圆的面积。在圆中所画最大正方形的对角线就等于圆的直径,圆的面积已知,可以求出半径平方的值,小正方形的对角线等于圆的直径,则小正方形的面积为对角线的平方的一半,也就能求出正方形的面积,据此解答即可。
32.10
解:4+4+2=10(只);
故答案为:10。
从观察到的三幅图可知,前面有2摞,每摞有4只碗,后面有1摞,这1摞有2只碗,据此解答。
33.
解:把单位“1”平均分成8份,阴影部分占其中的5份,用分数表示是;
故答案为:。
该图是把长方形面积看作单位“1”,把它平均分成8份,阴影部分占其中的5份,据此解答。
34.4;9;6
解:3÷0.75=4,所以3÷4=0.75;
12×0.75=9,所以9:12=0.75;
8×0.75=6,所以=0.75;
故答案为:4;9;6。
除数=被除数÷商;比的前项=比的后项×比值;分子=分母×分数值;据此解答。
35.2.35
解:235000000吨=2.35亿吨;
故答案为:2.35。
改写成亿为单位的数,就在亿位上数的右下角点上小数点,小数末尾的0省略,并在末尾添一个“亿”字;据此解答。
36.5;251.2
解:40÷2÷4=5(分米)
3.14×42×5
=3.14×16×5
=50.24×5
=251.2(立方分米)
故答案为:5,251.2。
由图可知,近似长方体的长相当于圆柱底面周长的一半,近似长方体的宽相当于圆柱的底面半径,近似长方体的高相当于圆柱的高,近似长方体的表面积比圆柱的表面积多两个侧面的面积,先根据增加部分面积求出圆柱的高,再利用“V圆柱=πr2h”求出这个圆柱的体积,据此解答。
37.150平方厘米
解:15×10=150(平方厘米)
故答案为:150平方厘米。
圆柱的表面积可以看做是两个圆的面积和一个长方形(或正方形)的面积,所以这个长方形围成的圆柱的侧面积就是这个长方形的面积,利用长方形的面积计算公式,长方形面积=长×宽,直接代入数据计算即可。
38.102.8
解:2×3.14×20÷2+20×2
=6.28×10+40
=62.8+40
=102.8(m)
故答案为:102.8。
半圆的周长=圆的周长的一半+一条直径的长度,先利用“C圆=2πr”表示出圆周长的一半,再加上一条直径的长度即可。
39.2
解:40÷20=2(厘米)
故答案为:2。
已知比例尺=图上距离:实际距离,则实际距离=图上距离÷比例尺,据此解答。
40.正
解:被除数÷除数=商
被除数÷商=除数
故答案为:正。
两种相关联的量,一种量变化,另一种量也随之变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫作正比例关系,据此解答。
41.8;51
解:18时22分-9时31分=8小时51分
故答案为:8,51。
用结束的时刻减去开始的时刻即可;分不够减时则向时借“1”,即60分。
42.7;70
解:(10×10-64)÷(10+2)
=36÷12
=3(道)
10-3=7(道)
7÷10×100%=70%
故答案为:7,70。
分析题干,假设10道题全做对,则得10×10=100(分),这样就少得100-64=36(分),错一题比对一题少10+2=12(分),也就是做错36÷12=3(道)题,进而得出做对题的数量;再用做对题的数量除以总数量,乘以100%即可求解。
43.12
解:(60,96)=12
故答案为:12。
两根绳子,一根长60米,一根长96米,要把这两根绳子剪成同样长的小段,每段最长为60米和96米的最大公因数;60=1×60=2×30=3×20=4×15=5×12=6×10,96=1×96=2×48=3×32=4×24=6×16=8×12,进而得出60和96的最大公因数为12,故每段最长是12米。
44.4.5,;﹣3,-1.5;0
解:4.5、是正数,-3、-1.5是负数,0既不是正数也不是负数
故答案为:4.5,,-3,-1.5,0。
大于0的数为正数,小于0的数为负数,负数前有负号“-”,0既不是正数也不是负数。
45.32;25;八;80
解:4:5=0.8=八成=80%
40×0.8=32
20÷0.8=25
故答案为:32,25,八,80。
已知所有值都为4:5=0.8,分子=分母×比值;除数=被除数÷商;小数化为百分数:将小数点向右移动2位,再加上百分号即可。
46.80;480;1.6
解:图中1厘米表示实际距离:1÷=8000000(厘米)=80千米;
济南到威海实际距离:6÷=48000000(厘米)=480千米;
济南到德州图上距离:128千米=12800000厘米,12800000×=1.6(厘米);
故答案为:80;480;1.6。
实际距离与图上距离及比例尺的关系是:实际距离=图上距离÷比例尺;据此解答。
47.12;36
解:底面积和体积相等的长方体、圆柱体和圆锥体,
长方体的高=圆柱体的高=12厘米,
圆锥体的高是圆柱体高的3倍,是12×3=36(厘米)。
故答案为:12;36。
长方体体积=底面积×高、圆柱体体积=底面积×高,圆锥体体积=底面积×高÷3。
48.12平方厘米
解:80米=8000厘米,60米=6000厘米,
8000×=4(厘米),6000×=3(厘米),
图上面积是4×3=12(平方厘米)。
故答案为:12平方厘米。
图上距离=实际距离×比例尺,据此求出长方形图上的长和宽,图上的长×图上的宽=图上的面积。
49.96;100
解:80×(1+20%)=80×1.2=96;
80÷(1-20%)=80÷0.8=100。
故答案为:96;100。
求比一个数多百分之几的数是多少用乘法,列式为:这个数×(1+多的百分之几)=所求的数;已知一个数比另一个数少百分之几,求另一个数,方法是:一个数÷(1-少的百分之几)。
同课章节目录
