2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题5 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题5 填空题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 179.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览




文档简介
2024-2025学年小升初数学备考真题分类汇编(山东地区专版)
专题5 填空题
一、填空题
1.(2024·五莲模拟)在商场里做随机问卷调查,随机抽取的25名顾客,至少有 人属相相同。
2.(2024·枣庄)甲乙两个数的差是4,比是3:5,则甲是 ,乙是 。
3.(2024·枣庄)一种洗衣机以八折出售,价格为1200元,它的原价是 元。
4.(2023·台儿庄) :40== = %。
5.(2023·德州)小丁,小亮、小敏3位同学排成一排照相,共有 种排法。
6.(2024·枣庄)三十五亿八千零六万写作 ,省略亿位后面的尾数记作 。
7.(2023·齐河)某服装店在搞活动,店内所有服装一律六折出售,若使用贵宾卡还可以再打八五折。一件羽绒服打折后活动价是660元,李叔叔如果用贵宾卡买这件羽绒服要花 元,这件羽绒服原价 元。
8.(2024·五莲模拟)把一根3米长的绳子平均分成5段,每段长 米,每段长是这根绳子的 ,每段是1米的 。
9.(2024·五莲模拟)李叔叔月工资6800元,扣除5000元个税免征额后的部分需要按3%的税率,缴纳个人所得税,李叔叔每月应缴纳个人所得税 元。
10.(2024·五莲模拟) = :15=3÷ =0.6= %= 成。
11.(2023·章丘)2022年12月31日,中国国家主席习近平在新年贺词中宣布,“中国空间站全面建成”,由于没有大气层的保护,在太阳光线直射下,空间站表面温度最高可达零上150℃以上,记作150℃;在背阳面,温度最低可达零下100℃以下,记作 ℃;空间站表面的最高温度和最低温度之间的温差是 ℃。
12.(2023·章丘)某砧板加工厂,准备把一根底面直径40厘米,长2米的圆柱形木料按照下图的方式加工成厚度为10厘米的砧板,每块砧板的体积是 dm3,每块砧板占这块圆柱形木料的 。
13.(2023·章丘)2023年6月4日神舟十五号载人飞船成功返航着陆,费俊龙、邓清明、张陆3位航天员在轨飞行距离一亿二千零九十六万千米,横线上的数写作 千米,省略亿后面的尾数约是 千米。
14.(2023·台儿庄)亮亮在比例尺为1:200000的路线图上,量得从家到少年宫的距离为4厘米。亮亮要乘出租车从家到少年宫,已知出租车3千米内(含3千米)按起步价10元计算,超过3千米,每增加1千米车费就增加2元,那么亮亮乘出租车从家到少年宫一共要付车费 元。
15.(2023·台儿庄)“地球是我家,绿化靠大家。”如图,太行林场去年共栽了三种树,其中栽柳树的面积占总面积的 %,如果松树栽了16公顷,那么杨树栽了 公顷。
16.(2023·台儿庄)8千克30克= 千克
9.6时= 时 分
17.(2023·台儿庄)一个正方体的棱长是5厘米,用两个这样的正方体拼成一个长方体。拼成的长方体的长是 厘米,表面积是 平方厘米。
18.(2023·台儿庄)中国古代数学名著《九章算术》中记载了圆柱、圆锥体积的计算方法。请看:如图实验可以得出,圆锥的体积等于与它等底等高的圆柱体积的 ,已知下面实验中的一个圆柱和一个圆锥体积相差36立方分米,那么一个圆锥的体积是 立方分米。
19.(2023·台儿庄)如果分母一定,分子和分数值成 比例;如果圆柱的体积一定,它的底面积和高成 比例。
20.(2023·五莲)如图,阴影部分的面积是5.6平方厘米,平行四边形的面积是 平方厘米。
21.(2023·五莲)2023年6月,小学生在校上学天数与在家休息天数的比为7:3,那么在校上学天数为 天,在家休息天数占总天数的 。
22.(2023·五莲)一个橘子占据的空间约为400 ,日照市海域面积约6000 。
23.(2023·五莲)一个三角形的三个内角的度数的比是2:3:4,这个三角形是 三角形.
24.(2023·五莲)“科技兴则民族兴,科技强则国家强”,比亚迪新能源技术的发展向世界证明中国的科技力量。今年1﹣5月累计生产1022890辆。1022890读作 ,改写成用“万”作单位的数是 万;1022890中的两个2相差 。
25.(2023·齐河)各边相等,各角也相等的多边形叫做正多边形。任一个正多边形都可以分成若干个三角形,请您根据如表提供的信息,寻找规律,探究正多边形的内角和与分成的三角形的个数之间的关系,将表格填写完整。
正多边形名称 正方形(正四边形) 正五边形 正六边形 正八边形 正n边形
画图表示 ……
分成三角形的个数 2 3
正多边形的内角和 2×180°=360° 3×180°=540°
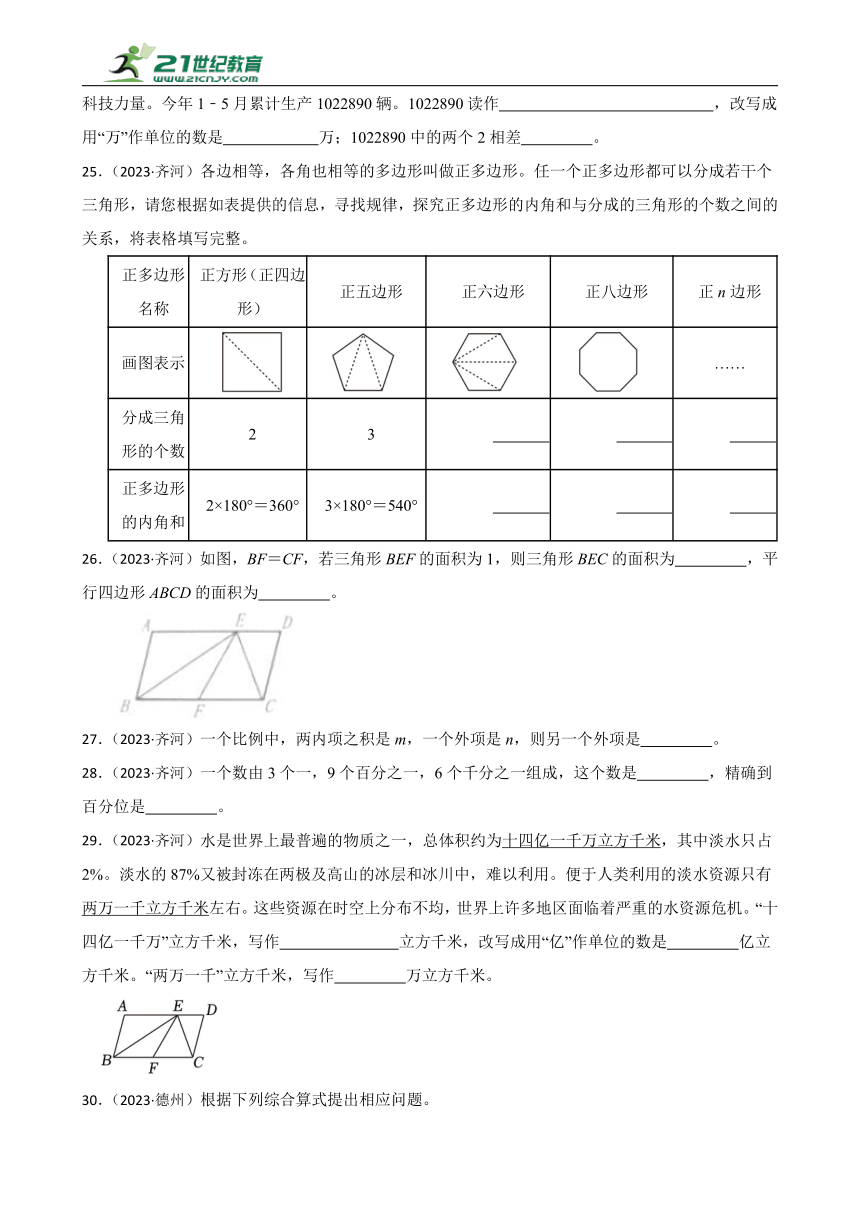
26.(2023·齐河)如图,BF=CF,若三角形BEF的面积为1,则三角形BEC的面积为 ,平行四边形ABCD的面积为 。
27.(2023·齐河)一个比例中,两内项之积是m,一个外项是n,则另一个外项是 。
28.(2023·齐河)一个数由3个一,9个百分之一,6个千分之一组成,这个数是 ,精确到百分位是 。
29.(2023·齐河)水是世界上最普遍的物质之一,总体积约为十四亿一千万立方千米,其中淡水只占2%。淡水的87%又被封冻在两极及高山的冰层和冰川中,难以利用。便于人类利用的淡水资源只有两万一千立方千米左右。这些资源在时空上分布不均,世界上许多地区面临着严重的水资源危机。“十四亿一千万”立方千米,写作 立方千米,改写成用“亿”作单位的数是 亿立方千米。“两万一千”立方千米,写作 万立方千米。
30.(2023·德州)根据下列综合算式提出相应问题。
(1)五年级一班原来有480本图书,这学期又购进60本, ?
列式:60÷480
(2)一袋面粉,吃了15千克,比剩下的 多5千克, ?
列式:(15﹣5)÷
31.(2023·德州)如图等腰三角形中阴影部分的面积是 .
32.(2023·德州)安全知识竞赛共15道题,答对一题得10分,答错一题倒扣5分。小华得了120分,她答对了 题。
33.(2023·德州)一个高10厘米的圆柱体,沿底面直径切拼成一个近似的长方体,表面积增加了200平方厘米。原来圆柱体的体积是 立方厘米。
34.(2023·德州)某机床厂男职工人数占全车间总人数的 ,男职工人数比女职工人数多 %。
35.(2023·德州)如果 =y(x、y都不为0),那么x与y成 比例。如果 x= y(x、y≠0),那么y:x= (填比)。
36.(2023·德州)把一个圆柱制成最大的圆锥,削去部分的体积是36立方分米,圆柱的体积是 立方分米,圆锥的体积是 立方分米。
37.(2023·德州)一根绳长9米,把它平均截成8段,每段是全长的 ,每段长 米。
38.(2023·德州)12: =0.75= ÷12= %= (折扣)
39.(2023·德州)3.07公顷= 公顷 平方米 4.25时= 时 分
8.03立方分米= 升 毫升
4千克40克= 千克
40.(2023·潍城)把两个完全一样的正方体拼成一个大长方体,拼成后表面积减少了 m2。
41.(2023·潍城)如图,三角形的底被平均分成了5份,阴影部分的面积和整个三角形面积的比是 。
42.(2023·潍城)学校买了5本《科学与天才》一共花了280元,写出书的总价与数量的比值。比值: ,比值表示的意义是 。
43.(2023·潍城)中百超市一种矿泉水,零售每瓶卖4元,超市为感谢广大客户对该产品的厚爱,特开展“买三赠一”大酬宾活动,超市的做法优惠了 %。
44.(2023·潍城)2.05升= 毫升
15分钟= 小时
2050千克= 吨
2.6立方分米= 毫升
45.(2023·潍城)如下图:制作一个底面直径20cm、长50cm的圆柱形通风管,至少需要用 平方厘米铁皮,这实际就是求圆柱的 。
46.(2023·潍城)一件商品原价为a元,现在促销打八五折销售,现在的价格是 元。
47.(2023·定陶)把两个完全相同的小正方体拼成一个长方体后,这个长方体的表面积比原来两个小正方体的表面积减少60平方厘米。那么原来每个小正方体的表面积是 平方厘米。
48.(2023·定陶)下图中圆和长方形面积相等,圆的半径等于长方形的宽.阴影部分面积是60cm2,圆的面积是 cm2。
49.(2023·定陶)把米长的铁丝焊接成正方形铁架,每条边是这根铁丝的 ,每条边的长是 米。
50.(2023·山亭) 150cm3= dm3 2500L= m3
4.5dm3= L 0.65m3= dm3
答案解析部分
1.3
解:25÷12=2······1,
2+1=3(人);
故答案为:3。
根据抽屉原理,将25名顾客放入12个属相中,每种属相都有2人,此时还多一人,则至少有一种属相有3人,据此求解。
2.6;10
解:设甲是3x,乙是5x
5x-3x=4
2x=4
x=2
3x=3×2=6
5x=5×2=10
故答案为:6,10。
分析题干,已知甲乙两个数的比是3:5,故可假设甲是3x,乙是5x,进而根据甲乙两个数的差是4建立等式方程5x-3x=4,解方程得出x的值,然后分别乘以3和5,即可得出甲和乙的值。
3.1500
解:1200÷80%=1500(元)
故答案为:1500。
分析题干,已知“现价=原价×折扣”,得到原价=现价÷折扣,故题中洗衣机的原价为1200÷80%=1500(元)。
4.12;30;30
解:=3:10=(3×4):(10×4)=12:40;
==;
===30%;
故答案为:12;30;30。
分数转化成比:分子作比的前项,分母作比的后项;比的基本性质:比的前项和比的后项同时乘或除以同一个数(不为0),比值不变;分数的基本性质:分数的分子和分母同时乘或除以同一个数(不为0),分数的大小不变;先将分数写成分母是100的分数,再去掉分母,在分子后面添上“%”接转化成百分数。
5.6
解:2×3=6(种),共有6种排法。
故答案为:6。
小丁排在第一位时,有2种排法;小亮排在第一位时,有2种排法;小敏排在第一位时,有2种排法;共6种排法。
6.3580060000;36亿
解:三十五亿八千零六万写作3580060000≈36亿
故答案为:3580060000,36亿。
写作方法:从高位写起,依次为十亿、亿、千万、百万、十万、万、千、百、十、个;省略亿位后的尾数,看千万位上的数,8大于5,故向上进一位,得到36亿。
7.561;1100
解:660×85%=561(元);
660÷60%=1100(元)。
故答案为:561;1100。
李叔叔用贵宾卡买羽绒服要花的钱是折后价的85%,求一个数的百分之几是多少,用乘法计算;打折后活动价是原价的60%,已知一个数的百分自己是多少,求这个数,用除法计算。
8.;;
解:3÷5=(米),
1÷5=,
÷1=;
故答案为:;;。
把一根3米长的绳子平均分成5段,每段的长度就是3÷5=米,将这条绳子看作单位”1“ ,平均分成5段,每段长是这根绳子的1÷5,每段的长度是米,占1米的多少就是用÷1,据此求解。
9.54
解:6800-5000=1800(元);
1800×3%=54(元);
故答案为:54。
计算出李叔叔的月工资中超过个税免征额的部分,将这个超过的部分乘3%的税率计算出需要缴纳的个人所得税。
10.20;9;5;60;六
解:0.6=60%=六成,
60%===,
=3÷5,
=3:5=(3×3):(5×3)=9:15;
故答案为:20;9;5;60;六。
将小数点向右移两位,再加上百分号即为百分数,百分之几十就是几成,60%=,根据分数的基本性质,的分子、分母都乘4就是;根据分数与除法的关系,=3÷5,根据比与分数的关系,=3:5,再根据比的基本性质比的前、后项都乘3就是9:15。
11.﹣100;250
解:零下100℃记作-100℃;
150℃+100℃=250℃;
所以最高温度和最低温度之间的温差是250℃。
故答案为:-100;250。
题中用150℃表示零上150℃,那么零下100℃就用负数进行表示,也就是在温度前面加上“-”号。求温差,也就是将最高温度与0℃之间的差值与最低温度与0℃之间的差值相加即可。
12.12.56;
解:(40÷2)2×3.14×10
=202×3.14×10
=400×3.14×10
=12560(cm3)
12560cm3=12.56dm3;
2米=200厘米
10÷200=
所以每块砧板的体积是12.56dm3,每块砧板占这块圆柱形木料的。
故答案为:12.56;。
第一问首先需要根据圆面积=半径×半径×π计算出砧板的底面积,再根据圆柱体积=底面积×高代入数值即可求出每块砧板的体积。第二问是将圆柱形木料的长看作单位“1”,根据对应量÷单位“1”=对应率代入数值进行解答。
13.120960000;1亿
解:一亿二千零九十六万写作:120960000;
120960000省略亿后面的尾数约是1亿
故答案为:120960000;1亿。
数的写法:从高位到低位,一级一级地写;哪一数位上一个单位也没有,就在那个数位上写0,即可写出此数。省略“亿”后面的尾数就是四舍五入到亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字。
14.20
解:家到少年宫的实际距离:4÷=800000(厘米)=8千米;
车费:10+(8-3)×2
=10+5×2
=10+10
=20(元);
故答案为:20。
先用图上距离除以比例尺求出家到少年宫的实际距离;再根据实际距离计算车费。
15.40;32
解:栽柳树的面积占总面积的:1-20%-40%
=80%-40%
=40%;
栽杨树面积:16÷20%×40%
=80×40%
=32(公顷);
故答案为:40;32。
林场总面积是单位“1”,用1减去其他两种树所占的百分比即可求出柳树所占的百分比;先用松树棵树除以其所占百分比求出总面积,再用总面积乘杨树所占百分比即可求出栽杨树的面积。
16.8.03;9;36
解:8+30÷1000
=8+0.03
=8.03,所以8千克30克=8.03千克;
0.6×60=36,所以9.6时=9时36分;
故答案为:8.03;9;36。
1千克=1000克,1时=60分,据此进行单位换算。
17.10;250
解:拼成的长方体的长是5×2=10(厘米),宽是5厘米,高是5厘米;
表面积是(10×5+10×5+5×5)×2
=(50+50+25)×2
=125×2
=250(平方厘米);
故答案为:10;250。
拼成的长方体的长等于正方体棱长×2,长方体的宽和高等于正方体的棱长;长方体表面积=(长×宽+长×高+宽×高)×2,据此解答。
18.;18
解:圆锥的体积等于与它等底等高的圆柱体积的;
36÷(3-1)
=36÷2
=18(立方分米);
故答案为:;18。
圆锥的体积等于与它等底等高的圆柱体积的;圆柱的体积就是与它等底等高的圆锥体积的3倍,那么圆柱和圆锥体积差就是圆锥体积的(3-1)倍;用相差的体积除以(3-1)即可求出圆锥的体积。
19.正;反
解:=分母(一定),比值一定,所以分子和分数值成正比例;
底面积×高=圆柱的体积(一定),乘积一定,所以底面积和高成反比例;
故答案为:正;反。
两种相关联的量,如果比值一定,那么这两种量成正比例;如果乘积一定,这两种量成反比例;据此解答。
20.11.2
解:5.6×2=11.2(平方厘米)
故答案为:11.2。
三角形面积=底×高÷2,平行四边形面积=底×高,图中空白的三角形与平行四边形等底等高,所以三角形面积是平行四边形的一半,那么阴影部分的面积也是平行四边形面积的一半,故平行四边形面积=阴影部分面积×2=5.6×2=11.2(平方厘米)。
21.21;
解:30÷(7+3)×7
=30÷10×7
=3×7
=21(天)
3÷(7+3)=
故答案为:21,。
6月有30天,可以采用设份数的方法,将上学的天数看作7份,在家休息的天数是3份,一共是10份,用60天除以10求出一份的天数,乘7即可求出在校上学的天数;用在家休息时间的份数除以时间的总份数即可求出在家休息天数占总天数的几分之几。
22.立方厘米;平方千米
解:一个橘子占据的空间约为400立方厘米,日照市海域面积约6000平方千米
故答案为:立方厘米,平方千米。
常见的体积单位有立方厘米、立方分米、立方米,1立方厘米相当于一个手指尖的体积,一个粉笔盒的体积接近1立方分米,棱长为1米的正方体的体积是1立方米,一个橘子的体积小于粉笔盒的体积,故占据的空间约为400立方厘米;面积单位有平方厘米、平方分米、平方米、公顷、平方千米,日照市的海域面积比较大,用“平方千米”作单位比较合适。
23.锐角
解:180°×
=180°×
=40°
180°×
=180°×
=60°
180°×
=180°×
=80°
故答案为:锐角。
已知三角形内角和为180°,三个内角的度数的比是2:3:4,根据分数乘法计算得出三个内角分别为180°×=40°、180°×=60°、180°×=80°,根据“三个内角都是锐角的三角形是锐角三角形”判断即可。
24.一百零二万二千八百九十;102.289;18000
解:1022890读作一百零二万二千八百九十
1022890=102.289万
20000-2000=18000
故答案为:一百零二万二千八百九十,102.289万,18000。
数位从大到小依次为个十百千万十万百万千万亿,据此读数;
改写成用“万”作单位的数:将数末位的小数点向左移动4位,即可;
一个2在万位,为20000,一个2在千位,为2000,作差即为答案。
25.4;6;(n﹣2);4×180°=720°;6×180°=1080°;(n﹣2)×180°
解:由图可知,正六边形可以分成4个三角形,正六边形的内角和是4×180°=720°;
正八边形可以分成6个三角形,正八边形的内角和是6×180°=1080°;
正n边形可以分成(n-2)个三角形,正n边形的内角和是(n-2)×180°;
故答案为:4;6;(n-2);4×180°=720°;6×180°=1080°;(n-2)×180°。
只从一个顶点出发的对角线把多边形分割的三角形的个数最少,有(n-2)个;正多边形可以分成几个三角形,内角和就是几个180°;据此解答。
26.2;4
解:三角形BEC面积=三角形BEC+三角形BEF面积
=1+1
=2;
平行四边形ABCD面积=三角形BEC面积×2
=2×2
=4;
故答案为:2;4。
三角形BFC与三角形BEF等底同高,所以三角形BFC与三角形BEF的面积相等,三角形BEC面积=三角形BEC+三角形BEF面积;平行四边形ABCD与三角形BEC等底等高,所以平行四边形ABCD的面积是三角形BEC面积的2倍;据此解答。
27.
解:m÷n=
故答案为:。
比例的基本性质:内项积等于外项积;据此解答。
28.3.096;3.10
解:3个一,9个百分之一,6个千分之一组成的数是3.096,精确到百分位是3.10。
故答案为:3.096;3.10。
有几个计数单位就在该数位上写几,中间数位上一个数都没有的就写0占位;精确到百分位要看千分位上的数,千分位上的数大于等于5,向百分位进1,并把百分位后的数字舍去;千分位上的数小于5,直接把百分位后的数字舍去。
29.1410000000;14.1;2.1
解:“十四亿一千万”写作1410000000;改写成用“亿”作单位的数是14.1亿。“两万一千”写作21000,改写成用“万”作单位的数是2.1万。
故答案为:1410000000;14.1;2.1。
数的写法:从最高位开始,一级一级地往下写;哪一个数位上一个数也没有,就在那个数位上写0;改写成用“亿”作单位的数:在亿位数的右下角点上小数点,去掉末尾的0,再在末尾添一个“亿”字;改写成用“万”作单位的数:在万位数的右下角点上小数点,去掉末尾的0,再在末尾添一个“万”字。
30.(1)这学期又购进的本数是原有图书本数的几分之几
(2)这袋面粉原来多少千克
解:(1)60÷480表示的意思是: 这学期又购进的本数是原有图书本数的几分之几?
(2)(15﹣5)÷ 表示的意思是:这袋面粉原来多少千克。
故答案为:(1) 这学期又购进的本数是原有图书本数的几分之几;(2)这袋面粉原来多少千克。
(1)求一个数是另一个数的几分之几用除法;
(2)(15千克-5千克)对应的是这袋面粉的;已知一个数的几分之几是多少,求这个数用除法。
31.2.86
解:如图:
4÷2=2
3.14×2×2÷4-2×2÷2=3.14-2=1.14
4×4÷2÷2=8÷2=4
4-1.14=2.86
阴影部分的面积是2.86
故答案为:2.86。
圆的面积-三角形面积=空白弧形的面积;等腰直角三角形的直角边×直角边÷2=等腰直角三角形的面积,等腰直角三角形的面积÷2=以4为底边的三角形面积,以4为底边的三角形面积-空白弧形的面积=阴影部分的面积。
32.13
解:假设15道全部答对,
15×10=150(分)
150-120=30(分)
10+5=15(分)
30÷15=2(道)
15-2=13(道)
故答案为:13。
五步解鸡兔同笼问题:(1)假设都是其中一个量;(2)计算假设和实际的差;(3)计算另一个差(有加有减);(4)两个差的商就是假设外的另一个值;(5)总数-假设外的另一个值=假设的值。
33.3140
解:表面积增加了左右2个面的面积,这两个面一样且都是长方形,长方形的长是圆柱的底面半径,长方形的宽是圆柱的高;
200÷2=100(平方厘米)
100÷10=10(厘米)
3.14×10×10×10=314×10=3140(立方厘米)
故答案为:3140。
增加的表面积÷2=1个面的面积,1个面的面积÷高=圆柱的底面半径;π×底面半径的平方×高=圆柱体的体积。
34.50
解:男职工人数占全车间总人数的 ,可以把全车间总人数看做5,男职工人数看做3,则女职工人数是2;
(3-2)÷2=1÷2=50%
故答案为:50。
求一个数比另一个数多百分之几,就用这两个数的差除以比后面的数。
35.反;15:8
解:由 =y得xy=5,那么x与y成反比例;
由 x= y得y:x=:;
y:x=:=15:8。
故答案为:反;15:8。
第一空:反比例的判断方法:相关联,能变化,积一定;
第二空:在 x= y中,根据比例的外项之积等于比例的内项之积。把 y看做比例的外项, x看做比例的內项,据此把反比例改写成正比例的形式。再根据比例的基本性质,比的前项和后项同时乘以或除以同一个数,化为最简整数比。
36.54;18
解:36÷=36×=54(立方分米)
54×=18(立方分米)
故答案为:54;18。
削去部分的体积占圆柱体积的;削去部分的体积÷削去部分的体积占圆柱体积的分率=圆柱体积;圆柱的体积×=圆锥的体积。
37.;
解:1÷8=;9÷8=(米)。
故答案为:;。
把绳子的长度看做单位1,单位1÷平均分的段数=每段绳子是这根绳子的几分之几;绳子的长度÷平均分的段数=每段绳子的长度。
38.16;9;75;七五折
解:0.75=75%=七五折;12÷0.75=16;12×0.75=9。
故答案为:16;9;75;七五折。
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;几折就表示十分之几,也就是百分之几十;比的后项=比的前项÷比值;被除数=除数×商。
39.3;700;4;15;8;30;4.04
解:0.07公顷×10000=700平方米,3.07公顷=3公顷700平方米;
0.25时×60=15分,4.25时=4时15分;
0.03升×1000=30毫升,8.03立方分米=8.03升=8升30毫升;
40克÷1000=0.04千克,4千克40克=4.04千克。
故答案为:3;700;4;15;8;30;4.04。
公顷×10000=平方米;时×60=分;1立方分米=1升;升×1000=毫升;克÷1000=千克。
40.50
解:5×5×2=25×2=50(m2);
故答案为:50。
减少的面积就是两个正方形的面积,据此求解。
41.2:5
解:因为高相等,底的比是2:5,
所以阴影部分的面积和整个三角形面积的比是2:5;
故答案为:2:5。
把三角形的底平均分成5份,分成的三角形等高,阴影部分的底和整个三角形底的比是2:5,三角形的面积=底×高÷2,高相等,根据比的意义即可写出阴影部分的面积和整个三角形面积的比。
42.56;《科学与天才》的单价
解:280:5
=280÷5
=56;
比值表示的意义是《科学与天才》的单价;
故答案为:56;《科学与天才》的单价。
已知买了5本《科学与天才》一共花了280元,先根据比的意义写出书的总价与数量的比,然后用比的前项除以后项,求出比值,再根据“单价=总价÷数量”,说明比值表示的意义。
43.25
解:原来买4瓶矿泉水需:4×4=16(元),
现在买4瓶矿泉水需:4×3=12(元),
(16-12)÷16×100%
=4÷16×100%
=0.25×100%
=25%;
故答案为:25%。
已知一种矿泉水每瓶4元,现在“买三赠一”,即现在只需花买3瓶的钱数就可以买到4瓶,求“买三赠一”优惠了百分之几,就是求现在买4瓶需要的钱数比原来便宜了百分之几,先根据“总价=单价×数量”,分别求出原来买4瓶需要的钱数与现在买4瓶需要的钱数;然后用减法求出它们的差值,再除以原来买4瓶需要的钱数,即可求解。
44.2050;0.25;2.05;2600
解:2.05升=2.05×1000=2050毫升;
15分钟=15÷60=0.25小时;
2050千克=2050÷1000=2.05吨;
2.6立方分米=2.6×1000=2600毫升;
故答案为:2050;0.25;2.05;2600。
1升=1000毫升,1小时=60分钟,1吨=1000千克,1立方分米=1000毫升,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率,据此求解。
45.3140;侧面积
解:3.14×20×50=3140(平方厘米);
这实际就是求圆柱的侧面积;
故答案为:3140;侧面积。
圆柱的侧面积公式为,需要的铁皮就是圆柱的侧面积,据此求解。
46.85%a
解:a×85%=85%a(元);
故答案为:85%a。
打八五折就是原价的85%,求现价就是用原价乘85%,据此求解。
47.180
解:60÷2×6
=30×6
=180(平方厘米);
故答案为:180。
两个完全相同的小正方体拼成一个长方体后,表面积减少了2个正方形面的面积,据此求出正方体的底面积,正方体表面积=底面积×6,据此解答。
48.80
解:60÷(1-)
=60÷
=80(cm2);
故答案为:80。
由图可知,阴影部分面积=长方形面积-扇形面积,而扇形面积是圆面积的,所以阴影部分面积=长方形面积-扇形面积=圆面积-圆面积=圆面积;已知一个数的几分之几是多少,求这个数,用除法计算。
49.;
解:1÷4=;
÷4=(米);
故答案为:;。
正方形有4条边,把单位“1”平均分成几份,每份就是它的几分之一;正方形边长=周长÷4;据此解答。
50.0.15;2.5;4.5;650
解:150cm3=0.15dm3;2500L=2.5m3;
4.5dm3=4.5L;0.65m3=650dm3。
故答案为:0.15;2.5;4.5;650。
1立方米=1000立方分米,1立方分米=1000立方厘米,1立方分米=1升,1立方厘米=1毫升。根据这些单位之间的进率换算单位即可。
专题5 填空题
一、填空题
1.(2024·五莲模拟)在商场里做随机问卷调查,随机抽取的25名顾客,至少有 人属相相同。
2.(2024·枣庄)甲乙两个数的差是4,比是3:5,则甲是 ,乙是 。
3.(2024·枣庄)一种洗衣机以八折出售,价格为1200元,它的原价是 元。
4.(2023·台儿庄) :40== = %。
5.(2023·德州)小丁,小亮、小敏3位同学排成一排照相,共有 种排法。
6.(2024·枣庄)三十五亿八千零六万写作 ,省略亿位后面的尾数记作 。
7.(2023·齐河)某服装店在搞活动,店内所有服装一律六折出售,若使用贵宾卡还可以再打八五折。一件羽绒服打折后活动价是660元,李叔叔如果用贵宾卡买这件羽绒服要花 元,这件羽绒服原价 元。
8.(2024·五莲模拟)把一根3米长的绳子平均分成5段,每段长 米,每段长是这根绳子的 ,每段是1米的 。
9.(2024·五莲模拟)李叔叔月工资6800元,扣除5000元个税免征额后的部分需要按3%的税率,缴纳个人所得税,李叔叔每月应缴纳个人所得税 元。
10.(2024·五莲模拟) = :15=3÷ =0.6= %= 成。
11.(2023·章丘)2022年12月31日,中国国家主席习近平在新年贺词中宣布,“中国空间站全面建成”,由于没有大气层的保护,在太阳光线直射下,空间站表面温度最高可达零上150℃以上,记作150℃;在背阳面,温度最低可达零下100℃以下,记作 ℃;空间站表面的最高温度和最低温度之间的温差是 ℃。
12.(2023·章丘)某砧板加工厂,准备把一根底面直径40厘米,长2米的圆柱形木料按照下图的方式加工成厚度为10厘米的砧板,每块砧板的体积是 dm3,每块砧板占这块圆柱形木料的 。
13.(2023·章丘)2023年6月4日神舟十五号载人飞船成功返航着陆,费俊龙、邓清明、张陆3位航天员在轨飞行距离一亿二千零九十六万千米,横线上的数写作 千米,省略亿后面的尾数约是 千米。
14.(2023·台儿庄)亮亮在比例尺为1:200000的路线图上,量得从家到少年宫的距离为4厘米。亮亮要乘出租车从家到少年宫,已知出租车3千米内(含3千米)按起步价10元计算,超过3千米,每增加1千米车费就增加2元,那么亮亮乘出租车从家到少年宫一共要付车费 元。
15.(2023·台儿庄)“地球是我家,绿化靠大家。”如图,太行林场去年共栽了三种树,其中栽柳树的面积占总面积的 %,如果松树栽了16公顷,那么杨树栽了 公顷。
16.(2023·台儿庄)8千克30克= 千克
9.6时= 时 分
17.(2023·台儿庄)一个正方体的棱长是5厘米,用两个这样的正方体拼成一个长方体。拼成的长方体的长是 厘米,表面积是 平方厘米。
18.(2023·台儿庄)中国古代数学名著《九章算术》中记载了圆柱、圆锥体积的计算方法。请看:如图实验可以得出,圆锥的体积等于与它等底等高的圆柱体积的 ,已知下面实验中的一个圆柱和一个圆锥体积相差36立方分米,那么一个圆锥的体积是 立方分米。
19.(2023·台儿庄)如果分母一定,分子和分数值成 比例;如果圆柱的体积一定,它的底面积和高成 比例。
20.(2023·五莲)如图,阴影部分的面积是5.6平方厘米,平行四边形的面积是 平方厘米。
21.(2023·五莲)2023年6月,小学生在校上学天数与在家休息天数的比为7:3,那么在校上学天数为 天,在家休息天数占总天数的 。
22.(2023·五莲)一个橘子占据的空间约为400 ,日照市海域面积约6000 。
23.(2023·五莲)一个三角形的三个内角的度数的比是2:3:4,这个三角形是 三角形.
24.(2023·五莲)“科技兴则民族兴,科技强则国家强”,比亚迪新能源技术的发展向世界证明中国的科技力量。今年1﹣5月累计生产1022890辆。1022890读作 ,改写成用“万”作单位的数是 万;1022890中的两个2相差 。
25.(2023·齐河)各边相等,各角也相等的多边形叫做正多边形。任一个正多边形都可以分成若干个三角形,请您根据如表提供的信息,寻找规律,探究正多边形的内角和与分成的三角形的个数之间的关系,将表格填写完整。
正多边形名称 正方形(正四边形) 正五边形 正六边形 正八边形 正n边形
画图表示 ……
分成三角形的个数 2 3
正多边形的内角和 2×180°=360° 3×180°=540°
26.(2023·齐河)如图,BF=CF,若三角形BEF的面积为1,则三角形BEC的面积为 ,平行四边形ABCD的面积为 。
27.(2023·齐河)一个比例中,两内项之积是m,一个外项是n,则另一个外项是 。
28.(2023·齐河)一个数由3个一,9个百分之一,6个千分之一组成,这个数是 ,精确到百分位是 。
29.(2023·齐河)水是世界上最普遍的物质之一,总体积约为十四亿一千万立方千米,其中淡水只占2%。淡水的87%又被封冻在两极及高山的冰层和冰川中,难以利用。便于人类利用的淡水资源只有两万一千立方千米左右。这些资源在时空上分布不均,世界上许多地区面临着严重的水资源危机。“十四亿一千万”立方千米,写作 立方千米,改写成用“亿”作单位的数是 亿立方千米。“两万一千”立方千米,写作 万立方千米。
30.(2023·德州)根据下列综合算式提出相应问题。
(1)五年级一班原来有480本图书,这学期又购进60本, ?
列式:60÷480
(2)一袋面粉,吃了15千克,比剩下的 多5千克, ?
列式:(15﹣5)÷
31.(2023·德州)如图等腰三角形中阴影部分的面积是 .
32.(2023·德州)安全知识竞赛共15道题,答对一题得10分,答错一题倒扣5分。小华得了120分,她答对了 题。
33.(2023·德州)一个高10厘米的圆柱体,沿底面直径切拼成一个近似的长方体,表面积增加了200平方厘米。原来圆柱体的体积是 立方厘米。
34.(2023·德州)某机床厂男职工人数占全车间总人数的 ,男职工人数比女职工人数多 %。
35.(2023·德州)如果 =y(x、y都不为0),那么x与y成 比例。如果 x= y(x、y≠0),那么y:x= (填比)。
36.(2023·德州)把一个圆柱制成最大的圆锥,削去部分的体积是36立方分米,圆柱的体积是 立方分米,圆锥的体积是 立方分米。
37.(2023·德州)一根绳长9米,把它平均截成8段,每段是全长的 ,每段长 米。
38.(2023·德州)12: =0.75= ÷12= %= (折扣)
39.(2023·德州)3.07公顷= 公顷 平方米 4.25时= 时 分
8.03立方分米= 升 毫升
4千克40克= 千克
40.(2023·潍城)把两个完全一样的正方体拼成一个大长方体,拼成后表面积减少了 m2。
41.(2023·潍城)如图,三角形的底被平均分成了5份,阴影部分的面积和整个三角形面积的比是 。
42.(2023·潍城)学校买了5本《科学与天才》一共花了280元,写出书的总价与数量的比值。比值: ,比值表示的意义是 。
43.(2023·潍城)中百超市一种矿泉水,零售每瓶卖4元,超市为感谢广大客户对该产品的厚爱,特开展“买三赠一”大酬宾活动,超市的做法优惠了 %。
44.(2023·潍城)2.05升= 毫升
15分钟= 小时
2050千克= 吨
2.6立方分米= 毫升
45.(2023·潍城)如下图:制作一个底面直径20cm、长50cm的圆柱形通风管,至少需要用 平方厘米铁皮,这实际就是求圆柱的 。
46.(2023·潍城)一件商品原价为a元,现在促销打八五折销售,现在的价格是 元。
47.(2023·定陶)把两个完全相同的小正方体拼成一个长方体后,这个长方体的表面积比原来两个小正方体的表面积减少60平方厘米。那么原来每个小正方体的表面积是 平方厘米。
48.(2023·定陶)下图中圆和长方形面积相等,圆的半径等于长方形的宽.阴影部分面积是60cm2,圆的面积是 cm2。
49.(2023·定陶)把米长的铁丝焊接成正方形铁架,每条边是这根铁丝的 ,每条边的长是 米。
50.(2023·山亭) 150cm3= dm3 2500L= m3
4.5dm3= L 0.65m3= dm3
答案解析部分
1.3
解:25÷12=2······1,
2+1=3(人);
故答案为:3。
根据抽屉原理,将25名顾客放入12个属相中,每种属相都有2人,此时还多一人,则至少有一种属相有3人,据此求解。
2.6;10
解:设甲是3x,乙是5x
5x-3x=4
2x=4
x=2
3x=3×2=6
5x=5×2=10
故答案为:6,10。
分析题干,已知甲乙两个数的比是3:5,故可假设甲是3x,乙是5x,进而根据甲乙两个数的差是4建立等式方程5x-3x=4,解方程得出x的值,然后分别乘以3和5,即可得出甲和乙的值。
3.1500
解:1200÷80%=1500(元)
故答案为:1500。
分析题干,已知“现价=原价×折扣”,得到原价=现价÷折扣,故题中洗衣机的原价为1200÷80%=1500(元)。
4.12;30;30
解:=3:10=(3×4):(10×4)=12:40;
==;
===30%;
故答案为:12;30;30。
分数转化成比:分子作比的前项,分母作比的后项;比的基本性质:比的前项和比的后项同时乘或除以同一个数(不为0),比值不变;分数的基本性质:分数的分子和分母同时乘或除以同一个数(不为0),分数的大小不变;先将分数写成分母是100的分数,再去掉分母,在分子后面添上“%”接转化成百分数。
5.6
解:2×3=6(种),共有6种排法。
故答案为:6。
小丁排在第一位时,有2种排法;小亮排在第一位时,有2种排法;小敏排在第一位时,有2种排法;共6种排法。
6.3580060000;36亿
解:三十五亿八千零六万写作3580060000≈36亿
故答案为:3580060000,36亿。
写作方法:从高位写起,依次为十亿、亿、千万、百万、十万、万、千、百、十、个;省略亿位后的尾数,看千万位上的数,8大于5,故向上进一位,得到36亿。
7.561;1100
解:660×85%=561(元);
660÷60%=1100(元)。
故答案为:561;1100。
李叔叔用贵宾卡买羽绒服要花的钱是折后价的85%,求一个数的百分之几是多少,用乘法计算;打折后活动价是原价的60%,已知一个数的百分自己是多少,求这个数,用除法计算。
8.;;
解:3÷5=(米),
1÷5=,
÷1=;
故答案为:;;。
把一根3米长的绳子平均分成5段,每段的长度就是3÷5=米,将这条绳子看作单位”1“ ,平均分成5段,每段长是这根绳子的1÷5,每段的长度是米,占1米的多少就是用÷1,据此求解。
9.54
解:6800-5000=1800(元);
1800×3%=54(元);
故答案为:54。
计算出李叔叔的月工资中超过个税免征额的部分,将这个超过的部分乘3%的税率计算出需要缴纳的个人所得税。
10.20;9;5;60;六
解:0.6=60%=六成,
60%===,
=3÷5,
=3:5=(3×3):(5×3)=9:15;
故答案为:20;9;5;60;六。
将小数点向右移两位,再加上百分号即为百分数,百分之几十就是几成,60%=,根据分数的基本性质,的分子、分母都乘4就是;根据分数与除法的关系,=3÷5,根据比与分数的关系,=3:5,再根据比的基本性质比的前、后项都乘3就是9:15。
11.﹣100;250
解:零下100℃记作-100℃;
150℃+100℃=250℃;
所以最高温度和最低温度之间的温差是250℃。
故答案为:-100;250。
题中用150℃表示零上150℃,那么零下100℃就用负数进行表示,也就是在温度前面加上“-”号。求温差,也就是将最高温度与0℃之间的差值与最低温度与0℃之间的差值相加即可。
12.12.56;
解:(40÷2)2×3.14×10
=202×3.14×10
=400×3.14×10
=12560(cm3)
12560cm3=12.56dm3;
2米=200厘米
10÷200=
所以每块砧板的体积是12.56dm3,每块砧板占这块圆柱形木料的。
故答案为:12.56;。
第一问首先需要根据圆面积=半径×半径×π计算出砧板的底面积,再根据圆柱体积=底面积×高代入数值即可求出每块砧板的体积。第二问是将圆柱形木料的长看作单位“1”,根据对应量÷单位“1”=对应率代入数值进行解答。
13.120960000;1亿
解:一亿二千零九十六万写作:120960000;
120960000省略亿后面的尾数约是1亿
故答案为:120960000;1亿。
数的写法:从高位到低位,一级一级地写;哪一数位上一个单位也没有,就在那个数位上写0,即可写出此数。省略“亿”后面的尾数就是四舍五入到亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字。
14.20
解:家到少年宫的实际距离:4÷=800000(厘米)=8千米;
车费:10+(8-3)×2
=10+5×2
=10+10
=20(元);
故答案为:20。
先用图上距离除以比例尺求出家到少年宫的实际距离;再根据实际距离计算车费。
15.40;32
解:栽柳树的面积占总面积的:1-20%-40%
=80%-40%
=40%;
栽杨树面积:16÷20%×40%
=80×40%
=32(公顷);
故答案为:40;32。
林场总面积是单位“1”,用1减去其他两种树所占的百分比即可求出柳树所占的百分比;先用松树棵树除以其所占百分比求出总面积,再用总面积乘杨树所占百分比即可求出栽杨树的面积。
16.8.03;9;36
解:8+30÷1000
=8+0.03
=8.03,所以8千克30克=8.03千克;
0.6×60=36,所以9.6时=9时36分;
故答案为:8.03;9;36。
1千克=1000克,1时=60分,据此进行单位换算。
17.10;250
解:拼成的长方体的长是5×2=10(厘米),宽是5厘米,高是5厘米;
表面积是(10×5+10×5+5×5)×2
=(50+50+25)×2
=125×2
=250(平方厘米);
故答案为:10;250。
拼成的长方体的长等于正方体棱长×2,长方体的宽和高等于正方体的棱长;长方体表面积=(长×宽+长×高+宽×高)×2,据此解答。
18.;18
解:圆锥的体积等于与它等底等高的圆柱体积的;
36÷(3-1)
=36÷2
=18(立方分米);
故答案为:;18。
圆锥的体积等于与它等底等高的圆柱体积的;圆柱的体积就是与它等底等高的圆锥体积的3倍,那么圆柱和圆锥体积差就是圆锥体积的(3-1)倍;用相差的体积除以(3-1)即可求出圆锥的体积。
19.正;反
解:=分母(一定),比值一定,所以分子和分数值成正比例;
底面积×高=圆柱的体积(一定),乘积一定,所以底面积和高成反比例;
故答案为:正;反。
两种相关联的量,如果比值一定,那么这两种量成正比例;如果乘积一定,这两种量成反比例;据此解答。
20.11.2
解:5.6×2=11.2(平方厘米)
故答案为:11.2。
三角形面积=底×高÷2,平行四边形面积=底×高,图中空白的三角形与平行四边形等底等高,所以三角形面积是平行四边形的一半,那么阴影部分的面积也是平行四边形面积的一半,故平行四边形面积=阴影部分面积×2=5.6×2=11.2(平方厘米)。
21.21;
解:30÷(7+3)×7
=30÷10×7
=3×7
=21(天)
3÷(7+3)=
故答案为:21,。
6月有30天,可以采用设份数的方法,将上学的天数看作7份,在家休息的天数是3份,一共是10份,用60天除以10求出一份的天数,乘7即可求出在校上学的天数;用在家休息时间的份数除以时间的总份数即可求出在家休息天数占总天数的几分之几。
22.立方厘米;平方千米
解:一个橘子占据的空间约为400立方厘米,日照市海域面积约6000平方千米
故答案为:立方厘米,平方千米。
常见的体积单位有立方厘米、立方分米、立方米,1立方厘米相当于一个手指尖的体积,一个粉笔盒的体积接近1立方分米,棱长为1米的正方体的体积是1立方米,一个橘子的体积小于粉笔盒的体积,故占据的空间约为400立方厘米;面积单位有平方厘米、平方分米、平方米、公顷、平方千米,日照市的海域面积比较大,用“平方千米”作单位比较合适。
23.锐角
解:180°×
=180°×
=40°
180°×
=180°×
=60°
180°×
=180°×
=80°
故答案为:锐角。
已知三角形内角和为180°,三个内角的度数的比是2:3:4,根据分数乘法计算得出三个内角分别为180°×=40°、180°×=60°、180°×=80°,根据“三个内角都是锐角的三角形是锐角三角形”判断即可。
24.一百零二万二千八百九十;102.289;18000
解:1022890读作一百零二万二千八百九十
1022890=102.289万
20000-2000=18000
故答案为:一百零二万二千八百九十,102.289万,18000。
数位从大到小依次为个十百千万十万百万千万亿,据此读数;
改写成用“万”作单位的数:将数末位的小数点向左移动4位,即可;
一个2在万位,为20000,一个2在千位,为2000,作差即为答案。
25.4;6;(n﹣2);4×180°=720°;6×180°=1080°;(n﹣2)×180°
解:由图可知,正六边形可以分成4个三角形,正六边形的内角和是4×180°=720°;
正八边形可以分成6个三角形,正八边形的内角和是6×180°=1080°;
正n边形可以分成(n-2)个三角形,正n边形的内角和是(n-2)×180°;
故答案为:4;6;(n-2);4×180°=720°;6×180°=1080°;(n-2)×180°。
只从一个顶点出发的对角线把多边形分割的三角形的个数最少,有(n-2)个;正多边形可以分成几个三角形,内角和就是几个180°;据此解答。
26.2;4
解:三角形BEC面积=三角形BEC+三角形BEF面积
=1+1
=2;
平行四边形ABCD面积=三角形BEC面积×2
=2×2
=4;
故答案为:2;4。
三角形BFC与三角形BEF等底同高,所以三角形BFC与三角形BEF的面积相等,三角形BEC面积=三角形BEC+三角形BEF面积;平行四边形ABCD与三角形BEC等底等高,所以平行四边形ABCD的面积是三角形BEC面积的2倍;据此解答。
27.
解:m÷n=
故答案为:。
比例的基本性质:内项积等于外项积;据此解答。
28.3.096;3.10
解:3个一,9个百分之一,6个千分之一组成的数是3.096,精确到百分位是3.10。
故答案为:3.096;3.10。
有几个计数单位就在该数位上写几,中间数位上一个数都没有的就写0占位;精确到百分位要看千分位上的数,千分位上的数大于等于5,向百分位进1,并把百分位后的数字舍去;千分位上的数小于5,直接把百分位后的数字舍去。
29.1410000000;14.1;2.1
解:“十四亿一千万”写作1410000000;改写成用“亿”作单位的数是14.1亿。“两万一千”写作21000,改写成用“万”作单位的数是2.1万。
故答案为:1410000000;14.1;2.1。
数的写法:从最高位开始,一级一级地往下写;哪一个数位上一个数也没有,就在那个数位上写0;改写成用“亿”作单位的数:在亿位数的右下角点上小数点,去掉末尾的0,再在末尾添一个“亿”字;改写成用“万”作单位的数:在万位数的右下角点上小数点,去掉末尾的0,再在末尾添一个“万”字。
30.(1)这学期又购进的本数是原有图书本数的几分之几
(2)这袋面粉原来多少千克
解:(1)60÷480表示的意思是: 这学期又购进的本数是原有图书本数的几分之几?
(2)(15﹣5)÷ 表示的意思是:这袋面粉原来多少千克。
故答案为:(1) 这学期又购进的本数是原有图书本数的几分之几;(2)这袋面粉原来多少千克。
(1)求一个数是另一个数的几分之几用除法;
(2)(15千克-5千克)对应的是这袋面粉的;已知一个数的几分之几是多少,求这个数用除法。
31.2.86
解:如图:
4÷2=2
3.14×2×2÷4-2×2÷2=3.14-2=1.14
4×4÷2÷2=8÷2=4
4-1.14=2.86
阴影部分的面积是2.86
故答案为:2.86。
圆的面积-三角形面积=空白弧形的面积;等腰直角三角形的直角边×直角边÷2=等腰直角三角形的面积,等腰直角三角形的面积÷2=以4为底边的三角形面积,以4为底边的三角形面积-空白弧形的面积=阴影部分的面积。
32.13
解:假设15道全部答对,
15×10=150(分)
150-120=30(分)
10+5=15(分)
30÷15=2(道)
15-2=13(道)
故答案为:13。
五步解鸡兔同笼问题:(1)假设都是其中一个量;(2)计算假设和实际的差;(3)计算另一个差(有加有减);(4)两个差的商就是假设外的另一个值;(5)总数-假设外的另一个值=假设的值。
33.3140
解:表面积增加了左右2个面的面积,这两个面一样且都是长方形,长方形的长是圆柱的底面半径,长方形的宽是圆柱的高;
200÷2=100(平方厘米)
100÷10=10(厘米)
3.14×10×10×10=314×10=3140(立方厘米)
故答案为:3140。
增加的表面积÷2=1个面的面积,1个面的面积÷高=圆柱的底面半径;π×底面半径的平方×高=圆柱体的体积。
34.50
解:男职工人数占全车间总人数的 ,可以把全车间总人数看做5,男职工人数看做3,则女职工人数是2;
(3-2)÷2=1÷2=50%
故答案为:50。
求一个数比另一个数多百分之几,就用这两个数的差除以比后面的数。
35.反;15:8
解:由 =y得xy=5,那么x与y成反比例;
由 x= y得y:x=:;
y:x=:=15:8。
故答案为:反;15:8。
第一空:反比例的判断方法:相关联,能变化,积一定;
第二空:在 x= y中,根据比例的外项之积等于比例的内项之积。把 y看做比例的外项, x看做比例的內项,据此把反比例改写成正比例的形式。再根据比例的基本性质,比的前项和后项同时乘以或除以同一个数,化为最简整数比。
36.54;18
解:36÷=36×=54(立方分米)
54×=18(立方分米)
故答案为:54;18。
削去部分的体积占圆柱体积的;削去部分的体积÷削去部分的体积占圆柱体积的分率=圆柱体积;圆柱的体积×=圆锥的体积。
37.;
解:1÷8=;9÷8=(米)。
故答案为:;。
把绳子的长度看做单位1,单位1÷平均分的段数=每段绳子是这根绳子的几分之几;绳子的长度÷平均分的段数=每段绳子的长度。
38.16;9;75;七五折
解:0.75=75%=七五折;12÷0.75=16;12×0.75=9。
故答案为:16;9;75;七五折。
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;几折就表示十分之几,也就是百分之几十;比的后项=比的前项÷比值;被除数=除数×商。
39.3;700;4;15;8;30;4.04
解:0.07公顷×10000=700平方米,3.07公顷=3公顷700平方米;
0.25时×60=15分,4.25时=4时15分;
0.03升×1000=30毫升,8.03立方分米=8.03升=8升30毫升;
40克÷1000=0.04千克,4千克40克=4.04千克。
故答案为:3;700;4;15;8;30;4.04。
公顷×10000=平方米;时×60=分;1立方分米=1升;升×1000=毫升;克÷1000=千克。
40.50
解:5×5×2=25×2=50(m2);
故答案为:50。
减少的面积就是两个正方形的面积,据此求解。
41.2:5
解:因为高相等,底的比是2:5,
所以阴影部分的面积和整个三角形面积的比是2:5;
故答案为:2:5。
把三角形的底平均分成5份,分成的三角形等高,阴影部分的底和整个三角形底的比是2:5,三角形的面积=底×高÷2,高相等,根据比的意义即可写出阴影部分的面积和整个三角形面积的比。
42.56;《科学与天才》的单价
解:280:5
=280÷5
=56;
比值表示的意义是《科学与天才》的单价;
故答案为:56;《科学与天才》的单价。
已知买了5本《科学与天才》一共花了280元,先根据比的意义写出书的总价与数量的比,然后用比的前项除以后项,求出比值,再根据“单价=总价÷数量”,说明比值表示的意义。
43.25
解:原来买4瓶矿泉水需:4×4=16(元),
现在买4瓶矿泉水需:4×3=12(元),
(16-12)÷16×100%
=4÷16×100%
=0.25×100%
=25%;
故答案为:25%。
已知一种矿泉水每瓶4元,现在“买三赠一”,即现在只需花买3瓶的钱数就可以买到4瓶,求“买三赠一”优惠了百分之几,就是求现在买4瓶需要的钱数比原来便宜了百分之几,先根据“总价=单价×数量”,分别求出原来买4瓶需要的钱数与现在买4瓶需要的钱数;然后用减法求出它们的差值,再除以原来买4瓶需要的钱数,即可求解。
44.2050;0.25;2.05;2600
解:2.05升=2.05×1000=2050毫升;
15分钟=15÷60=0.25小时;
2050千克=2050÷1000=2.05吨;
2.6立方分米=2.6×1000=2600毫升;
故答案为:2050;0.25;2.05;2600。
1升=1000毫升,1小时=60分钟,1吨=1000千克,1立方分米=1000毫升,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率,据此求解。
45.3140;侧面积
解:3.14×20×50=3140(平方厘米);
这实际就是求圆柱的侧面积;
故答案为:3140;侧面积。
圆柱的侧面积公式为,需要的铁皮就是圆柱的侧面积,据此求解。
46.85%a
解:a×85%=85%a(元);
故答案为:85%a。
打八五折就是原价的85%,求现价就是用原价乘85%,据此求解。
47.180
解:60÷2×6
=30×6
=180(平方厘米);
故答案为:180。
两个完全相同的小正方体拼成一个长方体后,表面积减少了2个正方形面的面积,据此求出正方体的底面积,正方体表面积=底面积×6,据此解答。
48.80
解:60÷(1-)
=60÷
=80(cm2);
故答案为:80。
由图可知,阴影部分面积=长方形面积-扇形面积,而扇形面积是圆面积的,所以阴影部分面积=长方形面积-扇形面积=圆面积-圆面积=圆面积;已知一个数的几分之几是多少,求这个数,用除法计算。
49.;
解:1÷4=;
÷4=(米);
故答案为:;。
正方形有4条边,把单位“1”平均分成几份,每份就是它的几分之一;正方形边长=周长÷4;据此解答。
50.0.15;2.5;4.5;650
解:150cm3=0.15dm3;2500L=2.5m3;
4.5dm3=4.5L;0.65m3=650dm3。
故答案为:0.15;2.5;4.5;650。
1立方米=1000立方分米,1立方分米=1000立方厘米,1立方分米=1升,1立方厘米=1毫升。根据这些单位之间的进率换算单位即可。
同课章节目录
