2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题6 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(山东地区专版)专题6 填空题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 114.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 10:11:58 | ||
图片预览




文档简介
2024-2025学年小升初数学备考真题分类汇编(山东地区专版)
专题6 填空题
一、填空题
1.(2024·沧县)把8000元存入银行2年,年利率是2.1%,到期后可得利息 元。
2.(2024·枣庄)如图,如果表示A的数对是(4,5),那么B( , ),C( , ),这个三角形的面积是 。
3.(2024·五莲模拟) 一条公路,甲队单独修8天完成,乙队单独修12天完成。两队合修4天,一共修了这项工程的 。
4.(2024·枣庄)用 块棱长1cm的正方体木块能摆成一个棱长1dm的正方体,将这些木块摆成一行,长 m。
5.(2024·五莲模拟)用小棒摆5正五边形,如图所示。
按照这样的方法,继续摆下去,摆第6幅图需要 根小棒,摆第n幅图需要 根小棒。
6.(2023·沂水)在横线里填写合适的分数。
已修的路程占这条路全长的 ,剩下的路程相当于已修路程的 。
7.(2024·五莲模拟)王奶奶把5000元钱存入银行,整存整取,年利率2.05%,到期后王奶奶可连本带息一共支取 元。
8.(2024·五莲模拟) 一幅地图的比例尺是1:5000000,在这幅地图上量得A、B两地的距离是3.2厘米,A、B两地的实际距离是 千米。
9.(2024·五莲模拟) 一根长3米圆柱形木材,锯成3段小圆柱后,表面积比原来增加了12.56平方分米,原来这根圆柱形木材的体积是 立方分米。
10.(2024·五莲模拟)如果a=b,(a、b均不为0),那么a与b成 比例,a:b= 。
11.(2023·鱼台)11只鸽子飞进4个鸽笼,总有一个鸽笼至少飞进了 只鸽子。
12.(2024·五莲模拟) 3升9毫升= 立方分米
4.2时= 时 分
2060平方米= 公顷
1.5吨= 千克
13.(2024·五莲模拟) 一个七位数,最高位上是最小的合数,万位上是最小的奇数,其他数位上都是0,这个数是 ,改写成用“万”作单位的数是 万,省略万位后面的尾数约是 万。
14.(2023·定陶)在比例尺是1:500000的地图上,量得甲、乙两地的距离约是12厘米,两地之间的实际距离大约是 千米。如在另一幅地图上量得甲、乙两地之间的距离是10厘米,这幅地图的比例尺是 。
15.(2023·定陶)如下图(单位:厘米)中,平行四边形的面积是72平方厘米,图中丙三角形的面积是甲三角形面积的 ,阴影部分的面积是 平方厘米。
16.(2023·定陶) 3÷4= :60= = %= (填小数)
17.(2023·定陶) 一个分数,分子分母的和是48,如果分子分母都加上1,所得分数约分后是,原来的分数是 。
18.(2023·定陶)在一条40米长的道路两边每隔2米放一盆花(两端都放),共放 盆花;把红、白、黄、蓝四种颜色的球各5个放到一个袋子里,至少取 个球,可以保证取到两个颜色相同的球。
19.(2023·定陶) 一个八位数,最高位上的数既是奇数又是合数,十万位上的数既是质数又是偶数,万位上的数的最大因数是6,千位上的数既不是质数也不是合数,其余各位上都是0,这个数写作 ,省略万位后面的尾数约是 万。
20.(2023·山亭)沿着物体不同的位置切下去,截面的形状居然也不相同,火腿肠沿不同的位置切下去,会有 种不同的截面。
21.(2023·山亭)生活中哪两种量成正比例关系: ,生活中哪两种量成反比例关系: 。
22.(2023·山亭)等底等高的一个圆柱和一个圆锥,体积相差60立方厘米,圆柱体的体积是 立方厘米,圆锥体的体积是 立方厘米。
23.(2023·鱼台)一种袋装食品标准净重为200g。质监部门为了解食品每袋净重与标准净重的误差,把食品净重205g记作+5g,那么食品净重为195g记作 g。
24.(2023·山亭)在下图中,正方形的面积是9平方厘米,这个圆的面积是 平方厘米。
25.(2023·鱼台)把一根长4米的木料截成7段,每段占全长的 ,每段长 米。
26.(2023·山亭)某银行的年利率是3.25%,5000元存一年,到期后应得利息 元。
27.(2023·山亭)山亭区水泉镇火樱桃采摘节期间,丰收火樱桃采摘园每斤打七五折销售,“七五折”表示现价是原价的 %,如果原价是20元,现价是 元。
28.(2023·沂水)如下图1所示,搭建单顶帐篷需要17根钢管,这样的帐篷按图2、图3的方式串起来搭建。如果想串起来搭建n顶帐篷,那么需要 根钢管。
29.(2023·沂水)如下图,△ABC绕点A顺时针旋转一定度数后得到△AB'C',已知∠B=20°,∠C=30°,这个三角形旋转了 °。
30.(2023·沂水)如下图直线上:若点C表示的数是,则点B表示的数是 ;若点D表示的数是150,则点A表示的数是 。
31.(2023·山亭)用8的4个因数组成一组比例是 。
32.(2023·沂水)把一根3米长的绳子剪成同样长的小段,每次剪一段,4次剪完。每段占全长的 ,每段长 米。
33.(2023·沂水) 80千米比 千米少20%;比60千克多20%是 千克。
34.(2023·沂水) 3÷8= = ÷64= (填小数)= %。
35.(2023·沂水) 2000平方米= 公顷 4吨50千克= 吨 3.05立方米= 立方厘米 1.3小时= 分
36.(2023·鱼台)一批货物,只用甲车运10次可运完,只用乙车运15次可运完。如果两辆车同时运 次可以运完。
37.(2023·山亭) 一个圆柱形油桶,从里面量底面直径是4分米,高是5分米。它的容积是 升。
38.(2023·鱼台)x与y是两种相关联的量,并且x÷y=12,那么x与y成 比例;如果,那么x与y成 比例。
39.(2023·鱼台)如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最大公因数是 。
40.(2023·山亭)要表示一位病人一天的体温变化情况,用 统计图比较合适。
41.(2023·高唐)一个三位小数取近似数后是2.00,这个三位小数最大是 ,最小是 。
42.(2023·鱼台)一个圆柱体积为75.36dm3,把它削成最大的圆锥,削去部分的是 dm3。
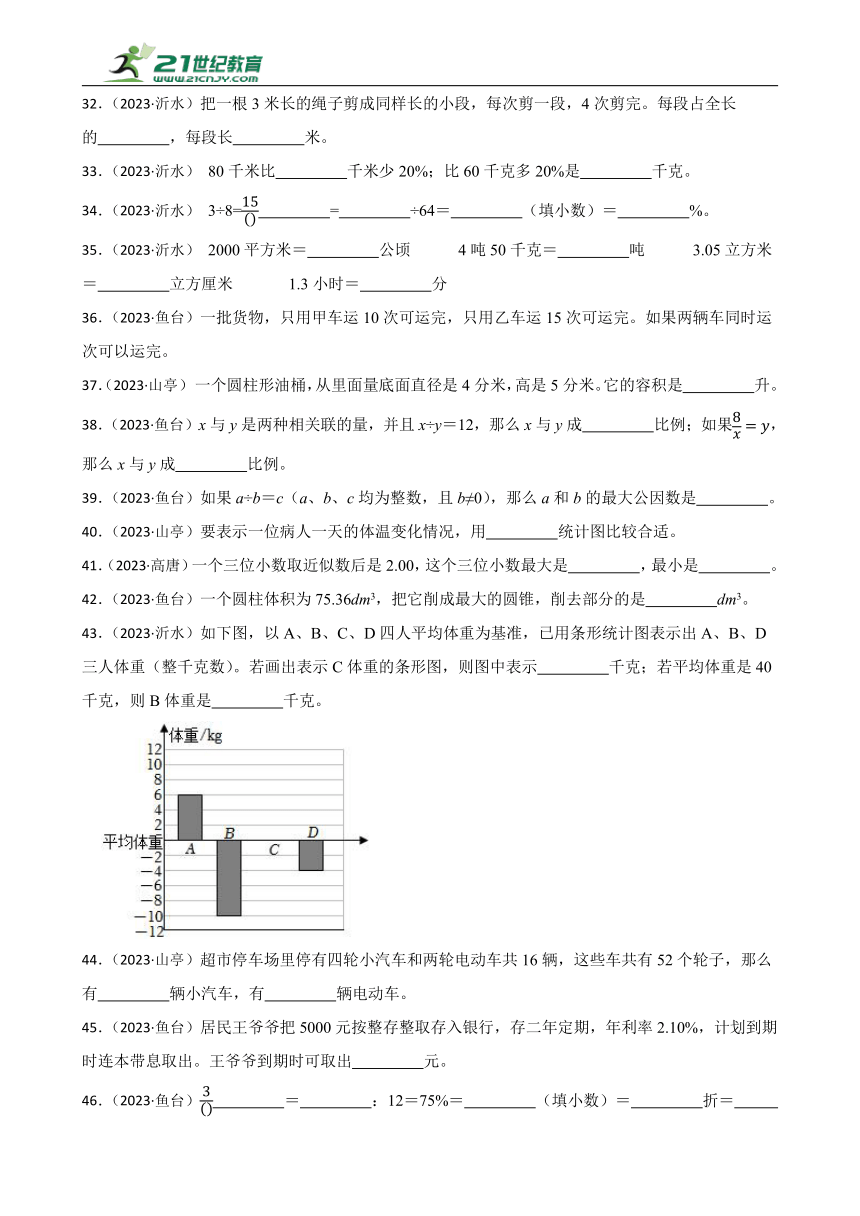
43.(2023·沂水)如下图,以A、B、C、D四人平均体重为基准,已用条形统计图表示出A、B、D三人体重(整千克数)。若画出表示C体重的条形图,则图中表示 千克;若平均体重是40千克,则B体重是 千克。
44.(2023·山亭)超市停车场里停有四轮小汽车和两轮电动车共16辆,这些车共有52个轮子,那么有 辆小汽车,有 辆电动车。
45.(2023·鱼台)居民王爷爷把5000元按整存整取存入银行,存二年定期,年利率2.10%,计划到期时连本带息取出。王爷爷到期时可取出 元。
46.(2023·鱼台) = :12=75%= (填小数)= 折= (填成数)
47.(2023·鱼台)2023年“五一”假期,经文化和旅游部数据中心测算,全国国内旅游出游合计接待游客二亿七千四百万人次,同比增长70.83%。二亿七千四百万写作 ,精确到亿位约是 。
48.(2023·高唐)一个等腰三角形的一个底角是m度,则顶角是 。
49.(2023·高唐)今年的植树活动中,光明小学五年级同学共植树80棵,结果成活了60棵,成活率为 ,后来补种了20棵,全部成活,这次植树活动最后的成活率为 。
50.(2023·鱼台)一个精密仪器零件实际长度是2毫米,画在一幅设计图上是10厘米。这幅图的比例尺是 。
答案解析部分
1.336
解:8000×2×2.1%=336元,所以到期后可得利息336元。
故答案为:336。
到期后可得的利息=存入银行的钱数×年份数×年利率,据此代入数据作答即可。
2.1;1;4;1;24cm2
解:B(1,1)
C(4,1)
S=(2×3)×(2×4)÷2
=6×8÷2
=48÷2
=24(cm2)
故答案为:1,1,4,1,24。
数对的第一个数表示列,第二个数表示行,据此得出B和C的数对;已知一个格子是2cm,三角形的底为3个格子,即2×3=6(cm),同样高为2×4=8(cm),然后根据“三角形面积=底×高÷2”计算得出该三角形的面积。
3.
解:
=
=;
故答案为:。
将这条公路看作单位”1“,甲队每天效率为,乙队每天效率为,工作总量=工作效率和×工作时间,据此求解。
4.1000;10
解:1dm=10cm
10×10×10=1000(块)
1000×1=1000(cm)=10m
故答案为:1000,10。
首先根据1dm=10cm,得到大正方体棱长为10cm,根据正方体体积=棱长×棱长×棱长,得到大正方体由10×10×10=1000(块)小正方体木块摆成,而每个小正方体棱长为1cm,故而摆成一行长1000×1=1000(cm),再根据1m=100cm换算单位即可。
5.25;4n+1
解:第一幅图:1+4=5(根),
第二幅图:1+4×2=9(根),
第三幅图:1+4×3=13(根),
第六幅图:1+4×6=25(根),
第n幅图:1+4×n=4n+1(根);
故答案为:25;4n+1。
观察图形,我们发现从第一幅图开始,每增加一幅图,小棒的数量就增加4根,第一幅图需要5根小棒,第二幅图需要9根小棒,第三幅图需要13根小棒,以此类推,由此可以推出第n幅图:1+4×n=4n+1(根);据此求解。
6.;
解:已修的路程占这条路全长的:5÷8=;
剩下的路程相当于已修路程的:3÷5=;
故答案为:;。
由图可知,整条路平均分成8份,已经修的路程是这样的5份,剩下的路程是这样的3份,求一个数是另一个数的几分之几,用除法计算;据此解答。
7.6025
解:5000×2.05%×3+5000
=1025+5000
=6025(元);
故答案为:6025。
根据利息=本金×利率×存期,求出利息,然后加上本金即可。
8.160
解:3.2÷=16000000厘米=160千米;
故答案为:160。
实际距离=图上距离÷比例尺,求出实际距离,再将厘米化成千米即可,据此求解。
9.94.2
解:12.56÷4=3.14(平方分米),
3米=30分米,
3.14×30=94.2(立方分米);
故答案为:94.2。
圆柱锯成3段,即锯了两次,每锯一次增加2个底面积,因此总共增加了4个底面积,先求出圆柱的底面积,再根据圆柱体积公式=底面积×高,据此求解。
10.正;3:4
解:a=b,所以a:b=:=3:4=,
比值一定,a与b成正比例;
故答案为:正;3:4。
根据比例的基本性质,两个外项的积等于两个内项的积,据此将式子变为比例,再化简,由于比值一定a与b成正比例,据此求解。
11.3
解:11÷4=2(只)……3(只)
2+1=3(只),即,总有一个鸽笼至少飞进了3只鸽子。
故答案为:3。
这是一个鸽巢问题,先把鸽子平均分到每一个鸽笼,鸽子总数÷鸽笼数量=平均每个鸽笼飞进的鸽子只数……剩下的鸽子只数,如果有剩余则不管飞到哪个鸽笼1只鸽子,则那个鸽笼都至少有(平均每个鸽笼飞进的鸽子只数+1)只鸽子,如果没有剩余,则总有一个鸽笼至少飞进了平均每个鸽笼飞进的鸽子只数。
12.3.009;4;12;0.206;1500
解:3升9毫升=3+9÷1000=3.009升=3.009立方分米;
4.2时=4时+0.2×60分=4时12分;
2060平方米=2060÷10000=0.206公顷;
1.5吨=1.5×1000=1500千克;
故答案为:3.009;4;12;0.206;1500。
1升=1立方分米=1000毫升,1时=60分,1公顷=10000平方米;1吨=1000千克,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
13.4010000;401;401
解:最小的合数是4,最小的奇数是1,
这个数是4010000,
4010000=401万;
故答案为:4010000;401;401。
根据整数的写法,从高位到低位,一级一级地写,最高位上是最小的合数,即4,万位上是最小的奇数,即1,其余数位上都是0,据此写出这个数,改写成以“万”作单位的数:改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字,省略“万”后面的尾数求它的近似数,要看万位的下一位千位上的数进行四舍五入,据此求解。
14.60;1:600000
解:12÷=6000000(厘米)=60千米;
10:6000000=1:600000;
故答案为:60;1:600000。
实际距离=图上距离÷比例尺;比例尺=图上距离:实际距离;据此解答。
15.;30
解:丙三角形的面积是甲三角形面积的: 7÷(5+7)
=7÷12
=;
阴影部分的面积是甲三角形面积的:5÷(5+7)
=5÷12
=,
阴影部分的面积:72××
=36×
=15(平方厘米);
故答案为:;15。
由图可知,丙三角形与甲三角形的高相等,丙的底边与甲的底边的比是7:(5+7);所以丙的面积与甲的面积的比也是7:(5+7);据此求出丙三角形的面积是甲三角形面积的几分之几。等底等高的三角形面积是平行四边形面积的一半,因此,乙面积+丙面积=甲面积=平行四边形面积;而乙的底边与甲的底边的比是5:(5+7),所以乙的面积与甲的面积的比也是5:(5+7);据此求出乙三角形面积是甲三角形面积的几分之几,再用甲三角形面积乘这个分率即可求出乙的面积。
16.45;12;75;0.75
解:3÷4=3:4=(3×15):(4×15)=45:60;
3÷4===;
3÷4=0.75=75%;
故答案为:45;12;75;0.75。
除法与比的关系:被除数作比的前项,除数作比的后项;比的基本性质:比的前项和后项同时乘或除以同一个数(不为0),比值不变;除法与分数的关系:被除数作分子,除数作分母;分数的基本性质:分子与分母同时乘或除以同一个数(不为0),分数的大小不变;小数转化成百分数:小数的小数点向右移动两位,再在后面添上“%”。
17.
解:48+1+1=50;
50÷(2+3)
=50÷5
=10;
得到的分数是:==;
原来的分数是:=;
故答案为:。
分子、分母都加上1,那么分子与分母的和就是(48+1+1);分数的基本性质:分子与分母同时乘或除以同一个数,分数的大小不变,因此,用所得分子与分母的和除以约分后分子与分母的和即可求出约分时,分子与分母同时除以的数;再用约分后的分数同时乘这个数即可求出所得的分数;最后用所得的分数的分子和分母同时减1求出原数;据此解答。
18.42;5
解:(40÷2+1)×2
=(20+1)×2
=21×2
=42(盆);
4+1=5(个);
故答案为:42;5。
两端植树问题中,全长÷间隔长度=间隔数,棵数=间隔数+1,据此求出一边的盆数,再乘2就是两边一共放的盆数。要想保证取到两个颜色相同的球,可以先考虑最坏情况是每种颜色各取一个,那么再去一个一定有两个颜色相同的球,据此解答。
19.90261000;9026
解:最高位也就是千万位上的数是9,十万位上的数是2,万位上的数是6,千位上的数是1,其余各位上都是0,这个数写作90261000;省略万位后面的尾数约是9026万。
故答案为:90261000;9026。
既是奇数又是合数的个位数是9,既是质数又是偶数的数是2,一个数的最大因数是它本身,既不是质数又不是合数的数是1,据此写出这个数;省略万位后面的尾数,在万位上数的右下角点上小数点,再看千位上的数四舍五入,最后在数的末尾添一个“万”字。
20.4
解:火腿肠是圆柱体,不同的切法有:①与底面平行切,切面是圆形;②沿着底面直径切,切面是长方形;③斜着切一部分,从上底面斜着向侧面切;④沿着底面直径的左端斜切到下底面直径的右端,共4种不同的截面。
故答案为:4。
可以动手切一切,然后想一想,共4种不同的截面。
21.速度一定,路程和时间是成正比例的量(答案不唯一);长方形的面积一定,长和宽是成反比例的量(答案不唯一)
解:生活中哪两种量成正比例关系:速度一定,路程和时间是成正比例的量,生活中哪两种量成反比例关系:长方形的面积一定,长和宽是成反比例的量。
故答案为:速度一定,路程和时间是成正比例的量;长方形的面积一定,长和宽是成反比例的量。(答案不唯一)
相关联的两个量,一个量变化,另一个量也随着变化。如果这两个量相对应的数的比值一定,这两个量就是成正比例的量,他们的关系叫做正比例关系。相关联的两个量,一个量变化,另一个量也随着变化。如果这两个量相对应的数的积一定,这两个量就是成反比例的量,他们的关系叫做反比例关系。
22.90;30
解:圆锥的体积:60÷(3-1)=30(立方厘米);圆柱的体积:30×3=90(立方厘米)。
故答案为:90;30。
等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,等底等高的圆柱体积就是3份。用体积差除以份数差求出每份的体积,也就是圆锥的体积,进而求出圆柱的体积。
23.﹣5
解:200-195=5(g),因此记作-5g。
故答案为:-5。
根据题意可知:标准净重是200g,比标准净重多的重量记为正,比标准净重轻的则记为负,因为195<200,即比标准净重轻,所以200-195=5g,这5g就是比标准净重轻的部分,应该记为负,即-5g。
24.28.26
解:3.14×9=28.26(平方厘米)
故答案为:28.26。
正方形的边长就是圆的半径,正方形面积是9平方厘米,说明圆半径的平方就是9;用圆周率乘半径的平方即可求出圆的面积。
25.;
解:1÷7=,4÷7=(米)。
故答案为:;。
根据题意可知:把这根木料的长度看作单位“1”,平均分成了7份,所以,1÷7=每段占全长的分率;这根木料的长度÷平均分成的份数=每段木料的长度。
26.162.5
解:5000×3.25%×1=162.5(元)
故答案为:162.5。
利息=本金×利率×存期,根据公式计算利息即可。
27.75;15
解:“七五折”表示现价是原价的75%;原价是20元,现价是20×75%=15(元)。
故答案为:75;15。
几折就是现价是原价的几分之几或百分之几十,用原价乘折扣即可求出现价。
28.11n+6
解:17+(n-1)×11
=17+11n-11
=11n+6(根);
故答案为:11n+6。
由图可知,搭1顶帐篷需要17根钢管,搭2顶帐篷需要(17+11)根钢管,搭3顶帐篷需要(17+11+11)根钢管,据此可得,搭n顶帐篷需要[17+(n-1)×11]根钢管;据此解答。
29.130
解:180°-20°-30°
=160°-30°
=130°;
故答案为:130。
由图可知想,旋转的度数刚好等于∠BAC的度数,∠BAC=内角和-∠B-∠C,据此解答。
30.;-30
解:OB=OC
=×
=,所以点B表示的数是;
OA=OC÷5
=150÷5
=30,点A在原点的左边,所以点A表示的数是-30。
故答案为:;-30。
由图可知,点B是线段OC的中点,所以OB=OC;线段OD被平均分成5段,线段OA等于其中一段的长度,点A在原点的左边,记为“-”;据此解答。
31.1:2=4:8(答案不唯一)
解:8的因数有1、2、4、8,组成的比例是1:2=4:8。
故答案为:1:2=4:8。(答案不唯一)
先找出8的所有因数,然后写出两个比值相等的比并组成比例。
32.;0.6
解:4+1=5(段);
每段占全长的:1÷5=;
每段长:3÷5=0.6(米);
故答案为:;0.6。
根据题意可知,4次剪完,是把整根绳子平均分成(4+1)段,把整根绳子看作单位“1”,平均分成几段,每段就是几分之一;每段长度=总长度÷段数;据此解答。
33.100;72
解:80÷(1-20%)
=80÷80%
=100(千米);
60×(1+20%)
=60×120%
=72(千克);
故答案为:100;72。
80千米比多少千米少20%,是把后面的长度看作单位“1”,80千米是单位“1”的(1-20%),求单位“1”,用除法计算。比60千克多20%,是把60千克看作单位“1”,求60的(1+20%)是多少,用乘法计算。
34.40;24;0.375;37.5
解:3÷8===;
3÷8=(3×8)÷(8×8)=24÷64;
3÷8=0.375=37.5%;
故答案为:40;24;0.375;37.5。
除法与分数的关系:被除数作分子,除数作分母;分数的基本性质:分子与分母同时乘或除以同一个数(不为0),分数的大小不变;商不变的性质:被除数和除数同时乘或除以同一个数(不为0),商不变;小数化成百分数:将小数的小数点向右移动两位,再在末尾添上“%”;据此解答。
35.0.2;4.05;3050;78
解:2000÷10000=0.2,所以2000平方米=0.2公顷;
4+50÷1000
=4+0.05
=4.05,所以4吨50千克=4.05吨;
3.05×1000=3050,所以3.05立方米=3050立方分米;
1.3×60=78,所以1.3小时=78分;
故答案为:0.2;4.05;3050;78。
1公顷=10000平方米,1吨=1000千克,1立方米=1000立方分米,1小时=60分,据此进行单位换算。
36.6
解:1÷()
=1÷
=6(次)
故答案为:6。
把这批货物的总量看作单位“1”,根据题意可得:甲车每次运的货物数量=货物总量÷甲车运的次数=1÷10=,同理,乙车每次运的货物数量=1÷15=,则,两车同运需要的次数=货物总量÷(甲车每次运的货物数量+乙车每次运的货物数量),据此可以解答。
37.62.8
解:3.14×(4÷2)2×5
=3.14×20
=62.8(立方分米)
62.8立方分米=62.8升
故答案为:62.8。
圆柱的体积=底面积×高,根据体积公式计算容积即可。
38.正;反
解:x和y是两种相关联的量,并且x÷y=12,即商一定,那么x与y成正比例;
因为,所以xy=8,即积一定,因此,x与y成反比例。
故答案为:正;反。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用 yx=k(k一定,k不等于0)来表示。
39.b
解:如果a÷b=c(a、b、c均为整数,且b0),那么a和b的最大公因数是b。
故答案为:b。
根据已知可知a是b的倍数,b是a的因数,即b是a和b的公因数,且b的因数中最大的因数就是它本身即b,所以a和b的最大公因数是b。
40.折线
要表示一位病人一天的体温变化情况,用折线统计图比较合适。
故答案为:折线。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。
41.2.004;1.995
解:一个三位小数取近似数后是2.00,则这个三位小数可能是1.995,1.996,1.997,1.998,1.999,2.000,2.001,2.002,2.003,2.004,所以,这个三位小数最大是2.004,最小是1.995。
故答案为:2.004;1.995。
求小数近似数时,保留整数,表示精确到个位,把十分位“四舍五入”到个位;保留一位小数,表示精确到十分位,把百分位“四舍五入”到十分位;保留两位小数,表示精确到百分位,把千分位“四舍五入”到百分位……注意:在表示近似数时,小数末尾的0不能去掉。
42.50.24
解:75.36×(1-)
=75.36×
=50.24(dm3)
故答案为:50.24。
根据题意可知:要把圆柱削成一个最大的圆锥,则圆锥与圆柱等底等高,等底等高的圆锥的体积是圆柱体积的,则削去部分的体积就是圆柱体积的1-=,因此,削去部分的体积=圆柱体积×(1-)。
43.8;30
解:10+4-6
=14-6
=8(千克);
40-10=30(千克);
故答案为:8;30。
正负数主要用来表示具有相反意义的两种量,如果规定其中一个为正,那么相反的量就用负表示,超过平均体重用“+”表示,那么低于平均体重用”-”表示,A超过平均体重6千克,B低于平均体重10千克,D低于平均体重4千克,求出三人的总体重低于平均体重多少千克,那么C的体重就超过平均体重多少千克;B低于平均体重10千克,B的体重=平均体重-10千克,据此解答。
44.10;6
解:假设都是电动车,则小汽车有:
(52-16×2)÷(4-2)
=(52-32)÷2
=20÷2
=10(辆)
电动车:16-10=6(辆)
故答案为:10;6。
假设都是电动车,则共有32个轮子,比52少,因为每个小汽车少算了2个轮子,因此用一共少算的轮子数除以每辆小汽车少算的轮子数求出小汽车的辆数,进而求出电动车的辆数。
45.5210
解:5000×2.10%×2+5000
=105×2+5000
=210+5000
=5210(元)
故答案为:5210。
根据题意可知:本金是5000元,年利率是2.10%,时间是二年,所以,本金×利率×时间=利息,本金×利率×时间+本金=到期时取出的钱。
46.4;9;0.75;七五;七成五
解:75%=;
=;
75%=0.75;
75%=七五折;
75%=七成五。
故答案为:4;9;0.75;七五;七成五。
百分数转化成分数:先将百分数写成分母是100的分数,再化简;
百分数转化成小数:先将百分数的小数点向左移动两位,再去掉百分号“%”;
成数表示一个数是另一个数的十分之几,通称“几成”。几成改写成百分数就是百分之几十,几成几改写成百分数就是百分之几十几;
折扣:几折就表示十分之几,也就是百分之几十,几折就是现价占原价的百分之几十;
先根据比与分数的关系:前项:后项=,把比转化成分数形式,再根据分数的基本性质:分数的分子与分母同时乘或除以相同的数(0除外),分数的大小不变,进行解答即可。
47.274000000;3亿
解:二亿七千四百万写作:274000000,2740000003亿。
故答案为:274000000;3亿。
大数的写法:先找到计数单位分级,然后从最高位一级一级的写起,哪个数位上一个单位也没有就在那个数位上写0。注意:除最高级外每级都要写满四位。
大数的改写:(1)只改写计数单位,先分级,找到需要改写的计数单位后点上小数点,最后千万不要忘了加上计数单位;(2)改写计数单位并求近似数,先改写,再根据要求用“四舍五入”求近似数,是“舍”还是“入”,要看省略的尾数部分的最高位上的数是小于5还是等于或大于5。
48.(180﹣2m)度
解:(180-2m)度
故答案为:(180-2m)度。
三角形的内角和是180°,等腰三角形的两个底角相等,所以,底角×2=两个底角和,三角形的内角和-底角×2=顶角。
49.75%;80%
解:60÷80×100%=75%
20+60=80(棵),80+20=100(棵)
80÷100×100%=80%
故答案为:75%;80%。
根据题意可得:补种前成活棵数÷补种前植树棵数×100%=补种前的成活率;补种的成活棵数+补种前的成活棵数=这次植树活动总成活棵数,补种的棵数+补种前植树棵数=这次植树活动总植树棵数,这次植树活动总成活棵数÷这次植树活动总植树棵数×100%=这次植树活动最后的成活率。
50.50:1
解:2毫米=0.2厘米
10:0.2
=(10×10÷2):(0.2×10÷2)
=50:1
故答案为:50:1。
先统一单位:1厘米=10毫米,小单位转化成大单位除以进率;再根据:图上距离:实际距离=比例尺,列式化简即可。
专题6 填空题
一、填空题
1.(2024·沧县)把8000元存入银行2年,年利率是2.1%,到期后可得利息 元。
2.(2024·枣庄)如图,如果表示A的数对是(4,5),那么B( , ),C( , ),这个三角形的面积是 。
3.(2024·五莲模拟) 一条公路,甲队单独修8天完成,乙队单独修12天完成。两队合修4天,一共修了这项工程的 。
4.(2024·枣庄)用 块棱长1cm的正方体木块能摆成一个棱长1dm的正方体,将这些木块摆成一行,长 m。
5.(2024·五莲模拟)用小棒摆5正五边形,如图所示。
按照这样的方法,继续摆下去,摆第6幅图需要 根小棒,摆第n幅图需要 根小棒。
6.(2023·沂水)在横线里填写合适的分数。
已修的路程占这条路全长的 ,剩下的路程相当于已修路程的 。
7.(2024·五莲模拟)王奶奶把5000元钱存入银行,整存整取,年利率2.05%,到期后王奶奶可连本带息一共支取 元。
8.(2024·五莲模拟) 一幅地图的比例尺是1:5000000,在这幅地图上量得A、B两地的距离是3.2厘米,A、B两地的实际距离是 千米。
9.(2024·五莲模拟) 一根长3米圆柱形木材,锯成3段小圆柱后,表面积比原来增加了12.56平方分米,原来这根圆柱形木材的体积是 立方分米。
10.(2024·五莲模拟)如果a=b,(a、b均不为0),那么a与b成 比例,a:b= 。
11.(2023·鱼台)11只鸽子飞进4个鸽笼,总有一个鸽笼至少飞进了 只鸽子。
12.(2024·五莲模拟) 3升9毫升= 立方分米
4.2时= 时 分
2060平方米= 公顷
1.5吨= 千克
13.(2024·五莲模拟) 一个七位数,最高位上是最小的合数,万位上是最小的奇数,其他数位上都是0,这个数是 ,改写成用“万”作单位的数是 万,省略万位后面的尾数约是 万。
14.(2023·定陶)在比例尺是1:500000的地图上,量得甲、乙两地的距离约是12厘米,两地之间的实际距离大约是 千米。如在另一幅地图上量得甲、乙两地之间的距离是10厘米,这幅地图的比例尺是 。
15.(2023·定陶)如下图(单位:厘米)中,平行四边形的面积是72平方厘米,图中丙三角形的面积是甲三角形面积的 ,阴影部分的面积是 平方厘米。
16.(2023·定陶) 3÷4= :60= = %= (填小数)
17.(2023·定陶) 一个分数,分子分母的和是48,如果分子分母都加上1,所得分数约分后是,原来的分数是 。
18.(2023·定陶)在一条40米长的道路两边每隔2米放一盆花(两端都放),共放 盆花;把红、白、黄、蓝四种颜色的球各5个放到一个袋子里,至少取 个球,可以保证取到两个颜色相同的球。
19.(2023·定陶) 一个八位数,最高位上的数既是奇数又是合数,十万位上的数既是质数又是偶数,万位上的数的最大因数是6,千位上的数既不是质数也不是合数,其余各位上都是0,这个数写作 ,省略万位后面的尾数约是 万。
20.(2023·山亭)沿着物体不同的位置切下去,截面的形状居然也不相同,火腿肠沿不同的位置切下去,会有 种不同的截面。
21.(2023·山亭)生活中哪两种量成正比例关系: ,生活中哪两种量成反比例关系: 。
22.(2023·山亭)等底等高的一个圆柱和一个圆锥,体积相差60立方厘米,圆柱体的体积是 立方厘米,圆锥体的体积是 立方厘米。
23.(2023·鱼台)一种袋装食品标准净重为200g。质监部门为了解食品每袋净重与标准净重的误差,把食品净重205g记作+5g,那么食品净重为195g记作 g。
24.(2023·山亭)在下图中,正方形的面积是9平方厘米,这个圆的面积是 平方厘米。
25.(2023·鱼台)把一根长4米的木料截成7段,每段占全长的 ,每段长 米。
26.(2023·山亭)某银行的年利率是3.25%,5000元存一年,到期后应得利息 元。
27.(2023·山亭)山亭区水泉镇火樱桃采摘节期间,丰收火樱桃采摘园每斤打七五折销售,“七五折”表示现价是原价的 %,如果原价是20元,现价是 元。
28.(2023·沂水)如下图1所示,搭建单顶帐篷需要17根钢管,这样的帐篷按图2、图3的方式串起来搭建。如果想串起来搭建n顶帐篷,那么需要 根钢管。
29.(2023·沂水)如下图,△ABC绕点A顺时针旋转一定度数后得到△AB'C',已知∠B=20°,∠C=30°,这个三角形旋转了 °。
30.(2023·沂水)如下图直线上:若点C表示的数是,则点B表示的数是 ;若点D表示的数是150,则点A表示的数是 。
31.(2023·山亭)用8的4个因数组成一组比例是 。
32.(2023·沂水)把一根3米长的绳子剪成同样长的小段,每次剪一段,4次剪完。每段占全长的 ,每段长 米。
33.(2023·沂水) 80千米比 千米少20%;比60千克多20%是 千克。
34.(2023·沂水) 3÷8= = ÷64= (填小数)= %。
35.(2023·沂水) 2000平方米= 公顷 4吨50千克= 吨 3.05立方米= 立方厘米 1.3小时= 分
36.(2023·鱼台)一批货物,只用甲车运10次可运完,只用乙车运15次可运完。如果两辆车同时运 次可以运完。
37.(2023·山亭) 一个圆柱形油桶,从里面量底面直径是4分米,高是5分米。它的容积是 升。
38.(2023·鱼台)x与y是两种相关联的量,并且x÷y=12,那么x与y成 比例;如果,那么x与y成 比例。
39.(2023·鱼台)如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最大公因数是 。
40.(2023·山亭)要表示一位病人一天的体温变化情况,用 统计图比较合适。
41.(2023·高唐)一个三位小数取近似数后是2.00,这个三位小数最大是 ,最小是 。
42.(2023·鱼台)一个圆柱体积为75.36dm3,把它削成最大的圆锥,削去部分的是 dm3。
43.(2023·沂水)如下图,以A、B、C、D四人平均体重为基准,已用条形统计图表示出A、B、D三人体重(整千克数)。若画出表示C体重的条形图,则图中表示 千克;若平均体重是40千克,则B体重是 千克。
44.(2023·山亭)超市停车场里停有四轮小汽车和两轮电动车共16辆,这些车共有52个轮子,那么有 辆小汽车,有 辆电动车。
45.(2023·鱼台)居民王爷爷把5000元按整存整取存入银行,存二年定期,年利率2.10%,计划到期时连本带息取出。王爷爷到期时可取出 元。
46.(2023·鱼台) = :12=75%= (填小数)= 折= (填成数)
47.(2023·鱼台)2023年“五一”假期,经文化和旅游部数据中心测算,全国国内旅游出游合计接待游客二亿七千四百万人次,同比增长70.83%。二亿七千四百万写作 ,精确到亿位约是 。
48.(2023·高唐)一个等腰三角形的一个底角是m度,则顶角是 。
49.(2023·高唐)今年的植树活动中,光明小学五年级同学共植树80棵,结果成活了60棵,成活率为 ,后来补种了20棵,全部成活,这次植树活动最后的成活率为 。
50.(2023·鱼台)一个精密仪器零件实际长度是2毫米,画在一幅设计图上是10厘米。这幅图的比例尺是 。
答案解析部分
1.336
解:8000×2×2.1%=336元,所以到期后可得利息336元。
故答案为:336。
到期后可得的利息=存入银行的钱数×年份数×年利率,据此代入数据作答即可。
2.1;1;4;1;24cm2
解:B(1,1)
C(4,1)
S=(2×3)×(2×4)÷2
=6×8÷2
=48÷2
=24(cm2)
故答案为:1,1,4,1,24。
数对的第一个数表示列,第二个数表示行,据此得出B和C的数对;已知一个格子是2cm,三角形的底为3个格子,即2×3=6(cm),同样高为2×4=8(cm),然后根据“三角形面积=底×高÷2”计算得出该三角形的面积。
3.
解:
=
=;
故答案为:。
将这条公路看作单位”1“,甲队每天效率为,乙队每天效率为,工作总量=工作效率和×工作时间,据此求解。
4.1000;10
解:1dm=10cm
10×10×10=1000(块)
1000×1=1000(cm)=10m
故答案为:1000,10。
首先根据1dm=10cm,得到大正方体棱长为10cm,根据正方体体积=棱长×棱长×棱长,得到大正方体由10×10×10=1000(块)小正方体木块摆成,而每个小正方体棱长为1cm,故而摆成一行长1000×1=1000(cm),再根据1m=100cm换算单位即可。
5.25;4n+1
解:第一幅图:1+4=5(根),
第二幅图:1+4×2=9(根),
第三幅图:1+4×3=13(根),
第六幅图:1+4×6=25(根),
第n幅图:1+4×n=4n+1(根);
故答案为:25;4n+1。
观察图形,我们发现从第一幅图开始,每增加一幅图,小棒的数量就增加4根,第一幅图需要5根小棒,第二幅图需要9根小棒,第三幅图需要13根小棒,以此类推,由此可以推出第n幅图:1+4×n=4n+1(根);据此求解。
6.;
解:已修的路程占这条路全长的:5÷8=;
剩下的路程相当于已修路程的:3÷5=;
故答案为:;。
由图可知,整条路平均分成8份,已经修的路程是这样的5份,剩下的路程是这样的3份,求一个数是另一个数的几分之几,用除法计算;据此解答。
7.6025
解:5000×2.05%×3+5000
=1025+5000
=6025(元);
故答案为:6025。
根据利息=本金×利率×存期,求出利息,然后加上本金即可。
8.160
解:3.2÷=16000000厘米=160千米;
故答案为:160。
实际距离=图上距离÷比例尺,求出实际距离,再将厘米化成千米即可,据此求解。
9.94.2
解:12.56÷4=3.14(平方分米),
3米=30分米,
3.14×30=94.2(立方分米);
故答案为:94.2。
圆柱锯成3段,即锯了两次,每锯一次增加2个底面积,因此总共增加了4个底面积,先求出圆柱的底面积,再根据圆柱体积公式=底面积×高,据此求解。
10.正;3:4
解:a=b,所以a:b=:=3:4=,
比值一定,a与b成正比例;
故答案为:正;3:4。
根据比例的基本性质,两个外项的积等于两个内项的积,据此将式子变为比例,再化简,由于比值一定a与b成正比例,据此求解。
11.3
解:11÷4=2(只)……3(只)
2+1=3(只),即,总有一个鸽笼至少飞进了3只鸽子。
故答案为:3。
这是一个鸽巢问题,先把鸽子平均分到每一个鸽笼,鸽子总数÷鸽笼数量=平均每个鸽笼飞进的鸽子只数……剩下的鸽子只数,如果有剩余则不管飞到哪个鸽笼1只鸽子,则那个鸽笼都至少有(平均每个鸽笼飞进的鸽子只数+1)只鸽子,如果没有剩余,则总有一个鸽笼至少飞进了平均每个鸽笼飞进的鸽子只数。
12.3.009;4;12;0.206;1500
解:3升9毫升=3+9÷1000=3.009升=3.009立方分米;
4.2时=4时+0.2×60分=4时12分;
2060平方米=2060÷10000=0.206公顷;
1.5吨=1.5×1000=1500千克;
故答案为:3.009;4;12;0.206;1500。
1升=1立方分米=1000毫升,1时=60分,1公顷=10000平方米;1吨=1000千克,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
13.4010000;401;401
解:最小的合数是4,最小的奇数是1,
这个数是4010000,
4010000=401万;
故答案为:4010000;401;401。
根据整数的写法,从高位到低位,一级一级地写,最高位上是最小的合数,即4,万位上是最小的奇数,即1,其余数位上都是0,据此写出这个数,改写成以“万”作单位的数:改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字,省略“万”后面的尾数求它的近似数,要看万位的下一位千位上的数进行四舍五入,据此求解。
14.60;1:600000
解:12÷=6000000(厘米)=60千米;
10:6000000=1:600000;
故答案为:60;1:600000。
实际距离=图上距离÷比例尺;比例尺=图上距离:实际距离;据此解答。
15.;30
解:丙三角形的面积是甲三角形面积的: 7÷(5+7)
=7÷12
=;
阴影部分的面积是甲三角形面积的:5÷(5+7)
=5÷12
=,
阴影部分的面积:72××
=36×
=15(平方厘米);
故答案为:;15。
由图可知,丙三角形与甲三角形的高相等,丙的底边与甲的底边的比是7:(5+7);所以丙的面积与甲的面积的比也是7:(5+7);据此求出丙三角形的面积是甲三角形面积的几分之几。等底等高的三角形面积是平行四边形面积的一半,因此,乙面积+丙面积=甲面积=平行四边形面积;而乙的底边与甲的底边的比是5:(5+7),所以乙的面积与甲的面积的比也是5:(5+7);据此求出乙三角形面积是甲三角形面积的几分之几,再用甲三角形面积乘这个分率即可求出乙的面积。
16.45;12;75;0.75
解:3÷4=3:4=(3×15):(4×15)=45:60;
3÷4===;
3÷4=0.75=75%;
故答案为:45;12;75;0.75。
除法与比的关系:被除数作比的前项,除数作比的后项;比的基本性质:比的前项和后项同时乘或除以同一个数(不为0),比值不变;除法与分数的关系:被除数作分子,除数作分母;分数的基本性质:分子与分母同时乘或除以同一个数(不为0),分数的大小不变;小数转化成百分数:小数的小数点向右移动两位,再在后面添上“%”。
17.
解:48+1+1=50;
50÷(2+3)
=50÷5
=10;
得到的分数是:==;
原来的分数是:=;
故答案为:。
分子、分母都加上1,那么分子与分母的和就是(48+1+1);分数的基本性质:分子与分母同时乘或除以同一个数,分数的大小不变,因此,用所得分子与分母的和除以约分后分子与分母的和即可求出约分时,分子与分母同时除以的数;再用约分后的分数同时乘这个数即可求出所得的分数;最后用所得的分数的分子和分母同时减1求出原数;据此解答。
18.42;5
解:(40÷2+1)×2
=(20+1)×2
=21×2
=42(盆);
4+1=5(个);
故答案为:42;5。
两端植树问题中,全长÷间隔长度=间隔数,棵数=间隔数+1,据此求出一边的盆数,再乘2就是两边一共放的盆数。要想保证取到两个颜色相同的球,可以先考虑最坏情况是每种颜色各取一个,那么再去一个一定有两个颜色相同的球,据此解答。
19.90261000;9026
解:最高位也就是千万位上的数是9,十万位上的数是2,万位上的数是6,千位上的数是1,其余各位上都是0,这个数写作90261000;省略万位后面的尾数约是9026万。
故答案为:90261000;9026。
既是奇数又是合数的个位数是9,既是质数又是偶数的数是2,一个数的最大因数是它本身,既不是质数又不是合数的数是1,据此写出这个数;省略万位后面的尾数,在万位上数的右下角点上小数点,再看千位上的数四舍五入,最后在数的末尾添一个“万”字。
20.4
解:火腿肠是圆柱体,不同的切法有:①与底面平行切,切面是圆形;②沿着底面直径切,切面是长方形;③斜着切一部分,从上底面斜着向侧面切;④沿着底面直径的左端斜切到下底面直径的右端,共4种不同的截面。
故答案为:4。
可以动手切一切,然后想一想,共4种不同的截面。
21.速度一定,路程和时间是成正比例的量(答案不唯一);长方形的面积一定,长和宽是成反比例的量(答案不唯一)
解:生活中哪两种量成正比例关系:速度一定,路程和时间是成正比例的量,生活中哪两种量成反比例关系:长方形的面积一定,长和宽是成反比例的量。
故答案为:速度一定,路程和时间是成正比例的量;长方形的面积一定,长和宽是成反比例的量。(答案不唯一)
相关联的两个量,一个量变化,另一个量也随着变化。如果这两个量相对应的数的比值一定,这两个量就是成正比例的量,他们的关系叫做正比例关系。相关联的两个量,一个量变化,另一个量也随着变化。如果这两个量相对应的数的积一定,这两个量就是成反比例的量,他们的关系叫做反比例关系。
22.90;30
解:圆锥的体积:60÷(3-1)=30(立方厘米);圆柱的体积:30×3=90(立方厘米)。
故答案为:90;30。
等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,等底等高的圆柱体积就是3份。用体积差除以份数差求出每份的体积,也就是圆锥的体积,进而求出圆柱的体积。
23.﹣5
解:200-195=5(g),因此记作-5g。
故答案为:-5。
根据题意可知:标准净重是200g,比标准净重多的重量记为正,比标准净重轻的则记为负,因为195<200,即比标准净重轻,所以200-195=5g,这5g就是比标准净重轻的部分,应该记为负,即-5g。
24.28.26
解:3.14×9=28.26(平方厘米)
故答案为:28.26。
正方形的边长就是圆的半径,正方形面积是9平方厘米,说明圆半径的平方就是9;用圆周率乘半径的平方即可求出圆的面积。
25.;
解:1÷7=,4÷7=(米)。
故答案为:;。
根据题意可知:把这根木料的长度看作单位“1”,平均分成了7份,所以,1÷7=每段占全长的分率;这根木料的长度÷平均分成的份数=每段木料的长度。
26.162.5
解:5000×3.25%×1=162.5(元)
故答案为:162.5。
利息=本金×利率×存期,根据公式计算利息即可。
27.75;15
解:“七五折”表示现价是原价的75%;原价是20元,现价是20×75%=15(元)。
故答案为:75;15。
几折就是现价是原价的几分之几或百分之几十,用原价乘折扣即可求出现价。
28.11n+6
解:17+(n-1)×11
=17+11n-11
=11n+6(根);
故答案为:11n+6。
由图可知,搭1顶帐篷需要17根钢管,搭2顶帐篷需要(17+11)根钢管,搭3顶帐篷需要(17+11+11)根钢管,据此可得,搭n顶帐篷需要[17+(n-1)×11]根钢管;据此解答。
29.130
解:180°-20°-30°
=160°-30°
=130°;
故答案为:130。
由图可知想,旋转的度数刚好等于∠BAC的度数,∠BAC=内角和-∠B-∠C,据此解答。
30.;-30
解:OB=OC
=×
=,所以点B表示的数是;
OA=OC÷5
=150÷5
=30,点A在原点的左边,所以点A表示的数是-30。
故答案为:;-30。
由图可知,点B是线段OC的中点,所以OB=OC;线段OD被平均分成5段,线段OA等于其中一段的长度,点A在原点的左边,记为“-”;据此解答。
31.1:2=4:8(答案不唯一)
解:8的因数有1、2、4、8,组成的比例是1:2=4:8。
故答案为:1:2=4:8。(答案不唯一)
先找出8的所有因数,然后写出两个比值相等的比并组成比例。
32.;0.6
解:4+1=5(段);
每段占全长的:1÷5=;
每段长:3÷5=0.6(米);
故答案为:;0.6。
根据题意可知,4次剪完,是把整根绳子平均分成(4+1)段,把整根绳子看作单位“1”,平均分成几段,每段就是几分之一;每段长度=总长度÷段数;据此解答。
33.100;72
解:80÷(1-20%)
=80÷80%
=100(千米);
60×(1+20%)
=60×120%
=72(千克);
故答案为:100;72。
80千米比多少千米少20%,是把后面的长度看作单位“1”,80千米是单位“1”的(1-20%),求单位“1”,用除法计算。比60千克多20%,是把60千克看作单位“1”,求60的(1+20%)是多少,用乘法计算。
34.40;24;0.375;37.5
解:3÷8===;
3÷8=(3×8)÷(8×8)=24÷64;
3÷8=0.375=37.5%;
故答案为:40;24;0.375;37.5。
除法与分数的关系:被除数作分子,除数作分母;分数的基本性质:分子与分母同时乘或除以同一个数(不为0),分数的大小不变;商不变的性质:被除数和除数同时乘或除以同一个数(不为0),商不变;小数化成百分数:将小数的小数点向右移动两位,再在末尾添上“%”;据此解答。
35.0.2;4.05;3050;78
解:2000÷10000=0.2,所以2000平方米=0.2公顷;
4+50÷1000
=4+0.05
=4.05,所以4吨50千克=4.05吨;
3.05×1000=3050,所以3.05立方米=3050立方分米;
1.3×60=78,所以1.3小时=78分;
故答案为:0.2;4.05;3050;78。
1公顷=10000平方米,1吨=1000千克,1立方米=1000立方分米,1小时=60分,据此进行单位换算。
36.6
解:1÷()
=1÷
=6(次)
故答案为:6。
把这批货物的总量看作单位“1”,根据题意可得:甲车每次运的货物数量=货物总量÷甲车运的次数=1÷10=,同理,乙车每次运的货物数量=1÷15=,则,两车同运需要的次数=货物总量÷(甲车每次运的货物数量+乙车每次运的货物数量),据此可以解答。
37.62.8
解:3.14×(4÷2)2×5
=3.14×20
=62.8(立方分米)
62.8立方分米=62.8升
故答案为:62.8。
圆柱的体积=底面积×高,根据体积公式计算容积即可。
38.正;反
解:x和y是两种相关联的量,并且x÷y=12,即商一定,那么x与y成正比例;
因为,所以xy=8,即积一定,因此,x与y成反比例。
故答案为:正;反。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用 yx=k(k一定,k不等于0)来表示。
39.b
解:如果a÷b=c(a、b、c均为整数,且b0),那么a和b的最大公因数是b。
故答案为:b。
根据已知可知a是b的倍数,b是a的因数,即b是a和b的公因数,且b的因数中最大的因数就是它本身即b,所以a和b的最大公因数是b。
40.折线
要表示一位病人一天的体温变化情况,用折线统计图比较合适。
故答案为:折线。
条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图能表示部分与整体之间的关系。
41.2.004;1.995
解:一个三位小数取近似数后是2.00,则这个三位小数可能是1.995,1.996,1.997,1.998,1.999,2.000,2.001,2.002,2.003,2.004,所以,这个三位小数最大是2.004,最小是1.995。
故答案为:2.004;1.995。
求小数近似数时,保留整数,表示精确到个位,把十分位“四舍五入”到个位;保留一位小数,表示精确到十分位,把百分位“四舍五入”到十分位;保留两位小数,表示精确到百分位,把千分位“四舍五入”到百分位……注意:在表示近似数时,小数末尾的0不能去掉。
42.50.24
解:75.36×(1-)
=75.36×
=50.24(dm3)
故答案为:50.24。
根据题意可知:要把圆柱削成一个最大的圆锥,则圆锥与圆柱等底等高,等底等高的圆锥的体积是圆柱体积的,则削去部分的体积就是圆柱体积的1-=,因此,削去部分的体积=圆柱体积×(1-)。
43.8;30
解:10+4-6
=14-6
=8(千克);
40-10=30(千克);
故答案为:8;30。
正负数主要用来表示具有相反意义的两种量,如果规定其中一个为正,那么相反的量就用负表示,超过平均体重用“+”表示,那么低于平均体重用”-”表示,A超过平均体重6千克,B低于平均体重10千克,D低于平均体重4千克,求出三人的总体重低于平均体重多少千克,那么C的体重就超过平均体重多少千克;B低于平均体重10千克,B的体重=平均体重-10千克,据此解答。
44.10;6
解:假设都是电动车,则小汽车有:
(52-16×2)÷(4-2)
=(52-32)÷2
=20÷2
=10(辆)
电动车:16-10=6(辆)
故答案为:10;6。
假设都是电动车,则共有32个轮子,比52少,因为每个小汽车少算了2个轮子,因此用一共少算的轮子数除以每辆小汽车少算的轮子数求出小汽车的辆数,进而求出电动车的辆数。
45.5210
解:5000×2.10%×2+5000
=105×2+5000
=210+5000
=5210(元)
故答案为:5210。
根据题意可知:本金是5000元,年利率是2.10%,时间是二年,所以,本金×利率×时间=利息,本金×利率×时间+本金=到期时取出的钱。
46.4;9;0.75;七五;七成五
解:75%=;
=;
75%=0.75;
75%=七五折;
75%=七成五。
故答案为:4;9;0.75;七五;七成五。
百分数转化成分数:先将百分数写成分母是100的分数,再化简;
百分数转化成小数:先将百分数的小数点向左移动两位,再去掉百分号“%”;
成数表示一个数是另一个数的十分之几,通称“几成”。几成改写成百分数就是百分之几十,几成几改写成百分数就是百分之几十几;
折扣:几折就表示十分之几,也就是百分之几十,几折就是现价占原价的百分之几十;
先根据比与分数的关系:前项:后项=,把比转化成分数形式,再根据分数的基本性质:分数的分子与分母同时乘或除以相同的数(0除外),分数的大小不变,进行解答即可。
47.274000000;3亿
解:二亿七千四百万写作:274000000,2740000003亿。
故答案为:274000000;3亿。
大数的写法:先找到计数单位分级,然后从最高位一级一级的写起,哪个数位上一个单位也没有就在那个数位上写0。注意:除最高级外每级都要写满四位。
大数的改写:(1)只改写计数单位,先分级,找到需要改写的计数单位后点上小数点,最后千万不要忘了加上计数单位;(2)改写计数单位并求近似数,先改写,再根据要求用“四舍五入”求近似数,是“舍”还是“入”,要看省略的尾数部分的最高位上的数是小于5还是等于或大于5。
48.(180﹣2m)度
解:(180-2m)度
故答案为:(180-2m)度。
三角形的内角和是180°,等腰三角形的两个底角相等,所以,底角×2=两个底角和,三角形的内角和-底角×2=顶角。
49.75%;80%
解:60÷80×100%=75%
20+60=80(棵),80+20=100(棵)
80÷100×100%=80%
故答案为:75%;80%。
根据题意可得:补种前成活棵数÷补种前植树棵数×100%=补种前的成活率;补种的成活棵数+补种前的成活棵数=这次植树活动总成活棵数,补种的棵数+补种前植树棵数=这次植树活动总植树棵数,这次植树活动总成活棵数÷这次植树活动总植树棵数×100%=这次植树活动最后的成活率。
50.50:1
解:2毫米=0.2厘米
10:0.2
=(10×10÷2):(0.2×10÷2)
=50:1
故答案为:50:1。
先统一单位:1厘米=10毫米,小单位转化成大单位除以进率;再根据:图上距离:实际距离=比例尺,列式化简即可。
同课章节目录
