河南省信阳市2024-2025学年高一下学期4月期中考试数学(pdf版,含详解)
文档属性
| 名称 | 河南省信阳市2024-2025学年高一下学期4月期中考试数学(pdf版,含详解) |

|
|
| 格式 | |||
| 文件大小 | 486.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 22:02:21 | ||
图片预览




文档简介
河南省信阳市 2024-2025 学年高一下学期 4 月期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
2
1.已知 i是虚数单位, 1 i ( )
A.-i B. i C.1- i D.1 i
2. cos
π
q
sin π -q π cos -q sin π q 的值等于( )
è 3 ÷ 6 ÷ 6 ÷ ÷
è è è 3
A 3. B.1 C.0 D 1.
2 2
r r 5π r r3.已知向量 a ,b 的夹角为 ,且 a 2 3 b ar
r
,则 在b 上的投影向量为(
6 )
r r r r
A. -3b B.- 3b C.3b D. 3b
y sin π 1 4.函数 - x ÷, x [-2π,2π]的单调递增区间是(3 2 )è
é π , 5π ù é 5π π ùA. ê- ú B. ê- , 3 3 3 3 ú
é
C. ê-2π,
π
- ù é
5π ,2πù é-2π, 5π- ù é π ù和 D. 和 ,2π
3 ú ê 3 ú ê 3 ú ê 3 ú
r r r r r r5.已知向量 a ,b 满足 a (1, 2)
r
,b (-2, y) r,且 a∥b ,则 a b ( )
A. 5 B.4 C.5 D.5 2
6.已知函数 f (x)
π
tan 2x - ÷ ,则下列说法错误的是(3 )è
π
A.函数 f (x) 的最小正周期为T 2
B.函数 f (x)
ì 5π kπ
的定义域为 íx x ,k
ü
Z
12 2
π kπC .函数 f (x) 的图象的对称中心为 ,0÷ , k Z
è 6 2
D.函数 f (x)
π kπ 5π kπ
的单调递增区间为 - , , k Z
è 12 2 12 2 ÷
7.将函数 f (x) sin x - 3 cos x 1图象上所有点的横坐标缩小为原来的 2 (纵坐标不变),再
将所得曲线上所有的点向左平移a(a > 0)个单位长度,得到函数 g(x)的图象,若 g(x)的图象
关于 y 轴对称,则 a的最小值是( )
5π 5π π πA. B. C12 .6 3
D.
6
8.在VABC 中,角A , B ,C 的对边分别为 a,b , c,且面积为S .若
bcosC c cos B a sin A, S
1
b2 a2 - c2 ,则角 B 等于( )4
p p p p
A. B. C. D.
2 3 6 4
二、多选题
z 2 11i9.已知 i是虚数单位,复数 ,则下列说法正确的是( )
2 i
A.复数 z 的虚部为 4i B. z 3- 4i
C. z 5 D. z 在复平面内对应的点在第二象限
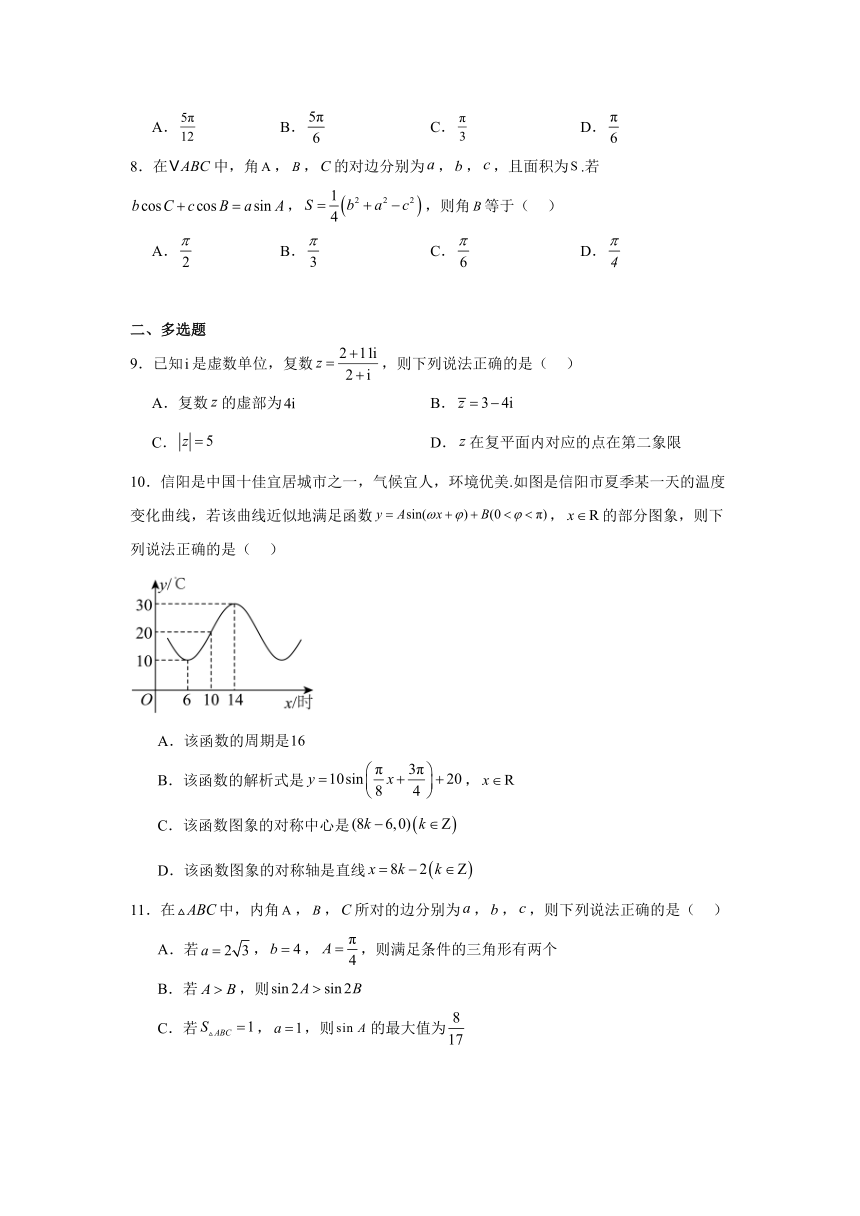
10.信阳是中国十佳宜居城市之一,气候宜人,环境优美.如图是信阳市夏季某一天的温度
变化曲线,若该曲线近似地满足函数 y Asin(wx j) B(0 < j < π), x R 的部分图象,则下
列说法正确的是( )
A.该函数的周期是16
y 10sin π x 3π B.该函数的解析式是 ÷ 20, x R
è 8 4
C.该函数图象的对称中心是 (8k - 6,0) k Z
D.该函数图象的对称轴是直线 x 8k - 2 k Z
11.在VABC中,内角A , B ,C 所对的边分别为 a,b , c,则下列说法正确的是( )
A πA.若a 2 3 ,b 4 , ,则满足条件的三角形有两个4
B.若 A > B ,则 sin 2A > sin 2B
8
C.若 SVABC 1, a 1,则 sin A 的最大值为17
uuur uuur uuur uuur
AB AC
uuur
÷ uAuBur uAuCur 1D.若 uuur uuur × BC 0,且 × ,则VABC 为等边三角形
è AB AC
÷ AB AC 2
三、填空题
uuur r uuur r uuur
12.如图,在VABC 中,D是BC 上靠近 B 的一个三等分点,AB=a ,AC b ,则 AD 可以用
r r
a ,b 表示为 .
π π
13 é ù.若j 是三角形的一个内角,且函数 y 2sin(3x j)在区间 ê- ,9 12 ú 上单调递增,则
j 的
取值范围为 .
π
14.已知函数 f (x) a cos x 1- a2 sin 2x(0 < a 1) 的图象关于直线 x 对称,若方程12
f (x) m(m R) é在 ê0,
π ù
4 ú上恰有
1 个实数根,则m 的取值范围是 .
四、解答题
r r
15.已知向量 a cos x,sin x ,b 3,- 3 , x 0, π .
r
(1) ar若 ^ b ,求 x 的值;
r
(2)记 f (x) r a ×b 1,求 f (x) 的最大值和最小值以及对应的 x 的值.
16.如图,在平面直角坐标系 xOy 中,以 x 轴正半轴为始边的锐角a 与钝角 b 的终边与单位
圆分别交于 A,B 两点,x 5轴正半轴与单位圆交于点 M,已知 SVOAM ,点 B 的纵坐标是5
2
.
10
(1)求 cos a - b 的值;
(2)求 2a - b 的值.
17.近年来,西安市长安区认真践行“绿水青山就是金山银山”生态文明理念,围绕良好的生
态禀赋和市场需求,深挖冷水鱼产业发展优势潜力,现已摸索出以虹鳟、鲟鱼等养殖为主方
向,为扩大养殖规模,某鲟鱼养殖场计划在如图所示的扇形区域OMN 内修建矩形水池
π
ABCD,矩形一边 AB 在OM 上,点C在圆弧MN 上,点D在边ON 上,且 MON ,OM 60
3
米,设 COM a .
(1)求扇形OMN 的面积;
(2)求矩形 ABCD的面积 S(a ) ;当a 为何值时, S(a ) 取得最大值,并求出这个最大值.
18.在VABC 中,内角 A,B,C 的对边分别为 a,b,c,已知 2cos A(c cos B bcosC) a .
(1)求 A;
(2)若VABC 为锐角三角形,且 a 3,求b2 c2 3bc的取值范围.
19.若函数 f (x) 在定义域区间[a,b]上连续,对任意 x , x [a,b]
x x
恒有 f ( 1 21 2 ) 2
f (x1) f (x2 ) ,则称函数 f (x) [a,b] f (
x1 x2 ) f (x1) f (x )是区间 上的上凸函数,若恒有 2 ,
2 2 2
则称函数 f (x) 是区间[a,b]上的下凸函数,当且仅当 x1 x2 时等号成立,这个性质称为函数
的凹凸性.上述不等式可以推广到取函数定义域中的任意 n 个点,即若 f (x) 是上凸函数,
x , x ,L, x [a,b] f ( x1 x2 ××× xn ) f (x1) f (x2 ) ××× f (x )则对任意 1 2 n 恒有 n ,若 f (x) 是下n n
凸函数,则对任意 x1, x2 ,L, x [a,b] f (
x1 x2 ××× xn ) f (x1) f (x2 ) ××× f (x恒有 n
)
n ,当n n
且仅当 x1 x2 × × × xn时等号成立.应用以上知识解决下列问题:
(1)判断函数 f (x) ax2 bx c ( a 0,x R ),g(x) sin x ,x (0, π)在定义域上是上凸函
数还是下凸函数;(只写出结论,不需证明)
(2)利用(1)中的结论,在VABC 中,求 sin A sin B sin(A B) 的最大值;
(3)证明函数 h(x) a ln
1
- x2 2- a 0 是上凸函数.
x x
河南省信阳市 2024-2025 学年高一下学期 4 月期中数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C A C A D BC ABD
题号 11
答案 ACD
1.C
2 2 1- i 2 - 2i
【详解】 1- i1 i 1 i 1- i 2 ,
故选:C.
2.B
π π π π π π π
【详解】 cos q ÷sin -q ÷ cos -q ÷sin q ÷ sin q -q ÷ sin 1,
è 3 è 6 è 6 è 3 è 3 6 2
故选:B.
3.A
r r
r r r 5π b r 3 b r
【详解】 a 在b 上的投影向量为 a cos r 2 3 b 6
-
2 ÷b ÷
r -3b .
è b
故选:A
4.C
π 1
【详解】 f (x) sin( - x) -sin(
1 x π- )
3 2 2 3 ,
z 1令 x
π
- ,
2 3
函数 y
π 3π
sin z é ù的单调递减区间为 ê2kπ , 2kπ 2 2 ú
(k Z) .
2kπ π 1 x π 2kπ 3π由 - , k Z,
2 2 3 2
得 4kπ+
5π
x 4kπ 11π , k Z ,
3 3
而 x -2π,2π é π ù 5π,所以所求单调递增区间是 ê-2π, - 3 ú 和
[ , 2π]
3 .
故选:C.
5.A
r ra (1, 2) b (-2, y) ar
r
【详解】因为 , , ∥b ,
r
所以1 y - 2 -2 0,则 y -4 ,故b (-2,-4),
ar
r r r
所以 b (-1, -2) ,则 a b -1 2 -2 2 5 .
故选:A.
6.C
f (x) tan 2x π- T π【详解】对于 A,函数 ÷ 的最小正周期 ,A 正确;
è 3 2
π π
对于 B,由 2x - kπ
5π kπ
, k Z,得 x , k Z,
3 2 12 2
ì 5π kπ ü
所以函数 f x 的定义域为 íx | x , k Z ,B 正确;
12 2
2x π kπ π kπ对于 C,由 - , k Z,得 x , k Z,
3 2 6 4
所以函数 f x π kπ的对称中心为 ,0
÷, k Z,C 错误;
è 6 4
π
对于 D,由- kπ<2x
π π kπ π kπ x 5π kπ- < , k Z,得- < < , k Z,
2 3 2 12 2 12 2
π kπ 5π kπ
所以函数 f x 的单调递增区间为 - , , k Z,D 正确.
è 12 2 12 2 ÷
故选:C
7.A
【详解】 f (x) sin x - 3 cos x 可化为 f (x) 2
1 3
sin x - cos x2 2 ÷÷
,
è
所以 f (x) 2sin
x
π
-
3 ÷
,
è
由条件可得 g(x) 2sin
2x 2a
π
- ÷ ,
è 3
因为函数 g(x)的图象关于 y 轴对称,所以函数 g x 为偶函数,
2a π kπ π所以 - , k Z,
3 2
a kπ 5π所以 , k Z,又 a > 0,
2 12
所以 a
5π
的最小值为 12 ,
故选:A.
8.D
【详解】因为bcosC c cos B a sin A,
所以由正弦定理得 sin B cosC sin C cos B sin Asin A ,
所以 sin(B C) sin(p - A) sin A sin2 A,
因为 sin A 0 ,所以 sin A 1,
因为 A (0,p ) A
p
,所以 ,
2
1 2 2 2 1 1
因为 S b a - c 2ab cosC absin C ,4 4 2
所以 tan C 1,
p
因为C
0, 2 ÷
,
è
p
所以C ,
4
p p p
所以B p - A - C p - - ,
2 4 4
故选:D
9.BC
2 11i 2 11i 2 - iz 4 - 2i 22i 11【详解】因为 3 4i2 i 2 i 2 ,- i 5
所以复数 z 的虚部为 4,A 错误;
因为 z 3 4i ,所以 z 3 - 4i ,B 正确,
因为 z 3 4i ,所以 z 32 42 5,C 正确;
复数 z 3 4i 在复平面内对应的点的坐标为 3,4 ,该点位于复平面的第一象限内,D 错误;
故选:BC.
10.ABD
【详解】对于 A 选项,由图象可知,该函数的最小正周期为T 2 14 - 6 16,A 选项正
确;
ì A B 30 ì A 10
对于 B 选项,由图象可得 í ,解得 ,
-A B 10
í
B 20
w 2p 2p p ,
T 16 8
Q图象经过点 14,30 ,
\30 10sin π 14 j
÷ 20,
è 8
\sin 7π j
÷ 1 .
è 4
Q0 < j < π 7π 7π j 11π 7π 5π 3π,\ < < ,则 j ,\j ,
4 4 4 4 2 4
y 10sin π x 3π 所以,函数解析式为 ÷ 20 , x R ,B 选项正确;
è 8 4
π 3π
对于 C 选项,令 x kπ, k Z,可得 x 8k - 6, k Z,
8 4
所以函数 y 10sin
π x 3π ÷ 20 图象的对称中心为 (8k - 6, 20) k Z ,C 选项错误;
è 8 4
π x 3π kπ+ π对于 D 选项,令 , k Z,可得 x 8k - 2, k Z,
8 4 2
所以函数 y 10sin
π
x
3π
÷ 20 图象的对称轴是直线 x 8k - 2 k Z ,故 D 选项正确.
è 8 4
故选:ABD.
11.ACD
π
【详解】A 选项,若 a 2 3 ,b 4 , A 4 ,
则bsinA 4 2 2 2 ,所以bsinA < a < b ,
2
所以满足条件的三角形有两个,所以 A 选项正确.
π π π
B 选项,若 A > B ,如 A ,B , 2A π , 2B ,
2 4 2
则 sin2A 0, sin2B 1,故 sin2A < sin2B ,所以 B 选项错误.
S 1C 选项, VABC bcsinA 1,bc
2
,
2 sinA
cosA b
2 c2 -1
余弦定理得 ,故 2bc ×cosA b2 c2 -1
2bc
2 2× ×cosA b2 c2 -1 2bc 2-1 2 × -1,
sinA sinA
4cosA 4
即 -1,当且仅当b c 时等号成立,
sinA sinA
1
由于三角形中, sinA > 0,所以 4cosA 4 - sinA, cosA 1- sinA > 0,
4
2
cos2 A 1 1- sinA 则 ,又 cos2 ÷ A 1- sin
2 A,
è 4
2
2 1 17 即1- sin A 1- sinA÷ ,整理得4
sinA -1÷ ×sinA 0,
è è 8
记得0 < sinA
8 8
,所以 sin A 的最大值为 ,所以 C 选项正确.
17 17
uuur uuur
uAuBur uuur
AC
D 选项, 表示 AB 方向的单位向量; uuur
uuur
AB 表示 AC 方向的单位向量,AC
uuur uuur
uAuBur uAuC根据平面向量加法的几何意义可知 ur 与 BACAB AC 的角平分线共线,
uuur uuur
uAuBur uAC
uuur
由 uur ÷ × BC 0可知 BAC 的角平分线与BC 垂直,
AB AC ֏
所以三角形 ABC 是等腰三角形.
uuur uuur
uAuBur uAC× uur 1 1 cosA cosA 1 > 0 A π而 A AB AC 2 ,所以 为锐角,且 ,3
所以VABC 是等边三角形.
故选:ACD
uuur 2 r 1 r
12. AD a b
3 3
uuur 1 uuur
【详解】因为D是BC 上靠近 B 的一个三等分点,所以BD BC ,
3
uuur r uuur r
又 AB=a , AC b ,
uuur uuur uuur uuur 1 uuur uuur 1 uuur uuur r r r r r所以 AD AB BD AB BC AB AC AB a 1 b 1 2 1- - a a b3 3 3 3 3 3 ,
uuur 2 r 1 r
故答案为: AD a b .
3 3
13. 0,
π ù
è 4 ú
π x π π π【详解】由- ,可得- j 3x j j ,
9 12 3 4
又j 是三角形的一个内角,所以0 < j < π,
π π
故- < - j
2π π π j 5π< , < < ,
3 3 3 4 4 4
é π π ù
因为函数 y 2sin(3x j)在区间 ê- ,9 12 ú 上单调递增,
ì π π
- - j
2 3 π π
í ,解得- j ,又0 < j < π,
π π j 6 4
4 2
j π ù所以 的取值范围为 0, ,
è 4 ú
π ù
故答案为: 0,
è 4 ú
.
ì 1 3 ü
14. ím m < m 1
或
2 2
【详解】因为 f x a cos 2x 1- a2 sin 2x sin 2x j ,其中 tanj
a
,
1- a2
π
又函数 f x 的图像关于直线 x 对称,且0 < a 1,
12
π π π 3 1 3
所以 f ÷ a cos 1- a
2 sin a 1- a2 1,解得 a ,
è12 6 6 2 2 2
f x 3 cos 2x 1 sin 2x sin 2x π 所以
2 2 3 ÷
,
è
x é π π π 5π当
ù é ù
ê
0, ú 时,令 t 2x 4 3 ê
,
3 6 ú
,
因为方程 f (x) m(m R) é0,
π ù é π π ù
在 ê ú上恰有 14 个实数根,且函数
g t sin t 在 ,
ê 3 2 ú
上单调递
é π , 5π ù增,在 ê ú上单调递减, 2 6
g π sin π 3 , g 5π π 1 sin , g π ÷ ÷ ÷ 1,
è 3 3 2 è 6 6 2 è 2
ì ü
所以 ím
1
m 3< 或m 1 .
2 2
ì 1 ü
故答案为: ím m
3
< 或m 1
2 2
π
15.(1)
3
5π
(2) x 0时, f (x) 的最大值为 4; x 时, f (x) 的最小值为
6 1- 2 3
r r
【详解】(1)因为 a cosx,sinx r,b 3,- 3 r, a ^ b ,
所以3cosx - 3sinx 0.
若 cosx 0,则 sinx 0,与 sin2x cos2x 1矛盾,
故 cosx 0,于是 tanx 3 .又 x 0, π ,
π
所以 x 3 .
f x ar
r
(2) ×b cosx,sinx × 3, - 3 1
3cosx - 3sinx 1 2 3cos x π
÷ 1.
è 6
因为 x 0, π x π π 7π,所以 é , ù -1 cos x π 3ê ,从而
6 6 6 ú 6 ÷
.
è 2
所以1- 2 3 2 3cos
x
π
÷ 1 4,
è 6
π π
于是,当 x ,即 x 0时, f x 取到最大值 4;
6 6
π 5π
当 x π ,即 x 时, f x 取到最小值
6 6 1- 2 3
.
16 1 10 π.( )- ;(2) 2α - β - .
10 4
【详解】解:(1)由题意,OA OM 1.
QS 1 5 aVOAM ×OAsina ×OM , 为锐角,2 5
\ sina 2 5 ,cosa 1-sin2 a 5 .
5 5
2
又点 B 的纵坐标是 且 b 为钝角,
10
\ sin b 2 , cos b - 1 7 2- sin2 b - .
10 10
\cos a - b cosa cos b sina sin b
5 7 2 2 5 2 10
- - .5 è 10
÷÷
5 10 10
2
2 5 (2)Qcos 2a 2cos a 3-1 2 ÷÷ -1 - ,
è 5 5
sin 2a 2sina cosa 2 5 5 4 2 ,
5 5 5
\2a p ,p
p
÷ , b ,p
p p
÷,\2a - b
- , ÷ .
è 2 è 2 è 2 2
又Qsin 2a - b sin 2a cos b - cos 2a sin b 4 7 2 - - 3 2 2 ÷÷ - ÷ - ,5 è 10 è 5 10 2
故 2α - β
π
- .
4
17.(1) 600π平方米;
(2) S(a ) 1200 3 sin(2a
π
) 600 3(0 a π π- < < ),当a 时,S a 取得最大值
6 3 6 600 3
平方
米.
MON π【详解】(1)依题意, ,扇形半径即OM 60米,
3
1 π
则扇形 OMN 2的面积为 60 600π平方米.
2 3
(2)在RtVOBC 中,BC 60sina ,OB 60cosa ,
在RtVOAD中, AD BC 60sina OA AD 3,则 60sina ,
3 3
于是 AB OB - OA 60cosa - 20 3 sina ,
则矩形 ABCD面积 S(a ) AB × BC 60sina (60cosa - 20 3 sina )
1200 3( 3 sina cosa - sin2 a ) 1200 3( 3 sin 2a 1 cos 2a 1- )
2 2 2
1200 3 sin(2a π ) - 600 3 0 a π, < < ,
6 3
π π
所以 S(a ) 1200 3 sin(2a ) - 600 3(0 < a < );
6 3
0 a π π 2a π 5π由 < < ,得 < < ,则当2a
π π π
时,即a 时, S(a ) 600 3 ,
3 6 6 6 6 2 6 max
π
所以当a 时, S a 取得最大值,最大值为600 3 平方米.6
π
18.(1)
3
(2) 11,15
【详解】(1)根据题意,由正弦定理得
2cos A(sin C cos B sin B cosC) 2cos Asin B C 2cos Asin A sin A,
又在VABC 中,有 A 0, π ,所以 sin A 0 ,
所以 cos A
1 π
,所以 A .
2 3
2π
(2 1 sin A 3)结合( )可得 ,B C π - A ,
2 3
a b c
由 a 3,则根据正弦定理有 2,得b 2sin B , c 2sin C ,sin A sin B sin C
根据余弦定理有 a2 b2 c2 - 2bc cos A,得b2 c2 3 bc,
b2 2所以 c 3bc 3 4bc 3 16sin B sin C 3 16sin B sin
2π
- B
3 ֏
3 8 3 sin B cos B 8sin2 B 7 4 3 sin 2B - 4cos 2B π 7 8sin 2B -
÷,
è 6
ABC B 0,
π 2π - B 0, π B π π , 又V 为锐角三角形,则有 , ,得 ,
è 2 ÷ 3 ÷ ÷ è 2 è 6 2
所以 2B
π π 5π π 1
- , sin 2B - ,所以
,1ù,
6 6 6 ÷ 6 ÷ è è è 2 ú
b2 c2 π故 3bc 7 8sin
2B -
6 ÷
11,15 .
è
19.(1)答案见解析;
(2) 3 3 ;
2
(3)证明见解析.
【详解】(1)函数 f (x) ax2 bx c a 0 "x , x R f ( x1 x2 ) f (x1) f (x2 ) , , 1 2 , -2 2
x x 2 2
a( 1 2 )2 b( x1 x2 ) c ax1 bx1 c ax2 bx2 c a- - (x 2
2 2 2 4 1
- x2 ) ,
a 0 f ( x1 x2 ) f (x ) f (x )当 > 时, 1 2 , f (x) 是下凸函数;
2 2
x x f (x ) f (x )
当 a < 0时, f ( 1 2 ) 1 2 , f (x) 是上凸函数,
2 2
"x , x (0, π), x x g( x1 x2 ) g(x1) g(x2 ) sin x1 x2 sin x1 sin x21 2 1 2 , - -2 2 2 2
sin x1 cos x2 x cos 1 sin x2 sin x1 cos x- 1 - cos x2 sin x2
2 2 2 2 2 2 2 2
(sin x2 - sin x1 )(cos x1 - cos x2 ) 0 x1 x2 π x x x x,显然 < < ,则 sin 2 sin 1 , cos 1 cos 2 ,
2 2 2 2 2 2 2 2 2 2 2
x
因此 g( 1
x2 ) g(x1) g(x 2 ) ,函数 g(x)是上凸函数.
2 2
(2)由(1)知函数 y sin x , x (0, π)是上凸函数,
在VABC 中, sin A sin B sin(A B) sin A sin B sin C A B C sin sin π 3 ,
3 3 2
3 3 π
即 sin A sin B sin(A B) ,当且仅当 A B C 取等号,
2 3
所以 sin A sin B sin(A B) 3 3的最大值是 .
2
(3)函数 h(x) a ln
1
- x2 2- (a 0)的定义域是 (0, ),
x x
要证函数h(x)是上凸函数,即证"x1, x2 (0, ) h(
x1 x2 ) h(x1) h(x ), 2 ,
2 2
h(x1) h(x2 ) - h( x1 x2 1因为 ) [a(ln
1 ln 1 ) - (x21 x
2
2 ) - 2(
1 1
)
2 2 2 x1 x2 x1 x2
[a ln 2 ( x1 x- - 2 )2 4- ]
x1 x2 2 x1 x2
a[ 1- ln(x 21x2 ) - ln ]-[
1 (x21 x
2 ) ( x1 x2 )2 ] ( x- - 1 x2 4- )
2 x1 x2 2
2 2 x1x2 x1 x2
2 x x 2 2
-a ln 1 2 (x1 - x2 ) (x x ) - 4x x- - 1 2 1 2
x1 x2 4 x1x2 (x1 x2 )
2 x x (x - x )2 (x 2
=-[a ln 1 2 1 2 1
- x2 ) ],
x1 x2 4 x1x2 (x1 x2 )
(x - x )2 (x - x )2
显然 x 1 21x2 > 0, x1 x2 > 0,则 0, 1 2 0,4 x1x2 (x1 x2 )
2 x1x2 2 x1x而 x1 x2 2 x
2
1x2 ,即0 < 1,则 ln 0,x1 x2 x1 x2
2 x x
a 0 h(x ) h(x ) x x x x h(x ) h(x )又 ,有 a ln 1 2 0,则 1 2 - h( 1 2 ) 0, h( 1 2 ) 1 2 ,
x1 x2 2 2 2 2
学校:___________姓名:___________班级:___________考号:___________
一、单选题
2
1.已知 i是虚数单位, 1 i ( )
A.-i B. i C.1- i D.1 i
2. cos
π
q
sin π -q π cos -q sin π q 的值等于( )
è 3 ÷ 6 ÷ 6 ÷ ÷
è è è 3
A 3. B.1 C.0 D 1.
2 2
r r 5π r r3.已知向量 a ,b 的夹角为 ,且 a 2 3 b ar
r
,则 在b 上的投影向量为(
6 )
r r r r
A. -3b B.- 3b C.3b D. 3b
y sin π 1 4.函数 - x ÷, x [-2π,2π]的单调递增区间是(3 2 )è
é π , 5π ù é 5π π ùA. ê- ú B. ê- , 3 3 3 3 ú
é
C. ê-2π,
π
- ù é
5π ,2πù é-2π, 5π- ù é π ù和 D. 和 ,2π
3 ú ê 3 ú ê 3 ú ê 3 ú
r r r r r r5.已知向量 a ,b 满足 a (1, 2)
r
,b (-2, y) r,且 a∥b ,则 a b ( )
A. 5 B.4 C.5 D.5 2
6.已知函数 f (x)
π
tan 2x - ÷ ,则下列说法错误的是(3 )è
π
A.函数 f (x) 的最小正周期为T 2
B.函数 f (x)
ì 5π kπ
的定义域为 íx x ,k
ü
Z
12 2
π kπC .函数 f (x) 的图象的对称中心为 ,0÷ , k Z
è 6 2
D.函数 f (x)
π kπ 5π kπ
的单调递增区间为 - , , k Z
è 12 2 12 2 ÷
7.将函数 f (x) sin x - 3 cos x 1图象上所有点的横坐标缩小为原来的 2 (纵坐标不变),再
将所得曲线上所有的点向左平移a(a > 0)个单位长度,得到函数 g(x)的图象,若 g(x)的图象
关于 y 轴对称,则 a的最小值是( )
5π 5π π πA. B. C12 .6 3
D.
6
8.在VABC 中,角A , B ,C 的对边分别为 a,b , c,且面积为S .若
bcosC c cos B a sin A, S
1
b2 a2 - c2 ,则角 B 等于( )4
p p p p
A. B. C. D.
2 3 6 4
二、多选题
z 2 11i9.已知 i是虚数单位,复数 ,则下列说法正确的是( )
2 i
A.复数 z 的虚部为 4i B. z 3- 4i
C. z 5 D. z 在复平面内对应的点在第二象限
10.信阳是中国十佳宜居城市之一,气候宜人,环境优美.如图是信阳市夏季某一天的温度
变化曲线,若该曲线近似地满足函数 y Asin(wx j) B(0 < j < π), x R 的部分图象,则下
列说法正确的是( )
A.该函数的周期是16
y 10sin π x 3π B.该函数的解析式是 ÷ 20, x R
è 8 4
C.该函数图象的对称中心是 (8k - 6,0) k Z
D.该函数图象的对称轴是直线 x 8k - 2 k Z
11.在VABC中,内角A , B ,C 所对的边分别为 a,b , c,则下列说法正确的是( )
A πA.若a 2 3 ,b 4 , ,则满足条件的三角形有两个4
B.若 A > B ,则 sin 2A > sin 2B
8
C.若 SVABC 1, a 1,则 sin A 的最大值为17
uuur uuur uuur uuur
AB AC
uuur
÷ uAuBur uAuCur 1D.若 uuur uuur × BC 0,且 × ,则VABC 为等边三角形
è AB AC
÷ AB AC 2
三、填空题
uuur r uuur r uuur
12.如图,在VABC 中,D是BC 上靠近 B 的一个三等分点,AB=a ,AC b ,则 AD 可以用
r r
a ,b 表示为 .
π π
13 é ù.若j 是三角形的一个内角,且函数 y 2sin(3x j)在区间 ê- ,9 12 ú 上单调递增,则
j 的
取值范围为 .
π
14.已知函数 f (x) a cos x 1- a2 sin 2x(0 < a 1) 的图象关于直线 x 对称,若方程12
f (x) m(m R) é在 ê0,
π ù
4 ú上恰有
1 个实数根,则m 的取值范围是 .
四、解答题
r r
15.已知向量 a cos x,sin x ,b 3,- 3 , x 0, π .
r
(1) ar若 ^ b ,求 x 的值;
r
(2)记 f (x) r a ×b 1,求 f (x) 的最大值和最小值以及对应的 x 的值.
16.如图,在平面直角坐标系 xOy 中,以 x 轴正半轴为始边的锐角a 与钝角 b 的终边与单位
圆分别交于 A,B 两点,x 5轴正半轴与单位圆交于点 M,已知 SVOAM ,点 B 的纵坐标是5
2
.
10
(1)求 cos a - b 的值;
(2)求 2a - b 的值.
17.近年来,西安市长安区认真践行“绿水青山就是金山银山”生态文明理念,围绕良好的生
态禀赋和市场需求,深挖冷水鱼产业发展优势潜力,现已摸索出以虹鳟、鲟鱼等养殖为主方
向,为扩大养殖规模,某鲟鱼养殖场计划在如图所示的扇形区域OMN 内修建矩形水池
π
ABCD,矩形一边 AB 在OM 上,点C在圆弧MN 上,点D在边ON 上,且 MON ,OM 60
3
米,设 COM a .
(1)求扇形OMN 的面积;
(2)求矩形 ABCD的面积 S(a ) ;当a 为何值时, S(a ) 取得最大值,并求出这个最大值.
18.在VABC 中,内角 A,B,C 的对边分别为 a,b,c,已知 2cos A(c cos B bcosC) a .
(1)求 A;
(2)若VABC 为锐角三角形,且 a 3,求b2 c2 3bc的取值范围.
19.若函数 f (x) 在定义域区间[a,b]上连续,对任意 x , x [a,b]
x x
恒有 f ( 1 21 2 ) 2
f (x1) f (x2 ) ,则称函数 f (x) [a,b] f (
x1 x2 ) f (x1) f (x )是区间 上的上凸函数,若恒有 2 ,
2 2 2
则称函数 f (x) 是区间[a,b]上的下凸函数,当且仅当 x1 x2 时等号成立,这个性质称为函数
的凹凸性.上述不等式可以推广到取函数定义域中的任意 n 个点,即若 f (x) 是上凸函数,
x , x ,L, x [a,b] f ( x1 x2 ××× xn ) f (x1) f (x2 ) ××× f (x )则对任意 1 2 n 恒有 n ,若 f (x) 是下n n
凸函数,则对任意 x1, x2 ,L, x [a,b] f (
x1 x2 ××× xn ) f (x1) f (x2 ) ××× f (x恒有 n
)
n ,当n n
且仅当 x1 x2 × × × xn时等号成立.应用以上知识解决下列问题:
(1)判断函数 f (x) ax2 bx c ( a 0,x R ),g(x) sin x ,x (0, π)在定义域上是上凸函
数还是下凸函数;(只写出结论,不需证明)
(2)利用(1)中的结论,在VABC 中,求 sin A sin B sin(A B) 的最大值;
(3)证明函数 h(x) a ln
1
- x2 2- a 0 是上凸函数.
x x
河南省信阳市 2024-2025 学年高一下学期 4 月期中数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C A C A D BC ABD
题号 11
答案 ACD
1.C
2 2 1- i 2 - 2i
【详解】 1- i1 i 1 i 1- i 2 ,
故选:C.
2.B
π π π π π π π
【详解】 cos q ÷sin -q ÷ cos -q ÷sin q ÷ sin q -q ÷ sin 1,
è 3 è 6 è 6 è 3 è 3 6 2
故选:B.
3.A
r r
r r r 5π b r 3 b r
【详解】 a 在b 上的投影向量为 a cos r 2 3 b 6
-
2 ÷b ÷
r -3b .
è b
故选:A
4.C
π 1
【详解】 f (x) sin( - x) -sin(
1 x π- )
3 2 2 3 ,
z 1令 x
π
- ,
2 3
函数 y
π 3π
sin z é ù的单调递减区间为 ê2kπ , 2kπ 2 2 ú
(k Z) .
2kπ π 1 x π 2kπ 3π由 - , k Z,
2 2 3 2
得 4kπ+
5π
x 4kπ 11π , k Z ,
3 3
而 x -2π,2π é π ù 5π,所以所求单调递增区间是 ê-2π, - 3 ú 和
[ , 2π]
3 .
故选:C.
5.A
r ra (1, 2) b (-2, y) ar
r
【详解】因为 , , ∥b ,
r
所以1 y - 2 -2 0,则 y -4 ,故b (-2,-4),
ar
r r r
所以 b (-1, -2) ,则 a b -1 2 -2 2 5 .
故选:A.
6.C
f (x) tan 2x π- T π【详解】对于 A,函数 ÷ 的最小正周期 ,A 正确;
è 3 2
π π
对于 B,由 2x - kπ
5π kπ
, k Z,得 x , k Z,
3 2 12 2
ì 5π kπ ü
所以函数 f x 的定义域为 íx | x , k Z ,B 正确;
12 2
2x π kπ π kπ对于 C,由 - , k Z,得 x , k Z,
3 2 6 4
所以函数 f x π kπ的对称中心为 ,0
÷, k Z,C 错误;
è 6 4
π
对于 D,由- kπ<2x
π π kπ π kπ x 5π kπ- < , k Z,得- < < , k Z,
2 3 2 12 2 12 2
π kπ 5π kπ
所以函数 f x 的单调递增区间为 - , , k Z,D 正确.
è 12 2 12 2 ÷
故选:C
7.A
【详解】 f (x) sin x - 3 cos x 可化为 f (x) 2
1 3
sin x - cos x2 2 ÷÷
,
è
所以 f (x) 2sin
x
π
-
3 ÷
,
è
由条件可得 g(x) 2sin
2x 2a
π
- ÷ ,
è 3
因为函数 g(x)的图象关于 y 轴对称,所以函数 g x 为偶函数,
2a π kπ π所以 - , k Z,
3 2
a kπ 5π所以 , k Z,又 a > 0,
2 12
所以 a
5π
的最小值为 12 ,
故选:A.
8.D
【详解】因为bcosC c cos B a sin A,
所以由正弦定理得 sin B cosC sin C cos B sin Asin A ,
所以 sin(B C) sin(p - A) sin A sin2 A,
因为 sin A 0 ,所以 sin A 1,
因为 A (0,p ) A
p
,所以 ,
2
1 2 2 2 1 1
因为 S b a - c 2ab cosC absin C ,4 4 2
所以 tan C 1,
p
因为C
0, 2 ÷
,
è
p
所以C ,
4
p p p
所以B p - A - C p - - ,
2 4 4
故选:D
9.BC
2 11i 2 11i 2 - iz 4 - 2i 22i 11【详解】因为 3 4i2 i 2 i 2 ,- i 5
所以复数 z 的虚部为 4,A 错误;
因为 z 3 4i ,所以 z 3 - 4i ,B 正确,
因为 z 3 4i ,所以 z 32 42 5,C 正确;
复数 z 3 4i 在复平面内对应的点的坐标为 3,4 ,该点位于复平面的第一象限内,D 错误;
故选:BC.
10.ABD
【详解】对于 A 选项,由图象可知,该函数的最小正周期为T 2 14 - 6 16,A 选项正
确;
ì A B 30 ì A 10
对于 B 选项,由图象可得 í ,解得 ,
-A B 10
í
B 20
w 2p 2p p ,
T 16 8
Q图象经过点 14,30 ,
\30 10sin π 14 j
÷ 20,
è 8
\sin 7π j
÷ 1 .
è 4
Q0 < j < π 7π 7π j 11π 7π 5π 3π,\ < < ,则 j ,\j ,
4 4 4 4 2 4
y 10sin π x 3π 所以,函数解析式为 ÷ 20 , x R ,B 选项正确;
è 8 4
π 3π
对于 C 选项,令 x kπ, k Z,可得 x 8k - 6, k Z,
8 4
所以函数 y 10sin
π x 3π ÷ 20 图象的对称中心为 (8k - 6, 20) k Z ,C 选项错误;
è 8 4
π x 3π kπ+ π对于 D 选项,令 , k Z,可得 x 8k - 2, k Z,
8 4 2
所以函数 y 10sin
π
x
3π
÷ 20 图象的对称轴是直线 x 8k - 2 k Z ,故 D 选项正确.
è 8 4
故选:ABD.
11.ACD
π
【详解】A 选项,若 a 2 3 ,b 4 , A 4 ,
则bsinA 4 2 2 2 ,所以bsinA < a < b ,
2
所以满足条件的三角形有两个,所以 A 选项正确.
π π π
B 选项,若 A > B ,如 A ,B , 2A π , 2B ,
2 4 2
则 sin2A 0, sin2B 1,故 sin2A < sin2B ,所以 B 选项错误.
S 1C 选项, VABC bcsinA 1,bc
2
,
2 sinA
cosA b
2 c2 -1
余弦定理得 ,故 2bc ×cosA b2 c2 -1
2bc
2 2× ×cosA b2 c2 -1 2bc 2-1 2 × -1,
sinA sinA
4cosA 4
即 -1,当且仅当b c 时等号成立,
sinA sinA
1
由于三角形中, sinA > 0,所以 4cosA 4 - sinA, cosA 1- sinA > 0,
4
2
cos2 A 1 1- sinA 则 ,又 cos2 ÷ A 1- sin
2 A,
è 4
2
2 1 17 即1- sin A 1- sinA÷ ,整理得4
sinA -1÷ ×sinA 0,
è è 8
记得0 < sinA
8 8
,所以 sin A 的最大值为 ,所以 C 选项正确.
17 17
uuur uuur
uAuBur uuur
AC
D 选项, 表示 AB 方向的单位向量; uuur
uuur
AB 表示 AC 方向的单位向量,AC
uuur uuur
uAuBur uAuC根据平面向量加法的几何意义可知 ur 与 BACAB AC 的角平分线共线,
uuur uuur
uAuBur uAC
uuur
由 uur ÷ × BC 0可知 BAC 的角平分线与BC 垂直,
AB AC ֏
所以三角形 ABC 是等腰三角形.
uuur uuur
uAuBur uAC× uur 1 1 cosA cosA 1 > 0 A π而 A AB AC 2 ,所以 为锐角,且 ,3
所以VABC 是等边三角形.
故选:ACD
uuur 2 r 1 r
12. AD a b
3 3
uuur 1 uuur
【详解】因为D是BC 上靠近 B 的一个三等分点,所以BD BC ,
3
uuur r uuur r
又 AB=a , AC b ,
uuur uuur uuur uuur 1 uuur uuur 1 uuur uuur r r r r r所以 AD AB BD AB BC AB AC AB a 1 b 1 2 1- - a a b3 3 3 3 3 3 ,
uuur 2 r 1 r
故答案为: AD a b .
3 3
13. 0,
π ù
è 4 ú
π x π π π【详解】由- ,可得- j 3x j j ,
9 12 3 4
又j 是三角形的一个内角,所以0 < j < π,
π π
故- < - j
2π π π j 5π< , < < ,
3 3 3 4 4 4
é π π ù
因为函数 y 2sin(3x j)在区间 ê- ,9 12 ú 上单调递增,
ì π π
- - j
2 3 π π
í ,解得- j ,又0 < j < π,
π π j 6 4
4 2
j π ù所以 的取值范围为 0, ,
è 4 ú
π ù
故答案为: 0,
è 4 ú
.
ì 1 3 ü
14. ím m < m 1
或
2 2
【详解】因为 f x a cos 2x 1- a2 sin 2x sin 2x j ,其中 tanj
a
,
1- a2
π
又函数 f x 的图像关于直线 x 对称,且0 < a 1,
12
π π π 3 1 3
所以 f ÷ a cos 1- a
2 sin a 1- a2 1,解得 a ,
è12 6 6 2 2 2
f x 3 cos 2x 1 sin 2x sin 2x π 所以
2 2 3 ÷
,
è
x é π π π 5π当
ù é ù
ê
0, ú 时,令 t 2x 4 3 ê
,
3 6 ú
,
因为方程 f (x) m(m R) é0,
π ù é π π ù
在 ê ú上恰有 14 个实数根,且函数
g t sin t 在 ,
ê 3 2 ú
上单调递
é π , 5π ù增,在 ê ú上单调递减, 2 6
g π sin π 3 , g 5π π 1 sin , g π ÷ ÷ ÷ 1,
è 3 3 2 è 6 6 2 è 2
ì ü
所以 ím
1
m 3< 或m 1 .
2 2
ì 1 ü
故答案为: ím m
3
< 或m 1
2 2
π
15.(1)
3
5π
(2) x 0时, f (x) 的最大值为 4; x 时, f (x) 的最小值为
6 1- 2 3
r r
【详解】(1)因为 a cosx,sinx r,b 3,- 3 r, a ^ b ,
所以3cosx - 3sinx 0.
若 cosx 0,则 sinx 0,与 sin2x cos2x 1矛盾,
故 cosx 0,于是 tanx 3 .又 x 0, π ,
π
所以 x 3 .
f x ar
r
(2) ×b cosx,sinx × 3, - 3 1
3cosx - 3sinx 1 2 3cos x π
÷ 1.
è 6
因为 x 0, π x π π 7π,所以 é , ù -1 cos x π 3ê ,从而
6 6 6 ú 6 ÷
.
è 2
所以1- 2 3 2 3cos
x
π
÷ 1 4,
è 6
π π
于是,当 x ,即 x 0时, f x 取到最大值 4;
6 6
π 5π
当 x π ,即 x 时, f x 取到最小值
6 6 1- 2 3
.
16 1 10 π.( )- ;(2) 2α - β - .
10 4
【详解】解:(1)由题意,OA OM 1.
QS 1 5 aVOAM ×OAsina ×OM , 为锐角,2 5
\ sina 2 5 ,cosa 1-sin2 a 5 .
5 5
2
又点 B 的纵坐标是 且 b 为钝角,
10
\ sin b 2 , cos b - 1 7 2- sin2 b - .
10 10
\cos a - b cosa cos b sina sin b
5 7 2 2 5 2 10
- - .5 è 10
÷÷
5 10 10
2
2 5 (2)Qcos 2a 2cos a 3-1 2 ÷÷ -1 - ,
è 5 5
sin 2a 2sina cosa 2 5 5 4 2 ,
5 5 5
\2a p ,p
p
÷ , b ,p
p p
÷,\2a - b
- , ÷ .
è 2 è 2 è 2 2
又Qsin 2a - b sin 2a cos b - cos 2a sin b 4 7 2 - - 3 2 2 ÷÷ - ÷ - ,5 è 10 è 5 10 2
故 2α - β
π
- .
4
17.(1) 600π平方米;
(2) S(a ) 1200 3 sin(2a
π
) 600 3(0 a π π- < < ),当a 时,S a 取得最大值
6 3 6 600 3
平方
米.
MON π【详解】(1)依题意, ,扇形半径即OM 60米,
3
1 π
则扇形 OMN 2的面积为 60 600π平方米.
2 3
(2)在RtVOBC 中,BC 60sina ,OB 60cosa ,
在RtVOAD中, AD BC 60sina OA AD 3,则 60sina ,
3 3
于是 AB OB - OA 60cosa - 20 3 sina ,
则矩形 ABCD面积 S(a ) AB × BC 60sina (60cosa - 20 3 sina )
1200 3( 3 sina cosa - sin2 a ) 1200 3( 3 sin 2a 1 cos 2a 1- )
2 2 2
1200 3 sin(2a π ) - 600 3 0 a π, < < ,
6 3
π π
所以 S(a ) 1200 3 sin(2a ) - 600 3(0 < a < );
6 3
0 a π π 2a π 5π由 < < ,得 < < ,则当2a
π π π
时,即a 时, S(a ) 600 3 ,
3 6 6 6 6 2 6 max
π
所以当a 时, S a 取得最大值,最大值为600 3 平方米.6
π
18.(1)
3
(2) 11,15
【详解】(1)根据题意,由正弦定理得
2cos A(sin C cos B sin B cosC) 2cos Asin B C 2cos Asin A sin A,
又在VABC 中,有 A 0, π ,所以 sin A 0 ,
所以 cos A
1 π
,所以 A .
2 3
2π
(2 1 sin A 3)结合( )可得 ,B C π - A ,
2 3
a b c
由 a 3,则根据正弦定理有 2,得b 2sin B , c 2sin C ,sin A sin B sin C
根据余弦定理有 a2 b2 c2 - 2bc cos A,得b2 c2 3 bc,
b2 2所以 c 3bc 3 4bc 3 16sin B sin C 3 16sin B sin
2π
- B
3 ֏
3 8 3 sin B cos B 8sin2 B 7 4 3 sin 2B - 4cos 2B π 7 8sin 2B -
÷,
è 6
ABC B 0,
π 2π - B 0, π B π π , 又V 为锐角三角形,则有 , ,得 ,
è 2 ÷ 3 ÷ ÷ è 2 è 6 2
所以 2B
π π 5π π 1
- , sin 2B - ,所以
,1ù,
6 6 6 ÷ 6 ÷ è è è 2 ú
b2 c2 π故 3bc 7 8sin
2B -
6 ÷
11,15 .
è
19.(1)答案见解析;
(2) 3 3 ;
2
(3)证明见解析.
【详解】(1)函数 f (x) ax2 bx c a 0 "x , x R f ( x1 x2 ) f (x1) f (x2 ) , , 1 2 , -2 2
x x 2 2
a( 1 2 )2 b( x1 x2 ) c ax1 bx1 c ax2 bx2 c a- - (x 2
2 2 2 4 1
- x2 ) ,
a 0 f ( x1 x2 ) f (x ) f (x )当 > 时, 1 2 , f (x) 是下凸函数;
2 2
x x f (x ) f (x )
当 a < 0时, f ( 1 2 ) 1 2 , f (x) 是上凸函数,
2 2
"x , x (0, π), x x g( x1 x2 ) g(x1) g(x2 ) sin x1 x2 sin x1 sin x21 2 1 2 , - -2 2 2 2
sin x1 cos x2 x cos 1 sin x2 sin x1 cos x- 1 - cos x2 sin x2
2 2 2 2 2 2 2 2
(sin x2 - sin x1 )(cos x1 - cos x2 ) 0 x1 x2 π x x x x,显然 < < ,则 sin 2 sin 1 , cos 1 cos 2 ,
2 2 2 2 2 2 2 2 2 2 2
x
因此 g( 1
x2 ) g(x1) g(x 2 ) ,函数 g(x)是上凸函数.
2 2
(2)由(1)知函数 y sin x , x (0, π)是上凸函数,
在VABC 中, sin A sin B sin(A B) sin A sin B sin C A B C sin sin π 3 ,
3 3 2
3 3 π
即 sin A sin B sin(A B) ,当且仅当 A B C 取等号,
2 3
所以 sin A sin B sin(A B) 3 3的最大值是 .
2
(3)函数 h(x) a ln
1
- x2 2- (a 0)的定义域是 (0, ),
x x
要证函数h(x)是上凸函数,即证"x1, x2 (0, ) h(
x1 x2 ) h(x1) h(x ), 2 ,
2 2
h(x1) h(x2 ) - h( x1 x2 1因为 ) [a(ln
1 ln 1 ) - (x21 x
2
2 ) - 2(
1 1
)
2 2 2 x1 x2 x1 x2
[a ln 2 ( x1 x- - 2 )2 4- ]
x1 x2 2 x1 x2
a[ 1- ln(x 21x2 ) - ln ]-[
1 (x21 x
2 ) ( x1 x2 )2 ] ( x- - 1 x2 4- )
2 x1 x2 2
2 2 x1x2 x1 x2
2 x x 2 2
-a ln 1 2 (x1 - x2 ) (x x ) - 4x x- - 1 2 1 2
x1 x2 4 x1x2 (x1 x2 )
2 x x (x - x )2 (x 2
=-[a ln 1 2 1 2 1
- x2 ) ],
x1 x2 4 x1x2 (x1 x2 )
(x - x )2 (x - x )2
显然 x 1 21x2 > 0, x1 x2 > 0,则 0, 1 2 0,4 x1x2 (x1 x2 )
2 x1x2 2 x1x而 x1 x2 2 x
2
1x2 ,即0 < 1,则 ln 0,x1 x2 x1 x2
2 x x
a 0 h(x ) h(x ) x x x x h(x ) h(x )又 ,有 a ln 1 2 0,则 1 2 - h( 1 2 ) 0, h( 1 2 ) 1 2 ,
x1 x2 2 2 2 2
同课章节目录
