北师大版七下数学 4.3 探索三角形全等的条件(3)复习 教案
文档属性
| 名称 | 北师大版七下数学 4.3 探索三角形全等的条件(3)复习 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 132.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览

文档简介
探索三角形全等的条件(三)命题人 命题日期
学习目标 1.通过分组画图比较,得出SAS的结论,培养学生思维的全面性。2.让学生在活动过程中,发展合作交流能力和语言表达能力。3.能够利用全等条件判定两个三角形全等并会用数学语言说明理由。4.在解决问题中发现问题,通过虚心交流解决问题,互相启发,互相受益。5.在活动过程中体会结论的客观真实性,感受数学与现实生活的密切联系增强学生的数学应用意识,初步培养学生依据已知结论分析问题解决问题的良好习惯。
学习重点 得出SAS的结论,培养学生思维的全面性
学习难点 能够利用全等条件判定两个三角形全等并会用数学语言说明理由。
学教内容:
【复习巩固】
1. 到目前为止,你知道哪些判定三角形全等的方法?
2.通过下面的题回顾证明三角形全等的三步走
如图(1),△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。△ABD与△ACD全等吗?请说明理由。
3. 当两个三角形满足六个条件中的三个时,有哪几种情况:
【新课探究】
活动一:探究两边及其夹角对应相等
按要求画图:已知两边分别为8厘米、10厘米,它们的夹角为45°。你能画出这个三角形吗?你画的三角形和同伴画的一定全等吗?
结论:三角形全等判定方法4
学生姓名:_____________组别______学生自评_________教师评价_____________
活动二:两边及其中一边的对角
按要求作图:以8厘米,10厘米为边,以8厘米的边所对的角为45°。分小组画图。情况又怎样?动手画一画,你发现了什么?
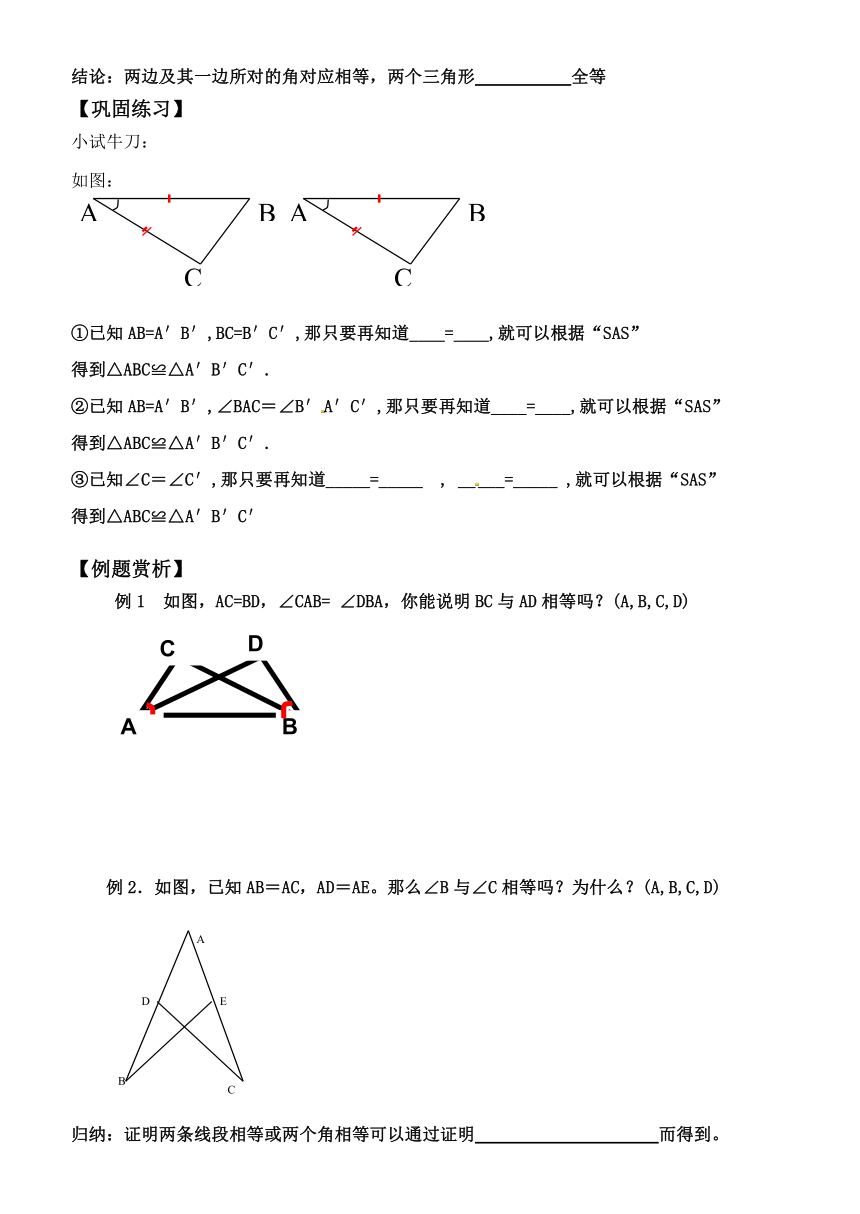
结论:两边及其一边所对的角对应相等,两个三角形 全等
【巩固练习】
小试牛刀:
如图:
①已知AB=A′B′,BC=B′C′,那只要再知道____=____,就可以根据“SAS”
得到△ABC≌△A′B′C′.
②已知AB=A′B′,∠BAC=∠B′A′C′,那只要再知道____=____,就可以根据“SAS”
得到△ABC≌△A′B′C′.
③已知∠C=∠C′,那只要再知道_____=_____ , _____=_____ ,就可以根据“SAS”
得到△ABC≌△A′B′C′
【例题赏析】
例1 如图,AC=BD,∠CAB= ∠DBA,你能说明BC与AD相等吗?(A,B,C,D)
例2.如图,已知AB=AC,AD=AE。那么∠B与∠C相等吗?为什么?(A,B,C,D)
归纳:证明两条线段相等或两个角相等可以通过证明 而得到。
你能选对吗?
如图,下列条件中,不能说明△ABD≌△ACD的是: ( )
A A.BD =DC,AB =AC
B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD
D. ∠B=∠C,BD=DC
D
B C
【开放探究】
如图,已知OA=OB,应填什么条件就得到: △AOC≌ △BOD(只允许添加一个条件)
说明全等的理由
【加油站】
1.如图,已知AB=AC,AD=AE,∠1=∠2.△ABD 与 △ ACE全等吗?说明理由。(A,B,C,D)
2.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C ,∠A与∠D相等吗?为什么?(A,B,C,D)
【拓展延伸】
1.如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?(C,D)
AC∥FD吗?为什么?
2. 如图,AC=BD,BC=AD ,求证:∠C=∠D(B,C,D)
变式: 如图,AC=BD,BC=AD,求证:∠A=∠B(B,C,D)
错题之家:
A
B
C
A
B
C
A
B
C
D
E
D
B
A
C
O
A
C
D
B
E
C
D
B
F
A
F
E
D
A
B
C
A
B
C
D
A
B
C
D
学习目标 1.通过分组画图比较,得出SAS的结论,培养学生思维的全面性。2.让学生在活动过程中,发展合作交流能力和语言表达能力。3.能够利用全等条件判定两个三角形全等并会用数学语言说明理由。4.在解决问题中发现问题,通过虚心交流解决问题,互相启发,互相受益。5.在活动过程中体会结论的客观真实性,感受数学与现实生活的密切联系增强学生的数学应用意识,初步培养学生依据已知结论分析问题解决问题的良好习惯。
学习重点 得出SAS的结论,培养学生思维的全面性
学习难点 能够利用全等条件判定两个三角形全等并会用数学语言说明理由。
学教内容:
【复习巩固】
1. 到目前为止,你知道哪些判定三角形全等的方法?
2.通过下面的题回顾证明三角形全等的三步走
如图(1),△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。△ABD与△ACD全等吗?请说明理由。
3. 当两个三角形满足六个条件中的三个时,有哪几种情况:
【新课探究】
活动一:探究两边及其夹角对应相等
按要求画图:已知两边分别为8厘米、10厘米,它们的夹角为45°。你能画出这个三角形吗?你画的三角形和同伴画的一定全等吗?
结论:三角形全等判定方法4
学生姓名:_____________组别______学生自评_________教师评价_____________
活动二:两边及其中一边的对角
按要求作图:以8厘米,10厘米为边,以8厘米的边所对的角为45°。分小组画图。情况又怎样?动手画一画,你发现了什么?
结论:两边及其一边所对的角对应相等,两个三角形 全等
【巩固练习】
小试牛刀:
如图:
①已知AB=A′B′,BC=B′C′,那只要再知道____=____,就可以根据“SAS”
得到△ABC≌△A′B′C′.
②已知AB=A′B′,∠BAC=∠B′A′C′,那只要再知道____=____,就可以根据“SAS”
得到△ABC≌△A′B′C′.
③已知∠C=∠C′,那只要再知道_____=_____ , _____=_____ ,就可以根据“SAS”
得到△ABC≌△A′B′C′
【例题赏析】
例1 如图,AC=BD,∠CAB= ∠DBA,你能说明BC与AD相等吗?(A,B,C,D)
例2.如图,已知AB=AC,AD=AE。那么∠B与∠C相等吗?为什么?(A,B,C,D)
归纳:证明两条线段相等或两个角相等可以通过证明 而得到。
你能选对吗?
如图,下列条件中,不能说明△ABD≌△ACD的是: ( )
A A.BD =DC,AB =AC
B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD
D. ∠B=∠C,BD=DC
D
B C
【开放探究】
如图,已知OA=OB,应填什么条件就得到: △AOC≌ △BOD(只允许添加一个条件)
说明全等的理由
【加油站】
1.如图,已知AB=AC,AD=AE,∠1=∠2.△ABD 与 △ ACE全等吗?说明理由。(A,B,C,D)
2.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C ,∠A与∠D相等吗?为什么?(A,B,C,D)
【拓展延伸】
1.如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?(C,D)
AC∥FD吗?为什么?
2. 如图,AC=BD,BC=AD ,求证:∠C=∠D(B,C,D)
变式: 如图,AC=BD,BC=AD,求证:∠A=∠B(B,C,D)
错题之家:
A
B
C
A
B
C
A
B
C
D
E
D
B
A
C
O
A
C
D
B
E
C
D
B
F
A
F
E
D
A
B
C
A
B
C
D
A
B
C
D
同课章节目录
