2025年中考数学冲刺复习课件:专题三 思维提升·化归与模型思想 课件(26张PPT)
文档属性
| 名称 | 2025年中考数学冲刺复习课件:专题三 思维提升·化归与模型思想 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
2025年数学中考冲刺复习
专题三 思维提升
化归与模型思想
经典试题解析
核心素养培优
将欲求解的复杂问题经过一次或多次转化,将其化为一个或几个已知
的或容易求解的问题,或将抽象的问题化为具体的问题,进而达到解决问
题的目的,在这个过程中所运用的转化方法就是化归思想。
化归思想方法是解决问题的重要方法。如:三元方程(组)化为二元
方程(组)、二元方程(组)化为一元方程来解答;在四边形的学习中,
常将四边形的问题转化为三角形的问题来解答;直角三角形借数量关系来
解答;几何问题借坐标来精确研究:一次函数、反比例函数、二次函数借
点在坐标系里的规律来研究它们的图像性质等。
数学模型通常是指从现实生活或具体情境中抽象出数学问题,如:
“垂线段最短”“将军饮马”“点圆最值”等,若注意将相关问题转化为对应的
模型进行求解,常可化难为易,化繁为简,达到简洁求解之目的。
化归与模型思想常见的类型:
(1)将不规则图形的面积化为可求的规则图形的面积;
(2)将非格点图形问题化为格点图形问题;
(3)将函数问题化为求点坐标的问题;
(4)将几何问题化为基本的几何模型的问题。
经典试题解析
01
类型1 不规则图形的面积转化
图3-1-1
例1 (2023·广元中考)如图3-1-1,半径为5的扇形
中, ,是上一点,, ,
垂足分别为,。若 ,则图中阴影部分的面积
为( )
B
A. B. C. D.
思路分析 连接,易证四边形 是正方形,进而得出
, ,把求阴影部分面积转化为求扇形面积即
可解答。
1
2
3
4
图3-1-2
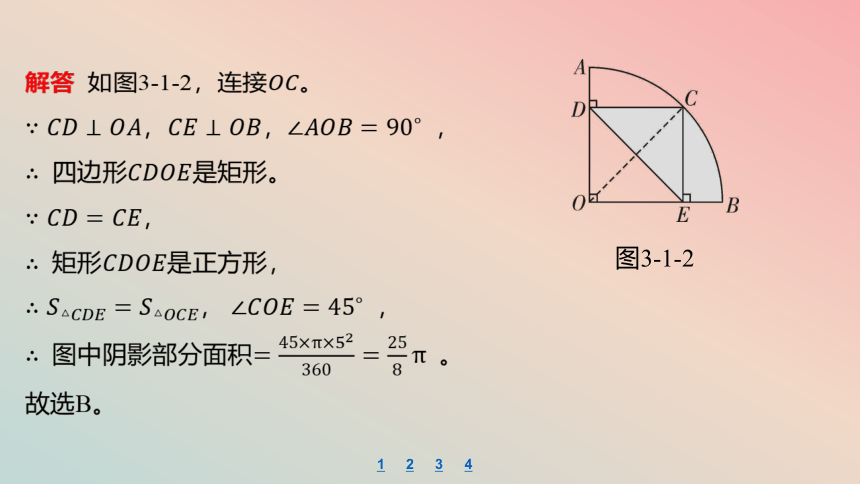
解答 如图3-1-2,连接 。
,, ,
四边形 是矩形。
,
矩形 是正方形,
, ,
图中阴影部分面积 。
故选B。
1
2
3
4
类型2 非格点图形问题的转化
图3-1-3
例2 (2023·济宁中考) 如图3-1-3,在正方形方格中,
每个小正方形的边长都是1个单位长度,点,,,, 均在
小正方形方格的顶点上,线段,交于点 。若
,则 等于( )
C
A. B. C. D.
思路分析 在正方形方格中构造三角形,利用三角形全等的性质和外角的
性质即可求解。
1
2
3
4
图3-1-4
解答 如图3-1-4,连接,,过点作,交
的延长线于点 。
由图可知,, ,
,
,
。
1
2
3
4
,
,
。
,
。
故选C。
1
2
3
4
类型3 函数问题的转化
图3-1-5
例3 (2023·达州中考)如图3-1-5,一次函数
与反比例函数的图像相交于, 两点,
以为边作等边三角形。若反比例函数 的
图像过点,则 的值为____。
思路分析 依据题意,点在 的垂直平分线上,可
得直线的解析式为,故可设 ,
再由求出的值,代入 即可求解。
1
2
3
4
图3-1-6
解答 如图3-1-6,连接 。
根据题意,建立方程组
解得或
, ,
点, 关于原点对称。
是等边三角形,
的垂直平分线过原点和点 。
1
2
3
4
直线的解析式为 ,
直线的解析式为 ,
设 。
又 为等边三角形,
,
根据两点间的距离公式可得
,
解得 。
1
2
3
4
点 在第二象限,
, ,
将点的坐标代入 ,得 。
故答案为 。
1
2
3
4
类型4 几何问题的转化
图3-1-7
例4 (2023·菏泽中考)如图3-1-7,在四边形
中, ,, ,
,点在线段上运动,点在线段 上,
,则线段 的最小值为 _________。
1
2
3
4
思路分析 已知,证明 ,即点在以点 为圆
心,长为直径的半圆上运动,求 的最小值转化成求圆外一点到圆
上一点的最小值问题(即点圆最值模型),当,,三点共线时, 最小,
最小值为 。
1
2
3
4
图3-1-8
解答 如图3-1-8,设的中点为,以点为圆心,
长为直径画半圆,连接, 。
,
,
。
,
,
点在以点为圆心,长为直径的半圆 上运动。
1
2
3
4
,
。
在中,, ,
,
又 ,
当,,三点共线时, 最小。
线段的最小值为 。
故答案为 。
1
2
3
4
核心素养培优
02
图3-1-9
1.(2023·连云港中考)如图3-1-9,矩形 内接于
,分别以,,, 为直径向外作半圆。若
, ,则阴影部分的面积是( )
D
A. B. C. D.20
1
2
3
4
5
图3-1-10
2.(2023·苏州中考)如图3-1-10,在正方形网格内,线
段的两个端点都在格点上,网格内另有,,,
四个格点,下面四个结论中,正确的是( )
B
A.连接,则 B.连接,则
C.连接,则 D.连接,则
1
2
3
4
5
图3-1-11
3.(2022·宿迁中考)如图3-1-11,点 在反比例函数
的图像上,以 为一边作等腰直角三角
形,其中 ,,则线段 的
长的最小值是( )
C
A.1 B. C. D.4
1
2
3
4
5
图3-1-12
4.(2023·广西中考)如图3-1-12,在边长为2的正方形
中,,分别是,上的动点,, 分别是
,的中点,则 的最大值为 ____。
1
2
3
4
5
图3-1-13
5.(2023·枣庄中考)银杏是著名的活化石植物,其
叶有细长的叶柄,呈扇形。图3-1-13是一片银杏叶标
本,叶片上两点,的坐标分别为, ,
将银杏叶绕原点顺时针旋转 后,叶柄上点 的对
应点的坐标为_______。
1
2
3
4
5
THE END
谢谢观看
2025年数学中考冲刺复习
专题三 思维提升
化归与模型思想
经典试题解析
核心素养培优
将欲求解的复杂问题经过一次或多次转化,将其化为一个或几个已知
的或容易求解的问题,或将抽象的问题化为具体的问题,进而达到解决问
题的目的,在这个过程中所运用的转化方法就是化归思想。
化归思想方法是解决问题的重要方法。如:三元方程(组)化为二元
方程(组)、二元方程(组)化为一元方程来解答;在四边形的学习中,
常将四边形的问题转化为三角形的问题来解答;直角三角形借数量关系来
解答;几何问题借坐标来精确研究:一次函数、反比例函数、二次函数借
点在坐标系里的规律来研究它们的图像性质等。
数学模型通常是指从现实生活或具体情境中抽象出数学问题,如:
“垂线段最短”“将军饮马”“点圆最值”等,若注意将相关问题转化为对应的
模型进行求解,常可化难为易,化繁为简,达到简洁求解之目的。
化归与模型思想常见的类型:
(1)将不规则图形的面积化为可求的规则图形的面积;
(2)将非格点图形问题化为格点图形问题;
(3)将函数问题化为求点坐标的问题;
(4)将几何问题化为基本的几何模型的问题。
经典试题解析
01
类型1 不规则图形的面积转化
图3-1-1
例1 (2023·广元中考)如图3-1-1,半径为5的扇形
中, ,是上一点,, ,
垂足分别为,。若 ,则图中阴影部分的面积
为( )
B
A. B. C. D.
思路分析 连接,易证四边形 是正方形,进而得出
, ,把求阴影部分面积转化为求扇形面积即
可解答。
1
2
3
4
图3-1-2
解答 如图3-1-2,连接 。
,, ,
四边形 是矩形。
,
矩形 是正方形,
, ,
图中阴影部分面积 。
故选B。
1
2
3
4
类型2 非格点图形问题的转化
图3-1-3
例2 (2023·济宁中考) 如图3-1-3,在正方形方格中,
每个小正方形的边长都是1个单位长度,点,,,, 均在
小正方形方格的顶点上,线段,交于点 。若
,则 等于( )
C
A. B. C. D.
思路分析 在正方形方格中构造三角形,利用三角形全等的性质和外角的
性质即可求解。
1
2
3
4
图3-1-4
解答 如图3-1-4,连接,,过点作,交
的延长线于点 。
由图可知,, ,
,
,
。
1
2
3
4
,
,
。
,
。
故选C。
1
2
3
4
类型3 函数问题的转化
图3-1-5
例3 (2023·达州中考)如图3-1-5,一次函数
与反比例函数的图像相交于, 两点,
以为边作等边三角形。若反比例函数 的
图像过点,则 的值为____。
思路分析 依据题意,点在 的垂直平分线上,可
得直线的解析式为,故可设 ,
再由求出的值,代入 即可求解。
1
2
3
4
图3-1-6
解答 如图3-1-6,连接 。
根据题意,建立方程组
解得或
, ,
点, 关于原点对称。
是等边三角形,
的垂直平分线过原点和点 。
1
2
3
4
直线的解析式为 ,
直线的解析式为 ,
设 。
又 为等边三角形,
,
根据两点间的距离公式可得
,
解得 。
1
2
3
4
点 在第二象限,
, ,
将点的坐标代入 ,得 。
故答案为 。
1
2
3
4
类型4 几何问题的转化
图3-1-7
例4 (2023·菏泽中考)如图3-1-7,在四边形
中, ,, ,
,点在线段上运动,点在线段 上,
,则线段 的最小值为 _________。
1
2
3
4
思路分析 已知,证明 ,即点在以点 为圆
心,长为直径的半圆上运动,求 的最小值转化成求圆外一点到圆
上一点的最小值问题(即点圆最值模型),当,,三点共线时, 最小,
最小值为 。
1
2
3
4
图3-1-8
解答 如图3-1-8,设的中点为,以点为圆心,
长为直径画半圆,连接, 。
,
,
。
,
,
点在以点为圆心,长为直径的半圆 上运动。
1
2
3
4
,
。
在中,, ,
,
又 ,
当,,三点共线时, 最小。
线段的最小值为 。
故答案为 。
1
2
3
4
核心素养培优
02
图3-1-9
1.(2023·连云港中考)如图3-1-9,矩形 内接于
,分别以,,, 为直径向外作半圆。若
, ,则阴影部分的面积是( )
D
A. B. C. D.20
1
2
3
4
5
图3-1-10
2.(2023·苏州中考)如图3-1-10,在正方形网格内,线
段的两个端点都在格点上,网格内另有,,,
四个格点,下面四个结论中,正确的是( )
B
A.连接,则 B.连接,则
C.连接,则 D.连接,则
1
2
3
4
5
图3-1-11
3.(2022·宿迁中考)如图3-1-11,点 在反比例函数
的图像上,以 为一边作等腰直角三角
形,其中 ,,则线段 的
长的最小值是( )
C
A.1 B. C. D.4
1
2
3
4
5
图3-1-12
4.(2023·广西中考)如图3-1-12,在边长为2的正方形
中,,分别是,上的动点,, 分别是
,的中点,则 的最大值为 ____。
1
2
3
4
5
图3-1-13
5.(2023·枣庄中考)银杏是著名的活化石植物,其
叶有细长的叶柄,呈扇形。图3-1-13是一片银杏叶标
本,叶片上两点,的坐标分别为, ,
将银杏叶绕原点顺时针旋转 后,叶柄上点 的对
应点的坐标为_______。
1
2
3
4
5
THE END
谢谢观看
同课章节目录
