2025年中考数学冲刺复习课件:专题三 思维提升· 数形结合思想 课件(21张PPT)
文档属性
| 名称 | 2025年中考数学冲刺复习课件:专题三 思维提升· 数形结合思想 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 21:10:34 | ||
图片预览








文档简介
(共21张PPT)
2025年数学中考冲刺复习
专题三 思维提升
数形结合思想
经典试题解析
核心素养培优
数形结合思想是数学教学内容的主线之一。如:用画线段图、框架图、
列表法来分析问题;借数轴表示数、确定不等式组的解集;借助图像研究函
数的性质,即图像的几何特征与数量特征;利用图像解释二元一次方程组的
解与两直线交点坐标的关系;处理不等式时,联系相关函数,分析其几何意
义,从图形上求解或寻找解题思路;利用图形解释、说明公式、法则的由来
与合理性;借勾股定理、锐角三角函数解三角形相关问题;用相似比精准描
述图形的大小关系;圆中的点、线与圆的位置,借数量关系精准定义;借直
角坐标系研究图形的变换问题;二次函数与几何的综合问题等。
“数”和“形”是从两个方面反映事物的特点,它主要是指数与形之间的一
一对应关系,即把抽象的数学语言、数量关系与直观的几何图形、位置关
系结合起来,通过“以形助数”或“以数解形”,把抽象思维与形象思维结合起
来,使复杂问题简单化、抽象问题具体化,从而起到简化解题过程的目的。
经典试题解析
01
类型1 以数解形
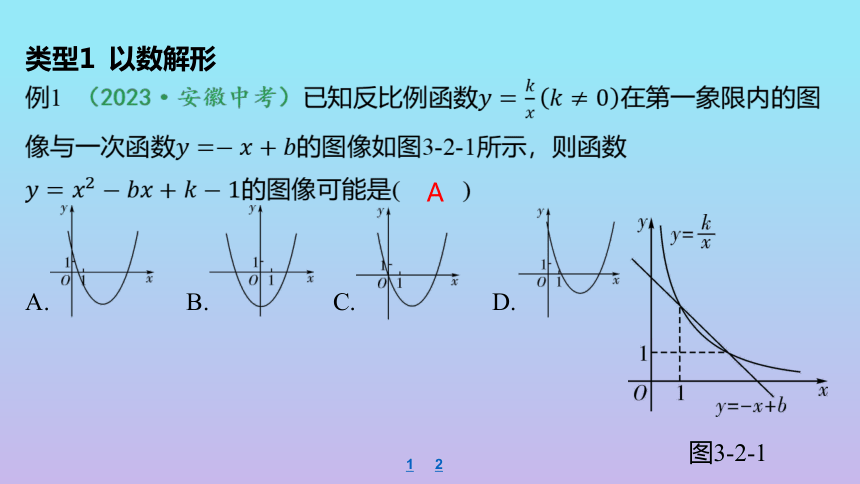
例1 (2023·安徽中考)已知反比例函数 在第一象限内的图
像与一次函数 的图像如图3-2-1所示,则函数
的图像可能是( )
A
图3-2-1
A. B. C. D.
1
2
思路分析 设,则,由图像可知,将点 代入
,得出,代入二次函数 ,可得出
抛物线的对称轴在直线的右侧,过定点,且与轴的交点在
轴的正半轴。
1
2
图3-2-2
解答 如图3-2-2,设,则 ,根据图像可得
,
将代入 ,
, 。
又, ,
二次函数 的对称轴为直线
。
1
2
当时, ,
二次函数的图像经过点 。
当时, 。
综上可知,二次函数图像的对称轴在直线的右侧,过定点 ,
且与轴的交点在 轴的正半轴。
故选A。
1
2
类型2 以形助数
图3-2-3
例2 (2023·烟台中考)如图3-2-3,将一个量角
器与一把无刻度直尺水平摆放,直尺的长边与量
角器的外弧分别交于点,,,,连接 ,
则 的度数为 ______。
思路分析 观察图形可以看出为圆周角,根据圆周角定理求出 所
对的圆心角的度数即可求解。
1
2
图3-2-4
解答 如图3-2-4,设量角器的圆心为 ,连接
, ,
,
。
故答案为 。
1
2
核心素养培优
02
1.(2023·内江中考)函数中,自变量 的取值范围在数轴上表
示为( )
D
A. B. C. D.
1
2
3
4
5
6
7
图3-2-5
2.(2023·乐山中考)我国汉代数学家赵爽在注解《周髀算
经》时给出“赵爽弦图”(如图3-2-5),它是由四个全等的
直角三角形与中间的小正方形拼成的一个大正方形。如果
大正方形的面积为25,小正方形的面积为1,那么
( )
A
A. B. C.4 D.
1
2
3
4
5
6
7
图3-2-6
3.(2023·福建中考)如图3-2-6,正方形的四个顶点分
别位于两个反比例函数和 的图像的四个分支上,
则实数 的值为( )
A
A. B. C. D.3
1
2
3
4
5
6
7
图3-2-7
4.(2023·眉山中考)如图3-2-7,二次函数
的图像与 轴的一个交点坐标为
,对称轴为直线 ,下列四个结论:
;; ;④当
时, 。其中正确结论的个数
为( )
D
A.1 B.2 C.3 D.4
1
2
3
4
5
6
7
图3-2-8
5.(2023·通辽中考)如图3-2-8,在平面直角坐标系
中,已知点,点,以点 为旋转中心,把
点按逆时针方向旋转 得到点。在 ,
,, 四个点中,直
线 经过的点是( )
B
A. B. C. D.
1
2
3
4
5
6
7
图3-2-9
6.(2023·扬州中考)如图3-2-9,已知正方形 的边
长为1,点,分别在边,上,将正方形沿着 翻
折,点恰好落在边上的点处。如果四边形 与
四边形的面积比为,那么线段 的长为__。
1
2
3
4
5
6
7
图3-2-10
7.(2023·河南中考)如图3-2-10
①,点从等边三角形 的顶点
出发,沿直线运动到三角形内部
一点,再从该点沿直线运动到顶
点。设点运动的路程为 ,
,图3-2-10②是点运动时
6
随变化的关系图像,则等边三角形 的边长为___。
1
2
3
4
5
6
7
THE END
谢谢观看
2025年数学中考冲刺复习
专题三 思维提升
数形结合思想
经典试题解析
核心素养培优
数形结合思想是数学教学内容的主线之一。如:用画线段图、框架图、
列表法来分析问题;借数轴表示数、确定不等式组的解集;借助图像研究函
数的性质,即图像的几何特征与数量特征;利用图像解释二元一次方程组的
解与两直线交点坐标的关系;处理不等式时,联系相关函数,分析其几何意
义,从图形上求解或寻找解题思路;利用图形解释、说明公式、法则的由来
与合理性;借勾股定理、锐角三角函数解三角形相关问题;用相似比精准描
述图形的大小关系;圆中的点、线与圆的位置,借数量关系精准定义;借直
角坐标系研究图形的变换问题;二次函数与几何的综合问题等。
“数”和“形”是从两个方面反映事物的特点,它主要是指数与形之间的一
一对应关系,即把抽象的数学语言、数量关系与直观的几何图形、位置关
系结合起来,通过“以形助数”或“以数解形”,把抽象思维与形象思维结合起
来,使复杂问题简单化、抽象问题具体化,从而起到简化解题过程的目的。
经典试题解析
01
类型1 以数解形
例1 (2023·安徽中考)已知反比例函数 在第一象限内的图
像与一次函数 的图像如图3-2-1所示,则函数
的图像可能是( )
A
图3-2-1
A. B. C. D.
1
2
思路分析 设,则,由图像可知,将点 代入
,得出,代入二次函数 ,可得出
抛物线的对称轴在直线的右侧,过定点,且与轴的交点在
轴的正半轴。
1
2
图3-2-2
解答 如图3-2-2,设,则 ,根据图像可得
,
将代入 ,
, 。
又, ,
二次函数 的对称轴为直线
。
1
2
当时, ,
二次函数的图像经过点 。
当时, 。
综上可知,二次函数图像的对称轴在直线的右侧,过定点 ,
且与轴的交点在 轴的正半轴。
故选A。
1
2
类型2 以形助数
图3-2-3
例2 (2023·烟台中考)如图3-2-3,将一个量角
器与一把无刻度直尺水平摆放,直尺的长边与量
角器的外弧分别交于点,,,,连接 ,
则 的度数为 ______。
思路分析 观察图形可以看出为圆周角,根据圆周角定理求出 所
对的圆心角的度数即可求解。
1
2
图3-2-4
解答 如图3-2-4,设量角器的圆心为 ,连接
, ,
,
。
故答案为 。
1
2
核心素养培优
02
1.(2023·内江中考)函数中,自变量 的取值范围在数轴上表
示为( )
D
A. B. C. D.
1
2
3
4
5
6
7
图3-2-5
2.(2023·乐山中考)我国汉代数学家赵爽在注解《周髀算
经》时给出“赵爽弦图”(如图3-2-5),它是由四个全等的
直角三角形与中间的小正方形拼成的一个大正方形。如果
大正方形的面积为25,小正方形的面积为1,那么
( )
A
A. B. C.4 D.
1
2
3
4
5
6
7
图3-2-6
3.(2023·福建中考)如图3-2-6,正方形的四个顶点分
别位于两个反比例函数和 的图像的四个分支上,
则实数 的值为( )
A
A. B. C. D.3
1
2
3
4
5
6
7
图3-2-7
4.(2023·眉山中考)如图3-2-7,二次函数
的图像与 轴的一个交点坐标为
,对称轴为直线 ,下列四个结论:
;; ;④当
时, 。其中正确结论的个数
为( )
D
A.1 B.2 C.3 D.4
1
2
3
4
5
6
7
图3-2-8
5.(2023·通辽中考)如图3-2-8,在平面直角坐标系
中,已知点,点,以点 为旋转中心,把
点按逆时针方向旋转 得到点。在 ,
,, 四个点中,直
线 经过的点是( )
B
A. B. C. D.
1
2
3
4
5
6
7
图3-2-9
6.(2023·扬州中考)如图3-2-9,已知正方形 的边
长为1,点,分别在边,上,将正方形沿着 翻
折,点恰好落在边上的点处。如果四边形 与
四边形的面积比为,那么线段 的长为__。
1
2
3
4
5
6
7
图3-2-10
7.(2023·河南中考)如图3-2-10
①,点从等边三角形 的顶点
出发,沿直线运动到三角形内部
一点,再从该点沿直线运动到顶
点。设点运动的路程为 ,
,图3-2-10②是点运动时
6
随变化的关系图像,则等边三角形 的边长为___。
1
2
3
4
5
6
7
THE END
谢谢观看
同课章节目录
