10.1.2 两角和与差的正弦 同步学案(含答案) 2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 10.1.2 两角和与差的正弦 同步学案(含答案) 2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 129.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 22:28:08 | ||
图片预览




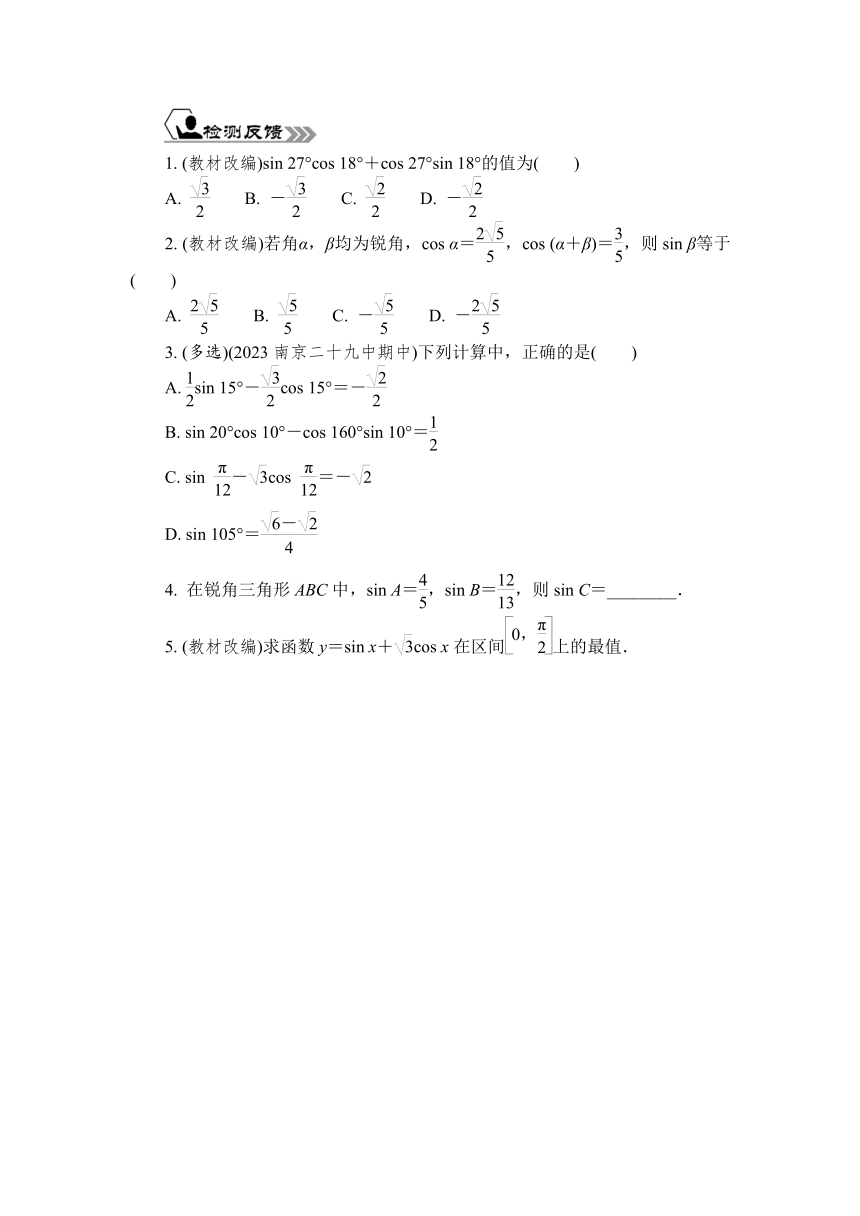
文档简介
10.1.2 两角和与差的正弦(1)
1. 能由两角和与差的余弦公式推导出两角和与差的正弦公式,体会化归思想的作用.
2. 能用两角和与差的正弦公式进行简单的三角函数式的化简与求值.
活动一 掌握两角和与差的正弦公式的推导
1. 回顾两角和与差的余弦公式.
2. 根据两角和与差的余弦公式和诱导公式,能否推导出两角和与差的正弦公式?如何推导?即如何用α,β的三角函数来表示sin (α+β),sin (α-β).
3. 写出两角和与差的正弦公式,并思考其结构特征.
活动二 利用两角和与差的正弦公式求简单三角函数式的值
例1 已知sin α=-,α是第四象限角,求sin ,sin 的值.
在使用两角和与差的正弦公式时,体会与两角和与差的余弦公式的不同.
已知sin α=,α∈,cos β=-,β∈,求sin (α+β)的值.
例2 已知cos (α+β)=,cos β=,α,β均是锐角,求sin α的值.
理解所求的角与已知角之间的关系,而不是简单地将已知的角α+β看成是α与β的和;当然将cos (α+β)展开也可以解决问题,但运算量较大.
已知0<α<<β<π,tan α=,cos (β-α)=,求sin β的值.
活动三 利用两角和与差的正弦公式化简简单的三角函数式
例3 化简:
(1) sin 2x cos x-cos 2x sin x;
(2) sin 13°cos 17°+cos 13°sin 17°;
充分利用两角和与差的正弦公式的特征去化简表达式,直至最简形式.
求值:sin 15°+cos 15°=________.
例4 (2023扬州期末)已知函数f(x)=-6(sin x+cos x)-3,x∈,求f(x)的最大值.
解决三角函数中的性质问题,其中一类问题就是将函数表达式化为y=A sin (ωx+φ)的形式,即一个角(将ωx+φ看成整体)的一个三角函数的形式.
求下列函数的值域:
(1) y=sin x+cos x;
(2) y=sin x-cos x,x∈.
思考
求函数y=a sin x+b cos x的最值.
1. (教材改编)sin 27°cos 18°+cos 27°sin 18°的值为( )
A. B. - C. D. -
2. (教材改编)若角α,β均为锐角,cos α=,cos (α+β)=,则sin β等于( )
A. B. C. - D. -
3. (多选)(2023南京二十九中期中)下列计算中,正确的是( )
A. sin 15°-cos 15°=-
B. sin 20°cos 10°-cos 160°sin 10°=
C. sin -cos =-
D. sin 105°=
4. 在锐角三角形ABC中,sin A=,sin B=,则sin C=________.
5. (教材改编)求函数y=sin x+cos x在区间上的最值.
10.1.2 两角和与差的正弦(2)
能用两角和与差的正弦公式进行简单的三角函数式的求值及恒等式证明.
活动一 掌握两角和与差的正弦公式的应用——求值
例1 已知α是锐角,且cos =,求sin α的值.
对于三角函数中的给值求值问题,主要先看角之间的关系,再看三角函数名称,然后合理使用公式.
若sin =,α∈,求sin α的值.
例2 设α,β是锐角,且sin α=,sin β=,求α+β的值.
对于三角函数中的给值求角问题,首先判断所求角的范围,然后求所求角的适当的三角函数值.
若α∈,β∈,且=tan β,则下列结论中正确的是( )
A. β-α= B. β+α=
C. 2β-α= D. 2β+α=
例3 求值:.
对于已知角的求值问题,尽量化到特殊角(如,,)的三角函数值去求解.
已知tan α=2tan ,求的值.
活动二 掌握两角和与差的正弦公式的应用——恒等式证明
例4 求证:-2cos (A+B)=.
对于三角函数中的证明问题,主要看等式两边的角和三角函数名称之间的关系,遵循从繁到简原则.
求证:sin (α+β)sin (α-β)=sin2α-sin2β.
活动三 掌握两角和与差的正弦公式的综合应用
例5 已知sin(α+β)=,sin (α-β)=-,求的值.
主要从形式上入手,找到已知条件和问题之间的关系.
已知在△ABC中,3sin A+4cos B=6,4sin B+3cos A=1,求角C的大小.
1. (2023南京外国语学校月考)化简的结果为( )
A. B. - C. sin 20° D. sin 10°
2. (教材改编)已知0<α<,cos =,则sin α的值为( )
A. B. C. D.
3. (多选)(2024济南期末)如图,已知角α,β的始边为x轴的非负半轴,终边与单位圆的交点分别为A,B,M为线段AB的中点,射线OM与单位圆交于点C,则下列结论中正确的是( )
A. ∠AOB=β-α
B. OM=cos
C. 点C的坐标为
D. 点M的坐标为
4. 已知2sin =cos α,则tan α=________.
5. (教材改编)已知角α,β满足sin =-,sin =,0<α<,<β<,求α+β的值.
10.1.2 两角和与差的正弦(1)
【活动方案】
1. cos (α+β)=cos αcos β-sin αsin β,
cos (α-β)=cos αcos β+sin αsin β.
2. sin (α+β)=cos =cos cos β+sin (-α)sin β=sin αcos β+cos αsin β,
sin (α-β)=cos =cos cos β-sin sin β=sin αcos β-cos αsin β.
3. sin (α+β)=sin αcos β+cos αsin β,
sin (α-β)=sin αcos β-cos αsin β,
异名三角函数相乘,符号相同.
例1 因为α是第四象限角,sin α=-,
所以cos α=,
所以sin =×=,
sin =×=.
跟踪训练 由sin α=,α∈,
得cos α=-,
同理可得sin β=-,
所以sin (α+β)=sin αcos β+cos αsin β=×+×=.
例2 由题意,得α+β∈(0,π),且cos (α+β)=,
所以sin (α+β)==.
同理可得sin β=,
所以sin α=sin [(α+β)-β]=×-×=.
跟踪训练 因为0<α<<β<π,tan α=,
所以sin α=,cos α=.
因为0<α<<β<π,
所以0<β-α<π.
又cos (β-α)=,
所以sin (β-α)==,
所以sin β=sin (β-α+α)=sin (β-α)cos α+cos (β-α)sin α=.
例3 (1) 原式=sin (2x-x)=sin x.
(2) 原式=sin (13°+17°)=sin 30°=.
跟踪训练 原式=2(sin 15°+cos 15°)=2(sin 15°cos 30°+cos 15°sin 30°)=2sin (15°+30°)=.
例4 (1) f(x)=-6(sin x+cos x)-3
=-6(sin x+cos x)-3
=-6sin (x+)-3.
因为x∈,所以x+∈,
所以f(x)在区间上单调递减,
所以f(x)max=f(0)=-9.
跟踪训练 (1) y=2sin ,值域为[-2,2].
(2) y=sin .
又x∈,所以x-∈,
所以值域为[-1,1].
思考:y=sin (x+φ),其中tan φ=,
所以最大值为,最小值为-.
【检测反馈】
1. C sin 27°cos 18°+cos 27°sin 18°=sin (27°+18°)=sin 45°=.
2. B 由角α,β均为锐角,得0<α+β<π.又cos (α+β)=,则sin (α+β)=.因为cos α=,所以sin α=,所以sin β=sin [(α+β)-α]=sin (α+β)cos α-cos (α+β)sin α=×-×=.
3. ABC 对于A,sin 15°-cos 15°=sin 15°cos 60°-cos 15°sin 60°=sin (15°-60°)=sin (-45°)=-,故A正确;对于B,sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin (20°+10°)=sin 30°=,故B正确;对于C,sin -cos =2×(sin cos -cos sin )=2sin =2sin =-,故C正确;对于D,sin 105°=sin (60°+45°)=sin 60°cos 45°+cos 60°sin 45°=×+×=,故D错误.故选ABC.
4. 因为△ABC是锐角三角形,sin A=,sin B=,所以cos A=,cos B=,所以sin C=sin (A+B)=×+×=.
5. y=sin x+cos x=2sin .
因为x∈,所以x+∈,
所以ymax=2,ymin=1.
10.1.2 两角和与差的正弦(2)
【活动方案】
例1 因为α∈,所以α+∈.
因为cos =,
所以sin =,
所以sin α=sin =×-×=.
跟踪训练 因为α∈,所以-α∈(-,).
因为sin =,
所以cos =,
所以sin α=sin =×-×=.
例2 因为α∈,β∈,
所以α+β∈(0,π).
又sin α=,sin β=,
所以cos α=,cos β=,
所以cos (α+β)=×-×=,
所以α+β=.
跟踪训练 C 由=tan β,得=,即cos β+cos βsin α=sin βcos α,故cos β=sin βcos α-cos βsin α=sin (β-α),即sin (-β)=sin (β-α).又因为α∈,β∈,所以-β∈,β-α∈.因为函数y=sin x在区间上单调递增,所以-β=β-α,即2β-α=.
例3 原式===.
跟踪训练 因为tan α=2tan ,
所以====3.
例4 左式=
===右式.
跟踪训练 左式=sin2αcos2β-sin2βcos2α
=sin2α(1-sin2β)-sin2β(1-sin2α)
=sin2α-sin2β=右式.
例5 由题意,得解得
所以==.
跟踪训练 (3sin A+4cos B)2+(4sin B+3cos A)2=37,
化简,得sin (A+B)=,
即sin C=,所以C=或C=.
因为3sin A=6-4cos B>2,
所以sin A>>,
所以A>,所以C≠,所以C=.
【检测反馈】
1. A 原式===tan 30°=.
2. A 因为0<α<,cos =>0,所以<α+<,sin ==,故sin α=sin (α+-)=sin cos -cos (α+)sin =×-×=.
3. ABC 对于A,因为∠AOx=α,∠BOx=β,0<α<β<,所以∠AOB=β-α,故A正确;对于B,因为M为线段AB的中点,所以OM⊥AB,则∠AOM=.又OA=1,所以OM=OA cos ∠AOM=cos ,故B正确;对于C,因为M为线段AB的中点,射线OM与单位圆交于点C,所以C为的中点,则∠COx=α+=.又OC=1,所以点C的坐标为,故C正确;对于D,xM=(xA+xB)=(cos α+cos β)=[cos (+)+cos ]=[cos cos -sin sin +cos cos +sin sin ]=×2cos cos =cos cos ,yM=(yA+yB)=(sin α+sin β)=[sin +sin (-)]=[sin cos +cos sin +sin cos -cos sin ]=×2sin cos =sin cos ,所以点M的坐标为(cos cos ,sin cos ),故D错误.故选ABC.
4. +1 因为2sin =cos α,所以2sin αcos -2cos αsin =cos α,整理,得sin α=(+1)cos α,即tan α=+1.
5. 因为0<α<,<β<,
所以-<-α<,<+β<,
所以<+β-<π,
即<α+β<π.
又sin =-,sin =,
所以cos =,cos =-,
所以cos (α+β)=cos =-×+×=-,
所以α+β=.
1. 能由两角和与差的余弦公式推导出两角和与差的正弦公式,体会化归思想的作用.
2. 能用两角和与差的正弦公式进行简单的三角函数式的化简与求值.
活动一 掌握两角和与差的正弦公式的推导
1. 回顾两角和与差的余弦公式.
2. 根据两角和与差的余弦公式和诱导公式,能否推导出两角和与差的正弦公式?如何推导?即如何用α,β的三角函数来表示sin (α+β),sin (α-β).
3. 写出两角和与差的正弦公式,并思考其结构特征.
活动二 利用两角和与差的正弦公式求简单三角函数式的值
例1 已知sin α=-,α是第四象限角,求sin ,sin 的值.
在使用两角和与差的正弦公式时,体会与两角和与差的余弦公式的不同.
已知sin α=,α∈,cos β=-,β∈,求sin (α+β)的值.
例2 已知cos (α+β)=,cos β=,α,β均是锐角,求sin α的值.
理解所求的角与已知角之间的关系,而不是简单地将已知的角α+β看成是α与β的和;当然将cos (α+β)展开也可以解决问题,但运算量较大.
已知0<α<<β<π,tan α=,cos (β-α)=,求sin β的值.
活动三 利用两角和与差的正弦公式化简简单的三角函数式
例3 化简:
(1) sin 2x cos x-cos 2x sin x;
(2) sin 13°cos 17°+cos 13°sin 17°;
充分利用两角和与差的正弦公式的特征去化简表达式,直至最简形式.
求值:sin 15°+cos 15°=________.
例4 (2023扬州期末)已知函数f(x)=-6(sin x+cos x)-3,x∈,求f(x)的最大值.
解决三角函数中的性质问题,其中一类问题就是将函数表达式化为y=A sin (ωx+φ)的形式,即一个角(将ωx+φ看成整体)的一个三角函数的形式.
求下列函数的值域:
(1) y=sin x+cos x;
(2) y=sin x-cos x,x∈.
思考
求函数y=a sin x+b cos x的最值.
1. (教材改编)sin 27°cos 18°+cos 27°sin 18°的值为( )
A. B. - C. D. -
2. (教材改编)若角α,β均为锐角,cos α=,cos (α+β)=,则sin β等于( )
A. B. C. - D. -
3. (多选)(2023南京二十九中期中)下列计算中,正确的是( )
A. sin 15°-cos 15°=-
B. sin 20°cos 10°-cos 160°sin 10°=
C. sin -cos =-
D. sin 105°=
4. 在锐角三角形ABC中,sin A=,sin B=,则sin C=________.
5. (教材改编)求函数y=sin x+cos x在区间上的最值.
10.1.2 两角和与差的正弦(2)
能用两角和与差的正弦公式进行简单的三角函数式的求值及恒等式证明.
活动一 掌握两角和与差的正弦公式的应用——求值
例1 已知α是锐角,且cos =,求sin α的值.
对于三角函数中的给值求值问题,主要先看角之间的关系,再看三角函数名称,然后合理使用公式.
若sin =,α∈,求sin α的值.
例2 设α,β是锐角,且sin α=,sin β=,求α+β的值.
对于三角函数中的给值求角问题,首先判断所求角的范围,然后求所求角的适当的三角函数值.
若α∈,β∈,且=tan β,则下列结论中正确的是( )
A. β-α= B. β+α=
C. 2β-α= D. 2β+α=
例3 求值:.
对于已知角的求值问题,尽量化到特殊角(如,,)的三角函数值去求解.
已知tan α=2tan ,求的值.
活动二 掌握两角和与差的正弦公式的应用——恒等式证明
例4 求证:-2cos (A+B)=.
对于三角函数中的证明问题,主要看等式两边的角和三角函数名称之间的关系,遵循从繁到简原则.
求证:sin (α+β)sin (α-β)=sin2α-sin2β.
活动三 掌握两角和与差的正弦公式的综合应用
例5 已知sin(α+β)=,sin (α-β)=-,求的值.
主要从形式上入手,找到已知条件和问题之间的关系.
已知在△ABC中,3sin A+4cos B=6,4sin B+3cos A=1,求角C的大小.
1. (2023南京外国语学校月考)化简的结果为( )
A. B. - C. sin 20° D. sin 10°
2. (教材改编)已知0<α<,cos =,则sin α的值为( )
A. B. C. D.
3. (多选)(2024济南期末)如图,已知角α,β的始边为x轴的非负半轴,终边与单位圆的交点分别为A,B,M为线段AB的中点,射线OM与单位圆交于点C,则下列结论中正确的是( )
A. ∠AOB=β-α
B. OM=cos
C. 点C的坐标为
D. 点M的坐标为
4. 已知2sin =cos α,则tan α=________.
5. (教材改编)已知角α,β满足sin =-,sin =,0<α<,<β<,求α+β的值.
10.1.2 两角和与差的正弦(1)
【活动方案】
1. cos (α+β)=cos αcos β-sin αsin β,
cos (α-β)=cos αcos β+sin αsin β.
2. sin (α+β)=cos =cos cos β+sin (-α)sin β=sin αcos β+cos αsin β,
sin (α-β)=cos =cos cos β-sin sin β=sin αcos β-cos αsin β.
3. sin (α+β)=sin αcos β+cos αsin β,
sin (α-β)=sin αcos β-cos αsin β,
异名三角函数相乘,符号相同.
例1 因为α是第四象限角,sin α=-,
所以cos α=,
所以sin =×=,
sin =×=.
跟踪训练 由sin α=,α∈,
得cos α=-,
同理可得sin β=-,
所以sin (α+β)=sin αcos β+cos αsin β=×+×=.
例2 由题意,得α+β∈(0,π),且cos (α+β)=,
所以sin (α+β)==.
同理可得sin β=,
所以sin α=sin [(α+β)-β]=×-×=.
跟踪训练 因为0<α<<β<π,tan α=,
所以sin α=,cos α=.
因为0<α<<β<π,
所以0<β-α<π.
又cos (β-α)=,
所以sin (β-α)==,
所以sin β=sin (β-α+α)=sin (β-α)cos α+cos (β-α)sin α=.
例3 (1) 原式=sin (2x-x)=sin x.
(2) 原式=sin (13°+17°)=sin 30°=.
跟踪训练 原式=2(sin 15°+cos 15°)=2(sin 15°cos 30°+cos 15°sin 30°)=2sin (15°+30°)=.
例4 (1) f(x)=-6(sin x+cos x)-3
=-6(sin x+cos x)-3
=-6sin (x+)-3.
因为x∈,所以x+∈,
所以f(x)在区间上单调递减,
所以f(x)max=f(0)=-9.
跟踪训练 (1) y=2sin ,值域为[-2,2].
(2) y=sin .
又x∈,所以x-∈,
所以值域为[-1,1].
思考:y=sin (x+φ),其中tan φ=,
所以最大值为,最小值为-.
【检测反馈】
1. C sin 27°cos 18°+cos 27°sin 18°=sin (27°+18°)=sin 45°=.
2. B 由角α,β均为锐角,得0<α+β<π.又cos (α+β)=,则sin (α+β)=.因为cos α=,所以sin α=,所以sin β=sin [(α+β)-α]=sin (α+β)cos α-cos (α+β)sin α=×-×=.
3. ABC 对于A,sin 15°-cos 15°=sin 15°cos 60°-cos 15°sin 60°=sin (15°-60°)=sin (-45°)=-,故A正确;对于B,sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin (20°+10°)=sin 30°=,故B正确;对于C,sin -cos =2×(sin cos -cos sin )=2sin =2sin =-,故C正确;对于D,sin 105°=sin (60°+45°)=sin 60°cos 45°+cos 60°sin 45°=×+×=,故D错误.故选ABC.
4. 因为△ABC是锐角三角形,sin A=,sin B=,所以cos A=,cos B=,所以sin C=sin (A+B)=×+×=.
5. y=sin x+cos x=2sin .
因为x∈,所以x+∈,
所以ymax=2,ymin=1.
10.1.2 两角和与差的正弦(2)
【活动方案】
例1 因为α∈,所以α+∈.
因为cos =,
所以sin =,
所以sin α=sin =×-×=.
跟踪训练 因为α∈,所以-α∈(-,).
因为sin =,
所以cos =,
所以sin α=sin =×-×=.
例2 因为α∈,β∈,
所以α+β∈(0,π).
又sin α=,sin β=,
所以cos α=,cos β=,
所以cos (α+β)=×-×=,
所以α+β=.
跟踪训练 C 由=tan β,得=,即cos β+cos βsin α=sin βcos α,故cos β=sin βcos α-cos βsin α=sin (β-α),即sin (-β)=sin (β-α).又因为α∈,β∈,所以-β∈,β-α∈.因为函数y=sin x在区间上单调递增,所以-β=β-α,即2β-α=.
例3 原式===.
跟踪训练 因为tan α=2tan ,
所以====3.
例4 左式=
===右式.
跟踪训练 左式=sin2αcos2β-sin2βcos2α
=sin2α(1-sin2β)-sin2β(1-sin2α)
=sin2α-sin2β=右式.
例5 由题意,得解得
所以==.
跟踪训练 (3sin A+4cos B)2+(4sin B+3cos A)2=37,
化简,得sin (A+B)=,
即sin C=,所以C=或C=.
因为3sin A=6-4cos B>2,
所以sin A>>,
所以A>,所以C≠,所以C=.
【检测反馈】
1. A 原式===tan 30°=.
2. A 因为0<α<,cos =>0,所以<α+<,sin ==,故sin α=sin (α+-)=sin cos -cos (α+)sin =×-×=.
3. ABC 对于A,因为∠AOx=α,∠BOx=β,0<α<β<,所以∠AOB=β-α,故A正确;对于B,因为M为线段AB的中点,所以OM⊥AB,则∠AOM=.又OA=1,所以OM=OA cos ∠AOM=cos ,故B正确;对于C,因为M为线段AB的中点,射线OM与单位圆交于点C,所以C为的中点,则∠COx=α+=.又OC=1,所以点C的坐标为,故C正确;对于D,xM=(xA+xB)=(cos α+cos β)=[cos (+)+cos ]=[cos cos -sin sin +cos cos +sin sin ]=×2cos cos =cos cos ,yM=(yA+yB)=(sin α+sin β)=[sin +sin (-)]=[sin cos +cos sin +sin cos -cos sin ]=×2sin cos =sin cos ,所以点M的坐标为(cos cos ,sin cos ),故D错误.故选ABC.
4. +1 因为2sin =cos α,所以2sin αcos -2cos αsin =cos α,整理,得sin α=(+1)cos α,即tan α=+1.
5. 因为0<α<,<β<,
所以-<-α<,<+β<,
所以<+β-<π,
即<α+β<π.
又sin =-,sin =,
所以cos =,cos =-,
所以cos (α+β)=cos =-×+×=-,
所以α+β=.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
