江苏省南通市海安市十三校2024-2025学年八年级下学期4月期中考试数学试卷(含答案)
文档属性
| 名称 | 江苏省南通市海安市十三校2024-2025学年八年级下学期4月期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 18:05:34 | ||
图片预览




文档简介
八年级数学期中试卷
一.选择题(共10小题,每题3分共30分)
1.要使式子在实数范围内有意义,字母a的取值必须满足( )
A.a≥3 B.a≤3 C.a≠3 D.a≠0
2.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
A.3,4,5 B.6,8,10 C.1,3, D.5,12,13
3.将直线y=2x向下平移3个单位长度后,得到的直线是( )
A.y=2x+3 B.y=2x-3 C.y=2(x+3) D.y=2(x-3)
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,AB∥CD B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
5.下列计算正确的有( )
A. B. C. D.
6.在直角坐标平面内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当y>1时,x>0 B.方程ax+b=0的解是x=2
C.当x<0时,1<y<2 D.不等式ax+b<0的解集是x<2
第6题 第7题 第8题
7.如图,在菱形ABCD中,若AB=5,AC=8,则菱形ABCD的面积为( )
A.24 B.20 C.16 D.12
8.甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:
①甲、乙同学都骑行了18km ②甲、乙同学同时到达B地
③甲停留前、后的骑行速度相同 ④乙的骑行速度是12km/h
其中正确的说法是( )
A.①③ B.①④ C.②④ D.②③
9.如图,在Rt△ABC中,∠A=90°,BD=4,CE=2,连接DE,若M、N分别为线段DE、BC的中点,则线段MN的长为( )
A. B. C. D.
第9题 第10题 第14题
10.如图,矩形纸片ABCD的边AB长为4,将这张纸片沿EF折叠,使点C与点A重合,已知折痕EF长为,则BC长为( )
A.4.8 B.6.4 C.8 D.10
二.填空题(共8小题,11,12每题3分,13~18每题4分,共30分)
11.已知正比例函数y=4x,当x=3时,函数值y= .
12.在平行四边形ABCD中,若∠B+∠D=160°,∠C= .
13.用一个x的值说明“”是错误的,则x的值可以是 .
14.如图,在平行四边形ABCD中,BC=10,DE=4,
∠ABC的平分线BE交AD于点E,则AB的长为 .
15.“尺”“寸”“丈”都是我国传统的长度单位,其中1丈=10尺,1尺=10寸.《九章算术》“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何.”大意是说:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?设门高x尺,根据题意,可列方程为 .
16.如图,菱形ABCD的对角线交于点O,点M为AB的中点,连接OM,
若AC=6,BD=8,则OM的长为 .
17.如图,在△ABC中,∠C=90°,∠A=30°,BC=2,E是AB上的动点,过点E分别作AC,BC的垂线段,垂足分别为F,G,连接FG,则FG的最小值为 .
18.已知一次函数y=x-k,若对于x<2范围内任意自变量x的值,其对应的函数值y都小于k,则k的取值范围是 .
三.解答题(共8小题,共90分)
19.(10分)计算:
.
(2);
20.(10分)在平面直角坐标系中有A(-1,4),B(-3,2),C(0,5)三点.
(1)求过A,B两点的直线的函数解析式;
(2)判断A,B,C三点是否在同一条直线上?并说明理由.
21.(10分)如图,在平面直角坐标系中,直线l1:y=kx+b(k≠0)与x轴交于点A(6,0),与y轴交于点B,与直线相交于点.
(1)求直线l1的函数表达式;
(2)点C为x轴上一点,若△ABC的面积为12,求点C的坐标.
22.(10分)如图,在△ABC中,AB=6,AC=4,点D为△ABC内一
点,且∠BDC=90°,CD=2,BD=AC.
(1)求BC的长;
(2)求图中阴影部分的面积.
23.(12分)如图,矩形ABCD的对角线AC,BD交于点O,且DE∥AC,CE∥BD.
(1)请判断四边形OCED的形状,并说明理由;
(2)若∠BAC=60°,CE=4,求矩形ABCD的面积.
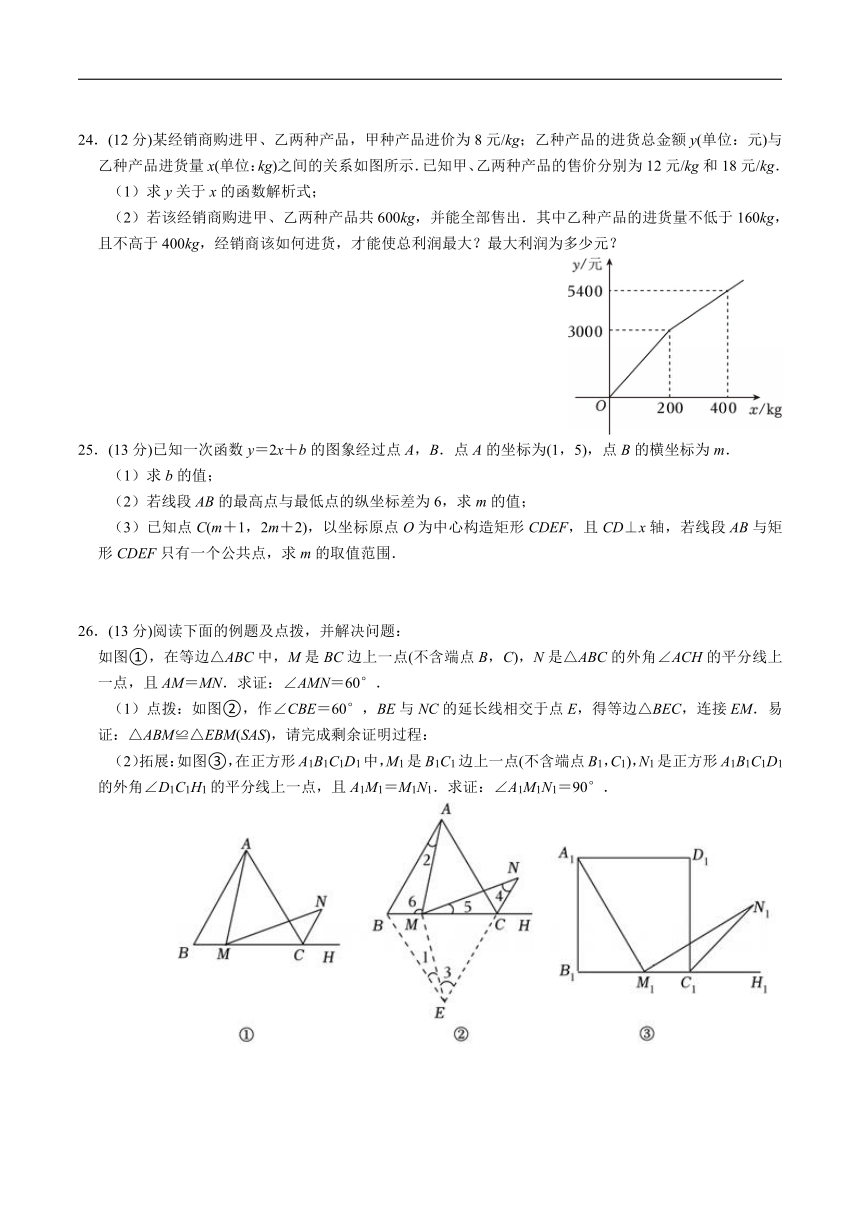
24.(12分)某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.
(1)求y关于x的函数解析式;
(2)若该经销商购进甲、乙两种产品共600kg,并能全部售出.其中乙种产品的进货量不低于160kg,且不高于400kg,经销商该如何进货,才能使总利润最大?最大利润为多少元?
25.(13分)已知一次函数y=2x+b的图象经过点A,B.点A的坐标为(1,5),点B的横坐标为m.
(1)求b的值;
(2)若线段AB的最高点与最低点的纵坐标差为6,求m的值;
(3)已知点C(m+1,2m+2),以坐标原点O为中心构造矩形CDEF,且CD⊥x轴,若线段AB与矩形CDEF只有一个公共点,求m的取值范围.
26.(13分)阅读下面的例题及点拨,并解决问题:
如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
(1)点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),请完成剩余证明过程:
(2)拓展:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C D B A B B C
二.填空题(共8小题)
11.12
12.100°
13. -2(答案不唯一)
14. 6
15. x2+(x-6.8)2=102
16.
17.
18.k≥1
三.解答题(共8小题)
19.(1)原式=-+=2-3+4=6-3. 5分
(2)4a2 2a
=2a2a
=0; 10分
20.解:(1)设过A,B两点的直线的函数解析式y=kx+b,
则,
解得,
∴直线AB的函数解析式为y=x+5; 5分
(2)A,B,C三点在同一条直线上,
理由:由(1)知,直线AB的解析式为y=x+5,
当x=0时,y=5,
∴点C(0,5)在直线AB上,
即A,B,C三点在同一条直线上. 10分
21.解:(1)∵点在直线l2上,
∴,解得m=3,
∴,
∵点A(6,0),M(3,)在直线l1上,
,解得,
∴直线l1的解析式为:y; 5分
(2)由直线解析式可知点B(0,3)即OB=3,
设点C的坐标为(n,0),则AC=|6-n|,
S△ABC12,
解得:n=-2或14, 9分
∴C(-2,0)或(14,0). 10分
22.解:(1)∵∠BDC=90°,CD=2,BD=AC,AC=4,
∴BC2; 5分
(2)∵AB=6,AC=4,BC=2,42+(2)2=62,即AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴S阴影=S△ABC-S△BCD
AC BCCD BD
4×22×4
=44. 10分
23.解:(1)四边形OCED是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵矩形ABCD的对角线AC,BD交于点O,
∴OC=OD,
∴ OCED是菱形; 6分
(2)∵四边形OCED是菱形,
∴OC=CE=4,
∴AC=2OC=8,
∵∠BAC=60°,∠ABC=90°,∠ACB=30°,
∴,
BC.
∴矩形ABCD的面积=4×416. 12分
24.解:(1)当0≤x≤200时,设y=k′x,
根据题意可得,200k′=3000,
解得k′=15,
∴y=15x; 3分
当x>200时,设y=kx+b,
根据题意可得,,
解得,
∴y=12x+600. 6分
∴综上所述,y关于x的函数解析式为y; 7分
(2)根据题意可知,设购进乙种产品x千克,则购进甲种产品(600-x)千克,
当160≤x≤200时,乙种产品进价为3000÷200=15(元/千克),
w=(12-8)(600-x)+18x-15x=-x+2400, 9分
∵-1<0,
∴w随x的增大而减小,
∴当x=160时,w的最大值为-1×160+2400=2240(元);
当200<x≤400时,w=(12-8)(600-x)+18x-(12x+600)=2x+1800,
∵2>0,
∴w随x的增大而增大,
∴当x=400时,w的最大值为800+1800=2600(元),
综上,购进甲产品200千克,乙产品400千克时利润最大,最大利润为2600元. 12分
25.解:(1)把点A的坐标为(1,5)代入y=2x+b得,5=2+b,
∴b=3,
即b的值为3; 3分
(2)∵点B的横坐标为m,
∴y=2m+3,
∴点B(m,2m+3),
∵线段AB的最高点与最低点的纵坐标差为6,
∴5-(2m+3)=6或2m+3-5=6,
∴m=-2或m=4;
(3)∵点C(m+1,2m+2),
∴点C在直线y=2x的图象上,
以坐标原点O为中心构造矩形CDEF,且CD⊥x轴,且与线段AB只有一个交点,则作图如上,
∴E(-m-1,-2m-2),D(m+1,-2m-2),F(-m-1,2m+2), 10分
当D在y=2x+3上,将D(m+1,-2m-2)代入表达式,
∴-2m-2=2(m+1)+3,
∴m;
当F在y=2x+3上,将F(-m-1,2m+2)代入表达式,
∴2m+2=-2(m+1)+3,
∴m; 12分
综上所述:m或; 13分
26.【解答】证明:(1)点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM,
易证△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2;
∵AM=MN,
∴EM=MN,
∴∠3=∠4;
∵∠3+∠1=∠4+∠5=60°,
∴∠1=∠2=∠5.
∵∠2+∠6=120,
∴∠5+∠6=120°,
∴∠AMN=60°; 6分
(2)拓展:延长AB至E,使EB=AB,连接EMC、EC,如图所示:
则EB=BC,∠EBM中=90°=∠ABM,
∴△EBC是等腰直角三角形,
∴∠BEC=∠BCE=45°,
∵N是正方形ABCD的外角∠DCH的平分线上一点,
∴∠MCN=90°+45°=135°,
∴∠BCE+∠MCN=180°,
∴E、C、N,三点共线,
在△ABM和△EBM中,
,
∴△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2,
∵AM=MN,
∴EM=MN,
∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,
∴∠1=∠2=∠5,
∵∠1+∠6=90°,
∴∠5+∠6=90°,
∴∠AMN=180°-90°=90°. 13分
一.选择题(共10小题,每题3分共30分)
1.要使式子在实数范围内有意义,字母a的取值必须满足( )
A.a≥3 B.a≤3 C.a≠3 D.a≠0
2.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
A.3,4,5 B.6,8,10 C.1,3, D.5,12,13
3.将直线y=2x向下平移3个单位长度后,得到的直线是( )
A.y=2x+3 B.y=2x-3 C.y=2(x+3) D.y=2(x-3)
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,AB∥CD B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
5.下列计算正确的有( )
A. B. C. D.
6.在直角坐标平面内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当y>1时,x>0 B.方程ax+b=0的解是x=2
C.当x<0时,1<y<2 D.不等式ax+b<0的解集是x<2
第6题 第7题 第8题
7.如图,在菱形ABCD中,若AB=5,AC=8,则菱形ABCD的面积为( )
A.24 B.20 C.16 D.12
8.甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:
①甲、乙同学都骑行了18km ②甲、乙同学同时到达B地
③甲停留前、后的骑行速度相同 ④乙的骑行速度是12km/h
其中正确的说法是( )
A.①③ B.①④ C.②④ D.②③
9.如图,在Rt△ABC中,∠A=90°,BD=4,CE=2,连接DE,若M、N分别为线段DE、BC的中点,则线段MN的长为( )
A. B. C. D.
第9题 第10题 第14题
10.如图,矩形纸片ABCD的边AB长为4,将这张纸片沿EF折叠,使点C与点A重合,已知折痕EF长为,则BC长为( )
A.4.8 B.6.4 C.8 D.10
二.填空题(共8小题,11,12每题3分,13~18每题4分,共30分)
11.已知正比例函数y=4x,当x=3时,函数值y= .
12.在平行四边形ABCD中,若∠B+∠D=160°,∠C= .
13.用一个x的值说明“”是错误的,则x的值可以是 .
14.如图,在平行四边形ABCD中,BC=10,DE=4,
∠ABC的平分线BE交AD于点E,则AB的长为 .
15.“尺”“寸”“丈”都是我国传统的长度单位,其中1丈=10尺,1尺=10寸.《九章算术》“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何.”大意是说:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?设门高x尺,根据题意,可列方程为 .
16.如图,菱形ABCD的对角线交于点O,点M为AB的中点,连接OM,
若AC=6,BD=8,则OM的长为 .
17.如图,在△ABC中,∠C=90°,∠A=30°,BC=2,E是AB上的动点,过点E分别作AC,BC的垂线段,垂足分别为F,G,连接FG,则FG的最小值为 .
18.已知一次函数y=x-k,若对于x<2范围内任意自变量x的值,其对应的函数值y都小于k,则k的取值范围是 .
三.解答题(共8小题,共90分)
19.(10分)计算:
.
(2);
20.(10分)在平面直角坐标系中有A(-1,4),B(-3,2),C(0,5)三点.
(1)求过A,B两点的直线的函数解析式;
(2)判断A,B,C三点是否在同一条直线上?并说明理由.
21.(10分)如图,在平面直角坐标系中,直线l1:y=kx+b(k≠0)与x轴交于点A(6,0),与y轴交于点B,与直线相交于点.
(1)求直线l1的函数表达式;
(2)点C为x轴上一点,若△ABC的面积为12,求点C的坐标.
22.(10分)如图,在△ABC中,AB=6,AC=4,点D为△ABC内一
点,且∠BDC=90°,CD=2,BD=AC.
(1)求BC的长;
(2)求图中阴影部分的面积.
23.(12分)如图,矩形ABCD的对角线AC,BD交于点O,且DE∥AC,CE∥BD.
(1)请判断四边形OCED的形状,并说明理由;
(2)若∠BAC=60°,CE=4,求矩形ABCD的面积.
24.(12分)某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.
(1)求y关于x的函数解析式;
(2)若该经销商购进甲、乙两种产品共600kg,并能全部售出.其中乙种产品的进货量不低于160kg,且不高于400kg,经销商该如何进货,才能使总利润最大?最大利润为多少元?
25.(13分)已知一次函数y=2x+b的图象经过点A,B.点A的坐标为(1,5),点B的横坐标为m.
(1)求b的值;
(2)若线段AB的最高点与最低点的纵坐标差为6,求m的值;
(3)已知点C(m+1,2m+2),以坐标原点O为中心构造矩形CDEF,且CD⊥x轴,若线段AB与矩形CDEF只有一个公共点,求m的取值范围.
26.(13分)阅读下面的例题及点拨,并解决问题:
如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.
(1)点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),请完成剩余证明过程:
(2)拓展:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B C D B A B B C
二.填空题(共8小题)
11.12
12.100°
13. -2(答案不唯一)
14. 6
15. x2+(x-6.8)2=102
16.
17.
18.k≥1
三.解答题(共8小题)
19.(1)原式=-+=2-3+4=6-3. 5分
(2)4a2 2a
=2a2a
=0; 10分
20.解:(1)设过A,B两点的直线的函数解析式y=kx+b,
则,
解得,
∴直线AB的函数解析式为y=x+5; 5分
(2)A,B,C三点在同一条直线上,
理由:由(1)知,直线AB的解析式为y=x+5,
当x=0时,y=5,
∴点C(0,5)在直线AB上,
即A,B,C三点在同一条直线上. 10分
21.解:(1)∵点在直线l2上,
∴,解得m=3,
∴,
∵点A(6,0),M(3,)在直线l1上,
,解得,
∴直线l1的解析式为:y; 5分
(2)由直线解析式可知点B(0,3)即OB=3,
设点C的坐标为(n,0),则AC=|6-n|,
S△ABC12,
解得:n=-2或14, 9分
∴C(-2,0)或(14,0). 10分
22.解:(1)∵∠BDC=90°,CD=2,BD=AC,AC=4,
∴BC2; 5分
(2)∵AB=6,AC=4,BC=2,42+(2)2=62,即AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴S阴影=S△ABC-S△BCD
AC BCCD BD
4×22×4
=44. 10分
23.解:(1)四边形OCED是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵矩形ABCD的对角线AC,BD交于点O,
∴OC=OD,
∴ OCED是菱形; 6分
(2)∵四边形OCED是菱形,
∴OC=CE=4,
∴AC=2OC=8,
∵∠BAC=60°,∠ABC=90°,∠ACB=30°,
∴,
BC.
∴矩形ABCD的面积=4×416. 12分
24.解:(1)当0≤x≤200时,设y=k′x,
根据题意可得,200k′=3000,
解得k′=15,
∴y=15x; 3分
当x>200时,设y=kx+b,
根据题意可得,,
解得,
∴y=12x+600. 6分
∴综上所述,y关于x的函数解析式为y; 7分
(2)根据题意可知,设购进乙种产品x千克,则购进甲种产品(600-x)千克,
当160≤x≤200时,乙种产品进价为3000÷200=15(元/千克),
w=(12-8)(600-x)+18x-15x=-x+2400, 9分
∵-1<0,
∴w随x的增大而减小,
∴当x=160时,w的最大值为-1×160+2400=2240(元);
当200<x≤400时,w=(12-8)(600-x)+18x-(12x+600)=2x+1800,
∵2>0,
∴w随x的增大而增大,
∴当x=400时,w的最大值为800+1800=2600(元),
综上,购进甲产品200千克,乙产品400千克时利润最大,最大利润为2600元. 12分
25.解:(1)把点A的坐标为(1,5)代入y=2x+b得,5=2+b,
∴b=3,
即b的值为3; 3分
(2)∵点B的横坐标为m,
∴y=2m+3,
∴点B(m,2m+3),
∵线段AB的最高点与最低点的纵坐标差为6,
∴5-(2m+3)=6或2m+3-5=6,
∴m=-2或m=4;
(3)∵点C(m+1,2m+2),
∴点C在直线y=2x的图象上,
以坐标原点O为中心构造矩形CDEF,且CD⊥x轴,且与线段AB只有一个交点,则作图如上,
∴E(-m-1,-2m-2),D(m+1,-2m-2),F(-m-1,2m+2), 10分
当D在y=2x+3上,将D(m+1,-2m-2)代入表达式,
∴-2m-2=2(m+1)+3,
∴m;
当F在y=2x+3上,将F(-m-1,2m+2)代入表达式,
∴2m+2=-2(m+1)+3,
∴m; 12分
综上所述:m或; 13分
26.【解答】证明:(1)点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM,
易证△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2;
∵AM=MN,
∴EM=MN,
∴∠3=∠4;
∵∠3+∠1=∠4+∠5=60°,
∴∠1=∠2=∠5.
∵∠2+∠6=120,
∴∠5+∠6=120°,
∴∠AMN=60°; 6分
(2)拓展:延长AB至E,使EB=AB,连接EMC、EC,如图所示:
则EB=BC,∠EBM中=90°=∠ABM,
∴△EBC是等腰直角三角形,
∴∠BEC=∠BCE=45°,
∵N是正方形ABCD的外角∠DCH的平分线上一点,
∴∠MCN=90°+45°=135°,
∴∠BCE+∠MCN=180°,
∴E、C、N,三点共线,
在△ABM和△EBM中,
,
∴△ABM≌△EBM(SAS),
∴AM=EM,∠1=∠2,
∵AM=MN,
∴EM=MN,
∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,
∴∠1=∠2=∠5,
∵∠1+∠6=90°,
∴∠5+∠6=90°,
∴∠AMN=180°-90°=90°. 13分
同课章节目录
