2025届中考数学预热模拟卷 【河南专用】(含解析)
文档属性
| 名称 | 2025届中考数学预热模拟卷 【河南专用】(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 18:15:08 | ||
图片预览



文档简介
2025届中考数学预热模拟卷 【河南专用】
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各数是无理数的是( )
A.3.14.5926 B. C. D.
2.长白山天池系由火山口积水成湖,天池湖水碧蓝,水平如镜,群峰倒映,风景秀丽,总蓄水量约达,数据用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.若关于x的一元二次方程没有实数根,则k的取值范围为( )
A. B. C. D.
5.在如图所示的电路图中,当开关闭合以后,滑动变阻器从左往右滑动的过程中,电流表的示数与关系用图象可近似表示为( )
A. B.
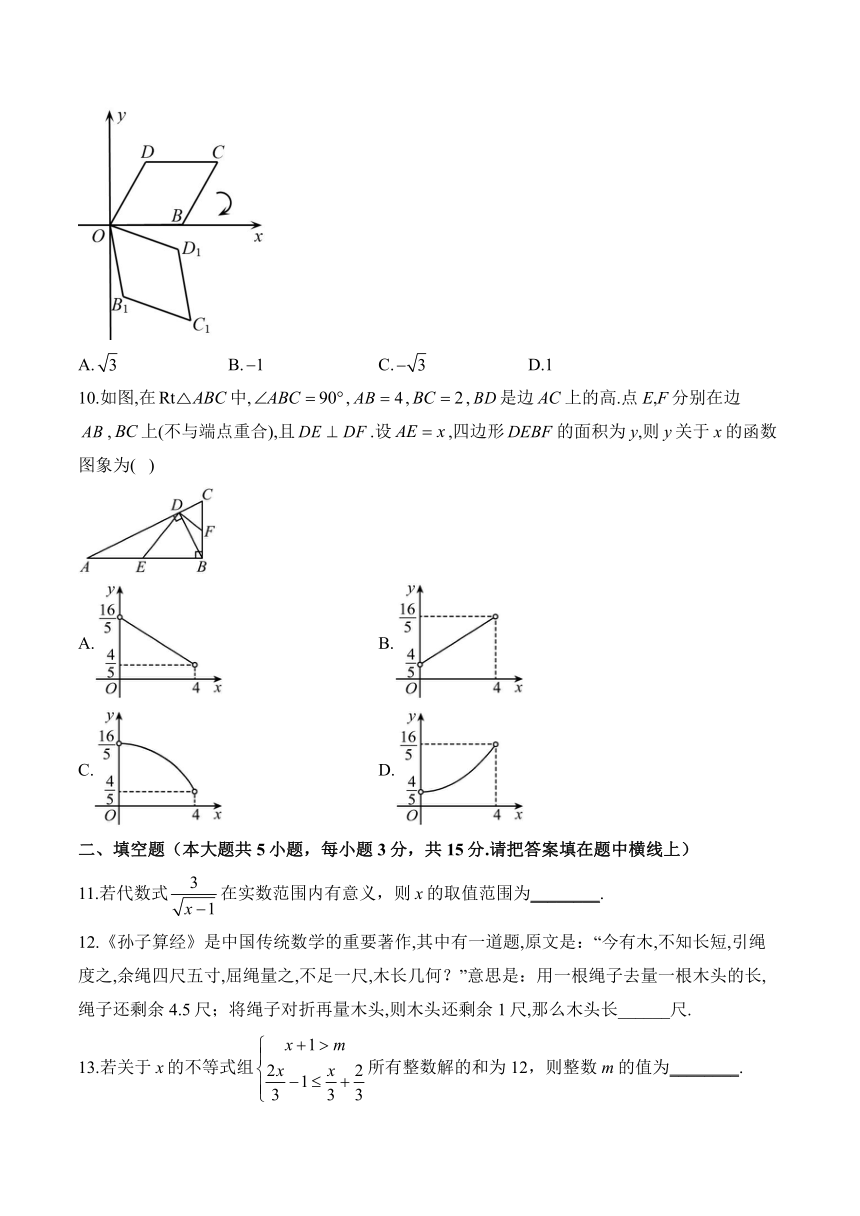
C. D.
6.“千门万户曈曈日,总把新桃换旧符”.春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在,人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.某商家在春节期间开展商品促销活动,顾客凡购物金额满100元,就可以从“福”字、春联、灯笼这三类礼品中免费领取一件.礼品领取规则:顾客每次从装有大小、形状、质地都相同的三张卡片(分别写有“福”字、春联、灯笼)的不透明袋子中,随机摸出一张卡片,然后领取一件与卡片上文字所对应的礼品.现有2名顾客都只领取了一件礼品,那么他们恰好领取同一类礼品的概率是( )
A. B. C. D.
7.如图,两个平面镜平行放置,光线经过平面镜反射时,,则的度数为( )
A. B. C. D.
8.如图,是的直径,点C是上一点,点D是的中点,连接,,,若,则的度数是( )
A. B. C. D.
9.如图,在平面直角坐标系中,四边形是菱形,,,将菱形绕点O旋转任意角度得到菱形,则点的纵坐标的最小值为( )
A. B. C. D.1
10.如图,在中,,,,是边上的高.点E,F分别在边,上(不与端点重合),且.设,四边形的面积为y,则y关于x的函数图象为( )
A. B.
C. D.
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
11.若代数式在实数范围内有意义,则x的取值范围为________.
12.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,那么木头长______尺.
13.若关于x的不等式组所有整数解的和为12,则整数m的值为________.
14.如图,点C是为直径的半圆O上一点,连接,将沿直线翻折,翻折后的圆弧恰好经过点O.若,则图中阴影部分的面积为______.
15.如图,在中,点E为的中点,点D在的延长线上,且,连接、,延长交于点F,若,,则的长为______.
三、解答题(本大题共8小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤)
16.(10分)(1)计算:;
(2)化简:.
17.(9分)随着科技的发展人工智能渐渐走进了人们的生活,现从甲、乙两款人工智能软件调查得分中分别随机抽取了20个用户的得分数据进行整理、描述和分析(得分用x表示),共分为四组,A:,B:,C:,D:,下面给出了部分信息.
甲款人工智能软件得分数据:
64,70,75,76,78,78,85,85,85,85,86,89,90,90,94,95,98,98,99,100.
乙款人工智能软件在C组内()的所有得分数据:
85,86,87,88,88,88,90,90.
甲、乙两款人工智能软件得分统计表:
软件 平均数 中位数 众数 方差
甲 86 85.5 b 96.6
乙 86 a 88
乙款人工智能软件得分扇形统计图:
根据以上信息,解答下列问题:
(1)填空:_______,______,______;
(2)根据以上数据,你认为哪款人工智能软件更受用户欢迎?请说明理由(写出一条理由即可);
(3)若本次调查有900名用户对甲款人工智能软件进行了调查评分,有1200名用户对乙款人工智能软件进行了评分,估计其中对甲、乙两款人工智能软件非常满意()的总用户数.
18.(9分)研学实践:钟鼓楼作为中国古代的传统建筑,一般都成为当地的地标,在古时主要承担报时之责.太原钟楼坐落于太原市府东街南侧,它始建于明代中期,是由傅山先生的祖父傅霖筹集资金修建而成.周末某学校研学小组对太原钟楼的高度进行测量.
方案设计:如图,观察员在地面上的点A处观察点C的仰角为.观察员在点A处竖直向上升起一架无人机,当无人机到达离地面的点B处时,测得钟楼顶端点D的俯角为,
数据应用:已知图中各点均在同一竖直平面内,C,D两点的水平距离,.请根据上述数据,计算太原钟楼的顶端到地面的距离.(结果精确到;参考数据:,,,,,)
19.(9分)某地消防中队在一座废弃高楼上开展消防技能比赛,在距离地面的点A处和其正上方的点B处各设置了一个火源,消防员站在水平地面上的点C处拿着水枪向A处喷水(水流出口与地面的距离忽略不计),水流路径为抛物线的一部分.据录像资料显示,水流路径的最高点到高楼的水平距离为,到水平地面的距离为.待A处火熄灭后,消防员退到点D处,调整水枪,使水流刚好落在点B处.已知点D到高楼的距离为,且两次灭火时水流路径的最高点到高楼的水平距离相等,建立如图所示的平面直角坐标系,其中水流的高度为,水流到高楼的水平距离为.
(1)求消防员灭A处的火源时水流路径所在抛物线的表达式;
(2)若消防员灭A,B两处的火源时水流路径所在抛物线的形状相同,求A,B两点之间的距离.
20.(9分)如图,一次函数的图象分别与反比例函数的图象在第一象限交于点,与y轴的负半轴交于点B,且.
(1)求函数和的表达式;
(2)已知点,试在该反比例函数图象上确定一点M,使得,求此时点M的坐标.
21.(9分)如图,已知的两边与以为直径的圆交于B,C两点.
(1)在射线上求作点M,使点M到点C的距离与点M到射线的距离相等;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若,,求的长.
22.(10分)如图(1)是我国明末《崇祯历书》之《割圆勾股八线表》中所绘的割圆八线图,如图(2),将图(1)中的丙、戊、乙、庚、辛、丁点分别表示A、B、C、D、E、D,扇形的圆心角为,切弧所在的于点A,交于点E.
(1)证明:是弧所在的的切线;
(2)若,扇形的半径为,求线段的长.
23.(10分)综合与探究
在数学课上,老师让同学们以“矩形的折叠”为主题开展活动.
实践操作:
如图,在矩形纸片中,,
第一步:如图1,将矩形纸片沿 过点C的直线折叠,使点B落在边上的点F处,得到折痕, 然后把纸片展平.
第二步:如图2,再将矩形纸片沿折叠,此时点A恰好落在上 的点N处,分别与交于点, 然后展平. 问题解决:
(1)求的长.
(2)判断与之间的数量关系,并说明理由.
拓展应用:
(3)如图3,延长相交于点P, 请直接写出的长.
答案以及解析
1.答案:B
解析:,,是有理数,故选项A,C,D不符合题意;
不能完全开方,是无理数,故选项B符合题意;
故选:B.
2.答案:B
解析:.
故选B.
3.答案:B
解析:A、,原计算错误,故此选项不符合题意;
B、,正确,故此选项符合题意;
C、,原计算错误,故此选项不符合题意;
D、,原计算错误,故此选项不符合题意;
故选:B.
4.答案:B
解析:∵一元二次方程没有实数根,
∴,
解得,
故选:B.
5.答案:C
解析:根据题意得:,即,
当从左往右滑动,即R增大时,
因为U一定,则I减小,
所以电流表的示数与关系用图象可近似表示为反比例函数图象,只有C选项符合题意.
故选:C.
6.答案:C
解析:分别用A,B,C表示写有“福”字、春联、灯笼的三张卡片,列表如下:
A B C
A A,A A,B A,C
B B,A B,B B,C
C C,A C,B C,C
共有9中等可能的结果,其中他们恰好领取同一类礼品有种等可能的结果,
∴;
故选C.
7.答案:C
解析:,
,
两个平面镜平行放置,
经过两次反射后的光线与入射光线平行,
;
故选C.
8.答案:D
解析:如图,连接,
∵是的直径,
∴,
∵,
∴,
∵点D是的中点,
∴,
∴,
∴,
∴.
故选:D.
9.答案:C
解析:如图,连接,过点C作轴于E,
∵四边形是菱形,
∴,
∴,
∵,
∴,
∴,
∴当点在y轴上时,点的纵坐标有最小值为
故选:C.
10.答案:A
解析:过点E作于点H,如下图:
∵,,,
∴,
∵是边上的高.
∴,
∴,
∵,,
∴,
∴,
解得:,
∴,
∵,,
∴,,
∴,
∴,
∴,
∴
∵,
∴当时,,
当时,.
故选:A.
11.答案:/
解析:由题意,得:,
解得:;
故答案为:.
12.答案:6.5
解析:设木头长x尺,则绳子长尺,
根据题意得:,
解得,
答:木头长6.5尺.
故答案为:6.5.
13.答案:
解析:,
解①得,
解②得,
∴,
∵所有整数解的和为12,
∴整数解是3,4,5.
∴,
解得:.
故答案为:.
14.答案:/
解析:如图,连接,作于点D,则,
由图可知,阴影部分的面积=扇形的面积,
由折叠性质可知:,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴扇形的面积是:,
故答案为:.
15.答案:/
解析:如图,延长到G,使,连接,
∵,,,
∴,
∴,,
∵,,
∴,
∴,即,
解得,,
∴,
∵,,
∴,
∴,即,
解得,,
∴,
解得,,
故答案为:.
16.答案:(1)
(2)
解析:(1)原式
.
(2)原式
.
17.答案:(1),,
(2)乙,理由见解析
(3)名
解析:(1)共个数据,乙组数据第10个、第11个数据分别为、,
中位数,
甲组数据中出现的次数最多,
众数,
,
,
故答案为:,,;
(2)乙款人工智能软件更受用户欢迎,理由如下:
因为甲、乙两款人工智能软件得分的平均数相等,但乙款人工智能软件得分的中位数和众数均高于甲,而且乙的方差小于甲的方差,乙更稳定,所以乙款人工智能软件更受用户欢迎(答案不唯一,合理即可),
答:乙款人工智能软件更受用户欢迎;
(3)(名),
估计其中对甲、乙两款人工智能软件非常满意()的总用户数约为名.
18.答案:太原钟楼的顶端D到地面的距离约为
解析:过点D作于点N,延长交于点M,如图所示:
则四边形、四边形都是矩形,,
∴,,.
设,则.
在中,,,,
∴.
在中,,,,
∴.
∵,
∴,解得.
∴.
∴.
答:太原钟楼的顶端D到地面的距离约为.
19.答案:(1)所在抛物线的表达式为;
(2).
解析:(1)由题意可知消防员灭A处的火源时水流路径所在抛物线的最高点的坐标为,
则设水流路径所在抛物线的表达式为,
将代入,得,
解得,
∴,
故消防员灭A处的火源时水流路径所在抛物线的表达式为;
(2)∵消防员灭A,B两处的火源时水流路径所在抛物线的形状相同,且两次灭火时水流路径的最高点到高楼的水平距离相等,
∴可设灭B处的火源时,水流路径所在抛物线的表达式为,
∵抛物线过点,
∴,解得,
故灭B处火源时,水流路径所在抛物线的表达式为,
令,则,
∴,
∴.
20.答案:(1),
(2)
解析:(1)∵,
∴,,
∴反比例函数的解析式为:,
∵,
∴,
把,代入,得:
,解得:,
∴一次函数的解析式为:;
(2)∵,
∴M在线段的中垂线上,
∵,,
∴B,C的中点坐标为:,
∴点M在直线上,
∴点M的纵坐标为:1,
∴点M的横坐标为:,
∴点M的坐标为:.
21.答案:(1)见解析
(2)
解析:(1)如图,作是平分线交于M,点M即为所作;
∵,
∴,
又∵,
∴,即,
如图1,作于H,
∴,
∴点M即为所作;
(2)由(1)可知,,
∵,
∴,即,
解得,,
由勾股定理得,,
∵,,
∴,
∴,
设,
∵,,
∴,
解得,,
由勾股定理得,,
∴的长为.
22.答案:(1)见解析
(2)
解析:证明:,,
,
,
又点D是半径的外端点,
是弧所在的的切线
(2),
,
切弧于点A,
,
,
,
在中:,
,
.
23.答案:(1)3;
(2),理由见解析;
(3)
解析:(1)四边形是矩形,
由折叠,可得.
设. 则.
在中,,
在中,,
即.
解得.
(2). 理由:
由第一步折叠,可得垂直平分.
由第二步折叠,可得.
在和中
(3)解析:四边形是矩形,
,
如图,连接.
垂直平分.
由(2)得.
四边形是菱形.
在中.
【满分120分 考试时间120分钟】
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各数是无理数的是( )
A.3.14.5926 B. C. D.
2.长白山天池系由火山口积水成湖,天池湖水碧蓝,水平如镜,群峰倒映,风景秀丽,总蓄水量约达,数据用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.若关于x的一元二次方程没有实数根,则k的取值范围为( )
A. B. C. D.
5.在如图所示的电路图中,当开关闭合以后,滑动变阻器从左往右滑动的过程中,电流表的示数与关系用图象可近似表示为( )
A. B.
C. D.
6.“千门万户曈曈日,总把新桃换旧符”.春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在,人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.某商家在春节期间开展商品促销活动,顾客凡购物金额满100元,就可以从“福”字、春联、灯笼这三类礼品中免费领取一件.礼品领取规则:顾客每次从装有大小、形状、质地都相同的三张卡片(分别写有“福”字、春联、灯笼)的不透明袋子中,随机摸出一张卡片,然后领取一件与卡片上文字所对应的礼品.现有2名顾客都只领取了一件礼品,那么他们恰好领取同一类礼品的概率是( )
A. B. C. D.
7.如图,两个平面镜平行放置,光线经过平面镜反射时,,则的度数为( )
A. B. C. D.
8.如图,是的直径,点C是上一点,点D是的中点,连接,,,若,则的度数是( )
A. B. C. D.
9.如图,在平面直角坐标系中,四边形是菱形,,,将菱形绕点O旋转任意角度得到菱形,则点的纵坐标的最小值为( )
A. B. C. D.1
10.如图,在中,,,,是边上的高.点E,F分别在边,上(不与端点重合),且.设,四边形的面积为y,则y关于x的函数图象为( )
A. B.
C. D.
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
11.若代数式在实数范围内有意义,则x的取值范围为________.
12.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,那么木头长______尺.
13.若关于x的不等式组所有整数解的和为12,则整数m的值为________.
14.如图,点C是为直径的半圆O上一点,连接,将沿直线翻折,翻折后的圆弧恰好经过点O.若,则图中阴影部分的面积为______.
15.如图,在中,点E为的中点,点D在的延长线上,且,连接、,延长交于点F,若,,则的长为______.
三、解答题(本大题共8小题,共75分.解答应写出必要的文字说明,证明过程或演算步骤)
16.(10分)(1)计算:;
(2)化简:.
17.(9分)随着科技的发展人工智能渐渐走进了人们的生活,现从甲、乙两款人工智能软件调查得分中分别随机抽取了20个用户的得分数据进行整理、描述和分析(得分用x表示),共分为四组,A:,B:,C:,D:,下面给出了部分信息.
甲款人工智能软件得分数据:
64,70,75,76,78,78,85,85,85,85,86,89,90,90,94,95,98,98,99,100.
乙款人工智能软件在C组内()的所有得分数据:
85,86,87,88,88,88,90,90.
甲、乙两款人工智能软件得分统计表:
软件 平均数 中位数 众数 方差
甲 86 85.5 b 96.6
乙 86 a 88
乙款人工智能软件得分扇形统计图:
根据以上信息,解答下列问题:
(1)填空:_______,______,______;
(2)根据以上数据,你认为哪款人工智能软件更受用户欢迎?请说明理由(写出一条理由即可);
(3)若本次调查有900名用户对甲款人工智能软件进行了调查评分,有1200名用户对乙款人工智能软件进行了评分,估计其中对甲、乙两款人工智能软件非常满意()的总用户数.
18.(9分)研学实践:钟鼓楼作为中国古代的传统建筑,一般都成为当地的地标,在古时主要承担报时之责.太原钟楼坐落于太原市府东街南侧,它始建于明代中期,是由傅山先生的祖父傅霖筹集资金修建而成.周末某学校研学小组对太原钟楼的高度进行测量.
方案设计:如图,观察员在地面上的点A处观察点C的仰角为.观察员在点A处竖直向上升起一架无人机,当无人机到达离地面的点B处时,测得钟楼顶端点D的俯角为,
数据应用:已知图中各点均在同一竖直平面内,C,D两点的水平距离,.请根据上述数据,计算太原钟楼的顶端到地面的距离.(结果精确到;参考数据:,,,,,)
19.(9分)某地消防中队在一座废弃高楼上开展消防技能比赛,在距离地面的点A处和其正上方的点B处各设置了一个火源,消防员站在水平地面上的点C处拿着水枪向A处喷水(水流出口与地面的距离忽略不计),水流路径为抛物线的一部分.据录像资料显示,水流路径的最高点到高楼的水平距离为,到水平地面的距离为.待A处火熄灭后,消防员退到点D处,调整水枪,使水流刚好落在点B处.已知点D到高楼的距离为,且两次灭火时水流路径的最高点到高楼的水平距离相等,建立如图所示的平面直角坐标系,其中水流的高度为,水流到高楼的水平距离为.
(1)求消防员灭A处的火源时水流路径所在抛物线的表达式;
(2)若消防员灭A,B两处的火源时水流路径所在抛物线的形状相同,求A,B两点之间的距离.
20.(9分)如图,一次函数的图象分别与反比例函数的图象在第一象限交于点,与y轴的负半轴交于点B,且.
(1)求函数和的表达式;
(2)已知点,试在该反比例函数图象上确定一点M,使得,求此时点M的坐标.
21.(9分)如图,已知的两边与以为直径的圆交于B,C两点.
(1)在射线上求作点M,使点M到点C的距离与点M到射线的距离相等;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若,,求的长.
22.(10分)如图(1)是我国明末《崇祯历书》之《割圆勾股八线表》中所绘的割圆八线图,如图(2),将图(1)中的丙、戊、乙、庚、辛、丁点分别表示A、B、C、D、E、D,扇形的圆心角为,切弧所在的于点A,交于点E.
(1)证明:是弧所在的的切线;
(2)若,扇形的半径为,求线段的长.
23.(10分)综合与探究
在数学课上,老师让同学们以“矩形的折叠”为主题开展活动.
实践操作:
如图,在矩形纸片中,,
第一步:如图1,将矩形纸片沿 过点C的直线折叠,使点B落在边上的点F处,得到折痕, 然后把纸片展平.
第二步:如图2,再将矩形纸片沿折叠,此时点A恰好落在上 的点N处,分别与交于点, 然后展平. 问题解决:
(1)求的长.
(2)判断与之间的数量关系,并说明理由.
拓展应用:
(3)如图3,延长相交于点P, 请直接写出的长.
答案以及解析
1.答案:B
解析:,,是有理数,故选项A,C,D不符合题意;
不能完全开方,是无理数,故选项B符合题意;
故选:B.
2.答案:B
解析:.
故选B.
3.答案:B
解析:A、,原计算错误,故此选项不符合题意;
B、,正确,故此选项符合题意;
C、,原计算错误,故此选项不符合题意;
D、,原计算错误,故此选项不符合题意;
故选:B.
4.答案:B
解析:∵一元二次方程没有实数根,
∴,
解得,
故选:B.
5.答案:C
解析:根据题意得:,即,
当从左往右滑动,即R增大时,
因为U一定,则I减小,
所以电流表的示数与关系用图象可近似表示为反比例函数图象,只有C选项符合题意.
故选:C.
6.答案:C
解析:分别用A,B,C表示写有“福”字、春联、灯笼的三张卡片,列表如下:
A B C
A A,A A,B A,C
B B,A B,B B,C
C C,A C,B C,C
共有9中等可能的结果,其中他们恰好领取同一类礼品有种等可能的结果,
∴;
故选C.
7.答案:C
解析:,
,
两个平面镜平行放置,
经过两次反射后的光线与入射光线平行,
;
故选C.
8.答案:D
解析:如图,连接,
∵是的直径,
∴,
∵,
∴,
∵点D是的中点,
∴,
∴,
∴,
∴.
故选:D.
9.答案:C
解析:如图,连接,过点C作轴于E,
∵四边形是菱形,
∴,
∴,
∵,
∴,
∴,
∴当点在y轴上时,点的纵坐标有最小值为
故选:C.
10.答案:A
解析:过点E作于点H,如下图:
∵,,,
∴,
∵是边上的高.
∴,
∴,
∵,,
∴,
∴,
解得:,
∴,
∵,,
∴,,
∴,
∴,
∴,
∴
∵,
∴当时,,
当时,.
故选:A.
11.答案:/
解析:由题意,得:,
解得:;
故答案为:.
12.答案:6.5
解析:设木头长x尺,则绳子长尺,
根据题意得:,
解得,
答:木头长6.5尺.
故答案为:6.5.
13.答案:
解析:,
解①得,
解②得,
∴,
∵所有整数解的和为12,
∴整数解是3,4,5.
∴,
解得:.
故答案为:.
14.答案:/
解析:如图,连接,作于点D,则,
由图可知,阴影部分的面积=扇形的面积,
由折叠性质可知:,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴扇形的面积是:,
故答案为:.
15.答案:/
解析:如图,延长到G,使,连接,
∵,,,
∴,
∴,,
∵,,
∴,
∴,即,
解得,,
∴,
∵,,
∴,
∴,即,
解得,,
∴,
解得,,
故答案为:.
16.答案:(1)
(2)
解析:(1)原式
.
(2)原式
.
17.答案:(1),,
(2)乙,理由见解析
(3)名
解析:(1)共个数据,乙组数据第10个、第11个数据分别为、,
中位数,
甲组数据中出现的次数最多,
众数,
,
,
故答案为:,,;
(2)乙款人工智能软件更受用户欢迎,理由如下:
因为甲、乙两款人工智能软件得分的平均数相等,但乙款人工智能软件得分的中位数和众数均高于甲,而且乙的方差小于甲的方差,乙更稳定,所以乙款人工智能软件更受用户欢迎(答案不唯一,合理即可),
答:乙款人工智能软件更受用户欢迎;
(3)(名),
估计其中对甲、乙两款人工智能软件非常满意()的总用户数约为名.
18.答案:太原钟楼的顶端D到地面的距离约为
解析:过点D作于点N,延长交于点M,如图所示:
则四边形、四边形都是矩形,,
∴,,.
设,则.
在中,,,,
∴.
在中,,,,
∴.
∵,
∴,解得.
∴.
∴.
答:太原钟楼的顶端D到地面的距离约为.
19.答案:(1)所在抛物线的表达式为;
(2).
解析:(1)由题意可知消防员灭A处的火源时水流路径所在抛物线的最高点的坐标为,
则设水流路径所在抛物线的表达式为,
将代入,得,
解得,
∴,
故消防员灭A处的火源时水流路径所在抛物线的表达式为;
(2)∵消防员灭A,B两处的火源时水流路径所在抛物线的形状相同,且两次灭火时水流路径的最高点到高楼的水平距离相等,
∴可设灭B处的火源时,水流路径所在抛物线的表达式为,
∵抛物线过点,
∴,解得,
故灭B处火源时,水流路径所在抛物线的表达式为,
令,则,
∴,
∴.
20.答案:(1),
(2)
解析:(1)∵,
∴,,
∴反比例函数的解析式为:,
∵,
∴,
把,代入,得:
,解得:,
∴一次函数的解析式为:;
(2)∵,
∴M在线段的中垂线上,
∵,,
∴B,C的中点坐标为:,
∴点M在直线上,
∴点M的纵坐标为:1,
∴点M的横坐标为:,
∴点M的坐标为:.
21.答案:(1)见解析
(2)
解析:(1)如图,作是平分线交于M,点M即为所作;
∵,
∴,
又∵,
∴,即,
如图1,作于H,
∴,
∴点M即为所作;
(2)由(1)可知,,
∵,
∴,即,
解得,,
由勾股定理得,,
∵,,
∴,
∴,
设,
∵,,
∴,
解得,,
由勾股定理得,,
∴的长为.
22.答案:(1)见解析
(2)
解析:证明:,,
,
,
又点D是半径的外端点,
是弧所在的的切线
(2),
,
切弧于点A,
,
,
,
在中:,
,
.
23.答案:(1)3;
(2),理由见解析;
(3)
解析:(1)四边形是矩形,
由折叠,可得.
设. 则.
在中,,
在中,,
即.
解得.
(2). 理由:
由第一步折叠,可得垂直平分.
由第二步折叠,可得.
在和中
(3)解析:四边形是矩形,
,
如图,连接.
垂直平分.
由(2)得.
四边形是菱形.
在中.
同课章节目录
