2025届中考数学预热模拟卷 【安徽专用】(含解析)
文档属性
| 名称 | 2025届中考数学预热模拟卷 【安徽专用】(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-10 18:17:17 | ||
图片预览



文档简介
2025届中考数学预热模拟卷 【安徽专用】
【满分150分 考试时间120分钟】
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.的相反数是( )
A. B. C.2025 D.
2.据光明网消息,今年“五一”假期,日均全社会跨区域人员流动量达亿人次以上,公路出行仍是主力,其中自驾出行比例达八成以上,将数据“亿”用科学记数法表示为( )
A. B. C. D.
3.斗拱是我国古建筑中特有的一种结构,体现了古代工匠的精湛技艺.如图是一种斗形构件“三才升”的示意图,则它的左视图为( )
A. B.
C. D.
4.下列计算正确的是( )
A. B. C. D.
5.关于x的一元二次方程有两个不相等的实数根,则k的值可以是( )
A.1 B. C. D.
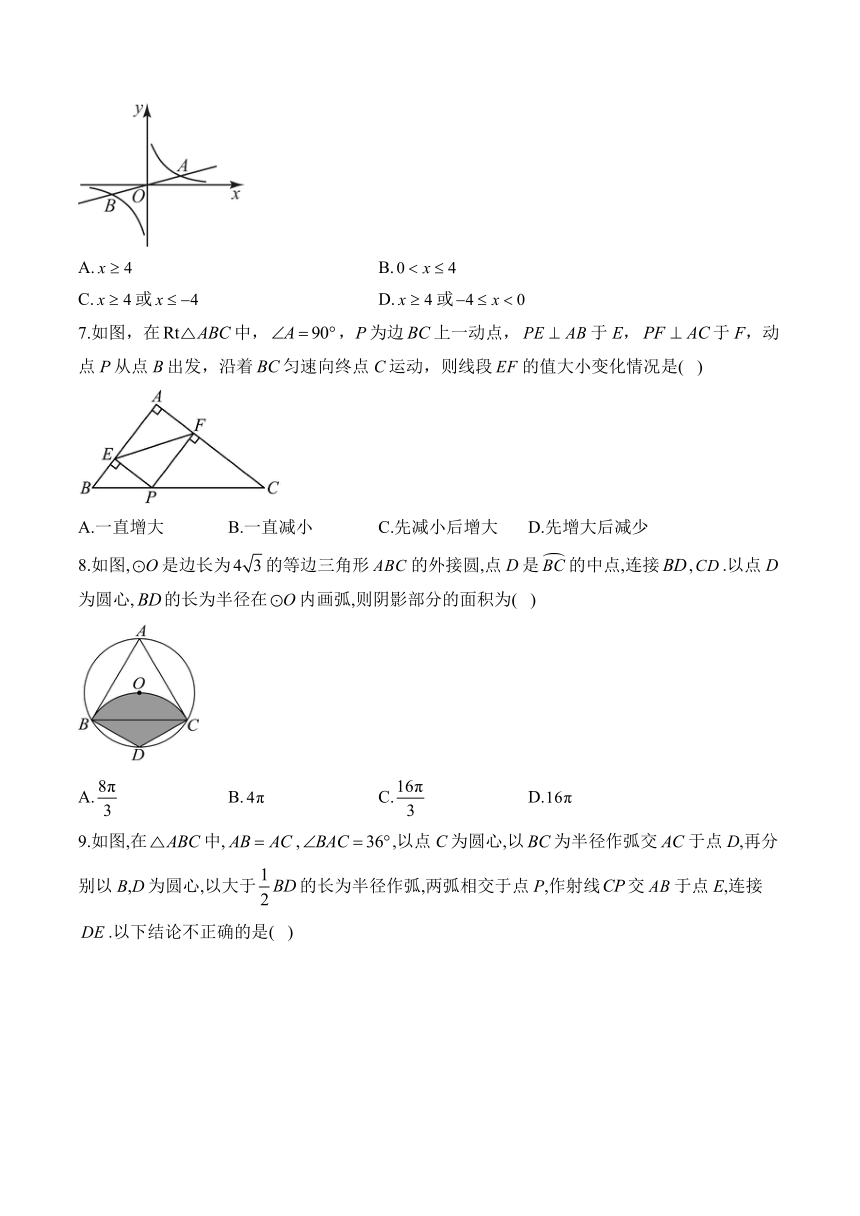
6.如图,直线与双曲线相交于点A和B,已知点A的坐标为,则不等式的解集为( )
A. B.
C.或 D.或
7.如图,在中,,P为边上一动点,于E,于F,动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是( )
A.一直增大 B.一直减小 C.先减小后增大 D.先增大后减少
8.如图,是边长为的等边三角形的外接圆,点D是的中点,连接,.以点D为圆心,的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
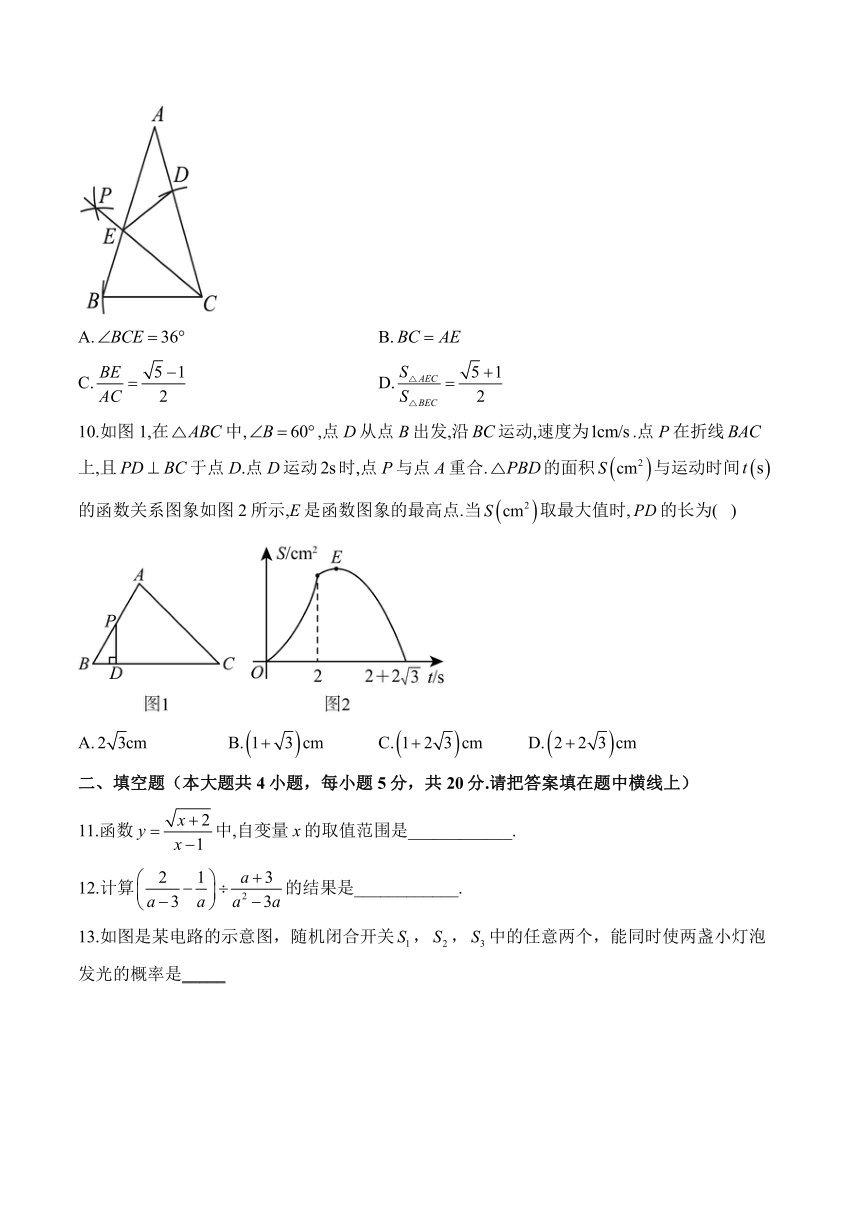
9.如图,在中,,,以点C为圆心,以为半径作弧交于点D,再分别以B,D为圆心,以大于的长为半径作弧,两弧相交于点P,作射线交于点E,连接.以下结论不正确的是( )
A. B.
C. D.
10.如图1,在中,,点D从点B出发,沿运动,速度为.点P在折线上,且于点D.点D运动时,点P与点A重合.的面积与运动时间的函数关系图象如图2所示,E是函数图象的最高点.当取最大值时,的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中横线上)
11.函数中,自变量x的取值范围是____________.
12.计算的结果是____________.
13.如图是某电路的示意图,随机闭合开关,,中的任意两个,能同时使两盏小灯泡发光的概率是_____
14.如图,在正方形中,G为边上一点,将沿翻折到处,延长交边于点E,过点F作分别交,,于点H,P,Q,请完成下列问题:
(1)______.
(2)若,则______.
三、解答题(本大题共9小题,共90分.解答应写出必要的文字说明,证明过程或演算步骤)
15.(8分)计算:.
16.(8分)宁陵酥梨产自河南省宁陵,最大可达1千克以上.成熟后的酥梨酥脆多汁、香甜味美、金黄发亮,是畅销海内外的佳品珍果.某水果商购进酥梨产品进行销售,酥梨鲜果以5元/千克的成本价购进,并以8元/千克的价格出售.梨膏以元/千克的成本价购进,并以元/千克的价格出售.请结合题意回答下列问题:
(1)该商店购进酥梨鲜果和梨膏共千克,花费元,则购进酥梨鲜果和梨膏各多少千克?
(2)该水果商店两天售完所有酥梨鲜果和梨膏后,决定再购进共千克的酥梨鲜果和梨膏(所购进梨膏重量不高于酥梨鲜果重量的2倍),则当该水果商店购进多少千克酥梨鲜果时,才能使利润最大?最大利润是多少?
17.(8分)观察以下等式:
第1个等式: 第2个等式:
第3个等式: 第4个等式:
…
按照以上规律,解决下列问题:
(1)写出第5个等式:__________________________;
(2)写出你猜想的第n个等式:______________________(用含n的等式表示),并证明.
18.(8分)如图,已知在平面直角坐标系中,点、、.请按如下要求画图:
(1)将绕点O逆时针旋转得到,请画出;
(2)以点O为位似中心,位似比为,将在位似中心的异侧进行放大得到,请画出;
(3)内部一点M的坐标为,写出M在中的对应点的坐标.
19.(10分)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为,主臂长为,测得主臂伸展角..(参考数据:,,,)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q到点N的距离为,求的度数.
20.(10分)如图,为的切线,C为切点,过点C作,垂足为D,交于点A,延长与的延长线交于点E.
(1)求证:为的切线.
(2)若,,求线段的长.
21.(12分)数学课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动,同学们随机收集芒果树、荔枝树的树叶各1片,通过测量得到这些树叶的长y(单位:),宽x(单位)的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 3.75 0.0424
荔枝树叶的长宽比 1.91 2.0 0.0669
(1)上述表格中:_______,______;
(2)通过数据,同学们总结出了一些结论:
①A同学说:“从树叶的长宽比的方差来看,芒果树叶的形状差别比荔枝树叶________”.
(填“小”或者“大”)
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的__________倍.”
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.
22.(12分)综合与实践在中,,,.
问题发现
(1)如图1,将绕点C按顺时针方向旋转得到,连接,,线段与之间的数量关系是___________,与的位置关系是___________.
类比探究
(2)如图2,将绕点C按顺时针方向旋转任意角度得到,连接,,线段与之间的数量关系、位置关系与(1)中的结论是否一致?请说明理由.
迁移应用
(3)如图3,将绕点C旋转一定的角度得到,当点D落到边上时,连接,求线段的长.
23.(14分)如图所示,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,已知点C的坐标为,且.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一点,连接,并将线段绕点P顺时针旋转90°,点A的对应点恰为点C,请直接写出点P的坐标;
(3)在(2)的前提下,将线段向上平移m个单位,若线段与抛物线有交点,求m的取值范围.
答案以及解析
1.答案:B
解析:根据相反数的定义(只有符号不同的两个数互为相反数),可知:的相反数是.
故选:B.
2.答案:B
解析:亿.
故选B.
3.答案:A
解析:斗形构件“三才升”的左视图为:
故选:A.
4.答案:D
解析:A.,原选项计算错误,不符合题意;
B. ,原选项计算错误,不符合题意;
C. ,原选项计算错误,不符合题意;
D. ,计算正确,符合题意,
故选:D.
5.答案:D
解析:由关于x的一元二次方程有两个不相等的实数根,可知:
,
解得:,
∴k的值可以是;
故选D.
6.答案:D
解析:直线与双曲线相交于点A和B,已知点A的坐标为,
点B的坐标为,
由图象可得,不等式的解集为或,
故选:D.
7.答案:C
解析:如图,连接.
,,
四边形是矩形,
,
由垂线段最短可得时,最短,则线段的值最小,
动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是先减小后增大.
故选:C.
8.答案:C
解析:过D作于E,
∵是边长为的等边三角形的外接圆,
∴,,,
∴,
∵点D是的中点,
∴,
∴,
∴,,
∴,
∴,
故选:C.
9.答案:C
解析:由题意得,,平分,
∵在中,,,
∴
∵平分,
∴,故A正确;
∵平分,
∴,
∴,
∵,,
∴,
∴,
∴,故B正确;
∵,,
∴,
∴,
设,,则,
∴,
∴,
解得,
∴,
∴,故C错误;
过点E作于G,于H,
∵平分,,,
∴
∴,故D正确;
故选:C.
10.答案:B
解析:由题意知,点D运动时,点P,D的位置如图1所示.
此时,在中,,,,
∴,
∴.
由函数图象得,
∴,
∴.
由题图2点E的位置可知,点P在上时,有最大值.
当时,点P在边上,如图2,
此时,,
∴.
∵,
又∵,
∴当时,的值最大,
此时.
故选:B.
11.答案:且
解析:由题意可得
解得且
故答案为:且.
12.答案:1
解析:
,
故答案为:1.
13.答案:
解析:画树状图如下:
共有6种等可能的结果,其中能让两个灯泡发光的结果数为4,
∴能同时使2盏小灯泡发光的概率是:,
故答案为:
14.答案:(1)
(2)
解析:(1)∵四边形为正方形,
∴,,
由折叠的性质可得:,,,
∴,,
在和中,
,
∴,
∴,
∴,
故答案为:;
(2)过点H作于M,如图:
∵,
∴,
∴,
在和中,
,
∴,
∴,,
∵,,
∴,
∴,
∵,
∴,
设,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
故答案为:.
15.答案:
解析:原式
.
16.答案:(1)购进酥梨鲜果千克,梨膏千克
(2)当该水果商店购进千克酥梨鲜果时,利润w最大,最大利润是元
解析:(1)设购进酥梨鲜果x千克,梨膏y千克.
根据题意,得:
解得:
答:购进酥梨鲜果千克,梨膏千克.
(2)设购进m千克酥梨鲜果,则购进梨膏千克,全部售出后获得的利润为w元.
购进梨膏重量不高于酥梨鲜果重量的2倍,
解得:
根据题意,得:
即:
随m的增大而减小.
当m取最小值时,w取得最大值,最大值为:(元)
答:当该水果商店购进千克酥梨鲜果时,利润w最大,最大利润是元.
17.答案:(1)
(2),证明见解析
解析:(1)根据题意,得:
故答案为:;
(2)∵第1个等式:
第2个等式:
第3个等式:
第4个等式:
…
∴第n个等式:
∵,
∴等式成立;
故答案为:.
18.答案:(1)见解析
(2)见解析
(3)
解析:如图所示,即为所求
(2)解析:如图所示,即为所求
(3)解析:如图所示,
过点分别作轴的垂线,垂足分别为,
∴
∵
∴,
∵,
∴
又
∴
∴
当,时,M在第四象限,在第一象限,
∴
当时,M在第一象限,在第二象限,
∴,
综上所述,
19.答案:(1)
(2)
解析:(1)过点P作,垂足为G,延长交于点F,
由题意得:,,,
在中,,,
,,
点P到地面的高度约为;
(2)由题意得:,
在中,,,
,,
,
,
在中,,
,,
的度数约为.
20.答案:(1)见解析
(2)6
解析:(1)证明:如图,连接,
为的切线,C为切点,
,
,O为圆心,
是的垂直平分线,
,
在和中,
,
,
,
,
为的半径,
为的切线.
(2)为的切线,
,
,,
,
,,
,
,
,
解得.
21.答案:(1)1.95,4.0
(2)小,2
(3)芒果树
解析:把片荔枝树叶的长宽比从小到大排列1.3,1.8,1.8,1.9,1.9,2.0,2.0,2.0,2.0,2.4
排在中间的两个数分别为1.9、2.0,
故;
片芒果树叶的长宽比中出现次数最多的是4.0,故;
故答案为:1.95,4.0;
(2)∵,
∴从树叶的长宽比的方差来看,芒果树叶的形状差别比荔枝树叶小”;
∵荔枝树叶的长宽比的平均数,中位数是,众数是,
∴从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的2倍.
故答案为:小,2;
(3)这片树叶更可能来自荔枝,理由如下:
∵一片长,宽的树叶,长宽比为3.75,接近3.74,
∴这片树叶更可能来自芒果树.
22.答案:(1),
(2)线段与的数量关系、位置关系与(1)中结论一致,理由见解析
(3)
解析:(1)∵将绕点C按顺时针方向旋转得到,连接,,
∴,,,,
∴,,
∴,,
∴与之间的数量关系是,
延长交于一点H,
∵,,
∴,
即,
∴与的位置关系是,
故答案为:,;
(2)线段与的数量关系、位置关系与(1)中结论一致,
理由如下:
如图,延长交于点H,
将绕点C按逆时针方向旋转任意角度得到,
,,,
,
,
,
,.
(3)如图,过点C作于点N,
,,,
,
,
又
,
,
,,
,
由(2)可知.
23.答案:(1)
(2)点P的坐标为
(3)线段AP与抛物线有交点,m的取值范围为
解析:(1)∵点C的坐标为,
∴,
∵,
∴,
∴,
把,代入得,
,
解得,,
∴抛物线的解析式为;
(2)对于抛物线,当时,
解得,,,
∴,
又
∴抛物线的对称轴为直线
∵点P为抛物线对称轴上一点,
∴设
∴;;
∵
∴,
∴,
解得,,,
又,即,
∴
解得,,
综上,t的值为1,
∴点P的坐标为:
(3)设直线的解析式为,
把,代入得,,
解得,,
∴直线的解析式为;
则直线向上平移m个单位后,所得直线解析式为,
联立方程组
得关于x的一元二次方程:
若直线与抛物线相切,则解得
结合图象可知:线段与抛物线有交点,m的取值范围为
【满分150分 考试时间120分钟】
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.的相反数是( )
A. B. C.2025 D.
2.据光明网消息,今年“五一”假期,日均全社会跨区域人员流动量达亿人次以上,公路出行仍是主力,其中自驾出行比例达八成以上,将数据“亿”用科学记数法表示为( )
A. B. C. D.
3.斗拱是我国古建筑中特有的一种结构,体现了古代工匠的精湛技艺.如图是一种斗形构件“三才升”的示意图,则它的左视图为( )
A. B.
C. D.
4.下列计算正确的是( )
A. B. C. D.
5.关于x的一元二次方程有两个不相等的实数根,则k的值可以是( )
A.1 B. C. D.
6.如图,直线与双曲线相交于点A和B,已知点A的坐标为,则不等式的解集为( )
A. B.
C.或 D.或
7.如图,在中,,P为边上一动点,于E,于F,动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是( )
A.一直增大 B.一直减小 C.先减小后增大 D.先增大后减少
8.如图,是边长为的等边三角形的外接圆,点D是的中点,连接,.以点D为圆心,的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
9.如图,在中,,,以点C为圆心,以为半径作弧交于点D,再分别以B,D为圆心,以大于的长为半径作弧,两弧相交于点P,作射线交于点E,连接.以下结论不正确的是( )
A. B.
C. D.
10.如图1,在中,,点D从点B出发,沿运动,速度为.点P在折线上,且于点D.点D运动时,点P与点A重合.的面积与运动时间的函数关系图象如图2所示,E是函数图象的最高点.当取最大值时,的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中横线上)
11.函数中,自变量x的取值范围是____________.
12.计算的结果是____________.
13.如图是某电路的示意图,随机闭合开关,,中的任意两个,能同时使两盏小灯泡发光的概率是_____
14.如图,在正方形中,G为边上一点,将沿翻折到处,延长交边于点E,过点F作分别交,,于点H,P,Q,请完成下列问题:
(1)______.
(2)若,则______.
三、解答题(本大题共9小题,共90分.解答应写出必要的文字说明,证明过程或演算步骤)
15.(8分)计算:.
16.(8分)宁陵酥梨产自河南省宁陵,最大可达1千克以上.成熟后的酥梨酥脆多汁、香甜味美、金黄发亮,是畅销海内外的佳品珍果.某水果商购进酥梨产品进行销售,酥梨鲜果以5元/千克的成本价购进,并以8元/千克的价格出售.梨膏以元/千克的成本价购进,并以元/千克的价格出售.请结合题意回答下列问题:
(1)该商店购进酥梨鲜果和梨膏共千克,花费元,则购进酥梨鲜果和梨膏各多少千克?
(2)该水果商店两天售完所有酥梨鲜果和梨膏后,决定再购进共千克的酥梨鲜果和梨膏(所购进梨膏重量不高于酥梨鲜果重量的2倍),则当该水果商店购进多少千克酥梨鲜果时,才能使利润最大?最大利润是多少?
17.(8分)观察以下等式:
第1个等式: 第2个等式:
第3个等式: 第4个等式:
…
按照以上规律,解决下列问题:
(1)写出第5个等式:__________________________;
(2)写出你猜想的第n个等式:______________________(用含n的等式表示),并证明.
18.(8分)如图,已知在平面直角坐标系中,点、、.请按如下要求画图:
(1)将绕点O逆时针旋转得到,请画出;
(2)以点O为位似中心,位似比为,将在位似中心的异侧进行放大得到,请画出;
(3)内部一点M的坐标为,写出M在中的对应点的坐标.
19.(10分)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为,主臂长为,测得主臂伸展角..(参考数据:,,,)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q到点N的距离为,求的度数.
20.(10分)如图,为的切线,C为切点,过点C作,垂足为D,交于点A,延长与的延长线交于点E.
(1)求证:为的切线.
(2)若,,求线段的长.
21.(12分)数学课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动,同学们随机收集芒果树、荔枝树的树叶各1片,通过测量得到这些树叶的长y(单位:),宽x(单位)的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 3.75 0.0424
荔枝树叶的长宽比 1.91 2.0 0.0669
(1)上述表格中:_______,______;
(2)通过数据,同学们总结出了一些结论:
①A同学说:“从树叶的长宽比的方差来看,芒果树叶的形状差别比荔枝树叶________”.
(填“小”或者“大”)
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的__________倍.”
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.
22.(12分)综合与实践在中,,,.
问题发现
(1)如图1,将绕点C按顺时针方向旋转得到,连接,,线段与之间的数量关系是___________,与的位置关系是___________.
类比探究
(2)如图2,将绕点C按顺时针方向旋转任意角度得到,连接,,线段与之间的数量关系、位置关系与(1)中的结论是否一致?请说明理由.
迁移应用
(3)如图3,将绕点C旋转一定的角度得到,当点D落到边上时,连接,求线段的长.
23.(14分)如图所示,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,已知点C的坐标为,且.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一点,连接,并将线段绕点P顺时针旋转90°,点A的对应点恰为点C,请直接写出点P的坐标;
(3)在(2)的前提下,将线段向上平移m个单位,若线段与抛物线有交点,求m的取值范围.
答案以及解析
1.答案:B
解析:根据相反数的定义(只有符号不同的两个数互为相反数),可知:的相反数是.
故选:B.
2.答案:B
解析:亿.
故选B.
3.答案:A
解析:斗形构件“三才升”的左视图为:
故选:A.
4.答案:D
解析:A.,原选项计算错误,不符合题意;
B. ,原选项计算错误,不符合题意;
C. ,原选项计算错误,不符合题意;
D. ,计算正确,符合题意,
故选:D.
5.答案:D
解析:由关于x的一元二次方程有两个不相等的实数根,可知:
,
解得:,
∴k的值可以是;
故选D.
6.答案:D
解析:直线与双曲线相交于点A和B,已知点A的坐标为,
点B的坐标为,
由图象可得,不等式的解集为或,
故选:D.
7.答案:C
解析:如图,连接.
,,
四边形是矩形,
,
由垂线段最短可得时,最短,则线段的值最小,
动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是先减小后增大.
故选:C.
8.答案:C
解析:过D作于E,
∵是边长为的等边三角形的外接圆,
∴,,,
∴,
∵点D是的中点,
∴,
∴,
∴,,
∴,
∴,
故选:C.
9.答案:C
解析:由题意得,,平分,
∵在中,,,
∴
∵平分,
∴,故A正确;
∵平分,
∴,
∴,
∵,,
∴,
∴,
∴,故B正确;
∵,,
∴,
∴,
设,,则,
∴,
∴,
解得,
∴,
∴,故C错误;
过点E作于G,于H,
∵平分,,,
∴
∴,故D正确;
故选:C.
10.答案:B
解析:由题意知,点D运动时,点P,D的位置如图1所示.
此时,在中,,,,
∴,
∴.
由函数图象得,
∴,
∴.
由题图2点E的位置可知,点P在上时,有最大值.
当时,点P在边上,如图2,
此时,,
∴.
∵,
又∵,
∴当时,的值最大,
此时.
故选:B.
11.答案:且
解析:由题意可得
解得且
故答案为:且.
12.答案:1
解析:
,
故答案为:1.
13.答案:
解析:画树状图如下:
共有6种等可能的结果,其中能让两个灯泡发光的结果数为4,
∴能同时使2盏小灯泡发光的概率是:,
故答案为:
14.答案:(1)
(2)
解析:(1)∵四边形为正方形,
∴,,
由折叠的性质可得:,,,
∴,,
在和中,
,
∴,
∴,
∴,
故答案为:;
(2)过点H作于M,如图:
∵,
∴,
∴,
在和中,
,
∴,
∴,,
∵,,
∴,
∴,
∵,
∴,
设,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
故答案为:.
15.答案:
解析:原式
.
16.答案:(1)购进酥梨鲜果千克,梨膏千克
(2)当该水果商店购进千克酥梨鲜果时,利润w最大,最大利润是元
解析:(1)设购进酥梨鲜果x千克,梨膏y千克.
根据题意,得:
解得:
答:购进酥梨鲜果千克,梨膏千克.
(2)设购进m千克酥梨鲜果,则购进梨膏千克,全部售出后获得的利润为w元.
购进梨膏重量不高于酥梨鲜果重量的2倍,
解得:
根据题意,得:
即:
随m的增大而减小.
当m取最小值时,w取得最大值,最大值为:(元)
答:当该水果商店购进千克酥梨鲜果时,利润w最大,最大利润是元.
17.答案:(1)
(2),证明见解析
解析:(1)根据题意,得:
故答案为:;
(2)∵第1个等式:
第2个等式:
第3个等式:
第4个等式:
…
∴第n个等式:
∵,
∴等式成立;
故答案为:.
18.答案:(1)见解析
(2)见解析
(3)
解析:如图所示,即为所求
(2)解析:如图所示,即为所求
(3)解析:如图所示,
过点分别作轴的垂线,垂足分别为,
∴
∵
∴,
∵,
∴
又
∴
∴
当,时,M在第四象限,在第一象限,
∴
当时,M在第一象限,在第二象限,
∴,
综上所述,
19.答案:(1)
(2)
解析:(1)过点P作,垂足为G,延长交于点F,
由题意得:,,,
在中,,,
,,
点P到地面的高度约为;
(2)由题意得:,
在中,,,
,,
,
,
在中,,
,,
的度数约为.
20.答案:(1)见解析
(2)6
解析:(1)证明:如图,连接,
为的切线,C为切点,
,
,O为圆心,
是的垂直平分线,
,
在和中,
,
,
,
,
为的半径,
为的切线.
(2)为的切线,
,
,,
,
,,
,
,
,
解得.
21.答案:(1)1.95,4.0
(2)小,2
(3)芒果树
解析:把片荔枝树叶的长宽比从小到大排列1.3,1.8,1.8,1.9,1.9,2.0,2.0,2.0,2.0,2.4
排在中间的两个数分别为1.9、2.0,
故;
片芒果树叶的长宽比中出现次数最多的是4.0,故;
故答案为:1.95,4.0;
(2)∵,
∴从树叶的长宽比的方差来看,芒果树叶的形状差别比荔枝树叶小”;
∵荔枝树叶的长宽比的平均数,中位数是,众数是,
∴从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的2倍.
故答案为:小,2;
(3)这片树叶更可能来自荔枝,理由如下:
∵一片长,宽的树叶,长宽比为3.75,接近3.74,
∴这片树叶更可能来自芒果树.
22.答案:(1),
(2)线段与的数量关系、位置关系与(1)中结论一致,理由见解析
(3)
解析:(1)∵将绕点C按顺时针方向旋转得到,连接,,
∴,,,,
∴,,
∴,,
∴与之间的数量关系是,
延长交于一点H,
∵,,
∴,
即,
∴与的位置关系是,
故答案为:,;
(2)线段与的数量关系、位置关系与(1)中结论一致,
理由如下:
如图,延长交于点H,
将绕点C按逆时针方向旋转任意角度得到,
,,,
,
,
,
,.
(3)如图,过点C作于点N,
,,,
,
,
又
,
,
,,
,
由(2)可知.
23.答案:(1)
(2)点P的坐标为
(3)线段AP与抛物线有交点,m的取值范围为
解析:(1)∵点C的坐标为,
∴,
∵,
∴,
∴,
把,代入得,
,
解得,,
∴抛物线的解析式为;
(2)对于抛物线,当时,
解得,,,
∴,
又
∴抛物线的对称轴为直线
∵点P为抛物线对称轴上一点,
∴设
∴;;
∵
∴,
∴,
解得,,,
又,即,
∴
解得,,
综上,t的值为1,
∴点P的坐标为:
(3)设直线的解析式为,
把,代入得,,
解得,,
∴直线的解析式为;
则直线向上平移m个单位后,所得直线解析式为,
联立方程组
得关于x的一元二次方程:
若直线与抛物线相切,则解得
结合图象可知:线段与抛物线有交点,m的取值范围为
同课章节目录
