2025年人教版八下数学下册第十八章 平行四边形 真题练习(含解析)
文档属性
| 名称 | 2025年人教版八下数学下册第十八章 平行四边形 真题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 605.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 11:22:34 | ||
图片预览



文档简介
2025年人教版八下数学下册第十八章
《平行四边形》真题练习
一、选择题
1.(2025八下·萧山期中)如图,在中,,,,点P为BC边上任意一点,连接PA,将PA沿BC方向平移至CQ,连接AQ、PQ,则当PQ取得最小值时,BP的长为( )
A. B. C. D.2
2.(2025八下·萧山期中)如图,在 ABCD中,E,F分别是AD,BC的中点,G,H是对角线BD上的两点,且.对于结论:①;②;③四边形EGFH是平行四边形;④.正确的是( )
A.①② B.②③ C.①②③ D.②③④
3.(2025八下·萧山期中)某社团统计成员10天的活动时间情况,列出了方差的计算公式:,则的值是( )
A.1 B.5 C.5.25 D.5.5
4.(2025八下·萧山期中)在平面直角坐标系中,平行四边形ABCD的两条对角线AC,BD交于直角坐标系的原点O,点D的坐标是(2,1),则点B的坐标是( )
A.(-2,-1) B.(2,1) C.(-1,2) D.(1,2)
5.(2025八下·萧山期中)下列式子中属于最简二次根式的是( )
A. B. C. D.
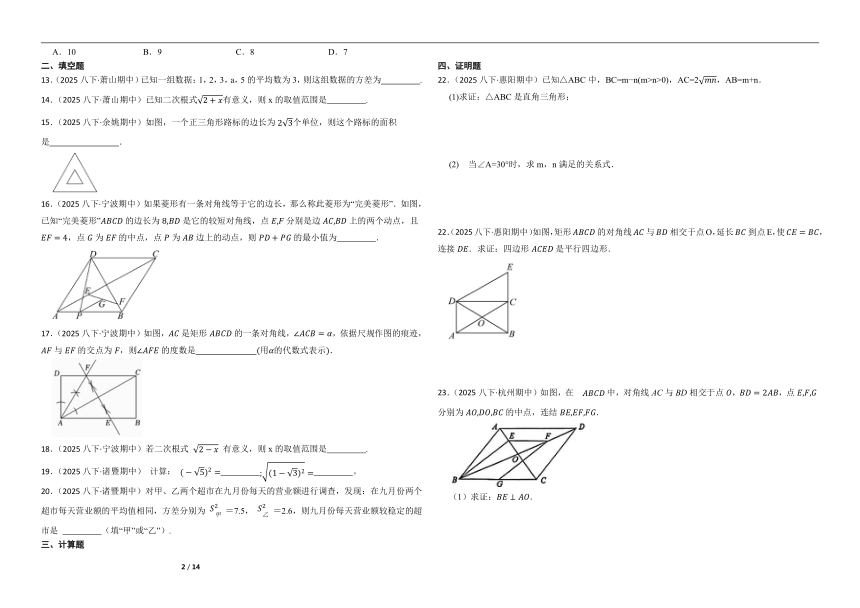
6.(2025八下·萧山期中)农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位:cm)进行了测量.根据统计的结果,绘制出如图所示的统计图.这组数据中,众数和中位数分别是( )
A.16,15 B.16,15.5 C.16,16 D.17,16
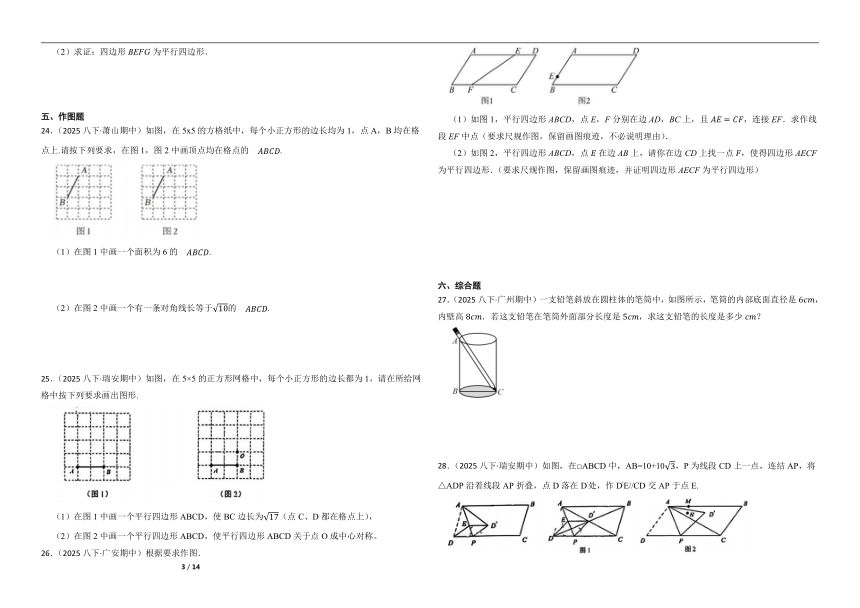
7.(2025八下·余姚期中)如图,在中,对角线,,直线过点,连接,的周长等于周长的一半,下列说法正确的是( )
①;②;③;④
A.①② B.①②③ C.②③④ D.③④
8.(2025八下·余姚期中)用两块相同的三角板能拼出多少个形状不同的平行四边形( )
A.3个 B.4个 C.3或4个 D.2或3个
9.(2025八下·南山期中)边长为2的等边三角形的面积是( )
A.2 B. C.3 D.6
10.(2025八下·宁波期中)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是 ,则射击成绩比较稳定的是( )
A.甲 B.乙 C.丙 D.丁
11.(2025八下·新昌期中)当时,二次根式的值为( )
A.1 B.2 C.3 D.4
12.(2025八下·诸暨期中)为备战体育中考,小明每日坚持引体向上,下表为其记录的一周中每日引体向上个数,
周一 周二 周三 周四 周五 周六 周日
10 9 9 10 7 8
其中一天数据缺失了,但这组数据中有唯一众数,则这组数据的中位数为( )
A.10 B.9 C.8 D.7
二、填空题
13.(2025八下·萧山期中)已知一组数据:1,2,3,a,5的平均数为3,则这组数据的方差为 .
14.(2025八下·萧山期中)已知二次根式有意义,则x的取值范围是 .
15.(2025八下·余姚期中)如图,一个正三角形路标的边长为个单位,则这个路标的面积是 .
16.(2025八下·宁波期中)如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为是它的较短对角线,点分别是边上的两个动点,且,点为的中点,点为边上的动点,则的最小值为 .
17.(2025八下·宁波期中)如图,是矩形的一条对角线,,依据尺规作图的痕迹,与的交点为,则的度数是 用的代数式表示.
18.(2025八下·宁波期中)若二次根式 有意义,则x的取值范围是 .
19.(2025八下·诸暨期中) 计算: 。
20.(2025八下·诸暨期中)对甲、乙两个超市在九月份每天的营业额进行调查,发现:在九月份两个超市每天营业额的平均值相同,方差分别为 =7.5, =2.6,则九月份每天营业额较稳定的超市是 (填“甲”或“乙”).
三、计算题
四、证明题
22.(2025八下·惠阳期中)已知△ABC中,BC=m n(m>n>0),AC=2,AB=m+n.
(1)求证:△ABC是直角三角形;
当∠A=30°时,求m,n满足的关系式.
22.(2025八下·惠阳期中)如图,矩形的对角线与相交于点O,延长到点E,使,连接.求证:四边形是平行四边形.
23.(2025八下·杭州期中)如图,在中,对角线AC与BD相交于点,,点分别为的中点,连结.
求证:.
求证:四边形BEFG为平行四边形.
五、作图题
24.(2025八下·萧山期中)如图,在5x5的方格纸中,每个小正方形的边长均为1,点A,B均在格点上.请按下列要求,在图1,图2中画顶点均在格点的.
在图1中画一个面积为6的.
在图2中画一个有一条对角线长等于的.
25.(2025八下·瑞安期中)如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
(1)在图1中画一个平行四边形ABCD,使BC边长为(点C、D都在格点上),
(2)在图2中画一个平行四边形ABCD,使平行四边形ABCD关于点O成中心对称。
26.(2025八下·广安期中)根据要求作图.
(1)如图1,平行四边形ABCD,点E,F分别在边AD,BC上,且,连接EF.求作线段EF中点(要求尺规作图,保留画图痕迹,不必说明理由).
(2)如图2,平行四边形ABCD,点在边AB上,请你在边CD上找一点,使得四边形AECF为平行四边形.(要求尺规作图,保留画图痕迹,并证明四边形AECF为平行四边形)
六、综合题
27.(2025八下·广州期中)一支铅笔斜放在圆柱体的笔筒中,如图所示,笔筒的内部底面直径是,内壁高.若这支铅笔在笔筒外面部分长度是,求这支铅笔的长度是多少?
28.(2025八下·瑞安期中)如图,在□ABCD中,AB=10+10,P为线段CD上一点,连结AP,将△ADP沿着线段AP折叠,点D落在D'处,作D'E//CD交AP于点E.
证明:四边形D'EDP为菱形.
如图1,若D'恰好落在平行四边形ABCD的对角线交点处,求此时DP的长度.
(3)如图2,连结AC,∠ADC=45°,∠DAC=105°,在AB上取一点M(AM答案解析部分
1.【答案】C
【知识点】垂线段最短及其应用;平行四边形的性质
【解析】【解答】解:
如图,令AC与PQ的交点为O
∵PA沿BC方向平移至CQ
∴AP平行且等于CQ
∴四边形APQC为平行四边形
∴PO=OQ=PQ,AO=OC=AC
当PQ取得最小值时,PO也取最小值
∵P为BC上的动点
∴当OP⊥BC时,此时OP最短,即PQ最短
作OP1⊥BC于P1,OQ1⊥AQ于Q1
此时Q1P1即为Rt△ABC斜边BC上的高
在Rt△ABC中,AC==4
根据三角形面积公式
∴=
∴=
∵OC=AC=2
∴在Rt△OP1C中
P1C==
∴BP1=BC-P1C=
故答案为:C.
【分析】 首先需明确PA沿BC方向平移至CQ形成平行四边形,进而利用平行四边形对边平行且相等的性质,将PQ的最小值转化为点P到AQ的最短距离问题,再结合垂线段最短的几何原理确定点P的位置,最后通过勾股定理计算BP长度.
2.【答案】B
【知识点】平行四边形的判定与性质
【解析】【解答】解:∵G,H是BD上两动点,只需满足BG=DH∴GF与BD不一定垂直故①不符合题意;
在中,有AD=BC,ADBC∴∠ADB=∠CBD∵ E,F分别是AD,BC的中点∴ED=AD,FB=BC∴ED=FB
又∵BG=DH∴△EDH≌△FBG(SAS)∴故②符合题意;
∵△EDH≌△FBG∴EH=GF,∠DHE=∠BGF∵∠DHE+∠EHG=180°,∠BGF+∠FGH=180°∴∠EHG=∠FGH∴EH∥GF又∵EH=GF∴ 四边形EGFH是平行四边形故③符合题意;∵G是BD上的动点∴EG的长度在变化∴EG不一定等于BD故④不符合题意;
故答案为:B.
【分析】 由F是BC的中点,G是BD上的动点,可知GF与BD不一定垂直,可判断①错误;由平行四边形的性质及E,F分别是AD,BC的中点,推导出∠EDH=∠FBG,DE=BF,而DH=BG,即可根据“SAS”证明△DEH≌△BFG,得∠DEH=∠BFG,可判断②正确;由等角的补角相等推导出∠EHG=∠FGH,则EH∥FG,因为EH=FG,所以四边形EGFH是平行四边形,可判断③正确;由EG是变量,而BD的值不变,可知EG与BD不一定相等,可判断④错误.
3.【答案】D
【知识点】方差
【解析】【解答】解:
由题意知,这组数据为2、5、5、5、6、6、6、6、6、8,
∴这组数据的平均数为
故答案为:D.
【分析】根据方差的计算公式,可得该组数据为有1个2,3个5,5个6,1个8,从而计算这组数据的平均值.
4.【答案】A
【知识点】坐标与图形性质;平行四边形的性质
【解析】【解答】解:
∵四边形ABCD是平行四边形,O为角线AC与BD的交点,
∴B与D关于原点O对称,
∵点D的坐标为(2,1),
∴点B的坐标为(-2,-1)
故答案为:A.
【分析】 利用平行四边形关于其对角线交点中心对称的性质 ,对角线上的B,D两点关于O点成中心对称.
5.【答案】A
【知识点】最简二次根式
【解析】【解答】解:A.是最简二次根式,故选项A符合题意;
B.,不是最简二次根式,故选项B不符合题意;
C.,不是最简二次根式,故选项C不符合题意;
D.,不是最简二次根式,故选项D不符合题意.
故答案为:A.
【分析】 最简二次根式需满足两点:被开方数不含能开得尽方的因数或因式,且被开方数不含分母.
6.【答案】C
【知识点】中位数;众数
7.【答案】A
【知识点】二次根式的混合运算;等边三角形的判定与性质;勾股定理;平行四边形的性质
8.【答案】D
【知识点】平行四边形的判定
9.【答案】B
【知识点】三角形的面积;等边三角形的性质;勾股定理
【解析】【分析】根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
【解答】AB=2,∵等边三角形高线即中点,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD==,
∴等边△ABC的面积为BC AD=×2×=,
故选:B.
【点评】本题考查了勾股定理在直角三角形中的运用,考查了等边三角形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.
10.【答案】D
【知识点】方差
【解析】【解答】解:∵四人10次射击成绩的平均数都是9环,S2丁<S2乙<S2丙<S2甲,
∴射击成绩比较稳定的是丁.
故答案为:D.
【分析】根据四人10次射击成绩的平均数都是9环,方差越小,成绩越稳定,据此即可得出正确答案.
11.【答案】B
【知识点】二次根式的化简求值
【解析】【解答】解:当时,
故答案为:B.
【分析】将代入二次根式,计算求解即可.
12.【答案】B
【知识点】中位数;众数
【解析】【解答】解:因为这组数据有唯一的众数,
所以这组数据可能是7,8,9,9,9,10,10或7,8,9,9,10,10,10,
中位数都是9.
故答案为:B.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),据此结合题意可得缺失的数据可能是9或10;中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数叫做这组数据的中位数,据此找出这组数据的中位数即可.
13.【答案】2
【知识点】平均数及其计算;方差
【解析】【解答】解:由平均数的公式得:(1+2+3+5+x)÷5=3,
解得x=4;
则方差=[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2
故答案为:2.
【分析】 根据平均数确定出x后,再根据方差的公式进行计算即可.
14.【答案】x≧-2
【知识点】二次根式有意义的条件
【解析】【解答】解:有意义
则2+x≥0,
解得:x≥-2.
故答案为:x≥-2.
【分析】直接利用二次根式的定义,得出2+x≥0,进而得出答案.
15.【答案】平方单位
【知识点】等边三角形的性质;勾股定理
16.【答案】
【知识点】菱形的性质;直角三角形斜边上的中线
【解析】【解答】解:设与的交点为,连接,,
四边形是菱形,
,
,
,
的最小值为,
作点关于的对称点,延长交于点,连接,,,
,
,
的最小值为,
四边形是菱形,,
,
四边形是“完美菱形”,
∴菱形的边只能和较短对角线相等,
∵的边长为8,
,,
,,
,,
由对称性和菱形的性质,知,
,
的最小值为,
故答案为:.
【分析】连接,,可得,根据,可得的最小值,根据将军饮马模型构造出的最小值时的线段,再根据勾股定理解答即可.
17.【答案】
【知识点】平行线的性质;矩形的性质
【解析】【解答】解:如图,设与交于点,
由作图可得:平分,垂直平分,
∴,,
∵四边形为矩形,
∴,
∴,
∴,
∴,
故答案为:.
【分析】设AC与EF交于点O,由作图可得:AF平分∠CAD,EF垂直平分AC,从而得出,∠AOF=90°,由矩形的性质即可求解.
18.【答案】x≤2
【知识点】二次根式有意义的条件
【解析】【解答】由题意得,2﹣x≥0,
解得x≤2.
故答案为:x≤2.
【分析】要使二次根式有意义,即是被开方数大于等于0,据此解答即可.
19.【答案】5;
【知识点】二次根式的性质与化简
【解析】【解答】解:
故答案为:5,.
【分析】本题考查的是二次根式的性质:;,根据性质依次解题即可.,
20.【答案】乙
【知识点】方差
【解析】【解答】解:∵ =7.5, =2.6,
∴ ,
∴九月份每天营业额较稳定的超市是乙,
故答案为:乙.
【分析】方差是反映一组数据的波动大小的一个量,方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好,据此解答即可.
21.【答案】解:(1)∵BC=m-n(m>n>0),AC=2,AB=m+n,
∴AC2+CB2=(m-n)2+4mn=m2+n2-2mn+4mn=m2+n2+2mn=(m+n)2=AB2.
∴∠C=90°.
∴△ABC是为直角三角形;
(2)∵∠A=30°,
∴,
∴m=3n.
【知识点】含30°角的直角三角形;勾股定理的逆定理
【解析】【分析】(1)由勾股定理的逆定理即可求出答案.
(2)根据含30°角的直角三角形性质即可求出答案.
22.【答案】证明:四边形是矩形,
,,
,
,
又∵,
四边形是平行四边形;
【知识点】平行四边形的判定;矩形的性质
【解析】【分析】根据矩形性质可得,,根据边之间的关系可得,再根据平行四边形判定定理即可求出答案.
23.【答案】(1)中,
是AO中点
(2)点E、F是AO、OD的中点,
且
中,
且
点G是BC的中点,
且
成立
【知识点】平行四边形的判定与性质;三角形的中位线定理;中点四边形模型
24.【答案】(1)解:不唯一
(2)解:一个
【知识点】勾股定理;平行四边形的判定与性质
【解析】【分析】 (1)结合平行四边形的性质按要求画图即可;
(2)结合勾股定理、平行四边形的性质按要求画图即可.
25.【答案】(1)解:如图,平行四边形ABCD即为所求(画法不唯一);
(2)解:如图,平行四边形ABCD即为所求.
【知识点】勾股定理;平行四边形的判定;作图﹣中心对称
【解析】【分析】(1)利用勾股定理,在网格中找一直角边分别为1和4的直角三角形,则斜边长为,据此确定点C,然后根据平行四边形的性质找出点D,按顺序连接顶点即可;
(2)根据对角线互相平分的四边形是平行四边形,连接AO并延长至点C,使CO=AO,连接BO并延长至点D,使DO=BO,再按顺序连接顶点即可.
26.【答案】(1)解:如图点O即为所求,
(2)解:如图,在CD上截取DF=BE,然后连接CE和AF,则四边形AECF是平行四边形;
证明:∵ABCD是平行四边形,
∴AB=CD,AB∥CD,
又∵BE=DF,
∴AE=CF,
∴AECF是平行四边形.
【知识点】平行四边形的判定与性质;尺规作图-垂直平分线
【解析】【分析】
(1) 作线段EF的垂直平分线交EF于点O,则点O即为所作;;
(2) 在CD上截取DF=BE,然后连接CE和AF,则四边形AECF是平行四边形;然后根据一组对边平行且相等的四边形是平行四边形证明即可.
27.【答案】
【知识点】勾股定理的应用
28.【答案】(1)证明:∵将沿线段AP折叠得到,
∴∠DEP=∠D'EP,∠DPE=∠D'PE,DE=D'E,DP=D'P,
∵D'E∥CD,
∴∠D'EP=∠DPE,
∴∠D'EP=∠DPE=∠DEP=∠D'PE,
∴DE=DP,D'E=D'P,
∴DE=DE'=D'P=DP,
∴四边形D'EDP为菱形;
(2)解:∵D'为AC中点,D'E∥CD,
∴D'E为中位线,
∴,即CP=2D'E,
由(1)得四边形D'EDP为菱形,
∴D'E=DP,
∴CD=DP+CP=3DP,
∵四边形ABCD是平行四边形,,
∴,
∴,
∴;
(3)
【知识点】菱形的判定与性质;轴对称的性质;翻折变换(折叠问题);三角形的中位线定理;四边形的综合
【解析】【解答】解:(3)解:∵四边形ABCD是平行四边形,,
∴AB∥CD,,
∴∠ADC+∠BAD=180°,
∵∠ADC=45°,
∴∠BAD=135°,
∵折叠的性质,
∴∠DAP=∠D'AP,
①如图,当点N在AP上时,
∵点M关于直线AD'的对称点为N,
∴∠D'AN=∠D'AM=∠DAP,
∵∠BAD=∠D'AN+∠D'AM+∠DAP=135°,
∴∠D'AN=∠D'AM=∠DAP=45°,
∵∠ADC=45°,∠DAC=105°,
∴∠APC=∠ADC+∠DAP=90°,∠ADC=∠DAP,∠ACP=180°-∠ADC-∠DAC=30°,
∴PA=PD,
设PA=PD=x,
∴AC=2PA=2x,
∴,
∴,
∴,
解得:,
∴DP=10,AC=20;
②如图,当点N在AC上时,过点P作PF⊥AC于F,
∴∠PFA=∠PFC=90°,
∵AB∥CD,∠ACP=30°,
∴∠BAC=∠ACP=30°,
∵点M关于直线AD'的对称点为N,
∴∠D'AN=∠D'AM=15°,
∵∠DAC=105°,
∴∠DAD'=∠DAC+∠D'AN=120°,
∴∠DAP=∠D'AP=60°,
∴∠PAF=∠D'AP-∠D'AN=45°,
∵∠PFA=90°,
∴∠APF=∠PAF=45°,
∴AF=PF,设AF=PF=y,
∵AC=20,
∴CF=AC-AF=20-y,
∵∠PFC=90°,∠ACP=30°,
∴PC=2PF=2y,
∴,
∴,
解得:,
∴,
∵,
∴;
综上所述,DP的取值范围为,
故答案为:.
【分析】(1)根据折叠的性质得∠DEP=∠D'EP,∠DPE=∠D'PE,DE=D'E,DP=D'P,然后根据平行线的性质得∠D'EP=∠D'PE,于是进行等量代换得∠D'EP=∠D'PE=∠DEP=∠DPE,从而根据等腰三角形的判定证出DE=DP,D'E=D'P,进而进行等量代换得DE=DE'=D'P=DP,最后根据菱形的判定即可得证结论;
(2)根据中位线定理得CP=2D'E,然后根据菱形的性质得D'E=DP,从而得CD=3DP,进而根据平行四边形的性质得AB=CD=3DP,据此即可求解;
(3)根据平行四边形的性质、平行线的性质、折叠的性质得,∠BAD=135°,∠DAP=∠D'AP,然后分情况讨论:①当点N在AP上时,根据轴对称的性质得∠D'AN=∠D'AM=∠DAP=45°,然后求出∠APC=90°,∠ADC=∠DAP,∠ACP=30°,从而根据等腰三角形的判定得设PA=PD=x,进而利用勾股定理得,于是可得,即可列出关于x的方程,解方程求出x的值,即可得DP=10,AC=20;
②当点N在AC上时,过点P作PF⊥AC于F,得∠PFA=∠PFC=90°,根据平行线的性质得∠BAC=∠ACP=30°,然后根据轴对称的性质得∠D'AN=∠D'AM=15°,从而求出∠DAD'=120°,∠DAP=∠D'AP=60°,进而得∠PAF=∠APF=45°,于是根据等腰三角形的判定得设AF=PF=y,得CF=20-y,接下来根据含30°的直角三角形的性质以及勾股定理得PC=2y,,即可列出关于y的方程,解方程求出y的值可得PC的值,于是得DP的值,最后综合以上两种情况得到答案.
试题分析部分
1、试卷总体分布分析
总分:57分
分值分布 客观题(占比) 30.0(52.6%)
主观题(占比) 27.0(47.4%)
题量分布 客观题(占比) 15(46.9%)
主观题(占比) 17(53.1%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
选择题 12(37.5%) 24.0(42.1%)
填空题 8(25.0%) 18.0(31.6%)
证明题 3(9.4%) 10.0(17.5%)
作图题 3(9.4%) 0.0(0.0%)
计算题 4(12.5%) 0.0(0.0%)
综合题 2(6.3%) 5.0(8.8%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (40.6%)
2 容易 (46.9%)
3 困难 (12.5%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 平均数及其计算 2.0(3.5%) 13
2 平方差公式及应用 0.0(0.0%) 21
3 含30°角的直角三角形 5.0(8.8%) 25
4 轴对称的性质 0.0(0.0%) 32
5 菱形的性质 2.0(3.5%) 16
6 三角形的中位线定理 0.0(0.0%) 27,32
7 菱形的判定与性质 0.0(0.0%) 32
8 坐标与图形性质 2.0(3.5%) 4
9 矩形的性质 7.0(12.3%) 17,26
10 二次根式有意义的条件 4.0(7.0%) 14,18
11 垂线段最短及其应用 2.0(3.5%) 1
12 完全平方公式及运用 0.0(0.0%) 21,23
13 方差 8.0(14.0%) 3,10,13,20
14 最简二次根式 2.0(3.5%) 5
15 平行四边形的性质 6.0(10.5%) 1,4,7
16 翻折变换(折叠问题) 0.0(0.0%) 32
17 中位数 4.0(7.0%) 6,12
18 等边三角形的判定与性质 2.0(3.5%) 7
19 等边三角形的性质 4.0(7.0%) 9,15
20 四边形的综合 0.0(0.0%) 32
21 二次根式的性质与化简 4.0(7.0%) 19
22 负整数指数幂 0.0(0.0%) 24
23 平行线的性质 2.0(3.5%) 17
24 勾股定理 6.0(10.5%) 7,9,15,28,29
25 二次根式的混合运算 2.0(3.5%) 7,21,23
26 平行四边形的判定 7.0(12.3%) 8,26,29
27 二次根式的化简求值 2.0(3.5%) 11
28 众数 4.0(7.0%) 6,12
29 三角形的面积 2.0(3.5%) 9
30 作图﹣中心对称 0.0(0.0%) 29
31 直角三角形斜边上的中线 2.0(3.5%) 16
32 平行四边形的判定与性质 2.0(3.5%) 2,27,28,30
33 尺规作图-垂直平分线 0.0(0.0%) 30
34 勾股定理的应用 5.0(8.8%) 31
35 中点四边形模型 0.0(0.0%) 27
36 二次根式的乘除法 0.0(0.0%) 22
37 零指数幂 0.0(0.0%) 24
38 二次根式的加减法 0.0(0.0%) 22,24
39 勾股定理的逆定理 5.0(8.8%) 25
1 / 1
《平行四边形》真题练习
一、选择题
1.(2025八下·萧山期中)如图,在中,,,,点P为BC边上任意一点,连接PA,将PA沿BC方向平移至CQ,连接AQ、PQ,则当PQ取得最小值时,BP的长为( )
A. B. C. D.2
2.(2025八下·萧山期中)如图,在 ABCD中,E,F分别是AD,BC的中点,G,H是对角线BD上的两点,且.对于结论:①;②;③四边形EGFH是平行四边形;④.正确的是( )
A.①② B.②③ C.①②③ D.②③④
3.(2025八下·萧山期中)某社团统计成员10天的活动时间情况,列出了方差的计算公式:,则的值是( )
A.1 B.5 C.5.25 D.5.5
4.(2025八下·萧山期中)在平面直角坐标系中,平行四边形ABCD的两条对角线AC,BD交于直角坐标系的原点O,点D的坐标是(2,1),则点B的坐标是( )
A.(-2,-1) B.(2,1) C.(-1,2) D.(1,2)
5.(2025八下·萧山期中)下列式子中属于最简二次根式的是( )
A. B. C. D.
6.(2025八下·萧山期中)农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位:cm)进行了测量.根据统计的结果,绘制出如图所示的统计图.这组数据中,众数和中位数分别是( )
A.16,15 B.16,15.5 C.16,16 D.17,16
7.(2025八下·余姚期中)如图,在中,对角线,,直线过点,连接,的周长等于周长的一半,下列说法正确的是( )
①;②;③;④
A.①② B.①②③ C.②③④ D.③④
8.(2025八下·余姚期中)用两块相同的三角板能拼出多少个形状不同的平行四边形( )
A.3个 B.4个 C.3或4个 D.2或3个
9.(2025八下·南山期中)边长为2的等边三角形的面积是( )
A.2 B. C.3 D.6
10.(2025八下·宁波期中)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是 ,则射击成绩比较稳定的是( )
A.甲 B.乙 C.丙 D.丁
11.(2025八下·新昌期中)当时,二次根式的值为( )
A.1 B.2 C.3 D.4
12.(2025八下·诸暨期中)为备战体育中考,小明每日坚持引体向上,下表为其记录的一周中每日引体向上个数,
周一 周二 周三 周四 周五 周六 周日
10 9 9 10 7 8
其中一天数据缺失了,但这组数据中有唯一众数,则这组数据的中位数为( )
A.10 B.9 C.8 D.7
二、填空题
13.(2025八下·萧山期中)已知一组数据:1,2,3,a,5的平均数为3,则这组数据的方差为 .
14.(2025八下·萧山期中)已知二次根式有意义,则x的取值范围是 .
15.(2025八下·余姚期中)如图,一个正三角形路标的边长为个单位,则这个路标的面积是 .
16.(2025八下·宁波期中)如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”的边长为是它的较短对角线,点分别是边上的两个动点,且,点为的中点,点为边上的动点,则的最小值为 .
17.(2025八下·宁波期中)如图,是矩形的一条对角线,,依据尺规作图的痕迹,与的交点为,则的度数是 用的代数式表示.
18.(2025八下·宁波期中)若二次根式 有意义,则x的取值范围是 .
19.(2025八下·诸暨期中) 计算: 。
20.(2025八下·诸暨期中)对甲、乙两个超市在九月份每天的营业额进行调查,发现:在九月份两个超市每天营业额的平均值相同,方差分别为 =7.5, =2.6,则九月份每天营业额较稳定的超市是 (填“甲”或“乙”).
三、计算题
四、证明题
22.(2025八下·惠阳期中)已知△ABC中,BC=m n(m>n>0),AC=2,AB=m+n.
(1)求证:△ABC是直角三角形;
当∠A=30°时,求m,n满足的关系式.
22.(2025八下·惠阳期中)如图,矩形的对角线与相交于点O,延长到点E,使,连接.求证:四边形是平行四边形.
23.(2025八下·杭州期中)如图,在中,对角线AC与BD相交于点,,点分别为的中点,连结.
求证:.
求证:四边形BEFG为平行四边形.
五、作图题
24.(2025八下·萧山期中)如图,在5x5的方格纸中,每个小正方形的边长均为1,点A,B均在格点上.请按下列要求,在图1,图2中画顶点均在格点的.
在图1中画一个面积为6的.
在图2中画一个有一条对角线长等于的.
25.(2025八下·瑞安期中)如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
(1)在图1中画一个平行四边形ABCD,使BC边长为(点C、D都在格点上),
(2)在图2中画一个平行四边形ABCD,使平行四边形ABCD关于点O成中心对称。
26.(2025八下·广安期中)根据要求作图.
(1)如图1,平行四边形ABCD,点E,F分别在边AD,BC上,且,连接EF.求作线段EF中点(要求尺规作图,保留画图痕迹,不必说明理由).
(2)如图2,平行四边形ABCD,点在边AB上,请你在边CD上找一点,使得四边形AECF为平行四边形.(要求尺规作图,保留画图痕迹,并证明四边形AECF为平行四边形)
六、综合题
27.(2025八下·广州期中)一支铅笔斜放在圆柱体的笔筒中,如图所示,笔筒的内部底面直径是,内壁高.若这支铅笔在笔筒外面部分长度是,求这支铅笔的长度是多少?
28.(2025八下·瑞安期中)如图,在□ABCD中,AB=10+10,P为线段CD上一点,连结AP,将△ADP沿着线段AP折叠,点D落在D'处,作D'E//CD交AP于点E.
证明:四边形D'EDP为菱形.
如图1,若D'恰好落在平行四边形ABCD的对角线交点处,求此时DP的长度.
(3)如图2,连结AC,∠ADC=45°,∠DAC=105°,在AB上取一点M(AM
1.【答案】C
【知识点】垂线段最短及其应用;平行四边形的性质
【解析】【解答】解:
如图,令AC与PQ的交点为O
∵PA沿BC方向平移至CQ
∴AP平行且等于CQ
∴四边形APQC为平行四边形
∴PO=OQ=PQ,AO=OC=AC
当PQ取得最小值时,PO也取最小值
∵P为BC上的动点
∴当OP⊥BC时,此时OP最短,即PQ最短
作OP1⊥BC于P1,OQ1⊥AQ于Q1
此时Q1P1即为Rt△ABC斜边BC上的高
在Rt△ABC中,AC==4
根据三角形面积公式
∴=
∴=
∵OC=AC=2
∴在Rt△OP1C中
P1C==
∴BP1=BC-P1C=
故答案为:C.
【分析】 首先需明确PA沿BC方向平移至CQ形成平行四边形,进而利用平行四边形对边平行且相等的性质,将PQ的最小值转化为点P到AQ的最短距离问题,再结合垂线段最短的几何原理确定点P的位置,最后通过勾股定理计算BP长度.
2.【答案】B
【知识点】平行四边形的判定与性质
【解析】【解答】解:∵G,H是BD上两动点,只需满足BG=DH∴GF与BD不一定垂直故①不符合题意;
在中,有AD=BC,ADBC∴∠ADB=∠CBD∵ E,F分别是AD,BC的中点∴ED=AD,FB=BC∴ED=FB
又∵BG=DH∴△EDH≌△FBG(SAS)∴故②符合题意;
∵△EDH≌△FBG∴EH=GF,∠DHE=∠BGF∵∠DHE+∠EHG=180°,∠BGF+∠FGH=180°∴∠EHG=∠FGH∴EH∥GF又∵EH=GF∴ 四边形EGFH是平行四边形故③符合题意;∵G是BD上的动点∴EG的长度在变化∴EG不一定等于BD故④不符合题意;
故答案为:B.
【分析】 由F是BC的中点,G是BD上的动点,可知GF与BD不一定垂直,可判断①错误;由平行四边形的性质及E,F分别是AD,BC的中点,推导出∠EDH=∠FBG,DE=BF,而DH=BG,即可根据“SAS”证明△DEH≌△BFG,得∠DEH=∠BFG,可判断②正确;由等角的补角相等推导出∠EHG=∠FGH,则EH∥FG,因为EH=FG,所以四边形EGFH是平行四边形,可判断③正确;由EG是变量,而BD的值不变,可知EG与BD不一定相等,可判断④错误.
3.【答案】D
【知识点】方差
【解析】【解答】解:
由题意知,这组数据为2、5、5、5、6、6、6、6、6、8,
∴这组数据的平均数为
故答案为:D.
【分析】根据方差的计算公式,可得该组数据为有1个2,3个5,5个6,1个8,从而计算这组数据的平均值.
4.【答案】A
【知识点】坐标与图形性质;平行四边形的性质
【解析】【解答】解:
∵四边形ABCD是平行四边形,O为角线AC与BD的交点,
∴B与D关于原点O对称,
∵点D的坐标为(2,1),
∴点B的坐标为(-2,-1)
故答案为:A.
【分析】 利用平行四边形关于其对角线交点中心对称的性质 ,对角线上的B,D两点关于O点成中心对称.
5.【答案】A
【知识点】最简二次根式
【解析】【解答】解:A.是最简二次根式,故选项A符合题意;
B.,不是最简二次根式,故选项B不符合题意;
C.,不是最简二次根式,故选项C不符合题意;
D.,不是最简二次根式,故选项D不符合题意.
故答案为:A.
【分析】 最简二次根式需满足两点:被开方数不含能开得尽方的因数或因式,且被开方数不含分母.
6.【答案】C
【知识点】中位数;众数
7.【答案】A
【知识点】二次根式的混合运算;等边三角形的判定与性质;勾股定理;平行四边形的性质
8.【答案】D
【知识点】平行四边形的判定
9.【答案】B
【知识点】三角形的面积;等边三角形的性质;勾股定理
【解析】【分析】根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
【解答】AB=2,∵等边三角形高线即中点,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD==,
∴等边△ABC的面积为BC AD=×2×=,
故选:B.
【点评】本题考查了勾股定理在直角三角形中的运用,考查了等边三角形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.
10.【答案】D
【知识点】方差
【解析】【解答】解:∵四人10次射击成绩的平均数都是9环,S2丁<S2乙<S2丙<S2甲,
∴射击成绩比较稳定的是丁.
故答案为:D.
【分析】根据四人10次射击成绩的平均数都是9环,方差越小,成绩越稳定,据此即可得出正确答案.
11.【答案】B
【知识点】二次根式的化简求值
【解析】【解答】解:当时,
故答案为:B.
【分析】将代入二次根式,计算求解即可.
12.【答案】B
【知识点】中位数;众数
【解析】【解答】解:因为这组数据有唯一的众数,
所以这组数据可能是7,8,9,9,9,10,10或7,8,9,9,10,10,10,
中位数都是9.
故答案为:B.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),据此结合题意可得缺失的数据可能是9或10;中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数叫做这组数据的中位数,据此找出这组数据的中位数即可.
13.【答案】2
【知识点】平均数及其计算;方差
【解析】【解答】解:由平均数的公式得:(1+2+3+5+x)÷5=3,
解得x=4;
则方差=[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2
故答案为:2.
【分析】 根据平均数确定出x后,再根据方差的公式进行计算即可.
14.【答案】x≧-2
【知识点】二次根式有意义的条件
【解析】【解答】解:有意义
则2+x≥0,
解得:x≥-2.
故答案为:x≥-2.
【分析】直接利用二次根式的定义,得出2+x≥0,进而得出答案.
15.【答案】平方单位
【知识点】等边三角形的性质;勾股定理
16.【答案】
【知识点】菱形的性质;直角三角形斜边上的中线
【解析】【解答】解:设与的交点为,连接,,
四边形是菱形,
,
,
,
的最小值为,
作点关于的对称点,延长交于点,连接,,,
,
,
的最小值为,
四边形是菱形,,
,
四边形是“完美菱形”,
∴菱形的边只能和较短对角线相等,
∵的边长为8,
,,
,,
,,
由对称性和菱形的性质,知,
,
的最小值为,
故答案为:.
【分析】连接,,可得,根据,可得的最小值,根据将军饮马模型构造出的最小值时的线段,再根据勾股定理解答即可.
17.【答案】
【知识点】平行线的性质;矩形的性质
【解析】【解答】解:如图,设与交于点,
由作图可得:平分,垂直平分,
∴,,
∵四边形为矩形,
∴,
∴,
∴,
∴,
故答案为:.
【分析】设AC与EF交于点O,由作图可得:AF平分∠CAD,EF垂直平分AC,从而得出,∠AOF=90°,由矩形的性质即可求解.
18.【答案】x≤2
【知识点】二次根式有意义的条件
【解析】【解答】由题意得,2﹣x≥0,
解得x≤2.
故答案为:x≤2.
【分析】要使二次根式有意义,即是被开方数大于等于0,据此解答即可.
19.【答案】5;
【知识点】二次根式的性质与化简
【解析】【解答】解:
故答案为:5,.
【分析】本题考查的是二次根式的性质:;,根据性质依次解题即可.,
20.【答案】乙
【知识点】方差
【解析】【解答】解:∵ =7.5, =2.6,
∴ ,
∴九月份每天营业额较稳定的超市是乙,
故答案为:乙.
【分析】方差是反映一组数据的波动大小的一个量,方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好,据此解答即可.
21.【答案】解:(1)∵BC=m-n(m>n>0),AC=2,AB=m+n,
∴AC2+CB2=(m-n)2+4mn=m2+n2-2mn+4mn=m2+n2+2mn=(m+n)2=AB2.
∴∠C=90°.
∴△ABC是为直角三角形;
(2)∵∠A=30°,
∴,
∴m=3n.
【知识点】含30°角的直角三角形;勾股定理的逆定理
【解析】【分析】(1)由勾股定理的逆定理即可求出答案.
(2)根据含30°角的直角三角形性质即可求出答案.
22.【答案】证明:四边形是矩形,
,,
,
,
又∵,
四边形是平行四边形;
【知识点】平行四边形的判定;矩形的性质
【解析】【分析】根据矩形性质可得,,根据边之间的关系可得,再根据平行四边形判定定理即可求出答案.
23.【答案】(1)中,
是AO中点
(2)点E、F是AO、OD的中点,
且
中,
且
点G是BC的中点,
且
成立
【知识点】平行四边形的判定与性质;三角形的中位线定理;中点四边形模型
24.【答案】(1)解:不唯一
(2)解:一个
【知识点】勾股定理;平行四边形的判定与性质
【解析】【分析】 (1)结合平行四边形的性质按要求画图即可;
(2)结合勾股定理、平行四边形的性质按要求画图即可.
25.【答案】(1)解:如图,平行四边形ABCD即为所求(画法不唯一);
(2)解:如图,平行四边形ABCD即为所求.
【知识点】勾股定理;平行四边形的判定;作图﹣中心对称
【解析】【分析】(1)利用勾股定理,在网格中找一直角边分别为1和4的直角三角形,则斜边长为,据此确定点C,然后根据平行四边形的性质找出点D,按顺序连接顶点即可;
(2)根据对角线互相平分的四边形是平行四边形,连接AO并延长至点C,使CO=AO,连接BO并延长至点D,使DO=BO,再按顺序连接顶点即可.
26.【答案】(1)解:如图点O即为所求,
(2)解:如图,在CD上截取DF=BE,然后连接CE和AF,则四边形AECF是平行四边形;
证明:∵ABCD是平行四边形,
∴AB=CD,AB∥CD,
又∵BE=DF,
∴AE=CF,
∴AECF是平行四边形.
【知识点】平行四边形的判定与性质;尺规作图-垂直平分线
【解析】【分析】
(1) 作线段EF的垂直平分线交EF于点O,则点O即为所作;;
(2) 在CD上截取DF=BE,然后连接CE和AF,则四边形AECF是平行四边形;然后根据一组对边平行且相等的四边形是平行四边形证明即可.
27.【答案】
【知识点】勾股定理的应用
28.【答案】(1)证明:∵将沿线段AP折叠得到,
∴∠DEP=∠D'EP,∠DPE=∠D'PE,DE=D'E,DP=D'P,
∵D'E∥CD,
∴∠D'EP=∠DPE,
∴∠D'EP=∠DPE=∠DEP=∠D'PE,
∴DE=DP,D'E=D'P,
∴DE=DE'=D'P=DP,
∴四边形D'EDP为菱形;
(2)解:∵D'为AC中点,D'E∥CD,
∴D'E为中位线,
∴,即CP=2D'E,
由(1)得四边形D'EDP为菱形,
∴D'E=DP,
∴CD=DP+CP=3DP,
∵四边形ABCD是平行四边形,,
∴,
∴,
∴;
(3)
【知识点】菱形的判定与性质;轴对称的性质;翻折变换(折叠问题);三角形的中位线定理;四边形的综合
【解析】【解答】解:(3)解:∵四边形ABCD是平行四边形,,
∴AB∥CD,,
∴∠ADC+∠BAD=180°,
∵∠ADC=45°,
∴∠BAD=135°,
∵折叠的性质,
∴∠DAP=∠D'AP,
①如图,当点N在AP上时,
∵点M关于直线AD'的对称点为N,
∴∠D'AN=∠D'AM=∠DAP,
∵∠BAD=∠D'AN+∠D'AM+∠DAP=135°,
∴∠D'AN=∠D'AM=∠DAP=45°,
∵∠ADC=45°,∠DAC=105°,
∴∠APC=∠ADC+∠DAP=90°,∠ADC=∠DAP,∠ACP=180°-∠ADC-∠DAC=30°,
∴PA=PD,
设PA=PD=x,
∴AC=2PA=2x,
∴,
∴,
∴,
解得:,
∴DP=10,AC=20;
②如图,当点N在AC上时,过点P作PF⊥AC于F,
∴∠PFA=∠PFC=90°,
∵AB∥CD,∠ACP=30°,
∴∠BAC=∠ACP=30°,
∵点M关于直线AD'的对称点为N,
∴∠D'AN=∠D'AM=15°,
∵∠DAC=105°,
∴∠DAD'=∠DAC+∠D'AN=120°,
∴∠DAP=∠D'AP=60°,
∴∠PAF=∠D'AP-∠D'AN=45°,
∵∠PFA=90°,
∴∠APF=∠PAF=45°,
∴AF=PF,设AF=PF=y,
∵AC=20,
∴CF=AC-AF=20-y,
∵∠PFC=90°,∠ACP=30°,
∴PC=2PF=2y,
∴,
∴,
解得:,
∴,
∵,
∴;
综上所述,DP的取值范围为,
故答案为:.
【分析】(1)根据折叠的性质得∠DEP=∠D'EP,∠DPE=∠D'PE,DE=D'E,DP=D'P,然后根据平行线的性质得∠D'EP=∠D'PE,于是进行等量代换得∠D'EP=∠D'PE=∠DEP=∠DPE,从而根据等腰三角形的判定证出DE=DP,D'E=D'P,进而进行等量代换得DE=DE'=D'P=DP,最后根据菱形的判定即可得证结论;
(2)根据中位线定理得CP=2D'E,然后根据菱形的性质得D'E=DP,从而得CD=3DP,进而根据平行四边形的性质得AB=CD=3DP,据此即可求解;
(3)根据平行四边形的性质、平行线的性质、折叠的性质得,∠BAD=135°,∠DAP=∠D'AP,然后分情况讨论:①当点N在AP上时,根据轴对称的性质得∠D'AN=∠D'AM=∠DAP=45°,然后求出∠APC=90°,∠ADC=∠DAP,∠ACP=30°,从而根据等腰三角形的判定得设PA=PD=x,进而利用勾股定理得,于是可得,即可列出关于x的方程,解方程求出x的值,即可得DP=10,AC=20;
②当点N在AC上时,过点P作PF⊥AC于F,得∠PFA=∠PFC=90°,根据平行线的性质得∠BAC=∠ACP=30°,然后根据轴对称的性质得∠D'AN=∠D'AM=15°,从而求出∠DAD'=120°,∠DAP=∠D'AP=60°,进而得∠PAF=∠APF=45°,于是根据等腰三角形的判定得设AF=PF=y,得CF=20-y,接下来根据含30°的直角三角形的性质以及勾股定理得PC=2y,,即可列出关于y的方程,解方程求出y的值可得PC的值,于是得DP的值,最后综合以上两种情况得到答案.
试题分析部分
1、试卷总体分布分析
总分:57分
分值分布 客观题(占比) 30.0(52.6%)
主观题(占比) 27.0(47.4%)
题量分布 客观题(占比) 15(46.9%)
主观题(占比) 17(53.1%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
选择题 12(37.5%) 24.0(42.1%)
填空题 8(25.0%) 18.0(31.6%)
证明题 3(9.4%) 10.0(17.5%)
作图题 3(9.4%) 0.0(0.0%)
计算题 4(12.5%) 0.0(0.0%)
综合题 2(6.3%) 5.0(8.8%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (40.6%)
2 容易 (46.9%)
3 困难 (12.5%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 平均数及其计算 2.0(3.5%) 13
2 平方差公式及应用 0.0(0.0%) 21
3 含30°角的直角三角形 5.0(8.8%) 25
4 轴对称的性质 0.0(0.0%) 32
5 菱形的性质 2.0(3.5%) 16
6 三角形的中位线定理 0.0(0.0%) 27,32
7 菱形的判定与性质 0.0(0.0%) 32
8 坐标与图形性质 2.0(3.5%) 4
9 矩形的性质 7.0(12.3%) 17,26
10 二次根式有意义的条件 4.0(7.0%) 14,18
11 垂线段最短及其应用 2.0(3.5%) 1
12 完全平方公式及运用 0.0(0.0%) 21,23
13 方差 8.0(14.0%) 3,10,13,20
14 最简二次根式 2.0(3.5%) 5
15 平行四边形的性质 6.0(10.5%) 1,4,7
16 翻折变换(折叠问题) 0.0(0.0%) 32
17 中位数 4.0(7.0%) 6,12
18 等边三角形的判定与性质 2.0(3.5%) 7
19 等边三角形的性质 4.0(7.0%) 9,15
20 四边形的综合 0.0(0.0%) 32
21 二次根式的性质与化简 4.0(7.0%) 19
22 负整数指数幂 0.0(0.0%) 24
23 平行线的性质 2.0(3.5%) 17
24 勾股定理 6.0(10.5%) 7,9,15,28,29
25 二次根式的混合运算 2.0(3.5%) 7,21,23
26 平行四边形的判定 7.0(12.3%) 8,26,29
27 二次根式的化简求值 2.0(3.5%) 11
28 众数 4.0(7.0%) 6,12
29 三角形的面积 2.0(3.5%) 9
30 作图﹣中心对称 0.0(0.0%) 29
31 直角三角形斜边上的中线 2.0(3.5%) 16
32 平行四边形的判定与性质 2.0(3.5%) 2,27,28,30
33 尺规作图-垂直平分线 0.0(0.0%) 30
34 勾股定理的应用 5.0(8.8%) 31
35 中点四边形模型 0.0(0.0%) 27
36 二次根式的乘除法 0.0(0.0%) 22
37 零指数幂 0.0(0.0%) 24
38 二次根式的加减法 0.0(0.0%) 22,24
39 勾股定理的逆定理 5.0(8.8%) 25
1 / 1
