第八章三角形单元测试(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章三角形单元测试华东师大版2024—2025学年七年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.若n边形的内角和等于它外角和的2倍,则边数n为( )
A.7 B.6 C.5 D.4
2.从n边形的一个顶点出发,可以作6条对角线,则n的值是( )
A.12 B.10 C.9 D.8
3.若一个多边形截去一个角后,变成五边形,则原来的多边形的边数可能为( )
A.5或6 B.4或5 C.3或4或5 D.4或5或6
4.如图,△ABC中∠B=40°,∠C=30°,延长BA到点D,则∠CAD的度数是( )
A.50° B.70° C.80° D.110°
5.某校校园里的一条小路使用正六边形、正方形、正三角形三种地砖按如图方式铺设.若这条小路共用了50块正六边形地砖,则正方形地砖的数量为( )
A.300块 B.301块 C.250块 D.251块
6.下列多边形的组合中,能够铺满地面的是( )
A.正方形与正六边形 B.正四边形和正八边形
C.正五边形和正八边形 D.正三角形和正十边形
7.如图,在△ABC中,点D在边AC上(不与端点重合),连接BD.则∠1,∠2,∠3的大小关系是( )
A.∠1<∠2<∠3 B.∠1<∠3<∠2 C.∠3<∠2<∠1 D.∠2<∠1<∠3
8.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
二.填空题(每小题5分,满分20分)
9.三角形的三边长分别为5,x,8,则x的取值范围是 .
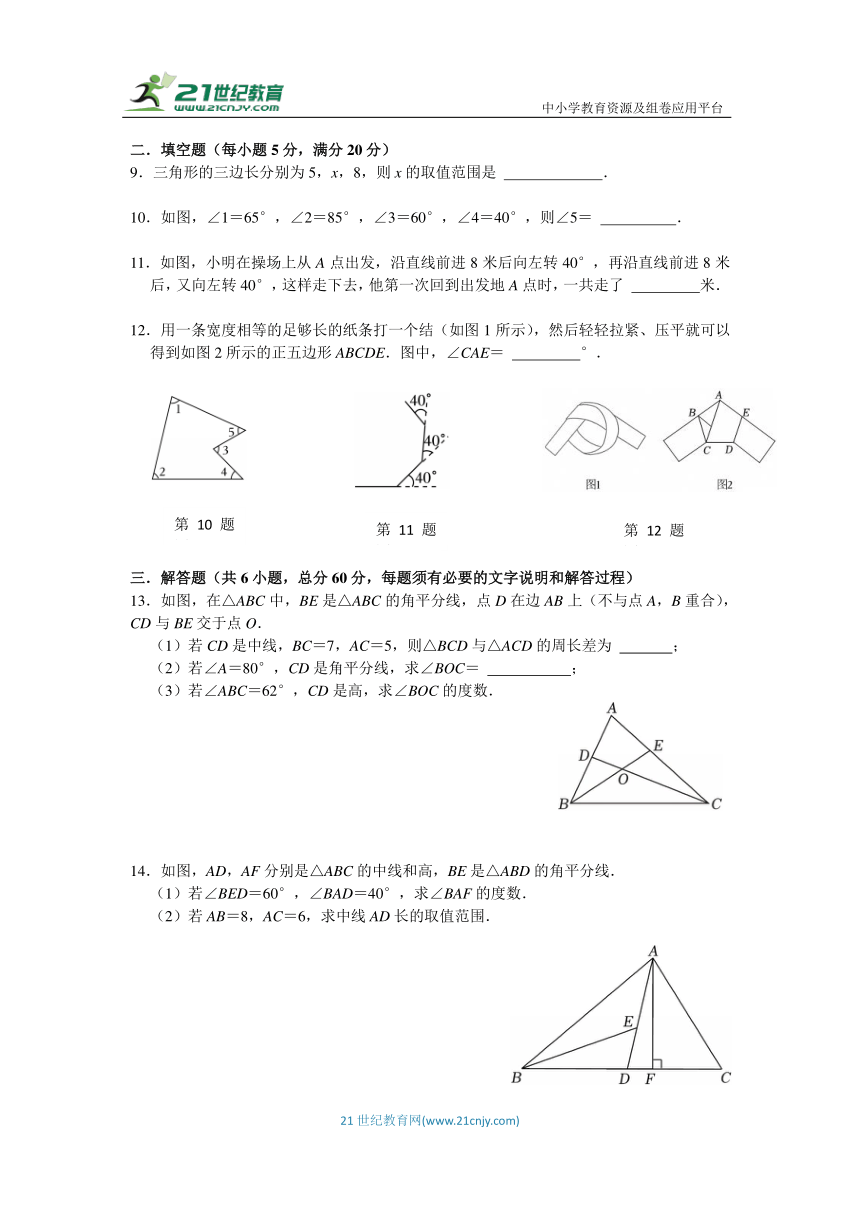
10.如图,∠1=65°,∠2=85°,∠3=60°,∠4=40°,则∠5= .
11.如图,小明在操场上从A点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地A点时,一共走了 米.
12.用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠CAE= °.
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,BE是△ABC的角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=7,AC=5,则△BCD与△ACD的周长差为 ;
(2)若∠A=80°,CD是角平分线,求∠BOC= ;
(3)若∠ABC=62°,CD是高,求∠BOC的度数.
14.如图,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若∠BED=60°,∠BAD=40°,求∠BAF的度数.
(2)若AB=8,AC=6,求中线AD长的取值范围.
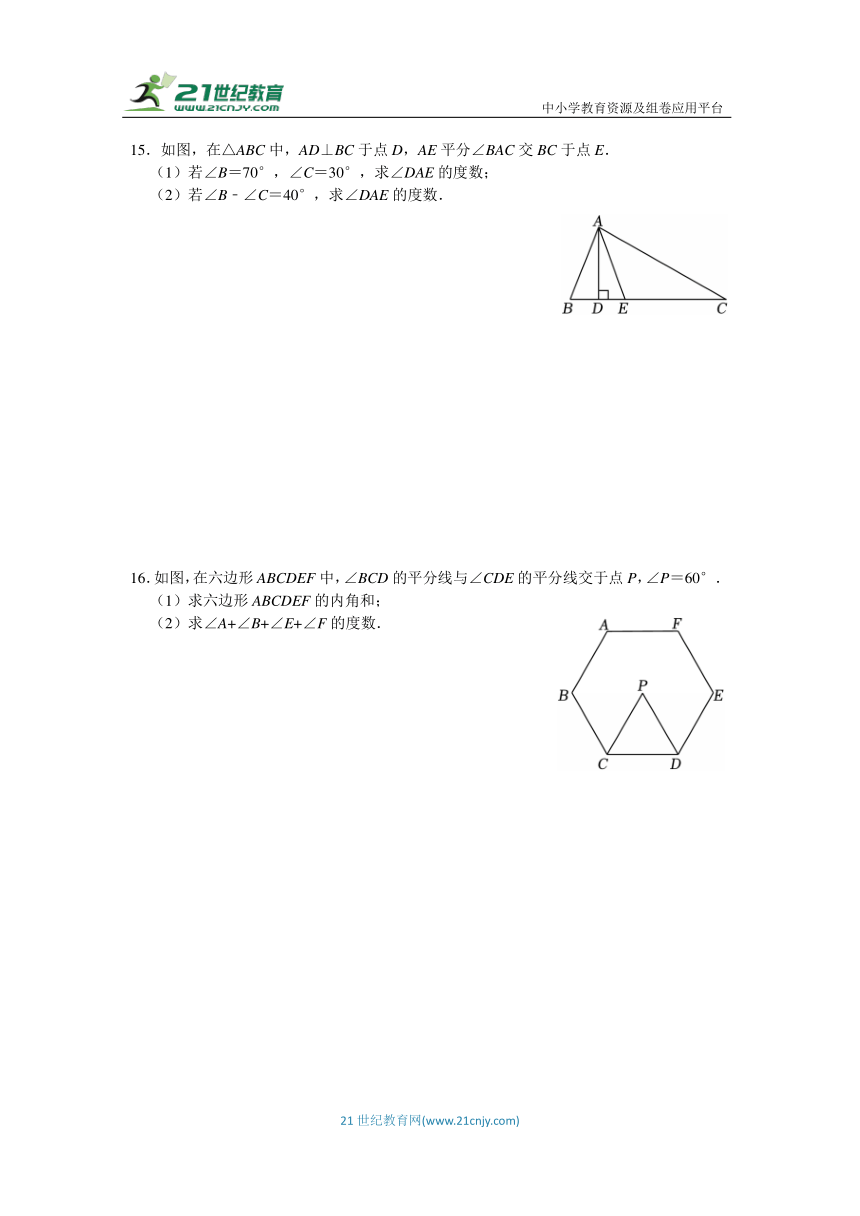
15.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC交BC于点E.
(1)若∠B=70°,∠C=30°,求∠DAE的度数;
(2)若∠B﹣∠C=40°,求∠DAE的度数.
16.如图,在六边形ABCDEF中,∠BCD的平分线与∠CDE的平分线交于点P,∠P=60°.
(1)求六边形ABCDEF的内角和;
(2)求∠A+∠B+∠E+∠F的度数.
17.如图,小明从点A出发,前进10m后向右转30°,再前进10m后又向右转30°,……,如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.
(1)求小明一共走了多少米;
(2)求这个正多边形的内角和.
18.我们在用边长相同的正多边形进行平面镶嵌时,各正多边形重合的顶点叫拼接点,如图1,O就是拼接点.我们发现,各正多边形的以拼接点为顶点的内角之和为360°(注:若不能等于360°,则不能镶嵌).
(1)如果我们只用一种边长相同的正多边形镶嵌,那么下面正多边形中,不能进行镶嵌的是 .(填序号)
①正三角形②正方形③正五边形④正六边形
(2)为了使镶嵌图案美丽多变,我们有时也可以用边长相同的两种正多边形进行镶嵌,如图2,正三角形与正方形的平面镶嵌,在一个拼接点的周围有3个正三角形和2个正方形.
①如果我们用边长相同的正三角形与正六边形进行镶嵌,求一个拼接点的周围有几个正三角形和几个正六边形;
②我们也可以用边长相同的正五边形和正 边形进行镶嵌.
参考答案
一、选择题
1—8:BCDBDBDD
二、填空题
9.【解答】解:根据三角形的三边关系,得:8﹣5<x<8+5,即:3<x<13.
故答案为:3<x<13.
10.【解答】解:如图,连接BC,
在△BCE中,∠3+∠EBC+∠ECB=180°,
∵∠3=60°,
∴∠EBC+∠ECB=120°,
在四边形ABCD中,∠1+∠2+∠4+∠EBC+∠ECB+∠5=(4﹣2)×180°=360°,
∵∠1=65°,∠2=85°,∠4=40°,
∴65°+85°+40°+120°+∠5=360°,
∴∠5=50°,
故答案为:50°.
11.【解答】解:∵小明需要转360÷40=9次才会回到原点,
∴小明共走了9×8=72(米),
故答案为:72.
12.【解答】解:∵五边形ABCDE是正五边形,
∴∠ABC=∠BAE,AB=BC,
∴∠BAC=∠ACB,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=∠ACB=36°,
∵∠BAE=∠BAC+∠CAE,
∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°,
故答案为:72.
三、解答题
13.【解答】解:(1)∵CD是AB的中线,
∴AD=DB,
∵BC=7,AC=5,
∴△BCD与△ACD的周长差为:(BC+CD+BD)﹣(AC+CD+AD)=BC﹣AC=2,
故答案为:2;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵BE是△ABC的角平分线,CD是角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=50°,
∴∠BOC=180°﹣50°=130°,
故答案为:130;
(3)∵CD是高,
∴∠CDB=90°,
∵∠ABC=62°,
∴∠BCD=90°﹣62°=28°,
∵BE平分∠ABC,
∴,
在△BOC中,∠BOC=180°﹣28°﹣31°=121°.
14.【解答】解:(1)∵∠BED=∠ABE+∠BAE,∠BED=60°,∠BAD=40°,
∴∠ABE=60°﹣40°=20°,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=40°,
∵AF为高,
∴∠AFB=90°,
∴∠BAF=90°﹣∠ABF=90°﹣40°=50°;
(2)延长AD至K,使AD=DK,连接CK.
∵AD是△ABC的中线,
∴BD=CD,
∵∠ADB=∠CDK,
∴△ADB≌△KDC,
∴AB=CK=8,而AC=6,
∴2<AK<14,
∴1<AD<7.
15.【解答】解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,
∴∠BAE∠BAC=40°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠BAD=90°﹣∠B=90°﹣70°=20°;
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE∠BAC(180°﹣∠B﹣∠C)=90°(∠B+∠C),
∵AD⊥BC,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°(∠B+∠C)﹣(90°﹣∠B)(∠B﹣∠C).
又∵∠B﹣∠C=40°,
∴∠DAE40°=20°.
16.【解答】解:(1)六边形ABCDEF的内角和=(6﹣2)×180°=720°;
(2)∵∠P=60°,
∴∠PCD+∠PDC=180°﹣∠P=180°﹣60°=120°,
∵PC平分∠BCD,PD平分∠EDC,
∴∠BCD+∠EDC=2∠PCD+2∠PDC=2×120°=240°,
∵∠A+∠B+∠E+∠F+∠BCD+∠EDC=720°,
∴∠A+∠B+∠E+∠F=720°﹣∠BCD﹣∠EDC=720°﹣240°=480°.
17.【解答】解:(1)∵所经过的路线正好构成一个外角是30度的正多边形,
∴360÷30=12,12×10=120(米);
答:小明一共走了120米;
(2)根据题意得:
(12﹣2)×180°=1800°,
答:这个多边形的内角和是1800°.
18.【解答】解:(1)①正三角形的内角为60°,360°÷60°=6,结果是整数,可以进行平面镶嵌;
②正方形内角为90°,360°÷90°=4,结果是整数,可以进行平面镶嵌;
③正五边形内角为108°,,结果不是整数,不可以进行平面镶嵌;
④正六边形内角为120°,360°÷120°=3,结果是整数,可以进行平面镶嵌;
故选:③;
(2)①设在平面镶嵌时,一个拼接点的周围有x个正三角形和y个正六边形,
根据题意得:60°x+120°y=360°,
∴x+2y=6,
∵x,y为正整数,
∴或,
答:在平面镶嵌时,一个拼接点的周围有2个正三角形和2个正六边形或4个正三角形和1个正六边形;
②由于正五边形内角为108°,设用边长相同的a个正五边形和b个正n边形进行镶嵌,
则,
整理得:,
∵a,b,n为正整数,
∴应为正整数,
则n=5或n=10,
当n=5时,3a+3b=10,此时a,b无正整数解,
当n=10时,3a+4b=10,解得正整数解为:,
故答案为:十.
21世纪教育网(www.21cnjy.com)
第八章三角形单元测试华东师大版2024—2025学年七年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.若n边形的内角和等于它外角和的2倍,则边数n为( )
A.7 B.6 C.5 D.4
2.从n边形的一个顶点出发,可以作6条对角线,则n的值是( )
A.12 B.10 C.9 D.8
3.若一个多边形截去一个角后,变成五边形,则原来的多边形的边数可能为( )
A.5或6 B.4或5 C.3或4或5 D.4或5或6
4.如图,△ABC中∠B=40°,∠C=30°,延长BA到点D,则∠CAD的度数是( )
A.50° B.70° C.80° D.110°
5.某校校园里的一条小路使用正六边形、正方形、正三角形三种地砖按如图方式铺设.若这条小路共用了50块正六边形地砖,则正方形地砖的数量为( )
A.300块 B.301块 C.250块 D.251块
6.下列多边形的组合中,能够铺满地面的是( )
A.正方形与正六边形 B.正四边形和正八边形
C.正五边形和正八边形 D.正三角形和正十边形
7.如图,在△ABC中,点D在边AC上(不与端点重合),连接BD.则∠1,∠2,∠3的大小关系是( )
A.∠1<∠2<∠3 B.∠1<∠3<∠2 C.∠3<∠2<∠1 D.∠2<∠1<∠3
8.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
二.填空题(每小题5分,满分20分)
9.三角形的三边长分别为5,x,8,则x的取值范围是 .
10.如图,∠1=65°,∠2=85°,∠3=60°,∠4=40°,则∠5= .
11.如图,小明在操场上从A点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地A点时,一共走了 米.
12.用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠CAE= °.
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,BE是△ABC的角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=7,AC=5,则△BCD与△ACD的周长差为 ;
(2)若∠A=80°,CD是角平分线,求∠BOC= ;
(3)若∠ABC=62°,CD是高,求∠BOC的度数.
14.如图,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若∠BED=60°,∠BAD=40°,求∠BAF的度数.
(2)若AB=8,AC=6,求中线AD长的取值范围.
15.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC交BC于点E.
(1)若∠B=70°,∠C=30°,求∠DAE的度数;
(2)若∠B﹣∠C=40°,求∠DAE的度数.
16.如图,在六边形ABCDEF中,∠BCD的平分线与∠CDE的平分线交于点P,∠P=60°.
(1)求六边形ABCDEF的内角和;
(2)求∠A+∠B+∠E+∠F的度数.
17.如图,小明从点A出发,前进10m后向右转30°,再前进10m后又向右转30°,……,如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.
(1)求小明一共走了多少米;
(2)求这个正多边形的内角和.
18.我们在用边长相同的正多边形进行平面镶嵌时,各正多边形重合的顶点叫拼接点,如图1,O就是拼接点.我们发现,各正多边形的以拼接点为顶点的内角之和为360°(注:若不能等于360°,则不能镶嵌).
(1)如果我们只用一种边长相同的正多边形镶嵌,那么下面正多边形中,不能进行镶嵌的是 .(填序号)
①正三角形②正方形③正五边形④正六边形
(2)为了使镶嵌图案美丽多变,我们有时也可以用边长相同的两种正多边形进行镶嵌,如图2,正三角形与正方形的平面镶嵌,在一个拼接点的周围有3个正三角形和2个正方形.
①如果我们用边长相同的正三角形与正六边形进行镶嵌,求一个拼接点的周围有几个正三角形和几个正六边形;
②我们也可以用边长相同的正五边形和正 边形进行镶嵌.
参考答案
一、选择题
1—8:BCDBDBDD
二、填空题
9.【解答】解:根据三角形的三边关系,得:8﹣5<x<8+5,即:3<x<13.
故答案为:3<x<13.
10.【解答】解:如图,连接BC,
在△BCE中,∠3+∠EBC+∠ECB=180°,
∵∠3=60°,
∴∠EBC+∠ECB=120°,
在四边形ABCD中,∠1+∠2+∠4+∠EBC+∠ECB+∠5=(4﹣2)×180°=360°,
∵∠1=65°,∠2=85°,∠4=40°,
∴65°+85°+40°+120°+∠5=360°,
∴∠5=50°,
故答案为:50°.
11.【解答】解:∵小明需要转360÷40=9次才会回到原点,
∴小明共走了9×8=72(米),
故答案为:72.
12.【解答】解:∵五边形ABCDE是正五边形,
∴∠ABC=∠BAE,AB=BC,
∴∠BAC=∠ACB,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=∠ACB=36°,
∵∠BAE=∠BAC+∠CAE,
∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°,
故答案为:72.
三、解答题
13.【解答】解:(1)∵CD是AB的中线,
∴AD=DB,
∵BC=7,AC=5,
∴△BCD与△ACD的周长差为:(BC+CD+BD)﹣(AC+CD+AD)=BC﹣AC=2,
故答案为:2;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵BE是△ABC的角平分线,CD是角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=50°,
∴∠BOC=180°﹣50°=130°,
故答案为:130;
(3)∵CD是高,
∴∠CDB=90°,
∵∠ABC=62°,
∴∠BCD=90°﹣62°=28°,
∵BE平分∠ABC,
∴,
在△BOC中,∠BOC=180°﹣28°﹣31°=121°.
14.【解答】解:(1)∵∠BED=∠ABE+∠BAE,∠BED=60°,∠BAD=40°,
∴∠ABE=60°﹣40°=20°,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=40°,
∵AF为高,
∴∠AFB=90°,
∴∠BAF=90°﹣∠ABF=90°﹣40°=50°;
(2)延长AD至K,使AD=DK,连接CK.
∵AD是△ABC的中线,
∴BD=CD,
∵∠ADB=∠CDK,
∴△ADB≌△KDC,
∴AB=CK=8,而AC=6,
∴2<AK<14,
∴1<AD<7.
15.【解答】解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,
∴∠BAE∠BAC=40°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠BAD=90°﹣∠B=90°﹣70°=20°;
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE∠BAC(180°﹣∠B﹣∠C)=90°(∠B+∠C),
∵AD⊥BC,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°(∠B+∠C)﹣(90°﹣∠B)(∠B﹣∠C).
又∵∠B﹣∠C=40°,
∴∠DAE40°=20°.
16.【解答】解:(1)六边形ABCDEF的内角和=(6﹣2)×180°=720°;
(2)∵∠P=60°,
∴∠PCD+∠PDC=180°﹣∠P=180°﹣60°=120°,
∵PC平分∠BCD,PD平分∠EDC,
∴∠BCD+∠EDC=2∠PCD+2∠PDC=2×120°=240°,
∵∠A+∠B+∠E+∠F+∠BCD+∠EDC=720°,
∴∠A+∠B+∠E+∠F=720°﹣∠BCD﹣∠EDC=720°﹣240°=480°.
17.【解答】解:(1)∵所经过的路线正好构成一个外角是30度的正多边形,
∴360÷30=12,12×10=120(米);
答:小明一共走了120米;
(2)根据题意得:
(12﹣2)×180°=1800°,
答:这个多边形的内角和是1800°.
18.【解答】解:(1)①正三角形的内角为60°,360°÷60°=6,结果是整数,可以进行平面镶嵌;
②正方形内角为90°,360°÷90°=4,结果是整数,可以进行平面镶嵌;
③正五边形内角为108°,,结果不是整数,不可以进行平面镶嵌;
④正六边形内角为120°,360°÷120°=3,结果是整数,可以进行平面镶嵌;
故选:③;
(2)①设在平面镶嵌时,一个拼接点的周围有x个正三角形和y个正六边形,
根据题意得:60°x+120°y=360°,
∴x+2y=6,
∵x,y为正整数,
∴或,
答:在平面镶嵌时,一个拼接点的周围有2个正三角形和2个正六边形或4个正三角形和1个正六边形;
②由于正五边形内角为108°,设用边长相同的a个正五边形和b个正n边形进行镶嵌,
则,
整理得:,
∵a,b,n为正整数,
∴应为正整数,
则n=5或n=10,
当n=5时,3a+3b=10,此时a,b无正整数解,
当n=10时,3a+4b=10,解得正整数解为:,
故答案为:十.
21世纪教育网(www.21cnjy.com)
