第八章三角形单元测试(一)(含答案)
文档属性
| 名称 | 第八章三角形单元测试(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 415.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 10:00:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章三角形单元测试(一)华东师大版2024—2025学年七年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.一位木工师傅有两根长分别是30cm和70cm的木条,他需要用第三根木条钉成一个封闭的三角形框架,则第三根木条的长度可以为( )
A.30cm B.40cm C.90cm D.110cm
2.△ABC的三角之比是1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.下列叙述中错误的一项是( )
A.三角形的中线、角平分线、高都是线段
B.三角形的三条高线中至少存在一条在三角形内部
C.三角形三条高的交点叫做三角形的重心
D.三角形的三条角平分线都在三角形内部
4.酷爱思考的可培同学在学面镶嵌的知识后,决定为家里新装修的房子选择一些不同样式的瓷砖来铺设地板,在以下正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
5.某校校园里的一条小路使用正六边形、正方形、正三角形三种地砖按如图方式铺设.若这条小路共用了50块正六边形地砖,则正方形地砖的数量为( )
A.300块 B.301块 C.250块 D.251块
6.如图,顺次连接图中六个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.270° C.360° D.720°
7.已知∠EOF=90°,现将一直角三角板ABC(∠A=30°、∠C=90°)按如图所示的位置摆放,则∠α+∠β=( )
A.210° B.200° C.190° D.180°
8.若一个多边形截去一个角后,变成五边形,则原来的多边形的边数可能为( )
A.5或6 B.4或5 C.3或4或5 D.4或5或6
二.填空题(每小题5分,满分20分)
9.如图,将五角星沿着虚线FG剪下.若∠B+∠C+∠D+∠E=5∠A,则∠CFG+∠DGF= .
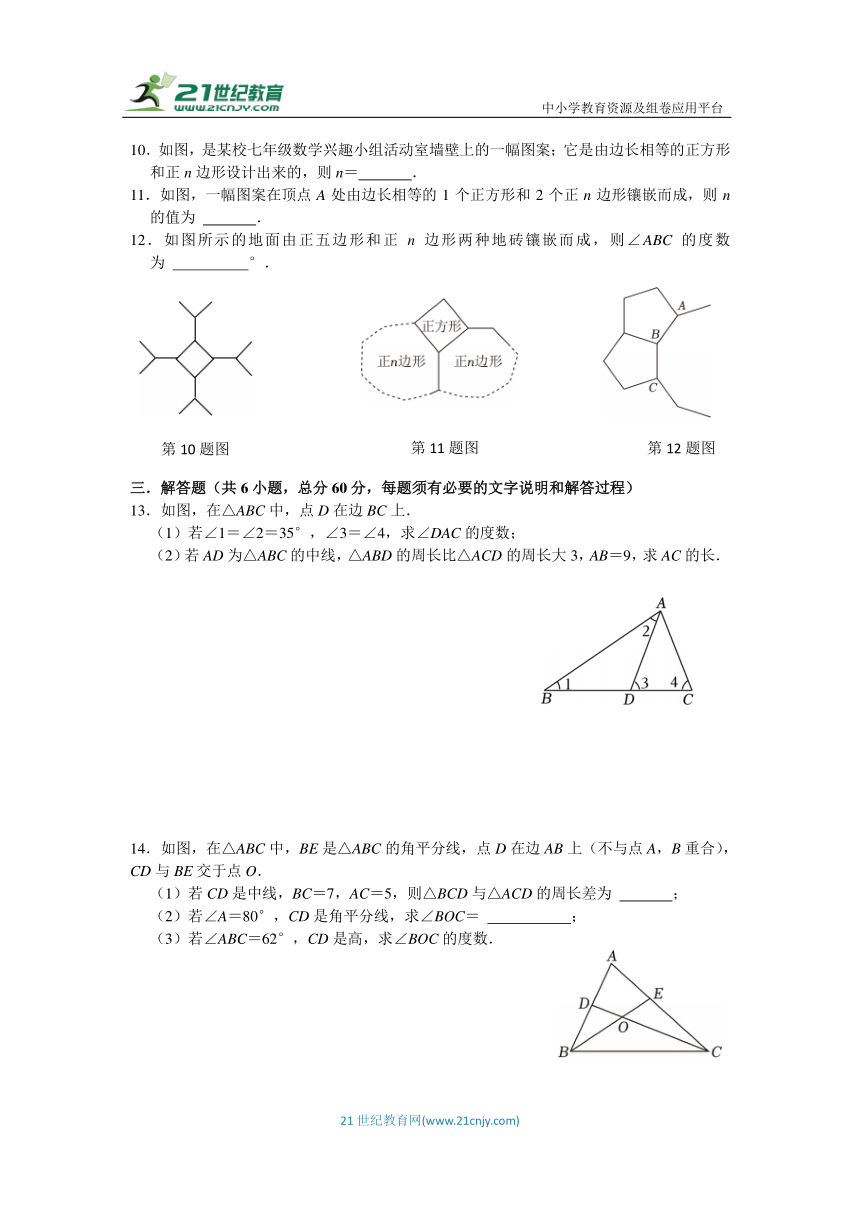
10.如图,是某校七年级数学兴趣小组活动室墙壁上的一幅图案;它是由边长相等的正方形和正n边形设计出来的,则n= .
11.如图,一幅图案在顶点A处由边长相等的1个正方形和2个正n边形镶嵌而成,则n的值为 .
12.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则∠ABC的度数为 °.
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,点D在边BC上.
(1)若∠1=∠2=35°,∠3=∠4,求∠DAC的度数;
(2)若AD为△ABC的中线,△ABD的周长比△ACD的周长大3,AB=9,求AC的长.
14.如图,在△ABC中,BE是△ABC的角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=7,AC=5,则△BCD与△ACD的周长差为 ;
(2)若∠A=80°,CD是角平分线,求∠BOC= ;
(3)若∠ABC=62°,CD是高,求∠BOC的度数.
15.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=80°,∠A=60°,求∠DCB的度数.
16.在△ABC中,AB=8,AC=2.
(1)若BC是偶数,求BC的长;
(2)已知AD是△ABC的中线,若△ACD的周长为10,求△ABD的周长.
17.已知△ABC的三边长分别为a,b,c.
(1)化简:|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|;
(2)若a=5,b=2,且三角形的周长为偶数.
①求c的值;
②试判断△ABC的形状.
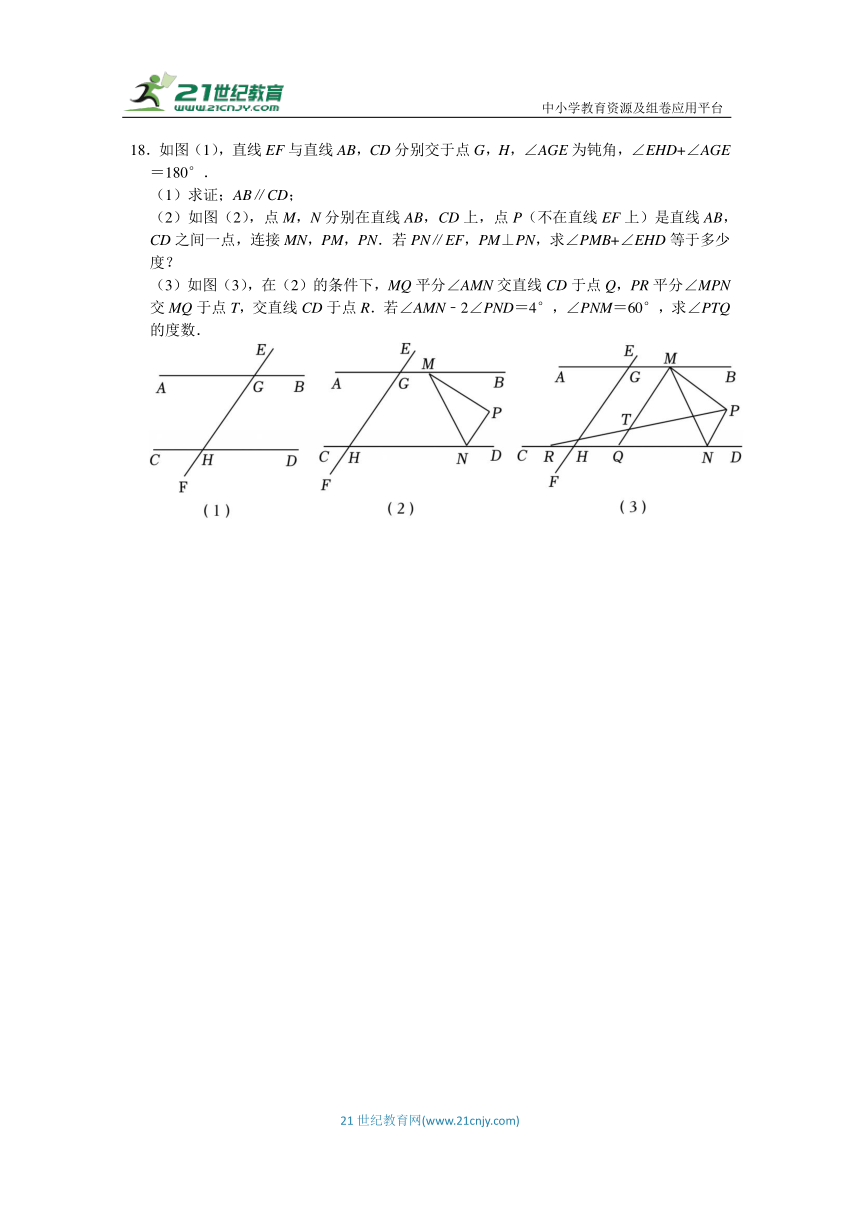
18.如图(1),直线EF与直线AB,CD分别交于点G,H,∠AGE为钝角,∠EHD+∠AGE=180°.
(1)求证;AB∥CD;
(2)如图(2),点M,N分别在直线AB,CD上,点P(不在直线EF上)是直线AB,CD之间一点,连接MN,PM,PN.若PN∥EF,PM⊥PN,求∠PMB+∠EHD等于多少度?
(3)如图(3),在(2)的条件下,MQ平分∠AMN交直线CD于点Q,PR平分∠MPN交MQ于点T,交直线CD于点R.若∠AMN﹣2∠PND=4°,∠PNM=60°,求∠PTQ 的度数.
参考答案
一、选择题
1—8:CBCBDCAD
二、填空题
9.【解答】解:如图,∵∠AMN=∠C+∠E,∠ANM=∠B+∠D,而∠AMN+∠ANM+∠A=180°,
∴∠C+∠E+∠B+∠D=180°﹣∠A,
即∠A+∠B+∠C+∠D+∠E=180°,
又∵∠B+∠C+∠D+∠E=5∠A,
∴∠A+5∠A=180°,
解得∠A=30°,
∴∠CFG+∠DGF=∠AFG+∠AGF+∠A+∠A=180°+30°=210°,
故答案为:210°.
10.【解答】解:正n边形的一个内角=(360°﹣90°)÷2=135°,
则135°n=(n﹣2) 180°,
解得n=8.
故答案为:8.
11.【解答】解:正方形的每个内角为90°,正n边形的每个内角为,根据题意得:
90°+2360°,
解得:n=8.
故答案为:8.
12.【解答】解:正五边形内角和 (5﹣2)×180°=540°,
所以每个内角度数540°÷8=108°,
∴∠ABC=360°﹣2×108°=144°.
故答案为:144.
三、解答题
13.【解答】解:(1)∵∠1=∠2=35°,
∴∠3=∠1+∠2=70°,
∴∠3=∠4=70°,
∴∠DAC=180°﹣∠3﹣∠4=40°;
(2)∵AD为△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD的周长大3,
∴AB+AD+BD﹣(AC+AD+CD)=3,
∴AB+AD+BD﹣AC﹣AD﹣CD=3,
∴AB﹣AC=3,
∵AB=9,
∴AC=6.
14.【解答】解:(1)∵CD是AB的中线,
∴AD=DB,
∵BC=7,AC=5,
∴△BCD与△ACD的周长差为:(BC+CD+BD)﹣(AC+CD+AD)=BC﹣AC=2,
故答案为:2;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵BE是△ABC的角平分线,CD是角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=50°,
∴∠BOC=180°﹣50°=130°,
故答案为:130;
(3)∵CD是高,
∴∠CDB=90°,
∵∠ABC=62°,
∴∠BCD=90°﹣62°=28°,
∵BE平分∠ABC,
∴,
在△BOC中,∠BOC=180°﹣28°﹣31°=121°.
15.【解答】(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=80°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=40°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣40°=50°.
16.【解答】解:(1)由三角形三边关系得:AB﹣AC<BC<AC+AB,
又∵AB=8,AC=2,
∴6<BC<10,
又∵BC是偶数,
∴BC=8,
所以BC的长为8;
(2)∵AD是△ABC的中线,
∴BD=CD.
∵△ACD的周长为10,
∴AC+AD+CD=10,
∵AC=2,
∴AD+CD=8,
∴AD+BD=8,
又∵AB=8,
∴△ABD的周长=AB+AD+BD=8+8=16.
17.【解答】解:(1)∵a,b,c是△ABC的三边长,
∴a﹣b﹣c<0,b﹣c﹣a<0,a+b﹣c>0,
∴|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|=﹣a+b+c+b﹣c﹣a+a+b﹣c=﹣a+3b﹣c;
(2)∵a=5,b=2,
∴5﹣2<c<5+2,
即3<c<7,
∵三角形的周长为偶数,
∴c=5;
②∵a=c=5,
∴△ABC是等腰三角形.
18.【解答】(1)证明:∵直线AB与直线EF交于点G,
∴∠AGE=∠BGF,
又∵∠EHD+∠AGE=180°,
∴∠EHD+∠BGF=180°,
∴AB∥CD;
(2)过点P作PK∥AB,如图所示:
由(1)可知:AB∥CD,
∴AB∥PK∥CD,
∴∠PMB=∠MPK,∠PND=∠NPK,
∴∠PMB+∠PND=∠MPK+∠NPK=∠MPN,
∵PM⊥PN,
∴∠MPN=90°,
∴∠PMB+∠PND=90°,
∵PN∥EF,
∴∠EHD=∠PND,
∴∠PMB+∠EHD=90°;
(3)设∠AMQ=α,
∵MQ平分∠AMN,
∴∠AMQ=∠QMN=α,
∴∠AMN=2α,
∵PM⊥PN,∠PNM=60°,
∴∠PMN=90°﹣60°=30°,
∴∠QMP=∠QMN+∠PMN=α+30°,
∠PMB=180°﹣∠AMN﹣∠PMN=180°﹣2α﹣30°=150°﹣2α,
由(2)可知:∠PMB+∠PND=90°,
∴∠PND=90°﹣∠PMB=90°﹣(150°﹣2α)=2α﹣60°,
∵∠AMN﹣2∠PND=4°,
∴2α﹣2(2α﹣60°)=4°,
解得:α=58°,
∴∠QMP=α+30°=88°,
∵PM⊥PN,PR平分∠MPN,
∴∠MPT=45°,
∴∠PTQ=∠QMP+∠MPT=45°+88°=133°.
21世纪教育网(www.21cnjy.com)
第八章三角形单元测试(一)华东师大版2024—2025学年七年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.一位木工师傅有两根长分别是30cm和70cm的木条,他需要用第三根木条钉成一个封闭的三角形框架,则第三根木条的长度可以为( )
A.30cm B.40cm C.90cm D.110cm
2.△ABC的三角之比是1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.下列叙述中错误的一项是( )
A.三角形的中线、角平分线、高都是线段
B.三角形的三条高线中至少存在一条在三角形内部
C.三角形三条高的交点叫做三角形的重心
D.三角形的三条角平分线都在三角形内部
4.酷爱思考的可培同学在学面镶嵌的知识后,决定为家里新装修的房子选择一些不同样式的瓷砖来铺设地板,在以下正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
5.某校校园里的一条小路使用正六边形、正方形、正三角形三种地砖按如图方式铺设.若这条小路共用了50块正六边形地砖,则正方形地砖的数量为( )
A.300块 B.301块 C.250块 D.251块
6.如图,顺次连接图中六个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.270° C.360° D.720°
7.已知∠EOF=90°,现将一直角三角板ABC(∠A=30°、∠C=90°)按如图所示的位置摆放,则∠α+∠β=( )
A.210° B.200° C.190° D.180°
8.若一个多边形截去一个角后,变成五边形,则原来的多边形的边数可能为( )
A.5或6 B.4或5 C.3或4或5 D.4或5或6
二.填空题(每小题5分,满分20分)
9.如图,将五角星沿着虚线FG剪下.若∠B+∠C+∠D+∠E=5∠A,则∠CFG+∠DGF= .
10.如图,是某校七年级数学兴趣小组活动室墙壁上的一幅图案;它是由边长相等的正方形和正n边形设计出来的,则n= .
11.如图,一幅图案在顶点A处由边长相等的1个正方形和2个正n边形镶嵌而成,则n的值为 .
12.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则∠ABC的度数为 °.
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,点D在边BC上.
(1)若∠1=∠2=35°,∠3=∠4,求∠DAC的度数;
(2)若AD为△ABC的中线,△ABD的周长比△ACD的周长大3,AB=9,求AC的长.
14.如图,在△ABC中,BE是△ABC的角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=7,AC=5,则△BCD与△ACD的周长差为 ;
(2)若∠A=80°,CD是角平分线,求∠BOC= ;
(3)若∠ABC=62°,CD是高,求∠BOC的度数.
15.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=80°,∠A=60°,求∠DCB的度数.
16.在△ABC中,AB=8,AC=2.
(1)若BC是偶数,求BC的长;
(2)已知AD是△ABC的中线,若△ACD的周长为10,求△ABD的周长.
17.已知△ABC的三边长分别为a,b,c.
(1)化简:|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|;
(2)若a=5,b=2,且三角形的周长为偶数.
①求c的值;
②试判断△ABC的形状.
18.如图(1),直线EF与直线AB,CD分别交于点G,H,∠AGE为钝角,∠EHD+∠AGE=180°.
(1)求证;AB∥CD;
(2)如图(2),点M,N分别在直线AB,CD上,点P(不在直线EF上)是直线AB,CD之间一点,连接MN,PM,PN.若PN∥EF,PM⊥PN,求∠PMB+∠EHD等于多少度?
(3)如图(3),在(2)的条件下,MQ平分∠AMN交直线CD于点Q,PR平分∠MPN交MQ于点T,交直线CD于点R.若∠AMN﹣2∠PND=4°,∠PNM=60°,求∠PTQ 的度数.
参考答案
一、选择题
1—8:CBCBDCAD
二、填空题
9.【解答】解:如图,∵∠AMN=∠C+∠E,∠ANM=∠B+∠D,而∠AMN+∠ANM+∠A=180°,
∴∠C+∠E+∠B+∠D=180°﹣∠A,
即∠A+∠B+∠C+∠D+∠E=180°,
又∵∠B+∠C+∠D+∠E=5∠A,
∴∠A+5∠A=180°,
解得∠A=30°,
∴∠CFG+∠DGF=∠AFG+∠AGF+∠A+∠A=180°+30°=210°,
故答案为:210°.
10.【解答】解:正n边形的一个内角=(360°﹣90°)÷2=135°,
则135°n=(n﹣2) 180°,
解得n=8.
故答案为:8.
11.【解答】解:正方形的每个内角为90°,正n边形的每个内角为,根据题意得:
90°+2360°,
解得:n=8.
故答案为:8.
12.【解答】解:正五边形内角和 (5﹣2)×180°=540°,
所以每个内角度数540°÷8=108°,
∴∠ABC=360°﹣2×108°=144°.
故答案为:144.
三、解答题
13.【解答】解:(1)∵∠1=∠2=35°,
∴∠3=∠1+∠2=70°,
∴∠3=∠4=70°,
∴∠DAC=180°﹣∠3﹣∠4=40°;
(2)∵AD为△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD的周长大3,
∴AB+AD+BD﹣(AC+AD+CD)=3,
∴AB+AD+BD﹣AC﹣AD﹣CD=3,
∴AB﹣AC=3,
∵AB=9,
∴AC=6.
14.【解答】解:(1)∵CD是AB的中线,
∴AD=DB,
∵BC=7,AC=5,
∴△BCD与△ACD的周长差为:(BC+CD+BD)﹣(AC+CD+AD)=BC﹣AC=2,
故答案为:2;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵BE是△ABC的角平分线,CD是角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=50°,
∴∠BOC=180°﹣50°=130°,
故答案为:130;
(3)∵CD是高,
∴∠CDB=90°,
∵∠ABC=62°,
∴∠BCD=90°﹣62°=28°,
∵BE平分∠ABC,
∴,
在△BOC中,∠BOC=180°﹣28°﹣31°=121°.
15.【解答】(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=80°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=40°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣40°=50°.
16.【解答】解:(1)由三角形三边关系得:AB﹣AC<BC<AC+AB,
又∵AB=8,AC=2,
∴6<BC<10,
又∵BC是偶数,
∴BC=8,
所以BC的长为8;
(2)∵AD是△ABC的中线,
∴BD=CD.
∵△ACD的周长为10,
∴AC+AD+CD=10,
∵AC=2,
∴AD+CD=8,
∴AD+BD=8,
又∵AB=8,
∴△ABD的周长=AB+AD+BD=8+8=16.
17.【解答】解:(1)∵a,b,c是△ABC的三边长,
∴a﹣b﹣c<0,b﹣c﹣a<0,a+b﹣c>0,
∴|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|=﹣a+b+c+b﹣c﹣a+a+b﹣c=﹣a+3b﹣c;
(2)∵a=5,b=2,
∴5﹣2<c<5+2,
即3<c<7,
∵三角形的周长为偶数,
∴c=5;
②∵a=c=5,
∴△ABC是等腰三角形.
18.【解答】(1)证明:∵直线AB与直线EF交于点G,
∴∠AGE=∠BGF,
又∵∠EHD+∠AGE=180°,
∴∠EHD+∠BGF=180°,
∴AB∥CD;
(2)过点P作PK∥AB,如图所示:
由(1)可知:AB∥CD,
∴AB∥PK∥CD,
∴∠PMB=∠MPK,∠PND=∠NPK,
∴∠PMB+∠PND=∠MPK+∠NPK=∠MPN,
∵PM⊥PN,
∴∠MPN=90°,
∴∠PMB+∠PND=90°,
∵PN∥EF,
∴∠EHD=∠PND,
∴∠PMB+∠EHD=90°;
(3)设∠AMQ=α,
∵MQ平分∠AMN,
∴∠AMQ=∠QMN=α,
∴∠AMN=2α,
∵PM⊥PN,∠PNM=60°,
∴∠PMN=90°﹣60°=30°,
∴∠QMP=∠QMN+∠PMN=α+30°,
∠PMB=180°﹣∠AMN﹣∠PMN=180°﹣2α﹣30°=150°﹣2α,
由(2)可知:∠PMB+∠PND=90°,
∴∠PND=90°﹣∠PMB=90°﹣(150°﹣2α)=2α﹣60°,
∵∠AMN﹣2∠PND=4°,
∴2α﹣2(2α﹣60°)=4°,
解得:α=58°,
∴∠QMP=α+30°=88°,
∵PM⊥PN,PR平分∠MPN,
∴∠MPT=45°,
∴∠PTQ=∠QMP+∠MPT=45°+88°=133°.
21世纪教育网(www.21cnjy.com)
