2025年九年级数学中考二轮复习专题:圆中切线的证明综合训练(含解析)
文档属性
| 名称 | 2025年九年级数学中考二轮复习专题:圆中切线的证明综合训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 341.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:46:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考二轮复习专题:圆中切线的证明综合训练
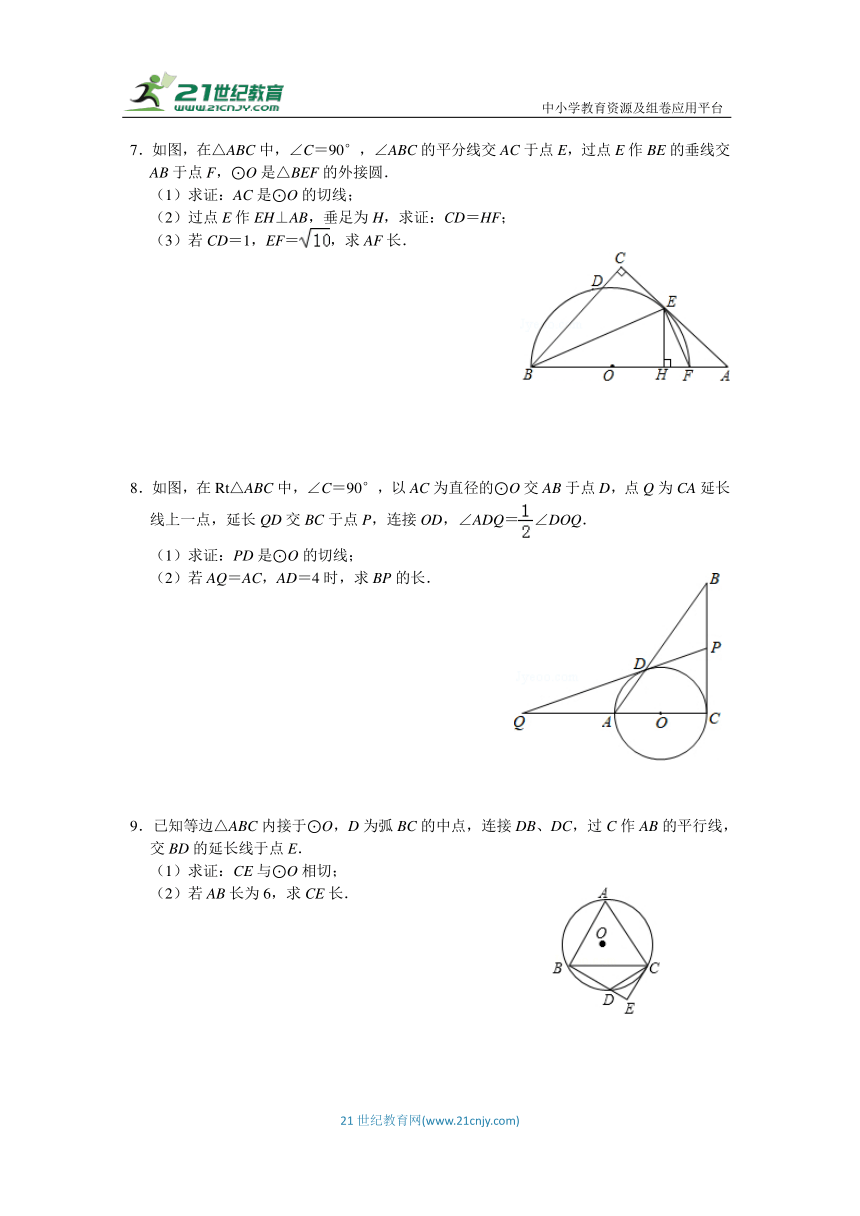
1.如图,点A、B在⊙O上,CB为⊙O的切线,AC=BC,求证:AC为⊙O的切线.
2.如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:DE是⊙O的切线.
(2)若BF=2,DH=,求⊙O的半径.
3.如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
4.如图,Rt△ABC中,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,交AC于点D,其中DE∥OC.
(1)求证:AC为⊙O的切线;
(2)若AD=,且AB、AE的长是关于x的方程x2﹣4x+k=0的两个实数根,求⊙O的半径、CD的长.
5.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AB=8,∠A=60°,求BD的长.
6.如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,在CD上有点N满足CN=CA,AN交圆O于点F,过点F的AC的平行线交CD的延长线于点M,交AB的延长线于点E
(1)求证:EM是圆O的切线;
(2)若AC:CD=5:8,AN=3,求圆O的直径长度;
(3)在(2)的条件下,直接写出FN的长度.
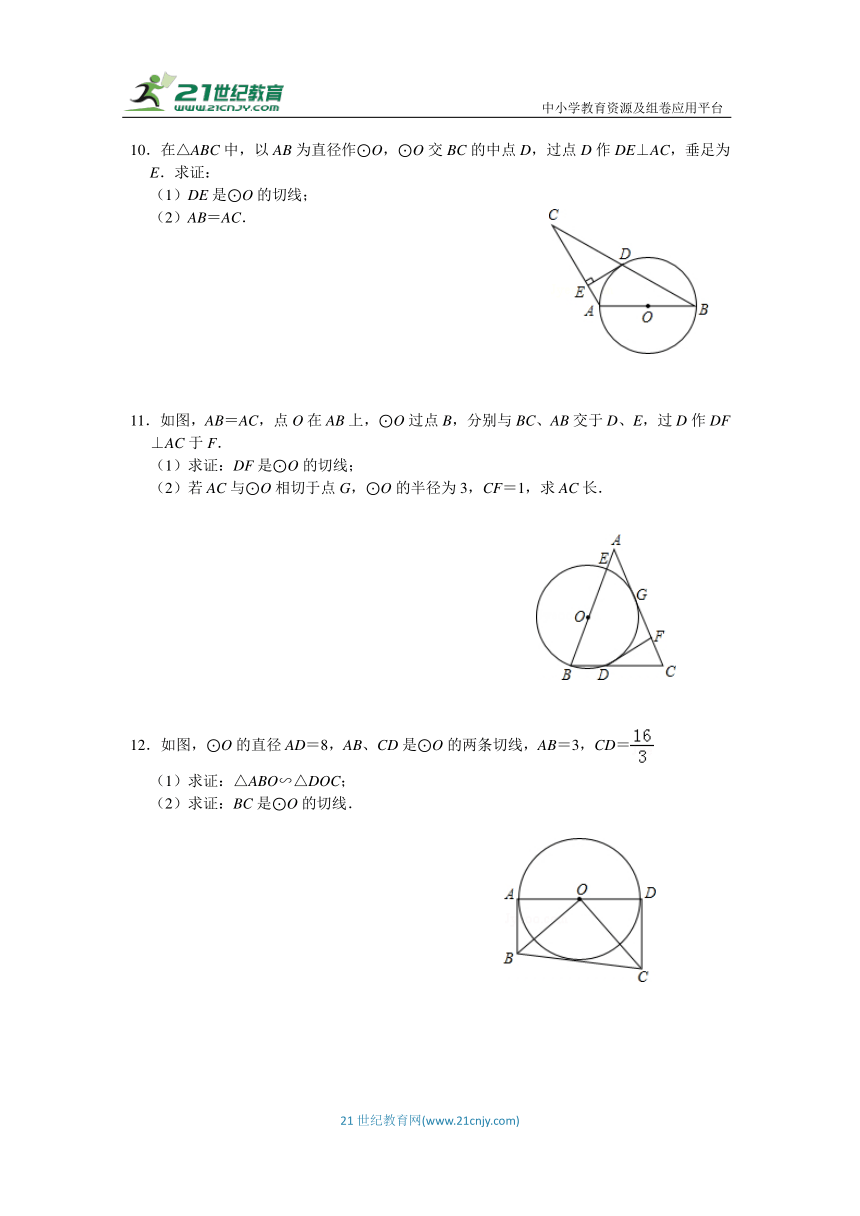
7.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EF=,求AF长.
8.如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=∠DOQ.
(1)求证:PD是⊙O的切线;
(2)若AQ=AC,AD=4时,求BP的长.
9.已知等边△ABC内接于⊙O,D为弧BC的中点,连接DB、DC,过C作AB的平行线,交BD的延长线于点E.
(1)求证:CE与⊙O相切;
(2)若AB长为6,求CE长.
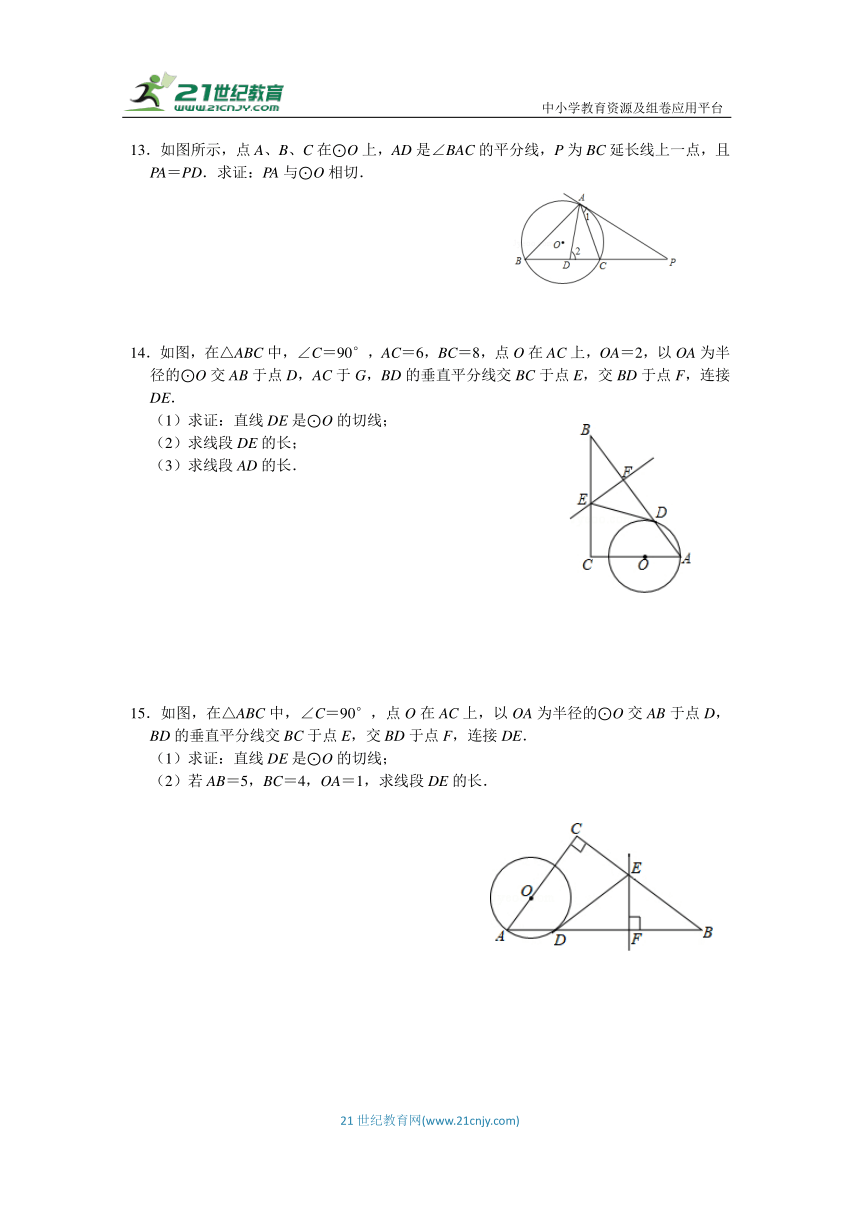
10.在△ABC中,以AB为直径作⊙O,⊙O交BC的中点D,过点D作DE⊥AC,垂足为E.求证:
(1)DE是⊙O的切线;
(2)AB=AC.
11.如图,AB=AC,点O在AB上,⊙O过点B,分别与BC、AB交于D、E,过D作DF⊥AC于F.
(1)求证:DF是⊙O的切线;
(2)若AC与⊙O相切于点G,⊙O的半径为3,CF=1,求AC长.
12.如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=
(1)求证:△ABO∽△DOC;
(2)求证:BC是⊙O的切线.
13.如图所示,点A、B、C在⊙O上,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
14.如图,在△ABC中,∠C=90°,AC=6,BC=8,点O在AC上,OA=2,以OA为半径的⊙O交AB于点D,AC于G,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求证:直线DE是⊙O的切线;
(2)求线段DE的长;
(3)求线段AD的长.
15.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求证:直线DE是⊙O的切线;
(2)若AB=5,BC=4,OA=1,求线段DE的长.
参考答案
1.【解答】证明:连接OC,如图所示:
∵点A、B在⊙O上,
∴OA=OB,
∵CB为⊙O的切线,
∴∠OBC=90°,
在△OAC和△OBC中,,
∴△OAC≌△OBC(SSS),
∴∠OAC=∠OBC=90°,
∵OA是⊙O的半径,
∴AC为⊙O的切线.
2.【解答】(1)证明:如图1,连接DF,
∵四边形ABCD为菱形,
∴AB=BC=CD=DA,AD∥BC,∠DAB=∠C,
∵BF=BE,
∴AB﹣BF=BC﹣BE,
即AF=CE,
∴△DAF≌△DCE(SAS),
∴∠DFA=∠DEC,
∵AD是⊙O的直径,
∴∠DFA=90°,
∴∠DEC=90°
∵AD∥BC,
∴∠ADE=∠DEC=90°,
∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:如图2,连接AH,
∵AD是⊙O的直径,
∴∠AHD=∠DFA=90°,
∴∠DFB=90°,
∵AD=AB,DH=,
∴DB=2DH=2,
在Rt△ADF和Rt△BDF中,
∵DF2=AD2﹣AF2,DF2=BD2﹣BF2,
∴AD2﹣AF2=DB2﹣BF2,
∴AD2﹣(AD﹣BF)2=DB2﹣BF2,
∴,
∴AD=5.
∴⊙O的半径为.
3.【解答】解:(1)∵∠ACB=90°,点B,D在⊙O上,
∴BD是⊙O的直径,∠BCE=∠BDE,
∵∠FDE=∠DCE,∠BCE+∠DCE=∠ACB=90°,
∴∠BDE+∠FDE=90°,
即∠BDF=90°,
∴DF⊥BD,
又∵BD是⊙O的直径,
∴DF是⊙O的切线.
(2)如图,∵∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=2×4=8,
∴=4,
∵点D是AC的中点,
∴,
∵BD是⊙O的直径,
∴∠DEB=90°,
∴∠DEA=180°﹣∠DEB=90°,
∴,
在Rt△BCD中,==2,
在Rt△BED中,BE===5,
∵∠FDE=∠DCE,∠DCE=∠DBE,
∴∠FDE=∠DBE,
∵∠DEF=∠BED=90°,
∴△FDE∽△DBE,
∴,即,
∴.
4.【解答】(1)证明:连接OD,如图1所示:
∵DE∥OC,
∴∠DEB=∠COB,∠DOC=∠ODE.
∵∠ODE=∠OED,
∴∠DOC=∠BOC.
∵OD=OD,OC=OC,
∴∠CDO=∠CBO=90°.
∴∠ODA=90°.
∴AC是⊙O的切线.
(2)解:∵AB、AE的长是关于x的方程x2﹣4x+k=0的两个实数根,
∴AB AE=k,
如图2,连接DB,
∵EB是⊙O的直径,
∴∠EDB=90°,
∴∠DEB+∠EBD=90°,
∵AD是⊙O的切线,
∴∠ADO=90°,
∴∠ADE+∠EDO=90°,
∵OD=OE,
∴∠DEO=∠EDO,
∴∠ADE=∠EBD,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴,
∴AD2=AE AB,
∵,
∴,
∴x2﹣4x+3=0,
∴x1=3,x2=1,
∴AE=1,AB=3,
∴BE=AB﹣AE=3﹣1=2,
∴⊙O的半径为1.
∵∠B=90°,AC是⊙O的切线,
∴DC=BC,
设CD=x,在Rt△ABC中,AC=x+,AB=3,BC=x,
∴,
解得:x=.
∴.
5.【解答】(1)证明:连接OD,AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵AB=AC,AD⊥BC,
∴∠BAD=∠BAC=30°,
∴BD=AB==4.
6.【解答】(1)证明:连接FO,
∵CN=AC,
∴∠CAN=∠CNA,
∵AC∥ME,
∴∠CAN=∠MFN,
∵∠CAN=∠FNM,
∴∠MFN=∠FNM=∠CAN,
∵CD⊥AB,
∴∠HAN+∠HNA=90°,
∵AO=FO,
∴∠OAF=∠OFA,
∴∠OFA+∠MFN=90°,即∠MFO=90°,
∴EM是圆O的切线;
(2)解:连接OC,
∵AC:CD=5:8,设AC=5a,则CD=8a,
∵CD⊥AB,
∴CH=DH=4a,AH=3a,
∵CA=CN,
∴NH=a,
∴AN===a=3,
∴a=3,AH=3a=9,CH=4a=12,
设圆的半径为r,则OH=r﹣9,
在Rt△OCH中,OC=r,CH=12,OH=r﹣9,
由OC2=CH2+OH2得r2=122+(r﹣9)2,
解得:r=,
∴圆O的直径为25;
(3)∵CH=DH=12,
∴CD=24,
∵AC:CD=5:8,
∴CN=AC=15,
∴DN=24﹣15=9,
∵∠AFD=∠ACD,∠FND=∠CNA,
∴△FND∽△CNA,
∴,
∵AN=3,
∴,
∴FN=.
7.【解答】证明:(1)如图1,连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF是圆O的直径.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)解:如图2,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
∴△CDE≌△HFE(AAS),
∴CD=HF.
(3)解:由(2)得CD=HF,又CD=1,
∴HF=1,
∵EF⊥BE,
∴∠BEF=90°,
∴∠EHF=∠BEF=90°,
∵∠EFH=∠BFE,
∴△EHF∽△BEF,
∴,即 ,
∴BF=10,
∴OE=BF=5,OH=5﹣1=4,
∴Rt△OHE中,cos∠EOA=,
∴Rt△EOA中,cos∠EOA=,
∴,
∴OA=,
∴AF=.
8.【解答】解:(1)连接DC,
∵=,
∴∠DCA=∠DOA,
∵∠ADQ=∠DOQ,
∴∠DCA=∠ADQ,
∵AC是⊙O的直径,
∴∠ADC=90°
∴∠DCA+∠DAC=90°,
∵∠ADQ+∠DAC=90°,∠ADO=∠DAO,
∴∠ADQ+∠ADO=90°,
∴DP是⊙O切线;
(2)∵∠C=90°,OC为半径.
∴PC是⊙O切线,
∴PD=PC,
连接OP,
∴∠DPO=∠CPO,
∴OP⊥CD,
∴OP∥AD,
∵AQ=AC=2OA,
∴==,
∵AD=4,
∴OP=6,
∵OP是△ACB的中位线,
∴AB=12,
∵CD⊥AB,∠C=90°,
∴BC2=BD BA=96,
∴BC=4,
∴BP=2.
9.【解答】(1)证明:连接OC,OB,
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,
∵AB∥CE,
∴∠BCE=∠ABC=60°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴∠OCE=∠OCB+∠BCE=30°+60°=90°,
∴CE与⊙O相切;
(2)∵四边形ABDC是圆的内接四边形,
∴∠A+∠BDC=180°,
∴∠BDC=120°,
∵D为弧BC的中点,
∴∠DBC=∠BCD=30°,
∴∠BEC=180°﹣∠EBC﹣∠BCE=90°,
∵AB=BC=6,
∴.
10.【解答】证明:(1)连接OD,
∵O是AB的中点,D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵D是BC的中点,
∴AD垂直平分BC,
∴AB=AC.
11.【解答】(1)证明:连接OD,
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
则DF为圆O的切线;
(2)解:连接OG,
∵AC与圆O相切,
∴OG⊥AC,
∴∠OGF=∠GFD=∠ODF=90°,且OG=OD,
∴四边形ODFG为边长为3的正方形,
设AB=AC=x,则有AG=x﹣3﹣1=x﹣4,AO=x﹣3,
在Rt△AOG中,利用勾股定理得:AO2=AG2+OG2,即(x﹣3)2=(x﹣4)2+32,
解得:x=8,
则AC=8.
12.【解答】(1)证明:∵AD、BC是⊙O的两条切线,
∴∠OAD=∠OBC=90°,
∵AB=3,CD=,AD=8,
∴OA=OD=4,
∴=,==,
∴=,
∴△ABO∽△DOC;
(3)证明:过O作OE⊥BC,交BC于点E,
∵△ABO∽△DOC,
∴∠ABO=∠COD,
∵∠ABO+∠AOB=90°,
∴∠AOB+∠COD=90°,
∵∠BOC=90°,
∵∠OBE=∠CBO,∠OEB=∠BOC=90°,
∴△BOE∽△BCO,
∴=,
由∵OB==5,OC==,
∴BC==,
∴=,
∴OE=4=OA,
∴BC是⊙O切线.
13.【解答】解:连接AO并延长交⊙O于点E,连接BE,
∵AE为⊙O的直径,
∴∠EBA=90°,
∵PA=PD,
∴∠1+∠CAD=∠2,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠ABD+∠BAD=∠2,
∴∠1=∠ABC,
∵∠CBE=∠EAC,∠ABC+∠CBE=90°,
∴∠CAE+∠1=90°,
∴PA与⊙O相切.
14.【解答】(1)证明:连接OD,
∵EF垂直平分BD,
∴EB=ED,
∴∠B=∠EDB,
∵OA=OD,
∴∠ODA=∠A,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠EDB+∠ODA=90°,
∴∠ODE=90°,
∴OD⊥DE于D,
∴DE是⊙O的切线.
(2)解:连接OE,
设DE=BE=x,CE=8﹣x,
∵OE2=DE2+OD2=EC2+OC2,
∴42+(8﹣x)2=22+x2,
解得x=4.75,
∴DE=4.75.
(3)连结BG,DG.
∵AG是直径,
∴GD⊥AB,
由S△ABG=AG BC=AB GD可得:4×8=10×GD,
∴GD=3.2,
∴AD==2.4,
15.【解答】(1)证明:连接OD,如图,
∵EF垂直平分BD,
∴ED=EB,
∴∠EDB=∠B,
∵OA=OD,
∴∠A=∠ODA,
∵∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴直线DE是⊙O的切线;
(2)解:作OH⊥AD于H,如图,则AH=DH,
在Rt△OAB中,sinA==,
在Rt△OAH中,sinA==,
∴OH=,
∴AH==,
∴AD=2AH=,
∴BD=5﹣=,
∴BF=BD=,
在Rt△ABC中,cosB=,
在Rt△BEF中,cosB==,
∴BE=×=,
∴线段DE的长为.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考二轮复习专题:圆中切线的证明综合训练
1.如图,点A、B在⊙O上,CB为⊙O的切线,AC=BC,求证:AC为⊙O的切线.
2.如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:DE是⊙O的切线.
(2)若BF=2,DH=,求⊙O的半径.
3.如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
4.如图,Rt△ABC中,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,交AC于点D,其中DE∥OC.
(1)求证:AC为⊙O的切线;
(2)若AD=,且AB、AE的长是关于x的方程x2﹣4x+k=0的两个实数根,求⊙O的半径、CD的长.
5.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AB=8,∠A=60°,求BD的长.
6.如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,在CD上有点N满足CN=CA,AN交圆O于点F,过点F的AC的平行线交CD的延长线于点M,交AB的延长线于点E
(1)求证:EM是圆O的切线;
(2)若AC:CD=5:8,AN=3,求圆O的直径长度;
(3)在(2)的条件下,直接写出FN的长度.
7.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EF=,求AF长.
8.如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=∠DOQ.
(1)求证:PD是⊙O的切线;
(2)若AQ=AC,AD=4时,求BP的长.
9.已知等边△ABC内接于⊙O,D为弧BC的中点,连接DB、DC,过C作AB的平行线,交BD的延长线于点E.
(1)求证:CE与⊙O相切;
(2)若AB长为6,求CE长.
10.在△ABC中,以AB为直径作⊙O,⊙O交BC的中点D,过点D作DE⊥AC,垂足为E.求证:
(1)DE是⊙O的切线;
(2)AB=AC.
11.如图,AB=AC,点O在AB上,⊙O过点B,分别与BC、AB交于D、E,过D作DF⊥AC于F.
(1)求证:DF是⊙O的切线;
(2)若AC与⊙O相切于点G,⊙O的半径为3,CF=1,求AC长.
12.如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=
(1)求证:△ABO∽△DOC;
(2)求证:BC是⊙O的切线.
13.如图所示,点A、B、C在⊙O上,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
14.如图,在△ABC中,∠C=90°,AC=6,BC=8,点O在AC上,OA=2,以OA为半径的⊙O交AB于点D,AC于G,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求证:直线DE是⊙O的切线;
(2)求线段DE的长;
(3)求线段AD的长.
15.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求证:直线DE是⊙O的切线;
(2)若AB=5,BC=4,OA=1,求线段DE的长.
参考答案
1.【解答】证明:连接OC,如图所示:
∵点A、B在⊙O上,
∴OA=OB,
∵CB为⊙O的切线,
∴∠OBC=90°,
在△OAC和△OBC中,,
∴△OAC≌△OBC(SSS),
∴∠OAC=∠OBC=90°,
∵OA是⊙O的半径,
∴AC为⊙O的切线.
2.【解答】(1)证明:如图1,连接DF,
∵四边形ABCD为菱形,
∴AB=BC=CD=DA,AD∥BC,∠DAB=∠C,
∵BF=BE,
∴AB﹣BF=BC﹣BE,
即AF=CE,
∴△DAF≌△DCE(SAS),
∴∠DFA=∠DEC,
∵AD是⊙O的直径,
∴∠DFA=90°,
∴∠DEC=90°
∵AD∥BC,
∴∠ADE=∠DEC=90°,
∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:如图2,连接AH,
∵AD是⊙O的直径,
∴∠AHD=∠DFA=90°,
∴∠DFB=90°,
∵AD=AB,DH=,
∴DB=2DH=2,
在Rt△ADF和Rt△BDF中,
∵DF2=AD2﹣AF2,DF2=BD2﹣BF2,
∴AD2﹣AF2=DB2﹣BF2,
∴AD2﹣(AD﹣BF)2=DB2﹣BF2,
∴,
∴AD=5.
∴⊙O的半径为.
3.【解答】解:(1)∵∠ACB=90°,点B,D在⊙O上,
∴BD是⊙O的直径,∠BCE=∠BDE,
∵∠FDE=∠DCE,∠BCE+∠DCE=∠ACB=90°,
∴∠BDE+∠FDE=90°,
即∠BDF=90°,
∴DF⊥BD,
又∵BD是⊙O的直径,
∴DF是⊙O的切线.
(2)如图,∵∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=2×4=8,
∴=4,
∵点D是AC的中点,
∴,
∵BD是⊙O的直径,
∴∠DEB=90°,
∴∠DEA=180°﹣∠DEB=90°,
∴,
在Rt△BCD中,==2,
在Rt△BED中,BE===5,
∵∠FDE=∠DCE,∠DCE=∠DBE,
∴∠FDE=∠DBE,
∵∠DEF=∠BED=90°,
∴△FDE∽△DBE,
∴,即,
∴.
4.【解答】(1)证明:连接OD,如图1所示:
∵DE∥OC,
∴∠DEB=∠COB,∠DOC=∠ODE.
∵∠ODE=∠OED,
∴∠DOC=∠BOC.
∵OD=OD,OC=OC,
∴∠CDO=∠CBO=90°.
∴∠ODA=90°.
∴AC是⊙O的切线.
(2)解:∵AB、AE的长是关于x的方程x2﹣4x+k=0的两个实数根,
∴AB AE=k,
如图2,连接DB,
∵EB是⊙O的直径,
∴∠EDB=90°,
∴∠DEB+∠EBD=90°,
∵AD是⊙O的切线,
∴∠ADO=90°,
∴∠ADE+∠EDO=90°,
∵OD=OE,
∴∠DEO=∠EDO,
∴∠ADE=∠EBD,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴,
∴AD2=AE AB,
∵,
∴,
∴x2﹣4x+3=0,
∴x1=3,x2=1,
∴AE=1,AB=3,
∴BE=AB﹣AE=3﹣1=2,
∴⊙O的半径为1.
∵∠B=90°,AC是⊙O的切线,
∴DC=BC,
设CD=x,在Rt△ABC中,AC=x+,AB=3,BC=x,
∴,
解得:x=.
∴.
5.【解答】(1)证明:连接OD,AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵AB=AC,AD⊥BC,
∴∠BAD=∠BAC=30°,
∴BD=AB==4.
6.【解答】(1)证明:连接FO,
∵CN=AC,
∴∠CAN=∠CNA,
∵AC∥ME,
∴∠CAN=∠MFN,
∵∠CAN=∠FNM,
∴∠MFN=∠FNM=∠CAN,
∵CD⊥AB,
∴∠HAN+∠HNA=90°,
∵AO=FO,
∴∠OAF=∠OFA,
∴∠OFA+∠MFN=90°,即∠MFO=90°,
∴EM是圆O的切线;
(2)解:连接OC,
∵AC:CD=5:8,设AC=5a,则CD=8a,
∵CD⊥AB,
∴CH=DH=4a,AH=3a,
∵CA=CN,
∴NH=a,
∴AN===a=3,
∴a=3,AH=3a=9,CH=4a=12,
设圆的半径为r,则OH=r﹣9,
在Rt△OCH中,OC=r,CH=12,OH=r﹣9,
由OC2=CH2+OH2得r2=122+(r﹣9)2,
解得:r=,
∴圆O的直径为25;
(3)∵CH=DH=12,
∴CD=24,
∵AC:CD=5:8,
∴CN=AC=15,
∴DN=24﹣15=9,
∵∠AFD=∠ACD,∠FND=∠CNA,
∴△FND∽△CNA,
∴,
∵AN=3,
∴,
∴FN=.
7.【解答】证明:(1)如图1,连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF是圆O的直径.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)解:如图2,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
∴△CDE≌△HFE(AAS),
∴CD=HF.
(3)解:由(2)得CD=HF,又CD=1,
∴HF=1,
∵EF⊥BE,
∴∠BEF=90°,
∴∠EHF=∠BEF=90°,
∵∠EFH=∠BFE,
∴△EHF∽△BEF,
∴,即 ,
∴BF=10,
∴OE=BF=5,OH=5﹣1=4,
∴Rt△OHE中,cos∠EOA=,
∴Rt△EOA中,cos∠EOA=,
∴,
∴OA=,
∴AF=.
8.【解答】解:(1)连接DC,
∵=,
∴∠DCA=∠DOA,
∵∠ADQ=∠DOQ,
∴∠DCA=∠ADQ,
∵AC是⊙O的直径,
∴∠ADC=90°
∴∠DCA+∠DAC=90°,
∵∠ADQ+∠DAC=90°,∠ADO=∠DAO,
∴∠ADQ+∠ADO=90°,
∴DP是⊙O切线;
(2)∵∠C=90°,OC为半径.
∴PC是⊙O切线,
∴PD=PC,
连接OP,
∴∠DPO=∠CPO,
∴OP⊥CD,
∴OP∥AD,
∵AQ=AC=2OA,
∴==,
∵AD=4,
∴OP=6,
∵OP是△ACB的中位线,
∴AB=12,
∵CD⊥AB,∠C=90°,
∴BC2=BD BA=96,
∴BC=4,
∴BP=2.
9.【解答】(1)证明:连接OC,OB,
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,
∵AB∥CE,
∴∠BCE=∠ABC=60°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴∠OCE=∠OCB+∠BCE=30°+60°=90°,
∴CE与⊙O相切;
(2)∵四边形ABDC是圆的内接四边形,
∴∠A+∠BDC=180°,
∴∠BDC=120°,
∵D为弧BC的中点,
∴∠DBC=∠BCD=30°,
∴∠BEC=180°﹣∠EBC﹣∠BCE=90°,
∵AB=BC=6,
∴.
10.【解答】证明:(1)连接OD,
∵O是AB的中点,D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵D是BC的中点,
∴AD垂直平分BC,
∴AB=AC.
11.【解答】(1)证明:连接OD,
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
则DF为圆O的切线;
(2)解:连接OG,
∵AC与圆O相切,
∴OG⊥AC,
∴∠OGF=∠GFD=∠ODF=90°,且OG=OD,
∴四边形ODFG为边长为3的正方形,
设AB=AC=x,则有AG=x﹣3﹣1=x﹣4,AO=x﹣3,
在Rt△AOG中,利用勾股定理得:AO2=AG2+OG2,即(x﹣3)2=(x﹣4)2+32,
解得:x=8,
则AC=8.
12.【解答】(1)证明:∵AD、BC是⊙O的两条切线,
∴∠OAD=∠OBC=90°,
∵AB=3,CD=,AD=8,
∴OA=OD=4,
∴=,==,
∴=,
∴△ABO∽△DOC;
(3)证明:过O作OE⊥BC,交BC于点E,
∵△ABO∽△DOC,
∴∠ABO=∠COD,
∵∠ABO+∠AOB=90°,
∴∠AOB+∠COD=90°,
∵∠BOC=90°,
∵∠OBE=∠CBO,∠OEB=∠BOC=90°,
∴△BOE∽△BCO,
∴=,
由∵OB==5,OC==,
∴BC==,
∴=,
∴OE=4=OA,
∴BC是⊙O切线.
13.【解答】解:连接AO并延长交⊙O于点E,连接BE,
∵AE为⊙O的直径,
∴∠EBA=90°,
∵PA=PD,
∴∠1+∠CAD=∠2,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠ABD+∠BAD=∠2,
∴∠1=∠ABC,
∵∠CBE=∠EAC,∠ABC+∠CBE=90°,
∴∠CAE+∠1=90°,
∴PA与⊙O相切.
14.【解答】(1)证明:连接OD,
∵EF垂直平分BD,
∴EB=ED,
∴∠B=∠EDB,
∵OA=OD,
∴∠ODA=∠A,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠EDB+∠ODA=90°,
∴∠ODE=90°,
∴OD⊥DE于D,
∴DE是⊙O的切线.
(2)解:连接OE,
设DE=BE=x,CE=8﹣x,
∵OE2=DE2+OD2=EC2+OC2,
∴42+(8﹣x)2=22+x2,
解得x=4.75,
∴DE=4.75.
(3)连结BG,DG.
∵AG是直径,
∴GD⊥AB,
由S△ABG=AG BC=AB GD可得:4×8=10×GD,
∴GD=3.2,
∴AD==2.4,
15.【解答】(1)证明:连接OD,如图,
∵EF垂直平分BD,
∴ED=EB,
∴∠EDB=∠B,
∵OA=OD,
∴∠A=∠ODA,
∵∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴直线DE是⊙O的切线;
(2)解:作OH⊥AD于H,如图,则AH=DH,
在Rt△OAB中,sinA==,
在Rt△OAH中,sinA==,
∴OH=,
∴AH==,
∴AD=2AH=,
∴BD=5﹣=,
∴BF=BD=,
在Rt△ABC中,cosB=,
在Rt△BEF中,cosB==,
∴BE=×=,
∴线段DE的长为.
21世纪教育网(www.21cnjy.com)
同课章节目录
