2025年九年级数学三轮冲刺训练圆中切线的判定和性质综合练习(含解析)
文档属性
| 名称 | 2025年九年级数学三轮冲刺训练圆中切线的判定和性质综合练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:44:23 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学三轮冲刺训练圆中切线的判定和性质综合练习
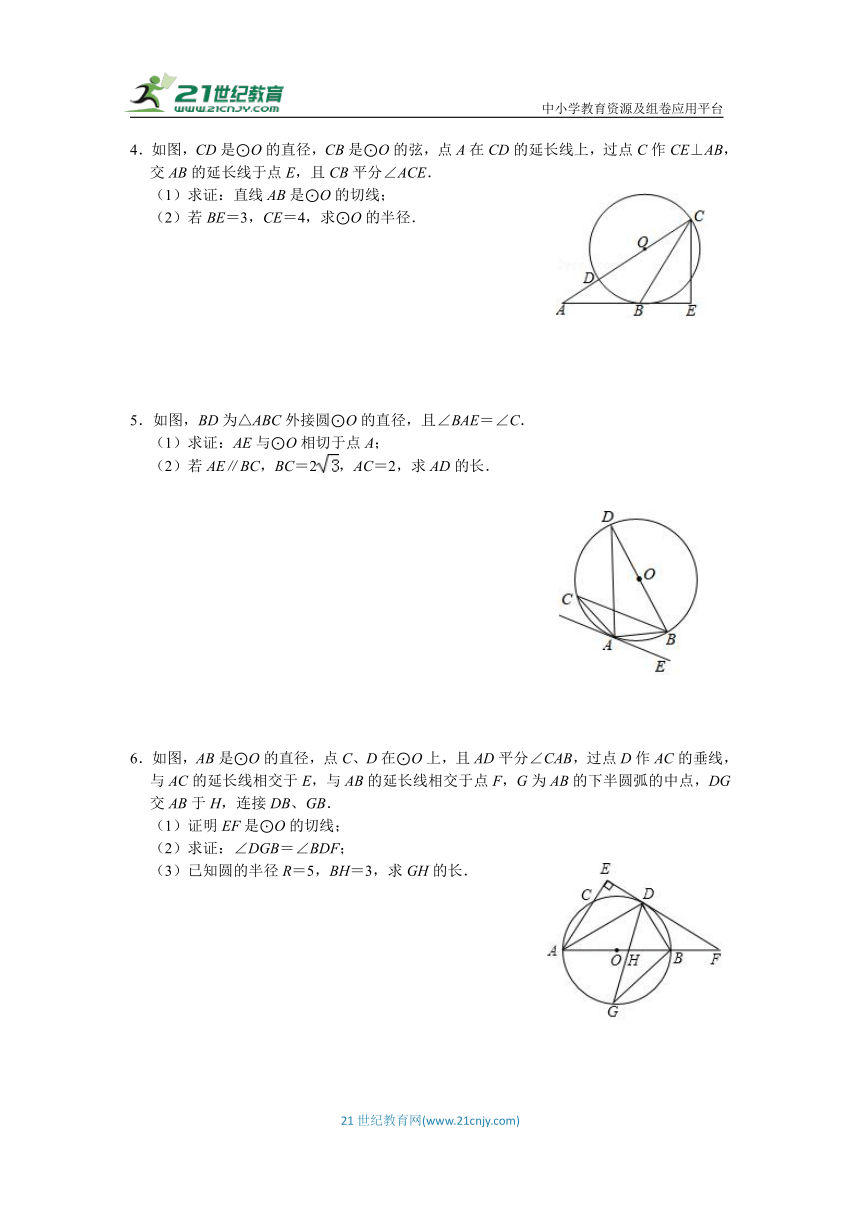
1.如图,AB是⊙O的直径,D是弦AC延长线上一点,且AB=BD,DB的延长线交⊙O于点E,过点C作CF⊥BD,垂足为点F.
(1)CF与⊙O有怎样的位置关系?请说明理由;
(2)若BF+CF=6,⊙O的半径为5,求BE的长度.
2.如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
3.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线;
(2)若DE+EA=8,AF=16,求⊙O的半径.
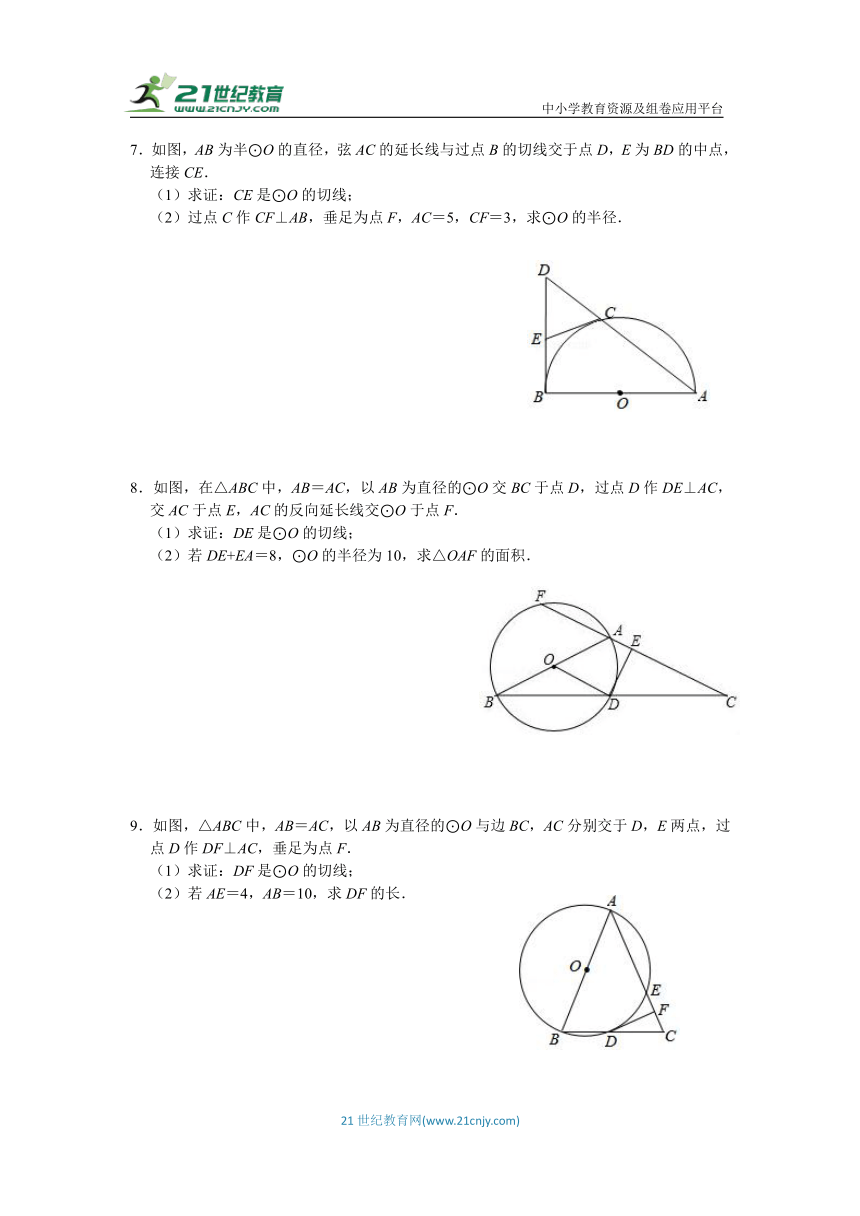
4.如图,CD是⊙O的直径,CB是⊙O的弦,点A在CD的延长线上,过点C作CE⊥AB,交AB的延长线于点E,且CB平分∠ACE.
(1)求证:直线AB是⊙O的切线;
(2)若BE=3,CE=4,求⊙O的半径.
5.如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2,AC=2,求AD的长.
6.如图,AB是⊙O的直径,点C、D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
(1)证明EF是⊙O的切线;
(2)求证:∠DGB=∠BDF;
(3)已知圆的半径R=5,BH=3,求GH的长.
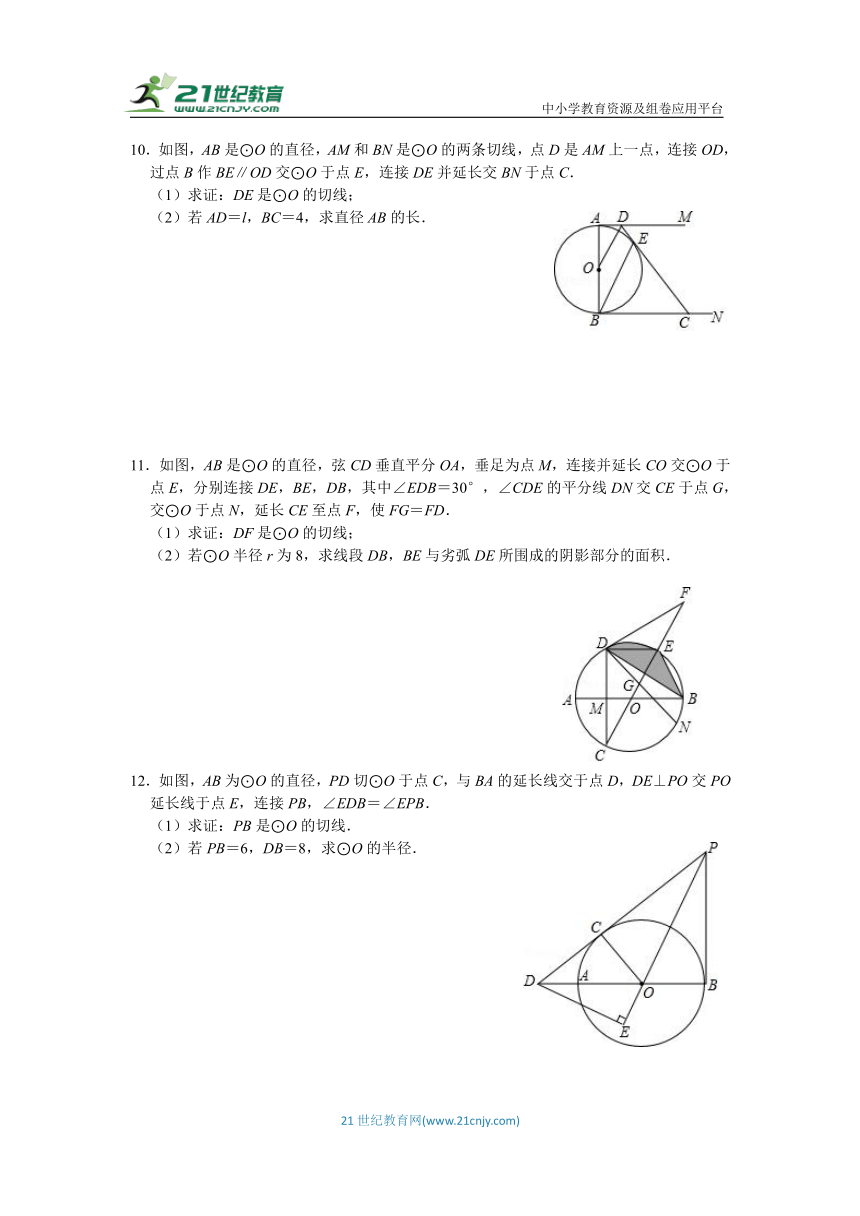
7.如图,AB为半⊙O的直径,弦AC的延长线与过点B的切线交于点D,E为BD的中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)过点C作CF⊥AB,垂足为点F,AC=5,CF=3,求⊙O的半径.
8.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线;
(2)若DE+EA=8,⊙O的半径为10,求△OAF的面积.
9.如图,△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)若AE=4,AB=10,求DF的长.
10.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,连接OD,过点B作BE∥OD交⊙O于点E,连接DE并延长交BN于点C.
(1)求证:DE是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.
11.如图,AB是⊙O的直径,弦CD垂直平分OA,垂足为点M,连接并延长CO交⊙O于点E,分别连接DE,BE,DB,其中∠EDB=30°,∠CDE的平分线DN交CE于点G,交⊙O于点N,延长CE至点F,使FG=FD.
(1)求证:DF是⊙O的切线;
(2)若⊙O半径r为8,求线段DB,BE与劣弧DE所围成的阴影部分的面积.
12.如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是⊙O的切线.
(2)若PB=6,DB=8,求⊙O的半径.
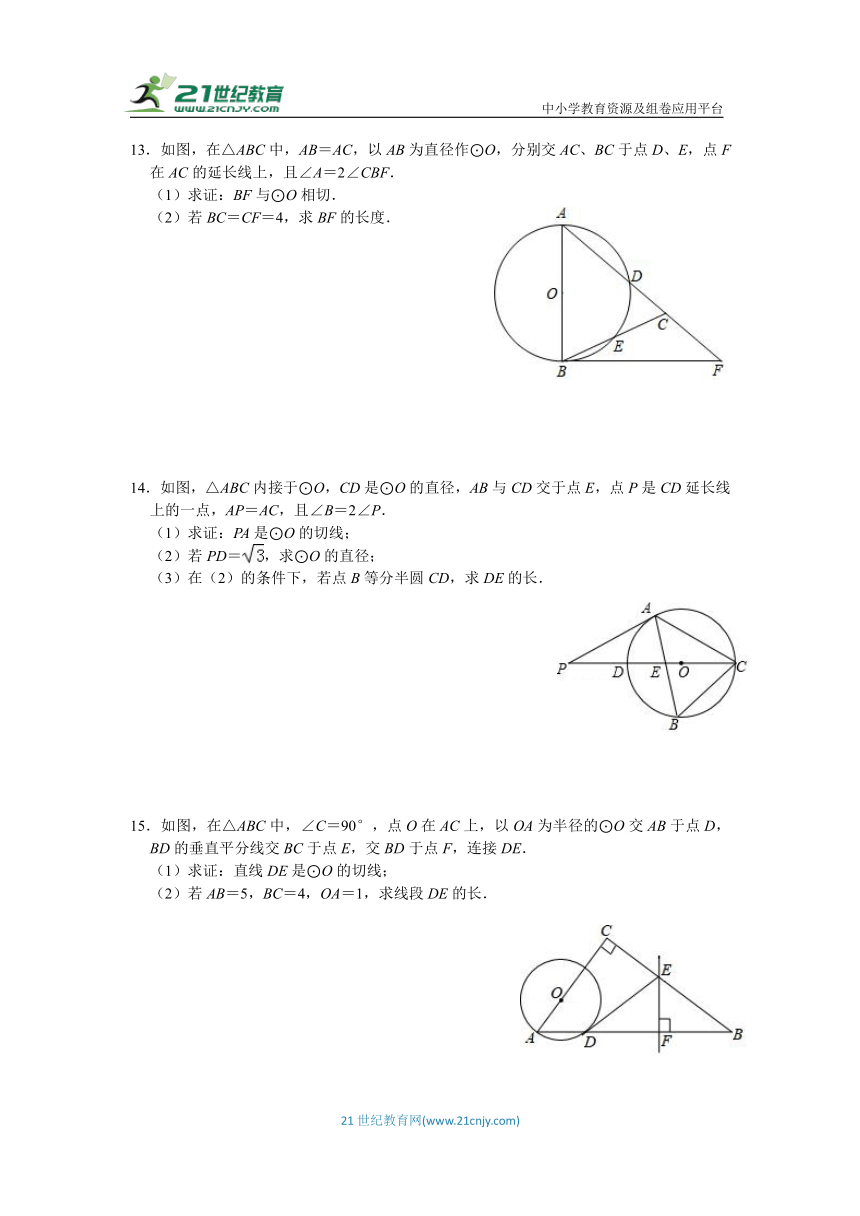
13.如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交AC、BC于点D、E,点F在AC的延长线上,且∠A=2∠CBF.
(1)求证:BF与⊙O相切.
(2)若BC=CF=4,求BF的长度.
14.如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径;
(3)在(2)的条件下,若点B等分半圆CD,求DE的长.
15.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求证:直线DE是⊙O的切线;
(2)若AB=5,BC=4,OA=1,求线段DE的长.
参考答案
1.【解答】解:(1)CF与⊙O相切.连接BC,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=BD,
∴∠A=∠D,
又∵OA=OB,
∴OC是△ABD的中位线.
∴OC∥BD,
∴∠OCF=∠CFD=90°,
即CF⊥OC.
∴CF与⊙O相切;
(2)过点O作OH⊥BE于点H,则∠OCF=∠CFH=∠OHB=90°,
∴四边形OCFH是矩形,
∴OC=FH,OH=CF,
设BH=x,
∵OC=5,BF+CF=6,
∴BF=5﹣x,OH=CF=6﹣(5﹣x)=x+1,
在Rt△BOH中,由勾股定理知:
BH2+OH2=OB2,即x2+(x+1)2=52,
解得x1=3,x2=﹣4(不合题意,舍去).
∴BH=3,
∵OH⊥BE,
∴BH=EH=BE,
∴BE=2BH=2×3=6.
2.【解答】(1)证明:连接OD,作OG⊥AB于G,如图1所示:
则∠OGB=90°,
∵△ABC为等边三角形,
∴∠OCD=∠OBG=∠ABC=60°,
∵O为BC的中点,
∴OB=OC,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=90°=∠OGB,
在△OBG和△OCD中,,
∴△OBG≌△OCD(AAS),
∴OG=OD,∴AB与⊙O相切;
(2)解:连接OA、OM,作OH⊥FM于H,如图2所示:
则∠OHB=90°,FH=MH,
∵CE=AC,AC=BC,
∴CE=BC,
∴∠CBE=∠CEB=∠ACB=30°,
∴∠ABE=∠ABC+∠CBE=90°,
∵∠OGB=90°,
∴四边形OHBG是矩形,
∴OH=BG,
∵△ABC是等边三角形,O为BC的中点,
∴OB=BC=AB=2,
∵∠BOG=90°﹣60°=30°,
∴OH=BG=OB=1,OG=BG=,
在Rt△OMH中,OM=OG=,OH=1,
∴MH==,
∴FM=2MH=2.
3.【解答】(1)证明:∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE⊥AC,OD是半径,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
∴AH=AF=8,
设AE=x.
∵DE+AE=8,
∴OH=DE=8﹣x,OA=OD=HE=AH+AE=8+x,
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即82+(8﹣x)2=(8+x)2,
解得:x=2,
∴OA=8+2=10.
∴⊙O的半径为10.
4.【解答】解:(1)连接OB,
∵OC=OB,
∴∠OCB=∠OBC,
∵CB平分∠ACE,
∴∠OCB=∠ECB,
∴∠OBC=∠BCE,
∴OB∥CE,
∵CE⊥AB,
∴OB⊥AE,
∴直线AB是⊙O的切线;
(2)连接DB,
∵∠E=90°,BE=3,CE=4,
∴BC=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠DBC=∠E,
∵∠DCB=∠BCE,
∴△BCD∽△ECB,
∴,
∴=,
∴CD=,
∴⊙O的半径=.
5.【解答】解:(1)连接AO并延长交⊙O于点F,连接BF,
则AF为直径,∠ABF=90°,
∵,
∴∠ACB=∠F,
∵∠BAE=∠ACB,
∴∠BAE=∠F,
∵∠FAB+∠F=90°,
∴∠FAB+∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
(2)连接OC,
∵AE∥BC,
∴∠BAE=∠ABC,
∵∠BAE=∠ACB,
∴∠ACB=∠ABC,
∴AC=AB=2,
∴∠AOC=∠AOB,
∵OC=OB,
∴OA⊥BC,
∴CH=BH=BC=,
在Rt△ABH中,
AH==1,
在Rt△OBH中,设OB=r,
∵OH2+BH2=OB2,
∴(r﹣1)2+()2=r2,
解得:r=2,
∴DB=2r=4,
在Rt△ABD中,AD===,
∴AD的长为.
6.【解答】解:(1)证明:连接OD,
∵OA=OD,
∴∠OAD=∠ODA
又∵AD平分∠BAC,
∴∠OAD=∠CAD
∴∠ODA=∠CAD,
∴OD∥AE,
又∵EF⊥AE,
∴OD⊥EF,
∴EF是⊙O的切线
(2)∵AB是⊙O的直径,
∴∠ADB=90°
∴∠DAB+∠OBD=90°
由(1)得,EF是⊙O的切线,
∴∠ODF=90°
∴∠BDF+∠ODB=90°
∵OD=OB,
∴∠ODB=∠OBD
∴∠DAB=∠BDF
又∠DAB=∠DGB
∴∠DGB=∠BDF
(3)连接OG,
∵G是半圆弧中点,
∴∠BOG=90°
在Rt△OGH中,OG=5,OH=OB﹣BH=5﹣3=2.
∴GH==
7.【解答】(1)证明:连接CO、EO、BC,
∵BD是⊙O的切线,
∴∠ABD=90°,
∵AB是直径,
∴∠BCA=∠BCD=90°,
∵Rt△BCD中,E是BD的中点,
∴CE=BE=ED,
∵OC=OB,OE=OE,
则△EBO≌△ECO(SSS),
∴∠ECO=∠EBO=90°,
∵点C在圆上,
∴CE是⊙O的切线;
(2)解:解法一:Rt△ACF中,∵AC=5,CF=3,
∴AF=4,
设圆O的半径为r,则OF=4﹣r,
由勾股定理得:CF2+OF2=CO2,
即32+(4﹣r)2=r2,r=;
解法二:Rt△ACF中,∵AC=5,CF=3,
∴AF=4,
设BF=x,
由勾股定理得:BC2=x2+32,
BC2+AC2=AB2,
x2+32+52=(x+4)2,
x=,
则r==,
则⊙O的半径为.
8.【解答】(1)证明:∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE⊥AC,OD是半径,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=8,OD=10,
∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2,
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,
解得x1=8,x2=﹣6(不合题意,舍去).
∴AH=8,OH=6,
∵OH⊥AF,
∴AH=FH=AF,
∴AF=2AH=2×8=16
∴△OAF的面积=×16×6=48.
9.【解答】(1)证明:如图,连接OD,作OG⊥AC于点G,
∵OB=OD,
∴∠ODB=∠B,
又∵AB=AC,
∴∠C=∠B,
∴∠ODB=∠C,
∵DF⊥AC,
∴∠DFC=90°,
∴∠ODF=∠DFC=90°,
∴DF是⊙O的切线;
(2)连接AD,BE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BD=CD,
∵AE=4,AB=10,
∴BE=2,
∵DF⊥AC,
∴DF∥BE,
∴DF=BE=.
10.【解答】(1)证明:连接OE,
∵OA=OE=OB,
∴∠OBE=∠PEB,
∵OD∥BE,
∴∠AOD=∠OBE,∠OEB=∠DOE,
∴∠AOD=∠EOD,
在△AOD和△EOD中
∴△AOD≌△EOD,
∴∠OAD=∠OED,
∵AM是⊙O的切线,
∴∠OAD=90°,
∴∠OED=90°,
即OE⊥DE,
∵OE为⊙O半径,
∴DE是⊙O的切线;
(2)解:
过D作DH⊥BC于H,
∵AM和BN是⊙O的两条切线,
∴∠DAB=∠ABH=∠DHB=90°,
∴四边形ABHD是矩形,
∴AB=DH,AD=BH,
∵AD=l,BC=4,
∴BH=1,CH=4﹣1=3,
∵AM和BN是⊙O的两条切线,DE切⊙O于E,AD=1,BC=4,
∴DE=AD=1,BC=CE=4,
∴DC=1+4=5,
在Rt△DHC中,由勾股定理得:DH===4,
即AB=4.
11.【解答】(1)证明:连接OD,
∵CD垂直平分OA,
∴OM=OA=OD,
∴∠ODC=30°,
∵CE为⊙O的直径,
∴∠CDE=90°,
∵DN平分∠CDE,
∴∠CDN=45°,
∴∠ODN=45°﹣30°=15°,
∵OD=OC,
∴∠DCO=∠ODC=30°,
∴∠FGD=45°+30°=75°,
∵FD=FG,
∴∠FDG=∠FGD=75°,
∴∠ODF=∠ODN+∠FDG=15°+75°=90°,
∴DF是⊙O的切线;
(2)解:∵∠EDB=30°,
∴∠EOB=60°,
Rt△CDE中,∠DEC=60°,
∴∠DEC=∠EOB=60°,
∴DE∥AB,
∴S△DOE=S△ODE,
∴S阴影=S扇形ODE==;
答:线段DB,BE与劣弧DE所围成的阴影部分的面积是,
12.【解答】解:(1)∵DE⊥PE,
∴∠E=90°,
∵∠EDB=∠EPB,∠DOE=∠POB,
∴∠EDB+∠DOE=∠EPB+∠POB,即∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2)在Rt△PBD中,PB=6,DB=8,
根据勾股定理得:PD==10,
∵PD与PB都为圆的切线,
∴PC=PB=6,
∴DC=PD﹣PC=10﹣6=4.
在Rt△CDO中,设OC=r,则有DO=8﹣r,
根据勾股定理得:(8﹣r)2=r2+42,
解得:r=3,
则圆的半径为3.
13.【解答】(1)证明:连接AE,如图,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,AE平分∠BAC,
∴∠1=∠2,
∵∠BAC=2∠4,
∴∠1=∠4,
∵∠1+∠3=90°,
∴∠3+∠4=90°,
∴AB⊥BF,
∴BF与⊙O相切;
(2)解:∵BC=CF=4,
∴∠F=∠4,
而∠BAC=2∠4,
∴∠BAC=2∠F,
∴∠F=30°,∠BAC=60°,
∴△ABC为等边三角形,
∴AB=AC=4,
∴BF===4.
14.【解答】(1)证明:连接OA、AD,如图,
∵∠B=2∠P,∠B=∠ADC,
∴∠ADC=2∠P,
∵AP=AC,
∴∠P=∠ACP,
∴∠ADC=2∠ACP,
∵CD为直径,
∴∠DAC=90°,
∴∠ADC=60°,∠C=30°,
∴△ADO为等边三角形,
∴∠AOP=60°,
而∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:在Rt△OAP中,∵∠P=30°,
∴OP=2OA,
∴PD=OD=,
∴⊙O的直径为2;
(3)解:作EH⊥AD于H,如图,
∵点B等分半圆CD,
∴∠BAC=45°,
∴∠DAE=45°,
设DH=x,
在Rt△DHE中,DE=2x,HE=x,
在Rt△AHE中,AH=HE=x,
∴AD=x+x=(+1)x,
即(+1)x=,
解得x=,
∴DE=2x=3﹣.
15.【解答】(1)证明:连接OD,如图,
∵EF垂直平分BD,
∴ED=EB,
∴∠EDB=∠B,
∵OA=OD,
∴∠A=∠ODA,
∵∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴直线DE是⊙O的切线;
(2)解:作OH⊥AD于H,如图,则AH=DH,
在Rt△OAB中,sinA==,
在Rt△OAH中,sinA==,
∴OH=,
∴AH==,
∴AD=2AH=,
∴BD=5﹣=,
∴BF=BD=,
在Rt△ABC中,cosB=,
在Rt△BEF中,cosB==,
∴BE=×=,
∴线段DE的长为.
21世纪教育网(www.21cnjy.com)
2025年九年级数学三轮冲刺训练圆中切线的判定和性质综合练习
1.如图,AB是⊙O的直径,D是弦AC延长线上一点,且AB=BD,DB的延长线交⊙O于点E,过点C作CF⊥BD,垂足为点F.
(1)CF与⊙O有怎样的位置关系?请说明理由;
(2)若BF+CF=6,⊙O的半径为5,求BE的长度.
2.如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
3.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线;
(2)若DE+EA=8,AF=16,求⊙O的半径.
4.如图,CD是⊙O的直径,CB是⊙O的弦,点A在CD的延长线上,过点C作CE⊥AB,交AB的延长线于点E,且CB平分∠ACE.
(1)求证:直线AB是⊙O的切线;
(2)若BE=3,CE=4,求⊙O的半径.
5.如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2,AC=2,求AD的长.
6.如图,AB是⊙O的直径,点C、D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
(1)证明EF是⊙O的切线;
(2)求证:∠DGB=∠BDF;
(3)已知圆的半径R=5,BH=3,求GH的长.
7.如图,AB为半⊙O的直径,弦AC的延长线与过点B的切线交于点D,E为BD的中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)过点C作CF⊥AB,垂足为点F,AC=5,CF=3,求⊙O的半径.
8.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线;
(2)若DE+EA=8,⊙O的半径为10,求△OAF的面积.
9.如图,△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)若AE=4,AB=10,求DF的长.
10.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,连接OD,过点B作BE∥OD交⊙O于点E,连接DE并延长交BN于点C.
(1)求证:DE是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.
11.如图,AB是⊙O的直径,弦CD垂直平分OA,垂足为点M,连接并延长CO交⊙O于点E,分别连接DE,BE,DB,其中∠EDB=30°,∠CDE的平分线DN交CE于点G,交⊙O于点N,延长CE至点F,使FG=FD.
(1)求证:DF是⊙O的切线;
(2)若⊙O半径r为8,求线段DB,BE与劣弧DE所围成的阴影部分的面积.
12.如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是⊙O的切线.
(2)若PB=6,DB=8,求⊙O的半径.
13.如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交AC、BC于点D、E,点F在AC的延长线上,且∠A=2∠CBF.
(1)求证:BF与⊙O相切.
(2)若BC=CF=4,求BF的长度.
14.如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径;
(3)在(2)的条件下,若点B等分半圆CD,求DE的长.
15.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求证:直线DE是⊙O的切线;
(2)若AB=5,BC=4,OA=1,求线段DE的长.
参考答案
1.【解答】解:(1)CF与⊙O相切.连接BC,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=BD,
∴∠A=∠D,
又∵OA=OB,
∴OC是△ABD的中位线.
∴OC∥BD,
∴∠OCF=∠CFD=90°,
即CF⊥OC.
∴CF与⊙O相切;
(2)过点O作OH⊥BE于点H,则∠OCF=∠CFH=∠OHB=90°,
∴四边形OCFH是矩形,
∴OC=FH,OH=CF,
设BH=x,
∵OC=5,BF+CF=6,
∴BF=5﹣x,OH=CF=6﹣(5﹣x)=x+1,
在Rt△BOH中,由勾股定理知:
BH2+OH2=OB2,即x2+(x+1)2=52,
解得x1=3,x2=﹣4(不合题意,舍去).
∴BH=3,
∵OH⊥BE,
∴BH=EH=BE,
∴BE=2BH=2×3=6.
2.【解答】(1)证明:连接OD,作OG⊥AB于G,如图1所示:
则∠OGB=90°,
∵△ABC为等边三角形,
∴∠OCD=∠OBG=∠ABC=60°,
∵O为BC的中点,
∴OB=OC,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=90°=∠OGB,
在△OBG和△OCD中,,
∴△OBG≌△OCD(AAS),
∴OG=OD,∴AB与⊙O相切;
(2)解:连接OA、OM,作OH⊥FM于H,如图2所示:
则∠OHB=90°,FH=MH,
∵CE=AC,AC=BC,
∴CE=BC,
∴∠CBE=∠CEB=∠ACB=30°,
∴∠ABE=∠ABC+∠CBE=90°,
∵∠OGB=90°,
∴四边形OHBG是矩形,
∴OH=BG,
∵△ABC是等边三角形,O为BC的中点,
∴OB=BC=AB=2,
∵∠BOG=90°﹣60°=30°,
∴OH=BG=OB=1,OG=BG=,
在Rt△OMH中,OM=OG=,OH=1,
∴MH==,
∴FM=2MH=2.
3.【解答】(1)证明:∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE⊥AC,OD是半径,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
∴AH=AF=8,
设AE=x.
∵DE+AE=8,
∴OH=DE=8﹣x,OA=OD=HE=AH+AE=8+x,
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即82+(8﹣x)2=(8+x)2,
解得:x=2,
∴OA=8+2=10.
∴⊙O的半径为10.
4.【解答】解:(1)连接OB,
∵OC=OB,
∴∠OCB=∠OBC,
∵CB平分∠ACE,
∴∠OCB=∠ECB,
∴∠OBC=∠BCE,
∴OB∥CE,
∵CE⊥AB,
∴OB⊥AE,
∴直线AB是⊙O的切线;
(2)连接DB,
∵∠E=90°,BE=3,CE=4,
∴BC=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠DBC=∠E,
∵∠DCB=∠BCE,
∴△BCD∽△ECB,
∴,
∴=,
∴CD=,
∴⊙O的半径=.
5.【解答】解:(1)连接AO并延长交⊙O于点F,连接BF,
则AF为直径,∠ABF=90°,
∵,
∴∠ACB=∠F,
∵∠BAE=∠ACB,
∴∠BAE=∠F,
∵∠FAB+∠F=90°,
∴∠FAB+∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
(2)连接OC,
∵AE∥BC,
∴∠BAE=∠ABC,
∵∠BAE=∠ACB,
∴∠ACB=∠ABC,
∴AC=AB=2,
∴∠AOC=∠AOB,
∵OC=OB,
∴OA⊥BC,
∴CH=BH=BC=,
在Rt△ABH中,
AH==1,
在Rt△OBH中,设OB=r,
∵OH2+BH2=OB2,
∴(r﹣1)2+()2=r2,
解得:r=2,
∴DB=2r=4,
在Rt△ABD中,AD===,
∴AD的长为.
6.【解答】解:(1)证明:连接OD,
∵OA=OD,
∴∠OAD=∠ODA
又∵AD平分∠BAC,
∴∠OAD=∠CAD
∴∠ODA=∠CAD,
∴OD∥AE,
又∵EF⊥AE,
∴OD⊥EF,
∴EF是⊙O的切线
(2)∵AB是⊙O的直径,
∴∠ADB=90°
∴∠DAB+∠OBD=90°
由(1)得,EF是⊙O的切线,
∴∠ODF=90°
∴∠BDF+∠ODB=90°
∵OD=OB,
∴∠ODB=∠OBD
∴∠DAB=∠BDF
又∠DAB=∠DGB
∴∠DGB=∠BDF
(3)连接OG,
∵G是半圆弧中点,
∴∠BOG=90°
在Rt△OGH中,OG=5,OH=OB﹣BH=5﹣3=2.
∴GH==
7.【解答】(1)证明:连接CO、EO、BC,
∵BD是⊙O的切线,
∴∠ABD=90°,
∵AB是直径,
∴∠BCA=∠BCD=90°,
∵Rt△BCD中,E是BD的中点,
∴CE=BE=ED,
∵OC=OB,OE=OE,
则△EBO≌△ECO(SSS),
∴∠ECO=∠EBO=90°,
∵点C在圆上,
∴CE是⊙O的切线;
(2)解:解法一:Rt△ACF中,∵AC=5,CF=3,
∴AF=4,
设圆O的半径为r,则OF=4﹣r,
由勾股定理得:CF2+OF2=CO2,
即32+(4﹣r)2=r2,r=;
解法二:Rt△ACF中,∵AC=5,CF=3,
∴AF=4,
设BF=x,
由勾股定理得:BC2=x2+32,
BC2+AC2=AB2,
x2+32+52=(x+4)2,
x=,
则r==,
则⊙O的半径为.
8.【解答】(1)证明:∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE⊥AC,OD是半径,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=8,OD=10,
∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2,
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,
解得x1=8,x2=﹣6(不合题意,舍去).
∴AH=8,OH=6,
∵OH⊥AF,
∴AH=FH=AF,
∴AF=2AH=2×8=16
∴△OAF的面积=×16×6=48.
9.【解答】(1)证明:如图,连接OD,作OG⊥AC于点G,
∵OB=OD,
∴∠ODB=∠B,
又∵AB=AC,
∴∠C=∠B,
∴∠ODB=∠C,
∵DF⊥AC,
∴∠DFC=90°,
∴∠ODF=∠DFC=90°,
∴DF是⊙O的切线;
(2)连接AD,BE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BD=CD,
∵AE=4,AB=10,
∴BE=2,
∵DF⊥AC,
∴DF∥BE,
∴DF=BE=.
10.【解答】(1)证明:连接OE,
∵OA=OE=OB,
∴∠OBE=∠PEB,
∵OD∥BE,
∴∠AOD=∠OBE,∠OEB=∠DOE,
∴∠AOD=∠EOD,
在△AOD和△EOD中
∴△AOD≌△EOD,
∴∠OAD=∠OED,
∵AM是⊙O的切线,
∴∠OAD=90°,
∴∠OED=90°,
即OE⊥DE,
∵OE为⊙O半径,
∴DE是⊙O的切线;
(2)解:
过D作DH⊥BC于H,
∵AM和BN是⊙O的两条切线,
∴∠DAB=∠ABH=∠DHB=90°,
∴四边形ABHD是矩形,
∴AB=DH,AD=BH,
∵AD=l,BC=4,
∴BH=1,CH=4﹣1=3,
∵AM和BN是⊙O的两条切线,DE切⊙O于E,AD=1,BC=4,
∴DE=AD=1,BC=CE=4,
∴DC=1+4=5,
在Rt△DHC中,由勾股定理得:DH===4,
即AB=4.
11.【解答】(1)证明:连接OD,
∵CD垂直平分OA,
∴OM=OA=OD,
∴∠ODC=30°,
∵CE为⊙O的直径,
∴∠CDE=90°,
∵DN平分∠CDE,
∴∠CDN=45°,
∴∠ODN=45°﹣30°=15°,
∵OD=OC,
∴∠DCO=∠ODC=30°,
∴∠FGD=45°+30°=75°,
∵FD=FG,
∴∠FDG=∠FGD=75°,
∴∠ODF=∠ODN+∠FDG=15°+75°=90°,
∴DF是⊙O的切线;
(2)解:∵∠EDB=30°,
∴∠EOB=60°,
Rt△CDE中,∠DEC=60°,
∴∠DEC=∠EOB=60°,
∴DE∥AB,
∴S△DOE=S△ODE,
∴S阴影=S扇形ODE==;
答:线段DB,BE与劣弧DE所围成的阴影部分的面积是,
12.【解答】解:(1)∵DE⊥PE,
∴∠E=90°,
∵∠EDB=∠EPB,∠DOE=∠POB,
∴∠EDB+∠DOE=∠EPB+∠POB,即∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2)在Rt△PBD中,PB=6,DB=8,
根据勾股定理得:PD==10,
∵PD与PB都为圆的切线,
∴PC=PB=6,
∴DC=PD﹣PC=10﹣6=4.
在Rt△CDO中,设OC=r,则有DO=8﹣r,
根据勾股定理得:(8﹣r)2=r2+42,
解得:r=3,
则圆的半径为3.
13.【解答】(1)证明:连接AE,如图,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,AE平分∠BAC,
∴∠1=∠2,
∵∠BAC=2∠4,
∴∠1=∠4,
∵∠1+∠3=90°,
∴∠3+∠4=90°,
∴AB⊥BF,
∴BF与⊙O相切;
(2)解:∵BC=CF=4,
∴∠F=∠4,
而∠BAC=2∠4,
∴∠BAC=2∠F,
∴∠F=30°,∠BAC=60°,
∴△ABC为等边三角形,
∴AB=AC=4,
∴BF===4.
14.【解答】(1)证明:连接OA、AD,如图,
∵∠B=2∠P,∠B=∠ADC,
∴∠ADC=2∠P,
∵AP=AC,
∴∠P=∠ACP,
∴∠ADC=2∠ACP,
∵CD为直径,
∴∠DAC=90°,
∴∠ADC=60°,∠C=30°,
∴△ADO为等边三角形,
∴∠AOP=60°,
而∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:在Rt△OAP中,∵∠P=30°,
∴OP=2OA,
∴PD=OD=,
∴⊙O的直径为2;
(3)解:作EH⊥AD于H,如图,
∵点B等分半圆CD,
∴∠BAC=45°,
∴∠DAE=45°,
设DH=x,
在Rt△DHE中,DE=2x,HE=x,
在Rt△AHE中,AH=HE=x,
∴AD=x+x=(+1)x,
即(+1)x=,
解得x=,
∴DE=2x=3﹣.
15.【解答】(1)证明:连接OD,如图,
∵EF垂直平分BD,
∴ED=EB,
∴∠EDB=∠B,
∵OA=OD,
∴∠A=∠ODA,
∵∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴直线DE是⊙O的切线;
(2)解:作OH⊥AD于H,如图,则AH=DH,
在Rt△OAB中,sinA==,
在Rt△OAH中,sinA==,
∴OH=,
∴AH==,
∴AD=2AH=,
∴BD=5﹣=,
∴BF=BD=,
在Rt△ABC中,cosB=,
在Rt△BEF中,cosB==,
∴BE=×=,
∴线段DE的长为.
21世纪教育网(www.21cnjy.com)
同课章节目录
