2025年九年级中考数学二轮专题复习反比例函数综合练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学二轮专题复习反比例函数综合练习(含解析) | 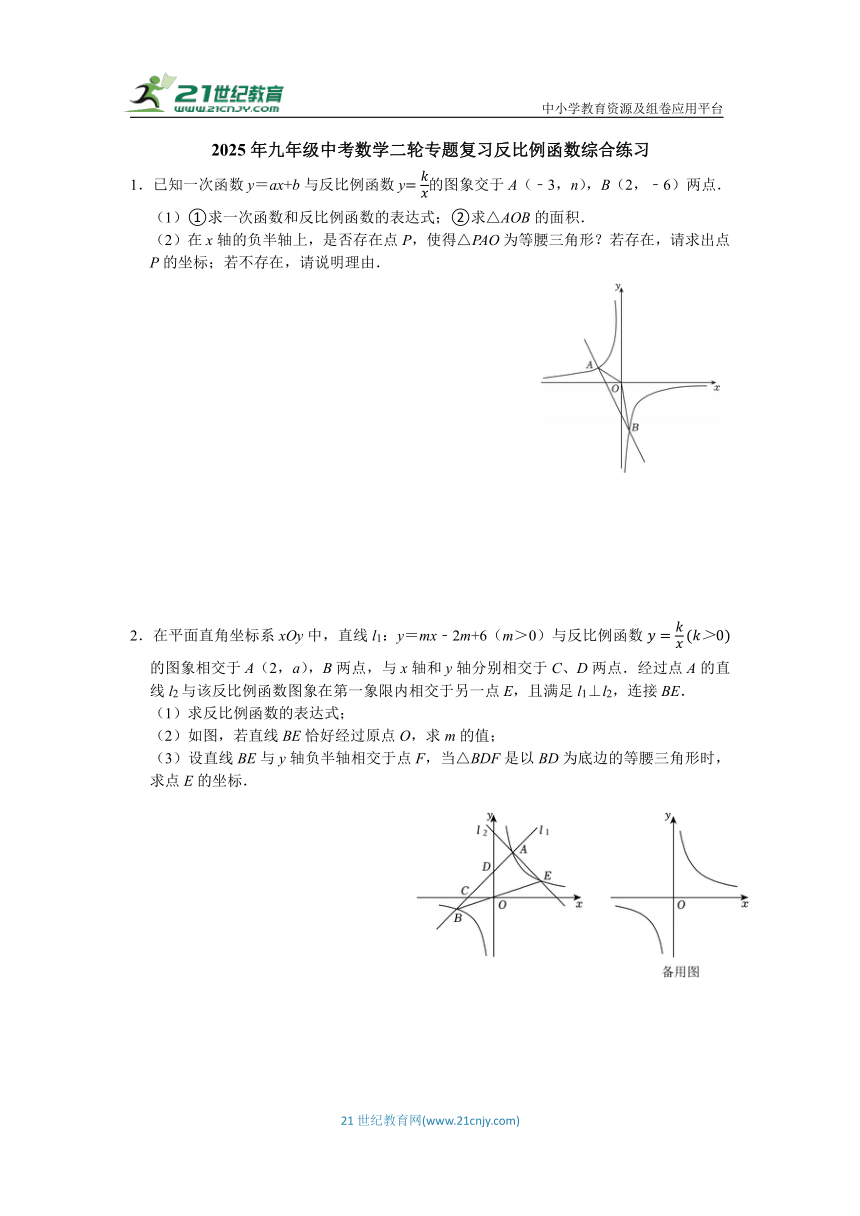 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:50:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学二轮专题复习反比例函数综合练习
1.已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点.
(1)①求一次函数和反比例函数的表达式;②求△AOB的面积.
(2)在x轴的负半轴上,是否存在点P,使得△PAO为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
2.在平面直角坐标系xOy中,直线l1:y=mx﹣2m+6(m>0)与反比例函数的图象相交于A(2,a),B两点,与x轴和y轴分别相交于C、D两点.经过点A的直线l2与该反比例函数图象在第一象限内相交于另一点E,且满足l1⊥l2,连接BE.
(1)求反比例函数的表达式;
(2)如图,若直线BE恰好经过原点O,求m的值;
(3)设直线BE与y轴负半轴相交于点F,当△BDF是以BD为底边的等腰三角形时,求点E的坐标.
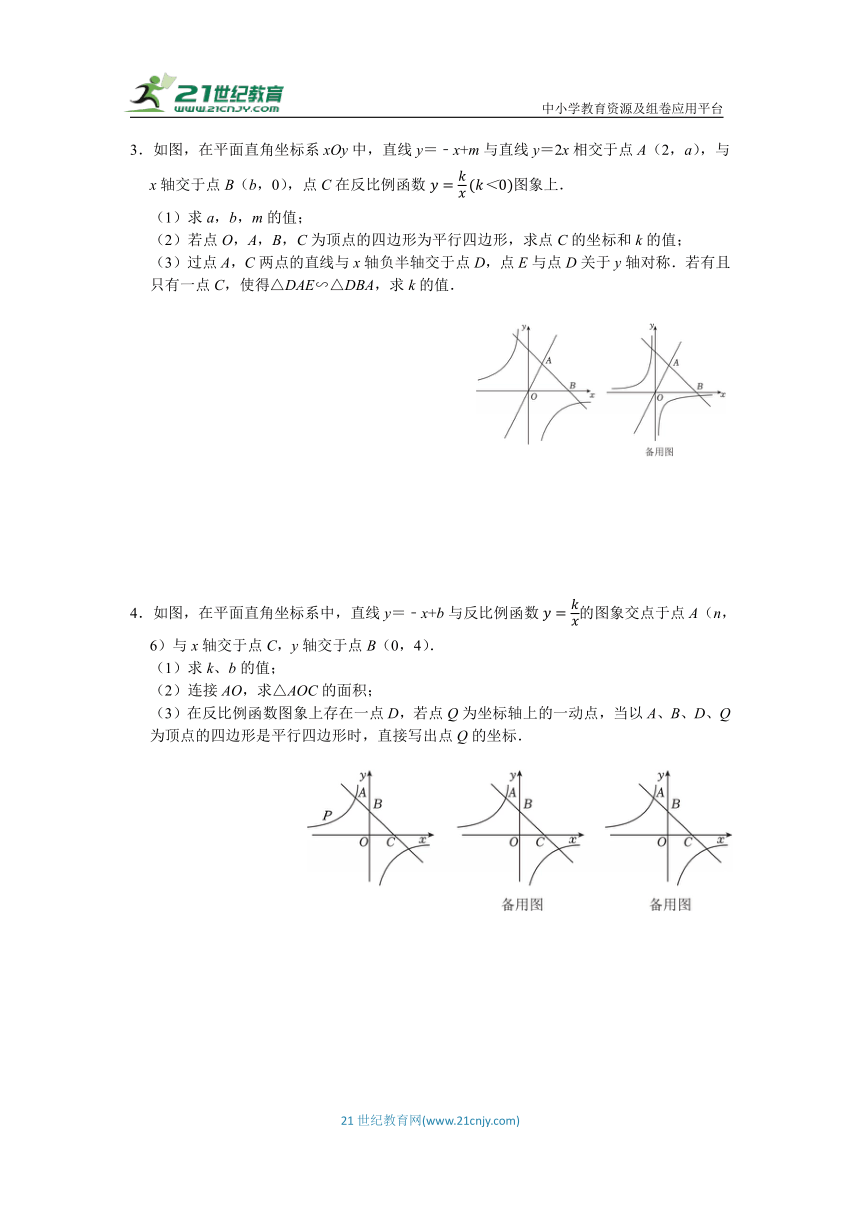
3.如图,在平面直角坐标系xOy中,直线y=﹣x+m与直线y=2x相交于点A(2,a),与x轴交于点B(b,0),点C在反比例函数图象上.
(1)求a,b,m的值;
(2)若点O,A,B,C为顶点的四边形为平行四边形,求点C的坐标和k的值;
(3)过点A,C两点的直线与x轴负半轴交于点D,点E与点D关于y轴对称.若有且只有一点C,使得△DAE∽△DBA,求k的值.
4.如图,在平面直角坐标系中,直线y=﹣x+b与反比例函数的图象交点于点A(n,6)与x轴交于点C,y轴交于点B(0,4).
(1)求k、b的值;
(2)连接AO,求△AOC的面积;
(3)在反比例函数图象上存在一点D,若点Q为坐标轴上的一动点,当以A、B、D、Q为顶点的四边形是平行四边形时,直接写出点Q的坐标.
5.如图所示,直线y=k1x+b与双曲线y交于A、B两点,已知点B的纵坐标为﹣3,直线AB与x轴交于点C,与y轴交于点D(0,﹣2),OA,tan∠AOC.
(1)求直线AB的解析式;
(2)若点P是第二象限内反比例函数图象上的一点,△OCP的面积是△ODB的面积的2倍,求点P的坐标;
(3)直接写出不等式k1x+b的解集.
6.已知在平面直角坐标系xOy中,点A是反比例函数y(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.
(1)如图1,过点B作BF⊥x轴,于点F,连接EF.
①若k=1,求证:四边形AEFO是平行四边形;
②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数y(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.
7.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于第二、四象限内的点A(a,4)和点B(8,b).过点A作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n的解集;
(3)在x轴上取点P,使PA﹣PB取得最大值时,求出点P的坐标.
8.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0且m≠3)的图象在第一象限交于点A、B,且该一次函数的图象与y轴正半轴交于点C,过A、B分别作y轴的垂线,垂足分别为E、D.已知A(4,1),CE=4CD.
(1)求m的值和反比例函数的解析式;
(2)若点M为一次函数图象上的动点,求OM长度的最小值.
9.如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的图象在第一象限内的交点为M(m,4).
(1)求一次函数和反比例函数的表达式;
(2)点C是线段AM上一点,若,求点C的坐标;
(3)若点P是x轴上一点,是否存在以点O、M、P为顶点的三角形是等腰三角形,若存在,求出点P的坐标;若不存在,说明理由.
10.如图,直线AB与x轴交于点A,与y轴交于点B.OB是一元二次方程x2﹣x﹣30=0的一个根,且tan∠OAB,点D为AB的中点,E为x轴正半轴上一点,BE=2,直线OD与BE相交于点F.
(1)求点A及点D的坐标;
(2)反比例函数y经过点F关于y轴的对称点F′,求k的值;
(3)在直线AB上是否存在点P,使△AEP为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
11.如图,P是反比例函数(x>0)的图象上的一点,PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数y=x+b的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线y=x+b与x轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的时,直接写出点Q的坐标.
12.如图1,在平面直角坐标系中,矩形OABC的边OC、OA分别在坐标轴上,且OA=3,OC=6,反比例函数的图象与AB、BC分别交于点D、E,连结DE.
(1)如图2,连结OD、OE,当△OAD的面积为2时:
①k= ;
②求△ODE的面积;
(2)如图3,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求k的值.
13.如图,在平面直角坐标系中,一次函数y=x+b的图象经过点C(0,2),与反比例函数的图象交于点A(1,a).
(1)求一次函数和反比例函数的表达式;
(2)一次函数y=x+b的图象与x轴交于B点,求△ABO的面积,并直接写出x为何值时双曲线位于直线上方;
(3)设M是反比例函数图象上一点,N是直线AB上一点,若以点O、M、C、N为顶点的四边形是平行四边形,求点N的坐标.
14.如图,一次函数y=kx+b与反比例函数y的图象交于点A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)连接OA、OB,求△AOB的面积;
(3)直线a经过点(0,1)且平行于x轴,点M在直线a上,点N在y轴上,以 A、B、M、N为顶点的四边形可以是平行四边形吗?如果可以,直接写出点M、N的坐标,如果不可以,说明理由.
15.如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y的另一个交点.
(1)点D的坐标为 ,点E的坐标为 ;
(2)动点P在第一象限内,且满足S△POBS△ODE
①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
16.如图,点A、B分别在x轴和y轴的正半轴上,以线段AB为边在第一象限作等边△ABC,S△ABC,且CA∥y轴,点C在反比例函数y(k≠0,x>0)的图象上.
(1)求该反比例函数的解析式;
(2)若点N是反比例函数图象上一点,当四边形ABCN是菱形时,求出点N坐标.
17.如图,在平面直角坐标系中,一次函数与反比例函数交于第一象限内A,B(6,1)两点(B在A右侧),分别交x轴,y轴于C,D两点.
(1)求k和b的值;
(2)求点A的坐标;
(3)在y轴上是否存在一点P,使以A,D,P为顶点的三角形与△CDO相似?若存在,求出点P的坐标.若不存在,请说明理由.
18.如图,正比例函数y=﹣3x与反比例函数y(k≠0)的图象交于A、B(1,m)两点,C点在x轴负半轴上,∠ACO=45°.
(1)m= ,k= ,点C的坐标为 ;
(2)点P在x轴上,若以B、O、P为顶点的三角形与△AOC相似,求点P的坐标.
参考答案
1.【解答】解:(1)①已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点,将点B的坐标代入y= 得:
﹣6= ,
解得:k=﹣12;
∴反比例函数的表达式为y= ;
将点A的坐标代入y= 得:
,
∴A(﹣3,4);
将点A,点B的坐标代入得:
,
解得:,
∴一次函数的表达式为:y=﹣2x﹣2
②设一次函数y=﹣2x﹣2与x轴交于点C,如图:
由0=﹣2x﹣2得x=﹣1;
∴C(﹣1,0),
∴;
(2)在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;理由如下:
设点P(p,0)(p<0),
①PA=PO,则,
解得:;
②AP=AO,则,
解得:p=﹣6或p=0(不合题意,舍去);
③OP=OA,则,
解得:p=﹣5;
综上所述,在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;点P的坐标为或(﹣6,0)或(﹣5,0).
2.【解答】解:(1)当x=2时,直线l1:y=mx﹣2m+6=6,
∴A(2,6),
∵点A在反比例函数图象上,
∴k=2×6=12,
∴反比例函数的表达式为y;
(2)∵l1⊥l2,
∴设直线l2:yx+b,
把A(2,6)代入得,62+b,
解得b6,
∴直线l2:yx6,
解得,,
∴E(6m,),
解得,,
∴,
设直线BE的解析式为y=cx,
∴,
解得m=±1,
∵m>0,
∴m=1.
方法二:过点A作MN∥x轴,过点B作BM⊥MN 于点M,过点E作 EN⊥MN 于点N.
∵∠M=∠N=∠BAE=90°,
∴∠BAM+∠EAN=∠BAM+∠ABM=90°,
∴∠ABM=∠EAN,
∴△BMA∽△ANE,
∴,
设,
∵直线BE过原点,且点B和点E在反比例函数图象上,
∴,
∴,整理,得,
即,
解得n1=6,n2=﹣6(舍去),
∴点B的坐标为(﹣6,﹣2),
将 B(﹣6,﹣2)代入 y=mx﹣2m+6,得﹣6m﹣2m+6=﹣2,
∴m=1.
(3)方法一:由(2)知B(,﹣2m),E(6m,),
设直线BE解析式为y=k'x+b',
将点B和点E代入得,
,
解得,
∴直线BE的解析式为yx,
∴F(0,),
由直线l1的解析式为y=mx﹣2m+6,可得D(0,﹣2m+6),
∴DF2=(﹣2m+62m)2=(6)2,
BF2=(0)2+(﹣2m2m)2,
∵△BDF是以BD为底边的等腰三角形,
∴DF=BF,即(6)2,
整理得3m2﹣2m+3=0,
解得m,
∵m>0,
∴E(2+2,).
方法二:∵△BDF 为等腰三角形,且BD 为底边,
∴∠CDO=∠ABE,
∵∠COD=∠BAE=90°,
∴△CDO∽△EAB,
∴,即,
∵lAB:y=mx﹣2m+6,
∴,D(0,﹣2m+6),
∴,即,
联立整理,得mx2+(﹣2m+6)x﹣12=0,
解得,x2=2(舍去),
∴点B的坐标为,
∵AB⊥AE,
∴kAB kAE=﹣1,
∴,
设,
将点A(2,6)代入,得,
联立,
整理,得,
解得x1=6m,x2=2(舍去),
∴点E的坐标为,
过点A作 GH∥x轴,过点B作 BG⊥GH于点G,过点E作 EH⊥GH 于点H.
∵∠G=∠H=∠BAE=90°,
∴∠BAG+∠EAH=∠BAG+∠ABG=90°,
∴∠ABG=∠EAH,
∴△BGA∽△AHE,
∴,
∵A(2,6),,,
∴BG=6+2m,AH=6m﹣2,
∴,
解得:,(舍去).
∴点E的坐标为.
方法三:由(2)知B(,﹣2m),E(6m,),
∴KBE,
∴tanα=m,tanθ,tanβ,
∵α=β+θ,
∴tanα=tan(β+θ)m,
∴m,
整理得3m2﹣2m﹣3=0,
解得m,
∵m>0,
∴E(2+2,).
3.【解答】解:(1)把点A(2,a)代入y=2x得a=4,
把点A(2,4)代入y=﹣x+m得m=6,即:y=﹣x+6,
当y=0时,0=﹣x+6,
解得b=6,
∴a=4,m=6,b=6;
(2)设C(t,),
由(1)知A(2,4),B(6,0),而O(0,0),
①当AC,BO为对角线时,AC,BO的中点重合,
∴,
解得,
经检验,t=4,k=﹣16符合题意,
此时点C的坐标为(4,﹣4);
②当CB,AO为对角线时,CB,AO的中点重合,
∴,
解得,
经检验,t=﹣4,k=﹣16符合题意,
此时点C的坐标为(﹣4,4);
③当CO,AB为对角线时,CO,AB的中点重合,
∴,
解得,
∵k=32>0,
∴这种情况不符合题意;
综上所述,C的坐标为(4,﹣4)或(﹣4,4),k的值为﹣16;
(3)设点D(t,0),则点E(﹣t,0),
∵△DAE∽△DBA,
∴AD2=DE DB,即:16+(2﹣t)2=﹣2t(6﹣t),
解得:t1=﹣2,t2=10(不合题意,舍去),
∴点D(﹣2,0),
设直线AD解析式为y=px+q,
将点A(2,4)、点D(﹣2,0)代入y=px+q,
,
解得,
∴直线AD解析式为y=x+2,
∵过AD两点的直线与双曲线有且只有一点C,
∴x+2,
化简得x2+2x﹣k=0,
∵方程x2+2x﹣k=0有且只有一个解,
∴Δ=4+4k=0,
得k=﹣1.
4.【解答】解:(1)由题意可得:4=﹣0+b,6=﹣n+b,
∴b=4,n=﹣2,
∴一次函数解析式为y=﹣x+4,点A(﹣2,6),
∵直线y=﹣x+4与反比例函数y的图象交于点A(﹣2,6),
∴k=6×(﹣2)=﹣12;
(2)令y=0,则y=﹣x+4=4,
∴C(4,0),
∴OC=4,
∴△AOC的面积OC yA4×6=12;
(3)当点Q在y轴上时,设点Q(0,c),点D(m,),
∵以A,B,D,Q为顶点的四边形为平行四边形,
∴BQ和AD是对角线,且互相平分,
∴,
∴m=2,
∴点D(2,﹣6),
∴,
∴c=﹣4,
∴点Q(0,﹣4);
当点Q在x轴上时,设点Q(t,0),点D(m,),
若AQ,BD为对角线,
则,,
∴m=﹣6,t=﹣4,
∴点Q(﹣4,0);
若AD,BQ为对角线,
则,,
∴m=6,t=4,
∴点Q(4,0),
此时点Q在AB的延长线上,不合题意舍去,
当AB,PQ为对角线时,同理可求点P(﹣1.2,10),点Q(﹣0.8,0),
综上所述:点Q(﹣4,0)或(0,﹣4)或(﹣0.8,0).
5.【解答】解:(1)如图1,
过点A作AE⊥x轴于E,
∴∠AEO=90°,
在Rt△AOE中,tan∠AOC,
设AE=m,则OE=2m,
根据勾股定理得,AE2+OE2=OA2,
∴m2+(2m)2=()2,
∴m=1或m=﹣1(舍),
∴OE=2,AE=1,
∴A(﹣2,1),
∵点A在双曲线y上,
∴k2=﹣2×1=﹣2,
∴双曲线的解析式为y,
∵点B在双曲线上,且纵坐标为﹣3,
∴﹣3,
∴x,
∴B(,﹣3),
将点A(﹣2,1),B(,﹣3)代入直线y=k1x+b中得,,
∴,
∴直线AB的解析式为yx﹣2;
(2)如图2,连接OB,PO,PC;
∵D(0,﹣2),
∴OD=2,
由(1)知,B(,﹣3),
∴S△ODBOD xB2,
∵△OCP的面积是△ODB的面积的2倍,
∴S△OCP=2S△ODB=2,
由(1)知,直线AB的解析式为yx﹣2,
令y=0,则x﹣2=0,
∴x,
∴OC,
设点P的纵坐标为n,
∴S△OCPOC yPn,
∴n=2,
由(1)知,双曲线的解析式为y,
∵点P在双曲线上,
∴2,
∴x=﹣1,
∴P(﹣1,2);
(3)由(1)知,A(﹣2,1),B(,﹣3),
由图象知,不等式k1x+b的解集为﹣2≤x<0或x.
6.【解答】(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,),
∴AE=OF=a,
∵AE⊥y轴,
∴AE∥OF,
∴四边形AEFO是平行四边形;
②解:过点B作BD⊥y轴于点D,如图1,
∵AE⊥y轴,
∴AE∥BD,
∴△AEO∽△BDO,
∴,
∴当k=4时,,
即,
∴S△BOE=2S△AOE=1;
(2)不改变.
理由如下:
过点P作PH⊥x轴于点H,PE与x轴交于点G,
设点A的坐标为(a,),点P的坐标为(b,),
则AE=a,OE,PH,
∵四边形AEGO是平行四边形,
∴∠EAO=∠EGO,AE=OG,
∵∠EGO=∠PGH,
∴∠EAO=∠PGH,
又∵∠PHG=∠AEO,
∴△AEO∽△GHP,
∴,
∵GH=OH﹣OG=﹣b﹣a,
∴,
∴k=0,
解得,
∵a,b异号,k>0,
∴,
∴S△POEOE×(﹣b)(﹣b),
∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.
7.【解答】解:(1)∵点A(a,4),
∴AC=4,
∵S△AOC=4,即,
∴OC=2,
∵点A(a,4)在第二象限,
∴a=﹣2 A(﹣2,4),
将A(﹣2,4)代入y得:k=﹣8,
∴反比例函数的关系式为:y,
把B(8,b)代入得:b=﹣1,
∴B(8,﹣1)
因此a=﹣2,b=﹣1;
(2)由图象可以看出mx+n的解集为:﹣2<x<0或x>8;
(3)如图,作点B关于x轴的对称点B′,直线AB′与x轴交于P,
此时PA﹣PB最大(PA﹣PB=PA﹣PB′≤AB′,共线时差最大)
∵B(8,﹣1)
∴B′(8,1)
设直线AP的关系式为y=mx+n,将 A(﹣2,4),B′(8,1)代入得:
,
解得:m,n,
∴直线AP的关系式为yx,
当y=0时,即x0,解得x,
∴P(,0).
8.【解答】解:(1)将点A(4,1)代入y,
得,m2﹣3m=4,
解得,m1=4,m2=﹣1,
∴m的值为4或﹣1;反比例函数解析式为:y;
(2)∵BD⊥y轴,AE⊥y轴,
∴∠CDB=∠CEA=90°,
∴△CDB∽△CEA,
∴,
∵CE=4CD,
∴AE=4BD,
∵A(4,1),
∴AE=4,
∴BD=1,
∴xB=1,
∴yB4,
∴B(1,4),
将A(4,1),B(1,4)代入y=kx+b,
得,,
解得,k=﹣1,b=5,
∴yAB=﹣x+5,
设直线AB与x轴交点为F,
当x=0时,y=5;当y=0时x=5,
∴C(0,5),F(5,0),
则OC=OF=5,
∴△OCF为等腰直角三角形,
∴CFOC=5,
则当OM垂直CF于M时,由垂线段最知可知,OM有最小值,
即OMCF.
9.【解答】解:(1)将A(0,﹣2),B(1,0)代入y=k1x+b,得:
,
解得k1=2,b=﹣2.
所以一次函数的表达式为y=2x﹣2,
将M(m,4)代入y=2x﹣2中,得:
4=2m﹣2,
解得m=3,
所以点M的坐标为(3,4),
因为反比例函数的图象过点M(3,4),得:
,
解得k2=12,
所以反比例函数的表达式为;
(2)根据题意,得:
,
则,
可得S△AOC=S△AMO﹣S△OCM=3﹣1=2,
由OA=2可知点C的横坐标为2,
将x=2代入y=2x﹣2中,得:y=2.
所以点C的坐标为(2,2);
(3)设点P的坐标为(n,0).
根据题意可得,
①如图1所示,
当点O为等腰三角形的顶角顶点时,OP=OM=5,则点P的坐标为(5,0)或(﹣5,0);
②如图2所示.
当点M为等腰三角形的顶角顶点时,MO=MP=5,则(n﹣3)2+42=52.
解得n1=0(舍去),n2=6.
所以,点P的坐标为(6,0);
③如图3所示.
当点P为等腰三角形的顶角顶点时,PO=PM,则:(n﹣3)2+42=n2,
解得,
所以,点P的坐标为.
综上所述,点P的坐标为(5,0),(﹣5,0),(6,0)或.
10.【解答】解:(1)∵x2﹣x﹣30=0,
∴x1=﹣5,x2=6,
∵直线AB与x轴交于点A,与y轴交于点B.OB是一元二次方程x2﹣x﹣30=0的一个根,
∴OB=6,
∵,
∴,
∴OA=8,
∴B(0,6),A(8,0),
∴点D的坐标为,即D(4,3).
(2),
∴E(2,0),
设直线BE的函数解析式为y=kx+b(k≠0),
把B(0,6),E(2,0)代入得:
,
解得:
∴直线BE的函数解析式为y=﹣3x+6,
∵D(4,3),
设直线OD的函数解析式为y=mx,
∴4m=3,解得,
∴直线OD的函数解析式为,
当时,,
此时,
∴,
∴F′为,
∴.
(3)设直线AB的解析式为y=ax+b,
将点AB的坐标代入得,
,解得:
∴直线AB的解析式为,
∵点P在直线AB上,
∴设点,
∴,,AE2=(8﹣2)2=36,
①当PE=AP时,,
解得:,
∴,
∴点P的坐标为;
②当PE=AE时,
解得:t1=8,
∴,此时点P不存在,
,
∴点P的坐标为;
③当AP=AE时,,
解得:,,
∴P或;
综上,P或或或.
11.【解答】解:(1)∵PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,
∴PN=2、
∴点P的坐标为(1,2).
∵反比例函数(x>0)的图象、一次函数y=x+b的图象都经过点P,
由,2=1+b得k=2,b=1、
∴反比例函数为,一次函数为y=x+1;
(2)Q1(0,1),Q2(0,﹣1).
12.【解答】解:(1)①∵△OAD的面积=2,
即,
∴k=4,
故答案为:4;
②在矩形OABC中,OA=BC=3,OC=AB=6,
∵k=4,
∴反比例函数的解析式是:y(x>0),
∵OA=3,
即点D的纵坐标是3,
令y3,
解得:x,
∴D(,3),
同理,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
∴S△ODE=S矩形OABC﹣S△OAD﹣S△OCE﹣S△BDE=OA OC;
(2)过点D作DG⊥x轴于点G,则DG=OA=3,
∵OA=3,即点D的纵坐标是3,
令y,
得:x,
∴D(,3),
同理可得,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
由折叠的性质可知:DF=BD=6,FE=BE=3,∠DFE=∠B=90°,
∴∠DFG+∠CFE=90°,
∵DG⊥x轴,
∴∠DFG+∠GDF=90°,
∴∠CFE=∠GDF,
∵∠CFE=∠GDF,∠FCE=∠DGF=90°,
∴△CFE∽△GDF,
∴,
即,
∴GF,
∵DG⊥x轴,
∴△GDF是直角三角形,DG2+GF2=DF2,
∴,
解得:k,
即k的值为.
13.【解答】解:(1)∵点C(0,2)在直线y=x+b上,
∴b=2,
∴一次函数的表达式为y=x+2;
∵点A(1,a)在直线y=x+2上,
∴a=1+2=3,
∴A(1,3),
∵点A(1,3)在反比例函数的图象上,
∴k=1×3=3,
∴反比例函数的表达式为;
(2)在y=x+2中,令y=0,
解得x=﹣2,
∴B(﹣2,0),
又∵A(1,3),
∴,
由函数图象得:当0<x<1时,双曲线位于直线上方;
(3)∵直线AB的表达式为y=x+2,反比例函数的表达式为,
设点,N(n,n+2),
若以点O、M、C、N为顶点的四边形是平行四边形,
则分情况讨论:
①以OC和MN为对角线时,
可得:,,
解得:,或(此时点M不在第一象限,舍去),
∴;
②以CN和OM为对角线时,
可得:,,
解得:或(此时点M不在第一象限,舍去),
∴,
③以CM和ON为对角线时,
可得:,,
∴或(此时点M不在第一象限,舍去),
∴,
综上,满足条件的点N的坐标为,,.
14.【解答】解:(1)将点A的坐标代入反比例函数表达式得:6,解得:m=6,
故反比例函数表达式为:y,
当x=3时,y2,即点B(3,2),
由题意得:,解得:,
故一次函数的表达式为:y=﹣2x+8;
(2)设AB交x轴于点H,
令y=﹣2x+8=0,解得:x=4,即OH=4,
则△AOB的面积=S△AOH﹣S△BOH4×64×2=8;
(3)设点M、N的坐标别为(m,1)、(0,n),
当AB是对角线时,由中点坐标公式得:,解得:,
即点M、N的坐标分别为(4,1)、(0,7);
当AM是对角线时,由中点坐标公式得:,解得:,
即点M、N的坐标分别为:(2,1)、(0,5);
当AN是对角线时,由中点坐标公式得:,解得:,
即即点M、N的坐标分别为:(﹣2,1)、(0,﹣3);
综上,点M、N的坐标分别为(4,1)、(0,7)或(2,1)、(0,5)或(﹣2,1)、(0,﹣3).
15.【解答】解:(1)∵四边形OACB是矩形,
∴AC=OB=6,
∴C(8,6),
∵点D是AC的中点,
∴D(8,3),
∴k=8×3=24,
∴y,
当y=6时,x=4,
∴E(4,6),
故答案为:(8,3),(4,6);
(2)①由题意知,S△ODE=S梯形OACE﹣S△OAD﹣S△ECD
(4+8)×63
=18,
∵S△PBOS△ODE.
∴6×xP18,
∴xP=3,
∴y=8,
∴P的坐标为(3,8);
②由①知,点P在直线x=3上,设直线x=3交x轴于H,
当AC=AP=6时,若点P在第一象限,
∴PH,
∴Q(3,6),
当点P在第四象限舍去,
当CA=CP时,
同理得,Q(3,),Q'(3,),
当PC=PA时,点P(3,3),
则点Q与P关于AC对称,
∴Q(13,3),
综上,点Q(3,6)或(3,)或(3,)或(13,3).
16.【解答】解:(1)根据题意,设C点的坐标为(a,b),
∴b,
∴ab=k,即得AC OA=k,
又∵CA∥y轴,
∴S△ABCAC OA,
∴k,
即k=2,
∴反比例函数的解析式为y;
(2)如图,根据菱形的性质可知,AC⊥BN,且AC与BN互相平分,
设菱形对角线的交点为P,设C点坐标为(a,b),
∵△ABC是等边三角形,四边形ABCN是菱形,
∴P(a,b),N(2a,b),
即BP=OA=a,AP=CPb,
∵∠BAC=60°,
∴BP=AP×tan60°,
即ab,
由(1)知ab=2,C点在第一象限,
∴a,b=2,
∴N(2,1).
17.【解答】解:(1)∵一次函数yx+b与反比例函数y交于B点,
∴16+b,1,
∴b=4,k=6;
(2)由(1)知一次函数的解析式为yx+4,反比例函数的解析式为y,
解得,,
∴A(2,3);
(3)存在以A,D,P为顶点的三角形与△CDO相似.
∵一次函数yx+4与x轴,y轴交于C,D两点,
∴C(8,0),D(0,4),
∴OC=8,OD=4,
设P(0,a),
∵∠COD=90°,∠APD=∠CDO,
①当∠APD=90°时,△APD∽△COD,
∵A(2,3),
∴AP=2,OP=3,
∴P(0,3);
②当∠PAD=90°时,△PAD∽△COD,
∴,
∵AD,CD4,PD=4﹣a,
∴,
解得a=﹣1,
∴P(0,﹣1),
综上所述,P(0,3)或(0,﹣1).
18.【解答】解:(1)当x=1时,y=﹣3x=﹣3=m,即点B(1,﹣3),
将点B的坐标代入反比例函数的表达式得:k=﹣3×1=﹣3,
即反比例函数的表达式为:y,
根据正比例函数的对称性,点A(﹣1,3),
由点O、A的坐标得,OA,过点A作AH⊥x轴于点H,
由直线AB的表达式知,tan∠AOH=3,
而∠ACO=45°,
设AH=3x=CH,则OH=x,则AOx,则x=1,
则AH=CH=3,OH=1,
则CO=CH+OH=4,
则点C的坐标为:(﹣4,0),
故答案为:﹣3,﹣3,(﹣4,0);
(2)当点P在x轴的负半轴时,
∵∠BOP>90°>∠AOC,
又∵∠BOP>∠ACO,∠BOP>∠CAO,
∴△BOP和△AOC不可能相似;
当点P在x轴的正半轴时,∠AOC=∠BOP,
若△AOC∽△BOP,则,
则OP=OC=4,
即点P(4,0);
若△AOC∽△POB,则,
即,
解得:OP=2.5,
即点P(2.5,0),
综上,点P的坐标为:(4,0)或(2.5,0).
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学二轮专题复习反比例函数综合练习
1.已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点.
(1)①求一次函数和反比例函数的表达式;②求△AOB的面积.
(2)在x轴的负半轴上,是否存在点P,使得△PAO为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
2.在平面直角坐标系xOy中,直线l1:y=mx﹣2m+6(m>0)与反比例函数的图象相交于A(2,a),B两点,与x轴和y轴分别相交于C、D两点.经过点A的直线l2与该反比例函数图象在第一象限内相交于另一点E,且满足l1⊥l2,连接BE.
(1)求反比例函数的表达式;
(2)如图,若直线BE恰好经过原点O,求m的值;
(3)设直线BE与y轴负半轴相交于点F,当△BDF是以BD为底边的等腰三角形时,求点E的坐标.
3.如图,在平面直角坐标系xOy中,直线y=﹣x+m与直线y=2x相交于点A(2,a),与x轴交于点B(b,0),点C在反比例函数图象上.
(1)求a,b,m的值;
(2)若点O,A,B,C为顶点的四边形为平行四边形,求点C的坐标和k的值;
(3)过点A,C两点的直线与x轴负半轴交于点D,点E与点D关于y轴对称.若有且只有一点C,使得△DAE∽△DBA,求k的值.
4.如图,在平面直角坐标系中,直线y=﹣x+b与反比例函数的图象交点于点A(n,6)与x轴交于点C,y轴交于点B(0,4).
(1)求k、b的值;
(2)连接AO,求△AOC的面积;
(3)在反比例函数图象上存在一点D,若点Q为坐标轴上的一动点,当以A、B、D、Q为顶点的四边形是平行四边形时,直接写出点Q的坐标.
5.如图所示,直线y=k1x+b与双曲线y交于A、B两点,已知点B的纵坐标为﹣3,直线AB与x轴交于点C,与y轴交于点D(0,﹣2),OA,tan∠AOC.
(1)求直线AB的解析式;
(2)若点P是第二象限内反比例函数图象上的一点,△OCP的面积是△ODB的面积的2倍,求点P的坐标;
(3)直接写出不等式k1x+b的解集.
6.已知在平面直角坐标系xOy中,点A是反比例函数y(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.
(1)如图1,过点B作BF⊥x轴,于点F,连接EF.
①若k=1,求证:四边形AEFO是平行四边形;
②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数y(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.
7.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于第二、四象限内的点A(a,4)和点B(8,b).过点A作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n的解集;
(3)在x轴上取点P,使PA﹣PB取得最大值时,求出点P的坐标.
8.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y(m≠0且m≠3)的图象在第一象限交于点A、B,且该一次函数的图象与y轴正半轴交于点C,过A、B分别作y轴的垂线,垂足分别为E、D.已知A(4,1),CE=4CD.
(1)求m的值和反比例函数的解析式;
(2)若点M为一次函数图象上的动点,求OM长度的最小值.
9.如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的图象在第一象限内的交点为M(m,4).
(1)求一次函数和反比例函数的表达式;
(2)点C是线段AM上一点,若,求点C的坐标;
(3)若点P是x轴上一点,是否存在以点O、M、P为顶点的三角形是等腰三角形,若存在,求出点P的坐标;若不存在,说明理由.
10.如图,直线AB与x轴交于点A,与y轴交于点B.OB是一元二次方程x2﹣x﹣30=0的一个根,且tan∠OAB,点D为AB的中点,E为x轴正半轴上一点,BE=2,直线OD与BE相交于点F.
(1)求点A及点D的坐标;
(2)反比例函数y经过点F关于y轴的对称点F′,求k的值;
(3)在直线AB上是否存在点P,使△AEP为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
11.如图,P是反比例函数(x>0)的图象上的一点,PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数y=x+b的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线y=x+b与x轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的时,直接写出点Q的坐标.
12.如图1,在平面直角坐标系中,矩形OABC的边OC、OA分别在坐标轴上,且OA=3,OC=6,反比例函数的图象与AB、BC分别交于点D、E,连结DE.
(1)如图2,连结OD、OE,当△OAD的面积为2时:
①k= ;
②求△ODE的面积;
(2)如图3,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求k的值.
13.如图,在平面直角坐标系中,一次函数y=x+b的图象经过点C(0,2),与反比例函数的图象交于点A(1,a).
(1)求一次函数和反比例函数的表达式;
(2)一次函数y=x+b的图象与x轴交于B点,求△ABO的面积,并直接写出x为何值时双曲线位于直线上方;
(3)设M是反比例函数图象上一点,N是直线AB上一点,若以点O、M、C、N为顶点的四边形是平行四边形,求点N的坐标.
14.如图,一次函数y=kx+b与反比例函数y的图象交于点A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)连接OA、OB,求△AOB的面积;
(3)直线a经过点(0,1)且平行于x轴,点M在直线a上,点N在y轴上,以 A、B、M、N为顶点的四边形可以是平行四边形吗?如果可以,直接写出点M、N的坐标,如果不可以,说明理由.
15.如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y的另一个交点.
(1)点D的坐标为 ,点E的坐标为 ;
(2)动点P在第一象限内,且满足S△POBS△ODE
①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
16.如图,点A、B分别在x轴和y轴的正半轴上,以线段AB为边在第一象限作等边△ABC,S△ABC,且CA∥y轴,点C在反比例函数y(k≠0,x>0)的图象上.
(1)求该反比例函数的解析式;
(2)若点N是反比例函数图象上一点,当四边形ABCN是菱形时,求出点N坐标.
17.如图,在平面直角坐标系中,一次函数与反比例函数交于第一象限内A,B(6,1)两点(B在A右侧),分别交x轴,y轴于C,D两点.
(1)求k和b的值;
(2)求点A的坐标;
(3)在y轴上是否存在一点P,使以A,D,P为顶点的三角形与△CDO相似?若存在,求出点P的坐标.若不存在,请说明理由.
18.如图,正比例函数y=﹣3x与反比例函数y(k≠0)的图象交于A、B(1,m)两点,C点在x轴负半轴上,∠ACO=45°.
(1)m= ,k= ,点C的坐标为 ;
(2)点P在x轴上,若以B、O、P为顶点的三角形与△AOC相似,求点P的坐标.
参考答案
1.【解答】解:(1)①已知一次函数y=ax+b与反比例函数y的图象交于A(﹣3,n),B(2,﹣6)两点,将点B的坐标代入y= 得:
﹣6= ,
解得:k=﹣12;
∴反比例函数的表达式为y= ;
将点A的坐标代入y= 得:
,
∴A(﹣3,4);
将点A,点B的坐标代入得:
,
解得:,
∴一次函数的表达式为:y=﹣2x﹣2
②设一次函数y=﹣2x﹣2与x轴交于点C,如图:
由0=﹣2x﹣2得x=﹣1;
∴C(﹣1,0),
∴;
(2)在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;理由如下:
设点P(p,0)(p<0),
①PA=PO,则,
解得:;
②AP=AO,则,
解得:p=﹣6或p=0(不合题意,舍去);
③OP=OA,则,
解得:p=﹣5;
综上所述,在x轴的负半轴上,存在点P,使得△PAO为等腰三角形;点P的坐标为或(﹣6,0)或(﹣5,0).
2.【解答】解:(1)当x=2时,直线l1:y=mx﹣2m+6=6,
∴A(2,6),
∵点A在反比例函数图象上,
∴k=2×6=12,
∴反比例函数的表达式为y;
(2)∵l1⊥l2,
∴设直线l2:yx+b,
把A(2,6)代入得,62+b,
解得b6,
∴直线l2:yx6,
解得,,
∴E(6m,),
解得,,
∴,
设直线BE的解析式为y=cx,
∴,
解得m=±1,
∵m>0,
∴m=1.
方法二:过点A作MN∥x轴,过点B作BM⊥MN 于点M,过点E作 EN⊥MN 于点N.
∵∠M=∠N=∠BAE=90°,
∴∠BAM+∠EAN=∠BAM+∠ABM=90°,
∴∠ABM=∠EAN,
∴△BMA∽△ANE,
∴,
设,
∵直线BE过原点,且点B和点E在反比例函数图象上,
∴,
∴,整理,得,
即,
解得n1=6,n2=﹣6(舍去),
∴点B的坐标为(﹣6,﹣2),
将 B(﹣6,﹣2)代入 y=mx﹣2m+6,得﹣6m﹣2m+6=﹣2,
∴m=1.
(3)方法一:由(2)知B(,﹣2m),E(6m,),
设直线BE解析式为y=k'x+b',
将点B和点E代入得,
,
解得,
∴直线BE的解析式为yx,
∴F(0,),
由直线l1的解析式为y=mx﹣2m+6,可得D(0,﹣2m+6),
∴DF2=(﹣2m+62m)2=(6)2,
BF2=(0)2+(﹣2m2m)2,
∵△BDF是以BD为底边的等腰三角形,
∴DF=BF,即(6)2,
整理得3m2﹣2m+3=0,
解得m,
∵m>0,
∴E(2+2,).
方法二:∵△BDF 为等腰三角形,且BD 为底边,
∴∠CDO=∠ABE,
∵∠COD=∠BAE=90°,
∴△CDO∽△EAB,
∴,即,
∵lAB:y=mx﹣2m+6,
∴,D(0,﹣2m+6),
∴,即,
联立整理,得mx2+(﹣2m+6)x﹣12=0,
解得,x2=2(舍去),
∴点B的坐标为,
∵AB⊥AE,
∴kAB kAE=﹣1,
∴,
设,
将点A(2,6)代入,得,
联立,
整理,得,
解得x1=6m,x2=2(舍去),
∴点E的坐标为,
过点A作 GH∥x轴,过点B作 BG⊥GH于点G,过点E作 EH⊥GH 于点H.
∵∠G=∠H=∠BAE=90°,
∴∠BAG+∠EAH=∠BAG+∠ABG=90°,
∴∠ABG=∠EAH,
∴△BGA∽△AHE,
∴,
∵A(2,6),,,
∴BG=6+2m,AH=6m﹣2,
∴,
解得:,(舍去).
∴点E的坐标为.
方法三:由(2)知B(,﹣2m),E(6m,),
∴KBE,
∴tanα=m,tanθ,tanβ,
∵α=β+θ,
∴tanα=tan(β+θ)m,
∴m,
整理得3m2﹣2m﹣3=0,
解得m,
∵m>0,
∴E(2+2,).
3.【解答】解:(1)把点A(2,a)代入y=2x得a=4,
把点A(2,4)代入y=﹣x+m得m=6,即:y=﹣x+6,
当y=0时,0=﹣x+6,
解得b=6,
∴a=4,m=6,b=6;
(2)设C(t,),
由(1)知A(2,4),B(6,0),而O(0,0),
①当AC,BO为对角线时,AC,BO的中点重合,
∴,
解得,
经检验,t=4,k=﹣16符合题意,
此时点C的坐标为(4,﹣4);
②当CB,AO为对角线时,CB,AO的中点重合,
∴,
解得,
经检验,t=﹣4,k=﹣16符合题意,
此时点C的坐标为(﹣4,4);
③当CO,AB为对角线时,CO,AB的中点重合,
∴,
解得,
∵k=32>0,
∴这种情况不符合题意;
综上所述,C的坐标为(4,﹣4)或(﹣4,4),k的值为﹣16;
(3)设点D(t,0),则点E(﹣t,0),
∵△DAE∽△DBA,
∴AD2=DE DB,即:16+(2﹣t)2=﹣2t(6﹣t),
解得:t1=﹣2,t2=10(不合题意,舍去),
∴点D(﹣2,0),
设直线AD解析式为y=px+q,
将点A(2,4)、点D(﹣2,0)代入y=px+q,
,
解得,
∴直线AD解析式为y=x+2,
∵过AD两点的直线与双曲线有且只有一点C,
∴x+2,
化简得x2+2x﹣k=0,
∵方程x2+2x﹣k=0有且只有一个解,
∴Δ=4+4k=0,
得k=﹣1.
4.【解答】解:(1)由题意可得:4=﹣0+b,6=﹣n+b,
∴b=4,n=﹣2,
∴一次函数解析式为y=﹣x+4,点A(﹣2,6),
∵直线y=﹣x+4与反比例函数y的图象交于点A(﹣2,6),
∴k=6×(﹣2)=﹣12;
(2)令y=0,则y=﹣x+4=4,
∴C(4,0),
∴OC=4,
∴△AOC的面积OC yA4×6=12;
(3)当点Q在y轴上时,设点Q(0,c),点D(m,),
∵以A,B,D,Q为顶点的四边形为平行四边形,
∴BQ和AD是对角线,且互相平分,
∴,
∴m=2,
∴点D(2,﹣6),
∴,
∴c=﹣4,
∴点Q(0,﹣4);
当点Q在x轴上时,设点Q(t,0),点D(m,),
若AQ,BD为对角线,
则,,
∴m=﹣6,t=﹣4,
∴点Q(﹣4,0);
若AD,BQ为对角线,
则,,
∴m=6,t=4,
∴点Q(4,0),
此时点Q在AB的延长线上,不合题意舍去,
当AB,PQ为对角线时,同理可求点P(﹣1.2,10),点Q(﹣0.8,0),
综上所述:点Q(﹣4,0)或(0,﹣4)或(﹣0.8,0).
5.【解答】解:(1)如图1,
过点A作AE⊥x轴于E,
∴∠AEO=90°,
在Rt△AOE中,tan∠AOC,
设AE=m,则OE=2m,
根据勾股定理得,AE2+OE2=OA2,
∴m2+(2m)2=()2,
∴m=1或m=﹣1(舍),
∴OE=2,AE=1,
∴A(﹣2,1),
∵点A在双曲线y上,
∴k2=﹣2×1=﹣2,
∴双曲线的解析式为y,
∵点B在双曲线上,且纵坐标为﹣3,
∴﹣3,
∴x,
∴B(,﹣3),
将点A(﹣2,1),B(,﹣3)代入直线y=k1x+b中得,,
∴,
∴直线AB的解析式为yx﹣2;
(2)如图2,连接OB,PO,PC;
∵D(0,﹣2),
∴OD=2,
由(1)知,B(,﹣3),
∴S△ODBOD xB2,
∵△OCP的面积是△ODB的面积的2倍,
∴S△OCP=2S△ODB=2,
由(1)知,直线AB的解析式为yx﹣2,
令y=0,则x﹣2=0,
∴x,
∴OC,
设点P的纵坐标为n,
∴S△OCPOC yPn,
∴n=2,
由(1)知,双曲线的解析式为y,
∵点P在双曲线上,
∴2,
∴x=﹣1,
∴P(﹣1,2);
(3)由(1)知,A(﹣2,1),B(,﹣3),
由图象知,不等式k1x+b的解集为﹣2≤x<0或x.
6.【解答】(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,),
∴AE=OF=a,
∵AE⊥y轴,
∴AE∥OF,
∴四边形AEFO是平行四边形;
②解:过点B作BD⊥y轴于点D,如图1,
∵AE⊥y轴,
∴AE∥BD,
∴△AEO∽△BDO,
∴,
∴当k=4时,,
即,
∴S△BOE=2S△AOE=1;
(2)不改变.
理由如下:
过点P作PH⊥x轴于点H,PE与x轴交于点G,
设点A的坐标为(a,),点P的坐标为(b,),
则AE=a,OE,PH,
∵四边形AEGO是平行四边形,
∴∠EAO=∠EGO,AE=OG,
∵∠EGO=∠PGH,
∴∠EAO=∠PGH,
又∵∠PHG=∠AEO,
∴△AEO∽△GHP,
∴,
∵GH=OH﹣OG=﹣b﹣a,
∴,
∴k=0,
解得,
∵a,b异号,k>0,
∴,
∴S△POEOE×(﹣b)(﹣b),
∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.
7.【解答】解:(1)∵点A(a,4),
∴AC=4,
∵S△AOC=4,即,
∴OC=2,
∵点A(a,4)在第二象限,
∴a=﹣2 A(﹣2,4),
将A(﹣2,4)代入y得:k=﹣8,
∴反比例函数的关系式为:y,
把B(8,b)代入得:b=﹣1,
∴B(8,﹣1)
因此a=﹣2,b=﹣1;
(2)由图象可以看出mx+n的解集为:﹣2<x<0或x>8;
(3)如图,作点B关于x轴的对称点B′,直线AB′与x轴交于P,
此时PA﹣PB最大(PA﹣PB=PA﹣PB′≤AB′,共线时差最大)
∵B(8,﹣1)
∴B′(8,1)
设直线AP的关系式为y=mx+n,将 A(﹣2,4),B′(8,1)代入得:
,
解得:m,n,
∴直线AP的关系式为yx,
当y=0时,即x0,解得x,
∴P(,0).
8.【解答】解:(1)将点A(4,1)代入y,
得,m2﹣3m=4,
解得,m1=4,m2=﹣1,
∴m的值为4或﹣1;反比例函数解析式为:y;
(2)∵BD⊥y轴,AE⊥y轴,
∴∠CDB=∠CEA=90°,
∴△CDB∽△CEA,
∴,
∵CE=4CD,
∴AE=4BD,
∵A(4,1),
∴AE=4,
∴BD=1,
∴xB=1,
∴yB4,
∴B(1,4),
将A(4,1),B(1,4)代入y=kx+b,
得,,
解得,k=﹣1,b=5,
∴yAB=﹣x+5,
设直线AB与x轴交点为F,
当x=0时,y=5;当y=0时x=5,
∴C(0,5),F(5,0),
则OC=OF=5,
∴△OCF为等腰直角三角形,
∴CFOC=5,
则当OM垂直CF于M时,由垂线段最知可知,OM有最小值,
即OMCF.
9.【解答】解:(1)将A(0,﹣2),B(1,0)代入y=k1x+b,得:
,
解得k1=2,b=﹣2.
所以一次函数的表达式为y=2x﹣2,
将M(m,4)代入y=2x﹣2中,得:
4=2m﹣2,
解得m=3,
所以点M的坐标为(3,4),
因为反比例函数的图象过点M(3,4),得:
,
解得k2=12,
所以反比例函数的表达式为;
(2)根据题意,得:
,
则,
可得S△AOC=S△AMO﹣S△OCM=3﹣1=2,
由OA=2可知点C的横坐标为2,
将x=2代入y=2x﹣2中,得:y=2.
所以点C的坐标为(2,2);
(3)设点P的坐标为(n,0).
根据题意可得,
①如图1所示,
当点O为等腰三角形的顶角顶点时,OP=OM=5,则点P的坐标为(5,0)或(﹣5,0);
②如图2所示.
当点M为等腰三角形的顶角顶点时,MO=MP=5,则(n﹣3)2+42=52.
解得n1=0(舍去),n2=6.
所以,点P的坐标为(6,0);
③如图3所示.
当点P为等腰三角形的顶角顶点时,PO=PM,则:(n﹣3)2+42=n2,
解得,
所以,点P的坐标为.
综上所述,点P的坐标为(5,0),(﹣5,0),(6,0)或.
10.【解答】解:(1)∵x2﹣x﹣30=0,
∴x1=﹣5,x2=6,
∵直线AB与x轴交于点A,与y轴交于点B.OB是一元二次方程x2﹣x﹣30=0的一个根,
∴OB=6,
∵,
∴,
∴OA=8,
∴B(0,6),A(8,0),
∴点D的坐标为,即D(4,3).
(2),
∴E(2,0),
设直线BE的函数解析式为y=kx+b(k≠0),
把B(0,6),E(2,0)代入得:
,
解得:
∴直线BE的函数解析式为y=﹣3x+6,
∵D(4,3),
设直线OD的函数解析式为y=mx,
∴4m=3,解得,
∴直线OD的函数解析式为,
当时,,
此时,
∴,
∴F′为,
∴.
(3)设直线AB的解析式为y=ax+b,
将点AB的坐标代入得,
,解得:
∴直线AB的解析式为,
∵点P在直线AB上,
∴设点,
∴,,AE2=(8﹣2)2=36,
①当PE=AP时,,
解得:,
∴,
∴点P的坐标为;
②当PE=AE时,
解得:t1=8,
∴,此时点P不存在,
,
∴点P的坐标为;
③当AP=AE时,,
解得:,,
∴P或;
综上,P或或或.
11.【解答】解:(1)∵PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,
∴PN=2、
∴点P的坐标为(1,2).
∵反比例函数(x>0)的图象、一次函数y=x+b的图象都经过点P,
由,2=1+b得k=2,b=1、
∴反比例函数为,一次函数为y=x+1;
(2)Q1(0,1),Q2(0,﹣1).
12.【解答】解:(1)①∵△OAD的面积=2,
即,
∴k=4,
故答案为:4;
②在矩形OABC中,OA=BC=3,OC=AB=6,
∵k=4,
∴反比例函数的解析式是:y(x>0),
∵OA=3,
即点D的纵坐标是3,
令y3,
解得:x,
∴D(,3),
同理,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
∴S△ODE=S矩形OABC﹣S△OAD﹣S△OCE﹣S△BDE=OA OC;
(2)过点D作DG⊥x轴于点G,则DG=OA=3,
∵OA=3,即点D的纵坐标是3,
令y,
得:x,
∴D(,3),
同理可得,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
由折叠的性质可知:DF=BD=6,FE=BE=3,∠DFE=∠B=90°,
∴∠DFG+∠CFE=90°,
∵DG⊥x轴,
∴∠DFG+∠GDF=90°,
∴∠CFE=∠GDF,
∵∠CFE=∠GDF,∠FCE=∠DGF=90°,
∴△CFE∽△GDF,
∴,
即,
∴GF,
∵DG⊥x轴,
∴△GDF是直角三角形,DG2+GF2=DF2,
∴,
解得:k,
即k的值为.
13.【解答】解:(1)∵点C(0,2)在直线y=x+b上,
∴b=2,
∴一次函数的表达式为y=x+2;
∵点A(1,a)在直线y=x+2上,
∴a=1+2=3,
∴A(1,3),
∵点A(1,3)在反比例函数的图象上,
∴k=1×3=3,
∴反比例函数的表达式为;
(2)在y=x+2中,令y=0,
解得x=﹣2,
∴B(﹣2,0),
又∵A(1,3),
∴,
由函数图象得:当0<x<1时,双曲线位于直线上方;
(3)∵直线AB的表达式为y=x+2,反比例函数的表达式为,
设点,N(n,n+2),
若以点O、M、C、N为顶点的四边形是平行四边形,
则分情况讨论:
①以OC和MN为对角线时,
可得:,,
解得:,或(此时点M不在第一象限,舍去),
∴;
②以CN和OM为对角线时,
可得:,,
解得:或(此时点M不在第一象限,舍去),
∴,
③以CM和ON为对角线时,
可得:,,
∴或(此时点M不在第一象限,舍去),
∴,
综上,满足条件的点N的坐标为,,.
14.【解答】解:(1)将点A的坐标代入反比例函数表达式得:6,解得:m=6,
故反比例函数表达式为:y,
当x=3时,y2,即点B(3,2),
由题意得:,解得:,
故一次函数的表达式为:y=﹣2x+8;
(2)设AB交x轴于点H,
令y=﹣2x+8=0,解得:x=4,即OH=4,
则△AOB的面积=S△AOH﹣S△BOH4×64×2=8;
(3)设点M、N的坐标别为(m,1)、(0,n),
当AB是对角线时,由中点坐标公式得:,解得:,
即点M、N的坐标分别为(4,1)、(0,7);
当AM是对角线时,由中点坐标公式得:,解得:,
即点M、N的坐标分别为:(2,1)、(0,5);
当AN是对角线时,由中点坐标公式得:,解得:,
即即点M、N的坐标分别为:(﹣2,1)、(0,﹣3);
综上,点M、N的坐标分别为(4,1)、(0,7)或(2,1)、(0,5)或(﹣2,1)、(0,﹣3).
15.【解答】解:(1)∵四边形OACB是矩形,
∴AC=OB=6,
∴C(8,6),
∵点D是AC的中点,
∴D(8,3),
∴k=8×3=24,
∴y,
当y=6时,x=4,
∴E(4,6),
故答案为:(8,3),(4,6);
(2)①由题意知,S△ODE=S梯形OACE﹣S△OAD﹣S△ECD
(4+8)×63
=18,
∵S△PBOS△ODE.
∴6×xP18,
∴xP=3,
∴y=8,
∴P的坐标为(3,8);
②由①知,点P在直线x=3上,设直线x=3交x轴于H,
当AC=AP=6时,若点P在第一象限,
∴PH,
∴Q(3,6),
当点P在第四象限舍去,
当CA=CP时,
同理得,Q(3,),Q'(3,),
当PC=PA时,点P(3,3),
则点Q与P关于AC对称,
∴Q(13,3),
综上,点Q(3,6)或(3,)或(3,)或(13,3).
16.【解答】解:(1)根据题意,设C点的坐标为(a,b),
∴b,
∴ab=k,即得AC OA=k,
又∵CA∥y轴,
∴S△ABCAC OA,
∴k,
即k=2,
∴反比例函数的解析式为y;
(2)如图,根据菱形的性质可知,AC⊥BN,且AC与BN互相平分,
设菱形对角线的交点为P,设C点坐标为(a,b),
∵△ABC是等边三角形,四边形ABCN是菱形,
∴P(a,b),N(2a,b),
即BP=OA=a,AP=CPb,
∵∠BAC=60°,
∴BP=AP×tan60°,
即ab,
由(1)知ab=2,C点在第一象限,
∴a,b=2,
∴N(2,1).
17.【解答】解:(1)∵一次函数yx+b与反比例函数y交于B点,
∴16+b,1,
∴b=4,k=6;
(2)由(1)知一次函数的解析式为yx+4,反比例函数的解析式为y,
解得,,
∴A(2,3);
(3)存在以A,D,P为顶点的三角形与△CDO相似.
∵一次函数yx+4与x轴,y轴交于C,D两点,
∴C(8,0),D(0,4),
∴OC=8,OD=4,
设P(0,a),
∵∠COD=90°,∠APD=∠CDO,
①当∠APD=90°时,△APD∽△COD,
∵A(2,3),
∴AP=2,OP=3,
∴P(0,3);
②当∠PAD=90°时,△PAD∽△COD,
∴,
∵AD,CD4,PD=4﹣a,
∴,
解得a=﹣1,
∴P(0,﹣1),
综上所述,P(0,3)或(0,﹣1).
18.【解答】解:(1)当x=1时,y=﹣3x=﹣3=m,即点B(1,﹣3),
将点B的坐标代入反比例函数的表达式得:k=﹣3×1=﹣3,
即反比例函数的表达式为:y,
根据正比例函数的对称性,点A(﹣1,3),
由点O、A的坐标得,OA,过点A作AH⊥x轴于点H,
由直线AB的表达式知,tan∠AOH=3,
而∠ACO=45°,
设AH=3x=CH,则OH=x,则AOx,则x=1,
则AH=CH=3,OH=1,
则CO=CH+OH=4,
则点C的坐标为:(﹣4,0),
故答案为:﹣3,﹣3,(﹣4,0);
(2)当点P在x轴的负半轴时,
∵∠BOP>90°>∠AOC,
又∵∠BOP>∠ACO,∠BOP>∠CAO,
∴△BOP和△AOC不可能相似;
当点P在x轴的正半轴时,∠AOC=∠BOP,
若△AOC∽△BOP,则,
则OP=OC=4,
即点P(4,0);
若△AOC∽△POB,则,
即,
解得:OP=2.5,
即点P(2.5,0),
综上,点P的坐标为:(4,0)或(2.5,0).
21世纪教育网(www.21cnjy.com)
同课章节目录
