2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 373.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:53:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练
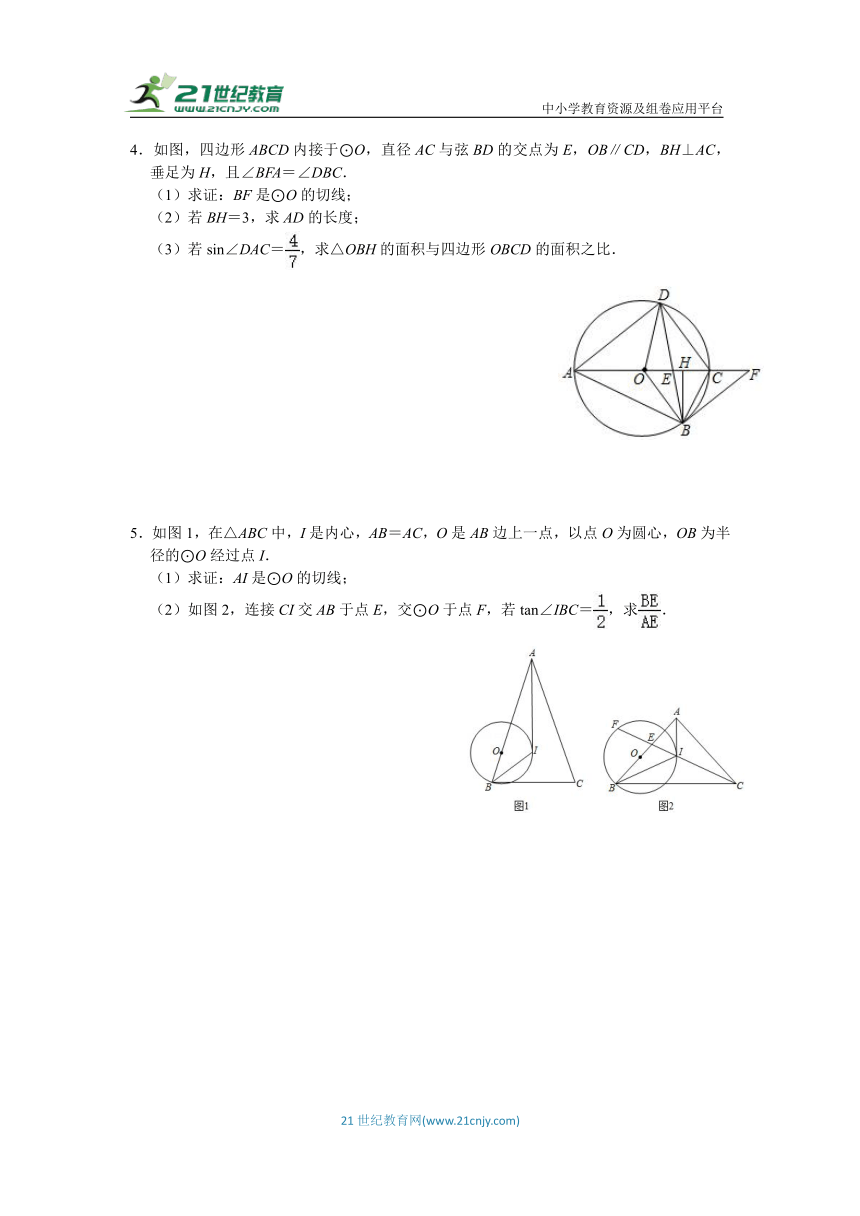
1.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=10,求AE的长;
(3)若△CDE的面积是△OBF面积的,求的值.
2.如图,在Rt△ABC中,∠C=90°,O在AB上,以O为圆心,以OA长为半径的圆分别与AC,AB交于点D,E,直线BD与⊙O相切于点 D.
(1)求证:∠CBD=∠A;
(2)若AC=6,AD:BC=1:.
①求线段BD的长;
②求⊙O的面积.
3.如图,四边形ABCD为正方形,取AB中点O,以AB为直径,O圆心作圆.
(1)如图1,取CD的中点P,连接BP交⊙O于Q,连接DQ并延长交AB的延长线于E,求证:QE2=BE AE;
(2)如图2,连接CO并延长交⊙O于M点,求tanM的值.
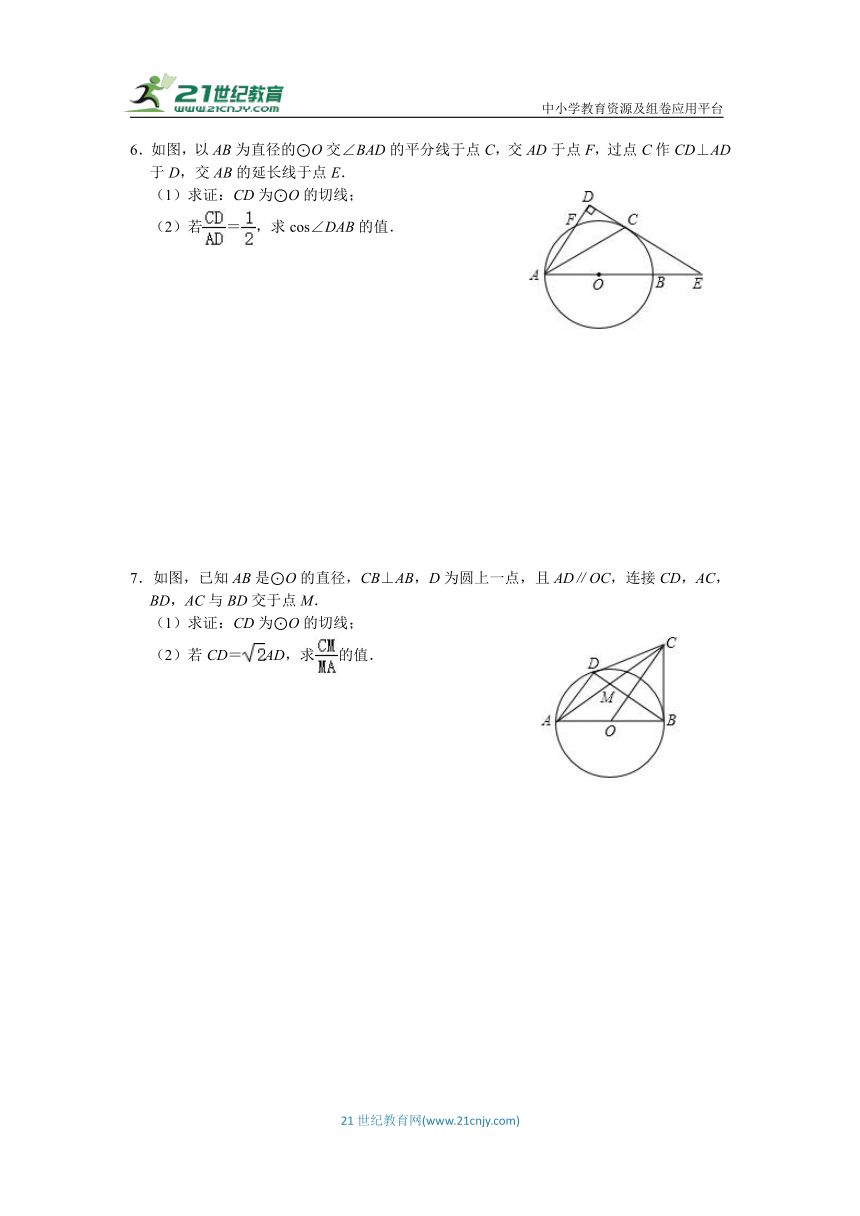
4.如图,四边形ABCD内接于⊙O,直径AC与弦BD的交点为E,OB∥CD,BH⊥AC,垂足为H,且∠BFA=∠DBC.
(1)求证:BF是⊙O的切线;
(2)若BH=3,求AD的长度;
(3)若sin∠DAC=,求△OBH的面积与四边形OBCD的面积之比.
5.如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=,求.
6.如图,以AB为直径的⊙O交∠BAD的平分线于点C,交AD于点F,过点C作CD⊥AD于D,交AB的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若=,求cos∠DAB的值.
7.如图,已知AB是⊙O的直径,CB⊥AB,D为圆上一点,且AD∥OC,连接CD,AC,BD,AC与BD交于点M.
(1)求证:CD为⊙O的切线;
(2)若CD=AD,求的值.
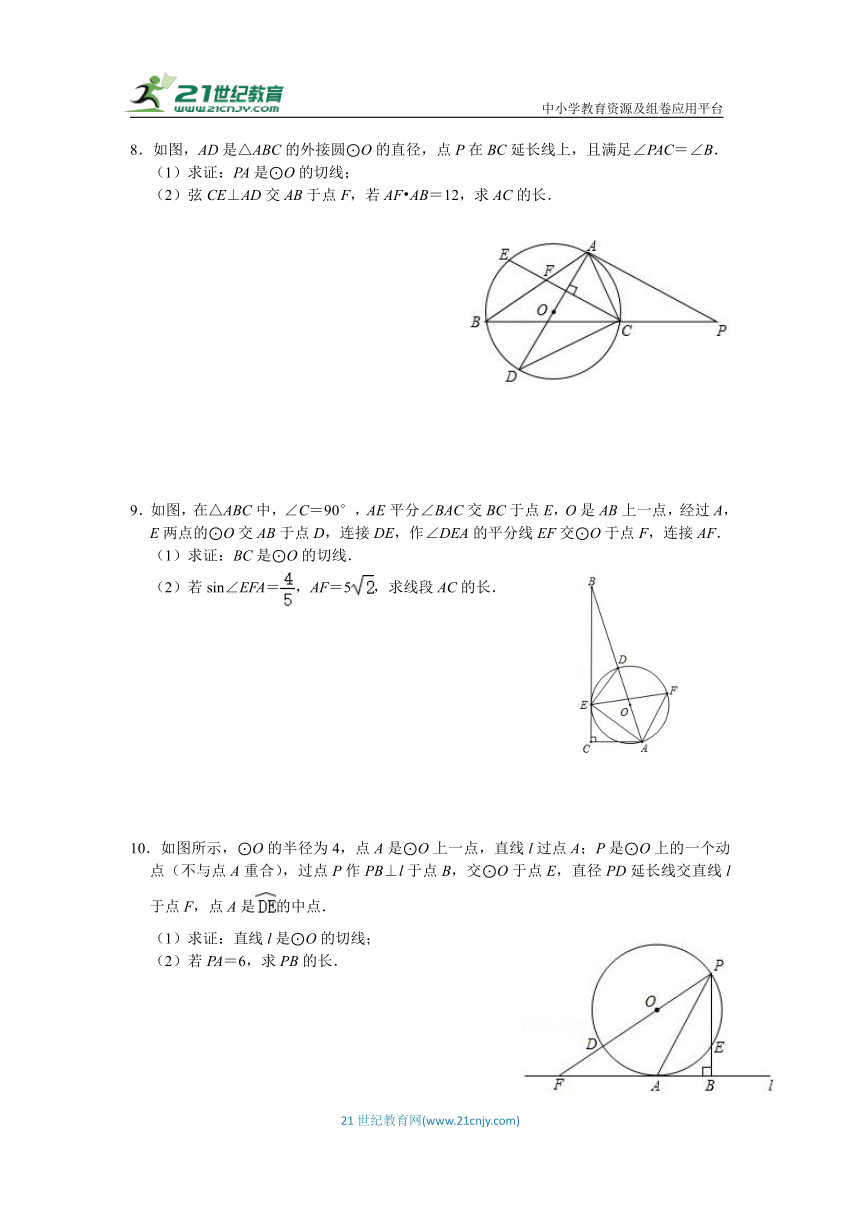
8.如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠PAC=∠B.
(1)求证:PA是⊙O的切线;
(2)弦CE⊥AD交AB于点F,若AF AB=12,求AC的长.
9.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
(1)求证:BC是⊙O的切线.
(2)若sin∠EFA=,AF=5,求线段AC的长.
10.如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.
11.如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.
(1)求证:DC为⊙O的切线;
(2)线段DF分别交AC,BC于点E,F且∠CEF=45°,⊙O的半径为5,sinB=,求CF的长.
12.如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.
(1)求证:AC∥PO;
(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求的值.
13.如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC;
(2)若BD=AD,AC=3,求CD的长.
14.已知:如图,在△ABC中,AB=AC,点P是底边BC上一点且满足PA=PB,⊙O是△PAB的外接圆,过点P作PD∥AB交AC于点D.
(1)求证:PD是⊙O的切线;
(2)若BC=8,tan∠ABC=,求⊙O的半径.
参考答案
1.【解答】解:(1)连接AD,
∵AB是⊙O直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴,即,
∴CE=2,
∴AE=AC﹣CE=AB﹣CE=8;
(3)∵,
∴设S△CDE=5k,S△OBF=6k,
∵BD=CD,
∴S△CDE=S△BDE=5k,
∵BD=CD,AO=BO,
∴OD∥AC,
∵△OBF∽△ABE,
∴,
∴S△ABE=4S△OBF,
∴S△ABE=4S△OBF=24k,
∴S△CAB=S△CDE+S△BDE+S△ABE=34k,
∵△CDE∽△CAB,
∴,
∴,
∵BC=2CD,
∴.
2.【解答】解:(1)证明:连接OD,
∵直线BD与⊙O相切于点D,
∴∠BDO=90°,
∴∠BDC+∠ODA=90°,
∵∠C=90°,
∴∠CBD+∠BDC=90°,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠BDC+∠OAD=90°,
∴∠CBD=∠A;
(2)①∵∠C=∠C,∠CBD=∠A,
∴△ACB∽△BCD,
∴=,
∵AC=6,AD:BC=1:.
∴设AD=x,BC=x,
∴=,
解得:x=3.
∴BC=3,CD=AC﹣AD=3
根据勾股定理得,BD=3;
②由①可知BC=3.
又∵∠C=90°,AC=6,
∴在Rt△ABC中,由勾股定理得:AB==3,
设OA=OD=r,则OB=3﹣r,
∴在Rt△OBD中,由勾股定理得:r2+=,
解得:r=,
∴⊙O的面积为:π×=.
3.【解答】(1)证明:如图1中,连接OD,OQ,设AQ交OD于K.
∵四边形ABCD是正方形,
∴CD=AB,CD∥AB,
∴DP=CD,OB=AB,
∴DP=OB,
∴四边形PDOB是平行四边形,
∴OD∥PB,
∵AB是直径,
∴∠AQB=90°,
∴∠AKO=∠AQB=90°,
∵OK∥BQ,AO=OB,
∴AK=KQ,
∴OD垂直平分线段AQ,
∴DA=DQ,
∵OD=OD,OA=OQ,
∴△ODA≌△ODQ(SSS),
∴∠DQO=∠DAO=90°,
∴∠EQO=90°,
∴∠EQB+∠OQB=90°,
∵OQ=OB,
∴∠OQB=∠OBQ,
∵∠QAB+∠ABQ=90°,
∴∠EQB=∠EAQ,
∵∠E=∠E,
∴△EQB∽△EAQ,
∴=,
∴EQ2=EA EB.
(2)解:如图2中,作BT⊥CM于T.设AB=BC=2a.
∵四边形ABCD是正方形,
∴∠OBC=90°,
∵OB=OA=a,BC=2a,
∴OC===a,
∵S△OBC= OB BC= OC BT,
∴BT=a,OT===a,
∴MT=OM+OT=a+a,
∴tanM===.
4.【解答】解:(1)证明:∵∠BFA=∠BDC,∠BDC=∠DAC,
∴∠DAC=∠BFA,
∵OB∥CD,
∴∠BOF=∠ACD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∴∠BOF+∠F=90°,
∴∠OBF=90°,
∴OB⊥BF,
∴BF是⊙O的切线;
(2)∵BH⊥AC,
∴∠OHB=90°,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ADC=∠OHB,
∵∠BOC=∠ACD,
∴△ACD∽△BOH,
∴,
∵BH=3,
∴AD=6;
(3)∵△ACD∽△BOH,
∴∠DAC=∠OBH,
∵sin∠DAC==,
∴sin∠OBH=,设OH=4a,OB=7a,
∴AC=2OB=14a,
∴DC=8a,
∴BH==a,
过C作CM⊥OB于M,
∵OB=OC,
∴CM=BH=a,
∵OB∥CD,CM⊥OB,
∴CM⊥CD,
∴S四边形OBCD=S△OCD+S△OCB
=CD CM+OB CM
=(8a+7a)×a
=,
S△OBH=OH×BH=4a×a=2a2,
∴=.
答:△OBH的面积与四边形OBCD的面积之比为.
5.【解答】(1)证明:延长AI交BC于D,连接OI.
∵I是△ABC的内心,
∴BI平分∠ABC,AI平分∠BAC.
∴∠1=∠3,
∵AB=AC,
∴AD⊥BC.
又∵OB=OI,
∴∠3=∠2.
∴∠1=∠2.
∴OI∥BD,
∴OI⊥AI.
∴AI为⊙O的切线;
(2)解:连接BF,过B作BM⊥CF于M
由(1)得AD垂直平分BC,
∴BI=CI,
∴∠1=∠4
故∠1=∠2=∠3=∠4=α,
∴∠BOI=180°﹣2α,
∴∠F=BOI=90°﹣α,
∴∠F+∠4=90°,
∴∠FBC=∠ADC=90°,
∴BF∥AD,
∴△AEI~△BEF,
∴.
∵DI∥BF,BD=CD,
∴CI=FI,
∴BF=2ID,
故,
设ID=a,
∵,
∴,
由面积法:,
∴,
又∠MIB=2∠1=∠ABD,
∴tan∠MIB=tan∠ABD,
∴,
∴,
∴,
∴.
6.【解答】(1)证明:连接OC,如图,
∵AC平分∠BAD,
∴∠DAC=∠EAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴CD为⊙O的切线;
(2)解:作OH⊥AD于H,如图,则AH=HF,
易得四边形OCDH为矩形,
∴OH=CD,OC=DH,
∵=,
∴设CD=x,则AD=2x,
设⊙O的半径为r,
∴AH=2x﹣r,OA=r,
在Rt△OAH中,x2+(2x﹣r)2=r2,解得x=r,
∴AH=r,
在Rt△OAH中,cos∠HAO===.
7.【解答】(1)证明:连接OD,设OC交BD于K.
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥AD,
∴OC⊥BD,
∴DK=KB,
∴CD=CB,
∵OD=OB,OC=OC,CD=CB,
∴△ODC≌△OBC(SSS),
∴∠ODC=∠OBC,
∵CB⊥AB,
∴∠OBC=90°,
∴∠ODC=90°,
∴OD⊥CD,
∴CD是⊙O的切线.
(2)解:∵CD=AD,
∴可以假设AD=a,CD=a,设KC=b.
∵DK=KB,AO=OB,
∴OK=AD=a,
∵∠DCK=∠DCO,∠CKD=∠CDO=90°,
∴△CDK∽△COD,
∴=,
∴=
整理得:2()2+()﹣4=0,
解得=或(舍弃),
∵CK∥AD,
∴===.
8.【解答】(1)∵AD是⊙O的直径
∴∠ACD=90°;
∴∠CAD+∠D=90°
∵∠PAC=∠PBA,∠D=∠PBA,
∴∠CAD+∠PAC=90°,
∴∠PAD=90°,
∴PA⊥AD,
∵点A在⊙O上,
∴PA是⊙O的切线
(2)∵CF⊥AD,
∴∠ACF+∠CAD=90°,
∵∠CAD+∠D=90°,
∴∠D=∠ACF,
∴∠B=∠ACF,
∵∠BAC=∠CAF,
∴△ABC∽△ACF,
∴,
∴AC2=AF AB
∵AF AB=12,
∴AC2=12,
∴AC=2.
9.【解答】证明:(1)连接OE,
∵OE=OA,
∴∠OEA=∠OAE,
∵AE平分∠BAC,
∴∠OAE=∠CAE,
∴∠CAE=∠OEA,
∴OE∥AC,
∴∠BEO=∠C=90°,
∴BC是⊙O的切线;
(2)过A作AH⊥EF于H,
Rt△AHF中,sin∠EFA=,
∵AF=5,
∴AH=4,
∵AD是⊙O的直径,
∴∠AED=90°,
∵EF平分∠AED,
∴∠AEF=45°,
∴△AEH是等腰直角三角形,
∴AE=AH=8,
∵sin∠EFA=sin∠ADE==,
∴AD=10,
∵∠DAE=∠EAC,∠DEA=∠ECA=90°,
∴△AED∽△ACE,
∴,
∴,
∴AC=6.4.
10.【解答】(1)证明:连接DE,OA.
∵PD是直径,
∴∠DEP=90°,
∵PB⊥FB,
∴∠DEP=∠FBP,
∴DE∥BF,
∵=,
∴OA⊥DE,
∴OA⊥BF,
∴直线l是⊙O的切线.
(2)解:作OH⊥PA于H.
∵OA=OP,OH⊥PA,
∴AH=PH=3,
∵OA∥PB,
∴∠OAH=∠APB,
∵∠AHO=∠ABP=90°,
∴△AOH∽△PAB,
∴=,
∴=,
∴PB=.
11.【解答】(1)证明:连接OC,
∵AB为⊙O的直径,
∴∠ACB=∠BCO+∠OCA=90°,
∵OB=OC,
∴∠B=∠BCO,
∵∠ACD=∠B,
∴∠ACD=∠BCO,
∴∠ACD+∠OCA=90°,即∠OCD=90°,
∴DC为⊙O的切线;
(2)解:Rt△ACB中,AB=10,
sinB=,
∴AC=6,BC=8,
∵∠ACD=∠B,∠ADC=∠CDB,
∴△CAD∽△BCD,
∴,
设AD=3x,CD=4x,
Rt△OCD中,OC2+CD2=OD2,
52+(4x)2=(5+3x)2,
x=0(舍)或,
∵∠CEF=45°,∠ACB=90°,
∴CE=CF,
设CF=a,
∵∠CEF=∠ACD+∠CDE,
∠CFE=∠B+∠BDF,
∴∠CDE=∠BDF,
∵∠ACD=∠B,
∴△CED∽△BFD,
∴,
∴,a=,
∴CF=.
12.【解答】(1)证明:∵PA、PB是⊙O的两条切线,A、B是切点,
∴PA=PB,且PO平分∠BPA,
∴PO⊥AB.
∵BC是直径,
∴∠CAB=90°,
∴AC⊥AB,
∴AC∥PO;
(2)解:连结OA、DF,如图,
∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAQ=∠PBQ=90°.
在Rt△OAQ中,OA=OC=3,∴OQ=5.
由QA2+OA2=OQ2,得QA=4.
在Rt△PBQ中,PA=PB,QB=OQ+OB=8,
由QB2+PB2=PQ2,得82+PB2=(PB+4)2,
解得PB=6,
∴PA=PB=6,
∵OP⊥AB,
∴BF=AF=AB.
又∵D为PB的中点,
∴DF∥AP,DF=PA=3,
∴△DFE∽△QEA,
∴==,
设AE=4t,FE=3t,则AF=AE+FE=7t,
∴BE=BF+FE=AF+FE=7t+3t=10t,
∴==.
13.【解答】(1)证明:连接OD,如图所示.
∵OB=OD,
∴∠OBD=∠ODB.
∵CD是⊙O的切线,OD是⊙O的半径,
∴∠ODB+∠BDC=90°.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠OBD+∠CAD=90°,
∴∠CAD=∠BDC.
(2)解:∵∠C=∠C,∠CAD=∠CDB,
∴△CDB∽△CAD,
∴=.
∵BD=AD,
∴=,
∴=,
又∵AC=3,
∴CD=2.
14.【解答】(1)证明:如图1,连接OP,
∵PA=PB,
∴,
∴OP⊥AB,
∵PD∥AB,
∴OP⊥PD,
∴PD是⊙O的切线;
(2)如图2,过A作AH⊥BC于H,连接OA,OP,OP交AB于E,
∵AB=AC,
∴BH=BC==4,
Rt△ABH中,tan∠ABC===,
∴AH=2,AB==2,
∴BE=,PE=,
设⊙O的半径为r,则OA=r,OE=r﹣,
由勾股定理得:,
r=,
答:⊙O的半径是.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练圆中相似三角形综合训练
1.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=10,求AE的长;
(3)若△CDE的面积是△OBF面积的,求的值.
2.如图,在Rt△ABC中,∠C=90°,O在AB上,以O为圆心,以OA长为半径的圆分别与AC,AB交于点D,E,直线BD与⊙O相切于点 D.
(1)求证:∠CBD=∠A;
(2)若AC=6,AD:BC=1:.
①求线段BD的长;
②求⊙O的面积.
3.如图,四边形ABCD为正方形,取AB中点O,以AB为直径,O圆心作圆.
(1)如图1,取CD的中点P,连接BP交⊙O于Q,连接DQ并延长交AB的延长线于E,求证:QE2=BE AE;
(2)如图2,连接CO并延长交⊙O于M点,求tanM的值.
4.如图,四边形ABCD内接于⊙O,直径AC与弦BD的交点为E,OB∥CD,BH⊥AC,垂足为H,且∠BFA=∠DBC.
(1)求证:BF是⊙O的切线;
(2)若BH=3,求AD的长度;
(3)若sin∠DAC=,求△OBH的面积与四边形OBCD的面积之比.
5.如图1,在△ABC中,I是内心,AB=AC,O是AB边上一点,以点O为圆心,OB为半径的⊙O经过点I.
(1)求证:AI是⊙O的切线;
(2)如图2,连接CI交AB于点E,交⊙O于点F,若tan∠IBC=,求.
6.如图,以AB为直径的⊙O交∠BAD的平分线于点C,交AD于点F,过点C作CD⊥AD于D,交AB的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若=,求cos∠DAB的值.
7.如图,已知AB是⊙O的直径,CB⊥AB,D为圆上一点,且AD∥OC,连接CD,AC,BD,AC与BD交于点M.
(1)求证:CD为⊙O的切线;
(2)若CD=AD,求的值.
8.如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠PAC=∠B.
(1)求证:PA是⊙O的切线;
(2)弦CE⊥AD交AB于点F,若AF AB=12,求AC的长.
9.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
(1)求证:BC是⊙O的切线.
(2)若sin∠EFA=,AF=5,求线段AC的长.
10.如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.
11.如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.
(1)求证:DC为⊙O的切线;
(2)线段DF分别交AC,BC于点E,F且∠CEF=45°,⊙O的半径为5,sinB=,求CF的长.
12.如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.
(1)求证:AC∥PO;
(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求的值.
13.如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC;
(2)若BD=AD,AC=3,求CD的长.
14.已知:如图,在△ABC中,AB=AC,点P是底边BC上一点且满足PA=PB,⊙O是△PAB的外接圆,过点P作PD∥AB交AC于点D.
(1)求证:PD是⊙O的切线;
(2)若BC=8,tan∠ABC=,求⊙O的半径.
参考答案
1.【解答】解:(1)连接AD,
∵AB是⊙O直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴,即,
∴CE=2,
∴AE=AC﹣CE=AB﹣CE=8;
(3)∵,
∴设S△CDE=5k,S△OBF=6k,
∵BD=CD,
∴S△CDE=S△BDE=5k,
∵BD=CD,AO=BO,
∴OD∥AC,
∵△OBF∽△ABE,
∴,
∴S△ABE=4S△OBF,
∴S△ABE=4S△OBF=24k,
∴S△CAB=S△CDE+S△BDE+S△ABE=34k,
∵△CDE∽△CAB,
∴,
∴,
∵BC=2CD,
∴.
2.【解答】解:(1)证明:连接OD,
∵直线BD与⊙O相切于点D,
∴∠BDO=90°,
∴∠BDC+∠ODA=90°,
∵∠C=90°,
∴∠CBD+∠BDC=90°,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠BDC+∠OAD=90°,
∴∠CBD=∠A;
(2)①∵∠C=∠C,∠CBD=∠A,
∴△ACB∽△BCD,
∴=,
∵AC=6,AD:BC=1:.
∴设AD=x,BC=x,
∴=,
解得:x=3.
∴BC=3,CD=AC﹣AD=3
根据勾股定理得,BD=3;
②由①可知BC=3.
又∵∠C=90°,AC=6,
∴在Rt△ABC中,由勾股定理得:AB==3,
设OA=OD=r,则OB=3﹣r,
∴在Rt△OBD中,由勾股定理得:r2+=,
解得:r=,
∴⊙O的面积为:π×=.
3.【解答】(1)证明:如图1中,连接OD,OQ,设AQ交OD于K.
∵四边形ABCD是正方形,
∴CD=AB,CD∥AB,
∴DP=CD,OB=AB,
∴DP=OB,
∴四边形PDOB是平行四边形,
∴OD∥PB,
∵AB是直径,
∴∠AQB=90°,
∴∠AKO=∠AQB=90°,
∵OK∥BQ,AO=OB,
∴AK=KQ,
∴OD垂直平分线段AQ,
∴DA=DQ,
∵OD=OD,OA=OQ,
∴△ODA≌△ODQ(SSS),
∴∠DQO=∠DAO=90°,
∴∠EQO=90°,
∴∠EQB+∠OQB=90°,
∵OQ=OB,
∴∠OQB=∠OBQ,
∵∠QAB+∠ABQ=90°,
∴∠EQB=∠EAQ,
∵∠E=∠E,
∴△EQB∽△EAQ,
∴=,
∴EQ2=EA EB.
(2)解:如图2中,作BT⊥CM于T.设AB=BC=2a.
∵四边形ABCD是正方形,
∴∠OBC=90°,
∵OB=OA=a,BC=2a,
∴OC===a,
∵S△OBC= OB BC= OC BT,
∴BT=a,OT===a,
∴MT=OM+OT=a+a,
∴tanM===.
4.【解答】解:(1)证明:∵∠BFA=∠BDC,∠BDC=∠DAC,
∴∠DAC=∠BFA,
∵OB∥CD,
∴∠BOF=∠ACD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∴∠BOF+∠F=90°,
∴∠OBF=90°,
∴OB⊥BF,
∴BF是⊙O的切线;
(2)∵BH⊥AC,
∴∠OHB=90°,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ADC=∠OHB,
∵∠BOC=∠ACD,
∴△ACD∽△BOH,
∴,
∵BH=3,
∴AD=6;
(3)∵△ACD∽△BOH,
∴∠DAC=∠OBH,
∵sin∠DAC==,
∴sin∠OBH=,设OH=4a,OB=7a,
∴AC=2OB=14a,
∴DC=8a,
∴BH==a,
过C作CM⊥OB于M,
∵OB=OC,
∴CM=BH=a,
∵OB∥CD,CM⊥OB,
∴CM⊥CD,
∴S四边形OBCD=S△OCD+S△OCB
=CD CM+OB CM
=(8a+7a)×a
=,
S△OBH=OH×BH=4a×a=2a2,
∴=.
答:△OBH的面积与四边形OBCD的面积之比为.
5.【解答】(1)证明:延长AI交BC于D,连接OI.
∵I是△ABC的内心,
∴BI平分∠ABC,AI平分∠BAC.
∴∠1=∠3,
∵AB=AC,
∴AD⊥BC.
又∵OB=OI,
∴∠3=∠2.
∴∠1=∠2.
∴OI∥BD,
∴OI⊥AI.
∴AI为⊙O的切线;
(2)解:连接BF,过B作BM⊥CF于M
由(1)得AD垂直平分BC,
∴BI=CI,
∴∠1=∠4
故∠1=∠2=∠3=∠4=α,
∴∠BOI=180°﹣2α,
∴∠F=BOI=90°﹣α,
∴∠F+∠4=90°,
∴∠FBC=∠ADC=90°,
∴BF∥AD,
∴△AEI~△BEF,
∴.
∵DI∥BF,BD=CD,
∴CI=FI,
∴BF=2ID,
故,
设ID=a,
∵,
∴,
由面积法:,
∴,
又∠MIB=2∠1=∠ABD,
∴tan∠MIB=tan∠ABD,
∴,
∴,
∴,
∴.
6.【解答】(1)证明:连接OC,如图,
∵AC平分∠BAD,
∴∠DAC=∠EAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴CD为⊙O的切线;
(2)解:作OH⊥AD于H,如图,则AH=HF,
易得四边形OCDH为矩形,
∴OH=CD,OC=DH,
∵=,
∴设CD=x,则AD=2x,
设⊙O的半径为r,
∴AH=2x﹣r,OA=r,
在Rt△OAH中,x2+(2x﹣r)2=r2,解得x=r,
∴AH=r,
在Rt△OAH中,cos∠HAO===.
7.【解答】(1)证明:连接OD,设OC交BD于K.
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥AD,
∴OC⊥BD,
∴DK=KB,
∴CD=CB,
∵OD=OB,OC=OC,CD=CB,
∴△ODC≌△OBC(SSS),
∴∠ODC=∠OBC,
∵CB⊥AB,
∴∠OBC=90°,
∴∠ODC=90°,
∴OD⊥CD,
∴CD是⊙O的切线.
(2)解:∵CD=AD,
∴可以假设AD=a,CD=a,设KC=b.
∵DK=KB,AO=OB,
∴OK=AD=a,
∵∠DCK=∠DCO,∠CKD=∠CDO=90°,
∴△CDK∽△COD,
∴=,
∴=
整理得:2()2+()﹣4=0,
解得=或(舍弃),
∵CK∥AD,
∴===.
8.【解答】(1)∵AD是⊙O的直径
∴∠ACD=90°;
∴∠CAD+∠D=90°
∵∠PAC=∠PBA,∠D=∠PBA,
∴∠CAD+∠PAC=90°,
∴∠PAD=90°,
∴PA⊥AD,
∵点A在⊙O上,
∴PA是⊙O的切线
(2)∵CF⊥AD,
∴∠ACF+∠CAD=90°,
∵∠CAD+∠D=90°,
∴∠D=∠ACF,
∴∠B=∠ACF,
∵∠BAC=∠CAF,
∴△ABC∽△ACF,
∴,
∴AC2=AF AB
∵AF AB=12,
∴AC2=12,
∴AC=2.
9.【解答】证明:(1)连接OE,
∵OE=OA,
∴∠OEA=∠OAE,
∵AE平分∠BAC,
∴∠OAE=∠CAE,
∴∠CAE=∠OEA,
∴OE∥AC,
∴∠BEO=∠C=90°,
∴BC是⊙O的切线;
(2)过A作AH⊥EF于H,
Rt△AHF中,sin∠EFA=,
∵AF=5,
∴AH=4,
∵AD是⊙O的直径,
∴∠AED=90°,
∵EF平分∠AED,
∴∠AEF=45°,
∴△AEH是等腰直角三角形,
∴AE=AH=8,
∵sin∠EFA=sin∠ADE==,
∴AD=10,
∵∠DAE=∠EAC,∠DEA=∠ECA=90°,
∴△AED∽△ACE,
∴,
∴,
∴AC=6.4.
10.【解答】(1)证明:连接DE,OA.
∵PD是直径,
∴∠DEP=90°,
∵PB⊥FB,
∴∠DEP=∠FBP,
∴DE∥BF,
∵=,
∴OA⊥DE,
∴OA⊥BF,
∴直线l是⊙O的切线.
(2)解:作OH⊥PA于H.
∵OA=OP,OH⊥PA,
∴AH=PH=3,
∵OA∥PB,
∴∠OAH=∠APB,
∵∠AHO=∠ABP=90°,
∴△AOH∽△PAB,
∴=,
∴=,
∴PB=.
11.【解答】(1)证明:连接OC,
∵AB为⊙O的直径,
∴∠ACB=∠BCO+∠OCA=90°,
∵OB=OC,
∴∠B=∠BCO,
∵∠ACD=∠B,
∴∠ACD=∠BCO,
∴∠ACD+∠OCA=90°,即∠OCD=90°,
∴DC为⊙O的切线;
(2)解:Rt△ACB中,AB=10,
sinB=,
∴AC=6,BC=8,
∵∠ACD=∠B,∠ADC=∠CDB,
∴△CAD∽△BCD,
∴,
设AD=3x,CD=4x,
Rt△OCD中,OC2+CD2=OD2,
52+(4x)2=(5+3x)2,
x=0(舍)或,
∵∠CEF=45°,∠ACB=90°,
∴CE=CF,
设CF=a,
∵∠CEF=∠ACD+∠CDE,
∠CFE=∠B+∠BDF,
∴∠CDE=∠BDF,
∵∠ACD=∠B,
∴△CED∽△BFD,
∴,
∴,a=,
∴CF=.
12.【解答】(1)证明:∵PA、PB是⊙O的两条切线,A、B是切点,
∴PA=PB,且PO平分∠BPA,
∴PO⊥AB.
∵BC是直径,
∴∠CAB=90°,
∴AC⊥AB,
∴AC∥PO;
(2)解:连结OA、DF,如图,
∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAQ=∠PBQ=90°.
在Rt△OAQ中,OA=OC=3,∴OQ=5.
由QA2+OA2=OQ2,得QA=4.
在Rt△PBQ中,PA=PB,QB=OQ+OB=8,
由QB2+PB2=PQ2,得82+PB2=(PB+4)2,
解得PB=6,
∴PA=PB=6,
∵OP⊥AB,
∴BF=AF=AB.
又∵D为PB的中点,
∴DF∥AP,DF=PA=3,
∴△DFE∽△QEA,
∴==,
设AE=4t,FE=3t,则AF=AE+FE=7t,
∴BE=BF+FE=AF+FE=7t+3t=10t,
∴==.
13.【解答】(1)证明:连接OD,如图所示.
∵OB=OD,
∴∠OBD=∠ODB.
∵CD是⊙O的切线,OD是⊙O的半径,
∴∠ODB+∠BDC=90°.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠OBD+∠CAD=90°,
∴∠CAD=∠BDC.
(2)解:∵∠C=∠C,∠CAD=∠CDB,
∴△CDB∽△CAD,
∴=.
∵BD=AD,
∴=,
∴=,
又∵AC=3,
∴CD=2.
14.【解答】(1)证明:如图1,连接OP,
∵PA=PB,
∴,
∴OP⊥AB,
∵PD∥AB,
∴OP⊥PD,
∴PD是⊙O的切线;
(2)如图2,过A作AH⊥BC于H,连接OA,OP,OP交AB于E,
∵AB=AC,
∴BH=BC==4,
Rt△ABH中,tan∠ABC===,
∴AH=2,AB==2,
∴BE=,PE=,
设⊙O的半径为r,则OA=r,OE=r﹣,
由勾股定理得:,
r=,
答:⊙O的半径是.
21世纪教育网(www.21cnjy.com)
同课章节目录
