2025年九年级数学中考三轮冲刺训练图形的旋转训练(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练图形的旋转训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 342.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:50:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练图形的旋转训练
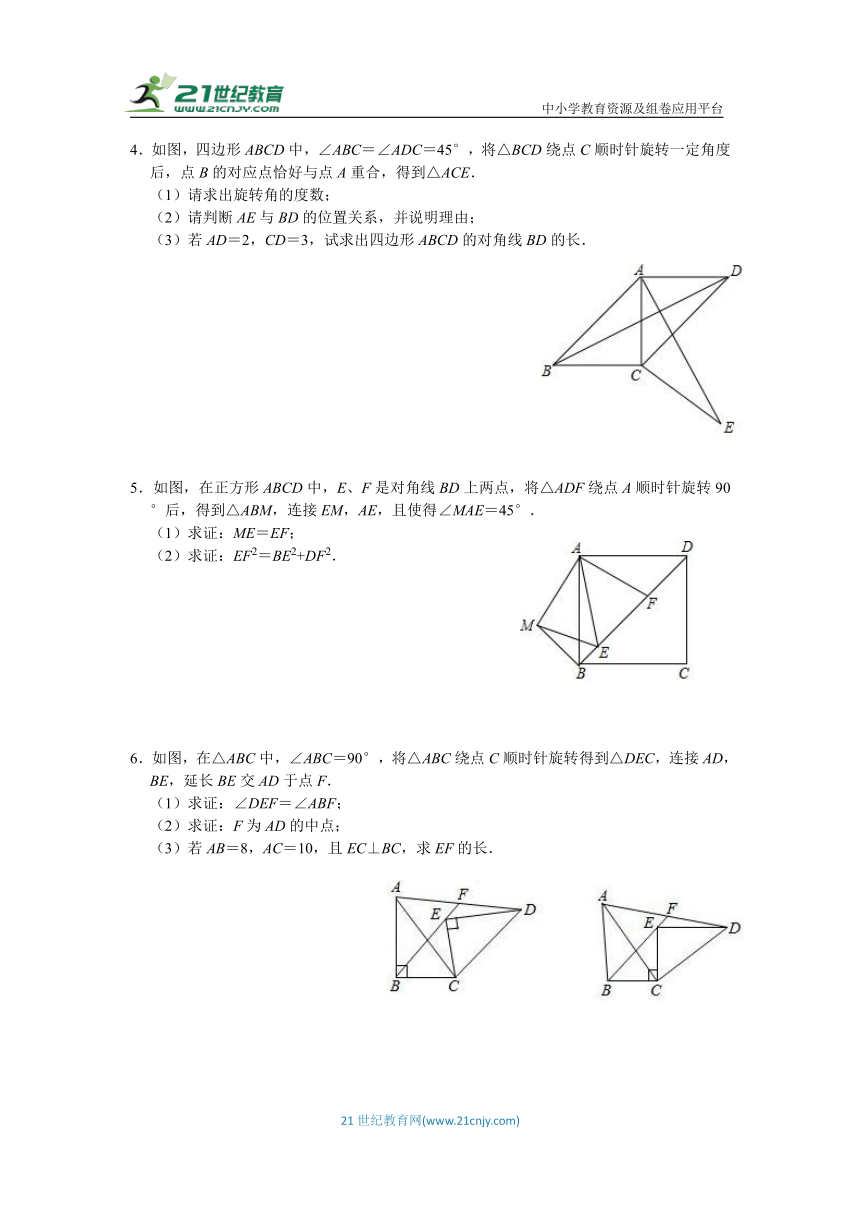
1.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连接EF,那么△AEF是怎样的三角形?
2.已知△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.
(1)如图,旋转中心是 ,∠DAE= °;
(2)如图,如果M是AB的中点,那么经过上述旋转后,点M转动了 度;
(3)如果点D为BC边上的三等分点,且△ABD的面积为3,那么四边形ADCE的面积为 .
3.如图,平面内三点A、B、C,AB=4,AC=3.以BC为对角线做正方形BDCE,连接AD.求AD的最大值.
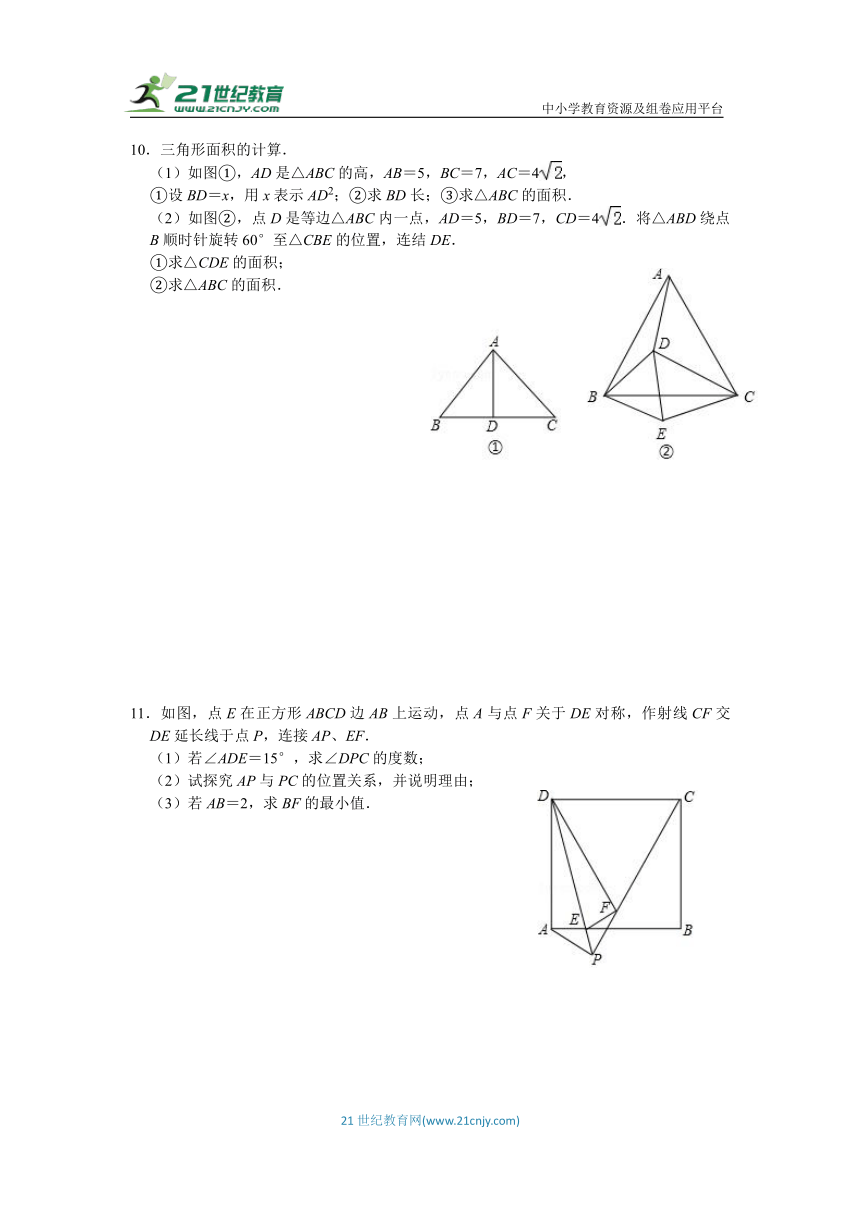
4.如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)请求出旋转角的度数;
(2)请判断AE与BD的位置关系,并说明理由;
(3)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.
5.如图,在正方形ABCD中,E、F是对角线BD上两点,将△ADF绕点A顺时针旋转90°后,得到△ABM,连接EM,AE,且使得∠MAE=45°.
(1)求证:ME=EF;
(2)求证:EF2=BE2+DF2.
6.如图,在△ABC中,∠ABC=90°,将△ABC绕点C顺时针旋转得到△DEC,连接AD,BE,延长BE交AD于点F.
(1)求证:∠DEF=∠ABF;
(2)求证:F为AD的中点;
(3)若AB=8,AC=10,且EC⊥BC,求EF的长.
7.如图, ABCD的对角线AC、BD相交于点O,对角线AC绕点O逆时针旋转,分别交边DC,AB于点E、F.
(1)求证:CE=AF
(2)若DB=2,BC=1,CD=.当AC绕点O逆时针方向旋转45°时,判断四边形BEDF的形状,并说明理由.
8.如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
9.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 ;
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围;
(3)在(2)条件下,当a取何值,代数式m2+2n+5取得最小值.
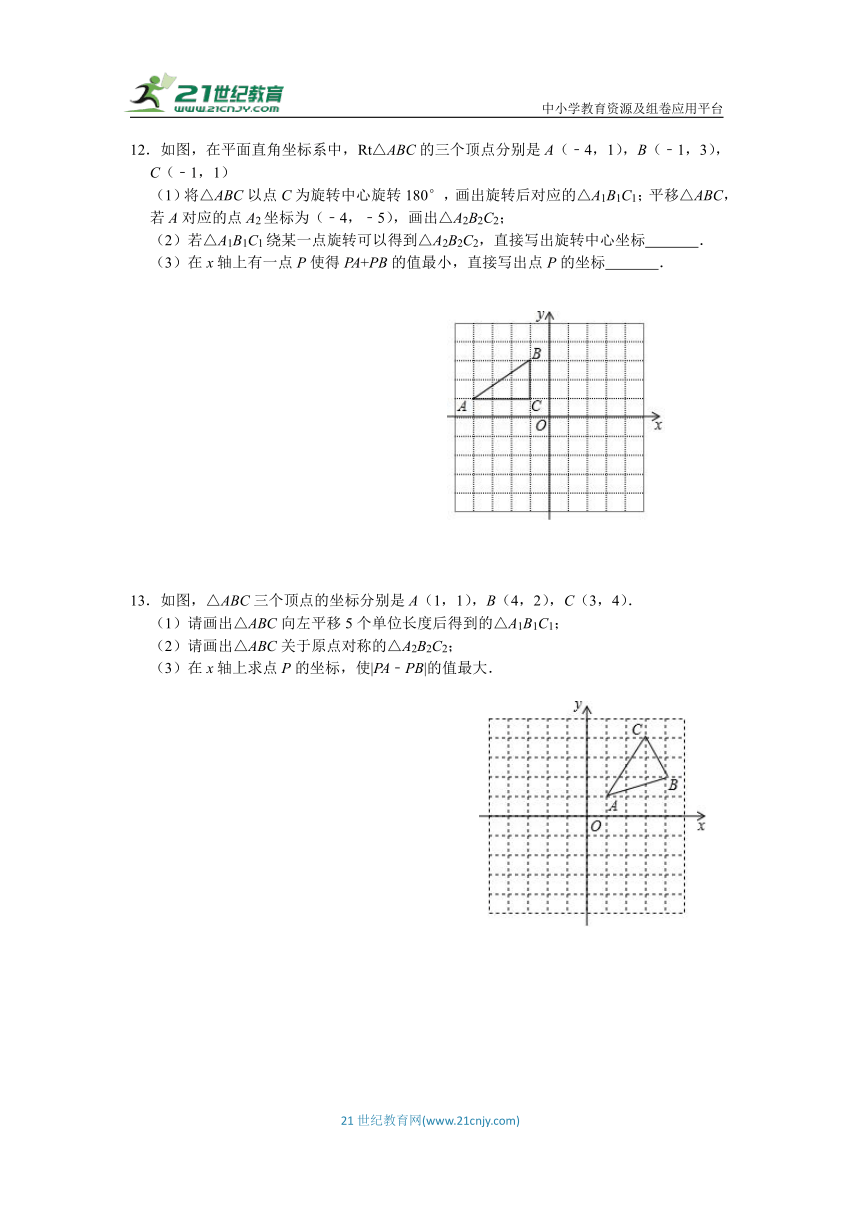
10.三角形面积的计算.
(1)如图①,AD是△ABC的高,AB=5,BC=7,AC=4,
①设BD=x,用x表示AD2;②求BD长;③求△ABC的面积.
(2)如图②,点D是等边△ABC内一点,AD=5,BD=7,CD=4.将△ABD绕点B顺时针旋转60°至△CBE的位置,连结DE.
①求△CDE的面积;
②求△ABC的面积.
11.如图,点E在正方形ABCD边AB上运动,点A与点F关于DE对称,作射线CF交DE延长线于点P,连接AP、EF.
(1)若∠ADE=15°,求∠DPC的度数;
(2)试探究AP与PC的位置关系,并说明理由;
(3)若AB=2,求BF的最小值.
12.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,1),B(﹣1,3),C(﹣1,1)
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;平移△ABC,若A对应的点A2坐标为(﹣4,﹣5),画出△A2B2C2;
(2)若△A1B1C1绕某一点旋转可以得到△A2B2C2,直接写出旋转中心坐标 .
(3)在x轴上有一点P使得PA+PB的值最小,直接写出点P的坐标 .
13.如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求点P的坐标,使|PA﹣PB|的值最大.
14.已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
(1)△ABP旋转的旋转中心是什么?旋转了多少度?
(2)若BP=2,求PE的长.
15.正方形ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.
16.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6,
(1)画出△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
17.已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
18.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
19.四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=3,求△AEF的面积.
20.如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.
参考答案
1.【解答】解:观察图形,由△ADE到△ABF的旋转可知:
(1)旋转中心是点A;
(2)∵△ABF是由△ADE旋转而成的
∴B是D的对应点
∴∠DAB=90°就是旋转角
(3)∵AD=1,DE=
∴
∵对应点到旋转中心的距离相等且F是E的对应点
∴
(4)∵∠EAF=90°且AF=AE
∴△EAF是等腰直角三角形
2.【解答】解:(1)∵△ABC为等边三角形,
∴∠BAC=60°
∵△ABD绕点A逆时针旋转到△ACE的位置,
∴旋转中心是点A,∠DAE=∠BAC=60°;
(2)∵AB和AC为对应边,
∴经过上述旋转后,点M转到了AC的中点位置,如图,
∴∠MAM′=60°,
∴点M转动了60°;
(3)∵△ABD绕点A逆时针旋转到△ACE的位置,
∴△ABD≌△ACE,
∵BD=BC,
∴CD=2BD,
∴S△ABC=S△ABD=×3=,
∴S四边形ADCE=S△ABC=.
故答案为点A,60;60;.
3.【解答】解:如图将△BDA绕点D顺时针旋转90°得到△CDM.
由旋转不变性可知:AB=CM=4,DA=DM.∠ADM=90°,
∴△ADM是等腰直角三角形,
∴AD=AM,
∴当AM的值最大时,AD的值最大,
∵AM≤AC+CM,
∴AM≤7,
∴AM的最大值为7,
∴AD的最大值为,
4.【解答】解:(1)∵将△BCD绕点C顺时针旋转得到△ACE
∴△BCD'≌△ACE
∴AC=BC,
又∵∠ABC=45°,
∴∠ABC=∠BAC=45°
∴∠ACB=90°
故旋转角的度数为90°
(2)AE⊥BD.
理由如下:
在Rt△BCM中,∠BCM=90°
∴∠MBC+∠BMC=90°
∵△BCD'≌△ACE
∴∠DBC=∠EAC
即∠MBC=∠NAM
又∵∠BMC=∠AMN
∴∠AMN+∠CAE=90°
∴∠AND=90°
∴AE⊥BD
(3)如图,连接DE,
由旋转图形的性质可知
CD=CE,BD=AE,旋转角∠DCE=90°
∴∠EDC=∠CED=45°
∵CD=3,
∴CE=3
在Rt△BCD中,∠DCE=90°
∴DE===3
∵∠ADC=45°
∴∠ADE=∠ADC+∠EDC=90°
在Rt△ADE中,∠ADE=90°
∴EA===
∴BD=
5.【解答】证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABM,
∴MB=DF,AM=AF,∠BAM=∠DAF,
∵∠EAM=45°,∠MAF=90°
∴∠FAE=45°,
∴∠MAE=∠FAE,
在△AME和△AFE中
,
∴△AME≌△AFE(SAS)
ME=EF.
(2)由(1)得△AME≌△AFE,
∴ME=EF,
∵∠ABM=∠ADF=45°,∠ABD=45°,
∴∠MBE=90°.
在Rt△MBE中,∵MB2+BE2=ME2,
又∵MB=DF,
∴EF2=BE2+DF2.
6.【解答】(1)证明:如图1中,
∵CB=CE,
∴∠CBE=∠CEB,
∵∠ABC=∠CED=90°,
∴∠DEF+∠CEB=90°,∠ABF+∠CBE=90°,
∴∠DEF=∠ABF.
(2)证明:如图1中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
∵∠ABN=∠DEM,∠ANB=∠M=90°,AB=DE,
∴△ANB≌△DME(AAS),
∴AN=DM,
∵∠ANF=∠M=90°,∠AFN=∠DFM,AN=DM,
∴△AFN≌△DFM(AAS),
∴AF=FD.
(3)解:如图2中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
在Rt△ABC中,∵∠ABC=90°,AC=10,AB=8,
∴BC=EC==6,
∵EC⊥BC,
∴∠BCE=∠ACD=90°,
∵AC=CD=10,
∴AD=10,
∴DF=AF=5,
∵∠MED=∠CEB=45°,
∴EM=MD=4,
在Rt△DFM中,FM==3,
∴EF=EM﹣FM=.
7.【解答】证明:(1)∵四边形ABCD是平行四边形
∴CD∥AB,AO=CO,AB=CD
∴∠DCO=∠BAO,且AO=CO,∠AOF=∠COE
∴△COE≌△AOF(ASA)
∴CE=AF,
(2)四边形BEDF是菱形
理由如下
如图,连接DF,BE,
∵DB=2,BC=1,CD=
∴DB2+BC2=5=CD2,
∴∠DBC=90°
由(1)可得AF=CE,且AB=CD
∴DE=BF,且DE∥BF
∴四边形DEBF是平行四边形
∴DO=BO=1,
∴OB=BC=1,且∠OBC=90°
∴∠BOC=45°,
∵当AC绕点O逆时针方向旋转45°时
∴∠EOC=45°
∴∠EOB=90°,即EF⊥BD
∴平行四边形DEBF是菱形
8.【解答】证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=AB=2
∵DF=AC=AB=2
∴BF=BD﹣DF=2﹣2
9.【解答】解:(1)由题意:Q(﹣3,1).
故答案为(﹣3,1).
(2)把点Q(﹣3,1)向右平移a个单位长度,向下平移a个单位长度后,
得到的点M的坐标为(﹣3+a,1﹣a),而M在第四象限,则有,
解得a>3,
即a的范围为a>3.
(3)由(2)得,m=﹣3+a,n=1﹣a
∴m2+2n+5=(a﹣3)2+2(1﹣a)+5
=a2﹣6a+9+2﹣2a+5
=a2﹣8a+16
=(a﹣4)2
∵(a﹣4)2≥0,
∴当a=4时,代数式m2+2n+5的最小值为0.
10.【解答】解:(1)①∵AD是△ABC的高,AB=5,
∴AD2=AB2﹣BD2=25﹣x2,
②∵AD是△ABC的高,AC=4
∴AD2=AC2﹣CD2,
∴25﹣x2=32﹣(7﹣x)2,
∴x=3
∴BD=3
③∵AD2=AB2﹣BD2=25﹣x2=16
∴AD=4
∴S△ABC=×BC×AD=14
(2)①∵将△ABD绕点B顺时针旋转60°至△CBE的位置,
∴BD=BE=7,∠DBE=60°,AD=CE=5,
∴△BDE是等边三角形,
∴DE=BD=7,
∴在△DEC中,DC=4,DE=7,CE=5
由(1)可得△DEC的面积=14
②∵S△ABD+S△BDC=S四边形BDCE,
∴S△ABD+S△BDC=×49+14=
同理可得:S△ABD+S△ADC=×25+14=+14,
S△ACD+S△BDC=×32+14=8+14
∴S△ABC=21+
11.【解答】解:(1)∵∠ADE=15°,
∴∠FDE=15°,∠CDF=60°.
∵DC=AD=DF,
∴∠CFD=60°.
又∠CFD=∠DPC+∠FDE=15°+∠DPC,
∴∠DPC=45°.
(2)AP与PC垂直,理由如下:
∵A、F关于DE对称,
∴∠APD=∠DPF.
设∠ADE=x,可得∠FDE=x,∠CDF=90°﹣2x,
∵DC=AD=DF,
∴∠CFD=45°+x.
又∠CFD=∠DPC+∠FDE=x+∠DPC,
∴∠DPC=45°,即∠APF=90°.
所以AP与PC垂直;
(3)点F始终在以点D为圆心,2为半径的圆上运动,根据两点之间线段最短,
可知当点D、F、B三点共线时,BF有最小值,最小值为BD﹣DF=.
12.【解答】解:(1)如图所示,△A1B1C1,△A2B2C2即为所求.
(2)如图所示,点Q即为所求,其坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2);
(3)如图所示,点P即为所求,
设直线A′B的解析式为y=kx+b,
将点A′(﹣4,﹣1),B(﹣1,3)代入,得:
,
解得:,
∴直线A′B的解析式为y=x+,
当y=0时,x+=0,
解得x=﹣,
∴点P的坐标为(﹣,0).
故答案为:(﹣,0).
13.【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示,此时|PA﹣PB|的值最大,P点坐标为:(﹣2,0).
14.【解答】解:(1)∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∵△ABP旋转后能与△CBE重合,
∴△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;
(2)∵△ABP旋转后能与△CBE重合,
∴BP=BE=2,∠PBE=90°,
∴PE=PB=2.
答:(1)△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;(2)PE为2.
15.【解答】解:(1)如图1,∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,
即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中
∵,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ;
(3)如图3,∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
16.【解答】解:(1)所画图形如下所示:
△ADE就是所作的图形.
(2)由(1)知:△ADE≌△BDC,
则CD=DE,AE=BC,
∴AE﹣AC<2CD<AE+AC,即BC﹣AC<2CD<BC+AC,
∴2<2CD<10,
解得:1<CD<5.
17.【解答】解:(1)旋转中心是点D.旋转角为90度.
(2)根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形.
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=20;
面积等于正方形ABCD的面积=16.
18.【解答】证明:(1)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,AD=OB=3,
又∵△COD是等边三角形,
∴∠ODC=60°,OD=OC=4
∴∠ADO=∠ADC﹣∠ODC=90°,
∴OA==5
19.【解答】证明:(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°
在△ADE和△ABF中
∴△ADE≌△ABF(SAS)
(2)△ABF可以由△ADE绕旋转中心点A,按顺时针方向旋转 90度得到.
故答案为:A,90
(3)∵四边形ABCD是正方形,
∴AD=BC=8
又∵DE=3,
∴AE==
由旋转性质得:
∴AE=AF=,∠EAF=90°
∴△AEF的面积=AE2=
20.【解答】解:(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)连接PQ,
在Rt△PBQ中
∵BP=BQ=2,
∴PQ2=BP2+BQ2=22+22=8,
在△PCQ中,
∵PC=3,QC=AP=1,
∴PC2=PQ2+QC2,
∴△PCQ是直角三角形,∠PQC=90°;
∵BP=BQ=2,∠PBQ=90°,
∴△PBQ是等腰直角三角形,
∴∠BQP=45°,
∵∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=45°+90°=135°,
∵△BQC由△BPA旋转而成,
∴∠APB=∠BQC=135°.
(3)如图,作CH⊥BQ交BQ的延长线于H.
∵∠BQC=135°,
∴∠CQH=∠QCH=45°,
∴CH=QH,∵CQ=QP=1,
∴CH=QH=,
∴BH=BQ+QH=2+,
在Rt△BCH中,BC===,
∴正方形ABCD的面积为5+2.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练图形的旋转训练
1.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连接EF,那么△AEF是怎样的三角形?
2.已知△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.
(1)如图,旋转中心是 ,∠DAE= °;
(2)如图,如果M是AB的中点,那么经过上述旋转后,点M转动了 度;
(3)如果点D为BC边上的三等分点,且△ABD的面积为3,那么四边形ADCE的面积为 .
3.如图,平面内三点A、B、C,AB=4,AC=3.以BC为对角线做正方形BDCE,连接AD.求AD的最大值.
4.如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)请求出旋转角的度数;
(2)请判断AE与BD的位置关系,并说明理由;
(3)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.
5.如图,在正方形ABCD中,E、F是对角线BD上两点,将△ADF绕点A顺时针旋转90°后,得到△ABM,连接EM,AE,且使得∠MAE=45°.
(1)求证:ME=EF;
(2)求证:EF2=BE2+DF2.
6.如图,在△ABC中,∠ABC=90°,将△ABC绕点C顺时针旋转得到△DEC,连接AD,BE,延长BE交AD于点F.
(1)求证:∠DEF=∠ABF;
(2)求证:F为AD的中点;
(3)若AB=8,AC=10,且EC⊥BC,求EF的长.
7.如图, ABCD的对角线AC、BD相交于点O,对角线AC绕点O逆时针旋转,分别交边DC,AB于点E、F.
(1)求证:CE=AF
(2)若DB=2,BC=1,CD=.当AC绕点O逆时针方向旋转45°时,判断四边形BEDF的形状,并说明理由.
8.如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
9.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是 ;
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围;
(3)在(2)条件下,当a取何值,代数式m2+2n+5取得最小值.
10.三角形面积的计算.
(1)如图①,AD是△ABC的高,AB=5,BC=7,AC=4,
①设BD=x,用x表示AD2;②求BD长;③求△ABC的面积.
(2)如图②,点D是等边△ABC内一点,AD=5,BD=7,CD=4.将△ABD绕点B顺时针旋转60°至△CBE的位置,连结DE.
①求△CDE的面积;
②求△ABC的面积.
11.如图,点E在正方形ABCD边AB上运动,点A与点F关于DE对称,作射线CF交DE延长线于点P,连接AP、EF.
(1)若∠ADE=15°,求∠DPC的度数;
(2)试探究AP与PC的位置关系,并说明理由;
(3)若AB=2,求BF的最小值.
12.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,1),B(﹣1,3),C(﹣1,1)
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;平移△ABC,若A对应的点A2坐标为(﹣4,﹣5),画出△A2B2C2;
(2)若△A1B1C1绕某一点旋转可以得到△A2B2C2,直接写出旋转中心坐标 .
(3)在x轴上有一点P使得PA+PB的值最小,直接写出点P的坐标 .
13.如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求点P的坐标,使|PA﹣PB|的值最大.
14.已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
(1)△ABP旋转的旋转中心是什么?旋转了多少度?
(2)若BP=2,求PE的长.
15.正方形ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.
16.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6,
(1)画出△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
17.已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
18.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
19.四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=3,求△AEF的面积.
20.如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.
参考答案
1.【解答】解:观察图形,由△ADE到△ABF的旋转可知:
(1)旋转中心是点A;
(2)∵△ABF是由△ADE旋转而成的
∴B是D的对应点
∴∠DAB=90°就是旋转角
(3)∵AD=1,DE=
∴
∵对应点到旋转中心的距离相等且F是E的对应点
∴
(4)∵∠EAF=90°且AF=AE
∴△EAF是等腰直角三角形
2.【解答】解:(1)∵△ABC为等边三角形,
∴∠BAC=60°
∵△ABD绕点A逆时针旋转到△ACE的位置,
∴旋转中心是点A,∠DAE=∠BAC=60°;
(2)∵AB和AC为对应边,
∴经过上述旋转后,点M转到了AC的中点位置,如图,
∴∠MAM′=60°,
∴点M转动了60°;
(3)∵△ABD绕点A逆时针旋转到△ACE的位置,
∴△ABD≌△ACE,
∵BD=BC,
∴CD=2BD,
∴S△ABC=S△ABD=×3=,
∴S四边形ADCE=S△ABC=.
故答案为点A,60;60;.
3.【解答】解:如图将△BDA绕点D顺时针旋转90°得到△CDM.
由旋转不变性可知:AB=CM=4,DA=DM.∠ADM=90°,
∴△ADM是等腰直角三角形,
∴AD=AM,
∴当AM的值最大时,AD的值最大,
∵AM≤AC+CM,
∴AM≤7,
∴AM的最大值为7,
∴AD的最大值为,
4.【解答】解:(1)∵将△BCD绕点C顺时针旋转得到△ACE
∴△BCD'≌△ACE
∴AC=BC,
又∵∠ABC=45°,
∴∠ABC=∠BAC=45°
∴∠ACB=90°
故旋转角的度数为90°
(2)AE⊥BD.
理由如下:
在Rt△BCM中,∠BCM=90°
∴∠MBC+∠BMC=90°
∵△BCD'≌△ACE
∴∠DBC=∠EAC
即∠MBC=∠NAM
又∵∠BMC=∠AMN
∴∠AMN+∠CAE=90°
∴∠AND=90°
∴AE⊥BD
(3)如图,连接DE,
由旋转图形的性质可知
CD=CE,BD=AE,旋转角∠DCE=90°
∴∠EDC=∠CED=45°
∵CD=3,
∴CE=3
在Rt△BCD中,∠DCE=90°
∴DE===3
∵∠ADC=45°
∴∠ADE=∠ADC+∠EDC=90°
在Rt△ADE中,∠ADE=90°
∴EA===
∴BD=
5.【解答】证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABM,
∴MB=DF,AM=AF,∠BAM=∠DAF,
∵∠EAM=45°,∠MAF=90°
∴∠FAE=45°,
∴∠MAE=∠FAE,
在△AME和△AFE中
,
∴△AME≌△AFE(SAS)
ME=EF.
(2)由(1)得△AME≌△AFE,
∴ME=EF,
∵∠ABM=∠ADF=45°,∠ABD=45°,
∴∠MBE=90°.
在Rt△MBE中,∵MB2+BE2=ME2,
又∵MB=DF,
∴EF2=BE2+DF2.
6.【解答】(1)证明:如图1中,
∵CB=CE,
∴∠CBE=∠CEB,
∵∠ABC=∠CED=90°,
∴∠DEF+∠CEB=90°,∠ABF+∠CBE=90°,
∴∠DEF=∠ABF.
(2)证明:如图1中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
∵∠ABN=∠DEM,∠ANB=∠M=90°,AB=DE,
∴△ANB≌△DME(AAS),
∴AN=DM,
∵∠ANF=∠M=90°,∠AFN=∠DFM,AN=DM,
∴△AFN≌△DFM(AAS),
∴AF=FD.
(3)解:如图2中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
在Rt△ABC中,∵∠ABC=90°,AC=10,AB=8,
∴BC=EC==6,
∵EC⊥BC,
∴∠BCE=∠ACD=90°,
∵AC=CD=10,
∴AD=10,
∴DF=AF=5,
∵∠MED=∠CEB=45°,
∴EM=MD=4,
在Rt△DFM中,FM==3,
∴EF=EM﹣FM=.
7.【解答】证明:(1)∵四边形ABCD是平行四边形
∴CD∥AB,AO=CO,AB=CD
∴∠DCO=∠BAO,且AO=CO,∠AOF=∠COE
∴△COE≌△AOF(ASA)
∴CE=AF,
(2)四边形BEDF是菱形
理由如下
如图,连接DF,BE,
∵DB=2,BC=1,CD=
∴DB2+BC2=5=CD2,
∴∠DBC=90°
由(1)可得AF=CE,且AB=CD
∴DE=BF,且DE∥BF
∴四边形DEBF是平行四边形
∴DO=BO=1,
∴OB=BC=1,且∠OBC=90°
∴∠BOC=45°,
∵当AC绕点O逆时针方向旋转45°时
∴∠EOC=45°
∴∠EOB=90°,即EF⊥BD
∴平行四边形DEBF是菱形
8.【解答】证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=AB=2
∵DF=AC=AB=2
∴BF=BD﹣DF=2﹣2
9.【解答】解:(1)由题意:Q(﹣3,1).
故答案为(﹣3,1).
(2)把点Q(﹣3,1)向右平移a个单位长度,向下平移a个单位长度后,
得到的点M的坐标为(﹣3+a,1﹣a),而M在第四象限,则有,
解得a>3,
即a的范围为a>3.
(3)由(2)得,m=﹣3+a,n=1﹣a
∴m2+2n+5=(a﹣3)2+2(1﹣a)+5
=a2﹣6a+9+2﹣2a+5
=a2﹣8a+16
=(a﹣4)2
∵(a﹣4)2≥0,
∴当a=4时,代数式m2+2n+5的最小值为0.
10.【解答】解:(1)①∵AD是△ABC的高,AB=5,
∴AD2=AB2﹣BD2=25﹣x2,
②∵AD是△ABC的高,AC=4
∴AD2=AC2﹣CD2,
∴25﹣x2=32﹣(7﹣x)2,
∴x=3
∴BD=3
③∵AD2=AB2﹣BD2=25﹣x2=16
∴AD=4
∴S△ABC=×BC×AD=14
(2)①∵将△ABD绕点B顺时针旋转60°至△CBE的位置,
∴BD=BE=7,∠DBE=60°,AD=CE=5,
∴△BDE是等边三角形,
∴DE=BD=7,
∴在△DEC中,DC=4,DE=7,CE=5
由(1)可得△DEC的面积=14
②∵S△ABD+S△BDC=S四边形BDCE,
∴S△ABD+S△BDC=×49+14=
同理可得:S△ABD+S△ADC=×25+14=+14,
S△ACD+S△BDC=×32+14=8+14
∴S△ABC=21+
11.【解答】解:(1)∵∠ADE=15°,
∴∠FDE=15°,∠CDF=60°.
∵DC=AD=DF,
∴∠CFD=60°.
又∠CFD=∠DPC+∠FDE=15°+∠DPC,
∴∠DPC=45°.
(2)AP与PC垂直,理由如下:
∵A、F关于DE对称,
∴∠APD=∠DPF.
设∠ADE=x,可得∠FDE=x,∠CDF=90°﹣2x,
∵DC=AD=DF,
∴∠CFD=45°+x.
又∠CFD=∠DPC+∠FDE=x+∠DPC,
∴∠DPC=45°,即∠APF=90°.
所以AP与PC垂直;
(3)点F始终在以点D为圆心,2为半径的圆上运动,根据两点之间线段最短,
可知当点D、F、B三点共线时,BF有最小值,最小值为BD﹣DF=.
12.【解答】解:(1)如图所示,△A1B1C1,△A2B2C2即为所求.
(2)如图所示,点Q即为所求,其坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2);
(3)如图所示,点P即为所求,
设直线A′B的解析式为y=kx+b,
将点A′(﹣4,﹣1),B(﹣1,3)代入,得:
,
解得:,
∴直线A′B的解析式为y=x+,
当y=0时,x+=0,
解得x=﹣,
∴点P的坐标为(﹣,0).
故答案为:(﹣,0).
13.【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示,此时|PA﹣PB|的值最大,P点坐标为:(﹣2,0).
14.【解答】解:(1)∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∵△ABP旋转后能与△CBE重合,
∴△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;
(2)∵△ABP旋转后能与△CBE重合,
∴BP=BE=2,∠PBE=90°,
∴PE=PB=2.
答:(1)△ABP旋转的旋转中心是点B,按顺时针方向旋转90°;(2)PE为2.
15.【解答】解:(1)如图1,∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,
即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中
∵,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ;
(3)如图3,∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
16.【解答】解:(1)所画图形如下所示:
△ADE就是所作的图形.
(2)由(1)知:△ADE≌△BDC,
则CD=DE,AE=BC,
∴AE﹣AC<2CD<AE+AC,即BC﹣AC<2CD<BC+AC,
∴2<2CD<10,
解得:1<CD<5.
17.【解答】解:(1)旋转中心是点D.旋转角为90度.
(2)根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形.
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=20;
面积等于正方形ABCD的面积=16.
18.【解答】证明:(1)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,AD=OB=3,
又∵△COD是等边三角形,
∴∠ODC=60°,OD=OC=4
∴∠ADO=∠ADC﹣∠ODC=90°,
∴OA==5
19.【解答】证明:(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°
在△ADE和△ABF中
∴△ADE≌△ABF(SAS)
(2)△ABF可以由△ADE绕旋转中心点A,按顺时针方向旋转 90度得到.
故答案为:A,90
(3)∵四边形ABCD是正方形,
∴AD=BC=8
又∵DE=3,
∴AE==
由旋转性质得:
∴AE=AF=,∠EAF=90°
∴△AEF的面积=AE2=
20.【解答】解:(1)作∠QBC=∠ABP,BP=BQ=2,连接QC即可得出△BCQ;
(2)连接PQ,
在Rt△PBQ中
∵BP=BQ=2,
∴PQ2=BP2+BQ2=22+22=8,
在△PCQ中,
∵PC=3,QC=AP=1,
∴PC2=PQ2+QC2,
∴△PCQ是直角三角形,∠PQC=90°;
∵BP=BQ=2,∠PBQ=90°,
∴△PBQ是等腰直角三角形,
∴∠BQP=45°,
∵∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=45°+90°=135°,
∵△BQC由△BPA旋转而成,
∴∠APB=∠BQC=135°.
(3)如图,作CH⊥BQ交BQ的延长线于H.
∵∠BQC=135°,
∴∠CQH=∠QCH=45°,
∴CH=QH,∵CQ=QP=1,
∴CH=QH=,
∴BH=BQ+QH=2+,
在Rt△BCH中,BC===,
∴正方形ABCD的面积为5+2.
21世纪教育网(www.21cnjy.com)
同课章节目录
