2025年九年级数学中考三轮冲刺训练四边形中的相似三角形综合问题(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练四边形中的相似三角形综合问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 340.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练四边形中的相似三角形综合问题
1.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
2.如图,点P是 ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交AD于点F,交CD的延长线于点G,已知.
(1)求的值.
(2)若四边形ABCD是菱形.
①求证:△APB≌△APD;
②若DP的长为6,求GF的长.
3.在矩形ABCD中,对角线AC、BD相交于点O,点E在BC上,且满足AE⊥BD;
(1)求证:AB2=BC BE;
(2)若AO=3,AE=4,求AB的长.
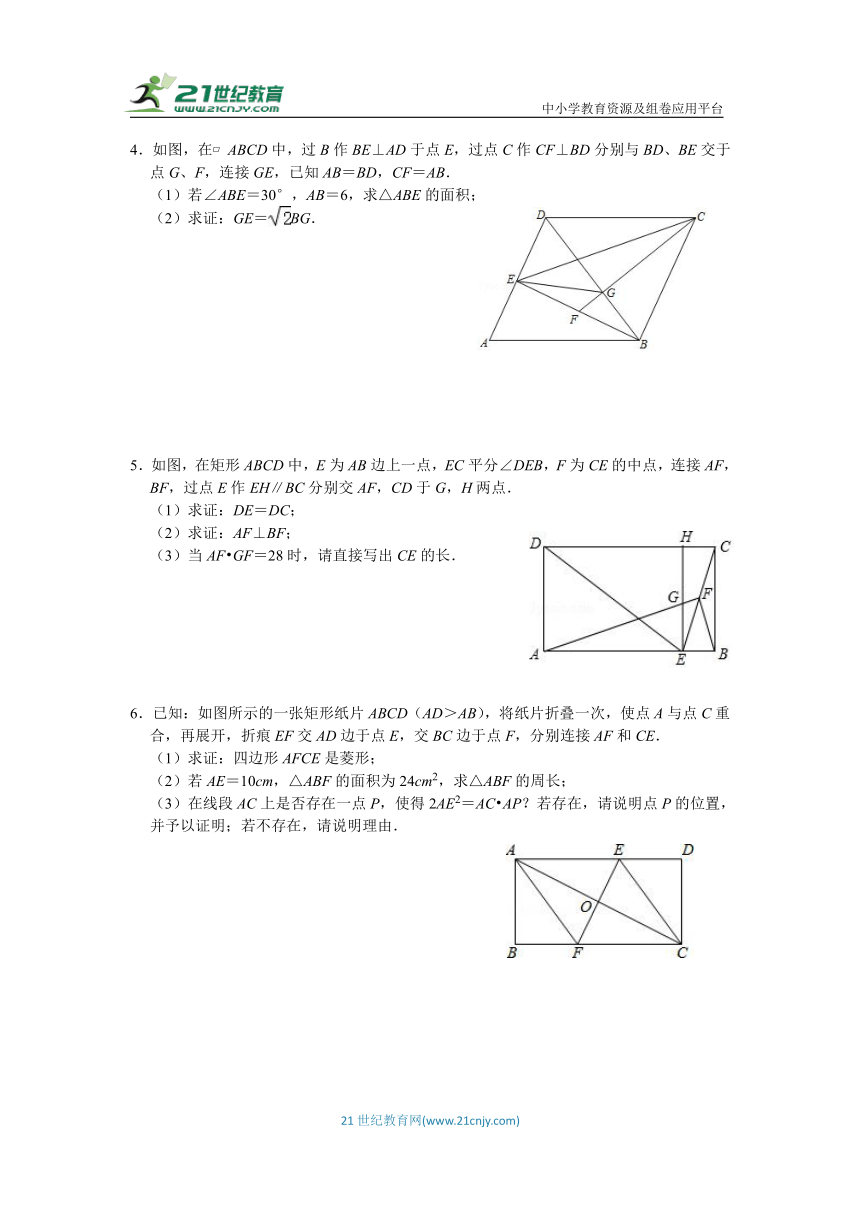
4.如图,在 ABCD中,过B作BE⊥AD于点E,过点C作CF⊥BD分别与BD、BE交于点G、F,连接GE,已知AB=BD,CF=AB.
(1)若∠ABE=30°,AB=6,求△ABE的面积;
(2)求证:GE=BG.
5.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AF GF=28时,请直接写出CE的长.
6.已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
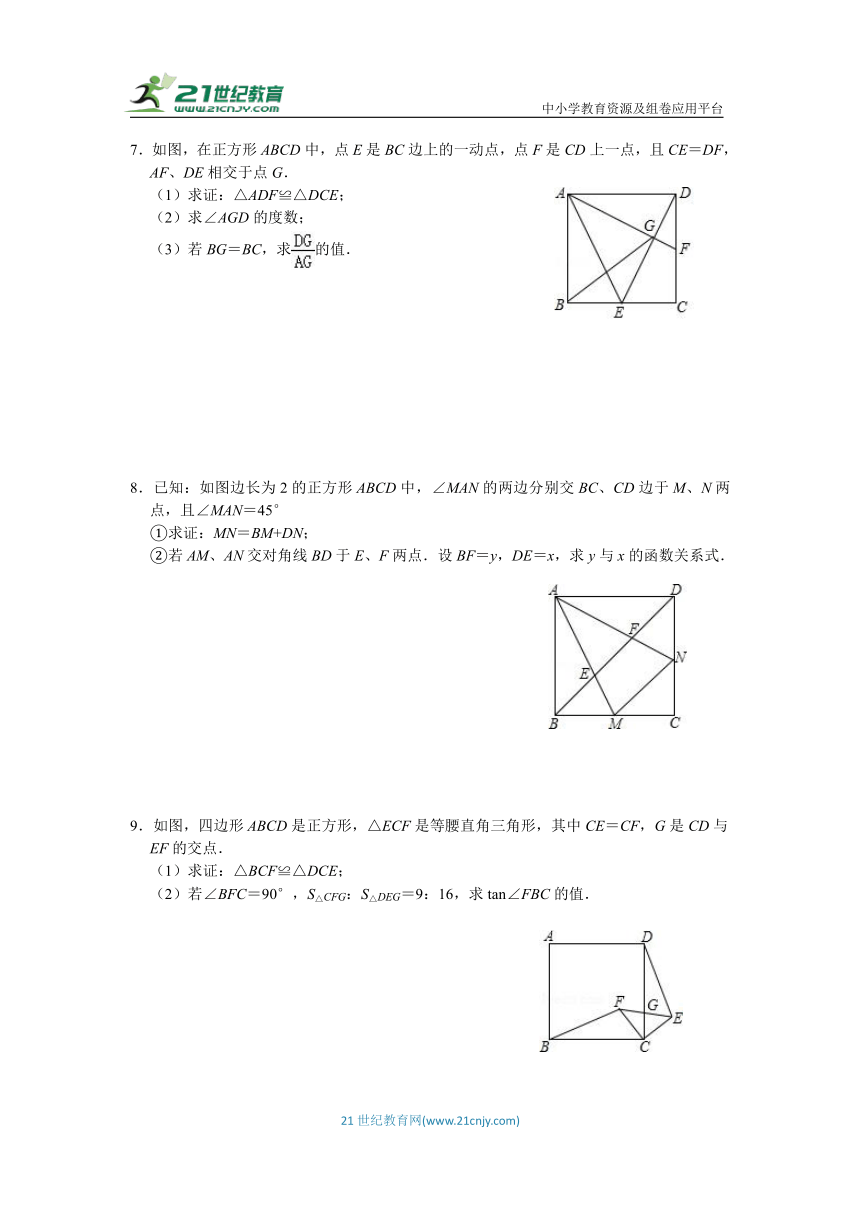
7.如图,在正方形ABCD中,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点G.
(1)求证:△ADF≌△DCE;
(2)求∠AGD的度数;
(3)若BG=BC,求的值.
8.已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
①求证:MN=BM+DN;
②若AM、AN交对角线BD于E、F两点.设BF=y,DE=x,求y与x的函数关系式.
9.如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
(1)求证:△BCF≌△DCE;
(2)若∠BFC=90°,S△CFG:S△DEG=9:16,求tan∠FBC的值.
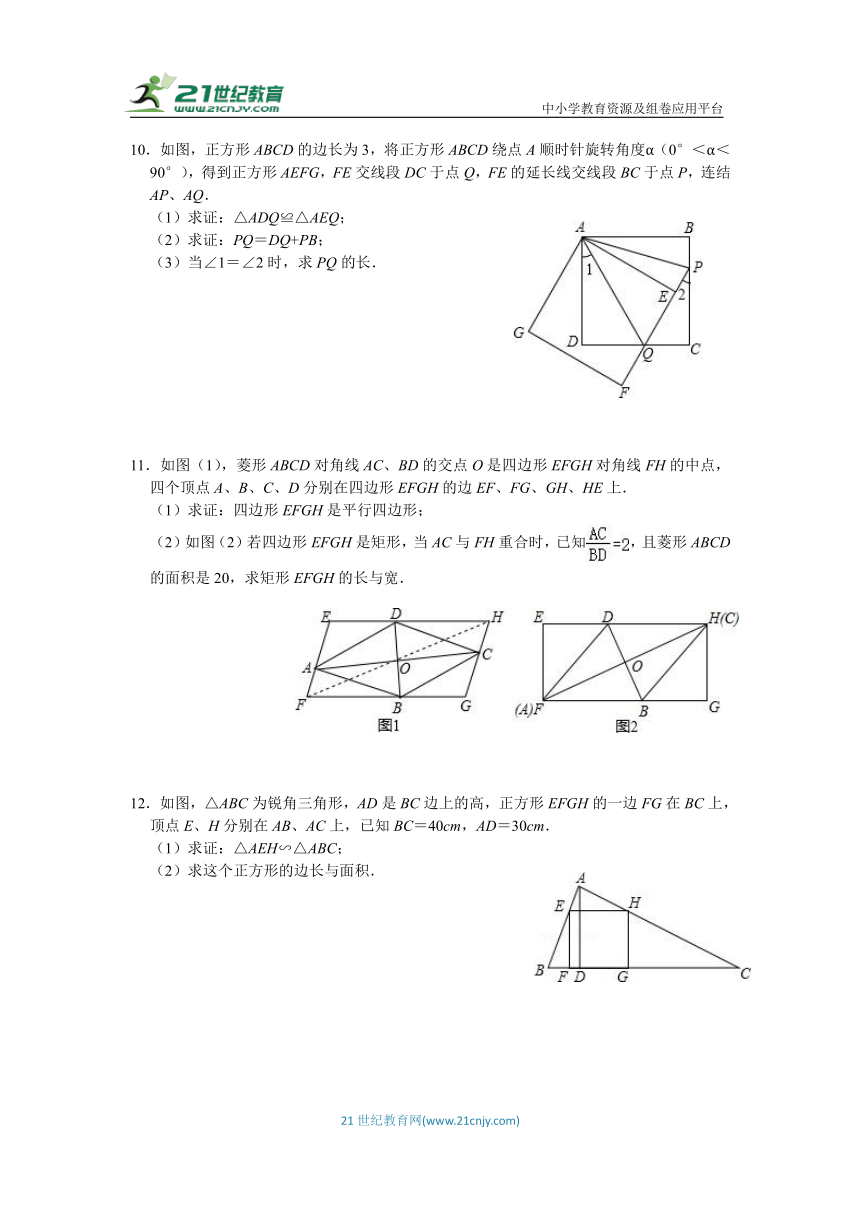
10.如图,正方形ABCD的边长为3,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到正方形AEFG,FE交线段DC于点Q,FE的延长线交线段BC于点P,连结AP、AQ.
(1)求证:△ADQ≌△AEQ;
(2)求证:PQ=DQ+PB;
(3)当∠1=∠2时,求PQ的长.
11.如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
12.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
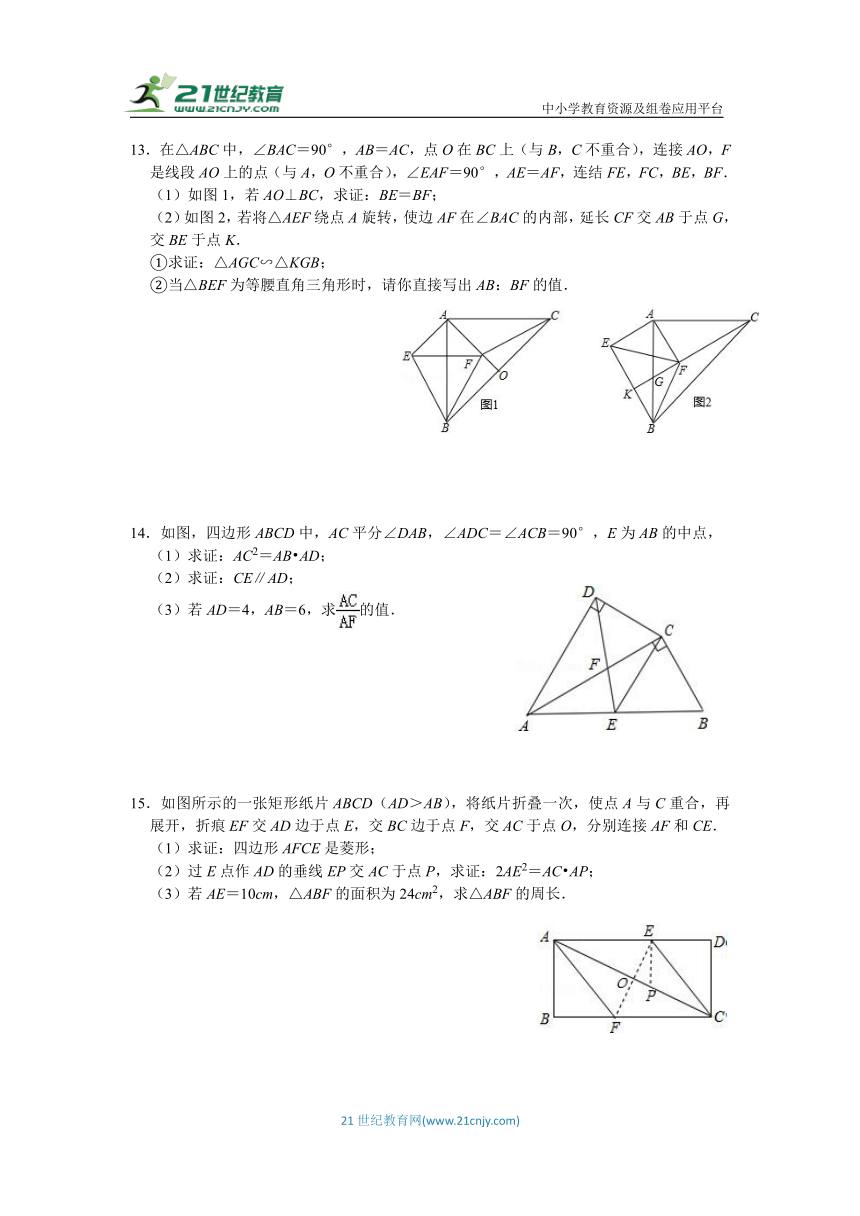
13.在△ABC中,∠BAC=90°,AB=AC,点O在BC上(与B,C不重合),连接AO,F是线段AO上的点(与A,O不重合),∠EAF=90°,AE=AF,连结FE,FC,BE,BF.
(1)如图1,若AO⊥BC,求证:BE=BF;
(2)如图2,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①求证:△AGC∽△KGB;
②当△BEF为等腰直角三角形时,请你直接写出AB:BF的值.
14.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
15.如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于点E,交BC边于点F,交AC于点O,分别连接AF和CE.
(1)求证:四边形AFCE是菱形;
(2)过E点作AD的垂线EP交AC于点P,求证:2AE2=AC AP;
(3)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长.
16.已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF.
(1)求证:BM⊥DF;
(2)若正方形ABCD的边长为2,求ME MB.
参考答案
1.【解答】(1)证明:∵四边形ABCD菱形,
∴AD=CD,∠ADP=∠CDP,
在△APD和△CPD中,
,
∴△APD≌△CPD(SAS);
(2)∵△APD≌△CPD,
∴∠DAP=∠DCP,
∵CD∥BF,
∴∠DCP=∠F,
∴∠DAP=∠F,
又∵∠APE=∠FPA,
∴△APE∽△FPA,
(3)∵△APE∽△FPA
∴,
∴PA2=PE PF,
∵△APD≌△CPD,
∴PA=PC,
∴PC2=PE PF,
∵PE=2,EF=6,
∴PF=PE+EF=2+6=8,
∴PC=4.
2.【解答】解:
∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC
∵.
∴设DF=x,则AF=2x
∴AD=3x
∴BC=AD=3x
∵AD∥BC
∴
(2)①∵四边形ABCD是菱形
∴AC平分∠BAD,
AB=AD
∴∠DAP=∠BAP
又AP=AP
∴△APB≌△APD(SAS)
②解:∵△APB≌△APD
∴DP=BP=6
∵
∴FP=4
∵四边形ABCD是平行四边形
∴AB∥DC
∴
∴,
∴GF=5
3.【解答】证明:如图所示:
(1)∵四边形ABCD是矩形,
∴OA=OB=OC,∠ABC=90°,
∴∠OAB=∠OBA,
又∵AE⊥BD,
∴∠AHB=∠EHB=90°,
又∵∠ABC=∠ABH+CBH=90°,
∠EBH+∠BEH=90°,
∴∠BEA=∠ABH,
∴∠CAB=∠AEB,
∴△ABE∽△CBA(AA),
∴,
∴AB2=BC BE;
(2)设AB=2x,由BC=3x,
由证明(1)得△ABE∽△CBA,
∴,
又∵AO=3,AE=4,
∴
∴在Rt△ABC中,由勾股定理得,
∴AB2+BC2=AC2,
∴(2x)2+(3x)2=62
解得:x=,
∴AB=.
4.【解答】(1)解:∵BE⊥AD,∠ABE=30°,
∴AE=AB=3,BE===3,
∴S△ABE=AE BE=×3×3=;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵∠FGB=∠BED=90°,∠FBG=∠DBE
∴∠BFC=∠BDE,
∴∠CBG=∠BFG,
∵∠CGB=∠BGF=90°,
∴∠BCF=∠DBE,
∴∠CBF=∠BCG+∠CBG=90°,
∵BE⊥AD,AB=BD,
∴AE=DE,
∵AB=BD,CF=AB,
∴CF=BD,
在△DEB和△FBC中,,
∴△DEB≌△FBC(AAS),
∴BF=DE,BE=BC=2DE,
设DE=x,则BE=BC=AD=2x,CF=BD=AB=x,
S△BCF=CF BG=BF BC,
即:x BG=x 2x,
∴BG=x,
∴DG=x﹣x=x,
过G作GH⊥AD于H,如图所示:
sin∠EDG==,即:=,
∴GH=x,
cos∠EDG==,即:=,
∴DH=x,
EH=DE﹣DH=x﹣x=x,
∴EG===,
∴==,
∴EG=BG.
5.【解答】解:(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DCE=∠CEB,
∵EC平分∠DEB,
∴∠DEC=∠CEB,
∴∠DCE=∠DEC,
∴DE=DC;
(2)如图,连接DF,
∵DE=DC,F为CE的中点,
∴DF⊥EC,
∴∠DFC=90°,
在矩形ABCD中,AB=DC,∠ABC=90°,
∴BF=CF=EF=EC,
∴∠ABF=∠CEB,
∵∠DCE=∠CEB,
∴∠ABF=∠DCF,
在△ABF和△DCF中,
,
∴△ABF≌△DCF(SAS),
∴∠AFB=∠DFC=90°,
∴AF⊥BF;
(3)CE=4.
理由如下:∵AF⊥BF,
∴∠BAF+∠ABF=90°,
∵EH∥BC,∠ABC=90°,
∴∠BEH=90°,
∴∠FEH+∠CEB=90°,
∵∠ABF=∠CEB,
∴∠BAF=∠FEH,
∵∠EFG=∠AFE,
∴△EFG∽△AFE,
∴=,即EF2=AF GF,
∵AF GF=28,
∴EF=2,
∴CE=2EF=4.
6.【解答】(1)证明:由题意可知OA=OC,EF⊥AO,
∵AD∥BC,
∴∠AEO=∠CFO,∠EAO=∠FCO,
∴△AOE≌△COF,
∴AE=CF,又AE∥CF,
∴四边形AECF是平行四边形,
由图形折叠的性质可知,AC⊥EF,
∴四边形AECF是菱形;
(2)解:∵四边形AECF是菱形,
∴AF=AE=10cm,
设AB=a,BF=b,
∵△ABF的面积为24cm2,
∴a2+b2=100,ab=48,
∴(a+b)2=196,
∴a+b=14或a+b=﹣14(不合题意,舍去),
∴△ABF的周长为14+10=24cm;
(3)解:存在,过点E作BC的垂线,交AC于点P,点P就是符合条件的点;
证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAO,
∴△AOE∽△AEP,
∴=,
∴AE2=AO AP,
∵四边形AECF是菱形,
∴AO=AC,
∴AE2=AC AP,
∴2AE2=AC AP.
7.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADF=∠DCE=90°,
∵CE=DF,
∴△ADF≌△DCE(SAS).
(2)解:∵△ADF≌△DCE,
∴∠DAF=∠CDE,
∵∠DAF+∠AFD=90°,
∴∠AFD+∠CDE=90°,
∴∠DGF=90°,
∴∠AGD=90°.
(3)解:∵BA=BG=BC,
∴∠BAG=∠BGA,∠BGC=∠BCG,
∵∠ABC=90°,2∠AGB+2∠GBC=270°,
∴∠AGB+∠CGB=135°,
∴∠CGF=45°,
∴∠CGE=∠FGC=45°,
∵∠ECF+∠EGF=90°,
∴E,C,F,G四点共圆,
∴∠CEF=∠CGF,∠CFE=∠CGE,
∴∠CFE=∠CEF,
∴CE=CF,
∵DF=EC,
∴FC=DF,
∴DF=CD=AD,
∵tan∠DAG===.
8.【解答】(1)证明:将△ABM绕点A逆时针旋转90°至△ADM′,
∵∠M′AN=∠DAN+∠MAB=45°,AM′=AM,BM=DM′,
∵M′AN=∠MAN=45°,AN=AN,
∴△AMN≌△AM′N′,
∴MN=NM′,
∴M′N=M′D+DN=BM+DN,
∴MN=BM+DN.
(2)解:∵∠AED=45°+∠BAE,∠FAB=45°+∠BAE,
∴∠AED=∠FAB,
∵∠ABF=∠ADE,
∴△BFA∽△DAE,
∴=,
∴=,
∴y=.
9.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
∵△ECF是等腰直角三角形,
∴∠FCE=90°,CF=CE,
∴∠BCD﹣∠FCD=∠ECF﹣∠FCD,即∠BCF=∠DCE,
在△BCF和△DCE中,
,
∴△BCF≌△DCE(SAS);
(2)由(1)知△BCF≌△DCE,
又∵∠BFC=90°,
∴∠DEC=∠BFC=90°,
∵∠FCE=90°,
∴FC∥DE,
∴∠CFG=∠DEG,
∵∠CGF=∠DGE,
∴△CFG∽△DEG,
∴=()2=,
∴=,
又由(1)知DE=BF,
∴=,
∵∠BFC=90°,
∴tan∠FBC==.
10.【解答】(1)证明:∵ABCD是正方形,
∴∠D=∠AEF=90°,AD=AE,
∵在Rt△ADQ和Rt△AEQ中
,
∴△ADQ≌△AEQ(HL);
(2)证明:与证△ADQ≌△AEQ类似,可证得:△AEP≌△ABP,
∴PB=PE,QD=QE,
∴PQ=QE+PE=DQ+PB;
(3)解:当∠1=∠2时,
∵∠D=∠C=90°,
∴Rt△ADQ∽Rt△PCQ,
∴∠AQD=∠PQC,
∵△ADQ≌△AEQ
∴∠AQD=∠AQE,
∴∠AQD=∠PQC=∠AQE,且∠AQD+∠AQE+∠PQC=180°,
∴∠AQD=60°,
∴∠1=30°
∴Rt△ADQ中,AD=3,DQ=,
∴QC=3﹣,
∵∠C=90°,∠PQC=60°,
∴∠2=30°,
∴PQ=2QC=6﹣2.
11.【解答】(1)证明:∵点O是菱形ABCD对角线AC、BD的交点,
∴OA=OC,OD=OB,
∵点O是线段FH的中点,
∴OF=OH.
在△AOF和△COH中,有,
∴△AOF≌△COH(SAS),
∴∠AFO=∠CHO,
∴AF∥CH.
同理可得:DH∥BF.
∴四边形EFGH是平行四边形.
(2)(方法一)设BD=m,则AC=2m,
∴S菱形ABCD=AC BD=m2=20,
∴m=2,
即BD=2,AC=4.
∵四边形ABCD为菱形,
∴OB=BD=,OA=AC=2,
∴AB==5.
∵四边形EFGH为矩形,
∴∠G=∠AOB=90°,
∴△AOB∽△AGC,
∴,
∴CG=4,AG=8.
∴矩形EFGH的长为8,宽为4.
(方法二)设BD=m,则AC=2m,
∴S菱形ABCD=AC BD=m2=20,
∴m=2,
即BD=2,AC=4.
∵四边形ABCD为菱形,
∴OB=BD=,OA=AC=2,
∴AB==5,
∴HG==4.
在Rt△BHG中,BH=5,HG=4,∠G=90°,
∴BG=3,
∴FG=AB+BG=8.
∴矩形EFGH的长为8,宽为4.
12.【解答】(1)证明:∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)解:如图设AD与EH交于点M.
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形,
∴EF=DM,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴=,
∴=,
∴x=,
∴正方形EFGH的边长为cm,面积为cm2.
13.【解答】(1)证明:∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF﹣∠BAF=45°,
∴∠EAB=∠BAF,
在△EAB和△FAB中,
,
∴△EAB≌△FAB(SAS),
∴BE=BF;
(2)①证明:∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
,
∴△AEB≌△AFC(SAS),
∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,
∴△AGC∽△KGB;
②当∠EBF=90°时,∵BE=BF,
∴∠BFE=45°,
∵∠EAF=90°,AE=AF,
∴∠AFE=45°,
∴∠AFB=90°,
此时,点F和点O重合(不符合题意),
当∠EFB=90°时,AB:BF=:2.
当∠BEF=90°时,AB:BF=:2.
14.【解答】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×6=3,
∵AD=4,
∴,
∴.
15.【解答】(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴平行四边形AFCE是菱形.
(2)证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAP,
∴△AOE∽△AEP,
∴=,
即AE2=AO AP,
∵AO=AC,
∴AE2=AC AP,
∴2AE2=AC AP.
(3)解:设AB=xcm,BF=ycm.
∵由(1)四边形AFCE是菱形,
∴AF=AE=10cm.
∵∠B=90°,
∴x2+y2=100.
∴(x+y)2﹣2xy=100①.
∵△ABF的面积为24cm2,
∴xy=24.即xy=48 ②.
由①、②得(x+y)2=196.
∴x+y=14或x+y=﹣14(不合题意,舍去).
∴△ABF的周长为:x+y+AF=14+10=24(cm).
16.【解答】(1)证明:在△BCE和△DCF中,
∵,
∴△BCE≌△DCF(SAS),
∴∠EBC=∠FDC(全等三角形的对应角相等),即∠EBC=∠EDM,
在△BCE和△DME中,
∵,
∴△BCE∽△DME,
∴∠BCE=∠DME=90°(相似三角形的对应角相等),即BM⊥DF;
(2)解:∵BC=2,
∴BD=2.
又∵BE平分∠DBC交DF于M,BM⊥DF,
∴BD=BF(等腰三角形“三合一”的性质),DM=FM,
∴CF=2﹣2.
在△BMF和△DME中,
∠MBF=∠MDE,∠BMF=∠DME=90°,
∴△BMF∽△DME,
∴=,
∴=,即ME MB=MD2,
∵DC2+FC2=(2DM)2,即22+(2﹣2)2=4DM2,
∴DM2=4﹣2,即ME MB=4﹣2.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练四边形中的相似三角形综合问题
1.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
2.如图,点P是 ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交AD于点F,交CD的延长线于点G,已知.
(1)求的值.
(2)若四边形ABCD是菱形.
①求证:△APB≌△APD;
②若DP的长为6,求GF的长.
3.在矩形ABCD中,对角线AC、BD相交于点O,点E在BC上,且满足AE⊥BD;
(1)求证:AB2=BC BE;
(2)若AO=3,AE=4,求AB的长.
4.如图,在 ABCD中,过B作BE⊥AD于点E,过点C作CF⊥BD分别与BD、BE交于点G、F,连接GE,已知AB=BD,CF=AB.
(1)若∠ABE=30°,AB=6,求△ABE的面积;
(2)求证:GE=BG.
5.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AF GF=28时,请直接写出CE的长.
6.已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
7.如图,在正方形ABCD中,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点G.
(1)求证:△ADF≌△DCE;
(2)求∠AGD的度数;
(3)若BG=BC,求的值.
8.已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
①求证:MN=BM+DN;
②若AM、AN交对角线BD于E、F两点.设BF=y,DE=x,求y与x的函数关系式.
9.如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
(1)求证:△BCF≌△DCE;
(2)若∠BFC=90°,S△CFG:S△DEG=9:16,求tan∠FBC的值.
10.如图,正方形ABCD的边长为3,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到正方形AEFG,FE交线段DC于点Q,FE的延长线交线段BC于点P,连结AP、AQ.
(1)求证:△ADQ≌△AEQ;
(2)求证:PQ=DQ+PB;
(3)当∠1=∠2时,求PQ的长.
11.如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
12.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
13.在△ABC中,∠BAC=90°,AB=AC,点O在BC上(与B,C不重合),连接AO,F是线段AO上的点(与A,O不重合),∠EAF=90°,AE=AF,连结FE,FC,BE,BF.
(1)如图1,若AO⊥BC,求证:BE=BF;
(2)如图2,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①求证:△AGC∽△KGB;
②当△BEF为等腰直角三角形时,请你直接写出AB:BF的值.
14.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
15.如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于点E,交BC边于点F,交AC于点O,分别连接AF和CE.
(1)求证:四边形AFCE是菱形;
(2)过E点作AD的垂线EP交AC于点P,求证:2AE2=AC AP;
(3)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长.
16.已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF.
(1)求证:BM⊥DF;
(2)若正方形ABCD的边长为2,求ME MB.
参考答案
1.【解答】(1)证明:∵四边形ABCD菱形,
∴AD=CD,∠ADP=∠CDP,
在△APD和△CPD中,
,
∴△APD≌△CPD(SAS);
(2)∵△APD≌△CPD,
∴∠DAP=∠DCP,
∵CD∥BF,
∴∠DCP=∠F,
∴∠DAP=∠F,
又∵∠APE=∠FPA,
∴△APE∽△FPA,
(3)∵△APE∽△FPA
∴,
∴PA2=PE PF,
∵△APD≌△CPD,
∴PA=PC,
∴PC2=PE PF,
∵PE=2,EF=6,
∴PF=PE+EF=2+6=8,
∴PC=4.
2.【解答】解:
∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC
∵.
∴设DF=x,则AF=2x
∴AD=3x
∴BC=AD=3x
∵AD∥BC
∴
(2)①∵四边形ABCD是菱形
∴AC平分∠BAD,
AB=AD
∴∠DAP=∠BAP
又AP=AP
∴△APB≌△APD(SAS)
②解:∵△APB≌△APD
∴DP=BP=6
∵
∴FP=4
∵四边形ABCD是平行四边形
∴AB∥DC
∴
∴,
∴GF=5
3.【解答】证明:如图所示:
(1)∵四边形ABCD是矩形,
∴OA=OB=OC,∠ABC=90°,
∴∠OAB=∠OBA,
又∵AE⊥BD,
∴∠AHB=∠EHB=90°,
又∵∠ABC=∠ABH+CBH=90°,
∠EBH+∠BEH=90°,
∴∠BEA=∠ABH,
∴∠CAB=∠AEB,
∴△ABE∽△CBA(AA),
∴,
∴AB2=BC BE;
(2)设AB=2x,由BC=3x,
由证明(1)得△ABE∽△CBA,
∴,
又∵AO=3,AE=4,
∴
∴在Rt△ABC中,由勾股定理得,
∴AB2+BC2=AC2,
∴(2x)2+(3x)2=62
解得:x=,
∴AB=.
4.【解答】(1)解:∵BE⊥AD,∠ABE=30°,
∴AE=AB=3,BE===3,
∴S△ABE=AE BE=×3×3=;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵∠FGB=∠BED=90°,∠FBG=∠DBE
∴∠BFC=∠BDE,
∴∠CBG=∠BFG,
∵∠CGB=∠BGF=90°,
∴∠BCF=∠DBE,
∴∠CBF=∠BCG+∠CBG=90°,
∵BE⊥AD,AB=BD,
∴AE=DE,
∵AB=BD,CF=AB,
∴CF=BD,
在△DEB和△FBC中,,
∴△DEB≌△FBC(AAS),
∴BF=DE,BE=BC=2DE,
设DE=x,则BE=BC=AD=2x,CF=BD=AB=x,
S△BCF=CF BG=BF BC,
即:x BG=x 2x,
∴BG=x,
∴DG=x﹣x=x,
过G作GH⊥AD于H,如图所示:
sin∠EDG==,即:=,
∴GH=x,
cos∠EDG==,即:=,
∴DH=x,
EH=DE﹣DH=x﹣x=x,
∴EG===,
∴==,
∴EG=BG.
5.【解答】解:(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DCE=∠CEB,
∵EC平分∠DEB,
∴∠DEC=∠CEB,
∴∠DCE=∠DEC,
∴DE=DC;
(2)如图,连接DF,
∵DE=DC,F为CE的中点,
∴DF⊥EC,
∴∠DFC=90°,
在矩形ABCD中,AB=DC,∠ABC=90°,
∴BF=CF=EF=EC,
∴∠ABF=∠CEB,
∵∠DCE=∠CEB,
∴∠ABF=∠DCF,
在△ABF和△DCF中,
,
∴△ABF≌△DCF(SAS),
∴∠AFB=∠DFC=90°,
∴AF⊥BF;
(3)CE=4.
理由如下:∵AF⊥BF,
∴∠BAF+∠ABF=90°,
∵EH∥BC,∠ABC=90°,
∴∠BEH=90°,
∴∠FEH+∠CEB=90°,
∵∠ABF=∠CEB,
∴∠BAF=∠FEH,
∵∠EFG=∠AFE,
∴△EFG∽△AFE,
∴=,即EF2=AF GF,
∵AF GF=28,
∴EF=2,
∴CE=2EF=4.
6.【解答】(1)证明:由题意可知OA=OC,EF⊥AO,
∵AD∥BC,
∴∠AEO=∠CFO,∠EAO=∠FCO,
∴△AOE≌△COF,
∴AE=CF,又AE∥CF,
∴四边形AECF是平行四边形,
由图形折叠的性质可知,AC⊥EF,
∴四边形AECF是菱形;
(2)解:∵四边形AECF是菱形,
∴AF=AE=10cm,
设AB=a,BF=b,
∵△ABF的面积为24cm2,
∴a2+b2=100,ab=48,
∴(a+b)2=196,
∴a+b=14或a+b=﹣14(不合题意,舍去),
∴△ABF的周长为14+10=24cm;
(3)解:存在,过点E作BC的垂线,交AC于点P,点P就是符合条件的点;
证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAO,
∴△AOE∽△AEP,
∴=,
∴AE2=AO AP,
∵四边形AECF是菱形,
∴AO=AC,
∴AE2=AC AP,
∴2AE2=AC AP.
7.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADF=∠DCE=90°,
∵CE=DF,
∴△ADF≌△DCE(SAS).
(2)解:∵△ADF≌△DCE,
∴∠DAF=∠CDE,
∵∠DAF+∠AFD=90°,
∴∠AFD+∠CDE=90°,
∴∠DGF=90°,
∴∠AGD=90°.
(3)解:∵BA=BG=BC,
∴∠BAG=∠BGA,∠BGC=∠BCG,
∵∠ABC=90°,2∠AGB+2∠GBC=270°,
∴∠AGB+∠CGB=135°,
∴∠CGF=45°,
∴∠CGE=∠FGC=45°,
∵∠ECF+∠EGF=90°,
∴E,C,F,G四点共圆,
∴∠CEF=∠CGF,∠CFE=∠CGE,
∴∠CFE=∠CEF,
∴CE=CF,
∵DF=EC,
∴FC=DF,
∴DF=CD=AD,
∵tan∠DAG===.
8.【解答】(1)证明:将△ABM绕点A逆时针旋转90°至△ADM′,
∵∠M′AN=∠DAN+∠MAB=45°,AM′=AM,BM=DM′,
∵M′AN=∠MAN=45°,AN=AN,
∴△AMN≌△AM′N′,
∴MN=NM′,
∴M′N=M′D+DN=BM+DN,
∴MN=BM+DN.
(2)解:∵∠AED=45°+∠BAE,∠FAB=45°+∠BAE,
∴∠AED=∠FAB,
∵∠ABF=∠ADE,
∴△BFA∽△DAE,
∴=,
∴=,
∴y=.
9.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
∵△ECF是等腰直角三角形,
∴∠FCE=90°,CF=CE,
∴∠BCD﹣∠FCD=∠ECF﹣∠FCD,即∠BCF=∠DCE,
在△BCF和△DCE中,
,
∴△BCF≌△DCE(SAS);
(2)由(1)知△BCF≌△DCE,
又∵∠BFC=90°,
∴∠DEC=∠BFC=90°,
∵∠FCE=90°,
∴FC∥DE,
∴∠CFG=∠DEG,
∵∠CGF=∠DGE,
∴△CFG∽△DEG,
∴=()2=,
∴=,
又由(1)知DE=BF,
∴=,
∵∠BFC=90°,
∴tan∠FBC==.
10.【解答】(1)证明:∵ABCD是正方形,
∴∠D=∠AEF=90°,AD=AE,
∵在Rt△ADQ和Rt△AEQ中
,
∴△ADQ≌△AEQ(HL);
(2)证明:与证△ADQ≌△AEQ类似,可证得:△AEP≌△ABP,
∴PB=PE,QD=QE,
∴PQ=QE+PE=DQ+PB;
(3)解:当∠1=∠2时,
∵∠D=∠C=90°,
∴Rt△ADQ∽Rt△PCQ,
∴∠AQD=∠PQC,
∵△ADQ≌△AEQ
∴∠AQD=∠AQE,
∴∠AQD=∠PQC=∠AQE,且∠AQD+∠AQE+∠PQC=180°,
∴∠AQD=60°,
∴∠1=30°
∴Rt△ADQ中,AD=3,DQ=,
∴QC=3﹣,
∵∠C=90°,∠PQC=60°,
∴∠2=30°,
∴PQ=2QC=6﹣2.
11.【解答】(1)证明:∵点O是菱形ABCD对角线AC、BD的交点,
∴OA=OC,OD=OB,
∵点O是线段FH的中点,
∴OF=OH.
在△AOF和△COH中,有,
∴△AOF≌△COH(SAS),
∴∠AFO=∠CHO,
∴AF∥CH.
同理可得:DH∥BF.
∴四边形EFGH是平行四边形.
(2)(方法一)设BD=m,则AC=2m,
∴S菱形ABCD=AC BD=m2=20,
∴m=2,
即BD=2,AC=4.
∵四边形ABCD为菱形,
∴OB=BD=,OA=AC=2,
∴AB==5.
∵四边形EFGH为矩形,
∴∠G=∠AOB=90°,
∴△AOB∽△AGC,
∴,
∴CG=4,AG=8.
∴矩形EFGH的长为8,宽为4.
(方法二)设BD=m,则AC=2m,
∴S菱形ABCD=AC BD=m2=20,
∴m=2,
即BD=2,AC=4.
∵四边形ABCD为菱形,
∴OB=BD=,OA=AC=2,
∴AB==5,
∴HG==4.
在Rt△BHG中,BH=5,HG=4,∠G=90°,
∴BG=3,
∴FG=AB+BG=8.
∴矩形EFGH的长为8,宽为4.
12.【解答】(1)证明:∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)解:如图设AD与EH交于点M.
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形,
∴EF=DM,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴=,
∴=,
∴x=,
∴正方形EFGH的边长为cm,面积为cm2.
13.【解答】(1)证明:∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF﹣∠BAF=45°,
∴∠EAB=∠BAF,
在△EAB和△FAB中,
,
∴△EAB≌△FAB(SAS),
∴BE=BF;
(2)①证明:∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
,
∴△AEB≌△AFC(SAS),
∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,
∴△AGC∽△KGB;
②当∠EBF=90°时,∵BE=BF,
∴∠BFE=45°,
∵∠EAF=90°,AE=AF,
∴∠AFE=45°,
∴∠AFB=90°,
此时,点F和点O重合(不符合题意),
当∠EFB=90°时,AB:BF=:2.
当∠BEF=90°时,AB:BF=:2.
14.【解答】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=AB,
∴CE=×6=3,
∵AD=4,
∴,
∴.
15.【解答】(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴平行四边形AFCE是菱形.
(2)证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAP,
∴△AOE∽△AEP,
∴=,
即AE2=AO AP,
∵AO=AC,
∴AE2=AC AP,
∴2AE2=AC AP.
(3)解:设AB=xcm,BF=ycm.
∵由(1)四边形AFCE是菱形,
∴AF=AE=10cm.
∵∠B=90°,
∴x2+y2=100.
∴(x+y)2﹣2xy=100①.
∵△ABF的面积为24cm2,
∴xy=24.即xy=48 ②.
由①、②得(x+y)2=196.
∴x+y=14或x+y=﹣14(不合题意,舍去).
∴△ABF的周长为:x+y+AF=14+10=24(cm).
16.【解答】(1)证明:在△BCE和△DCF中,
∵,
∴△BCE≌△DCF(SAS),
∴∠EBC=∠FDC(全等三角形的对应角相等),即∠EBC=∠EDM,
在△BCE和△DME中,
∵,
∴△BCE∽△DME,
∴∠BCE=∠DME=90°(相似三角形的对应角相等),即BM⊥DF;
(2)解:∵BC=2,
∴BD=2.
又∵BE平分∠DBC交DF于M,BM⊥DF,
∴BD=BF(等腰三角形“三合一”的性质),DM=FM,
∴CF=2﹣2.
在△BMF和△DME中,
∠MBF=∠MDE,∠BMF=∠DME=90°,
∴△BMF∽△DME,
∴=,
∴=,即ME MB=MD2,
∵DC2+FC2=(2DM)2,即22+(2﹣2)2=4DM2,
∴DM2=4﹣2,即ME MB=4﹣2.
21世纪教育网(www.21cnjy.com)
同课章节目录
