2025年九年级数学中考三轮冲刺训练二次函数中相似三角形存在性问题(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练二次函数中相似三角形存在性问题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 541.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:51:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练二次函数中相似三角形存在性问题
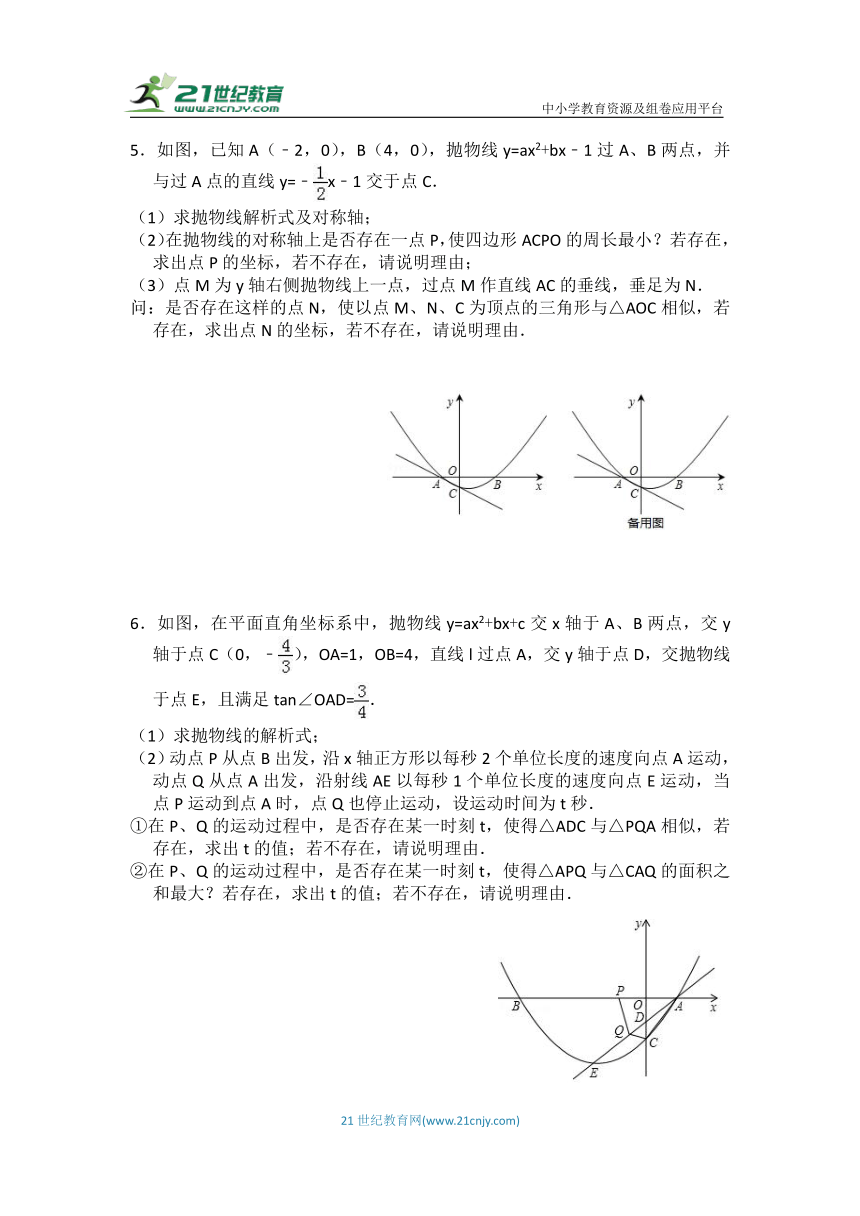
1.如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
2.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
3.如图,抛物线y=ax2+bx+c与坐标轴交点分别为A(﹣1,0),B(3,0),C(0,2),作直线BC.
(1)求抛物线的解析式;
(2)点P为抛物线上第一象限内一动点,过点P作PD⊥x轴于点D,设点P的横坐标为t(0<t<3),求△ABP的面积S与t的函数关系式;
(3)条件同(2),若△ODP与△COB相似,求点P的坐标.
4.已知抛物线y=x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
5.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.
问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
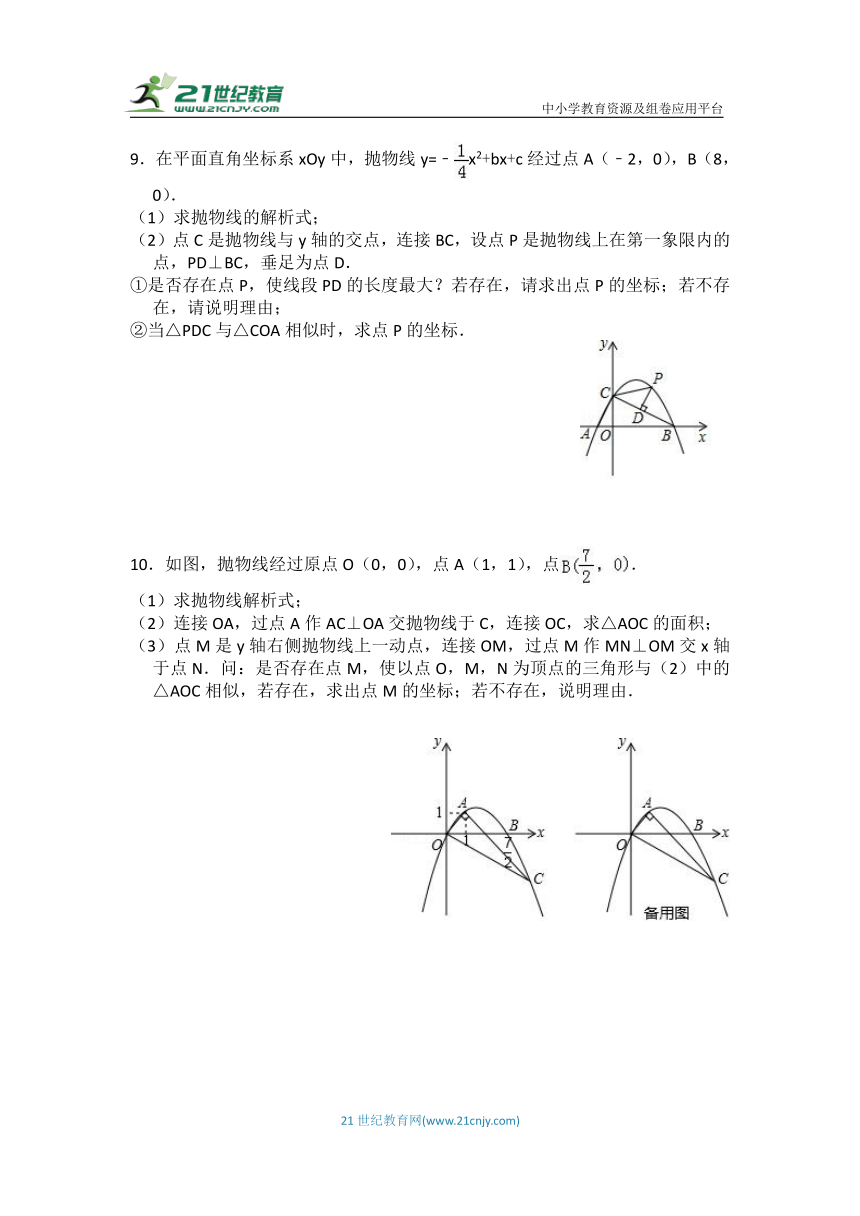
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,﹣),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=.
(1)求抛物线的解析式;
(2)动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒.
①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由.
②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.
7.如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
8.如图,已知抛物线y=x2+bx+c与直线y=x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求此抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P,使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
9.在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣2,0),B(8,0).
(1)求抛物线的解析式;
(2)点C是抛物线与y轴的交点,连接BC,设点P是抛物线上在第一象限内的点,PD⊥BC,垂足为点D.
①是否存在点P,使线段PD的长度最大?若存在,请求出点P的坐标;若不存在,请说明理由;
②当△PDC与△COA相似时,求点P的坐标.
10.如图,抛物线经过原点O(0,0),点A(1,1),点.
(1)求抛物线解析式;
(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;
(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.
11.如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
12.如图,已知二次函数的图象过点O(0,0).A(8,4),与x轴交于另一点B,且对称轴是直线x=3.
(1)求该二次函数的解析式;
(2)若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求M的坐标;
(3)P是x轴上的点,过P作PQ⊥x轴与抛物线交于Q.过A作AC⊥x轴于C,当以O,P,Q为顶点的三角形与以O,A,C为顶点的三角形相似时,求P点的坐标.
13.如图,在平面直角坐标系中,二次函数y=(x﹣a)(x﹣3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.
14.如图,已知抛物线y=ax2+bx(a≠0)过点A(,﹣3)和点B(3,0).过点A作直线AC∥x轴,交y轴于点C.
(1)求抛物线的解析式;
(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D.连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;
(3)抛物线上是否存在点Q,使得S△AOC=S△AOQ?若存在,求出点Q的坐标;若不存在,请说明理由.
参考答案
1.【解答】解:(1)将A(﹣1,0)、B(4,0)代入y=ax2+bx+2,得:
,解得:,
∴抛物线的解析式为y=﹣x2+x+2.
(2)当x=0时,y=﹣x2+x+2=2,
∴点C的坐标为(0,2).
①过点D作DE⊥x轴于点E,如图1所示.
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴OA=EB,OC=ED.
∵A(﹣1,0),O(0,0),C(0,2),B(4,0),
∴BE=1,DE=2,OE=3,
∴点D的坐标为(3,﹣2).
②四边形ADBC为矩形,理由如下:
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OC=2,OB=4,AB=5,
∴AC==,BC==2.
∵AC2+BC2=25=AB2,
∴∠ACB=90°.
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴∠ABC=∠BAD,BC=AD,
∴BC∥AD且BC=AD,
∴四边形ADBC为平行四边形.
又∵∠ACB=90°,
∴四边形ADBC为矩形.
(3)假设存在,设点P的坐标为(,m).
∵点M为AB的中点,
∴∠BPD=∠ADB=90°,
∴有两种情况(如图2所示).
①当△PMB∽△BDA时,有==,即=,
解得:m=±,
∴点P的坐标为(,)或(,﹣);
②当△BMP∽△BDA时,有==2,即=2,
解得:m=±5,
∴点P的坐标为(,5)或(,﹣5).
综上所述:在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(,)或(,﹣)或(,5)或(,﹣5).
2.【解答】解:(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3).
把y=0代入y=﹣x+3得:x=3,
∴B(3,0),A(﹣1,0)
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:,解得b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图所示:作点O关于BC的对称点O′,则O′(3,3).
∵O′与O关于BC对称,
∴PO=PO′.
∴OP+AP=O′P+AP≤AO′.
∴当A、P、O′在一条直线上时,OP+AP有最小值.
设AP的解析式为y=kx+b,则,解得:k=,b=.
∴AP的解析式为y=x+.
将y=x+与y=﹣x+3联立,解得:y=,x=,
∴点P的坐标为(,).
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
又∵C(0,3,B(3,0),
∴CD=,BC=3,DB=2.
∴CD2+CB2=BD2,
∴∠DCB=90°.
∵A(﹣1,0),C(0,3),
∴OA=1,CO=3.
∴==.
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图所示:连接AC,过点C作CQ⊥AC,交x轴与点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB.
∴=,即=,解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
3.【解答】解:(1)把A(﹣1,0),B(3,0),C(0,2)代入y=ax2+bx+c得:,
解得:a=﹣,b=,c=2,
∴抛物线的解析式为y=﹣x2+x+2.
(2)设点P的坐标为(t,﹣t2+t+2).
∵A(﹣1,0),B(3,0),
∴AB=4.
∴S=AB PD=×4×(﹣t2+t+2)=﹣t2+t+4(0<t<3);
(3)当△ODP∽△COB时,=即=,
整理得:4t2+t﹣12=0,
解得:t=或t=(舍去).
∴OD=t=,DP=OD=,
∴点P的坐标为(,).
当△ODP∽△BOC,则=,即=,
整理得t2﹣t﹣3=0,
解得:t=或t=(舍去).
∴OD=t=,DP=OD=,
∴点P的坐标为(,).
综上所述点P的坐标为(,)或(,).
4.【解答】解:(1)把点A(﹣2,0),B(0、﹣4)代入抛物线y=x2+bx+c中得:
,解得:,
∴抛物线的解析式为:y=x2﹣x﹣4;
(2)当y=0时,x2﹣x﹣4=0,
解得:x=﹣2或4,
∴C(4,0),
如图1,过O作OE⊥BP于E,过C作CF⊥BP于F,设PB交x轴于G,
∵S△PBO=S△PBC,
∴,
∴OE=CF,
易得△OEG≌△CFG,
∴OG=CG=2,
设P(x,x2﹣x﹣4),过P作PM⊥y轴于M,
tan∠PBM===,
∴BM=2PM,
∴4+x2﹣x﹣4=2x,
x2﹣6x=0,
x1=0(舍),x2=6,
∴P(6,8),
易得AP的解析式为:y=x+2,
BC的解析式为:y=x﹣4,
∴AP∥BC;
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
∵∠BAE=∠BAC,∠ABE≠∠ABC,
∴∠ABE=∠ACB=45°,
∴△ABE∽△ACB,
∴,
∴,
∴AE=,OE=﹣2=
∴E(,0),
∵B(0,﹣4),
易得BE:y=3x﹣4,
则x2﹣x﹣4=3x﹣4,
x1=0(舍),x2=8,
∴D(8,20);
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,
∵∠BEA=∠BEC,
∴当∠ABE=∠BCE时,△ABE∽△BCE,
∴==,
设BE=2m,CE=4m,
Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴,
3m2﹣8m+8=0,
(m﹣2)(3m﹣2)=0,
m1=2,m2=,
∴OE=4m﹣4=12或,
∵OE=<2,∠AEB是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,
∴E(﹣12,0);
同理得BE的解析式为:y=﹣x﹣4,
﹣x﹣4=x2﹣x﹣4,
x=或0(舍)
∴D(,﹣);
综上,点D的坐标为(8,20)或(,﹣).
5.【解答】解:(1)把A(﹣2,0),B(4,0)代入抛物线y=ax2+bx﹣1,得
解得
∴抛物线解析式为:y=
∴抛物线对称轴为直线x=﹣
(2)存在
使四边形ACPO的周长最小,只需PC+PO最小
∴取点C(0,﹣1)关于直线x=1的对称点C′(2,﹣1),连C′O与直线x=1的交点即为P点.
设过点C′、O直线解析式为:y=kx
∴k=﹣
∴y=﹣
则P点坐标为(1,﹣)
(3)当△AOC∽△MNC时,
如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E
∵∠ACO=∠NCD,∠AOC=∠CND=90°
∴∠CDN=∠CAO
由相似,∠CAO=∠CMN
∴∠CDN=∠CMN
∵MN⊥AC
∴M、D关于AN对称,则N为DM中点
设点N坐标为(a,﹣a﹣1)
由△EDN∽△OAC
∴ED=2a
∴点D坐标为(0,﹣)
∵N为DM中点
∴点M坐标为(2a,)
把M代入y=,解得
a=0(舍去)或a=4
∴a=4
则N点坐标为(4,﹣3)
当△AOC∽△CNM时,∠CAO=∠NCM
∴CM∥AB则点C关于直线x=1的对称点C′即为点M
由(2)M为(2,﹣1)
∴由相似CN=,MN=
由面积法求N到MC距离为
则N点坐标为(,﹣)
∴N点坐标为(4,﹣3)或(,﹣)
6.【解答】解:(1)∵OA=1,OB=4
∴A(1,0),B(﹣4,0)
设抛物线的解析式为y=a(x+4)(x﹣1)
∵点C(0,﹣)在抛物线上
∴﹣
解得a=
∴抛物线的解析式为y=
(2)存在t,使得△ADC与△PQA相似.
理由:①在Rt△AOC中,OA=1,OC=
则tan∠ACO=
∵tan∠OAD=
∴∠OAD=∠ACO
∵直线l的解析式为y=
∴D(0,﹣)
∵点C(0,﹣)
∴CD=
由AC2=OC2+OA2,得AC=
在△AQP中,AP=AB﹣PB=5﹣2t,AQ=t
由∠PAQ=∠ACD,要使△ADC与△PQA相似
只需或
则有或
解得t1=,t2=
∵t1<2.5,t2<2.5
∴存在t=或t=,使得△ADC与△PQA相似
②存在t,使得△APQ与△CAQ的面积之和最大
理由:作PF⊥AQ于点F,CN⊥AQ于N
在△APF中,PF=AP sin∠PAF=
在△AOD中,由AD2=OD2+OA2,得AD=
在△ADC中,由S△ADC=
∴CN=
∴S△AQP+S△AQC=
=﹣
∴当t=时,△APQ与△CAQ的面积之和最大
7.【解答】解:(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),
将点C(0,2)代入,得:﹣4a=2,
解得:a=﹣,
则抛物线解析式为y=﹣(x+1)(x﹣4)=﹣x2+x+2;
(2)由题意知点D坐标为(0,﹣2),
设直线BD解析式为y=kx+b,
将B(4,0)、D(0,﹣2)代入,得:,
解得:,
∴直线BD解析式为y=x﹣2,
∵QM⊥x轴,P(m,0),
∴Q(m,﹣m2+m+2)、M(m,m﹣2),
则QM=﹣m2+m+2﹣(m﹣2)=﹣m2+m+4,
∵F(0,)、D(0,﹣2),
∴DF=,
∵QM∥DF,
∴当﹣m2+m+4=时,四边形DMQF是平行四边形,
解得:m=﹣1或m=3,
即m=﹣1或m=3时,四边形DMQF是平行四边形;
(3)如图所示:
∵QM∥DF,
∴∠ODB=∠QMB,
分以下两种情况:
①当∠DOB=∠MBQ=90°时,△DOB∽△MBQ,
则===,
∵∠MBQ=90°,
∴∠MBP+∠PBQ=90°,
∵∠MPB=∠BPQ=90°,
∴∠MBP+∠BMP=90°,
∴∠BMP=∠PBQ,
∴△MBQ∽△BPQ,
∴=,即=,
解得:m1=3、m2=4,
当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,
∴m=3,点Q的坐标为(3,2);
②当∠BQM=90°时,此时点Q与点A重合,△BOD∽△BQM′,
此时m=﹣1,点Q的坐标为(﹣1,0);
综上,点Q的坐标为(3,2)或(﹣1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.
8.【解答】解:(1)将A(0,3),C(﹣3,0)代入函数解析式,得
,
解得,
抛物线的解析式是y=x2+x+3;
(2)由抛物线的对称性可知,点D与点C关于对称轴对称,
∴对l上任意一点有MD=MC,
联立方程组,
解得(不符合题意,舍),,
∴B(﹣4,1),
当点B,C,M共线时,|MB﹣MD|取最大值,即为BC的长,
过点B作BE⊥x轴于点E,
在Rt△BEC中,由勾股定理,得
BC==,
|MB﹣MD|取最大值为;
(3)存在点P使得以A,P,Q为顶点的三角形与△ABC相似,
在Rt△BEC中,∵BE=CE=1,
∴∠BCE=45°,
在Rt△ACO中,
∵AO=CO=3,
∴∠ACO=45°,
∴∠ACB=180°﹣45°﹣45°=90°,
过点P作PQ⊥y轴于Q点,∠PQA=90°,
设P点坐标为(x,x2+x+3)(x>0)
①当∠PAQ=∠BAC时,△PAQ∽△CAB,
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,
∴△PGA∽△BCA,
∴=,
即==,
∴=,
解得x1=1,x2=0(舍去),
∴P点的纵坐标为×12+×1+3=6,
∴P(1,6),
②当∠PAQ=∠ABC时,△PAQ∽△CBA,
∵∠PGA=∠ACB=90°,∠PAQ=∠ABC,
∴△PGA∽△ACB,
∴=,
即==3,
∴=3,
解得x1=﹣(舍去),x2=0(舍去)
∴此时无符合条件的点P,
综上所述,存在点P(1,6).
9.【解答】解:(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣x2+bx+c,
得:,解得:,
∴抛物线的解析式为:y=﹣x2+x+4;
(2)由(1)知C(0,4),∵B(8,0),
易得直线BC的解析式为:y=﹣x+4,
①如图1,过P作PG⊥x轴于G,PG交BC于E,
Rt△BOC中,OC=4,OB=8,
∴BC==4,
在Rt△PDE中,PD=PE sin∠PED=PE sin∠OCB=PE,
∴当线段PE最长时,PD的长最大,
设P(t,),则E(t,),
∴PG=﹣,EG=﹣t+4,
∴PE=PG﹣EG=(﹣)﹣(﹣t+4)=﹣t2+2t=﹣(t﹣4)2+4,(0<t<8),
当t=4时,PE有最大值是4,此时P(4,6),
∴PD==,
即当P(4,6)时,PD的长度最大,最大值是;
②∵A(﹣2,0),B(8,0),C(0,4),
∴OA=2,OB=8,OC=4,
∴AC2=22+42=20,AB2=(2+8)2=100,BC2=42+82=80,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴△COA∽△BOC,
当△PDC与△COA相似时,就有△PDC与△BOC相似,
∵相似三角形的对应角相等,
∴∠PCD=∠CBO或∠PCD=∠BCO,
(I)若∠PCD=∠CBO时,即Rt△PDC∽Rt△COB,
此时CP∥OB,
∵C(0,4),
∴yP=4,
∴﹣=4,
解得:x1=6,x2=0(舍),
即Rt△PDC∽Rt△COB时,P(6,4);
(II)若∠PCD=∠BCO时,即Rt△PDC∽Rt△BOC,
如图2,过P作x轴的垂线PG,交直线BC于F,
∴PF∥OC,
∴∠PFC=∠BCO,
∴∠PCD=∠PFC,
∴PC=PF,
设P(n,﹣+n+4),则PF=﹣+2n,
过P作PN⊥y轴于N,
Rt△PNC中,PC2=PN2+CN2=PF2,
∴n2+(﹣+n+4﹣4)2=(﹣+2n)2,
解得:n=3,
即Rt△PDC∽Rt△BOC时,P(3,);
综上所述,当△PDC与△COA相似时,点P的坐标为(6,4)或(3,).
10.【解答】解:(1)设抛物线解析式为y=ax(x﹣),
把A(1,1)代入得a 1(1﹣)=1,解得a=﹣,
∴抛物线解析式为y=﹣x(x﹣),
即y=﹣x2+x;
(2)延长CA交y轴于D,如图1,
∵A(1,1),
∴OA=,∠DOA=45°,
∴△AOD为等腰直角三角形,
∵OA⊥AC,
∴OD=OA=2,
∴D(0,2),
易得直线AD的解析式为y=﹣x+2,
解方程组得或,则C(5,﹣3),
∴S△AOC=S△COD﹣S△AOD
=×2×5﹣×2×1
=4;
(3)存在.
如图2,作MH⊥x轴于H,AC==4,OA=,
设M(x,﹣x2+x)(x>0),
∵∠OHM=∠OAC,
∴当=时,△OHM∽△OAC,即=,
解方程﹣x2+x=4x得x1=0(舍去),x2=﹣(舍去),
解方程﹣x2+x=﹣4x得x1=0(舍去),x2=,此时M点坐标为(,﹣54);
当=时,△OHM∽△CAO,即=,
解方程﹣x2+x=x得x1=0(舍去),x2=,此时M点的坐标为(,),
解方程﹣x2+x=﹣x得x1=0(舍去),x2=,此时M点坐标为(,﹣);
∵MN⊥OM,
∴∠OMN=90°,∴∠MON=∠HOM,∴△OMH∽△ONM,
∴当M点的坐标为(,﹣54)或(,)或(,﹣)时,以点O,M,N为顶点的三角形与(2)中的△AOC相似.
11.【解答】解:(1)①如图1,
∵y=﹣2x2+2x+4=﹣2(x﹣)2+,
∴顶点为M的坐标为(,),
当x=时,y=﹣2×+4=3,则点N坐标为(,3);
②不存在.
理由如下:
MN=﹣3=,
设P点坐标为(m,﹣2m+4),则D(m,﹣2m2+2m+4),
∴PD=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m,
∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即﹣2m2+4m=,解得m1=(舍去),m2=,此时P点坐标为(,1),
∵PN==,
∴PN≠MN,
∴平行四边形MNPD不为菱形,
∴不存在点P,使四边形MNPD为菱形;
(2)存在.
如图2,OB=4,OA=2,则AB==2,
当x=1时,y=﹣2x+4=2,则P(1,2),
∴PB==,
设抛物线的解析式为y=ax2+bx+4,
把A(2,0)代入得4a+2b+4=0,解得b=﹣2a﹣2,
∴抛物线的解析式为y=ax2﹣2(a+1)x+4,
当x=1时,y=ax2﹣2(a+1)x+4=a﹣2a﹣2+4=2﹣a,则D(1,2﹣a),
∴PD=2﹣a﹣2=﹣a,
∵DC∥OB,
∴∠DPB=∠OBA,
∴当=时,△PDB∽△BOA,即=,解得a=﹣2,此时抛物线解析式为y=﹣2x2+2x+4;
当=时,△PDB∽△BAO,即=,解得a=﹣,此时抛物线解析式为y=﹣x2+3x+4;
综上所述,满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=﹣x2+3x+4.
12.【解答】解:(1)∵抛物线过原点,对称轴是直线x=3,
∴B点坐标为(6,0),
设抛物线解析式为y=ax(x﹣6),
把A(8,4)代入得a 8 2=4,解得a=,
∴抛物线解析式为y=x(x﹣6),即y=x2﹣x;
(2)设M(t,0),
易得直线OA的解析式为y=x,
设直线AB的解析式为y=kx+b,
把B(6,0),A(8,4)代入得,解得,
∴直线AB的解析式为y=2x﹣12,
∵MN∥AB,
∴设直线MN的解析式为y=2x+n,
把M(t,0)代入得2t+n=0,解得n=﹣2t,
∴直线MN的解析式为y=2x﹣2t,
解方程组得,则N(t,t),
∴S△AMN=S△AOM﹣S△NOM
= 4 t﹣ t t
=﹣t2+2t
=﹣(t﹣3)2+3,
当t=3时,S△AMN有最大值3,此时M点坐标为(3,0);
(3)设Q(m,m2﹣m),
∵∠OPQ=∠ACO,
∴当=时,△PQO∽△COA,即=,
∴PQ=2PO,即|m2﹣m|=2|m|,
解方程m2﹣m=2m得m1=0(舍去),m2=14,此时P点坐标为(14,0);
解方程m2﹣m=﹣2m得m1=0(舍去),m2=﹣2,此时P点坐标为(﹣2,0);
∴当=时,△PQO∽△CAO,即=,
∴PQ=PO,即|m2﹣m|=|m|,
解方程m2﹣m=m得m1=0(舍去),m2=8(舍去),
解方程m2﹣m=﹣m得m1=0(舍去),m2=4,此时P点坐标为(4,0);
综上所述,P点坐标为(14,0)或(﹣2,0)或(4,0).
13.【解答】解:(1)∵y=(x﹣a)(x﹣3)(0<a<3),
∴A(a,0),B(3,0).
当x=0时,y=3a,
∴D(0,3a);
(2)∵A(a,0),B(3,0),
∴对称轴直线方程为:x=.
当x=时,y=﹣()2,
∴C(,﹣()2),
PB=3﹣,PC=()2,
①若△AOD∽△BPC时,则=,即=,
解得a=±3(舍去);
②若△AOD∽△CPB时,则=,即=,
解得a=3(舍去)或a=.
所以a的值是.
(3)能.理由如下:
联结BD,取中点M
∵D、O、B在同一个圆上,且圆心M为(,a).
若点C也在圆上,则MC=MB.即(﹣)2+(a+()2)2=(﹣3)2+(a﹣0)2,
整理,得
a4﹣14a2+45=0,
所以(a2﹣5)(a2﹣9)=0,
解得a1=,a2=﹣(舍),a3=3(舍),a4=﹣3(舍),
∴a=.
14.【解答】解:(1)把A(,﹣3)和点B(3,0)代入抛物线得:,
解得:a=,b=﹣,
则抛物线解析式为y=x2﹣x;
(2)当P在直线AD上方时,
设P坐标为(x,x2﹣x),则有AD=x﹣,PD=x2﹣x+3,
当△OCA∽△ADP时,=,即=,
整理得:3x2﹣9x+18=2x﹣6,即3x2﹣11x+24=0,
解得:x=,即x=或x=(舍去),
此时P(,﹣);
当△OCA∽△PDA时,=,即=,
整理得:x2﹣9x+6=6x﹣6,即x2﹣5x+12=0,
解得:x=,即x=4或(舍去),
此时P(4,6);
当点P(0,0)时,也满足△OCA∽△PDA;
当P在直线AD下方时,同理可得:P的坐标为(,﹣),
综上,P的坐标为(,﹣)或(4,6)或(,﹣)或(0,0);
(3)在Rt△AOC中,OC=3,AC=,
根据勾股定理得:OA=2,
∵OC AC=OA h,
∴h=,
∵S△AOC=S△AOQ=,
∴△AOQ边OA上的高为,
过O作OM⊥OA,截取OM=,过M作MN∥OA,交y轴于点N,如图所示:
在Rt△OMN中,ON=2OM=9,即N(0,9),
过M作MH⊥x轴,
在Rt△OMH中,MH=OM=,OH=OM=,即M(,),
设直线MN解析式为y=kx+9,
把M坐标代入得:=k+9,即k=﹣,即y=﹣x+9,
联立得:,
解得:或,即Q(3,0)或(﹣2,15),
则抛物线上存在点Q,使得S△AOC=S△AOQ,此时点Q的坐标为(3,0)或(﹣2,15).
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练二次函数中相似三角形存在性问题
1.如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
2.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
3.如图,抛物线y=ax2+bx+c与坐标轴交点分别为A(﹣1,0),B(3,0),C(0,2),作直线BC.
(1)求抛物线的解析式;
(2)点P为抛物线上第一象限内一动点,过点P作PD⊥x轴于点D,设点P的横坐标为t(0<t<3),求△ABP的面积S与t的函数关系式;
(3)条件同(2),若△ODP与△COB相似,求点P的坐标.
4.已知抛物线y=x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
5.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.
问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
6.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,﹣),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=.
(1)求抛物线的解析式;
(2)动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒.
①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由.
②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.
7.如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
8.如图,已知抛物线y=x2+bx+c与直线y=x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求此抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P,使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
9.在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣2,0),B(8,0).
(1)求抛物线的解析式;
(2)点C是抛物线与y轴的交点,连接BC,设点P是抛物线上在第一象限内的点,PD⊥BC,垂足为点D.
①是否存在点P,使线段PD的长度最大?若存在,请求出点P的坐标;若不存在,请说明理由;
②当△PDC与△COA相似时,求点P的坐标.
10.如图,抛物线经过原点O(0,0),点A(1,1),点.
(1)求抛物线解析式;
(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;
(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.
11.如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
12.如图,已知二次函数的图象过点O(0,0).A(8,4),与x轴交于另一点B,且对称轴是直线x=3.
(1)求该二次函数的解析式;
(2)若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求M的坐标;
(3)P是x轴上的点,过P作PQ⊥x轴与抛物线交于Q.过A作AC⊥x轴于C,当以O,P,Q为顶点的三角形与以O,A,C为顶点的三角形相似时,求P点的坐标.
13.如图,在平面直角坐标系中,二次函数y=(x﹣a)(x﹣3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.
14.如图,已知抛物线y=ax2+bx(a≠0)过点A(,﹣3)和点B(3,0).过点A作直线AC∥x轴,交y轴于点C.
(1)求抛物线的解析式;
(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D.连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;
(3)抛物线上是否存在点Q,使得S△AOC=S△AOQ?若存在,求出点Q的坐标;若不存在,请说明理由.
参考答案
1.【解答】解:(1)将A(﹣1,0)、B(4,0)代入y=ax2+bx+2,得:
,解得:,
∴抛物线的解析式为y=﹣x2+x+2.
(2)当x=0时,y=﹣x2+x+2=2,
∴点C的坐标为(0,2).
①过点D作DE⊥x轴于点E,如图1所示.
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴OA=EB,OC=ED.
∵A(﹣1,0),O(0,0),C(0,2),B(4,0),
∴BE=1,DE=2,OE=3,
∴点D的坐标为(3,﹣2).
②四边形ADBC为矩形,理由如下:
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OC=2,OB=4,AB=5,
∴AC==,BC==2.
∵AC2+BC2=25=AB2,
∴∠ACB=90°.
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴∠ABC=∠BAD,BC=AD,
∴BC∥AD且BC=AD,
∴四边形ADBC为平行四边形.
又∵∠ACB=90°,
∴四边形ADBC为矩形.
(3)假设存在,设点P的坐标为(,m).
∵点M为AB的中点,
∴∠BPD=∠ADB=90°,
∴有两种情况(如图2所示).
①当△PMB∽△BDA时,有==,即=,
解得:m=±,
∴点P的坐标为(,)或(,﹣);
②当△BMP∽△BDA时,有==2,即=2,
解得:m=±5,
∴点P的坐标为(,5)或(,﹣5).
综上所述:在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(,)或(,﹣)或(,5)或(,﹣5).
2.【解答】解:(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3).
把y=0代入y=﹣x+3得:x=3,
∴B(3,0),A(﹣1,0)
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:,解得b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图所示:作点O关于BC的对称点O′,则O′(3,3).
∵O′与O关于BC对称,
∴PO=PO′.
∴OP+AP=O′P+AP≤AO′.
∴当A、P、O′在一条直线上时,OP+AP有最小值.
设AP的解析式为y=kx+b,则,解得:k=,b=.
∴AP的解析式为y=x+.
将y=x+与y=﹣x+3联立,解得:y=,x=,
∴点P的坐标为(,).
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
又∵C(0,3,B(3,0),
∴CD=,BC=3,DB=2.
∴CD2+CB2=BD2,
∴∠DCB=90°.
∵A(﹣1,0),C(0,3),
∴OA=1,CO=3.
∴==.
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图所示:连接AC,过点C作CQ⊥AC,交x轴与点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB.
∴=,即=,解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
3.【解答】解:(1)把A(﹣1,0),B(3,0),C(0,2)代入y=ax2+bx+c得:,
解得:a=﹣,b=,c=2,
∴抛物线的解析式为y=﹣x2+x+2.
(2)设点P的坐标为(t,﹣t2+t+2).
∵A(﹣1,0),B(3,0),
∴AB=4.
∴S=AB PD=×4×(﹣t2+t+2)=﹣t2+t+4(0<t<3);
(3)当△ODP∽△COB时,=即=,
整理得:4t2+t﹣12=0,
解得:t=或t=(舍去).
∴OD=t=,DP=OD=,
∴点P的坐标为(,).
当△ODP∽△BOC,则=,即=,
整理得t2﹣t﹣3=0,
解得:t=或t=(舍去).
∴OD=t=,DP=OD=,
∴点P的坐标为(,).
综上所述点P的坐标为(,)或(,).
4.【解答】解:(1)把点A(﹣2,0),B(0、﹣4)代入抛物线y=x2+bx+c中得:
,解得:,
∴抛物线的解析式为:y=x2﹣x﹣4;
(2)当y=0时,x2﹣x﹣4=0,
解得:x=﹣2或4,
∴C(4,0),
如图1,过O作OE⊥BP于E,过C作CF⊥BP于F,设PB交x轴于G,
∵S△PBO=S△PBC,
∴,
∴OE=CF,
易得△OEG≌△CFG,
∴OG=CG=2,
设P(x,x2﹣x﹣4),过P作PM⊥y轴于M,
tan∠PBM===,
∴BM=2PM,
∴4+x2﹣x﹣4=2x,
x2﹣6x=0,
x1=0(舍),x2=6,
∴P(6,8),
易得AP的解析式为:y=x+2,
BC的解析式为:y=x﹣4,
∴AP∥BC;
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
∵∠BAE=∠BAC,∠ABE≠∠ABC,
∴∠ABE=∠ACB=45°,
∴△ABE∽△ACB,
∴,
∴,
∴AE=,OE=﹣2=
∴E(,0),
∵B(0,﹣4),
易得BE:y=3x﹣4,
则x2﹣x﹣4=3x﹣4,
x1=0(舍),x2=8,
∴D(8,20);
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,
∵∠BEA=∠BEC,
∴当∠ABE=∠BCE时,△ABE∽△BCE,
∴==,
设BE=2m,CE=4m,
Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴,
3m2﹣8m+8=0,
(m﹣2)(3m﹣2)=0,
m1=2,m2=,
∴OE=4m﹣4=12或,
∵OE=<2,∠AEB是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,
∴E(﹣12,0);
同理得BE的解析式为:y=﹣x﹣4,
﹣x﹣4=x2﹣x﹣4,
x=或0(舍)
∴D(,﹣);
综上,点D的坐标为(8,20)或(,﹣).
5.【解答】解:(1)把A(﹣2,0),B(4,0)代入抛物线y=ax2+bx﹣1,得
解得
∴抛物线解析式为:y=
∴抛物线对称轴为直线x=﹣
(2)存在
使四边形ACPO的周长最小,只需PC+PO最小
∴取点C(0,﹣1)关于直线x=1的对称点C′(2,﹣1),连C′O与直线x=1的交点即为P点.
设过点C′、O直线解析式为:y=kx
∴k=﹣
∴y=﹣
则P点坐标为(1,﹣)
(3)当△AOC∽△MNC时,
如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E
∵∠ACO=∠NCD,∠AOC=∠CND=90°
∴∠CDN=∠CAO
由相似,∠CAO=∠CMN
∴∠CDN=∠CMN
∵MN⊥AC
∴M、D关于AN对称,则N为DM中点
设点N坐标为(a,﹣a﹣1)
由△EDN∽△OAC
∴ED=2a
∴点D坐标为(0,﹣)
∵N为DM中点
∴点M坐标为(2a,)
把M代入y=,解得
a=0(舍去)或a=4
∴a=4
则N点坐标为(4,﹣3)
当△AOC∽△CNM时,∠CAO=∠NCM
∴CM∥AB则点C关于直线x=1的对称点C′即为点M
由(2)M为(2,﹣1)
∴由相似CN=,MN=
由面积法求N到MC距离为
则N点坐标为(,﹣)
∴N点坐标为(4,﹣3)或(,﹣)
6.【解答】解:(1)∵OA=1,OB=4
∴A(1,0),B(﹣4,0)
设抛物线的解析式为y=a(x+4)(x﹣1)
∵点C(0,﹣)在抛物线上
∴﹣
解得a=
∴抛物线的解析式为y=
(2)存在t,使得△ADC与△PQA相似.
理由:①在Rt△AOC中,OA=1,OC=
则tan∠ACO=
∵tan∠OAD=
∴∠OAD=∠ACO
∵直线l的解析式为y=
∴D(0,﹣)
∵点C(0,﹣)
∴CD=
由AC2=OC2+OA2,得AC=
在△AQP中,AP=AB﹣PB=5﹣2t,AQ=t
由∠PAQ=∠ACD,要使△ADC与△PQA相似
只需或
则有或
解得t1=,t2=
∵t1<2.5,t2<2.5
∴存在t=或t=,使得△ADC与△PQA相似
②存在t,使得△APQ与△CAQ的面积之和最大
理由:作PF⊥AQ于点F,CN⊥AQ于N
在△APF中,PF=AP sin∠PAF=
在△AOD中,由AD2=OD2+OA2,得AD=
在△ADC中,由S△ADC=
∴CN=
∴S△AQP+S△AQC=
=﹣
∴当t=时,△APQ与△CAQ的面积之和最大
7.【解答】解:(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),
将点C(0,2)代入,得:﹣4a=2,
解得:a=﹣,
则抛物线解析式为y=﹣(x+1)(x﹣4)=﹣x2+x+2;
(2)由题意知点D坐标为(0,﹣2),
设直线BD解析式为y=kx+b,
将B(4,0)、D(0,﹣2)代入,得:,
解得:,
∴直线BD解析式为y=x﹣2,
∵QM⊥x轴,P(m,0),
∴Q(m,﹣m2+m+2)、M(m,m﹣2),
则QM=﹣m2+m+2﹣(m﹣2)=﹣m2+m+4,
∵F(0,)、D(0,﹣2),
∴DF=,
∵QM∥DF,
∴当﹣m2+m+4=时,四边形DMQF是平行四边形,
解得:m=﹣1或m=3,
即m=﹣1或m=3时,四边形DMQF是平行四边形;
(3)如图所示:
∵QM∥DF,
∴∠ODB=∠QMB,
分以下两种情况:
①当∠DOB=∠MBQ=90°时,△DOB∽△MBQ,
则===,
∵∠MBQ=90°,
∴∠MBP+∠PBQ=90°,
∵∠MPB=∠BPQ=90°,
∴∠MBP+∠BMP=90°,
∴∠BMP=∠PBQ,
∴△MBQ∽△BPQ,
∴=,即=,
解得:m1=3、m2=4,
当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,
∴m=3,点Q的坐标为(3,2);
②当∠BQM=90°时,此时点Q与点A重合,△BOD∽△BQM′,
此时m=﹣1,点Q的坐标为(﹣1,0);
综上,点Q的坐标为(3,2)或(﹣1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.
8.【解答】解:(1)将A(0,3),C(﹣3,0)代入函数解析式,得
,
解得,
抛物线的解析式是y=x2+x+3;
(2)由抛物线的对称性可知,点D与点C关于对称轴对称,
∴对l上任意一点有MD=MC,
联立方程组,
解得(不符合题意,舍),,
∴B(﹣4,1),
当点B,C,M共线时,|MB﹣MD|取最大值,即为BC的长,
过点B作BE⊥x轴于点E,
在Rt△BEC中,由勾股定理,得
BC==,
|MB﹣MD|取最大值为;
(3)存在点P使得以A,P,Q为顶点的三角形与△ABC相似,
在Rt△BEC中,∵BE=CE=1,
∴∠BCE=45°,
在Rt△ACO中,
∵AO=CO=3,
∴∠ACO=45°,
∴∠ACB=180°﹣45°﹣45°=90°,
过点P作PQ⊥y轴于Q点,∠PQA=90°,
设P点坐标为(x,x2+x+3)(x>0)
①当∠PAQ=∠BAC时,△PAQ∽△CAB,
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,
∴△PGA∽△BCA,
∴=,
即==,
∴=,
解得x1=1,x2=0(舍去),
∴P点的纵坐标为×12+×1+3=6,
∴P(1,6),
②当∠PAQ=∠ABC时,△PAQ∽△CBA,
∵∠PGA=∠ACB=90°,∠PAQ=∠ABC,
∴△PGA∽△ACB,
∴=,
即==3,
∴=3,
解得x1=﹣(舍去),x2=0(舍去)
∴此时无符合条件的点P,
综上所述,存在点P(1,6).
9.【解答】解:(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣x2+bx+c,
得:,解得:,
∴抛物线的解析式为:y=﹣x2+x+4;
(2)由(1)知C(0,4),∵B(8,0),
易得直线BC的解析式为:y=﹣x+4,
①如图1,过P作PG⊥x轴于G,PG交BC于E,
Rt△BOC中,OC=4,OB=8,
∴BC==4,
在Rt△PDE中,PD=PE sin∠PED=PE sin∠OCB=PE,
∴当线段PE最长时,PD的长最大,
设P(t,),则E(t,),
∴PG=﹣,EG=﹣t+4,
∴PE=PG﹣EG=(﹣)﹣(﹣t+4)=﹣t2+2t=﹣(t﹣4)2+4,(0<t<8),
当t=4时,PE有最大值是4,此时P(4,6),
∴PD==,
即当P(4,6)时,PD的长度最大,最大值是;
②∵A(﹣2,0),B(8,0),C(0,4),
∴OA=2,OB=8,OC=4,
∴AC2=22+42=20,AB2=(2+8)2=100,BC2=42+82=80,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴△COA∽△BOC,
当△PDC与△COA相似时,就有△PDC与△BOC相似,
∵相似三角形的对应角相等,
∴∠PCD=∠CBO或∠PCD=∠BCO,
(I)若∠PCD=∠CBO时,即Rt△PDC∽Rt△COB,
此时CP∥OB,
∵C(0,4),
∴yP=4,
∴﹣=4,
解得:x1=6,x2=0(舍),
即Rt△PDC∽Rt△COB时,P(6,4);
(II)若∠PCD=∠BCO时,即Rt△PDC∽Rt△BOC,
如图2,过P作x轴的垂线PG,交直线BC于F,
∴PF∥OC,
∴∠PFC=∠BCO,
∴∠PCD=∠PFC,
∴PC=PF,
设P(n,﹣+n+4),则PF=﹣+2n,
过P作PN⊥y轴于N,
Rt△PNC中,PC2=PN2+CN2=PF2,
∴n2+(﹣+n+4﹣4)2=(﹣+2n)2,
解得:n=3,
即Rt△PDC∽Rt△BOC时,P(3,);
综上所述,当△PDC与△COA相似时,点P的坐标为(6,4)或(3,).
10.【解答】解:(1)设抛物线解析式为y=ax(x﹣),
把A(1,1)代入得a 1(1﹣)=1,解得a=﹣,
∴抛物线解析式为y=﹣x(x﹣),
即y=﹣x2+x;
(2)延长CA交y轴于D,如图1,
∵A(1,1),
∴OA=,∠DOA=45°,
∴△AOD为等腰直角三角形,
∵OA⊥AC,
∴OD=OA=2,
∴D(0,2),
易得直线AD的解析式为y=﹣x+2,
解方程组得或,则C(5,﹣3),
∴S△AOC=S△COD﹣S△AOD
=×2×5﹣×2×1
=4;
(3)存在.
如图2,作MH⊥x轴于H,AC==4,OA=,
设M(x,﹣x2+x)(x>0),
∵∠OHM=∠OAC,
∴当=时,△OHM∽△OAC,即=,
解方程﹣x2+x=4x得x1=0(舍去),x2=﹣(舍去),
解方程﹣x2+x=﹣4x得x1=0(舍去),x2=,此时M点坐标为(,﹣54);
当=时,△OHM∽△CAO,即=,
解方程﹣x2+x=x得x1=0(舍去),x2=,此时M点的坐标为(,),
解方程﹣x2+x=﹣x得x1=0(舍去),x2=,此时M点坐标为(,﹣);
∵MN⊥OM,
∴∠OMN=90°,∴∠MON=∠HOM,∴△OMH∽△ONM,
∴当M点的坐标为(,﹣54)或(,)或(,﹣)时,以点O,M,N为顶点的三角形与(2)中的△AOC相似.
11.【解答】解:(1)①如图1,
∵y=﹣2x2+2x+4=﹣2(x﹣)2+,
∴顶点为M的坐标为(,),
当x=时,y=﹣2×+4=3,则点N坐标为(,3);
②不存在.
理由如下:
MN=﹣3=,
设P点坐标为(m,﹣2m+4),则D(m,﹣2m2+2m+4),
∴PD=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m,
∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即﹣2m2+4m=,解得m1=(舍去),m2=,此时P点坐标为(,1),
∵PN==,
∴PN≠MN,
∴平行四边形MNPD不为菱形,
∴不存在点P,使四边形MNPD为菱形;
(2)存在.
如图2,OB=4,OA=2,则AB==2,
当x=1时,y=﹣2x+4=2,则P(1,2),
∴PB==,
设抛物线的解析式为y=ax2+bx+4,
把A(2,0)代入得4a+2b+4=0,解得b=﹣2a﹣2,
∴抛物线的解析式为y=ax2﹣2(a+1)x+4,
当x=1时,y=ax2﹣2(a+1)x+4=a﹣2a﹣2+4=2﹣a,则D(1,2﹣a),
∴PD=2﹣a﹣2=﹣a,
∵DC∥OB,
∴∠DPB=∠OBA,
∴当=时,△PDB∽△BOA,即=,解得a=﹣2,此时抛物线解析式为y=﹣2x2+2x+4;
当=时,△PDB∽△BAO,即=,解得a=﹣,此时抛物线解析式为y=﹣x2+3x+4;
综上所述,满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=﹣x2+3x+4.
12.【解答】解:(1)∵抛物线过原点,对称轴是直线x=3,
∴B点坐标为(6,0),
设抛物线解析式为y=ax(x﹣6),
把A(8,4)代入得a 8 2=4,解得a=,
∴抛物线解析式为y=x(x﹣6),即y=x2﹣x;
(2)设M(t,0),
易得直线OA的解析式为y=x,
设直线AB的解析式为y=kx+b,
把B(6,0),A(8,4)代入得,解得,
∴直线AB的解析式为y=2x﹣12,
∵MN∥AB,
∴设直线MN的解析式为y=2x+n,
把M(t,0)代入得2t+n=0,解得n=﹣2t,
∴直线MN的解析式为y=2x﹣2t,
解方程组得,则N(t,t),
∴S△AMN=S△AOM﹣S△NOM
= 4 t﹣ t t
=﹣t2+2t
=﹣(t﹣3)2+3,
当t=3时,S△AMN有最大值3,此时M点坐标为(3,0);
(3)设Q(m,m2﹣m),
∵∠OPQ=∠ACO,
∴当=时,△PQO∽△COA,即=,
∴PQ=2PO,即|m2﹣m|=2|m|,
解方程m2﹣m=2m得m1=0(舍去),m2=14,此时P点坐标为(14,0);
解方程m2﹣m=﹣2m得m1=0(舍去),m2=﹣2,此时P点坐标为(﹣2,0);
∴当=时,△PQO∽△CAO,即=,
∴PQ=PO,即|m2﹣m|=|m|,
解方程m2﹣m=m得m1=0(舍去),m2=8(舍去),
解方程m2﹣m=﹣m得m1=0(舍去),m2=4,此时P点坐标为(4,0);
综上所述,P点坐标为(14,0)或(﹣2,0)或(4,0).
13.【解答】解:(1)∵y=(x﹣a)(x﹣3)(0<a<3),
∴A(a,0),B(3,0).
当x=0时,y=3a,
∴D(0,3a);
(2)∵A(a,0),B(3,0),
∴对称轴直线方程为:x=.
当x=时,y=﹣()2,
∴C(,﹣()2),
PB=3﹣,PC=()2,
①若△AOD∽△BPC时,则=,即=,
解得a=±3(舍去);
②若△AOD∽△CPB时,则=,即=,
解得a=3(舍去)或a=.
所以a的值是.
(3)能.理由如下:
联结BD,取中点M
∵D、O、B在同一个圆上,且圆心M为(,a).
若点C也在圆上,则MC=MB.即(﹣)2+(a+()2)2=(﹣3)2+(a﹣0)2,
整理,得
a4﹣14a2+45=0,
所以(a2﹣5)(a2﹣9)=0,
解得a1=,a2=﹣(舍),a3=3(舍),a4=﹣3(舍),
∴a=.
14.【解答】解:(1)把A(,﹣3)和点B(3,0)代入抛物线得:,
解得:a=,b=﹣,
则抛物线解析式为y=x2﹣x;
(2)当P在直线AD上方时,
设P坐标为(x,x2﹣x),则有AD=x﹣,PD=x2﹣x+3,
当△OCA∽△ADP时,=,即=,
整理得:3x2﹣9x+18=2x﹣6,即3x2﹣11x+24=0,
解得:x=,即x=或x=(舍去),
此时P(,﹣);
当△OCA∽△PDA时,=,即=,
整理得:x2﹣9x+6=6x﹣6,即x2﹣5x+12=0,
解得:x=,即x=4或(舍去),
此时P(4,6);
当点P(0,0)时,也满足△OCA∽△PDA;
当P在直线AD下方时,同理可得:P的坐标为(,﹣),
综上,P的坐标为(,﹣)或(4,6)或(,﹣)或(0,0);
(3)在Rt△AOC中,OC=3,AC=,
根据勾股定理得:OA=2,
∵OC AC=OA h,
∴h=,
∵S△AOC=S△AOQ=,
∴△AOQ边OA上的高为,
过O作OM⊥OA,截取OM=,过M作MN∥OA,交y轴于点N,如图所示:
在Rt△OMN中,ON=2OM=9,即N(0,9),
过M作MH⊥x轴,
在Rt△OMH中,MH=OM=,OH=OM=,即M(,),
设直线MN解析式为y=kx+9,
把M坐标代入得:=k+9,即k=﹣,即y=﹣x+9,
联立得:,
解得:或,即Q(3,0)或(﹣2,15),
则抛物线上存在点Q,使得S△AOC=S△AOQ,此时点Q的坐标为(3,0)或(﹣2,15).
21世纪教育网(www.21cnjy.com)
同课章节目录
