2025年九年级数学三轮冲刺训练圆的综合题训练(含解析)
文档属性
| 名称 | 2025年九年级数学三轮冲刺训练圆的综合题训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 12:58:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学三轮冲刺训练圆的综合题训练
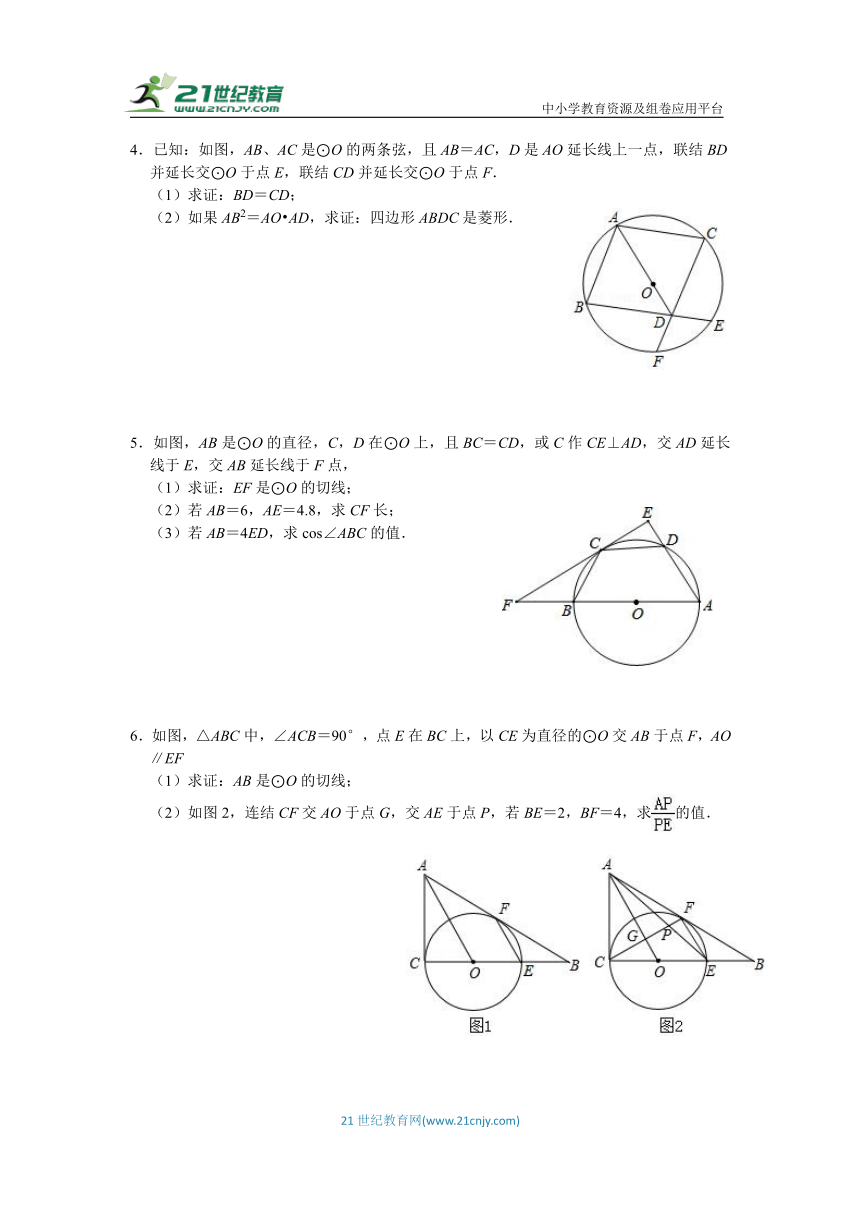
1.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为的中点,过点D作DE∥AC,交BC的延长线于点E.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为5,AB=8,求CE的长.
2.如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
3.如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
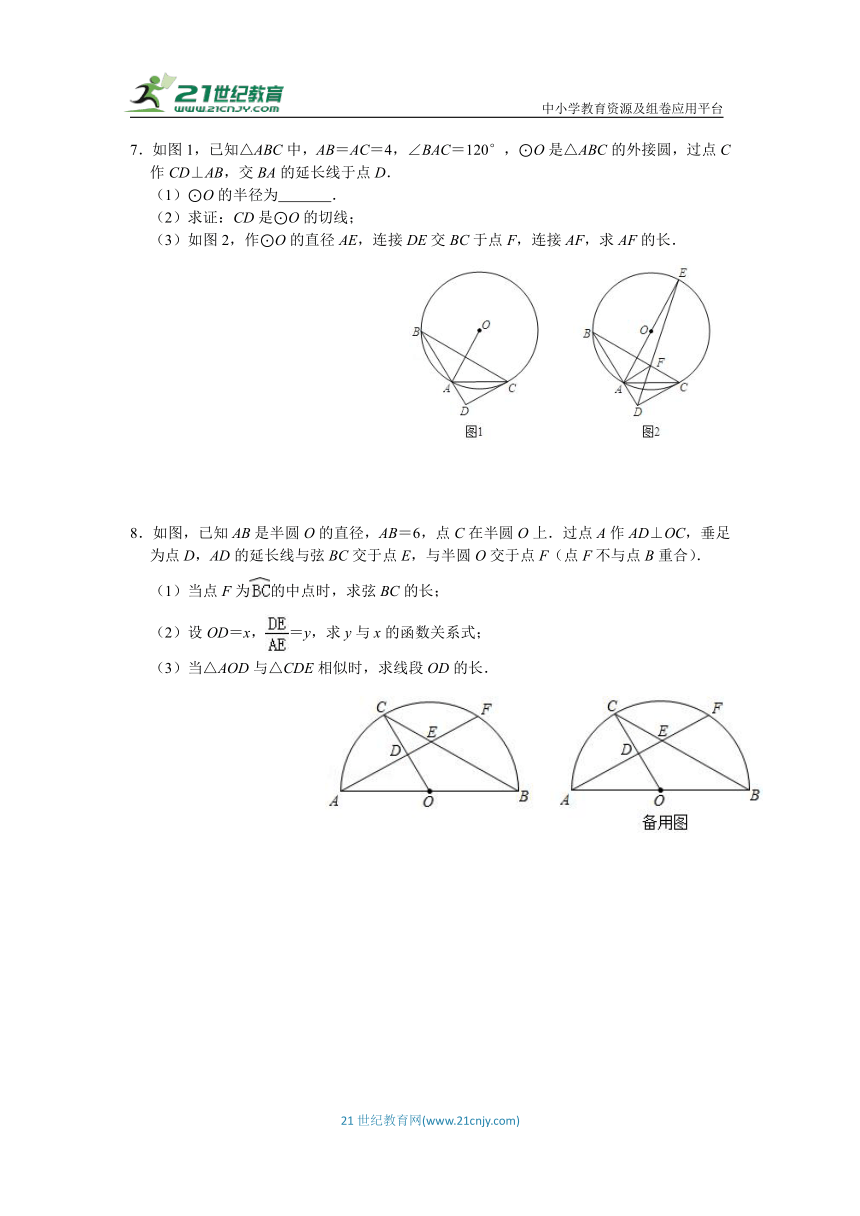
4.已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.
(1)求证:BD=CD;
(2)如果AB2=AO AD,求证:四边形ABDC是菱形.
5.如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,或C作CE⊥AD,交AD延长线于E,交AB延长线于F点,
(1)求证:EF是⊙O的切线;
(2)若AB=6,AE=4.8,求CF长;
(3)若AB=4ED,求cos∠ABC的值.
6.如图,△ABC中,∠ACB=90°,点E在BC上,以CE为直径的⊙O交AB于点F,AO∥EF
(1)求证:AB是⊙O的切线;
(2)如图2,连结CF交AO于点G,交AE于点P,若BE=2,BF=4,求的值.
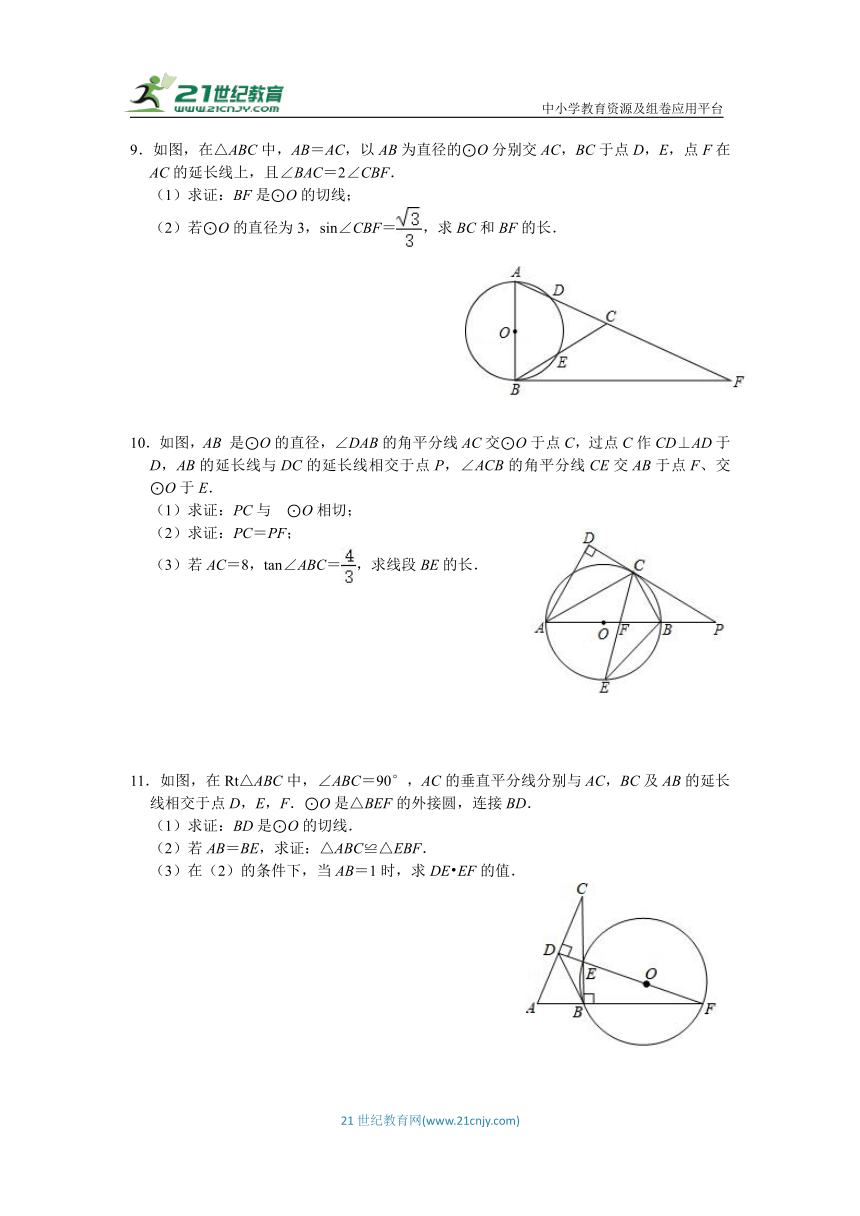
7.如图1,已知△ABC中,AB=AC=4,∠BAC=120°,⊙O是△ABC的外接圆,过点C作CD⊥AB,交BA的延长线于点D.
(1)⊙O的半径为 .
(2)求证:CD是⊙O的切线;
(3)如图2,作⊙O的直径AE,连接DE交BC于点F,连接AF,求AF的长.
8.如图,已知AB是半圆O的直径,AB=6,点C在半圆O上.过点A作AD⊥OC,垂足为点D,AD的延长线与弦BC交于点E,与半圆O交于点F(点F不与点B重合).
(1)当点F为的中点时,求弦BC的长;
(2)设OD=x,=y,求y与x的函数关系式;
(3)当△AOD与△CDE相似时,求线段OD的长.
9.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.
(1)求证:BF是⊙O的切线;
(2)若⊙O的直径为3,sin∠CBF=,求BC和BF的长.
10.如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
(1)求证:PC与 ⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=,求线段BE的长.
11.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,连接BD.
(1)求证:BD是⊙O的切线.
(2)若AB=BE,求证:△ABC≌△EBF.
(3)在(2)的条件下,当AB=1时,求DE EF的值.
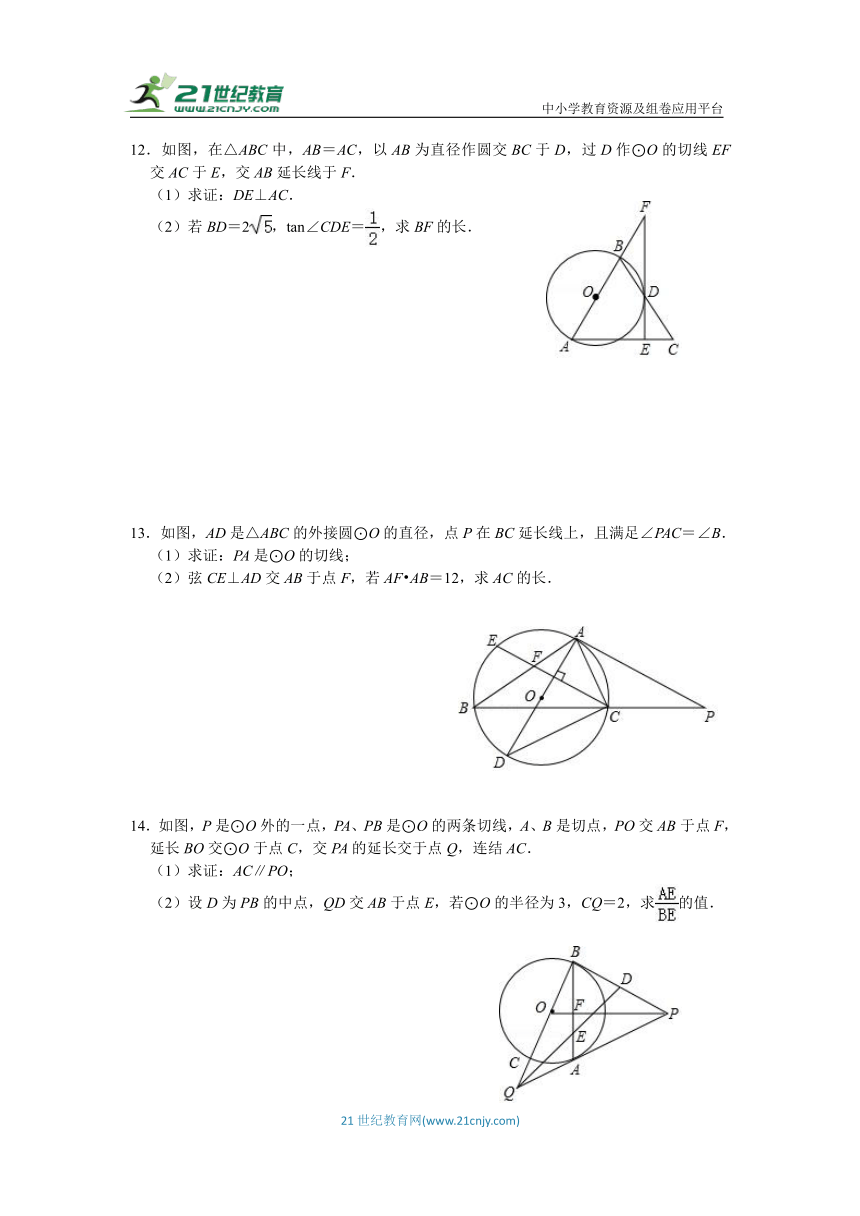
12.如图,在△ABC中,AB=AC,以AB为直径作圆交BC于D,过D作⊙O的切线EF交AC于E,交AB延长线于F.
(1)求证:DE⊥AC.
(2)若BD=2,tan∠CDE=,求BF的长.
13.如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠PAC=∠B.
(1)求证:PA是⊙O的切线;
(2)弦CE⊥AD交AB于点F,若AF AB=12,求AC的长.
14.如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.
(1)求证:AC∥PO;
(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求的值.
15.如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC;
(2)若BD=AD,AC=3,求CD的长.
16.已知:如图,在△ABC中,AB=AC,点P是底边BC上一点且满足PA=PB,⊙O是△PAB的外接圆,过点P作PD∥AB交AC于点D.
(1)求证:PD是⊙O的切线;
(2)若BC=8,tan∠ABC=,求⊙O的半径.
17.如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CE CP的值.
18.如图,AB是⊙O的直径,AB=4,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当=时,求劣弧的长度(结果保留π)
参考答案
1.【解答】解:(1)DE与⊙O相切,
理由:连接OD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∵D为的中点,
∴=,
∴AD=CD,
∴∠ACD=45°,
∵O是AC的中点,
∴∠ODC=45°,
∵DE∥AC,
∴∠CDE=∠DCA=45°,
∴∠ODE=90°,
∴DE与⊙O相切;
(2)∵⊙O的半径为5,
∴AC=10,
∴AD=CD=5,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB=8,
∴BC=6,
∵∠BAD=∠DCE,
∵∠ABD=∠CDE=45°,
∴△ABD∽△CDE,
∴=,
∴=,
∴CE=.
2.【解答】解:(1)如图1,连接OD,AD
∵AB是⊙O的直径,CD⊥AB
∴AB垂直平分CD
∵M是OA的中点,
∴OM=OA=OD
∴cos∠DOM==
∴∠DOM=60°
又:OA=OD
∴△OAD是等边三角形
∴∠OAD=60°
故答案为:60°
(2)∵CD⊥AB,AB是⊙O的直径,
∴CM=MD.
∵M是OA的中点,
∴AM=MO.
又∵∠AMC=∠DMO,
∴△AMC≌△OMD.
∴∠ACM=∠ODM.
∴CA∥OD.
∵DE⊥CA,
∴∠E=90°.
∴∠ODE=180°﹣∠E=90°.
∴DE⊥OD.
∴DE与⊙O相切.
(3)如图2,连接CF,CN,
∵OA⊥CD于M,
∴M是CD中点.
∴NC=ND.
∵∠CDF=45°,
∴∠NCD=∠NDC=45°.
∴∠CND=90°.
∴∠CNF=90°.
由(1)可知∠AOD=60°.
∴.
在Rt△CDE中,∠E=90°,∠ECD=30°,DE=3,
∴.
在Rt△CND中,∠CND=90°,∠CDN=45°,CD=6,
∴.
由(1)知∠CAD=2∠OAD=120°,
∴∠CFD=180°﹣∠CAD=60°.
在Rt△CNF中,∠CNF=90°,∠CFN=60°,,
∴.
3.【解答】(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O时AB的中点,
∴S△POB=S△PAB=×AP PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
4.【解答】证明:(1)如图1,连接BC,OB,OC,
∵AB、AC是⊙O的两条弦,且AB=AC,
∴A在BC的垂直平分线上,
∵OB=OA=OC,
∴O在BC的垂直平分线上,
∴AO垂直平分BC,
∴BD=CD;
(2)如图2,连接OB,
∵AB2=AO AD,
∴=,
∵∠BAO=∠DAB,
∴△ABO∽△ADB,
∴∠OBA=∠ADB,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠OAB=∠BDA,
∴AB=BD,
∵AB=AC,BD=CD,
∴AB=AC=BD=CD,
∴四边形ABDC是菱形.
5.【解答】(1)证明:连接OC、AC
∵CE⊥AD
∴∠EAC+∠ECA=90°
∵OC=OA
∴∠OCA=∠OAC
又∵BC=CD
∴∠OAC=∠EAC
∴∠OCA=∠EAC
∴∠ECA+∠OCA=90°
∴EF是⊙O的切线.
(2)解:∵EF是⊙O的切线
∴∠OCF=90°
又∵∠AEF=90°∠EFA=∠CFO
∴△COF∽△EAF
∴
即
解得:OF=5
在Rt△OCF中
CF===4
(3)解:∵EF是⊙O的切线
∴∠ECD=∠EAC
又∵BC=CD
∴∠EAC=∠BAC
∴∠ECD=∠BAC
又∵AB是直径
∴∠BCA=90°
在△BAC和△DCE中
∠BCA=∠DEC=90°
∠ECD=∠CAB
∴△CDE∽△ABC
∴
又∵AB=4DE,CD=BC
∴
∴BC=
∴cos∠ABC==
6.【解答】(1)证明:连接OF,如图1,
∵OA∥EF,
∴∠1=∠3,∠2=∠4,
∵OE=OF,
∴∠3=∠4,
∴∠1=∠2,
在△AOC和△AOF中,
,
∴△AOC≌△AOF,
∴∠ACO=∠AFO=90°,
∴OF⊥AB,
∴AB是⊙O的切线;
(2)解:如图2,在Rt△OFB中,设OE=OF=r,
∵OF2+BF2=OB2,
∴r2+42=(r+2)2,解得r=3,
∴OB=5,
设AC=AF=t,则AB=4+t,
在Rt△ACB中,t2+82=(t+4)2,解得t=6,
即AC=6,
∴AO==3,
∵AC2=AO AG,
∴AG==,
∴AO=AG,
∵OA∥EF,
∴△BEF∽△BOA,
∴==,
∴=,
∴=,
∵EF∥GA,
∴△PEF∽△PAG,
∴==2.
7.【解答】(1)解:如图1,连接OB,
∵AB=AC,
∴∠ABC=∠ACB=30°,
由圆周角定理得,∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∴OA=AB=4,
故答案为:4;
(2)证明:如图1,连接OC,
∵AB=AC,
∴=,
∴∠AOC=∠AOB=60°,
∴△AOC为等边三角形,
∴四边形OBAC为菱形,
∴OC∥BD,
∵CD⊥AB,
∴CD⊥OC,即CD是⊙O的切线;
(3)解:如图2,连接BE,
∵=,
∴OA⊥BC于H,
∵∠ABC=30°,
∴AH=AB=2,
由勾股定理得,BH==2,
∴BC=2BH=4,
在Rt△BDC中,∠ABC=30°,
∴CD=BC=2,
∵AE是⊙O的直径,
∴∠EBA=90°,
∴BE=AB tan∠BAE=4,
∵∠DBE=∠BDC=90°,
∴CD∥BE,
∴==2,
∠DAC=180°﹣∠BAC=60°,
∴DA=AC=AB,
∴=,
∴AF∥CD,
∴==,即=,
解得,AF=.
8.【解答】解:(1)如图1,联结OF,交BC于点H.
∵F是中点,
∴OF⊥BC,BC=2BH.
∴∠BOF=∠COF.
∵OA=OF,OC⊥AF,
∴∠AOC=∠COF,
∴∠AOC=∠COF=∠BOF=60°,
在Rt△BOH中,sin∠BOH==,
∵AB=6,
∴OB=3,
∴BH=,
∴BC=2BH=3;
(2)如图2,联结BF.
∵AF⊥OC,垂足为点=D,
∴AD=DF.
又∵OA=OB,
∴OD∥BF,BF=2OD=2x.
∴,
∴,
即,
∴,
∴y=.
(3)△AOD∽△CDE,分两种情况:①当∠DCE=∠DOA时,AB∥CB,不符合题意,舍去.
②当∠DCE=∠DAO时,联结OF.
∵OA=OF,OB=OC,
∴∠OAF=∠OFA,∠OCB=∠OBC.
∵∠DCE=∠DAO,
∴∠OAF=∠OFA=∠OCB=∠OBC.
∵∠AOD=∠OCB+∠OBC=2∠OAF,
∴∠OAF=30°,
∴OD=.
即线段OD的长为.
9.【解答】(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴2∠1=∠CAB.
∵∠BAC=2∠CBF,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线;
(2)解:过点C作CH⊥BF于H.
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=,
∵在Rt△AEB中,∠AEB=90°,AB=3,
∴BE=AB sin∠1=3×=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
∵sin∠CBF==,
∴CH=2,
∵CH∥AB,
∴=,即=,
∴CF=6,
∴AF=AC+CF=9,
∴BF==6.
10.【解答】解:(1)如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC是∠DAB的角平分线,
∴∠DAC=∠OAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴PC与 ⊙O相切;
(2)∵CF是∠ACB的角平分线,
∴∠ACF=∠BCF,
∵∠CAF=∠PCB,
∴∠ACF+∠CAF=∠BCF+∠PCB,
∴∠PFC=∠PCF,
∴PC=PF.
(3)∵AB 是⊙O的直径,
∴∠ACB=90°,
∵AC=8,tan∠ABC==,
∴BC=6,
∴AB==10,
∴OB=OE=5,
∵∠ACE=∠BCE,
∴=,
∴EO⊥AB,
∴BE==5.
11.【解答】解:(1)BD与⊙O相切,如图1,连接OB.
证明如下:∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,
∴∠C=∠DBC,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)证明:∵∠ABC=90°,
∴∠EBF=90°,
∵DF⊥AC,
∴∠ADF=90°,
∴∠C+∠A=∠A+∠AFD=90°,
∴∠C=∠BFE,
在△ABC与△EBF中,,
∴△ABC≌△EBF;
(3)解:如图2,连接CF,
∵△ABC≌△EBF,
∴BC=BF,
∵∠CBF=90°,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴BF=BC=+1,
∴EC﹣BC﹣BE=,
∵∠CED=∠BEF,∠CDE=∠EBF,
∴△CED∽△FEB,
∴=,
∴DE EF=BE EC=
12.【解答】(1)证明:连接OD,AD,如图:
∵EF是⊙O的切线,
∴OD⊥DE,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=DC,
又∵OB=OA,
∴OD是△ABC的中位线,
∴OD∥AC,
∴DE⊥AC.
(2)解:由(1)得,
∵DE⊥AC,AD⊥BC,
∴∠CDE+∠C=90°,∠DAC+∠C=90°,
∴∠CDE=∠DAC,
∴,
∴,
∴.
在Rt△ABD中,,
∴OA=OD=OB=5,AC=AB=10,
在Rt△CDE中,DE2+CE2=CD2,
∴2,
解得CE=2,
∴AE=AC﹣CE=10﹣2=8,
∵∠AEF=∠ODF=90°,∠F=∠F,
∴△AEF~△ODF,
∴,即,
解得.
13.【解答】(1)∵AD是⊙O的直径
∴∠ACD=90°;
∴∠CAD+∠D=90°
∵∠PAC=∠PBA,∠D=∠PBA,
∴∠CAD+∠PAC=90°,
∴∠PAD=90°,
∴PA⊥AD,
∵点A在⊙O上,
∴PA是⊙O的切线
(2)∵CF⊥AD,
∴∠ACF+∠CAD=90°,
∵∠CAD+∠D=90°,
∴∠D=∠ACF,
∴∠B=∠ACF,
∵∠BAC=∠CAF,
∴△ABC∽△ACF,
∴,
∴AC2=AF AB
∵AF AB=12,
∴AC2=12,
∴AC=2.
14.【解答】(1)证明:∵PA、PB是⊙O的两条切线,A、B是切点,
∴PA=PB,且PO平分∠BPA,
∴PO⊥AB.
∵BC是直径,
∴∠CAB=90°,
∴AC⊥AB,
∴AC∥PO;
(2)解:连结OA、DF,如图,
∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAQ=∠PBQ=90°.
在Rt△OAQ中,OA=OC=3,∴OQ=5.
由QA2+OA2=OQ2,得QA=4.
在Rt△PBQ中,PA=PB,QB=OQ+OB=8,
由QB2+PB2=PQ2,得82+PB2=(PB+4)2,
解得PB=6,
∴PA=PB=6,
∵OP⊥AB,
∴BF=AF=AB.
又∵D为PB的中点,
∴DF∥AP,DF=PA=3,
∴△DFE∽△QEA,
∴==,
设AE=4t,FE=3t,则AF=AE+FE=7t,
∴BE=BF+FE=AF+FE=7t+3t=10t,
∴==.
15.【解答】(1)证明:连接OD,如图所示.
∵OB=OD,
∴∠OBD=∠ODB.
∵CD是⊙O的切线,OD是⊙O的半径,
∴∠ODB+∠BDC=90°.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠OBD+∠CAD=90°,
∴∠CAD=∠BDC.
(2)解:∵∠C=∠C,∠CAD=∠CDB,
∴△CDB∽△CAD,
∴=.
∵BD=AD,
∴=,
∴=,
又∵AC=3,
∴CD=2.
16.【解答】(1)证明:如图1,连接OP,
∵PA=PB,
∴,
∴OP⊥AB,
∵PD∥AB,
∴OP⊥PD,
∴PD是⊙O的切线;
(2)如图2,过A作AH⊥BC于H,连接OA,OP,OP交AB于E,
∵AB=AC,
∴BH=BC==4,
Rt△ABH中,tan∠ABC===,
∴AH=2,AB==2,
∴BE=,PE=,
设⊙O的半径为r,则OA=r,OE=r﹣,
由勾股定理得:,
r=,
答:⊙O的半径是.
17.【解答】解:(1)如图,PD是⊙O的切线.
证明如下:
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=4,.
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴,
∴CP CE=CA2=(2)2=8.
18.【解答】(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵PF是⊙O的切线,CE⊥AB,
∴∠OCP=∠CEB=90°,
∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,
∴∠BCE=∠BCP,
∴BC平分∠PCE.
(2)证明:连接AC.
∵AB是直径,
∴∠ACB=90°,
∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,
∵∠BCP=∠BCE,
∴∠ACF=∠ACE,
∵∠F=∠AEC=90°,AC=AC,
∴△ACF≌△ACE,
∴CF=CE.
解法二:证明:连接AC.
∵OA=OC
∴∠BAC=∠ACO,
∵CD平行AF,
∴∠FAC=∠ACD,
∴∠FAC=∠CAO,∵CF⊥AF,CE⊥AB,
∴CF=CE.
(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=3a,PC=4a,PM=a,
∵∠MCB+∠P=90°,∠P+∠PBM=90°,
∴∠MCB=∠PBM,
∵CD是直径,BM⊥PC,
∴∠CMB=∠BMP=90°,
∴△BMC∽△PMB,
∴=,
∴BM2=CM PM=3a2,
∴BM=a,
∴tan∠BCM==,
∴∠BCM=30°,
∴∠OCB=∠OBC=∠BOC=60°,
∴的长==π.
21世纪教育网(www.21cnjy.com)
2025年九年级数学三轮冲刺训练圆的综合题训练
1.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为的中点,过点D作DE∥AC,交BC的延长线于点E.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为5,AB=8,求CE的长.
2.如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
3.如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
4.已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.
(1)求证:BD=CD;
(2)如果AB2=AO AD,求证:四边形ABDC是菱形.
5.如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,或C作CE⊥AD,交AD延长线于E,交AB延长线于F点,
(1)求证:EF是⊙O的切线;
(2)若AB=6,AE=4.8,求CF长;
(3)若AB=4ED,求cos∠ABC的值.
6.如图,△ABC中,∠ACB=90°,点E在BC上,以CE为直径的⊙O交AB于点F,AO∥EF
(1)求证:AB是⊙O的切线;
(2)如图2,连结CF交AO于点G,交AE于点P,若BE=2,BF=4,求的值.
7.如图1,已知△ABC中,AB=AC=4,∠BAC=120°,⊙O是△ABC的外接圆,过点C作CD⊥AB,交BA的延长线于点D.
(1)⊙O的半径为 .
(2)求证:CD是⊙O的切线;
(3)如图2,作⊙O的直径AE,连接DE交BC于点F,连接AF,求AF的长.
8.如图,已知AB是半圆O的直径,AB=6,点C在半圆O上.过点A作AD⊥OC,垂足为点D,AD的延长线与弦BC交于点E,与半圆O交于点F(点F不与点B重合).
(1)当点F为的中点时,求弦BC的长;
(2)设OD=x,=y,求y与x的函数关系式;
(3)当△AOD与△CDE相似时,求线段OD的长.
9.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.
(1)求证:BF是⊙O的切线;
(2)若⊙O的直径为3,sin∠CBF=,求BC和BF的长.
10.如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
(1)求证:PC与 ⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=,求线段BE的长.
11.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,连接BD.
(1)求证:BD是⊙O的切线.
(2)若AB=BE,求证:△ABC≌△EBF.
(3)在(2)的条件下,当AB=1时,求DE EF的值.
12.如图,在△ABC中,AB=AC,以AB为直径作圆交BC于D,过D作⊙O的切线EF交AC于E,交AB延长线于F.
(1)求证:DE⊥AC.
(2)若BD=2,tan∠CDE=,求BF的长.
13.如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠PAC=∠B.
(1)求证:PA是⊙O的切线;
(2)弦CE⊥AD交AB于点F,若AF AB=12,求AC的长.
14.如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.
(1)求证:AC∥PO;
(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求的值.
15.如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC;
(2)若BD=AD,AC=3,求CD的长.
16.已知:如图,在△ABC中,AB=AC,点P是底边BC上一点且满足PA=PB,⊙O是△PAB的外接圆,过点P作PD∥AB交AC于点D.
(1)求证:PD是⊙O的切线;
(2)若BC=8,tan∠ABC=,求⊙O的半径.
17.如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CE CP的值.
18.如图,AB是⊙O的直径,AB=4,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当=时,求劣弧的长度(结果保留π)
参考答案
1.【解答】解:(1)DE与⊙O相切,
理由:连接OD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∵D为的中点,
∴=,
∴AD=CD,
∴∠ACD=45°,
∵O是AC的中点,
∴∠ODC=45°,
∵DE∥AC,
∴∠CDE=∠DCA=45°,
∴∠ODE=90°,
∴DE与⊙O相切;
(2)∵⊙O的半径为5,
∴AC=10,
∴AD=CD=5,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB=8,
∴BC=6,
∵∠BAD=∠DCE,
∵∠ABD=∠CDE=45°,
∴△ABD∽△CDE,
∴=,
∴=,
∴CE=.
2.【解答】解:(1)如图1,连接OD,AD
∵AB是⊙O的直径,CD⊥AB
∴AB垂直平分CD
∵M是OA的中点,
∴OM=OA=OD
∴cos∠DOM==
∴∠DOM=60°
又:OA=OD
∴△OAD是等边三角形
∴∠OAD=60°
故答案为:60°
(2)∵CD⊥AB,AB是⊙O的直径,
∴CM=MD.
∵M是OA的中点,
∴AM=MO.
又∵∠AMC=∠DMO,
∴△AMC≌△OMD.
∴∠ACM=∠ODM.
∴CA∥OD.
∵DE⊥CA,
∴∠E=90°.
∴∠ODE=180°﹣∠E=90°.
∴DE⊥OD.
∴DE与⊙O相切.
(3)如图2,连接CF,CN,
∵OA⊥CD于M,
∴M是CD中点.
∴NC=ND.
∵∠CDF=45°,
∴∠NCD=∠NDC=45°.
∴∠CND=90°.
∴∠CNF=90°.
由(1)可知∠AOD=60°.
∴.
在Rt△CDE中,∠E=90°,∠ECD=30°,DE=3,
∴.
在Rt△CND中,∠CND=90°,∠CDN=45°,CD=6,
∴.
由(1)知∠CAD=2∠OAD=120°,
∴∠CFD=180°﹣∠CAD=60°.
在Rt△CNF中,∠CNF=90°,∠CFN=60°,,
∴.
3.【解答】(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O时AB的中点,
∴S△POB=S△PAB=×AP PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
4.【解答】证明:(1)如图1,连接BC,OB,OC,
∵AB、AC是⊙O的两条弦,且AB=AC,
∴A在BC的垂直平分线上,
∵OB=OA=OC,
∴O在BC的垂直平分线上,
∴AO垂直平分BC,
∴BD=CD;
(2)如图2,连接OB,
∵AB2=AO AD,
∴=,
∵∠BAO=∠DAB,
∴△ABO∽△ADB,
∴∠OBA=∠ADB,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠OAB=∠BDA,
∴AB=BD,
∵AB=AC,BD=CD,
∴AB=AC=BD=CD,
∴四边形ABDC是菱形.
5.【解答】(1)证明:连接OC、AC
∵CE⊥AD
∴∠EAC+∠ECA=90°
∵OC=OA
∴∠OCA=∠OAC
又∵BC=CD
∴∠OAC=∠EAC
∴∠OCA=∠EAC
∴∠ECA+∠OCA=90°
∴EF是⊙O的切线.
(2)解:∵EF是⊙O的切线
∴∠OCF=90°
又∵∠AEF=90°∠EFA=∠CFO
∴△COF∽△EAF
∴
即
解得:OF=5
在Rt△OCF中
CF===4
(3)解:∵EF是⊙O的切线
∴∠ECD=∠EAC
又∵BC=CD
∴∠EAC=∠BAC
∴∠ECD=∠BAC
又∵AB是直径
∴∠BCA=90°
在△BAC和△DCE中
∠BCA=∠DEC=90°
∠ECD=∠CAB
∴△CDE∽△ABC
∴
又∵AB=4DE,CD=BC
∴
∴BC=
∴cos∠ABC==
6.【解答】(1)证明:连接OF,如图1,
∵OA∥EF,
∴∠1=∠3,∠2=∠4,
∵OE=OF,
∴∠3=∠4,
∴∠1=∠2,
在△AOC和△AOF中,
,
∴△AOC≌△AOF,
∴∠ACO=∠AFO=90°,
∴OF⊥AB,
∴AB是⊙O的切线;
(2)解:如图2,在Rt△OFB中,设OE=OF=r,
∵OF2+BF2=OB2,
∴r2+42=(r+2)2,解得r=3,
∴OB=5,
设AC=AF=t,则AB=4+t,
在Rt△ACB中,t2+82=(t+4)2,解得t=6,
即AC=6,
∴AO==3,
∵AC2=AO AG,
∴AG==,
∴AO=AG,
∵OA∥EF,
∴△BEF∽△BOA,
∴==,
∴=,
∴=,
∵EF∥GA,
∴△PEF∽△PAG,
∴==2.
7.【解答】(1)解:如图1,连接OB,
∵AB=AC,
∴∠ABC=∠ACB=30°,
由圆周角定理得,∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∴OA=AB=4,
故答案为:4;
(2)证明:如图1,连接OC,
∵AB=AC,
∴=,
∴∠AOC=∠AOB=60°,
∴△AOC为等边三角形,
∴四边形OBAC为菱形,
∴OC∥BD,
∵CD⊥AB,
∴CD⊥OC,即CD是⊙O的切线;
(3)解:如图2,连接BE,
∵=,
∴OA⊥BC于H,
∵∠ABC=30°,
∴AH=AB=2,
由勾股定理得,BH==2,
∴BC=2BH=4,
在Rt△BDC中,∠ABC=30°,
∴CD=BC=2,
∵AE是⊙O的直径,
∴∠EBA=90°,
∴BE=AB tan∠BAE=4,
∵∠DBE=∠BDC=90°,
∴CD∥BE,
∴==2,
∠DAC=180°﹣∠BAC=60°,
∴DA=AC=AB,
∴=,
∴AF∥CD,
∴==,即=,
解得,AF=.
8.【解答】解:(1)如图1,联结OF,交BC于点H.
∵F是中点,
∴OF⊥BC,BC=2BH.
∴∠BOF=∠COF.
∵OA=OF,OC⊥AF,
∴∠AOC=∠COF,
∴∠AOC=∠COF=∠BOF=60°,
在Rt△BOH中,sin∠BOH==,
∵AB=6,
∴OB=3,
∴BH=,
∴BC=2BH=3;
(2)如图2,联结BF.
∵AF⊥OC,垂足为点=D,
∴AD=DF.
又∵OA=OB,
∴OD∥BF,BF=2OD=2x.
∴,
∴,
即,
∴,
∴y=.
(3)△AOD∽△CDE,分两种情况:①当∠DCE=∠DOA时,AB∥CB,不符合题意,舍去.
②当∠DCE=∠DAO时,联结OF.
∵OA=OF,OB=OC,
∴∠OAF=∠OFA,∠OCB=∠OBC.
∵∠DCE=∠DAO,
∴∠OAF=∠OFA=∠OCB=∠OBC.
∵∠AOD=∠OCB+∠OBC=2∠OAF,
∴∠OAF=30°,
∴OD=.
即线段OD的长为.
9.【解答】(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴2∠1=∠CAB.
∵∠BAC=2∠CBF,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线;
(2)解:过点C作CH⊥BF于H.
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=,
∵在Rt△AEB中,∠AEB=90°,AB=3,
∴BE=AB sin∠1=3×=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
∵sin∠CBF==,
∴CH=2,
∵CH∥AB,
∴=,即=,
∴CF=6,
∴AF=AC+CF=9,
∴BF==6.
10.【解答】解:(1)如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC是∠DAB的角平分线,
∴∠DAC=∠OAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴PC与 ⊙O相切;
(2)∵CF是∠ACB的角平分线,
∴∠ACF=∠BCF,
∵∠CAF=∠PCB,
∴∠ACF+∠CAF=∠BCF+∠PCB,
∴∠PFC=∠PCF,
∴PC=PF.
(3)∵AB 是⊙O的直径,
∴∠ACB=90°,
∵AC=8,tan∠ABC==,
∴BC=6,
∴AB==10,
∴OB=OE=5,
∵∠ACE=∠BCE,
∴=,
∴EO⊥AB,
∴BE==5.
11.【解答】解:(1)BD与⊙O相切,如图1,连接OB.
证明如下:∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,
∴∠C=∠DBC,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)证明:∵∠ABC=90°,
∴∠EBF=90°,
∵DF⊥AC,
∴∠ADF=90°,
∴∠C+∠A=∠A+∠AFD=90°,
∴∠C=∠BFE,
在△ABC与△EBF中,,
∴△ABC≌△EBF;
(3)解:如图2,连接CF,
∵△ABC≌△EBF,
∴BC=BF,
∵∠CBF=90°,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴BF=BC=+1,
∴EC﹣BC﹣BE=,
∵∠CED=∠BEF,∠CDE=∠EBF,
∴△CED∽△FEB,
∴=,
∴DE EF=BE EC=
12.【解答】(1)证明:连接OD,AD,如图:
∵EF是⊙O的切线,
∴OD⊥DE,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=DC,
又∵OB=OA,
∴OD是△ABC的中位线,
∴OD∥AC,
∴DE⊥AC.
(2)解:由(1)得,
∵DE⊥AC,AD⊥BC,
∴∠CDE+∠C=90°,∠DAC+∠C=90°,
∴∠CDE=∠DAC,
∴,
∴,
∴.
在Rt△ABD中,,
∴OA=OD=OB=5,AC=AB=10,
在Rt△CDE中,DE2+CE2=CD2,
∴2,
解得CE=2,
∴AE=AC﹣CE=10﹣2=8,
∵∠AEF=∠ODF=90°,∠F=∠F,
∴△AEF~△ODF,
∴,即,
解得.
13.【解答】(1)∵AD是⊙O的直径
∴∠ACD=90°;
∴∠CAD+∠D=90°
∵∠PAC=∠PBA,∠D=∠PBA,
∴∠CAD+∠PAC=90°,
∴∠PAD=90°,
∴PA⊥AD,
∵点A在⊙O上,
∴PA是⊙O的切线
(2)∵CF⊥AD,
∴∠ACF+∠CAD=90°,
∵∠CAD+∠D=90°,
∴∠D=∠ACF,
∴∠B=∠ACF,
∵∠BAC=∠CAF,
∴△ABC∽△ACF,
∴,
∴AC2=AF AB
∵AF AB=12,
∴AC2=12,
∴AC=2.
14.【解答】(1)证明:∵PA、PB是⊙O的两条切线,A、B是切点,
∴PA=PB,且PO平分∠BPA,
∴PO⊥AB.
∵BC是直径,
∴∠CAB=90°,
∴AC⊥AB,
∴AC∥PO;
(2)解:连结OA、DF,如图,
∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAQ=∠PBQ=90°.
在Rt△OAQ中,OA=OC=3,∴OQ=5.
由QA2+OA2=OQ2,得QA=4.
在Rt△PBQ中,PA=PB,QB=OQ+OB=8,
由QB2+PB2=PQ2,得82+PB2=(PB+4)2,
解得PB=6,
∴PA=PB=6,
∵OP⊥AB,
∴BF=AF=AB.
又∵D为PB的中点,
∴DF∥AP,DF=PA=3,
∴△DFE∽△QEA,
∴==,
设AE=4t,FE=3t,则AF=AE+FE=7t,
∴BE=BF+FE=AF+FE=7t+3t=10t,
∴==.
15.【解答】(1)证明:连接OD,如图所示.
∵OB=OD,
∴∠OBD=∠ODB.
∵CD是⊙O的切线,OD是⊙O的半径,
∴∠ODB+∠BDC=90°.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠OBD+∠CAD=90°,
∴∠CAD=∠BDC.
(2)解:∵∠C=∠C,∠CAD=∠CDB,
∴△CDB∽△CAD,
∴=.
∵BD=AD,
∴=,
∴=,
又∵AC=3,
∴CD=2.
16.【解答】(1)证明:如图1,连接OP,
∵PA=PB,
∴,
∴OP⊥AB,
∵PD∥AB,
∴OP⊥PD,
∴PD是⊙O的切线;
(2)如图2,过A作AH⊥BC于H,连接OA,OP,OP交AB于E,
∵AB=AC,
∴BH=BC==4,
Rt△ABH中,tan∠ABC===,
∴AH=2,AB==2,
∴BE=,PE=,
设⊙O的半径为r,则OA=r,OE=r﹣,
由勾股定理得:,
r=,
答:⊙O的半径是.
17.【解答】解:(1)如图,PD是⊙O的切线.
证明如下:
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=4,.
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴,
∴CP CE=CA2=(2)2=8.
18.【解答】(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵PF是⊙O的切线,CE⊥AB,
∴∠OCP=∠CEB=90°,
∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,
∴∠BCE=∠BCP,
∴BC平分∠PCE.
(2)证明:连接AC.
∵AB是直径,
∴∠ACB=90°,
∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,
∵∠BCP=∠BCE,
∴∠ACF=∠ACE,
∵∠F=∠AEC=90°,AC=AC,
∴△ACF≌△ACE,
∴CF=CE.
解法二:证明:连接AC.
∵OA=OC
∴∠BAC=∠ACO,
∵CD平行AF,
∴∠FAC=∠ACD,
∴∠FAC=∠CAO,∵CF⊥AF,CE⊥AB,
∴CF=CE.
(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=3a,PC=4a,PM=a,
∵∠MCB+∠P=90°,∠P+∠PBM=90°,
∴∠MCB=∠PBM,
∵CD是直径,BM⊥PC,
∴∠CMB=∠BMP=90°,
∴△BMC∽△PMB,
∴=,
∴BM2=CM PM=3a2,
∴BM=a,
∴tan∠BCM==,
∴∠BCM=30°,
∴∠OCB=∠OBC=∠BOC=60°,
∴的长==π.
21世纪教育网(www.21cnjy.com)
同课章节目录
