数学:正切函数的图像与性质课件(1)(沪教版高一下)
文档属性
| 名称 | 数学:正切函数的图像与性质课件(1)(沪教版高一下) |

|
|
| 格式 | rar | ||
| 文件大小 | 320.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-08 00:00:00 | ||
图片预览





文档简介
课件18张PPT。正切函数的图像与性质(1)上海市南洋中学 卢久红 复习引入请同学们画出其它象限的三角函数线一、复习三角函数线当α在第一象限时:
正弦线: sinα=BM>0
余弦线: cosα=0B>0
正切线:tanα=AT>0
我们将考虑将区间 进行
八等分,9个点分别为
分别画出其中
的正切线,
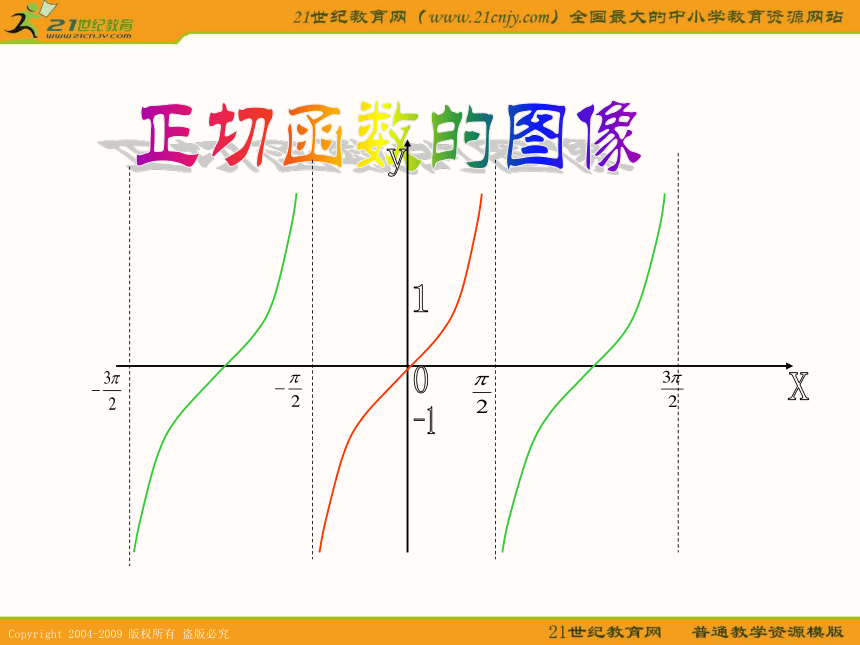
然后利用描点法画出正切函数的大致图象。
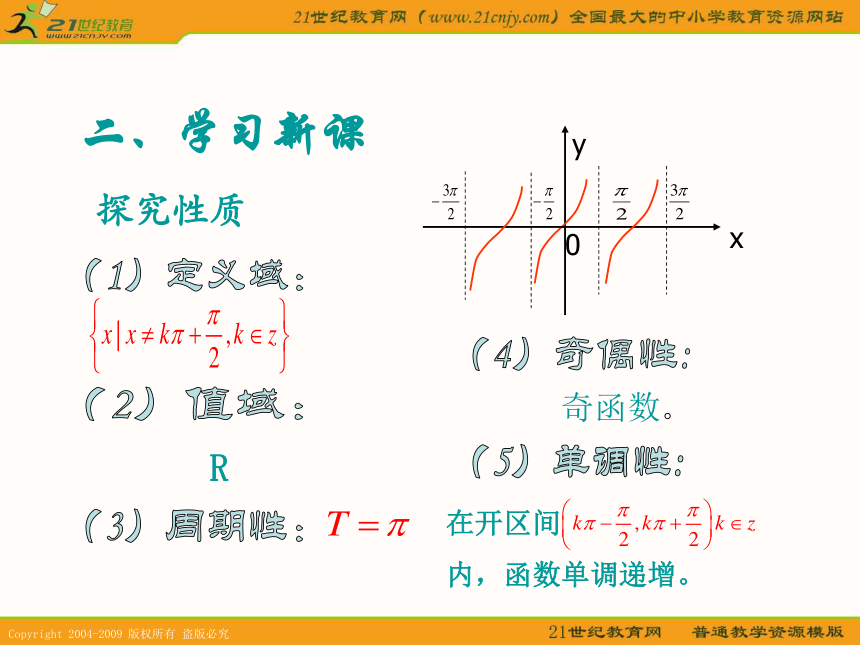
正切函数的图像0-11xy二、学习新课??
? 探究性质
(1)定义域:(2)值域:(3)周期性:(4)奇偶性:(5)单调性:R 奇函数。
在开区间
内,函数单调递增。
从图象上看出函数y=tanx的单调区间是
,但是我们怎样从理论上去加以证明
呢?
思考一:我们先考察 这个区间内的函数y=tanx的单调性.
在这个区间内任意取x1,x2.且 x1= =
因为 ,所以 则cosx1、
Cosx2>0 sin(x1-x2)<0,从而tanx1-tanx2<0,y1即正切函数y=tanx在 上是增函数.由奇函数的性
质可知,在 上正切函数y=tanx也是增函数。
由于y=tanx的周期为 ,则函数y=tanx在开区间
内单调递增。 解法二 :在 内任意取x1,x2,且x1
tanx1-tanx2= 因为
tan(x1-x2)<0, 而tanx1≥0,tanx2>0.
因此1+tanx1·tanx2>0.
则tanx1-tanx2<0, tanx1是增函数.接下来的证明同前一种方法.说明 在考虑正切函数单调性的时候,一
定要讲是在 每一个单调
区间上的增函数,而不能讲它在定义
域上是增函数,为什么?请同学们思
考并说明之。
例题分析例1、不通过求值,比较下列各组中两个正切函数值的大小:
与
(2)比较 与 的大小.
例2、讨论函数 的性质;
问题拓展例3、求下列函数的单调区间:
区间是: 是增函数,
递增区间: 说明在考虑正切函数与其他函数复合的问题时,需要分别注意这两个函数的单调性,然后根据复合函数的规则:增增得增,增减得减,来确定单调区间.
例4、求下列函数的周期: 变式问题2:求解
思考由上面的例4及其变式,请你归纳一下函数
y=Atan(ωx+Ф)的周期是什么?( )
三、巩固练习 求函数y=tan 的定义域、值域,并指出
它的奇偶性、单调性以及周期.
四、课堂小结(一)正切函数y=tanx的性质(略)
(二)在求解有关正切函数与其它函数(如一次函数)复合的函数的增减性的时候,一定要将构成此复合函数的每一个函数的单调性都搞清楚,然后根据增增得增、增减得减的原则来确定该函数的单调区间。
(三)在求解函数周期性的时候,一定要借助y=tanx的周期是的结论,然后再利用周期函数定义f(x)=f(x+T),来求出函数的周期.
?
五、布置作业(略)谢谢大家
正弦线: sinα=BM>0
余弦线: cosα=0B>0
正切线:tanα=AT>0
我们将考虑将区间 进行
八等分,9个点分别为
分别画出其中
的正切线,
然后利用描点法画出正切函数的大致图象。
正切函数的图像0-11xy二、学习新课??
? 探究性质
(1)定义域:(2)值域:(3)周期性:(4)奇偶性:(5)单调性:R 奇函数。
在开区间
内,函数单调递增。
从图象上看出函数y=tanx的单调区间是
,但是我们怎样从理论上去加以证明
呢?
思考一:我们先考察 这个区间内的函数y=tanx的单调性.
在这个区间内任意取x1,x2.且 x1
因为 ,所以 则cosx1、
Cosx2>0 sin(x1-x2)<0,从而tanx1-tanx2<0,y1
质可知,在 上正切函数y=tanx也是增函数。
由于y=tanx的周期为 ,则函数y=tanx在开区间
内单调递增。 解法二 :在 内任意取x1,x2,且x1
tanx1-tanx2= 因为
tan(x1-x2)<0, 而tanx1≥0,tanx2>0.
因此1+tanx1·tanx2>0.
则tanx1-tanx2<0, tanx1
定要讲是在 每一个单调
区间上的增函数,而不能讲它在定义
域上是增函数,为什么?请同学们思
考并说明之。
例题分析例1、不通过求值,比较下列各组中两个正切函数值的大小:
与
(2)比较 与 的大小.
例2、讨论函数 的性质;
问题拓展例3、求下列函数的单调区间:
区间是: 是增函数,
递增区间: 说明在考虑正切函数与其他函数复合的问题时,需要分别注意这两个函数的单调性,然后根据复合函数的规则:增增得增,增减得减,来确定单调区间.
例4、求下列函数的周期: 变式问题2:求解
思考由上面的例4及其变式,请你归纳一下函数
y=Atan(ωx+Ф)的周期是什么?( )
三、巩固练习 求函数y=tan 的定义域、值域,并指出
它的奇偶性、单调性以及周期.
四、课堂小结(一)正切函数y=tanx的性质(略)
(二)在求解有关正切函数与其它函数(如一次函数)复合的函数的增减性的时候,一定要将构成此复合函数的每一个函数的单调性都搞清楚,然后根据增增得增、增减得减的原则来确定该函数的单调区间。
(三)在求解函数周期性的时候,一定要借助y=tanx的周期是的结论,然后再利用周期函数定义f(x)=f(x+T),来求出函数的周期.
?
五、布置作业(略)谢谢大家
