【中考押题卷】2025年中考数学高频易错考前冲刺:函数基础知识(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:函数基础知识(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 779.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 07:10:25 | ||
图片预览

文档简介
2025年中考数学高频易错考前冲刺:函数基础知识
一.选择题(共10小题)
1.(2024 红谷滩区校级期末)在球的体积公式VπR3中,下列说法正确的是( )
A.V、π、R是变量,为常量
B.V、π是变量,R为常量
C.V、R是变量,、π为常量
D.以上都不对
2.(2023 蜀山区模拟)小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,那么从家到火车站路程是( )
A.1300米 B.1400米 C.1600米 D.1500米
3.(2024 百色)已知函数y,当x=2时,函数值y为( )
A.5 B.6 C.7 D.8
4.(2024 连州市一模)如图所示,△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,正方形DEFG边长也为2,且AC与DE在同一直线上,△ABC从C点与D点重合开始,沿直线DE向右平移,直到点A与点E重合为止,设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A. B.
C. D.
5.(2024 安徽)如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A.
B.
C.
D.
6.(2024 杭州)两个不相等的正数满足a+b=2,ab=t﹣1,设S=(a﹣b)2,则S关于t的函数图象是( )
A.射线(不含端点) B.线段(不含端点)
C.直线 D.抛物线的一部分
7.(2024 英德市一模)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. B.
C. D.
8.(2024 淄博)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A. B.
C. D.
9.(2024 恩施州)函数y的自变量x的取值范围是( )
A.x≥1 B.x≥1且x≠3 C.x≠3 D.1≤x≤3
10.(2024 锦州)如图,在△ABC中,∠C=90°,AC=BC=3cm,动点P从点A出发,以cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A. B.
C. D.
二.填空题(共5小题)
11.(2023秋 惠来县校级期末)函数y中,自变量x的取值范围是 .
12.(2024 柳城县一模)甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.则甲的速度为每秒 米.
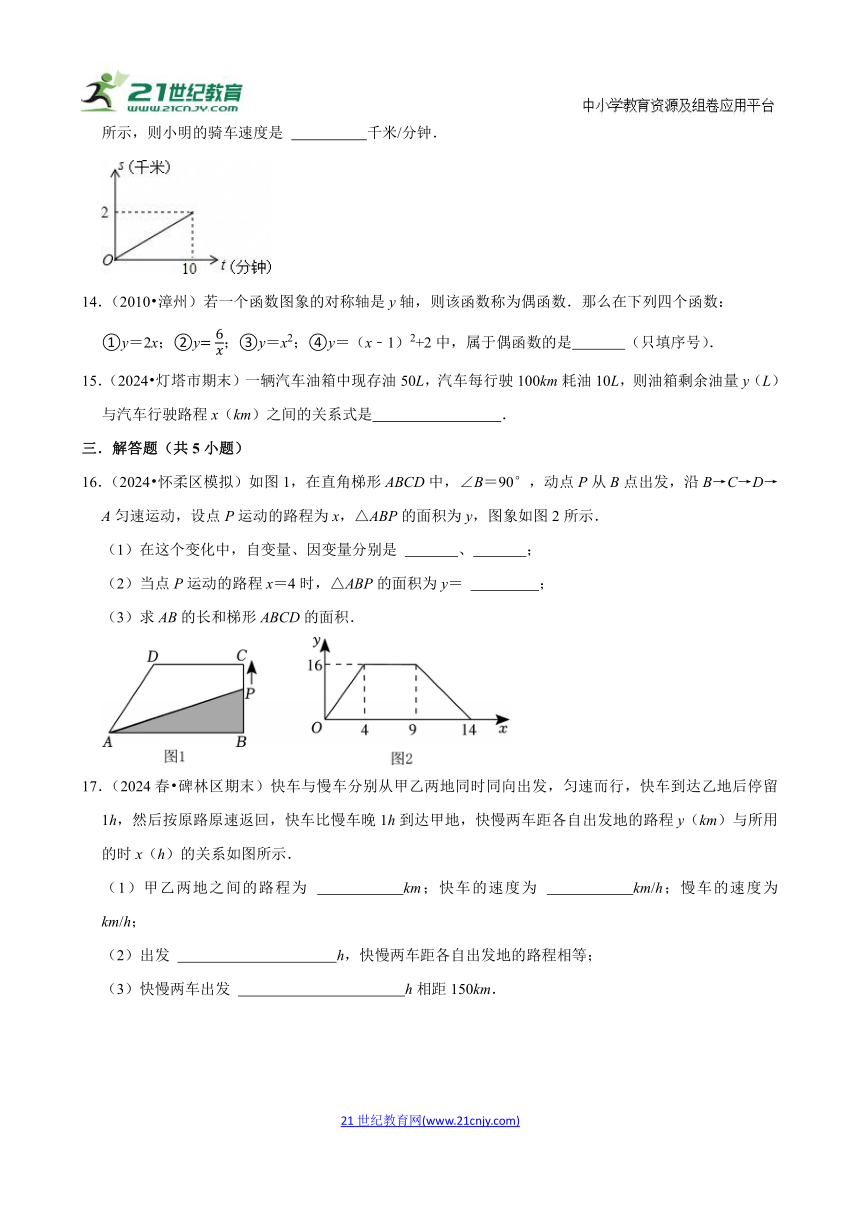
13.(2024 湖州)放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
14.(2010 漳州)若一个函数图象的对称轴是y轴,则该函数称为偶函数.那么在下列四个函数:
①y=2x;②y;③y=x2;④y=(x﹣1)2+2中,属于偶函数的是 (只填序号).
15.(2024 灯塔市期末)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 .
三.解答题(共5小题)
16.(2024 怀柔区模拟)如图1,在直角梯形ABCD中,∠B=90°,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.
17.(2024春 碑林区期末)快车与慢车分别从甲乙两地同时同向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程为 km;快车的速度为 km/h;慢车的速度为 km/h;
(2)出发 h,快慢两车距各自出发地的路程相等;
(3)快慢两车出发 h相距150km.
18.(2024 灵石县期末)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)朱老师的速度为 米/秒;小明的速度为 米/秒;
(3)小明与朱老师相遇 次,相遇时距起点的距离分别为 米.
19.(2024 莱西市期末)父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2 ﹣4 ﹣10
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
20.(2024 雁塔区校级期末)一列快车、一列慢车同时从相距300km的两地出发,相向而行.如图,l1和l2分别表示两车到甲地的距离s(km)与行驶时间t(h)的关系.
(1)快车的速度为 km/h,慢车的速度为 km/h;
(2)经过多久两车第一次相遇?
(3)当快车到达目的地时,慢车距离目的地多远?
2025年中考数学高频易错考前冲刺:函数基础知识
参考答案与试题解析
一.选择题(共10小题)
1.(2024 红谷滩区校级期末)在球的体积公式VπR3中,下列说法正确的是( )
A.V、π、R是变量,为常量
B.V、π是变量,R为常量
C.V、R是变量,、π为常量
D.以上都不对
【考点】常量与变量.
【专题】函数及其图象;数感.
【答案】C
【分析】根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案.
【解答】解:在球的体积公式VπR3中,V,R是变量,,π是常量,
故选:C.
【点评】此题主要考查了常量和变量,关键是掌握两个量的定义.
2.(2023 蜀山区模拟)小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,那么从家到火车站路程是( )
A.1300米 B.1400米 C.1600米 D.1500米
【考点】函数的图象.
【专题】数形结合;一次函数及其应用;应用意识.
【答案】C
【分析】先由函数图象步行6分钟,离家480米,可求得步行的速度,再根据小元以同样的速度回家取物品,便可求得返回到家时的时间,进而得出此时点的坐标,再用待定系数法求出后来乘出租车过程中S与t的函数解析式,最后设步行到达的时间为t,根据“然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.”列出方程求出t即可进一步求得家到火车站的路程.
【解答】解:步行的速度为:480÷6=80米/分钟,
∵小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品,
∴小元回到家时的时间为6×2=12(分钟)
则返回时函数图象的点坐标是(12,0)
设后来乘出租车中S与t的函数解析式为S=kt+b(k≠0),
把(12,0)和(16,1280)代入得,
,
解得,
所以S=320t﹣3840;
设步行到达的时间为t,则实际到达的时间为t﹣3,
由题意得,80t=320(t﹣3)﹣3840,
解得t=20.
所以家到火车站的距离为80×20=1600m.
故选:C.
【点评】本题考查的是用一次函数解决实际问题,主要利用了路程、速度、时间三者之间的关系,待定系数法求一次函数解析式,难点在于找出等量关系列出方程.
3.(2024 百色)已知函数y,当x=2时,函数值y为( )
A.5 B.6 C.7 D.8
【考点】函数值.
【答案】A
【分析】利用已知函数关系式结合x的取值范围,进而将x=2代入求出即可.
【解答】解:∵x≥0时,y=2x+1,
∴当x=2时,y=2×2+1=5.
故选:A.
【点评】此题主要考查了函数值,注意x的取值不同对应函数解析式不同,进而得出是解题关键.
4.(2024 连州市一模)如图所示,△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,正方形DEFG边长也为2,且AC与DE在同一直线上,△ABC从C点与D点重合开始,沿直线DE向右平移,直到点A与点E重合为止,设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A. B.
C. D.
【考点】动点问题的函数图象.
【专题】函数及其图象;模型思想.
【答案】A
【分析】此题可分为两段求解,即C从D点运动到E点和A从D点运动到E点,列出面积随动点变化的函数关系式即可.
【解答】解:设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,
当C从D点运动到E点时,即0≤x≤2时,y2×2(2﹣x)×(2﹣x)x2+2x.
当A从D点运动到E点时,即2<x≤4时,y[2﹣(x﹣2)]×[2﹣(x﹣2)]x2﹣4x+8,
∴y与x之间的函数关系 由函数关系式可看出A中的函数图象与所求的分段函数对应.
故选:A.
【点评】本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.
5.(2024 安徽)如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A.
B.
C.
D.
【考点】动点问题的函数图象.
【专题】二次函数图象及其性质;二次函数的应用;模型思想.
【答案】A
【分析】分为0<x≤2、2<x≤4两种情况,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
【解答】解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GHEJx,
∴yEJ GHx2.
当x=2时,y,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
yFJ GH(4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
【点评】本题主要考查的是动点问题的函数图象,求得函数的解析式是解题的关键.
6.(2024 杭州)两个不相等的正数满足a+b=2,ab=t﹣1,设S=(a﹣b)2,则S关于t的函数图象是( )
A.射线(不含端点) B.线段(不含端点)
C.直线 D.抛物线的一部分
【考点】函数的图象.
【答案】B
【分析】要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
【解答】解:首先根据题意,消去字母a和b,得到S和t的关系式.
S=(a﹣b)2=(a+b)2﹣4ab=22﹣4(t﹣1)=8﹣4t.
然后根据题意,因为ab=t﹣1,所以t=ab+1,又因为ab>0,故t>1;
①又因为S=(a﹣b)2>0,所以8﹣4t>0,所以t<2.
②由①②得1<t<2,故S关于t的函数图象是一条不含端点的线段.
故选:B.
【点评】本题考查了有自变量取值范围的函数的图象.
7.(2024 英德市一模)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. B.
C. D.
【考点】动点问题的函数图象;二次函数的图象.
【专题】计算题;压轴题;推理填空题.
【答案】A
【分析】由勾股定理求出AB、AC的长,进一步求出△ABC的面积,根据移动特点有三种情况(1)(2)(3),分别求出每种情况y与x的关系式,利用关系式的特点(是一次函数还是二次函数)就能选出答案.
【解答】解:已知∠C=90°,BC=2cm,∠A=30°,
∴AB=4,
由勾股定理得:AC=2,
∵四边形DEFG为矩形,∠C=90,
∴DE=GF=2,∠C=∠DEF=90°,
∴AC∥DE,
此题有三种情况:(1)当0<x<2时,AB交DE于H,
如图
∵DE∥AC,
∴,
即,
解得:EHx,
所以y x xx2,
∵y是关于x的二次函数,
所以所选答案C错误,答案D错误,
∵a0,开口向上;
(2)当2≤x≤6时,如图,
此时y2×22,
(3)当6<x≤8时,如图,设GF交AB于N,设△ABC的面积是s1,△FNB的面积是s2.
BF=x﹣6,与(1)类同,同法可求FNx﹣6,
∴y=s1﹣s2,
2×2(x﹣6)×(x﹣6),
x2+6x﹣16,
∵0,
∴开口向下,
所以答案A正确,答案B错误,
故选:A.
【点评】本题主要考查了一次函数,二次函数的性质三角形的面积公式等知识点,解此题的关键是能根据移动规律把问题分成三种情况,并能求出每种情况的y与x的关系式.
8.(2024 淄博)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A. B.
C. D.
【考点】函数的图象.
【答案】D
【分析】根据用一注水管向小玻璃杯内注水,即可分段求出小水杯内水面的高度h(cm)与注水时间t(min)的函数图象.
【解答】解:一注水管向小玻璃杯内注水,水面在逐渐升高,当小杯中水满时,开始向鱼缸内流,这时水位高度不变,
当鱼缸水面高度与小杯一样后,再继续注水,水面高度在升高,升高的比开始慢.
故选:D.
【点评】此题主要考查了函数图象,关键是问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.
9.(2024 恩施州)函数y的自变量x的取值范围是( )
A.x≥1 B.x≥1且x≠3 C.x≠3 D.1≤x≤3
【考点】函数自变量的取值范围.
【答案】B
【分析】根据被开方数是非负数,分母不能为零,可得答案.
【解答】解:由题意,得
x﹣1≥0且x﹣3≠0,
解得x≥1且x≠3,
故选:B.
【点评】本题考查了函数自变量的取值范围,利用被开方数是非负数,分母不能为零是解题关键.
10.(2024 锦州)如图,在△ABC中,∠C=90°,AC=BC=3cm,动点P从点A出发,以cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A. B.
C. D.
【考点】动点问题的函数图象.
【专题】常规题型;分类讨论;函数及其图象.
【答案】D
【分析】作QD⊥AB,分点Q在AC、CB上运动这两种情况,由直角三角形的性质表示出QD的长,利用三角形面积公式得出函数解析式即可判断.
【解答】解:(1)过点Q作QD⊥AB于点D,
①如图1,当点Q在AC上运动时,即0≤x≤3,
由题意知AQ=x、APx,
∵∠A=45°,
∴QDAQx,
则y x xx2;
②如图2,当点Q在CB上运动时,即3<x≤6,此时点P与点B重合,
由题意知BQ=6﹣x、AP=AB=3,
∵∠B=45°,
∴QDBQ(6﹣x),
则y3(6﹣x)x+9;
故选:D.
【点评】本题主要考查动点问题的函数图象,解题的关键是根据题意弄清两点的运动路线,据此分类讨论并得出函数解析式.
二.填空题(共5小题)
11.(2023秋 惠来县校级期末)函数y中,自变量x的取值范围是 x≥2且x≠3 .
【考点】函数自变量的取值范围.
【答案】见试题解答内容
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
【解答】解:根据题意得:,
解得:x≥2且x≠3.
故答案为:x≥2且x≠3.
【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.
12.(2024 柳城县一模)甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.则甲的速度为每秒 6 米.
【考点】函数的图象.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】设甲的速度为x米/秒,根据50秒时,甲追上乙列方程求出甲的速度.
【解答】解:由图可知:①50秒时,甲追上乙,②300秒时,乙到达目的地,
∴乙的速度为:4,
设甲的速度为x米/秒,
则50x﹣50×4=100,
x=6,
故答案为:6
【点评】本题是函数图象的信息题,又是行程问题,首先要明确三个量:路程、时间和速度,正确读出图形中甲、乙相遇及到达目的地的时间是本题的关键;重点理解图象中x与y所表示的含义,也是本题的难点.
13.(2024 湖州)放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 0.2 千米/分钟.
【考点】函数的图象.
【答案】见试题解答内容
【分析】根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得答案.
【解答】解:由纵坐标看出路程是2千米,
由横坐标看出时间是10分钟,
小明的骑车速度是2÷10=0.2(千米/分钟),
故答案为:0.2.
【点评】本题考查了函数图象,观察函数图象的纵坐标得出路程,观察函数图象的横坐标得出时间,利用了路程与时间的关系.
14.(2010 漳州)若一个函数图象的对称轴是y轴,则该函数称为偶函数.那么在下列四个函数:
①y=2x;②y;③y=x2;④y=(x﹣1)2+2中,属于偶函数的是 ③ (只填序号).
【考点】函数的概念.
【专题】压轴题.
【答案】见试题解答内容
【分析】根据对称轴是y轴,排除①②选项,再根据④不是偶函数,即可确定答案.
【解答】解:①y=2x,是正比例函数,函数图象的对称轴不是y轴,错误;
②y是反比例函数,函数图象的对称轴不是y轴,错误;
③y=x2是抛物线,对称轴是y轴,是偶函数,正确;
④y=(x﹣1)2+2对称轴是直线x=1,错误.
故属于偶函数的是③.
【点评】本题主要考查正比例函数、反比例函数、二次函数的对称性和二次函数是偶函数的性质.
15.(2024 灯塔市期末)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 y=﹣0.1x+50 .
【考点】函数关系式.
【专题】函数及其图象;运算能力;应用意识.
【答案】见试题解答内容
【分析】由于汽车每行驶100km耗油10L,那么汽车行驶路程x千米耗油0.1xL,而汽车油箱中能盛汽油50L,由此即可确定加满油后,油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数关系式.
【解答】解:∵汽车每行驶100km耗油10L,
∴汽车行驶路程xkm耗油0.1xL,
∵汽车油箱中现存油50L,
∴油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是y=﹣0.1x+50.
故答案为:y=﹣0.1x+50.
【点评】此题主要考查了根据实际问题中包含的数量关系列出函数关系式,解题关键是正确理解和把握题目中隐含的数量关系,只有充分理解已知条件,才能求出函数关系式.
三.解答题(共5小题)
16.(2024 怀柔区模拟)如图1,在直角梯形ABCD中,∠B=90°,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 x 、 y ;
(2)当点P运动的路程x=4时,△ABP的面积为y= 16 ;
(3)求AB的长和梯形ABCD的面积.
【考点】动点问题的函数图象.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】(1)依据点P运动的路程为x,△ABP的面积为y,即可得到自变量和因变量;
(2)依据函数图象,即可得到点P运动的路程x=4时,△ABP的面积;
(3)根据图象得出BC的长,以及此时三角形ABP面积,利用三角形面积公式求出AB的长即可;由函数图象得出DC的长,利用梯形面积公式求出梯形ABCD面积即可.
【解答】解:(1)∵点P运动的路程为x,△ABP的面积为y,
∴自变量为x,因变量为y,
故答案为:x,y;
(2)由图可得,当点P运动的路程x=4时,△ABP的面积为y=16,
故答案为:16;
(3)根据图象得:BC=4,此时△ABP为16,
∴AB BC=16,即AB×4=16,
解得:AB=8;
由图象得:DC=9﹣4=5,
则S梯形ABCDBC×(DC+AB)4×(5+8)=26.
【点评】此题考查了动点问题的函数图象,弄清函数图象上的信息是解本题的关键.
17.(2024春 碑林区期末)快车与慢车分别从甲乙两地同时同向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程为 420 km;快车的速度为 140 km/h;慢车的速度为 70 km/h;
(2)出发 h,快慢两车距各自出发地的路程相等;
(3)快慢两车出发 h或h或 h相距150km.
【考点】函数的图象.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】(1)先得两地的距离,根据速度=路程÷时间列式计算即可求出快车和慢车的速度;
(2)由图可知:快车返程时,两车距各自出发地的路程相等,根据慢车的路程=2个总路程﹣快车的路程,列方程即可得出答案;
(3)分别根据两车相遇以及两车相遇后两车距离为150km时,列方程可解答.
【解答】解:(1)由图可知:甲乙两地之间的路程为420km;
快车的速度为:140km/h;
由题意得:快车7小时到达甲地,则慢车6小时到达甲地,
则慢车的速度为:70km/h;
故答案为:420,140,70;
(2)∵快车速度为:140km/h,
∴A点坐标为:(3,420),
∴B点坐标为(4,420),
由图可知:快车返程时,两车距各自出发地的路程相等,
设出发x小时,两车距各自出发地的路程相等,
70x=2×420﹣140(x﹣1),
70x=980﹣140x,
解得:x,
答:出发小时,快、慢两车距各自出发地的路程相等;
故答案为:;
(3)第一种情形第一次没有相遇前,相距150km,
则140x+70x+150=420,
解得:x,
第二种情形应是相遇后而快车没到乙地前140x+70x﹣420=150,
解得:x,
第三种情形是快车从乙往甲返回:70x﹣140(x﹣4)=150,
解得:x,
综上所述:快慢两车出发h或h或h相距150km.
故答案为:h或h或.
【点评】本题考查了函数的应用,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于(2)表示出快车距离出发地的路程.
18.(2024 灵石县期末)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 自变量为小明出发的时间t ,因变量是 因变量为距起点的距离s ;
(2)朱老师的速度为 2 米/秒;小明的速度为 6 米/秒;
(3)小明与朱老师相遇 2 次,相遇时距起点的距离分别为 300或420 米.
【考点】函数的图象;常量与变量.
【答案】见试题解答内容
【分析】(1)观察函数图象即可找出谁是自变量谁是因变量;
(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;
(3)根据函数图象即可得到结论.
【解答】解:(1)观察函数图象可得出:自变量为小明出发的时间t,因变量为距起点的距离s.
故答案为:小明出发的时间t;距起点的距离s.
(2)朱老师的速度为:(300﹣200)÷50=2(米/秒);
小明的速度为:300÷50=6(米/秒).
故答案为:2;6.
(3)小明与朱老师相遇2次,相遇时距起点的距离分别为300米或420米,
故答案为:300米或420米.
【点评】本题考查了一次函数的应用,观察函数图象找出点的坐标利用待定系数法求出函数解析式是解题的关键.
19.(2024 莱西市期末)父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2 ﹣4 ﹣10
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
【考点】函数的表示方法.
【专题】应用题.
【答案】见试题解答内容
【分析】(1)根据图表,反映的是距离地面的高度和温度两个量,所以温度和高度是两个变化的量,温度随高度的变化而变化;
(2)根据表格数据,高度越大,温度越低,所以随着高度的h的增大,温度t在减小;
(3)求出当h=6时温度t的值即可.
【解答】解:(1)上表反映了温度和高度两个变量之间.高度是自变量,温度是因变量.
(2)如果用h表示距离地面的高度,用t表示温度,那么随着高度h的增大,温度t逐渐减小(或降低).
(3)距离地面6千米的高空温度是﹣16℃.
【点评】本题是对函数定义的考查和图表的识别,自变量、因变量的区分对初学函数的同学来说比较困难,需要在学习上多下功夫.
20.(2024 雁塔区校级期末)一列快车、一列慢车同时从相距300km的两地出发,相向而行.如图,l1和l2分别表示两车到甲地的距离s(km)与行驶时间t(h)的关系.
(1)快车的速度为 45 km/h,慢车的速度为 30 km/h;
(2)经过多久两车第一次相遇?
(3)当快车到达目的地时,慢车距离目的地多远?
【考点】函数的图象.
【答案】见试题解答内容
【分析】(1)分别用各自的总路程除以总时间即可得各自的速度;
(2)用总路程除以快车与慢车的速度和即可得两车第一次相遇时间;
(3)用慢车到目的地的时间减去快车到目的地的时间,再乘以慢车的速度即可.
【解答】解:(1)快车的速度为30045km/h,慢车的速度为300÷10=30km/h,
故答案为:45,30;
(2)4h
答:经过4h两车第一次相遇;
(3)(10)×30=100km,
答:当快车到达目的地时,慢车距离目的地100km.
【点评】本题考查了一次函数的图象的性质的运用,行程问题的数量关系的运用,相遇问题的数量关系的运用,解答时认真分析函数图象的意义是关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024 红谷滩区校级期末)在球的体积公式VπR3中,下列说法正确的是( )
A.V、π、R是变量,为常量
B.V、π是变量,R为常量
C.V、R是变量,、π为常量
D.以上都不对
2.(2023 蜀山区模拟)小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,那么从家到火车站路程是( )
A.1300米 B.1400米 C.1600米 D.1500米
3.(2024 百色)已知函数y,当x=2时,函数值y为( )
A.5 B.6 C.7 D.8
4.(2024 连州市一模)如图所示,△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,正方形DEFG边长也为2,且AC与DE在同一直线上,△ABC从C点与D点重合开始,沿直线DE向右平移,直到点A与点E重合为止,设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A. B.
C. D.
5.(2024 安徽)如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A.
B.
C.
D.
6.(2024 杭州)两个不相等的正数满足a+b=2,ab=t﹣1,设S=(a﹣b)2,则S关于t的函数图象是( )
A.射线(不含端点) B.线段(不含端点)
C.直线 D.抛物线的一部分
7.(2024 英德市一模)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. B.
C. D.
8.(2024 淄博)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A. B.
C. D.
9.(2024 恩施州)函数y的自变量x的取值范围是( )
A.x≥1 B.x≥1且x≠3 C.x≠3 D.1≤x≤3
10.(2024 锦州)如图,在△ABC中,∠C=90°,AC=BC=3cm,动点P从点A出发,以cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A. B.
C. D.
二.填空题(共5小题)
11.(2023秋 惠来县校级期末)函数y中,自变量x的取值范围是 .
12.(2024 柳城县一模)甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.则甲的速度为每秒 米.
13.(2024 湖州)放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
14.(2010 漳州)若一个函数图象的对称轴是y轴,则该函数称为偶函数.那么在下列四个函数:
①y=2x;②y;③y=x2;④y=(x﹣1)2+2中,属于偶函数的是 (只填序号).
15.(2024 灯塔市期末)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 .
三.解答题(共5小题)
16.(2024 怀柔区模拟)如图1,在直角梯形ABCD中,∠B=90°,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.
17.(2024春 碑林区期末)快车与慢车分别从甲乙两地同时同向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程为 km;快车的速度为 km/h;慢车的速度为 km/h;
(2)出发 h,快慢两车距各自出发地的路程相等;
(3)快慢两车出发 h相距150km.
18.(2024 灵石县期末)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)朱老师的速度为 米/秒;小明的速度为 米/秒;
(3)小明与朱老师相遇 次,相遇时距起点的距离分别为 米.
19.(2024 莱西市期末)父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2 ﹣4 ﹣10
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
20.(2024 雁塔区校级期末)一列快车、一列慢车同时从相距300km的两地出发,相向而行.如图,l1和l2分别表示两车到甲地的距离s(km)与行驶时间t(h)的关系.
(1)快车的速度为 km/h,慢车的速度为 km/h;
(2)经过多久两车第一次相遇?
(3)当快车到达目的地时,慢车距离目的地多远?
2025年中考数学高频易错考前冲刺:函数基础知识
参考答案与试题解析
一.选择题(共10小题)
1.(2024 红谷滩区校级期末)在球的体积公式VπR3中,下列说法正确的是( )
A.V、π、R是变量,为常量
B.V、π是变量,R为常量
C.V、R是变量,、π为常量
D.以上都不对
【考点】常量与变量.
【专题】函数及其图象;数感.
【答案】C
【分析】根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案.
【解答】解:在球的体积公式VπR3中,V,R是变量,,π是常量,
故选:C.
【点评】此题主要考查了常量和变量,关键是掌握两个量的定义.
2.(2023 蜀山区模拟)小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,那么从家到火车站路程是( )
A.1300米 B.1400米 C.1600米 D.1500米
【考点】函数的图象.
【专题】数形结合;一次函数及其应用;应用意识.
【答案】C
【分析】先由函数图象步行6分钟,离家480米,可求得步行的速度,再根据小元以同样的速度回家取物品,便可求得返回到家时的时间,进而得出此时点的坐标,再用待定系数法求出后来乘出租车过程中S与t的函数解析式,最后设步行到达的时间为t,根据“然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.”列出方程求出t即可进一步求得家到火车站的路程.
【解答】解:步行的速度为:480÷6=80米/分钟,
∵小元步行从家去火车站,走到6分钟时,以同样的速度回家取物品,
∴小元回到家时的时间为6×2=12(分钟)
则返回时函数图象的点坐标是(12,0)
设后来乘出租车中S与t的函数解析式为S=kt+b(k≠0),
把(12,0)和(16,1280)代入得,
,
解得,
所以S=320t﹣3840;
设步行到达的时间为t,则实际到达的时间为t﹣3,
由题意得,80t=320(t﹣3)﹣3840,
解得t=20.
所以家到火车站的距离为80×20=1600m.
故选:C.
【点评】本题考查的是用一次函数解决实际问题,主要利用了路程、速度、时间三者之间的关系,待定系数法求一次函数解析式,难点在于找出等量关系列出方程.
3.(2024 百色)已知函数y,当x=2时,函数值y为( )
A.5 B.6 C.7 D.8
【考点】函数值.
【答案】A
【分析】利用已知函数关系式结合x的取值范围,进而将x=2代入求出即可.
【解答】解:∵x≥0时,y=2x+1,
∴当x=2时,y=2×2+1=5.
故选:A.
【点评】此题主要考查了函数值,注意x的取值不同对应函数解析式不同,进而得出是解题关键.
4.(2024 连州市一模)如图所示,△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,正方形DEFG边长也为2,且AC与DE在同一直线上,△ABC从C点与D点重合开始,沿直线DE向右平移,直到点A与点E重合为止,设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A. B.
C. D.
【考点】动点问题的函数图象.
【专题】函数及其图象;模型思想.
【答案】A
【分析】此题可分为两段求解,即C从D点运动到E点和A从D点运动到E点,列出面积随动点变化的函数关系式即可.
【解答】解:设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,
当C从D点运动到E点时,即0≤x≤2时,y2×2(2﹣x)×(2﹣x)x2+2x.
当A从D点运动到E点时,即2<x≤4时,y[2﹣(x﹣2)]×[2﹣(x﹣2)]x2﹣4x+8,
∴y与x之间的函数关系 由函数关系式可看出A中的函数图象与所求的分段函数对应.
故选:A.
【点评】本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.
5.(2024 安徽)如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A.
B.
C.
D.
【考点】动点问题的函数图象.
【专题】二次函数图象及其性质;二次函数的应用;模型思想.
【答案】A
【分析】分为0<x≤2、2<x≤4两种情况,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
【解答】解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GHEJx,
∴yEJ GHx2.
当x=2时,y,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
yFJ GH(4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
【点评】本题主要考查的是动点问题的函数图象,求得函数的解析式是解题的关键.
6.(2024 杭州)两个不相等的正数满足a+b=2,ab=t﹣1,设S=(a﹣b)2,则S关于t的函数图象是( )
A.射线(不含端点) B.线段(不含端点)
C.直线 D.抛物线的一部分
【考点】函数的图象.
【答案】B
【分析】要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
【解答】解:首先根据题意,消去字母a和b,得到S和t的关系式.
S=(a﹣b)2=(a+b)2﹣4ab=22﹣4(t﹣1)=8﹣4t.
然后根据题意,因为ab=t﹣1,所以t=ab+1,又因为ab>0,故t>1;
①又因为S=(a﹣b)2>0,所以8﹣4t>0,所以t<2.
②由①②得1<t<2,故S关于t的函数图象是一条不含端点的线段.
故选:B.
【点评】本题考查了有自变量取值范围的函数的图象.
7.(2024 英德市一模)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. B.
C. D.
【考点】动点问题的函数图象;二次函数的图象.
【专题】计算题;压轴题;推理填空题.
【答案】A
【分析】由勾股定理求出AB、AC的长,进一步求出△ABC的面积,根据移动特点有三种情况(1)(2)(3),分别求出每种情况y与x的关系式,利用关系式的特点(是一次函数还是二次函数)就能选出答案.
【解答】解:已知∠C=90°,BC=2cm,∠A=30°,
∴AB=4,
由勾股定理得:AC=2,
∵四边形DEFG为矩形,∠C=90,
∴DE=GF=2,∠C=∠DEF=90°,
∴AC∥DE,
此题有三种情况:(1)当0<x<2时,AB交DE于H,
如图
∵DE∥AC,
∴,
即,
解得:EHx,
所以y x xx2,
∵y是关于x的二次函数,
所以所选答案C错误,答案D错误,
∵a0,开口向上;
(2)当2≤x≤6时,如图,
此时y2×22,
(3)当6<x≤8时,如图,设GF交AB于N,设△ABC的面积是s1,△FNB的面积是s2.
BF=x﹣6,与(1)类同,同法可求FNx﹣6,
∴y=s1﹣s2,
2×2(x﹣6)×(x﹣6),
x2+6x﹣16,
∵0,
∴开口向下,
所以答案A正确,答案B错误,
故选:A.
【点评】本题主要考查了一次函数,二次函数的性质三角形的面积公式等知识点,解此题的关键是能根据移动规律把问题分成三种情况,并能求出每种情况的y与x的关系式.
8.(2024 淄博)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A. B.
C. D.
【考点】函数的图象.
【答案】D
【分析】根据用一注水管向小玻璃杯内注水,即可分段求出小水杯内水面的高度h(cm)与注水时间t(min)的函数图象.
【解答】解:一注水管向小玻璃杯内注水,水面在逐渐升高,当小杯中水满时,开始向鱼缸内流,这时水位高度不变,
当鱼缸水面高度与小杯一样后,再继续注水,水面高度在升高,升高的比开始慢.
故选:D.
【点评】此题主要考查了函数图象,关键是问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.
9.(2024 恩施州)函数y的自变量x的取值范围是( )
A.x≥1 B.x≥1且x≠3 C.x≠3 D.1≤x≤3
【考点】函数自变量的取值范围.
【答案】B
【分析】根据被开方数是非负数,分母不能为零,可得答案.
【解答】解:由题意,得
x﹣1≥0且x﹣3≠0,
解得x≥1且x≠3,
故选:B.
【点评】本题考查了函数自变量的取值范围,利用被开方数是非负数,分母不能为零是解题关键.
10.(2024 锦州)如图,在△ABC中,∠C=90°,AC=BC=3cm,动点P从点A出发,以cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2),运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A. B.
C. D.
【考点】动点问题的函数图象.
【专题】常规题型;分类讨论;函数及其图象.
【答案】D
【分析】作QD⊥AB,分点Q在AC、CB上运动这两种情况,由直角三角形的性质表示出QD的长,利用三角形面积公式得出函数解析式即可判断.
【解答】解:(1)过点Q作QD⊥AB于点D,
①如图1,当点Q在AC上运动时,即0≤x≤3,
由题意知AQ=x、APx,
∵∠A=45°,
∴QDAQx,
则y x xx2;
②如图2,当点Q在CB上运动时,即3<x≤6,此时点P与点B重合,
由题意知BQ=6﹣x、AP=AB=3,
∵∠B=45°,
∴QDBQ(6﹣x),
则y3(6﹣x)x+9;
故选:D.
【点评】本题主要考查动点问题的函数图象,解题的关键是根据题意弄清两点的运动路线,据此分类讨论并得出函数解析式.
二.填空题(共5小题)
11.(2023秋 惠来县校级期末)函数y中,自变量x的取值范围是 x≥2且x≠3 .
【考点】函数自变量的取值范围.
【答案】见试题解答内容
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
【解答】解:根据题意得:,
解得:x≥2且x≠3.
故答案为:x≥2且x≠3.
【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.
12.(2024 柳城县一模)甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.则甲的速度为每秒 6 米.
【考点】函数的图象.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】设甲的速度为x米/秒,根据50秒时,甲追上乙列方程求出甲的速度.
【解答】解:由图可知:①50秒时,甲追上乙,②300秒时,乙到达目的地,
∴乙的速度为:4,
设甲的速度为x米/秒,
则50x﹣50×4=100,
x=6,
故答案为:6
【点评】本题是函数图象的信息题,又是行程问题,首先要明确三个量:路程、时间和速度,正确读出图形中甲、乙相遇及到达目的地的时间是本题的关键;重点理解图象中x与y所表示的含义,也是本题的难点.
13.(2024 湖州)放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 0.2 千米/分钟.
【考点】函数的图象.
【答案】见试题解答内容
【分析】根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得答案.
【解答】解:由纵坐标看出路程是2千米,
由横坐标看出时间是10分钟,
小明的骑车速度是2÷10=0.2(千米/分钟),
故答案为:0.2.
【点评】本题考查了函数图象,观察函数图象的纵坐标得出路程,观察函数图象的横坐标得出时间,利用了路程与时间的关系.
14.(2010 漳州)若一个函数图象的对称轴是y轴,则该函数称为偶函数.那么在下列四个函数:
①y=2x;②y;③y=x2;④y=(x﹣1)2+2中,属于偶函数的是 ③ (只填序号).
【考点】函数的概念.
【专题】压轴题.
【答案】见试题解答内容
【分析】根据对称轴是y轴,排除①②选项,再根据④不是偶函数,即可确定答案.
【解答】解:①y=2x,是正比例函数,函数图象的对称轴不是y轴,错误;
②y是反比例函数,函数图象的对称轴不是y轴,错误;
③y=x2是抛物线,对称轴是y轴,是偶函数,正确;
④y=(x﹣1)2+2对称轴是直线x=1,错误.
故属于偶函数的是③.
【点评】本题主要考查正比例函数、反比例函数、二次函数的对称性和二次函数是偶函数的性质.
15.(2024 灯塔市期末)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 y=﹣0.1x+50 .
【考点】函数关系式.
【专题】函数及其图象;运算能力;应用意识.
【答案】见试题解答内容
【分析】由于汽车每行驶100km耗油10L,那么汽车行驶路程x千米耗油0.1xL,而汽车油箱中能盛汽油50L,由此即可确定加满油后,油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数关系式.
【解答】解:∵汽车每行驶100km耗油10L,
∴汽车行驶路程xkm耗油0.1xL,
∵汽车油箱中现存油50L,
∴油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是y=﹣0.1x+50.
故答案为:y=﹣0.1x+50.
【点评】此题主要考查了根据实际问题中包含的数量关系列出函数关系式,解题关键是正确理解和把握题目中隐含的数量关系,只有充分理解已知条件,才能求出函数关系式.
三.解答题(共5小题)
16.(2024 怀柔区模拟)如图1,在直角梯形ABCD中,∠B=90°,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 x 、 y ;
(2)当点P运动的路程x=4时,△ABP的面积为y= 16 ;
(3)求AB的长和梯形ABCD的面积.
【考点】动点问题的函数图象.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】(1)依据点P运动的路程为x,△ABP的面积为y,即可得到自变量和因变量;
(2)依据函数图象,即可得到点P运动的路程x=4时,△ABP的面积;
(3)根据图象得出BC的长,以及此时三角形ABP面积,利用三角形面积公式求出AB的长即可;由函数图象得出DC的长,利用梯形面积公式求出梯形ABCD面积即可.
【解答】解:(1)∵点P运动的路程为x,△ABP的面积为y,
∴自变量为x,因变量为y,
故答案为:x,y;
(2)由图可得,当点P运动的路程x=4时,△ABP的面积为y=16,
故答案为:16;
(3)根据图象得:BC=4,此时△ABP为16,
∴AB BC=16,即AB×4=16,
解得:AB=8;
由图象得:DC=9﹣4=5,
则S梯形ABCDBC×(DC+AB)4×(5+8)=26.
【点评】此题考查了动点问题的函数图象,弄清函数图象上的信息是解本题的关键.
17.(2024春 碑林区期末)快车与慢车分别从甲乙两地同时同向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程为 420 km;快车的速度为 140 km/h;慢车的速度为 70 km/h;
(2)出发 h,快慢两车距各自出发地的路程相等;
(3)快慢两车出发 h或h或 h相距150km.
【考点】函数的图象.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】(1)先得两地的距离,根据速度=路程÷时间列式计算即可求出快车和慢车的速度;
(2)由图可知:快车返程时,两车距各自出发地的路程相等,根据慢车的路程=2个总路程﹣快车的路程,列方程即可得出答案;
(3)分别根据两车相遇以及两车相遇后两车距离为150km时,列方程可解答.
【解答】解:(1)由图可知:甲乙两地之间的路程为420km;
快车的速度为:140km/h;
由题意得:快车7小时到达甲地,则慢车6小时到达甲地,
则慢车的速度为:70km/h;
故答案为:420,140,70;
(2)∵快车速度为:140km/h,
∴A点坐标为:(3,420),
∴B点坐标为(4,420),
由图可知:快车返程时,两车距各自出发地的路程相等,
设出发x小时,两车距各自出发地的路程相等,
70x=2×420﹣140(x﹣1),
70x=980﹣140x,
解得:x,
答:出发小时,快、慢两车距各自出发地的路程相等;
故答案为:;
(3)第一种情形第一次没有相遇前,相距150km,
则140x+70x+150=420,
解得:x,
第二种情形应是相遇后而快车没到乙地前140x+70x﹣420=150,
解得:x,
第三种情形是快车从乙往甲返回:70x﹣140(x﹣4)=150,
解得:x,
综上所述:快慢两车出发h或h或h相距150km.
故答案为:h或h或.
【点评】本题考查了函数的应用,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于(2)表示出快车距离出发地的路程.
18.(2024 灵石县期末)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 自变量为小明出发的时间t ,因变量是 因变量为距起点的距离s ;
(2)朱老师的速度为 2 米/秒;小明的速度为 6 米/秒;
(3)小明与朱老师相遇 2 次,相遇时距起点的距离分别为 300或420 米.
【考点】函数的图象;常量与变量.
【答案】见试题解答内容
【分析】(1)观察函数图象即可找出谁是自变量谁是因变量;
(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;
(3)根据函数图象即可得到结论.
【解答】解:(1)观察函数图象可得出:自变量为小明出发的时间t,因变量为距起点的距离s.
故答案为:小明出发的时间t;距起点的距离s.
(2)朱老师的速度为:(300﹣200)÷50=2(米/秒);
小明的速度为:300÷50=6(米/秒).
故答案为:2;6.
(3)小明与朱老师相遇2次,相遇时距起点的距离分别为300米或420米,
故答案为:300米或420米.
【点评】本题考查了一次函数的应用,观察函数图象找出点的坐标利用待定系数法求出函数解析式是解题的关键.
19.(2024 莱西市期末)父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2 ﹣4 ﹣10
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
【考点】函数的表示方法.
【专题】应用题.
【答案】见试题解答内容
【分析】(1)根据图表,反映的是距离地面的高度和温度两个量,所以温度和高度是两个变化的量,温度随高度的变化而变化;
(2)根据表格数据,高度越大,温度越低,所以随着高度的h的增大,温度t在减小;
(3)求出当h=6时温度t的值即可.
【解答】解:(1)上表反映了温度和高度两个变量之间.高度是自变量,温度是因变量.
(2)如果用h表示距离地面的高度,用t表示温度,那么随着高度h的增大,温度t逐渐减小(或降低).
(3)距离地面6千米的高空温度是﹣16℃.
【点评】本题是对函数定义的考查和图表的识别,自变量、因变量的区分对初学函数的同学来说比较困难,需要在学习上多下功夫.
20.(2024 雁塔区校级期末)一列快车、一列慢车同时从相距300km的两地出发,相向而行.如图,l1和l2分别表示两车到甲地的距离s(km)与行驶时间t(h)的关系.
(1)快车的速度为 45 km/h,慢车的速度为 30 km/h;
(2)经过多久两车第一次相遇?
(3)当快车到达目的地时,慢车距离目的地多远?
【考点】函数的图象.
【答案】见试题解答内容
【分析】(1)分别用各自的总路程除以总时间即可得各自的速度;
(2)用总路程除以快车与慢车的速度和即可得两车第一次相遇时间;
(3)用慢车到目的地的时间减去快车到目的地的时间,再乘以慢车的速度即可.
【解答】解:(1)快车的速度为30045km/h,慢车的速度为300÷10=30km/h,
故答案为:45,30;
(2)4h
答:经过4h两车第一次相遇;
(3)(10)×30=100km,
答:当快车到达目的地时,慢车距离目的地100km.
【点评】本题考查了一次函数的图象的性质的运用,行程问题的数量关系的运用,相遇问题的数量关系的运用,解答时认真分析函数图象的意义是关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
