【中考押题卷】2025年中考数学高频易错考前冲刺:命题与证明(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:命题与证明(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 07:10:01 | ||
图片预览




文档简介
2025年中考数学高频易错考前冲刺:命题与证明
一.选择题(共10小题)
1.(2024秋 石狮市期末)用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )
A.∠B≥90° B.∠B>90° C.∠B<90° D.AB≠AC
2.(2024 常州)判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )
A.﹣2 B. C.0 D.
3.(2024 榆树市校级期末)用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45°
B.每一个内角都小于45°
C.有一个内角大于等于45°
D.每一个内角都大于等于45°
4.(2024 深圳)下列哪一个是假命题( )
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
5.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
6.(2023秋 青龙县期末)对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )
A.a⊥c B.b⊥c C.a与c相交 D.b与c相交
7.(2023 攸县一模)已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①② B.③④②① C.①②③④ D.③④①②
8.(2024秋 栾城区期末)已知:在△ABC中,AB≠AC,求证:∠B≠∠C.若用反证法来证明这个结论,可以假设( )
A.∠A=∠B B.AB=BC C.∠B=∠C D.∠A=∠C
9.(2024 钦州期末)下列命题中,是真命题的是( )
A.一条线段上只有一个黄金分割点
B.各角分别相等,各边成比例的两个多边形相似
C.两条直线被一组平行线所截,所得的线段成比例
D.若2x=3y,则
10.(2024 浙江)在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
二.填空题(共5小题)
11.(2024 东台市一模)如图,已知点A(﹣3,0),B(0,3),C(﹣1,4),动点P在线段AB上,点P、C、M按逆时针顺序排列,且∠CPM=90°,CP=MP,当点P从点A运动到点B时,则点M运动的路径长为 .
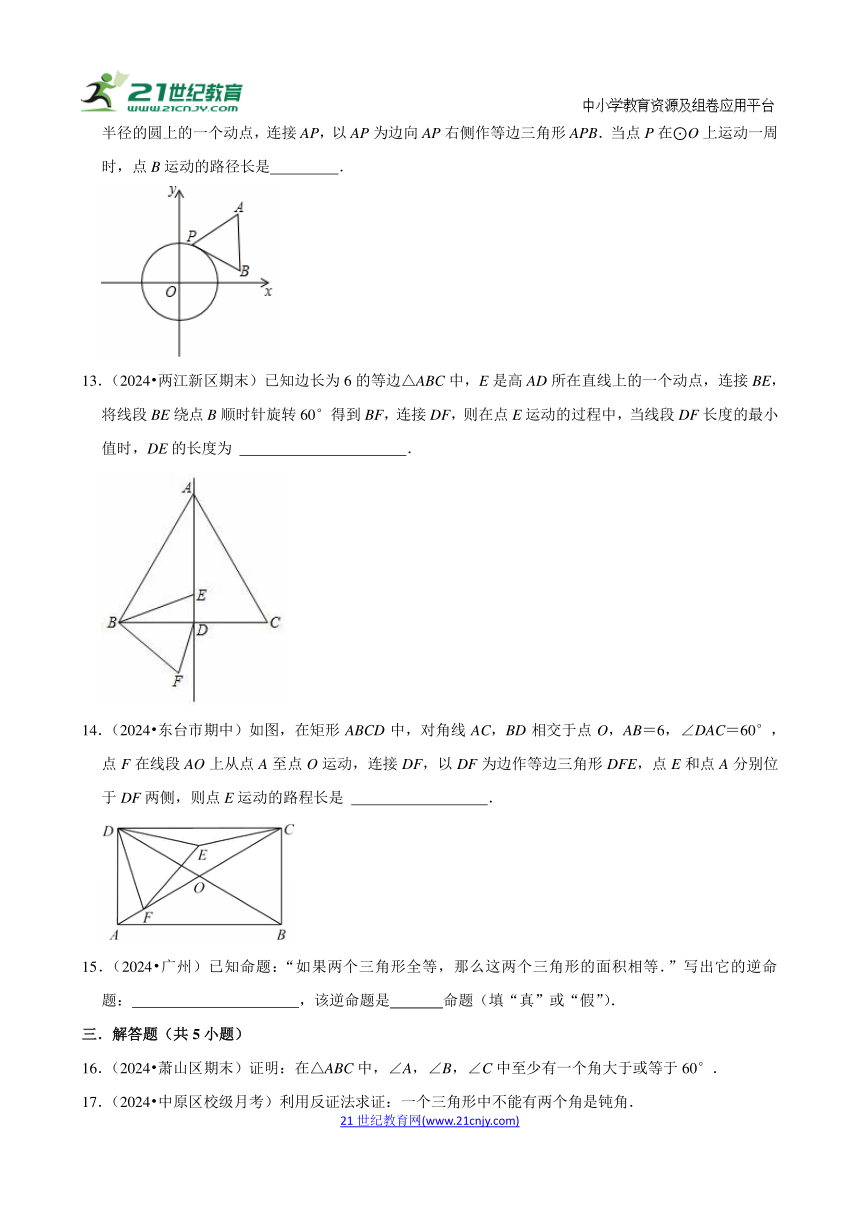
12.(2024 江阴市期中)如图,已知点A是第一象限内的一个定点,若点P是以O为圆心,2个单位长为半径的圆上的一个动点,连接AP,以AP为边向AP右侧作等边三角形APB.当点P在⊙O上运动一周时,点B运动的路径长是 .
13.(2024 两江新区期末)已知边长为6的等边△ABC中,E是高AD所在直线上的一个动点,连接BE,将线段BE绕点B顺时针旋转60°得到BF,连接DF,则在点E运动的过程中,当线段DF长度的最小值时,DE的长度为 .
14.(2024 东台市期中)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上从点A至点O运动,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,则点E运动的路程长是 .
15.(2024 广州)已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题: ,该逆命题是 命题(填“真”或“假”).
三.解答题(共5小题)
16.(2024 萧山区期末)证明:在△ABC中,∠A,∠B,∠C中至少有一个角大于或等于60°.
17.(2024 中原区校级月考)利用反证法求证:一个三角形中不能有两个角是钝角.
18.(2024 鞍山)用反证法证明:等腰三角形的底角是锐角.
19.(2024 莘县期末)(用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
20.(2024 盐山县期末)图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
(1)如图,EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小丽添加的条件:∠B+∠BDG=180°.
请你帮小丽将下面的证明过程补充完整.
证明:∵EF∥CD(已知)
∴∠BEF= ( )
∵∠B+∠BDG=180°(已知)
∴BC∥ ( )
∴∠CDG= ( )
∴∠BEF=∠CDG(等量代换)
(2)拓展:如图,请你从三个选项①DG∥BC,②DG平分∠ADC,③∠B=∠BCD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
①条件: ,结论: (填序号).
②证明: .
2025年中考数学高频易错考前冲刺:命题与证明
参考答案与试题解析
一.选择题(共10小题)
1.(2024秋 石狮市期末)用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )
A.∠B≥90° B.∠B>90° C.∠B<90° D.AB≠AC
【考点】反证法.
【专题】反证法;运算能力.
【答案】A
【分析】直接利用反证法的第一步分析得出答案.
【解答】解:用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设∠B≥90°.
故选:A.
【点评】此题主要考查了反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.
2.(2024 常州)判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )
A.﹣2 B. C.0 D.
【考点】命题与定理.
【专题】一元一次不等式(组)及应用.
【答案】A
【分析】反例中的n满足n<1,使n2﹣1≥0,从而对各选项进行判断.
【解答】解:当n=﹣2时,满足n<1,但n2﹣1=3>0,
所以判断命题“如果n<1,那么n2﹣1<0”是假命题,举出n=﹣2.
故选:A.
【点评】本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
3.(2024 榆树市校级期末)用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45°
B.每一个内角都小于45°
C.有一个内角大于等于45°
D.每一个内角都大于等于45°
【考点】反证法.
【答案】D
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立.
【解答】解:用反证法证明“钝角三角形中必有一个内角小于45°”时,
应先假设这个三角形中每一个内角都不小于45°,即每一个内角都大于或等于45°.
故选:D.
【点评】此题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
4.(2024 深圳)下列哪一个是假命题( )
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
【考点】命题与定理.
【答案】C
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:A、五边形外角和为360°是真命题,故A不符合题意;
B、切线垂直于经过切点的半径是真命题,故B不符合题意;
C、(3,﹣2)关于y轴的对称点为(﹣3,2)是假命题,故C符合题意;
D、抛物线y=x2﹣4x+2017对称轴为直线x=2是真命题,故D不符合题意;
故选:C.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
5.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
【考点】命题与定理.
【专题】几何图形.
【答案】D
【分析】根据线段、对顶角、补角、平行线的性质判断即可.
【解答】解:A、两点之间,线段最短是真命题;
B、对顶角相等是真命题;
C、直角的补角仍然是直角是真命题;
D、如果两直线不平行,同旁内角不互补,所以同旁内角互补是假命题;
故选:D.
【点评】此题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
6.(2023秋 青龙县期末)对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )
A.a⊥c B.b⊥c C.a与c相交 D.b与c相交
【考点】反证法.
【专题】反证法.
【答案】D
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
【解答】解:c与b的位置关系有c∥b和c与b相交两种,因此用反证法证明“c∥b”时,应先假设c与b相交.
故选:D.
【点评】本题结合直线的位置关系考查反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
7.(2023 攸县一模)已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①② B.③④②① C.①②③④ D.③④①②
【考点】反证法;等腰三角形的性质.
【专题】反证法;推理能力.
【答案】D
【分析】根据反证法的一般步骤判断即可.
【解答】解:运用反证法证明这个命题的四个步骤:1、假设在△ABC中,∠B≥90°,
2、由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°,
3、∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾,
4、因此假设不成立.∴∠B<90°,
故选:D.
【点评】本题考查的是反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.
8.(2024秋 栾城区期末)已知:在△ABC中,AB≠AC,求证:∠B≠∠C.若用反证法来证明这个结论,可以假设( )
A.∠A=∠B B.AB=BC C.∠B=∠C D.∠A=∠C
【考点】反证法.
【专题】推理能力.
【答案】C
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
【解答】解:∠B≠∠C的反面是∠B=∠C.
故可以假设∠B=∠C.
故选:C.
【点评】本题主要考查了反证法的基本步骤,正确确定∠B≠∠C的反面,是解决本题的关键
9.(2024 钦州期末)下列命题中,是真命题的是( )
A.一条线段上只有一个黄金分割点
B.各角分别相等,各边成比例的两个多边形相似
C.两条直线被一组平行线所截,所得的线段成比例
D.若2x=3y,则
【考点】命题与定理.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据黄金分割的定义对A选项进行判断;根据相似多边形的定义对B选项进行判断;根据平行线分线段成比例定理对C选项进行判断;根据比例的性质对D选项进行判断.
【解答】解:A.一条线段上有两个黄金分割点,所以A选项不符合题意;
B.各角分别相等,各边成比例的两个多边形相似,所以B选项符合题意;
C.两条直线被一组平行线所截,所得的对应线段成比例,所以C选项不符合题意;
D.若2x=3y,则,所以D选项不符合题意.
故选:B.
【点评】本题考查了命题:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
10.(2024 浙江)在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
【考点】命题与定理.
【专题】综合题.
【答案】C
【分析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.两组对边平行的四边形是平行四边形;有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;有一组邻边相等的平行四边形是菱形;对角线互相垂直平分且相等的四边形是正方形.
【解答】解:A、应为两组对边平行的四边形是平行四边形;
B、有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;
C、符合菱形定义;
D、应为对角线互相垂直平分且相等的四边形是正方形.
故选:C.
【点评】本题考查平行四边形、矩形和菱形及正方形的判定与命题的真假区别.
二.填空题(共5小题)
11.(2024 东台市一模)如图,已知点A(﹣3,0),B(0,3),C(﹣1,4),动点P在线段AB上,点P、C、M按逆时针顺序排列,且∠CPM=90°,CP=MP,当点P从点A运动到点B时,则点M运动的路径长为 6 .
【考点】轨迹;坐标与图形性质;全等三角形的判定与性质;等腰直角三角形.
【专题】动点型;模型思想.
【答案】6.
【分析】P为主动点,M为从动点,C为定点,则P运动路径(AB)与M运动路径之比等于可得答案.
【解答】解:∵点A(﹣3,0),B(0,3),
∴AB,
∵C(﹣1,4),动点P在线段AB上,∠CPM=90°,CP=MP,
∴,P为主动点,M为从动点,C为定点,
由“瓜豆原理”得P运动路径(AB)与M运动路径之比等于,
∴点M运动的路径长为6,
故答案为:6.
【点评】本题考查等腰直角三角形、动点问题,关键是要理解掌握“瓜豆原理”:主动点、从动点与定点距离之比等于主动点、从动点运动路径之比.
12.(2024 江阴市期中)如图,已知点A是第一象限内的一个定点,若点P是以O为圆心,2个单位长为半径的圆上的一个动点,连接AP,以AP为边向AP右侧作等边三角形APB.当点P在⊙O上运动一周时,点B运动的路径长是 4π .
【考点】轨迹;等边三角形的性质.
【专题】模型思想.
【答案】4π.
【分析】根据已知条件得到点B的运动轨迹也为圆,根据全等三角形的性质得到OP=O'B=2,即可求出路径长.
【解答】解:如图,连接AO、OP,将AO绕点A逆时针旋转60°,得线段AO',连接O'B、OO',
∵AO=AO',∠OAO'=60°,
∴△OAO'为正三角形,
∵△APB为正三角形,
∴∠PAB=60°,PA=BA,
∴∠PAB﹣∠OAB=∠OAO'﹣∠OAB,
∴∠PAO=∠BAO,
在△APO与△ABO′中,
,
∴△APO≌△ABO′,
∴OP=O'B=2,
∴⊙O'即为动点B运动的路径,
∴当点P在⊙O上运动一周时,点B运动的路径长是4π,
【点评】此题考查了动点路径长,关键在于确定从动点的运动轨迹,考查了旋转、全等知识,“瓜豆原理”.
13.(2024 两江新区期末)已知边长为6的等边△ABC中,E是高AD所在直线上的一个动点,连接BE,将线段BE绕点B顺时针旋转60°得到BF,连接DF,则在点E运动的过程中,当线段DF长度的最小值时,DE的长度为 .
【考点】轨迹;旋转的性质;全等三角形的判定与性质;等边三角形的性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】连接CF,F点在直线CF上运动;由已知可证明△ABE≌△BCF(ASA),当DF⊥CF时,DF最小,求出AE,即可求解.
【解答】解:连接CF,
∵等边△ABC,
∴AB=BC,
∵线段BE绕点B顺时针旋转60°得到BF,
∴BE=BF,∠ABE=∠CBF,
∴△ABE≌△BCF(ASA),
F点在直线CF上运动,
∴CF=AE,∠BCF=30°,
∴F点在直线CF上运动,
当DF⊥CF时,DF最小,
∵CD=3,
∴CF,
∴AE,
∵AD=3,
∴DE,
故答案为.
【点评】本题考查等边三角形的性质,点的轨迹;熟练掌握等边三角形的性质,能够通过主动点的运动确定从动点的运动轨迹是解题的关键.
14.(2024 东台市期中)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上从点A至点O运动,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,则点E运动的路程长是 2 .
【考点】轨迹;等边三角形的判定与性质;矩形的性质.
【专题】图形的全等;推理能力.
【答案】2.
【分析】连接OE,利用SAS证明△ADF≌△ODE(SAS),得OE=AF,∠DOE=∠DAO,则点E在射线OE上运动,且OE=AF,当点F在线段AO上从点A至点O运动时,故点E的运动路程是AO,利用勾股定理求出AO的长即可.
【解答】解:连接OE,
∵四边形ABCD是矩形,
∴AO=DO,∠DAB=90°,
∵∠DAC=60°,
∴△DAO是等边三角形,
∴DA=DO,∠ADO=60°,
∵△DFE是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠ADF=∠ODE,
又AD=DO,DF=DE,
∴△ADF≌△ODE(SAS),
∴OE=AF,∠DOE=∠DAO,
∴点E在射线OE上运动,且OE=AF,
当点F在线段AO上从点A至点O运动时,
∴点E的运动路程是AO,
在Rt△ADB中,设AD=x,则BD=2x,
∴(2x)2﹣x2=62,
解得x=2(负值舍去),
∴AD=AO=2,
即点E的运动路程为2,
故答案为:2.
【点评】本题主要考查了矩形的性质,等边三角形的判定与性质,全等三角形的判定与性质,勾股定理等知识,确定点E的运动路径是解题的关键.
15.(2024 广州)已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题: 如果两个三角形的面积相等,那么这两个三角形全等 ,该逆命题是 假 命题(填“真”或“假”).
【考点】命题与定理.
【答案】见试题解答内容
【分析】交换原命题的题设和结论即可得到该命题的逆命题.
【解答】解:“如果两个三角形全等,那么这两个三角形的面积相等.”写成它的逆命题:如果两个三角形的面积相等,那么这两个三角形全等,该逆命题是假命题,
故答案为:如果两个三角形的面积相等,那么这两个三角形全等;假.
【点评】本题考查逆命题的概念,以及判断真假命题的能力以及全等三角形的判定和性质.
三.解答题(共5小题)
16.(2024 萧山区期末)证明:在△ABC中,∠A,∠B,∠C中至少有一个角大于或等于60°.
【考点】反证法.
【专题】证明题.
【答案】见试题解答内容
【分析】利用反证法的步骤,首先假设原命题错误,进而得出与三角形内角和定理矛盾,从而证明原命题正确.
【解答】证明:假设△ABC中每个内角都小于60°,
则∠A+∠B+∠C<180°,
这与三角形内角和定理矛盾,
故假设错误,即原结论成立,在△ABC中,∠A,∠B,∠C中至少有一个角大于或等于60°.
【点评】此题主要考查了反证法,正确把握反证法的证明步骤是解题关键.
17.(2024 中原区校级月考)利用反证法求证:一个三角形中不能有两个角是钝角.
【考点】反证法.
【答案】见试题解答内容
【分析】根据反证法的证明方法假设出命题,进而证明即可.
【解答】证明:假设∠A、∠B、∠C中有两个角是钝角,不妨设∠A、∠B为钝角,
∴∠A+∠B>180°,这与三角形内角和定理相矛盾,故假设不成立原命题正确.
【点评】此题主要考查了反证法,需熟练掌握反证法的一般步骤:
①假设命题的结论不成立;
②从这个假设出发,经过推理论证,得出矛盾;
③由矛盾判定假设不正确,从而肯定原命题的结论正确.
18.(2024 鞍山)用反证法证明:等腰三角形的底角是锐角.
【考点】反证法.
【专题】证明题.
【答案】见试题解答内容
【分析】根据反证法的步骤进行证明.
【解答】证明:用反证法.
假设等腰三角形的底角不是锐角,则大于或等于90°.
根据等腰三角形的两个底角相等,则两个底角的和大于或等于180°.
则该三角形的三个内角的和一定大于180°,这与三角形的内角和定理相矛盾,故假设不成立.
所以等腰三角形的底角是锐角.
【点评】反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
19.(2024 莘县期末)(用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
【考点】反证法;平行公理及推论.
【专题】证明题.
【答案】见试题解答内容
【分析】用反证法进行证明;先假设原命题不成立,然后经过推导得出与已知或定理相矛盾,从而证得原结论正确.
【解答】证明:假设a与b相交,
则过M点有两条直线平行于直线c,
这与过直线外一点平行于已知直线的直线有且只有一条相矛盾,
所以a∥b.
【点评】考查了反证法.解此题关键要懂得反证法的意义及步骤.反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,只要否定其一即可.
20.(2024 盐山县期末)图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
(1)如图,EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小丽添加的条件:∠B+∠BDG=180°.
请你帮小丽将下面的证明过程补充完整.
证明:∵EF∥CD(已知)
∴∠BEF= ∠BCD ( 两直线平行,同位角相等 )
∵∠B+∠BDG=180°(已知)
∴BC∥ DG ( 同旁内角互补,两直线平行 )
∴∠CDG= ∠BCD ( 两直线平行,内错角相等 )
∴∠BEF=∠CDG(等量代换)
(2)拓展:如图,请你从三个选项①DG∥BC,②DG平分∠ADC,③∠B=∠BCD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
①条件: ①③ ,结论: ②(答案不唯一) (填序号).
②证明: ∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC .
【考点】命题与定理.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】(1)根据平行线的判定定理和性质定理解答;
(2)根据真命题的概念写出命题的条件和结论,根据平行线的判定定理和性质定理、角平分线的定义解答.
【解答】(1)证明:∵EF∥CD(已知),
∴∠BEF=∠BCD(两直线平行,同位角相等),
∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠BEF=∠CDG(等量代换);
(2)①条件:DG∥BC,∠B=∠BCD(答案不唯一),
结论:DG平分∠ADC,
②证明:∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
故答案为:(1)∠BCD;两直线平行,同位角相等;DG;同旁内角互补,两直线平行;∠BCD;两直线平行,内错角相等;
(2)①、①③;②,
∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
【点评】本题考查的是命题的真假判断、平行线的判定和性质,掌握平行线的判定定理和性质定理是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 石狮市期末)用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )
A.∠B≥90° B.∠B>90° C.∠B<90° D.AB≠AC
2.(2024 常州)判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )
A.﹣2 B. C.0 D.
3.(2024 榆树市校级期末)用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45°
B.每一个内角都小于45°
C.有一个内角大于等于45°
D.每一个内角都大于等于45°
4.(2024 深圳)下列哪一个是假命题( )
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
5.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
6.(2023秋 青龙县期末)对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )
A.a⊥c B.b⊥c C.a与c相交 D.b与c相交
7.(2023 攸县一模)已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①② B.③④②① C.①②③④ D.③④①②
8.(2024秋 栾城区期末)已知:在△ABC中,AB≠AC,求证:∠B≠∠C.若用反证法来证明这个结论,可以假设( )
A.∠A=∠B B.AB=BC C.∠B=∠C D.∠A=∠C
9.(2024 钦州期末)下列命题中,是真命题的是( )
A.一条线段上只有一个黄金分割点
B.各角分别相等,各边成比例的两个多边形相似
C.两条直线被一组平行线所截,所得的线段成比例
D.若2x=3y,则
10.(2024 浙江)在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
二.填空题(共5小题)
11.(2024 东台市一模)如图,已知点A(﹣3,0),B(0,3),C(﹣1,4),动点P在线段AB上,点P、C、M按逆时针顺序排列,且∠CPM=90°,CP=MP,当点P从点A运动到点B时,则点M运动的路径长为 .
12.(2024 江阴市期中)如图,已知点A是第一象限内的一个定点,若点P是以O为圆心,2个单位长为半径的圆上的一个动点,连接AP,以AP为边向AP右侧作等边三角形APB.当点P在⊙O上运动一周时,点B运动的路径长是 .
13.(2024 两江新区期末)已知边长为6的等边△ABC中,E是高AD所在直线上的一个动点,连接BE,将线段BE绕点B顺时针旋转60°得到BF,连接DF,则在点E运动的过程中,当线段DF长度的最小值时,DE的长度为 .
14.(2024 东台市期中)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上从点A至点O运动,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,则点E运动的路程长是 .
15.(2024 广州)已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题: ,该逆命题是 命题(填“真”或“假”).
三.解答题(共5小题)
16.(2024 萧山区期末)证明:在△ABC中,∠A,∠B,∠C中至少有一个角大于或等于60°.
17.(2024 中原区校级月考)利用反证法求证:一个三角形中不能有两个角是钝角.
18.(2024 鞍山)用反证法证明:等腰三角形的底角是锐角.
19.(2024 莘县期末)(用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
20.(2024 盐山县期末)图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
(1)如图,EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小丽添加的条件:∠B+∠BDG=180°.
请你帮小丽将下面的证明过程补充完整.
证明:∵EF∥CD(已知)
∴∠BEF= ( )
∵∠B+∠BDG=180°(已知)
∴BC∥ ( )
∴∠CDG= ( )
∴∠BEF=∠CDG(等量代换)
(2)拓展:如图,请你从三个选项①DG∥BC,②DG平分∠ADC,③∠B=∠BCD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
①条件: ,结论: (填序号).
②证明: .
2025年中考数学高频易错考前冲刺:命题与证明
参考答案与试题解析
一.选择题(共10小题)
1.(2024秋 石狮市期末)用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )
A.∠B≥90° B.∠B>90° C.∠B<90° D.AB≠AC
【考点】反证法.
【专题】反证法;运算能力.
【答案】A
【分析】直接利用反证法的第一步分析得出答案.
【解答】解:用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设∠B≥90°.
故选:A.
【点评】此题主要考查了反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.
2.(2024 常州)判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举出一个反例.反例中的n可以为( )
A.﹣2 B. C.0 D.
【考点】命题与定理.
【专题】一元一次不等式(组)及应用.
【答案】A
【分析】反例中的n满足n<1,使n2﹣1≥0,从而对各选项进行判断.
【解答】解:当n=﹣2时,满足n<1,但n2﹣1=3>0,
所以判断命题“如果n<1,那么n2﹣1<0”是假命题,举出n=﹣2.
故选:A.
【点评】本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
3.(2024 榆树市校级期末)用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45°
B.每一个内角都小于45°
C.有一个内角大于等于45°
D.每一个内角都大于等于45°
【考点】反证法.
【答案】D
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立.
【解答】解:用反证法证明“钝角三角形中必有一个内角小于45°”时,
应先假设这个三角形中每一个内角都不小于45°,即每一个内角都大于或等于45°.
故选:D.
【点评】此题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
4.(2024 深圳)下列哪一个是假命题( )
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
【考点】命题与定理.
【答案】C
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【解答】解:A、五边形外角和为360°是真命题,故A不符合题意;
B、切线垂直于经过切点的半径是真命题,故B不符合题意;
C、(3,﹣2)关于y轴的对称点为(﹣3,2)是假命题,故C符合题意;
D、抛物线y=x2﹣4x+2017对称轴为直线x=2是真命题,故D不符合题意;
故选:C.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
5.(2024秋 新田县期末)下列命题中,是假命题的是( )
A.两点之间,线段最短
B.对顶角相等
C.直角的补角仍然是直角
D.同旁内角互补
【考点】命题与定理.
【专题】几何图形.
【答案】D
【分析】根据线段、对顶角、补角、平行线的性质判断即可.
【解答】解:A、两点之间,线段最短是真命题;
B、对顶角相等是真命题;
C、直角的补角仍然是直角是真命题;
D、如果两直线不平行,同旁内角不互补,所以同旁内角互补是假命题;
故选:D.
【点评】此题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
6.(2023秋 青龙县期末)对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )
A.a⊥c B.b⊥c C.a与c相交 D.b与c相交
【考点】反证法.
【专题】反证法.
【答案】D
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
【解答】解:c与b的位置关系有c∥b和c与b相交两种,因此用反证法证明“c∥b”时,应先假设c与b相交.
故选:D.
【点评】本题结合直线的位置关系考查反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
7.(2023 攸县一模)已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾
②因此假设不成立.∴∠B<90°
③假设在△ABC中,∠B≥90°
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A.④③①② B.③④②① C.①②③④ D.③④①②
【考点】反证法;等腰三角形的性质.
【专题】反证法;推理能力.
【答案】D
【分析】根据反证法的一般步骤判断即可.
【解答】解:运用反证法证明这个命题的四个步骤:1、假设在△ABC中,∠B≥90°,
2、由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°,
3、∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾,
4、因此假设不成立.∴∠B<90°,
故选:D.
【点评】本题考查的是反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.
8.(2024秋 栾城区期末)已知:在△ABC中,AB≠AC,求证:∠B≠∠C.若用反证法来证明这个结论,可以假设( )
A.∠A=∠B B.AB=BC C.∠B=∠C D.∠A=∠C
【考点】反证法.
【专题】推理能力.
【答案】C
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
【解答】解:∠B≠∠C的反面是∠B=∠C.
故可以假设∠B=∠C.
故选:C.
【点评】本题主要考查了反证法的基本步骤,正确确定∠B≠∠C的反面,是解决本题的关键
9.(2024 钦州期末)下列命题中,是真命题的是( )
A.一条线段上只有一个黄金分割点
B.各角分别相等,各边成比例的两个多边形相似
C.两条直线被一组平行线所截,所得的线段成比例
D.若2x=3y,则
【考点】命题与定理.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据黄金分割的定义对A选项进行判断;根据相似多边形的定义对B选项进行判断;根据平行线分线段成比例定理对C选项进行判断;根据比例的性质对D选项进行判断.
【解答】解:A.一条线段上有两个黄金分割点,所以A选项不符合题意;
B.各角分别相等,各边成比例的两个多边形相似,所以B选项符合题意;
C.两条直线被一组平行线所截,所得的对应线段成比例,所以C选项不符合题意;
D.若2x=3y,则,所以D选项不符合题意.
故选:B.
【点评】本题考查了命题:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
10.(2024 浙江)在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
【考点】命题与定理.
【专题】综合题.
【答案】C
【分析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.两组对边平行的四边形是平行四边形;有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;有一组邻边相等的平行四边形是菱形;对角线互相垂直平分且相等的四边形是正方形.
【解答】解:A、应为两组对边平行的四边形是平行四边形;
B、有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;
C、符合菱形定义;
D、应为对角线互相垂直平分且相等的四边形是正方形.
故选:C.
【点评】本题考查平行四边形、矩形和菱形及正方形的判定与命题的真假区别.
二.填空题(共5小题)
11.(2024 东台市一模)如图,已知点A(﹣3,0),B(0,3),C(﹣1,4),动点P在线段AB上,点P、C、M按逆时针顺序排列,且∠CPM=90°,CP=MP,当点P从点A运动到点B时,则点M运动的路径长为 6 .
【考点】轨迹;坐标与图形性质;全等三角形的判定与性质;等腰直角三角形.
【专题】动点型;模型思想.
【答案】6.
【分析】P为主动点,M为从动点,C为定点,则P运动路径(AB)与M运动路径之比等于可得答案.
【解答】解:∵点A(﹣3,0),B(0,3),
∴AB,
∵C(﹣1,4),动点P在线段AB上,∠CPM=90°,CP=MP,
∴,P为主动点,M为从动点,C为定点,
由“瓜豆原理”得P运动路径(AB)与M运动路径之比等于,
∴点M运动的路径长为6,
故答案为:6.
【点评】本题考查等腰直角三角形、动点问题,关键是要理解掌握“瓜豆原理”:主动点、从动点与定点距离之比等于主动点、从动点运动路径之比.
12.(2024 江阴市期中)如图,已知点A是第一象限内的一个定点,若点P是以O为圆心,2个单位长为半径的圆上的一个动点,连接AP,以AP为边向AP右侧作等边三角形APB.当点P在⊙O上运动一周时,点B运动的路径长是 4π .
【考点】轨迹;等边三角形的性质.
【专题】模型思想.
【答案】4π.
【分析】根据已知条件得到点B的运动轨迹也为圆,根据全等三角形的性质得到OP=O'B=2,即可求出路径长.
【解答】解:如图,连接AO、OP,将AO绕点A逆时针旋转60°,得线段AO',连接O'B、OO',
∵AO=AO',∠OAO'=60°,
∴△OAO'为正三角形,
∵△APB为正三角形,
∴∠PAB=60°,PA=BA,
∴∠PAB﹣∠OAB=∠OAO'﹣∠OAB,
∴∠PAO=∠BAO,
在△APO与△ABO′中,
,
∴△APO≌△ABO′,
∴OP=O'B=2,
∴⊙O'即为动点B运动的路径,
∴当点P在⊙O上运动一周时,点B运动的路径长是4π,
【点评】此题考查了动点路径长,关键在于确定从动点的运动轨迹,考查了旋转、全等知识,“瓜豆原理”.
13.(2024 两江新区期末)已知边长为6的等边△ABC中,E是高AD所在直线上的一个动点,连接BE,将线段BE绕点B顺时针旋转60°得到BF,连接DF,则在点E运动的过程中,当线段DF长度的最小值时,DE的长度为 .
【考点】轨迹;旋转的性质;全等三角形的判定与性质;等边三角形的性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】连接CF,F点在直线CF上运动;由已知可证明△ABE≌△BCF(ASA),当DF⊥CF时,DF最小,求出AE,即可求解.
【解答】解:连接CF,
∵等边△ABC,
∴AB=BC,
∵线段BE绕点B顺时针旋转60°得到BF,
∴BE=BF,∠ABE=∠CBF,
∴△ABE≌△BCF(ASA),
F点在直线CF上运动,
∴CF=AE,∠BCF=30°,
∴F点在直线CF上运动,
当DF⊥CF时,DF最小,
∵CD=3,
∴CF,
∴AE,
∵AD=3,
∴DE,
故答案为.
【点评】本题考查等边三角形的性质,点的轨迹;熟练掌握等边三角形的性质,能够通过主动点的运动确定从动点的运动轨迹是解题的关键.
14.(2024 东台市期中)如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=6,∠DAC=60°,点F在线段AO上从点A至点O运动,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,则点E运动的路程长是 2 .
【考点】轨迹;等边三角形的判定与性质;矩形的性质.
【专题】图形的全等;推理能力.
【答案】2.
【分析】连接OE,利用SAS证明△ADF≌△ODE(SAS),得OE=AF,∠DOE=∠DAO,则点E在射线OE上运动,且OE=AF,当点F在线段AO上从点A至点O运动时,故点E的运动路程是AO,利用勾股定理求出AO的长即可.
【解答】解:连接OE,
∵四边形ABCD是矩形,
∴AO=DO,∠DAB=90°,
∵∠DAC=60°,
∴△DAO是等边三角形,
∴DA=DO,∠ADO=60°,
∵△DFE是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠ADF=∠ODE,
又AD=DO,DF=DE,
∴△ADF≌△ODE(SAS),
∴OE=AF,∠DOE=∠DAO,
∴点E在射线OE上运动,且OE=AF,
当点F在线段AO上从点A至点O运动时,
∴点E的运动路程是AO,
在Rt△ADB中,设AD=x,则BD=2x,
∴(2x)2﹣x2=62,
解得x=2(负值舍去),
∴AD=AO=2,
即点E的运动路程为2,
故答案为:2.
【点评】本题主要考查了矩形的性质,等边三角形的判定与性质,全等三角形的判定与性质,勾股定理等知识,确定点E的运动路径是解题的关键.
15.(2024 广州)已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题: 如果两个三角形的面积相等,那么这两个三角形全等 ,该逆命题是 假 命题(填“真”或“假”).
【考点】命题与定理.
【答案】见试题解答内容
【分析】交换原命题的题设和结论即可得到该命题的逆命题.
【解答】解:“如果两个三角形全等,那么这两个三角形的面积相等.”写成它的逆命题:如果两个三角形的面积相等,那么这两个三角形全等,该逆命题是假命题,
故答案为:如果两个三角形的面积相等,那么这两个三角形全等;假.
【点评】本题考查逆命题的概念,以及判断真假命题的能力以及全等三角形的判定和性质.
三.解答题(共5小题)
16.(2024 萧山区期末)证明:在△ABC中,∠A,∠B,∠C中至少有一个角大于或等于60°.
【考点】反证法.
【专题】证明题.
【答案】见试题解答内容
【分析】利用反证法的步骤,首先假设原命题错误,进而得出与三角形内角和定理矛盾,从而证明原命题正确.
【解答】证明:假设△ABC中每个内角都小于60°,
则∠A+∠B+∠C<180°,
这与三角形内角和定理矛盾,
故假设错误,即原结论成立,在△ABC中,∠A,∠B,∠C中至少有一个角大于或等于60°.
【点评】此题主要考查了反证法,正确把握反证法的证明步骤是解题关键.
17.(2024 中原区校级月考)利用反证法求证:一个三角形中不能有两个角是钝角.
【考点】反证法.
【答案】见试题解答内容
【分析】根据反证法的证明方法假设出命题,进而证明即可.
【解答】证明:假设∠A、∠B、∠C中有两个角是钝角,不妨设∠A、∠B为钝角,
∴∠A+∠B>180°,这与三角形内角和定理相矛盾,故假设不成立原命题正确.
【点评】此题主要考查了反证法,需熟练掌握反证法的一般步骤:
①假设命题的结论不成立;
②从这个假设出发,经过推理论证,得出矛盾;
③由矛盾判定假设不正确,从而肯定原命题的结论正确.
18.(2024 鞍山)用反证法证明:等腰三角形的底角是锐角.
【考点】反证法.
【专题】证明题.
【答案】见试题解答内容
【分析】根据反证法的步骤进行证明.
【解答】证明:用反证法.
假设等腰三角形的底角不是锐角,则大于或等于90°.
根据等腰三角形的两个底角相等,则两个底角的和大于或等于180°.
则该三角形的三个内角的和一定大于180°,这与三角形的内角和定理相矛盾,故假设不成立.
所以等腰三角形的底角是锐角.
【点评】反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
19.(2024 莘县期末)(用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
【考点】反证法;平行公理及推论.
【专题】证明题.
【答案】见试题解答内容
【分析】用反证法进行证明;先假设原命题不成立,然后经过推导得出与已知或定理相矛盾,从而证得原结论正确.
【解答】证明:假设a与b相交,
则过M点有两条直线平行于直线c,
这与过直线外一点平行于已知直线的直线有且只有一条相矛盾,
所以a∥b.
【点评】考查了反证法.解此题关键要懂得反证法的意义及步骤.反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,只要否定其一即可.
20.(2024 盐山县期末)图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
(1)如图,EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小丽添加的条件:∠B+∠BDG=180°.
请你帮小丽将下面的证明过程补充完整.
证明:∵EF∥CD(已知)
∴∠BEF= ∠BCD ( 两直线平行,同位角相等 )
∵∠B+∠BDG=180°(已知)
∴BC∥ DG ( 同旁内角互补,两直线平行 )
∴∠CDG= ∠BCD ( 两直线平行,内错角相等 )
∴∠BEF=∠CDG(等量代换)
(2)拓展:如图,请你从三个选项①DG∥BC,②DG平分∠ADC,③∠B=∠BCD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
①条件: ①③ ,结论: ②(答案不唯一) (填序号).
②证明: ∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC .
【考点】命题与定理.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】(1)根据平行线的判定定理和性质定理解答;
(2)根据真命题的概念写出命题的条件和结论,根据平行线的判定定理和性质定理、角平分线的定义解答.
【解答】(1)证明:∵EF∥CD(已知),
∴∠BEF=∠BCD(两直线平行,同位角相等),
∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠BEF=∠CDG(等量代换);
(2)①条件:DG∥BC,∠B=∠BCD(答案不唯一),
结论:DG平分∠ADC,
②证明:∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
故答案为:(1)∠BCD;两直线平行,同位角相等;DG;同旁内角互补,两直线平行;∠BCD;两直线平行,内错角相等;
(2)①、①③;②,
∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
【点评】本题考查的是命题的真假判断、平行线的判定和性质,掌握平行线的判定定理和性质定理是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
