初中数学苏科版九年级下册 5.3 用待定系数法确定二次函数表达式 同步练习(含解析)
文档属性
| 名称 | 初中数学苏科版九年级下册 5.3 用待定系数法确定二次函数表达式 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 336.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 11:35:17 | ||
图片预览



文档简介
5.3用待定系数法确定二次函数表达式
一、单选题
1.将二次函数y=x2﹣4x+8转化为y=a(x﹣m)2+k的形式,其结果为( )
A.y=(x﹣2)2+4 B.y=(x+4)2+4
C.y=(x﹣4)2+8 D.y=(x﹣2)2﹣4
2.已知二次函数y=ax2﹣2ax+c(其中x是自变量),当2≤x≤3时,5≤y≤8,则a的值为( )
A.1 B.2 C.±1 D.±2
3.设函数y=a(x+m)2+n(a≠0,m,n是实数),当x=1时,y=1;当x=6时,y=6.则( )
A.若m=﹣3,则a<0 B.若m=﹣4,则a>0
C.若m=﹣5,则a<0 D.若m=﹣6,则a>0
4.已知抛物线y=x2+(3m﹣1)x﹣3m(m>0)的最低点的纵坐标为﹣4,则抛物线的表达式是( )
A.y=x2﹣6x+5 B.y=x2+2x﹣3 C.y=x2+5x﹣6 D.y=x2+4x﹣5
5.二次函数y=﹣x2﹣2x+1配方后,结果正确的是( )
A.y=﹣(x+1)2+2 B.y=﹣(x﹣1)2+2
C.y=﹣(x+1)2﹣2 D.y=﹣(x﹣1)2﹣2
二、填空题
6.一个二次函数y=ax2+bx+c图象的顶点在x轴负半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是 .
7.请写出一个开口向上,并且对称轴为直线x=1的抛物线的表达式y=
8.一个二次函数的图象经过(0,0),(﹣1,﹣1),(1,9)三点.则这个二次函数的解析式为 .
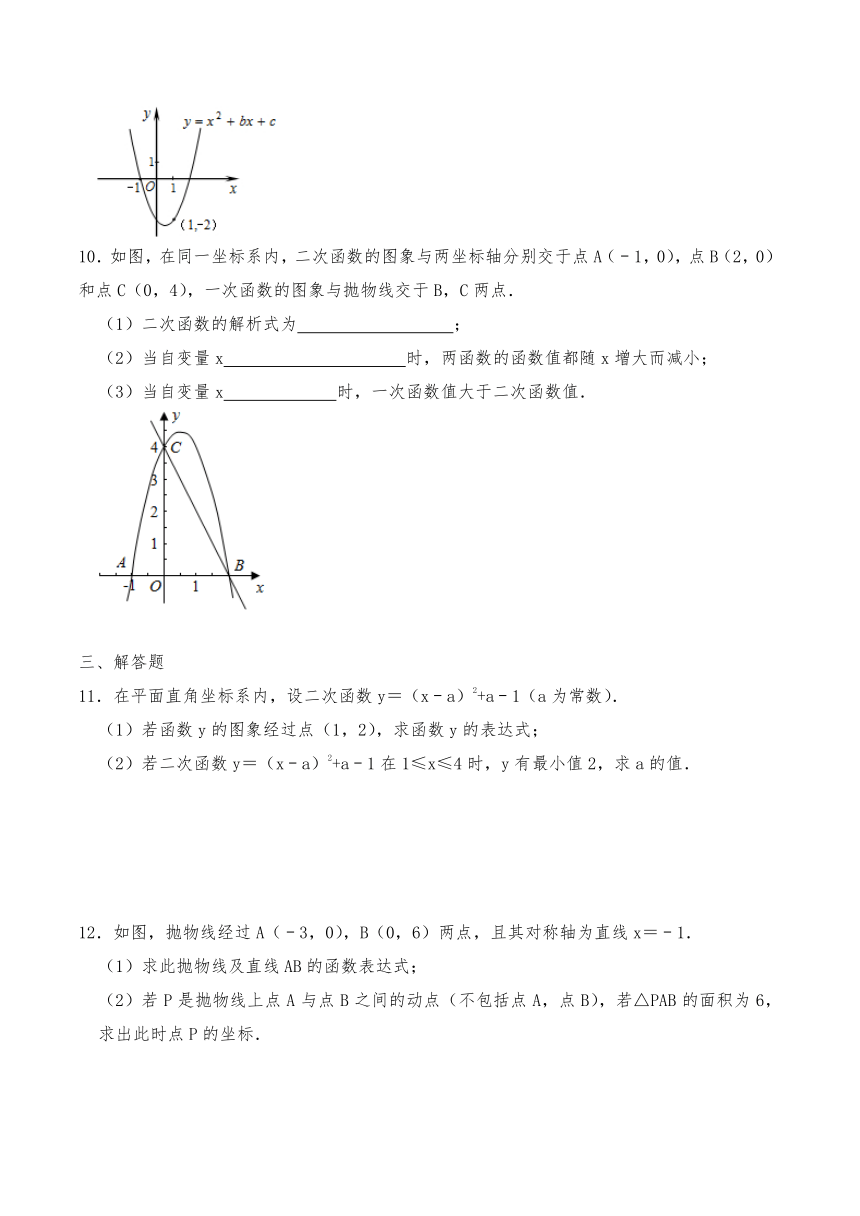
9.如图,已知二次函数y=x2+bx+c的图象经过点(﹣1,0),(1,﹣2),当y随x的增大而增大时,x的取值范围是 .
10.如图,在同一坐标系内,二次函数的图象与两坐标轴分别交于点A(﹣1,0),点B(2,0)和点C(0,4),一次函数的图象与抛物线交于B,C两点.
(1)二次函数的解析式为 ;
(2)当自变量x 时,两函数的函数值都随x增大而减小;
(3)当自变量x 时,一次函数值大于二次函数值.
三、解答题
11.在平面直角坐标系内,设二次函数y=(x﹣a)2+a﹣1(a为常数).
(1)若函数y的图象经过点(1,2),求函数y的表达式;
(2)若二次函数y=(x﹣a)2+a﹣1在1≤x≤4时,y有最小值2,求a的值.
12.如图,抛物线经过A(﹣3,0),B(0,6)两点,且其对称轴为直线x=﹣1.
(1)求此抛物线及直线AB的函数表达式;
(2)若P是抛物线上点A与点B之间的动点(不包括点A,点B),若△PAB的面积为6,求出此时点P的坐标.
13.如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标;
(2)当y≤﹣2时,请根据图象直接写出x的取值范围是 ;
(3)若关于x的方程|x2+bx+c|﹣m=0有且只有四个解,则m的取值范围是 .
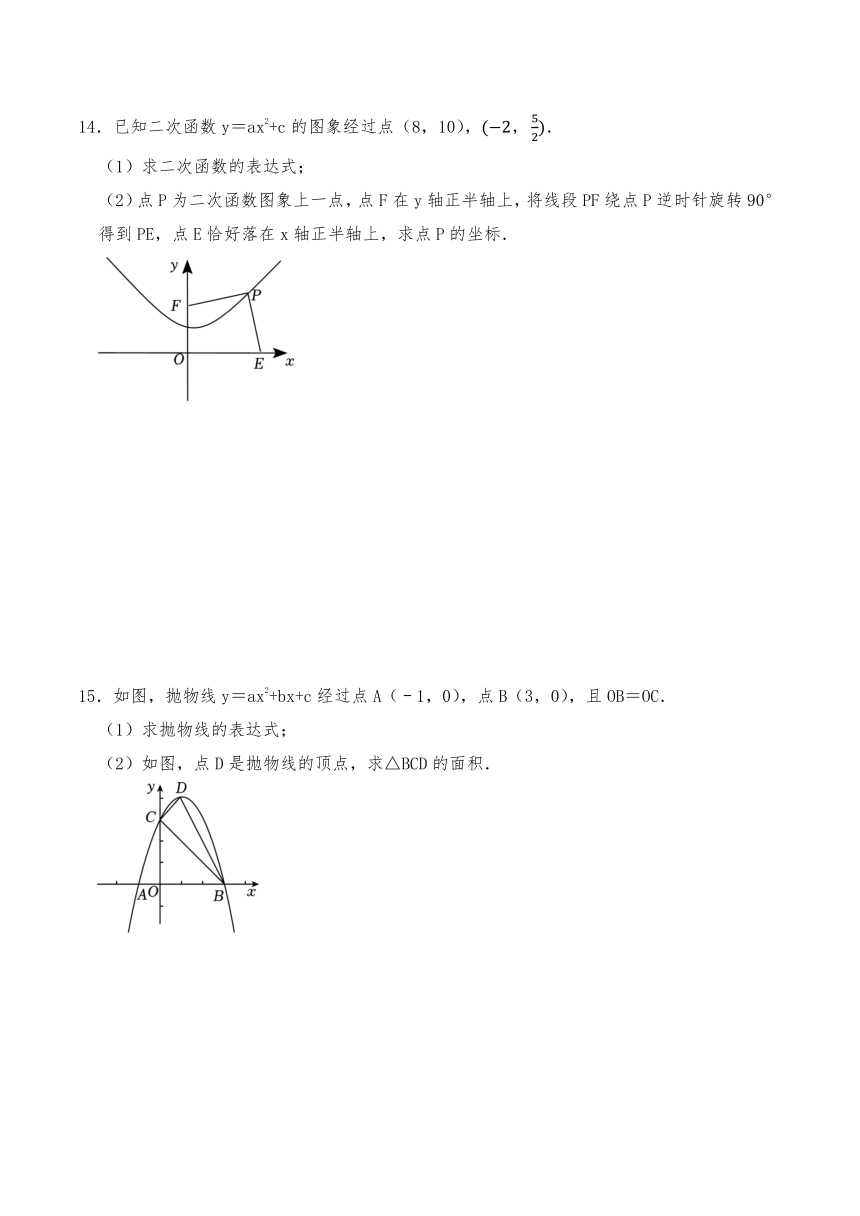
14.已知二次函数y=ax2+c的图象经过点(8,10),.
(1)求二次函数的表达式;
(2)点P为二次函数图象上一点,点F在y轴正半轴上,将线段PF绕点P逆时针旋转90°得到PE,点E恰好落在x轴正半轴上,求点P的坐标.
15.如图,抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0),且OB=OC.
(1)求抛物线的表达式;
(2)如图,点D是抛物线的顶点,求△BCD的面积.
16.已知直线y=2x﹣2与抛物线y=mx2+mx+n交于点A(1,0)和点B,且m<n.
(1)当m=﹣2时,直接写出该抛物线顶点的坐标.
(2)求点B的坐标(用含m的代数式表示).
(3)设抛物线顶点为C,记△ABC的面积为S.
①若﹣1≤m,求线段AB长度的取值范围;
②当S时,求对应的抛物线的函数表达式.
17.已知二次函数y=﹣x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当﹣1≤x≤3时,求y的取值范围;
(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.
18.如图,抛物线y=x2+bx+c经过点A(﹣1,0),点B(2,﹣3),与y轴交于点C,抛物线的顶点为D.
(1)求抛物线的解析式;
(2)抛物线上是否存在点P,使△PBC的面积是△BCD面积的4倍,若存在,请直接写出点P的坐标;若不存在,请说明理由.
19.已知如图,在平面直角坐标系中,二次函数的图象经过点,
(1)求抛物线的表达式;
(2)如图1,点E是抛物线上的第一象限的点,求的最大值,并求取得最大值时E点坐标;
(3)如图2,在抛物线对称轴上是否存在一点P,使是等腰三角形?若存在,直接写出点P的坐标,若不存在请说明理由.
参考答案
一、单选题
1.
【分析】利用配方法把二次函数的一般式化为顶点式即可.
【解答】解:y=x2﹣4x+8
=x2﹣4x+4+4
=(x﹣2)2+4,
故选:A.
2.
【分析】分两种情况,根据待定系数法即可求得a的值.
【解答】解:当x=2时,y=5;x=3时,y=8,则,解得;
当x=2时,y=8;x=3时,y=5,则,解得,
∴a的值为±1,
故选:C.
3.
【分析】根据所给解析式得出抛物线的对称轴为直线x=﹣m,再根据选项中所给出的m的值都a的正负依次进行判断即可.
【解答】解:由所给函数解析式可知,
抛物线的对称轴为直线x=﹣m.
当m=﹣3时,抛物线的对称轴为直线x=3,
因为(1,1)和(6,6)在抛物线上,
则点(1,1)关于直线x=3的对称点为(5,1),
因为6>5,6>1,
所以在对称轴的右侧y随x的增大而增大,
则抛物线的开口向上,
即a>0.
故A选择不符合题意.
当m=﹣4时,抛物线的对称轴为直线x=4,
所以点(1,1)关于直线x=4的对称点为(7,1),
因为6<7,6>1,
所以在对称轴的右侧y随x的增大而减小,
则抛物线的开口向下,
即a<0.
故B选项不符合题意.
当m=﹣5时,抛物线的对称轴为直线x=5,
所以点(1,1)关于直线x=5的对称点为(9,1),
因为6<9,6>1,
所以在对称轴的右侧y随x的增大而减小,
则抛物线的开口向下,
即a<0.
故C选项符合题意.
当m=﹣6时,抛物线的对称轴为直线x=6,
因为6>1,
所以顶点的纵坐标为抛物线上所有点纵坐标中最大的,
则抛物线的开口向下,
即a<0.
故D选项不符合题意.
故选:C.
4.
【分析】根据顶点的纵坐标求出m的值,再代入计算即可.
【解答】解:∵抛物线y=x2+(3m﹣1)x﹣3m(m>0)的最低点的纵坐标为﹣4,
∴,
即,
∴(3m﹣1)2+12m=16,
(3m+1)2=16,
∴3m+1=±4,
解得:m1=1,,
当m=1时,抛物线为y=x2+2x﹣3.
故选:B.
5.
【分析】化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
【解答】解:y=﹣x2﹣2x+1,
=﹣(x2+2x)+1,
=﹣[(x2+2x)+1]+1+1,
=y=﹣(x+1)2+2.
故选:A.
二、填空题
6.
【分析】按照题目对二次函数的要求,写出符合要求的解析式即可.
【解答】解:由题知,
因为二次函数图象的顶点在x轴的负半轴上,
不妨令其顶点坐标为(﹣1,0).
又因为在其对称轴左侧的部分是上升的,
所以抛物线的开口向下,则a<0,
不妨令a的值为﹣1,
所以这个二次函数的解析式可以是:y=﹣(x+1)2.
故答案为:y=﹣(x+1)2(答案不唯一).
7.
【分析】此题是一道开放型的题目,答案不唯一,只要写出一个符合的即可.
【解答】解:符合的表达式是y=(x﹣1)2,
故答案为:(x﹣1)2.
8.
【分析】设这个二次函数的解析式为y=ax2+bx+c,把三点的坐标代入得出方程组,求出方程组的解即可.
【解答】解:设这个二次函数的解析式为y=ax2+bx+c,
∵二次函数的图象经过(0,0),(﹣1,﹣1),(1,9)三点,
∴代入得:
解得:a=4,b=5,c=0,
即二次函数的解析式是y=4x2+5x,
故答案为:y=4x2+5x.
9.
【分析】先把(﹣1,0),(1,﹣2)代入二次函数y=x2+bx+c中,得到关于b、c的方程,解出b、c,即可求解析式.
【解答】解:把(﹣1,0),(1,﹣2)代入二次函数y=x2+bx+c中,得
,
解得
,
那么二次函数的解析式是y=x2﹣x﹣2.
函数的对称轴是:x
因而当y随x的增大而增大时,x的取值范围是:x.
故答案为:x.
10.
【分析】(1)可设二次函数解析式为y=ax2+bx+c,分别把点A(﹣1,0),点B(2,0)和点C(0,4)代入解析式求解系数即可.
(2)和(3)都可以根据函数图象直接观察.
【解答】解:(1)根据题意,可设二次函数解析式为y=ax2+bx+c,
∵二次函数的图象与两坐标轴分别交于点A(﹣1,0),点B(2,0)和点C(0,4),
∴分别把点A(﹣1,0),点B(2,0)和点C(0,4)代入解析式得,
0=a﹣b+c,①
0=4a+2b+c,②
4=c,③
由①②③得,a=﹣2,b=2,c=4,
∴二次函数解析式为y=﹣2x2+2x+4.
(2)根据图象可知,当x时,两函数的函数值都随x增大而减小.
(3)一次函数值大于二次函数值即一次函数图象在二次函数上方,根据图象知x范围为:x<0或x>2.
故答案为:(1)y=﹣2x2+2x+4;
(2);
(3)<0或x>2.
三、解答题
11.解:(1)把(1,2)代入y=(x﹣a)2+a﹣1 得:2=(1﹣a)2+a﹣1,
解得a=2或a=﹣1,
∴函数y的表达式为y=(x﹣2)2+1 y=(x+1)2﹣2;
(2)抛物线y=(x﹣a)2+a﹣1开口向上,对称轴是直线 x=a,
当a<1时,x=1时y取最小值2,
∴(1﹣a)2+a﹣1=2,解得a=2(舍去)或a=﹣1;
当1≤a≤4时,x=a时y取最小值2,
∴a﹣1=2,
解得 a=3,
当a>4时,x=4时y取最小值2,
∴(4﹣a)2+a﹣1=2,方程无实数解,
综上所述,二次函数 y=(x﹣a)2+a﹣1在1≤x≤4时,y有最小值2,a的值为﹣1或3.
12.解:(1)设抛物线解析式为y=ax2+bx+c(a≠0),
∵抛物线对称轴为直线x=﹣1,
∴,即b=2a
把A(﹣3,0),B(0,6)代入y=ax2+bx+c(a≠0)中得,
∴,
∴,
∴抛物线解析式为y=﹣2x2﹣4x+6;
设直线AB的解析式为y=kx+b′,
把A(﹣3,0),B(0,6)代入y=kx+b′中得:,
∴,
∴直线AB的解析式为y=2x+6;
(2)如图所示,过点P作PH⊥x轴于H,
设P(m,﹣2m2﹣4m+6),则OH=﹣m,PH=﹣2m2﹣4m+6,
∴AH=OA﹣OH=m+3,
∵S四边形AOBP=S△APB+S△AOB=S△APH+S梯形OBPH,
∴,
∴,
∴﹣2m3﹣6m2﹣4m2﹣12m+6m+18+2m3+4m2﹣12m=30,
∴m2+3m+2=0,
解得m=﹣1或m=﹣2,
当m=﹣1时,﹣2m2﹣4m+6=8,
当m=﹣2时,﹣2m2﹣4m+6=6,
∴点P的坐标为(﹣1,8)或(﹣2,6).
13.解:(1)将点A(1,﹣2)和B(0,﹣5)代入解析式,得:
,
解得,
所以函数解析式为y=x2+2x﹣5,
∵y=x2+2x﹣5=(x+1)2﹣6,
∴函数图象的顶点坐标为(﹣1,﹣6);
(2)当y≤﹣2时,x2+2x﹣5≤﹣2,
∴x2+2x﹣3≤0,
解得﹣3≤x≤1,
故答案为:﹣3≤x≤1;
(3)由|x2+bx+c|﹣m=0知|x2+bx+c|=m,
如图所示,
由图知,当0<m<6时,直线y=m与函数y=|x2+2x﹣5|有4个交点,即此时|x2+bx+c|﹣m=0有4个解.
故答案为:0<m<6.
14.解:(1)∵二次函数y=ax2+c的图象经过点(8,10),,
∴,
解得:,
∴二次函数的表达式为y2;
(2)过点P作PA⊥x轴于点A,PB⊥y轴于点B,如图,
∵线段PF绕点P逆时针旋转90°得到PE,点E恰好落在x轴正半轴上,
∴∠FPE=90°,PF=PE
∴∠FPA+∠EPA=90°.
∵作PA⊥x轴,PB⊥y轴,OF⊥OE,
∴四边形APBO为矩形,
∴∠APB=90°,
∴∠BPF+∠FPA=90°,
∴∠FPB=∠EPA.
在△BPF和△APE中,
,
∴△BPF≌△APE(AAS),
∴PB=PA.
∴点P的横纵坐标相等,
设P(m,m),
∵点P为二次函数图象上一点,
∴2=m,
解得:m1=m2=4,
∴点P的坐标为(4,4).
15.解:(1)∵抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0),且OB=OC,
∴OC=OB=3,
∴C(0,3),
设抛物线的解析式为y=a(x+1)(x﹣3),将C(0,3)代入得,
﹣3a=3,
∴a=﹣1,
∴抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
如图,过点D作DF⊥AB于点F,交BC于点E.
设直线BC的解析式为y=kx+3,将(3,0)代入得,0=3k+3,
∴k=﹣1,
∴直线BC的解析式为y=﹣x+3,
当x=1时,y=2,
∴E(1,2),
∴DE=4﹣2=2,
∴S△CDB DE OB2×3=3
16.解:(1)∵抛物线y=mx2+mx+n过点A(1,0),得n=﹣2m,
当m=﹣2时,y=﹣2x2﹣2x+4
=﹣2(x2+x﹣2)
=﹣2(x)2,
则抛物线顶点坐标为(,);
(2)由题意得,,
整理得,mx2+(m﹣2)x﹣2m+2=0,即x2+(1)x﹣20,
解得x=1或x2,
∴B点坐标为(2,6);
(3)①由勾股定理可得AB2=[(2)﹣1]2+(6)2=5(3)2,
∵,
∴﹣31,
∴AB2随的增大而减小,
∴当3时,AB2有最大值405,则AB有最大值9,
当1时,AB2有最小值125,则AB有最小值5,
∴线段AB长度的取值范围为5AB≤9;
②如图,设抛物线对称轴交直线y=2x﹣2于点E,
由题意得:点C的坐标为(,m)
∵抛物线对称轴为x,点E在直线AB:y=2x﹣2上,
∴E(,﹣3),
∵A(1,0),B(2,6),且m<0,
∴△ABC的面积S=S△CEB+S△ACE(3)(3),
解得m=﹣1或m,
对应的抛物线的函数表达式为y=﹣x2﹣x+2或yx2x.
17.解:(1)①∵b=4,c=3 时,
∴y=﹣x2+4x+3=﹣(x﹣2)2+7,
∴顶点坐标为(2,7).
②∵﹣1≤x≤3中含有顶点(2,7),
∴当 x=2 时,y有最大值7,
∵2﹣(﹣1)>3﹣2,
∴当x=﹣1 时,y有最小值为:﹣2,
∴当﹣1≤x≤3时,﹣2≤y≤7.
(2)∵x≤0时,y的最大值为2;x>0时,y的最大值为3,
∴抛物线的对称轴 在y轴的右侧,
∴b>0,
∵抛物线开口向下,x≤0时,y的最大值为2,
∴c=2,
又∵,
∴b=±2,
∵b>0,
∴b=2.
∴二次函数的表达式为 y=﹣x2+2x+2.
18.解:(1)∵抛物线y=x2+bx+c经过点A(﹣1,0),点B(2,﹣3),
∴,
解得b=﹣2,c=﹣3,
∴抛物线的解析式:y=x2﹣2x﹣3;
(2)存在,理由如下:
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D点坐标为(1,﹣4),
令x=0,则y=x2﹣2x﹣3=﹣3,
∴C点坐标为(0,﹣3),
又∵B点坐标为(2,﹣3),
∴BC∥x轴,
∴S△BCD=×2×1=1,
设抛物线上的点P坐标为(m,m2﹣2m﹣3),
∴S△PBC=×2×|m2﹣2m﹣3﹣(﹣3)|=|m2﹣2m|,
当|m2﹣2m|=4×1时,
解得m=1±,
当m=1+时,m2﹣2m﹣3=1,
当m=1﹣时,m2﹣2m﹣3=1,
综上,P点坐标为(1+,1)或(1﹣,1).
19.(1)解:将点,代入,
得:,
解得:,
抛物线解析式为:;
(2)解:如图1,过点作轴于点,
设点,
则,,,
,
则当时,取得最大值4,
∴
(3)解:由(1)可知抛物线的对称轴为直线,设点,当是等腰三角形时,可分:
①当时,根据两点距离公式可得:,
解得:,
∴点;
②当时,根据两点距离公式可得:,
解得:,
∴点或;
③当时,根据两点距离公式可得:,
解得:,
∴点或;
综上所述:当是等腰三角形时,点或或或或.
一、单选题
1.将二次函数y=x2﹣4x+8转化为y=a(x﹣m)2+k的形式,其结果为( )
A.y=(x﹣2)2+4 B.y=(x+4)2+4
C.y=(x﹣4)2+8 D.y=(x﹣2)2﹣4
2.已知二次函数y=ax2﹣2ax+c(其中x是自变量),当2≤x≤3时,5≤y≤8,则a的值为( )
A.1 B.2 C.±1 D.±2
3.设函数y=a(x+m)2+n(a≠0,m,n是实数),当x=1时,y=1;当x=6时,y=6.则( )
A.若m=﹣3,则a<0 B.若m=﹣4,则a>0
C.若m=﹣5,则a<0 D.若m=﹣6,则a>0
4.已知抛物线y=x2+(3m﹣1)x﹣3m(m>0)的最低点的纵坐标为﹣4,则抛物线的表达式是( )
A.y=x2﹣6x+5 B.y=x2+2x﹣3 C.y=x2+5x﹣6 D.y=x2+4x﹣5
5.二次函数y=﹣x2﹣2x+1配方后,结果正确的是( )
A.y=﹣(x+1)2+2 B.y=﹣(x﹣1)2+2
C.y=﹣(x+1)2﹣2 D.y=﹣(x﹣1)2﹣2
二、填空题
6.一个二次函数y=ax2+bx+c图象的顶点在x轴负半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是 .
7.请写出一个开口向上,并且对称轴为直线x=1的抛物线的表达式y=
8.一个二次函数的图象经过(0,0),(﹣1,﹣1),(1,9)三点.则这个二次函数的解析式为 .
9.如图,已知二次函数y=x2+bx+c的图象经过点(﹣1,0),(1,﹣2),当y随x的增大而增大时,x的取值范围是 .
10.如图,在同一坐标系内,二次函数的图象与两坐标轴分别交于点A(﹣1,0),点B(2,0)和点C(0,4),一次函数的图象与抛物线交于B,C两点.
(1)二次函数的解析式为 ;
(2)当自变量x 时,两函数的函数值都随x增大而减小;
(3)当自变量x 时,一次函数值大于二次函数值.
三、解答题
11.在平面直角坐标系内,设二次函数y=(x﹣a)2+a﹣1(a为常数).
(1)若函数y的图象经过点(1,2),求函数y的表达式;
(2)若二次函数y=(x﹣a)2+a﹣1在1≤x≤4时,y有最小值2,求a的值.
12.如图,抛物线经过A(﹣3,0),B(0,6)两点,且其对称轴为直线x=﹣1.
(1)求此抛物线及直线AB的函数表达式;
(2)若P是抛物线上点A与点B之间的动点(不包括点A,点B),若△PAB的面积为6,求出此时点P的坐标.
13.如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标;
(2)当y≤﹣2时,请根据图象直接写出x的取值范围是 ;
(3)若关于x的方程|x2+bx+c|﹣m=0有且只有四个解,则m的取值范围是 .
14.已知二次函数y=ax2+c的图象经过点(8,10),.
(1)求二次函数的表达式;
(2)点P为二次函数图象上一点,点F在y轴正半轴上,将线段PF绕点P逆时针旋转90°得到PE,点E恰好落在x轴正半轴上,求点P的坐标.
15.如图,抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0),且OB=OC.
(1)求抛物线的表达式;
(2)如图,点D是抛物线的顶点,求△BCD的面积.
16.已知直线y=2x﹣2与抛物线y=mx2+mx+n交于点A(1,0)和点B,且m<n.
(1)当m=﹣2时,直接写出该抛物线顶点的坐标.
(2)求点B的坐标(用含m的代数式表示).
(3)设抛物线顶点为C,记△ABC的面积为S.
①若﹣1≤m,求线段AB长度的取值范围;
②当S时,求对应的抛物线的函数表达式.
17.已知二次函数y=﹣x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当﹣1≤x≤3时,求y的取值范围;
(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.
18.如图,抛物线y=x2+bx+c经过点A(﹣1,0),点B(2,﹣3),与y轴交于点C,抛物线的顶点为D.
(1)求抛物线的解析式;
(2)抛物线上是否存在点P,使△PBC的面积是△BCD面积的4倍,若存在,请直接写出点P的坐标;若不存在,请说明理由.
19.已知如图,在平面直角坐标系中,二次函数的图象经过点,
(1)求抛物线的表达式;
(2)如图1,点E是抛物线上的第一象限的点,求的最大值,并求取得最大值时E点坐标;
(3)如图2,在抛物线对称轴上是否存在一点P,使是等腰三角形?若存在,直接写出点P的坐标,若不存在请说明理由.
参考答案
一、单选题
1.
【分析】利用配方法把二次函数的一般式化为顶点式即可.
【解答】解:y=x2﹣4x+8
=x2﹣4x+4+4
=(x﹣2)2+4,
故选:A.
2.
【分析】分两种情况,根据待定系数法即可求得a的值.
【解答】解:当x=2时,y=5;x=3时,y=8,则,解得;
当x=2时,y=8;x=3时,y=5,则,解得,
∴a的值为±1,
故选:C.
3.
【分析】根据所给解析式得出抛物线的对称轴为直线x=﹣m,再根据选项中所给出的m的值都a的正负依次进行判断即可.
【解答】解:由所给函数解析式可知,
抛物线的对称轴为直线x=﹣m.
当m=﹣3时,抛物线的对称轴为直线x=3,
因为(1,1)和(6,6)在抛物线上,
则点(1,1)关于直线x=3的对称点为(5,1),
因为6>5,6>1,
所以在对称轴的右侧y随x的增大而增大,
则抛物线的开口向上,
即a>0.
故A选择不符合题意.
当m=﹣4时,抛物线的对称轴为直线x=4,
所以点(1,1)关于直线x=4的对称点为(7,1),
因为6<7,6>1,
所以在对称轴的右侧y随x的增大而减小,
则抛物线的开口向下,
即a<0.
故B选项不符合题意.
当m=﹣5时,抛物线的对称轴为直线x=5,
所以点(1,1)关于直线x=5的对称点为(9,1),
因为6<9,6>1,
所以在对称轴的右侧y随x的增大而减小,
则抛物线的开口向下,
即a<0.
故C选项符合题意.
当m=﹣6时,抛物线的对称轴为直线x=6,
因为6>1,
所以顶点的纵坐标为抛物线上所有点纵坐标中最大的,
则抛物线的开口向下,
即a<0.
故D选项不符合题意.
故选:C.
4.
【分析】根据顶点的纵坐标求出m的值,再代入计算即可.
【解答】解:∵抛物线y=x2+(3m﹣1)x﹣3m(m>0)的最低点的纵坐标为﹣4,
∴,
即,
∴(3m﹣1)2+12m=16,
(3m+1)2=16,
∴3m+1=±4,
解得:m1=1,,
当m=1时,抛物线为y=x2+2x﹣3.
故选:B.
5.
【分析】化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
【解答】解:y=﹣x2﹣2x+1,
=﹣(x2+2x)+1,
=﹣[(x2+2x)+1]+1+1,
=y=﹣(x+1)2+2.
故选:A.
二、填空题
6.
【分析】按照题目对二次函数的要求,写出符合要求的解析式即可.
【解答】解:由题知,
因为二次函数图象的顶点在x轴的负半轴上,
不妨令其顶点坐标为(﹣1,0).
又因为在其对称轴左侧的部分是上升的,
所以抛物线的开口向下,则a<0,
不妨令a的值为﹣1,
所以这个二次函数的解析式可以是:y=﹣(x+1)2.
故答案为:y=﹣(x+1)2(答案不唯一).
7.
【分析】此题是一道开放型的题目,答案不唯一,只要写出一个符合的即可.
【解答】解:符合的表达式是y=(x﹣1)2,
故答案为:(x﹣1)2.
8.
【分析】设这个二次函数的解析式为y=ax2+bx+c,把三点的坐标代入得出方程组,求出方程组的解即可.
【解答】解:设这个二次函数的解析式为y=ax2+bx+c,
∵二次函数的图象经过(0,0),(﹣1,﹣1),(1,9)三点,
∴代入得:
解得:a=4,b=5,c=0,
即二次函数的解析式是y=4x2+5x,
故答案为:y=4x2+5x.
9.
【分析】先把(﹣1,0),(1,﹣2)代入二次函数y=x2+bx+c中,得到关于b、c的方程,解出b、c,即可求解析式.
【解答】解:把(﹣1,0),(1,﹣2)代入二次函数y=x2+bx+c中,得
,
解得
,
那么二次函数的解析式是y=x2﹣x﹣2.
函数的对称轴是:x
因而当y随x的增大而增大时,x的取值范围是:x.
故答案为:x.
10.
【分析】(1)可设二次函数解析式为y=ax2+bx+c,分别把点A(﹣1,0),点B(2,0)和点C(0,4)代入解析式求解系数即可.
(2)和(3)都可以根据函数图象直接观察.
【解答】解:(1)根据题意,可设二次函数解析式为y=ax2+bx+c,
∵二次函数的图象与两坐标轴分别交于点A(﹣1,0),点B(2,0)和点C(0,4),
∴分别把点A(﹣1,0),点B(2,0)和点C(0,4)代入解析式得,
0=a﹣b+c,①
0=4a+2b+c,②
4=c,③
由①②③得,a=﹣2,b=2,c=4,
∴二次函数解析式为y=﹣2x2+2x+4.
(2)根据图象可知,当x时,两函数的函数值都随x增大而减小.
(3)一次函数值大于二次函数值即一次函数图象在二次函数上方,根据图象知x范围为:x<0或x>2.
故答案为:(1)y=﹣2x2+2x+4;
(2);
(3)<0或x>2.
三、解答题
11.解:(1)把(1,2)代入y=(x﹣a)2+a﹣1 得:2=(1﹣a)2+a﹣1,
解得a=2或a=﹣1,
∴函数y的表达式为y=(x﹣2)2+1 y=(x+1)2﹣2;
(2)抛物线y=(x﹣a)2+a﹣1开口向上,对称轴是直线 x=a,
当a<1时,x=1时y取最小值2,
∴(1﹣a)2+a﹣1=2,解得a=2(舍去)或a=﹣1;
当1≤a≤4时,x=a时y取最小值2,
∴a﹣1=2,
解得 a=3,
当a>4时,x=4时y取最小值2,
∴(4﹣a)2+a﹣1=2,方程无实数解,
综上所述,二次函数 y=(x﹣a)2+a﹣1在1≤x≤4时,y有最小值2,a的值为﹣1或3.
12.解:(1)设抛物线解析式为y=ax2+bx+c(a≠0),
∵抛物线对称轴为直线x=﹣1,
∴,即b=2a
把A(﹣3,0),B(0,6)代入y=ax2+bx+c(a≠0)中得,
∴,
∴,
∴抛物线解析式为y=﹣2x2﹣4x+6;
设直线AB的解析式为y=kx+b′,
把A(﹣3,0),B(0,6)代入y=kx+b′中得:,
∴,
∴直线AB的解析式为y=2x+6;
(2)如图所示,过点P作PH⊥x轴于H,
设P(m,﹣2m2﹣4m+6),则OH=﹣m,PH=﹣2m2﹣4m+6,
∴AH=OA﹣OH=m+3,
∵S四边形AOBP=S△APB+S△AOB=S△APH+S梯形OBPH,
∴,
∴,
∴﹣2m3﹣6m2﹣4m2﹣12m+6m+18+2m3+4m2﹣12m=30,
∴m2+3m+2=0,
解得m=﹣1或m=﹣2,
当m=﹣1时,﹣2m2﹣4m+6=8,
当m=﹣2时,﹣2m2﹣4m+6=6,
∴点P的坐标为(﹣1,8)或(﹣2,6).
13.解:(1)将点A(1,﹣2)和B(0,﹣5)代入解析式,得:
,
解得,
所以函数解析式为y=x2+2x﹣5,
∵y=x2+2x﹣5=(x+1)2﹣6,
∴函数图象的顶点坐标为(﹣1,﹣6);
(2)当y≤﹣2时,x2+2x﹣5≤﹣2,
∴x2+2x﹣3≤0,
解得﹣3≤x≤1,
故答案为:﹣3≤x≤1;
(3)由|x2+bx+c|﹣m=0知|x2+bx+c|=m,
如图所示,
由图知,当0<m<6时,直线y=m与函数y=|x2+2x﹣5|有4个交点,即此时|x2+bx+c|﹣m=0有4个解.
故答案为:0<m<6.
14.解:(1)∵二次函数y=ax2+c的图象经过点(8,10),,
∴,
解得:,
∴二次函数的表达式为y2;
(2)过点P作PA⊥x轴于点A,PB⊥y轴于点B,如图,
∵线段PF绕点P逆时针旋转90°得到PE,点E恰好落在x轴正半轴上,
∴∠FPE=90°,PF=PE
∴∠FPA+∠EPA=90°.
∵作PA⊥x轴,PB⊥y轴,OF⊥OE,
∴四边形APBO为矩形,
∴∠APB=90°,
∴∠BPF+∠FPA=90°,
∴∠FPB=∠EPA.
在△BPF和△APE中,
,
∴△BPF≌△APE(AAS),
∴PB=PA.
∴点P的横纵坐标相等,
设P(m,m),
∵点P为二次函数图象上一点,
∴2=m,
解得:m1=m2=4,
∴点P的坐标为(4,4).
15.解:(1)∵抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0),且OB=OC,
∴OC=OB=3,
∴C(0,3),
设抛物线的解析式为y=a(x+1)(x﹣3),将C(0,3)代入得,
﹣3a=3,
∴a=﹣1,
∴抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
如图,过点D作DF⊥AB于点F,交BC于点E.
设直线BC的解析式为y=kx+3,将(3,0)代入得,0=3k+3,
∴k=﹣1,
∴直线BC的解析式为y=﹣x+3,
当x=1时,y=2,
∴E(1,2),
∴DE=4﹣2=2,
∴S△CDB DE OB2×3=3
16.解:(1)∵抛物线y=mx2+mx+n过点A(1,0),得n=﹣2m,
当m=﹣2时,y=﹣2x2﹣2x+4
=﹣2(x2+x﹣2)
=﹣2(x)2,
则抛物线顶点坐标为(,);
(2)由题意得,,
整理得,mx2+(m﹣2)x﹣2m+2=0,即x2+(1)x﹣20,
解得x=1或x2,
∴B点坐标为(2,6);
(3)①由勾股定理可得AB2=[(2)﹣1]2+(6)2=5(3)2,
∵,
∴﹣31,
∴AB2随的增大而减小,
∴当3时,AB2有最大值405,则AB有最大值9,
当1时,AB2有最小值125,则AB有最小值5,
∴线段AB长度的取值范围为5AB≤9;
②如图,设抛物线对称轴交直线y=2x﹣2于点E,
由题意得:点C的坐标为(,m)
∵抛物线对称轴为x,点E在直线AB:y=2x﹣2上,
∴E(,﹣3),
∵A(1,0),B(2,6),且m<0,
∴△ABC的面积S=S△CEB+S△ACE(3)(3),
解得m=﹣1或m,
对应的抛物线的函数表达式为y=﹣x2﹣x+2或yx2x.
17.解:(1)①∵b=4,c=3 时,
∴y=﹣x2+4x+3=﹣(x﹣2)2+7,
∴顶点坐标为(2,7).
②∵﹣1≤x≤3中含有顶点(2,7),
∴当 x=2 时,y有最大值7,
∵2﹣(﹣1)>3﹣2,
∴当x=﹣1 时,y有最小值为:﹣2,
∴当﹣1≤x≤3时,﹣2≤y≤7.
(2)∵x≤0时,y的最大值为2;x>0时,y的最大值为3,
∴抛物线的对称轴 在y轴的右侧,
∴b>0,
∵抛物线开口向下,x≤0时,y的最大值为2,
∴c=2,
又∵,
∴b=±2,
∵b>0,
∴b=2.
∴二次函数的表达式为 y=﹣x2+2x+2.
18.解:(1)∵抛物线y=x2+bx+c经过点A(﹣1,0),点B(2,﹣3),
∴,
解得b=﹣2,c=﹣3,
∴抛物线的解析式:y=x2﹣2x﹣3;
(2)存在,理由如下:
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D点坐标为(1,﹣4),
令x=0,则y=x2﹣2x﹣3=﹣3,
∴C点坐标为(0,﹣3),
又∵B点坐标为(2,﹣3),
∴BC∥x轴,
∴S△BCD=×2×1=1,
设抛物线上的点P坐标为(m,m2﹣2m﹣3),
∴S△PBC=×2×|m2﹣2m﹣3﹣(﹣3)|=|m2﹣2m|,
当|m2﹣2m|=4×1时,
解得m=1±,
当m=1+时,m2﹣2m﹣3=1,
当m=1﹣时,m2﹣2m﹣3=1,
综上,P点坐标为(1+,1)或(1﹣,1).
19.(1)解:将点,代入,
得:,
解得:,
抛物线解析式为:;
(2)解:如图1,过点作轴于点,
设点,
则,,,
,
则当时,取得最大值4,
∴
(3)解:由(1)可知抛物线的对称轴为直线,设点,当是等腰三角形时,可分:
①当时,根据两点距离公式可得:,
解得:,
∴点;
②当时,根据两点距离公式可得:,
解得:,
∴点或;
③当时,根据两点距离公式可得:,
解得:,
∴点或;
综上所述:当是等腰三角形时,点或或或或.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
