13.1.1 棱柱、棱锥和棱台 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.1.1 棱柱、棱锥和棱台 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 401.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 21:03:21 | ||
图片预览


文档简介
13.1.1 棱柱、棱锥和棱台
1. 利用实物、计算机软件等观察空间图形,认识棱柱、棱锥和棱台的结构特征.
2. 能运用这些特征描述现实生活中简单物体的结构.
3. 了解棱柱、棱锥和棱台的概念.
活动一 了解常见的空间图形
在我们周围的生活中,存在不少有特色的建筑物,你能举出一些例子吗?这些建筑的几何结构特征如何?
思考1
我们发现建筑物大多是由一些简单的空间图形组合而成的,你能通过观察,根据某种标准对这些空间图形进行分类吗?
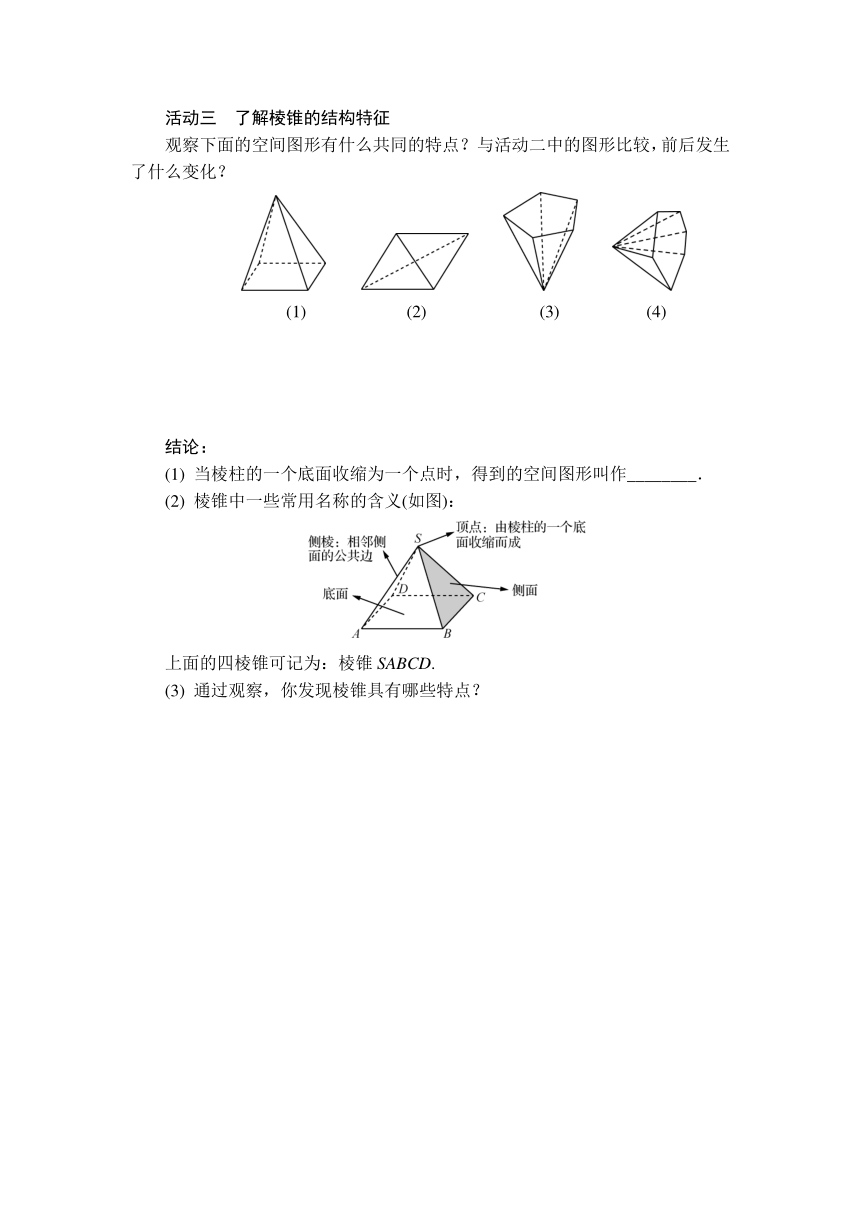
活动二 了解棱柱的结构特征
仔细观察下面的空间图形,你能发现它们可以怎样形成?
(2) (3) (4)
图(1)和(3)中的空间图形分别是由平行四边形和五边形沿某一方向平移而得.
思考2
图(2)和(4)中的空间图形分别是由怎样的平面图形平移而得?
探究:
(1) 棱柱的定义:
(2) 棱柱中一些常用名称的含义(如图):
思考3
通过观察,你发现棱柱具有哪些特点?
思考4
各种这样的棱柱,相互之间有什么区别和联系?可不可以根据这些区别和联系对棱柱分类?
活动三 了解棱锥的结构特征
观察下面的空间图形有什么共同的特点?与活动二中的图形比较,前后发生了什么变化?
(2) (3) (4)
结论:
(1) 当棱柱的一个底面收缩为一个点时,得到的空间图形叫作________.
(2) 棱锥中一些常用名称的含义(如图):
上面的四棱锥可记为:棱锥SABCD.
(3) 通过观察,你发现棱锥具有哪些特点?
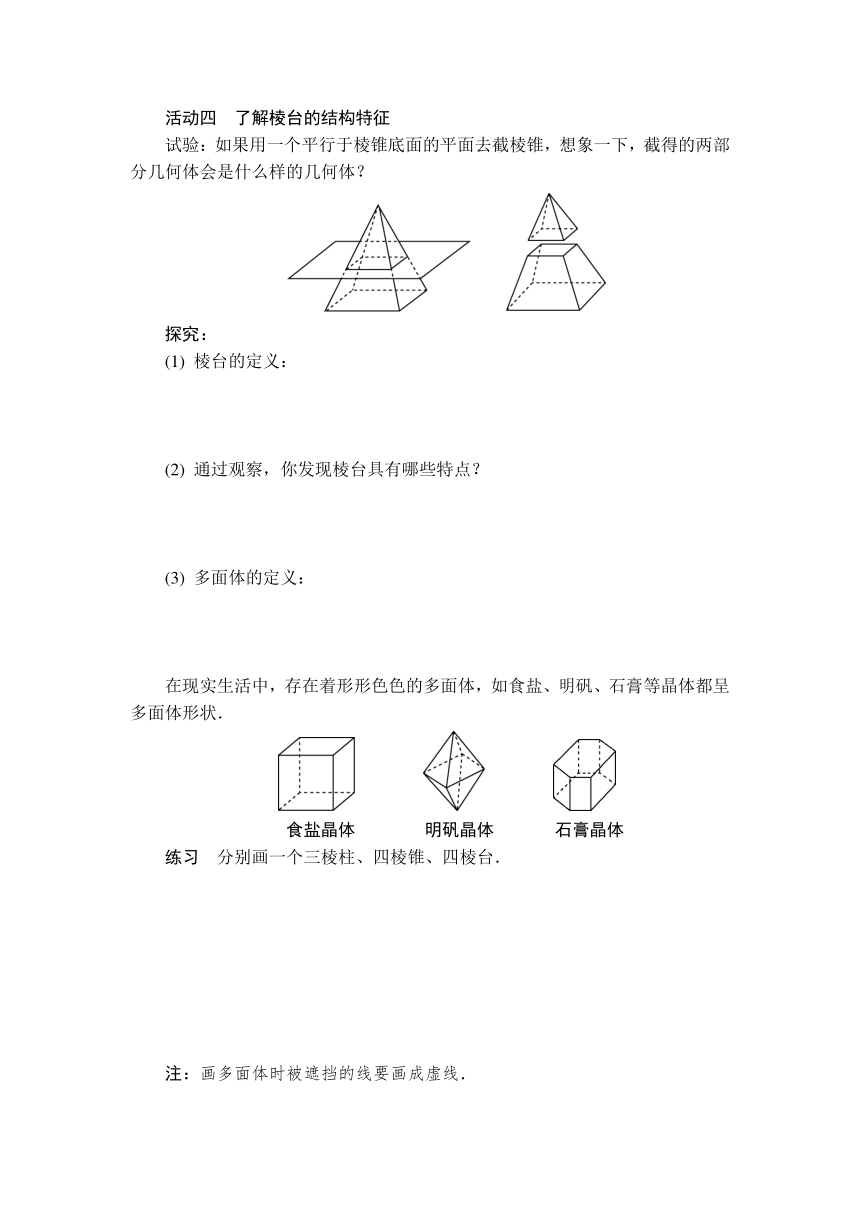
活动四 了解棱台的结构特征
试验:如果用一个平行于棱锥底面的平面去截棱锥,想象一下,截得的两部分几何体会是什么样的几何体?
探究:
(1) 棱台的定义:
(2) 通过观察,你发现棱台具有哪些特点?
(3) 多面体的定义:
在现实生活中,存在着形形色色的多面体,如食盐、明矾、石膏等晶体都呈多面体形状.
食盐晶体 明矾晶体 石膏晶体
练习 分别画一个三棱柱、四棱锥、四棱台.
注:画多面体时被遮挡的线要画成虚线.
巩固棱柱、棱锥、棱台的基本概念.
名称 定义 图形及表示 相关概念 分类
棱柱 由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱 如图可记作: 棱柱ABCDEF-A′B′C′D′E′F′ 底面:平移起止位置的两个面 侧面:多边形的边平移所形成的面 侧棱:相邻侧面的公共边 顶点:侧棱与底面的公共点 底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱……
棱锥 当棱柱的一个底面收缩为一个点时,得到的空间图形叫作棱锥 如图可记作:棱锥S-ABCD 底面:多边形的面 侧面:有公共顶点的各个三角形的面 侧棱:相邻侧面的公共边 顶点:由棱柱的一个底面收缩而成 按底面多边形的边数分为:三棱锥、四棱锥……
棱台 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分称之为棱台 如图可记作:棱台ABCD-A′B′C′D′ 上底面:原棱锥的截面 下底面:原棱锥的底面 侧面:其余各面 侧棱:相邻侧面的公共边 顶点:侧棱与上(下)底面的公共点 由三棱锥、四棱锥、五棱锥……截得的棱台分别叫作三棱台、四棱台、五棱台……
1. (2024湖北月考)有一个多面体,由五个面围成,只有一个面不是三角形,则这个多面体为( )
A. 四棱柱 B. 四棱锥 C. 三棱柱 D. 三棱锥
2. (教材改编)如图,在三棱台ABC-A′B′C′中,沿平面A′BC截去三棱锥A′-ABC,则剩余的部分是( )
A. 三棱锥
B. 四棱锥
C. 三棱柱
D. 三棱台
3. (多选)(2024河南期中)两个三棱锥、一个四棱锥拼在一起,可能拼成的空间图形是 ( )
A. 一个三棱锥 B. 一个四棱锥
C. 一个三棱柱 D. 一个四棱柱
4. (2024宿州期中)现有一块如图所示的三棱锥木料,其中∠AVB=∠AVC=∠BVC=40°,VA=VB=VC=6,木工师傅打算过点A将木料切成两部分,则截面△AEF周长的最小值为________.
5. (教材改编)画六面体.
(1) 使它是一个四棱柱;
(2) 使它是由两个三棱锥组成;
(3) 使它是一个五棱锥.
13.1.1 棱柱、棱锥和棱台
【活动方案】
背景引入:略
思考1:略
思考2:分别是由三角形和六边形沿某一方向平移而得.
探究:(1) 一般地,由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱.
思考3:①两个底面是全等的多边形,且对应边互相平行;②侧面都是平行四边形.
思考4:底面的平面图形不同,侧面都是平行四边形,由三角形平移构成三棱柱,由六边形平移构成六棱柱.
底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱……
结论:(1) 棱锥 (3) ①底面是一个多边形;②侧面是有一个公共顶点的三角形.
探究:(1) 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分称之为棱台.
(2) ①上、下两底面平行且相似;②侧面是梯形;③侧棱延长后交于一点.
(3) 棱柱、棱锥和棱台都是由一些平面多边形围成的空间图形.由若干个平面多边形围成的空间图形叫作多面体.
练习:略
【检测反馈】
1. B 有一个面是多边形,其余四个面都是有一个公共顶点的三角形,由这些面所围成的多面体是四棱锥.
2. B 在三棱台ABC-A′B′C′中,沿平面A′BC截去三棱锥A′-ABC,剩余的部分是以A′为顶点,四边形BCC′B′为底面的四棱锥A′-BCC′B′.
3. ABC 对于A,如图1,在三棱锥A-BCD中,分别取BC,BD的中点为E,F,再取EF的中点M,连接AM,则三棱锥A-BCD可拆割成三棱锥A-BEM,A-BFM和四棱锥A-CDFE,故A正确;对于B,如图2,在四棱锥P-ABCD中,分别取BC,AD的中点为E,F,则四棱锥PABCD可拆割成三棱锥P-ABF,P-BEF和四棱锥P-CDFE,故B正确;对于C,如图3,在三棱柱ABC-A1B1C1中,取B1C1的中点E,则三棱柱ABC-A1B1C1可拆割为三棱锥B1-A1BE,C1-A1BE和四棱锥B-ACC1A1,故C正确;对于D,一个四棱柱割去一个四棱锥后的空间图形不可能由两个三棱锥拼成,故D错误.故选ABC.
图1 图2 图3
4. 6 如图,将三棱锥的侧面沿着VA展开,则VA=VA′=6,∠AVA′=120°,由余弦定理可得AA′2=62+62-2×6×6cos 120°=108,则AA′=6,所以截面△AEF周长的最小值为6.
5. 略
1. 利用实物、计算机软件等观察空间图形,认识棱柱、棱锥和棱台的结构特征.
2. 能运用这些特征描述现实生活中简单物体的结构.
3. 了解棱柱、棱锥和棱台的概念.
活动一 了解常见的空间图形
在我们周围的生活中,存在不少有特色的建筑物,你能举出一些例子吗?这些建筑的几何结构特征如何?
思考1
我们发现建筑物大多是由一些简单的空间图形组合而成的,你能通过观察,根据某种标准对这些空间图形进行分类吗?
活动二 了解棱柱的结构特征
仔细观察下面的空间图形,你能发现它们可以怎样形成?
(2) (3) (4)
图(1)和(3)中的空间图形分别是由平行四边形和五边形沿某一方向平移而得.
思考2
图(2)和(4)中的空间图形分别是由怎样的平面图形平移而得?
探究:
(1) 棱柱的定义:
(2) 棱柱中一些常用名称的含义(如图):
思考3
通过观察,你发现棱柱具有哪些特点?
思考4
各种这样的棱柱,相互之间有什么区别和联系?可不可以根据这些区别和联系对棱柱分类?
活动三 了解棱锥的结构特征
观察下面的空间图形有什么共同的特点?与活动二中的图形比较,前后发生了什么变化?
(2) (3) (4)
结论:
(1) 当棱柱的一个底面收缩为一个点时,得到的空间图形叫作________.
(2) 棱锥中一些常用名称的含义(如图):
上面的四棱锥可记为:棱锥SABCD.
(3) 通过观察,你发现棱锥具有哪些特点?
活动四 了解棱台的结构特征
试验:如果用一个平行于棱锥底面的平面去截棱锥,想象一下,截得的两部分几何体会是什么样的几何体?
探究:
(1) 棱台的定义:
(2) 通过观察,你发现棱台具有哪些特点?
(3) 多面体的定义:
在现实生活中,存在着形形色色的多面体,如食盐、明矾、石膏等晶体都呈多面体形状.
食盐晶体 明矾晶体 石膏晶体
练习 分别画一个三棱柱、四棱锥、四棱台.
注:画多面体时被遮挡的线要画成虚线.
巩固棱柱、棱锥、棱台的基本概念.
名称 定义 图形及表示 相关概念 分类
棱柱 由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱 如图可记作: 棱柱ABCDEF-A′B′C′D′E′F′ 底面:平移起止位置的两个面 侧面:多边形的边平移所形成的面 侧棱:相邻侧面的公共边 顶点:侧棱与底面的公共点 底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱……
棱锥 当棱柱的一个底面收缩为一个点时,得到的空间图形叫作棱锥 如图可记作:棱锥S-ABCD 底面:多边形的面 侧面:有公共顶点的各个三角形的面 侧棱:相邻侧面的公共边 顶点:由棱柱的一个底面收缩而成 按底面多边形的边数分为:三棱锥、四棱锥……
棱台 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分称之为棱台 如图可记作:棱台ABCD-A′B′C′D′ 上底面:原棱锥的截面 下底面:原棱锥的底面 侧面:其余各面 侧棱:相邻侧面的公共边 顶点:侧棱与上(下)底面的公共点 由三棱锥、四棱锥、五棱锥……截得的棱台分别叫作三棱台、四棱台、五棱台……
1. (2024湖北月考)有一个多面体,由五个面围成,只有一个面不是三角形,则这个多面体为( )
A. 四棱柱 B. 四棱锥 C. 三棱柱 D. 三棱锥
2. (教材改编)如图,在三棱台ABC-A′B′C′中,沿平面A′BC截去三棱锥A′-ABC,则剩余的部分是( )
A. 三棱锥
B. 四棱锥
C. 三棱柱
D. 三棱台
3. (多选)(2024河南期中)两个三棱锥、一个四棱锥拼在一起,可能拼成的空间图形是 ( )
A. 一个三棱锥 B. 一个四棱锥
C. 一个三棱柱 D. 一个四棱柱
4. (2024宿州期中)现有一块如图所示的三棱锥木料,其中∠AVB=∠AVC=∠BVC=40°,VA=VB=VC=6,木工师傅打算过点A将木料切成两部分,则截面△AEF周长的最小值为________.
5. (教材改编)画六面体.
(1) 使它是一个四棱柱;
(2) 使它是由两个三棱锥组成;
(3) 使它是一个五棱锥.
13.1.1 棱柱、棱锥和棱台
【活动方案】
背景引入:略
思考1:略
思考2:分别是由三角形和六边形沿某一方向平移而得.
探究:(1) 一般地,由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱.
思考3:①两个底面是全等的多边形,且对应边互相平行;②侧面都是平行四边形.
思考4:底面的平面图形不同,侧面都是平行四边形,由三角形平移构成三棱柱,由六边形平移构成六棱柱.
底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱……
结论:(1) 棱锥 (3) ①底面是一个多边形;②侧面是有一个公共顶点的三角形.
探究:(1) 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分称之为棱台.
(2) ①上、下两底面平行且相似;②侧面是梯形;③侧棱延长后交于一点.
(3) 棱柱、棱锥和棱台都是由一些平面多边形围成的空间图形.由若干个平面多边形围成的空间图形叫作多面体.
练习:略
【检测反馈】
1. B 有一个面是多边形,其余四个面都是有一个公共顶点的三角形,由这些面所围成的多面体是四棱锥.
2. B 在三棱台ABC-A′B′C′中,沿平面A′BC截去三棱锥A′-ABC,剩余的部分是以A′为顶点,四边形BCC′B′为底面的四棱锥A′-BCC′B′.
3. ABC 对于A,如图1,在三棱锥A-BCD中,分别取BC,BD的中点为E,F,再取EF的中点M,连接AM,则三棱锥A-BCD可拆割成三棱锥A-BEM,A-BFM和四棱锥A-CDFE,故A正确;对于B,如图2,在四棱锥P-ABCD中,分别取BC,AD的中点为E,F,则四棱锥PABCD可拆割成三棱锥P-ABF,P-BEF和四棱锥P-CDFE,故B正确;对于C,如图3,在三棱柱ABC-A1B1C1中,取B1C1的中点E,则三棱柱ABC-A1B1C1可拆割为三棱锥B1-A1BE,C1-A1BE和四棱锥B-ACC1A1,故C正确;对于D,一个四棱柱割去一个四棱锥后的空间图形不可能由两个三棱锥拼成,故D错误.故选ABC.
图1 图2 图3
4. 6 如图,将三棱锥的侧面沿着VA展开,则VA=VA′=6,∠AVA′=120°,由余弦定理可得AA′2=62+62-2×6×6cos 120°=108,则AA′=6,所以截面△AEF周长的最小值为6.
5. 略
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
